Hydrodynamic Controls of Particulate Metals Partitioning Along the Lower Selenga River—Main Tributary of The Lake Baikal
Abstract
:1. Introduction
2. Data and Methods
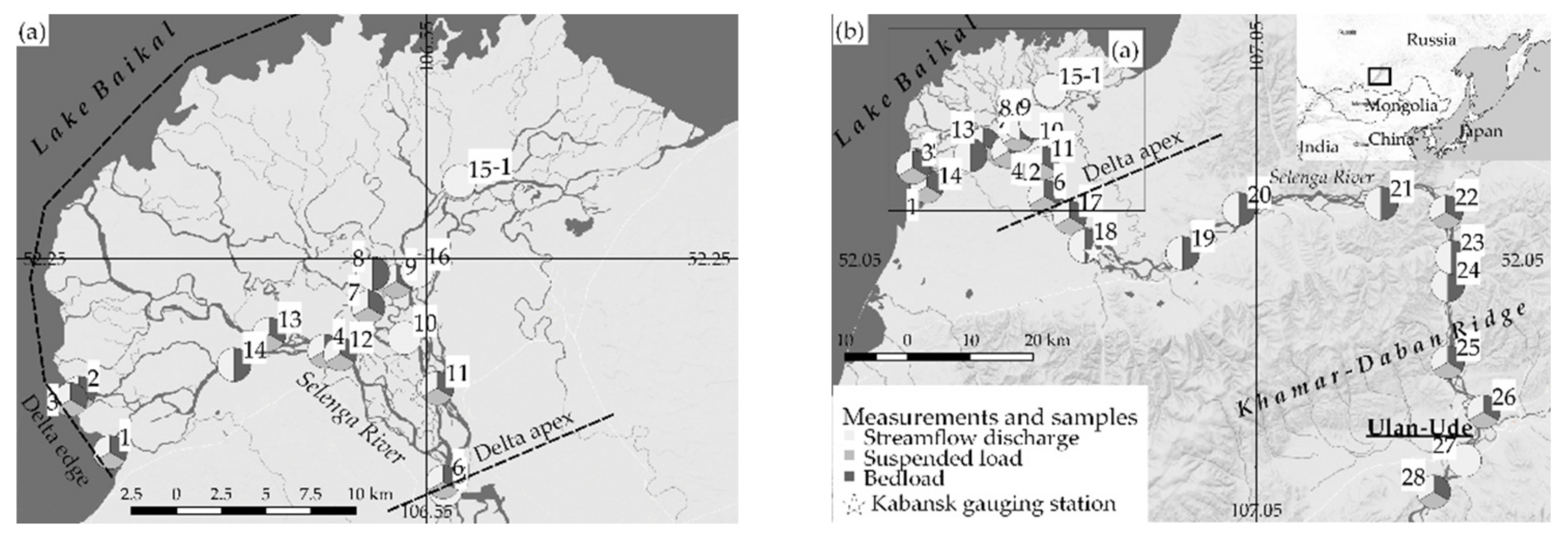
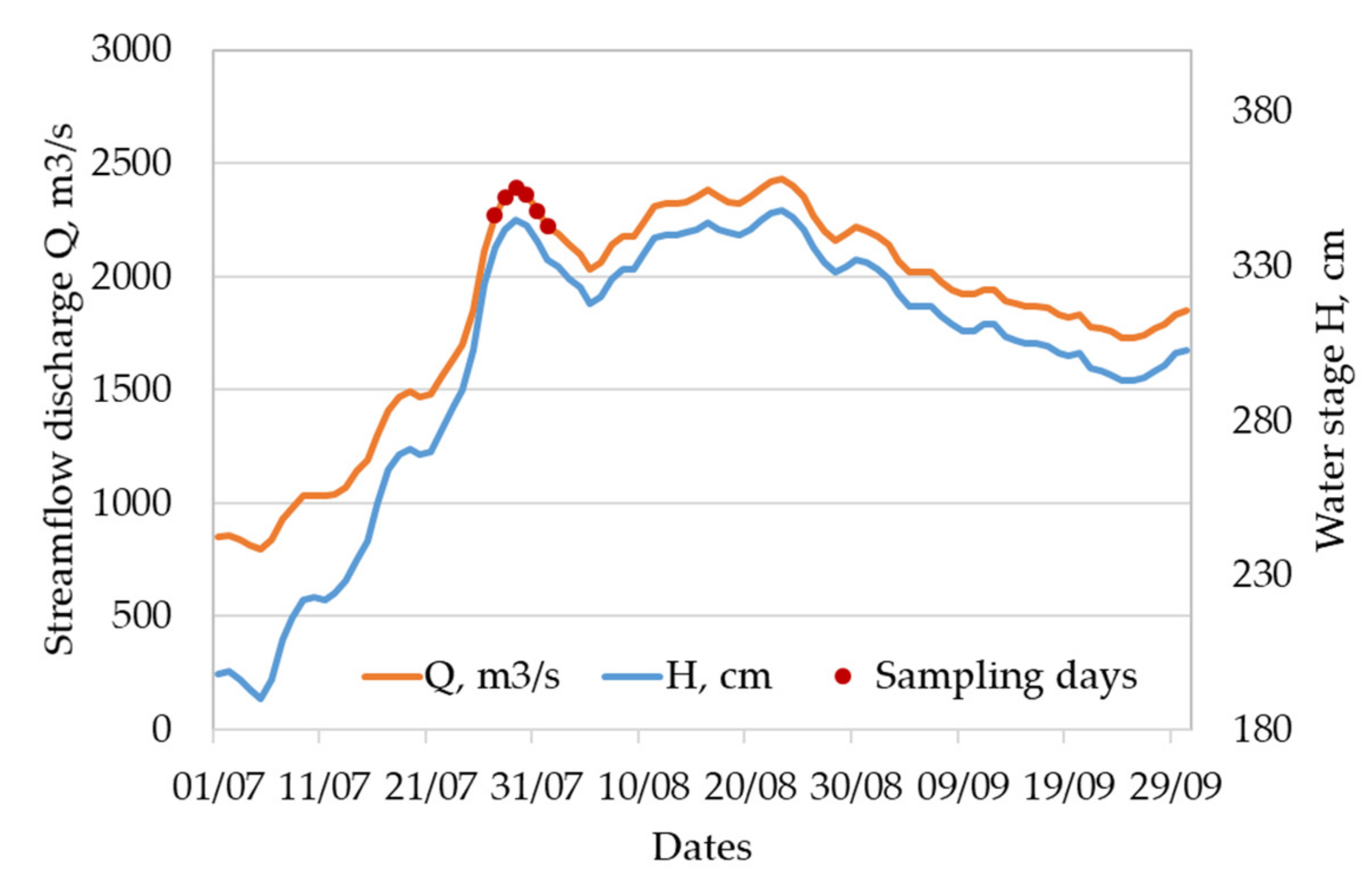
2.1. Sampling and Samples Processing
2.2. Hydrodynamic Modelling of Sediment Transport
2.3. Grain Size and Hydrogeochemical Analyses
3. Results
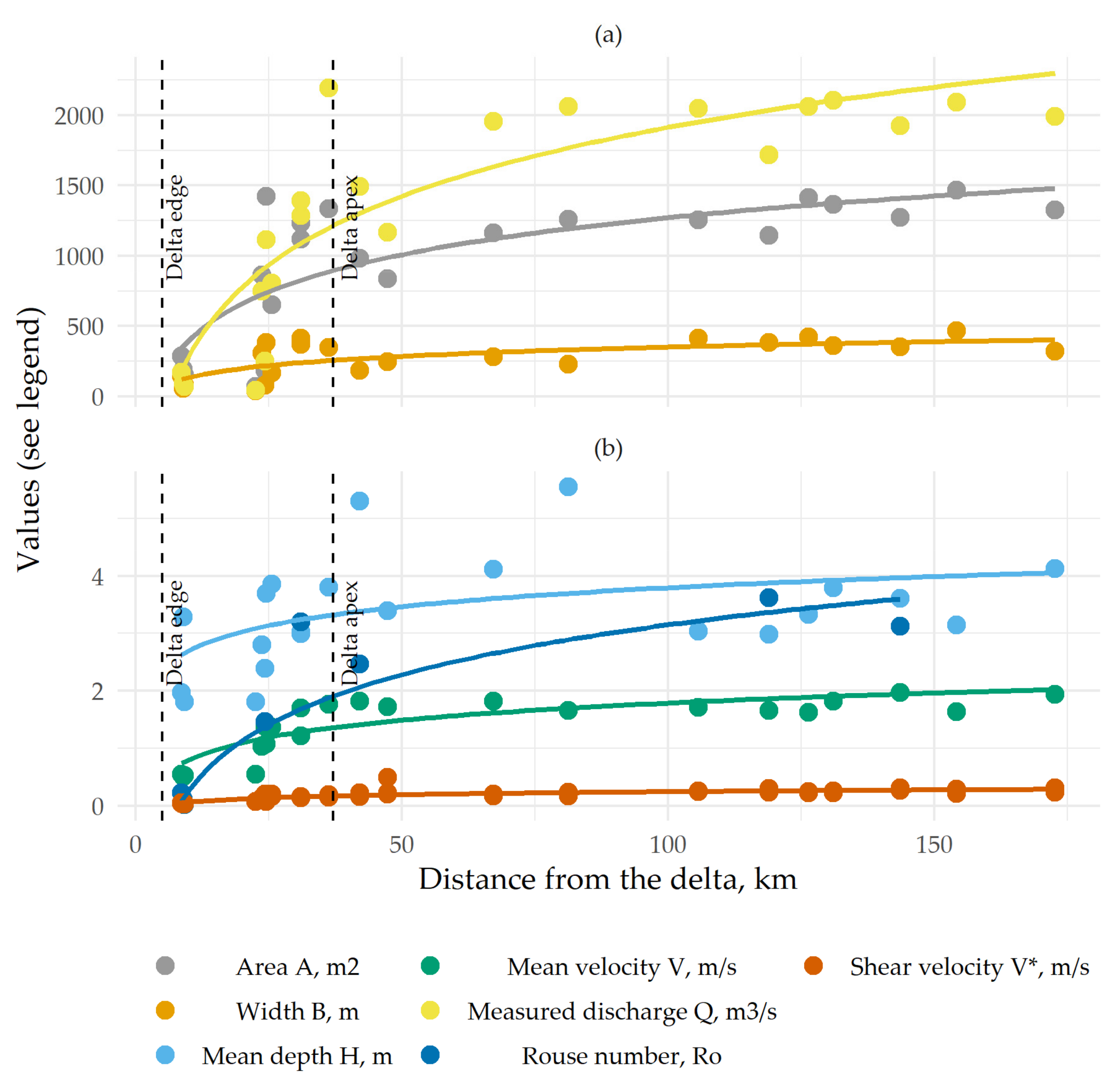
3.1. Downstream Variations of Sediment Transport
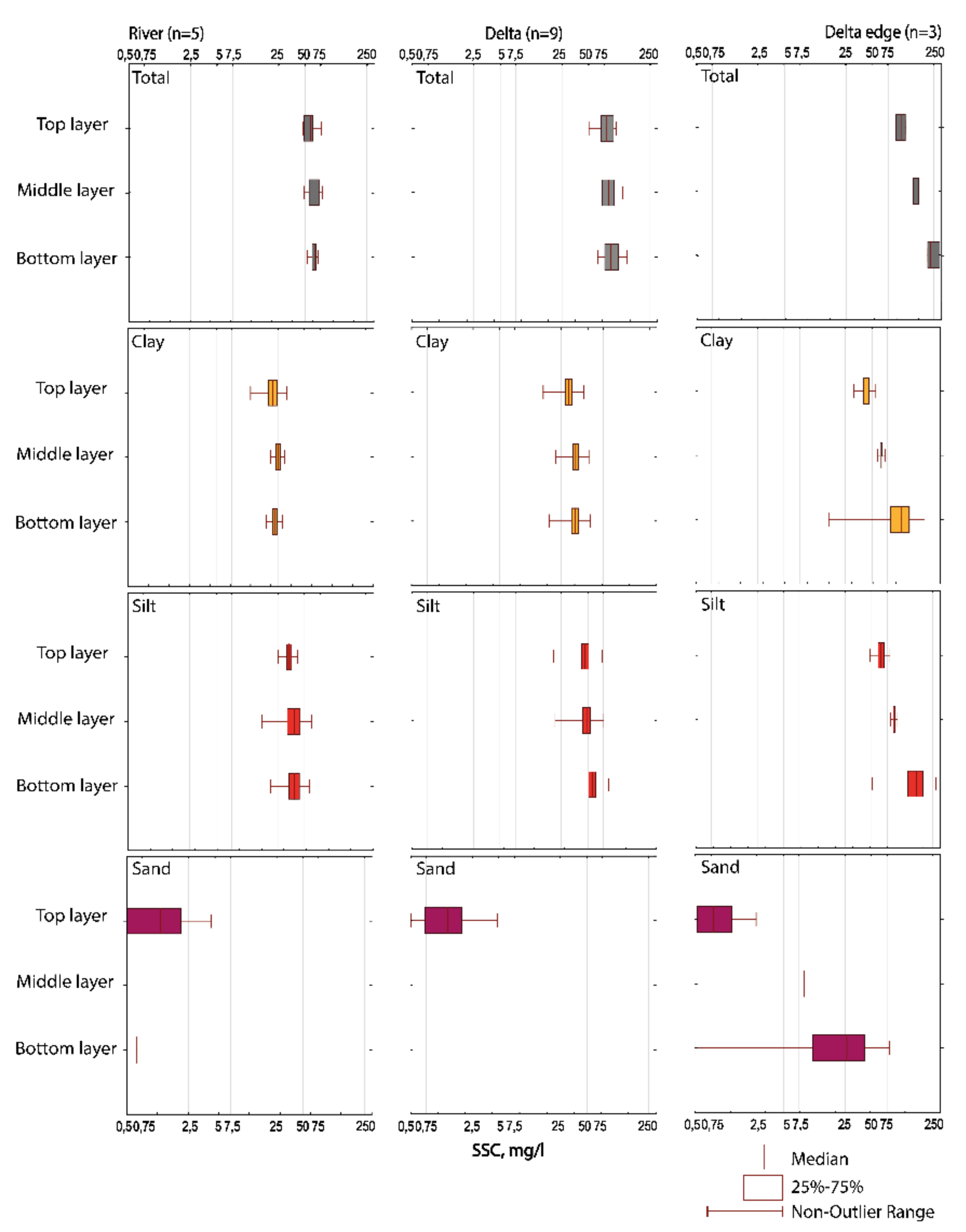
3.2. Sediment Grain Sizes and Geochemistry
4. Discussion
4.1. Bed and Suspended Sediment Fluxes
4.2. Particulate Metals Behavior and SB-Analyses
5. Conclusions
- Due to hydrodynamic impacts of varying channel patterns along the river continuum, various patterns of heavy metals are observed along the river course. Depositional channels such as Selenga delta branches act as a better “sorting machine” of heavy metals (30% to 40% vertical distribution is higher in the delta than in the gravel–boulder main channel of the Selenga river).
- This increase can be attributed to a higher concentration of the clay-silt fraction near the bed in the deltaic channels due to its heavier mineral structure containing specific microelements. The SSC gradient towards the bottom is further pronounced (Kssc = 1.75 vs. Kssc = 0.99 in the main channel).
- This vertical variability is also caused by the pronounced increase of coarse mineral fractions (50–2000 mm) in the near-bottom layer in the depositional delta pattern (K (sand (%)) = 1.75) compared to the unbraided main stem of the Selenga river where sediments are deposited on the bottom, thus having increased content in the near-bottom layers.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Horowitz, A.J.; Rinella, F.A.; Lamothe, P.; Miller, T.L.; Edwards, T.K.; Roche, R.; Rickert, D.A. Variations in Suspended Sediment and Associated Trace Element Concentrations in Selected Riverine Cross Sections. Environ. Sci. Technol. 1990, 24, 1313–1320. [Google Scholar] [CrossRef]
- Rouse, H. Fluid Mechanics for Hydraulic Engineers, 1st ed.; McGraw-Hill: New York, NY, USA, 1938. [Google Scholar]
- Dupré, B.; Gaillardet, J.; Rousseau, D.; Allègre, C.J. Major and trace elements of river-borne material: The Congo Basin. Geochim. Cosmochim. Acta. 1996, 60, 1301–1321. [Google Scholar] [CrossRef]
- Meybeck, M.; Ragu, A. River discharges to the oceans: an assessment of suspended solids, major ions and nutrients; UNEP: Nairobi, Kenya, 1997; pp. 3–14. [Google Scholar]
- Bouchez, J.; Maurice, L.; France-Lanord, C.; Dutra-Maia, P.; Gaillardet, J. Grain size control of river suspended sediment geochemistry: Clues from Amazon River depth profiles. Geochem. Geophys. Geosystems. 2011, 12, 12. [Google Scholar] [CrossRef] [Green Version]
- Lupker, M.; France-Lanord, C.; Lavé, J.; Bouchez, J.; Galy, V.; Métivier, F.; Gaillardet, J.; Lartiges, B.; Mugnier, J.-L. A Rouse-based method to integrate the chemical composition of river sediments: Application to the Ganga basin. J. Geophys. Res. Space Phys. 2011, 116, 116. [Google Scholar] [CrossRef] [Green Version]
- Dong, T.Y.; Nittrouer, J.A.; Il’Icheva, E.; Pavlov, M.; McElroy, B.; Czapiga, M.J.; Ma, H.; Parker, G. Controls on gravel termination in seven distributary channels of the Selenga River Delta, Baikal Rift basin, Russia. GSA Bull. 2016, 128, 1297–1312. [Google Scholar] [CrossRef] [Green Version]
- Pietroń, J.; Nittrouer, J.A.; Chalov, S.R.; Dong, T.Y.; Kasimov, N.; Shinkareva, G.; Jarsjö, J. Sedimentation patterns in the Selenga River delta under changing hydroclimatic conditions. Hydrol. Process. 2018, 32, 278–292. [Google Scholar] [CrossRef]
- Karthe, D.; Chalov, S.; Gradel, A.; Kusbach, A. Special issue «environmental change on the Mongolian plateau: Atmosphere, forests, soils and water». Geogr. Environ. Sustain. 2019, 12, 60–65. [Google Scholar] [CrossRef] [Green Version]
- Shinkareva, G.L.; Lychagin, M.Y.; Tarasov, M.K.; Pietroń, J.; Chichaeva, M.A.; Chalov, S.R. Biogeochemical specialization of macrophytes and their role as a biofilter in the Selenga delta. Geogr. Environ. Sustain. 2019, 12, 240–263. [Google Scholar] [CrossRef] [Green Version]
- Garmaev, E.Z.; Kulikov, A.I.; Tsydypov, B.Z.; Sodnomov, B.V.; Ayurzhanaev, A.A. Environmental Conditions of Zakamensk Town (Dzhida River Basin Hotspot). Geogr. Environ. Sustain. 2019, 12, 224–239. [Google Scholar] [CrossRef] [Green Version]
- Timofeev, I.V.; Kosheleva, N.E.; Kasimov, N.S.; Gunin, P.D.; Sandag, E.-A. Geochemical transformation of soil cover in copper–molybdenum mining areas (Erdenet, Mongolia). J. Soils Sediments. 2015, 16, 1225–1237. [Google Scholar] [CrossRef]
- Chalov, S.R.; Thorslund, J.; Kasimov, N.; Aybullatov, D.; Ilyicheva, E.; Karthe, D.; Kositsky, A.; Lychagin, M.; Nittrouer, J.; Pavlov, M.; et al. The Selenga River delta: a geochemical barrier protecting Lake Baikal waters. Reg. Environ. Chang. 2016, 17, 2039–2053. [Google Scholar] [CrossRef]
- Popovskaya, G.I.; Tashlykova, N.A. The Selenga River Delta–Natural Biofilter and Indicator of the Condition of Lake Baikal; Tulokhonov, A.K., Ed.; Publishing house of SB RAS: Novosibirsk, Russia, 2008; pp. 167–181. [Google Scholar]
- Chalov, S.R.; Potemkina, T.G.; Pashkina, M.P.; Kasimov, N.S. Evolution of Suspended Sediment Budget in the Deltas of Lake Baikal Tributaries. Russ. Meteorol. Hydrol. 2019, 44, 667–673. [Google Scholar] [CrossRef]
- Ivanov, V.V.; Korotayev, V.N.; Labutina, I.A. Morphology and dynamics of the Selenga River delta; Vestnik Moskovskogo Universiteta: Moscow, Russia, 2007; pp. 48–54. [Google Scholar]
- Sinyukovich, V.N. The water balance of the Selenga river basin. Geogr. Nat. Resour. 2008, 29, 54–56. [Google Scholar] [CrossRef]
- Chalov, S.; Golosov, V.; Tsyplenkov, A.; Theuring, P.; Zakerinejad, R.; Märker, M.; Samokhin, M. A toolbox for sediment budget research in small catchments. Geogr. Environ. Sustain. 2017, 10, 43–68. [Google Scholar]
- Chalov, S.R.; Bazilova, V.O.; Tarasov, M.K. Modelling suspended sediment distribution in the Selenga River Delta using LandSat data. Proc. Int. Assoc. Hydrol. Sci. 2017, 375, 19–22. [Google Scholar] [CrossRef] [Green Version]
- Dong, T.; Nittrouer, J.A.; Czapiga, M.J.; Ma, H.; McElroy, B.; Il’Icheva, E.; Pavlov, M.; Chalov, S.; Parker, G. Roles of Bank Material in Setting Bankfull Hydraulic Geometry as Informed by the Selenga River Delta, Russia. Water Resour. Res. 2019, 55, 827–846. [Google Scholar] [CrossRef]
- Gyninova, А.В.; Korsunov, V.M.; Beshentsev, A.N.; Balsanova, L.D.; Ubugunova, V.I.; Gyninova, B.D. Accumulation of substances on geochemical barriers in the Selenga delta. Geogr. Nat. Resour. 2007, 2, 65–69. [Google Scholar]
- Sorokovikova, L.M.; Popovskaya, G.I.; Sinyukovich, V.N.; Tomberg, I.V.; Bashenkhaeva, N.V.; Tashlykova, N.A. Water chemistry and phytoplankton in water bodies in the Selenga River’s delta under ice cover. Water Resour. 2006, 33, 321–328. [Google Scholar] [CrossRef]
- Karthe, D.; Kasimov, N.S.; Chalov, S.R.; Shinkareva, G.L.; Malsy, M.; Menzel, L.; Theuring, P.; Hartwig, M.; Schweitzer, C.; Hofmann, J.; et al. Integrating multi-scale data for the assessment of water availability and quality in the Kharaa - Orkhon - Selenga river system. Geogr. Environ. Sustain. 2014, 7, 65–86. [Google Scholar] [CrossRef] [Green Version]
- Parker, G. The uses of sediment transport and morphodynamic modeling in stream restoration. In Proceedings of the 2004 World Water and Environmetal Resources Congress: Critical Transitions in Water and Environmetal Resources Management, Salt Lake City, UT, USA, 27 June–1 July 2004; pp. 812–815. [Google Scholar]
- Whiting, P.J.; Dietrich, W.E. Convective accelerations and boundary shear stress over a Channel Bar. Water Resour. Res. 1991, 27, 783–796. [Google Scholar] [CrossRef]
- Wilcock, P.R. Estimating local bed shear stress from velocity observations. Water Resour. Res. 1996, 32, 3361–3366. [Google Scholar] [CrossRef]
- Dietrich, E.W. Settling Velocity of Natural Particles. Water Resour. Res. 1982, 18, 1615–1626. [Google Scholar] [CrossRef]
- Van Rijn L., C. Principles of Sediment. Transport. in Rivers, Estuaries and Coastal Seas; Aquapublications: Blokzijl, The Netherlands, 1993; pp. 1–17. [Google Scholar]
- Van Rijn, L.C. Sediment Transport, Part I: Bed Load Transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef] [Green Version]
- Van Rijn, L.C. Unified View of Sediment Transport by Currents and Waves. I: Initiation of Motion, Bed Roughness, and Bed-Load Transport. J. Hydraul. Eng. 2007, 133, 649–667. [Google Scholar] [CrossRef] [Green Version]
- Kasimov, N.; Kosheleva, N.; Lychagin, M.; Chalov, S.R.; Alekseenko, A.V.; Bazilova, V.; Beshentsev, A.; Bogdanova, M.; Chernov, A.V.; Dorjgotov, D.; et al. Environmental Atlas Selenga-Baikal; Faculty of Geography, Lomonosov Moscow State University: Moscow, Russia, 2019; p. 288. [Google Scholar]
- Chalov, S.R.; Jarsjö, J.; Kasimov, N.; Romanchenko, A.; Pietron, J.; Thorslund, J.; Belozerova, E. Spatio-temporal variation of sediment transport in the Selenga River Basin, Mongolia and Russia. Environ. Earth Scie. 2014, 73, 663–680. [Google Scholar] [CrossRef]
- Horowitz, A.J. Primer on trace metal-sediment chemistry; US Government Printing Office: Washington, DC, USA, 1985; p. 2277. [Google Scholar]
- Horowitz, A.; Elrick, K.A. The relation of stream sediment surface area, grain size and composition to trace element chemistry. Appl. Geochem. 1987, 2, 437–451. [Google Scholar] [CrossRef]
- Miller, J.; Lechler, P.J.; Mackin, G.; Germanoski, D.; Villarroel, L.F. Evaluation of particle dispersal from mining and milling operations using lead isotopic fingerprinting techniques, Rio Pilcomayo Basin, Bolivia. Sci. Total. Environ. 2007, 384, 355–373. [Google Scholar] [CrossRef]
- Tansel, B.; Rafiuddin, S.; Tanse, B.; Rafiuddi, S. Heavy metal content in relation to particle size and organic content of surficial sediments in Miami River and transport potential. Int. J. Sediment. Res. 2016, 31, 324–329. [Google Scholar] [CrossRef]
- Yao, Q.; Wang, X.; Jian, H.; Chen, H.; Yu, Z. Characterization of the particle size fraction associated with heavy metals in suspended sediments of the yellow river. Int. J. Environ. Res. Public. Health. 2015, 12, 6725–6744. [Google Scholar] [CrossRef]
- Middleton, G.V.; Southard, J.B. Mechanics of Sediment. Movement; SEPM Society for Sedimentary Geology: Tulsa, OK, USA, 1984. [Google Scholar]
- Huston, D. Particulate organic carbon trapping efficiency in the stream bed for cobbles and gravels: A laboratory test. Kaleidoscope 2014, 11, 73. [Google Scholar]
- Lynds, R.M.; Mohrig, D.; Hajek, E.A.; Heller, P.L. Paleoslope Reconstruction in Sandy Suspended-Load-Dominant Rivers. J. Sediment. Res. 2014, 84, 825–836. [Google Scholar] [CrossRef]
- Guy, H.; Simons, D.; Richardson, E. Summary of Alluvial Channel Data from Flume Experiments 1956-61; US Government Printing Office: Washington, DC, USA, 1966; pp. 1–104. [Google Scholar]
- Shah-Fairbank, S.C.; Julien, P.Y. Sediment load calculations from point measurements in sand-bed rivers. Int. J. Sediment. Res. 2015, 30, 1–12. [Google Scholar] [CrossRef]
- Julien, P.Y. Erosion and Sedimentation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010; p. 371. [Google Scholar]
- Pietroń, J.; Jarsjö, J.; Romanchenko, A.O.; Chalov, S.R. Model analyses of the contribution of in-channel processes to sediment concentration hysteresis loops. J. Hydrol. 2015, 527, 576–589. [Google Scholar] [CrossRef] [Green Version]
- Bouchez, J.; Métivier, F.; Lupker, M.; Maurice, L.; Pérez, M.; Gaillardet, J.; France-Lanord, C. Prediction of depth-integrated fluxes of suspended sediment in the Amazon River: Particle aggregation as a complicating factor. Hydrol. Process. 2010, 25, 778–794. [Google Scholar] [CrossRef]
- Antokhina, O.Y.; Latysheva, I.V.; Mordvinov, V.I. A Cases Study Of Mongolian Cyclogenesis During The July 2018 Blocking Events. Geogr. Environ. Sustain. 2019, 12, 66–78. [Google Scholar] [CrossRef] [Green Version]
- Frolova, N.; Belyakova, P.; Grigor’Ev, V.Y.; Sazonov, A.A.; Zotov, L.V. Many-year variations of river runoff in the Selenga basin. Water Resour. 2017, 44, 359–371. [Google Scholar] [CrossRef]
- Moreido, V.M.; Kalugin, A.S. Assessing possible changes in Selenga R. water regime in the XXI century based on a runoff formation model. Water Resour. 2017, 44, 390–398. [Google Scholar] [CrossRef]
- Sorokovikova, L.M.; Sinyukovich, V.N.; Tomberg, I.V.; Popovskaya, G.I.; Chernyshev, M.S.; Ivanov, V.G.; Khodzher, T.V. The status of the aquatic ecosystem of the Selenga river delta under long-duration low-water conditions. Geogr. Nat. Resour. 2017, 38, 60–67. [Google Scholar] [CrossRef]
- Tomberg, I.V.; Sorokovikova, L.M.; Sinyukovich, V.N.; Pogodaeva, T.V. Ion flow in the Selenga river Delta under low water content conditions. Meteorol. and Hydrol. 2006, 12, 87–95. [Google Scholar]
- Qiao, S.; Yang, Z.; Pan, Y.; Guo, Z. Metals in suspended sediments from the Changjiang (Yangtze River) and Huanghe (Yellow River) to the sea, and their comparison. Estuarine Coast. Shelf. Sci. 2007, 74, 539–548. [Google Scholar] [CrossRef]
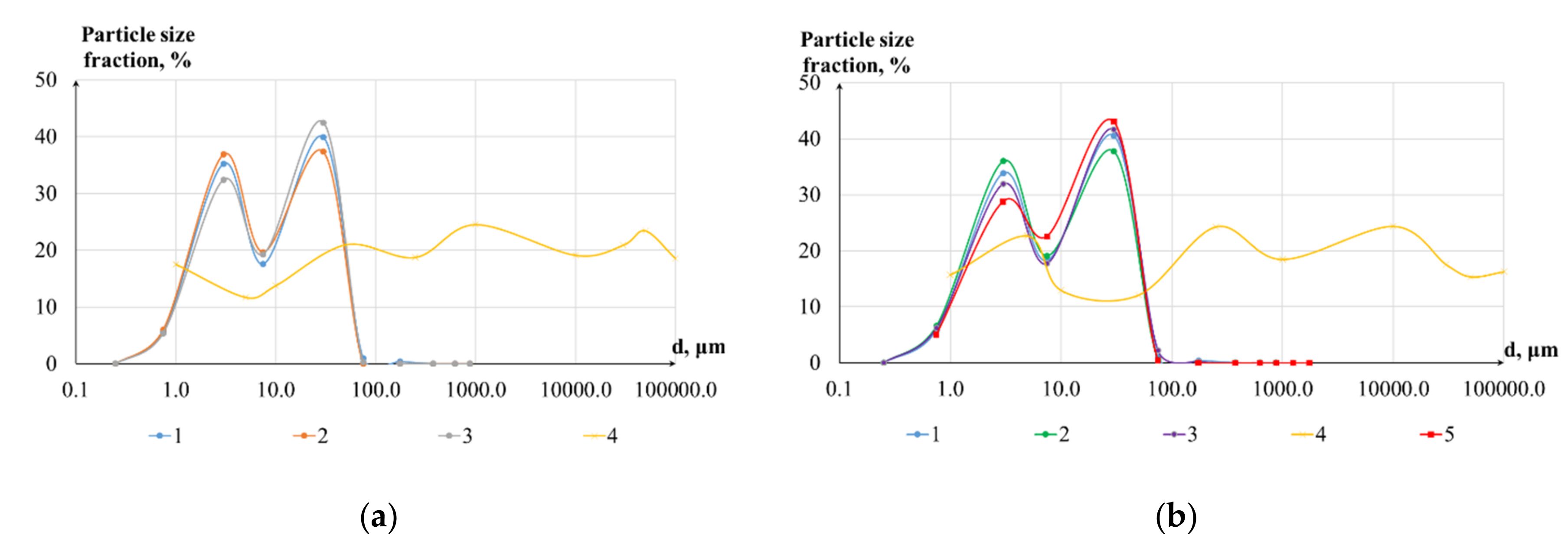
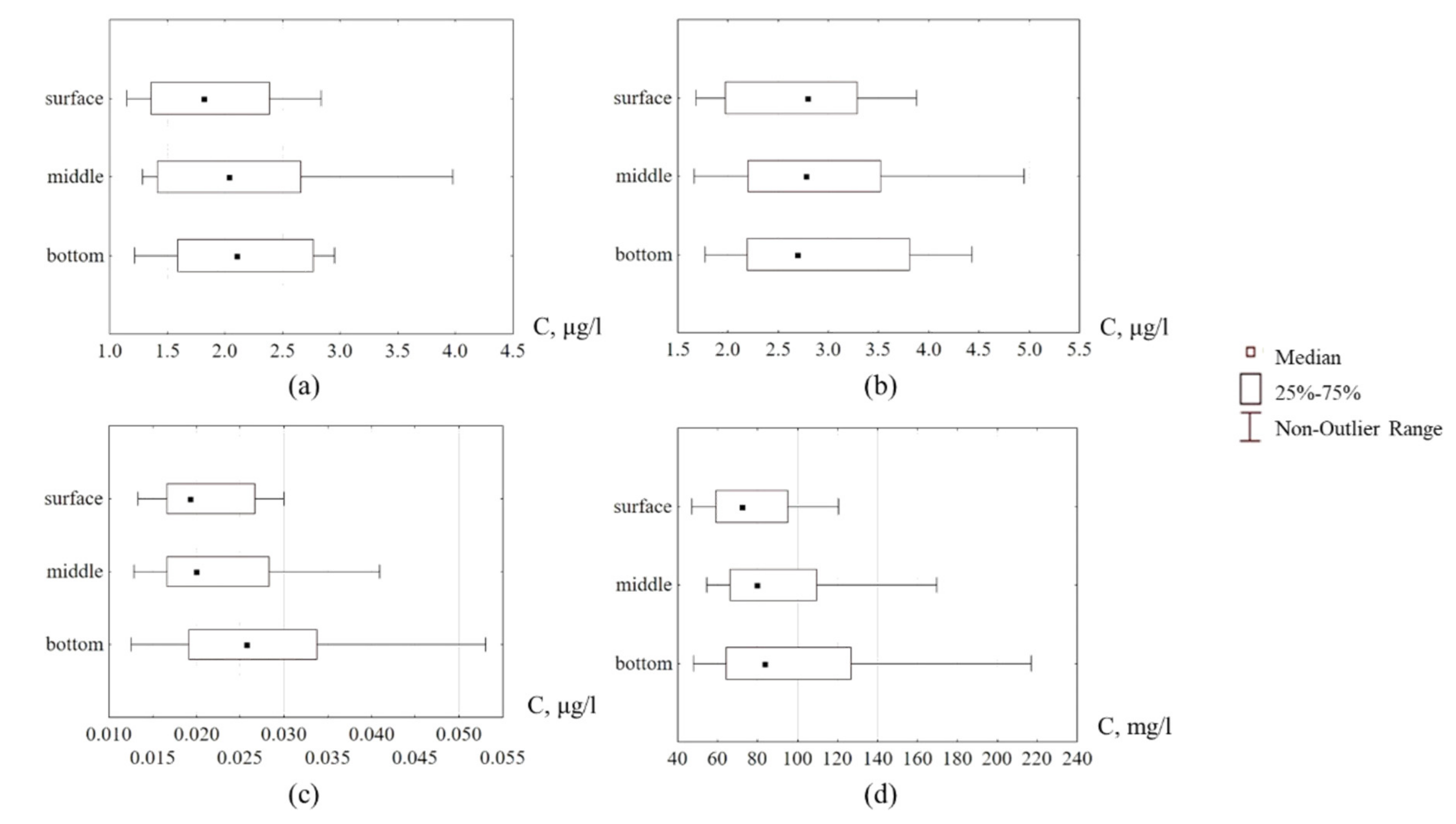
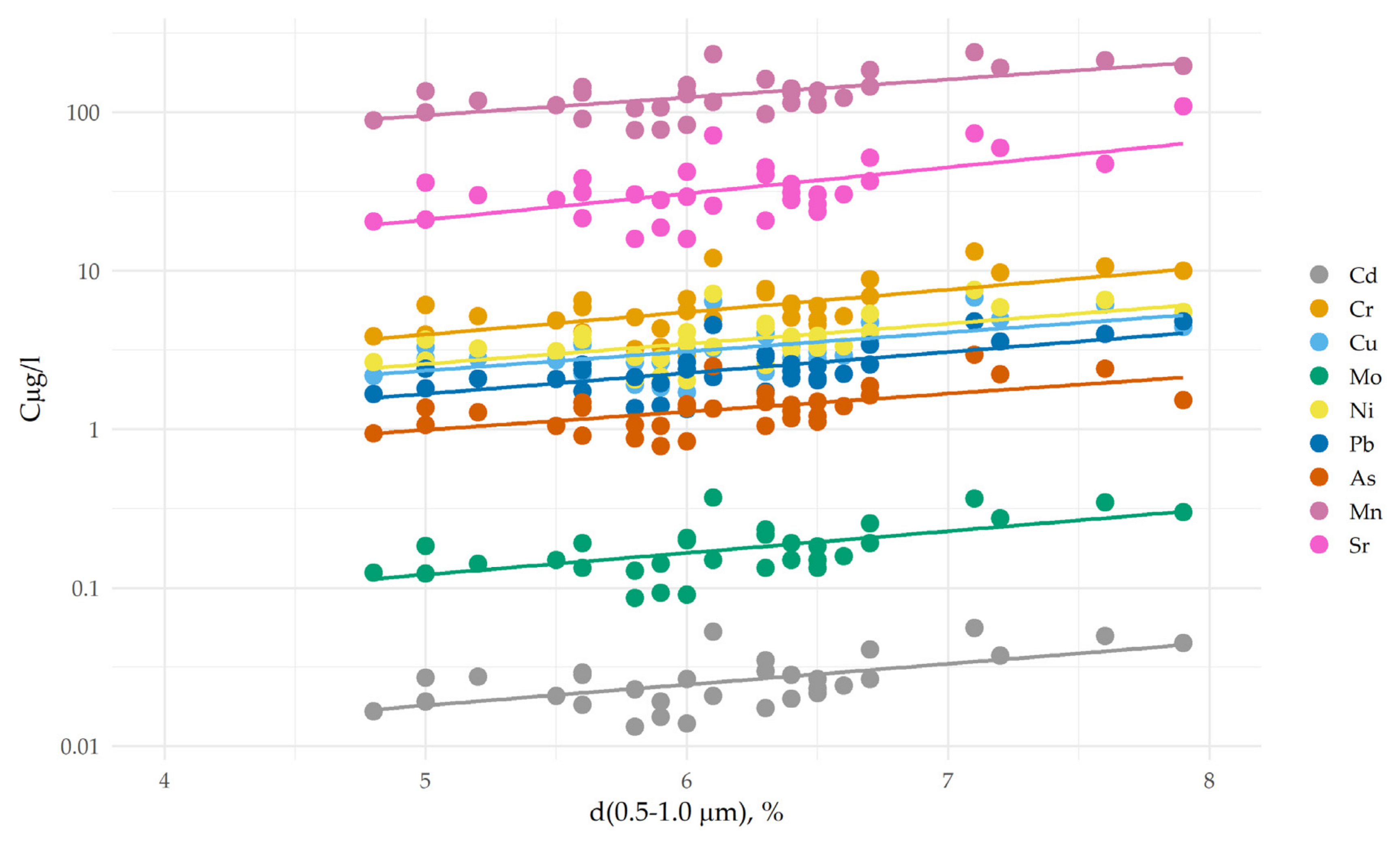
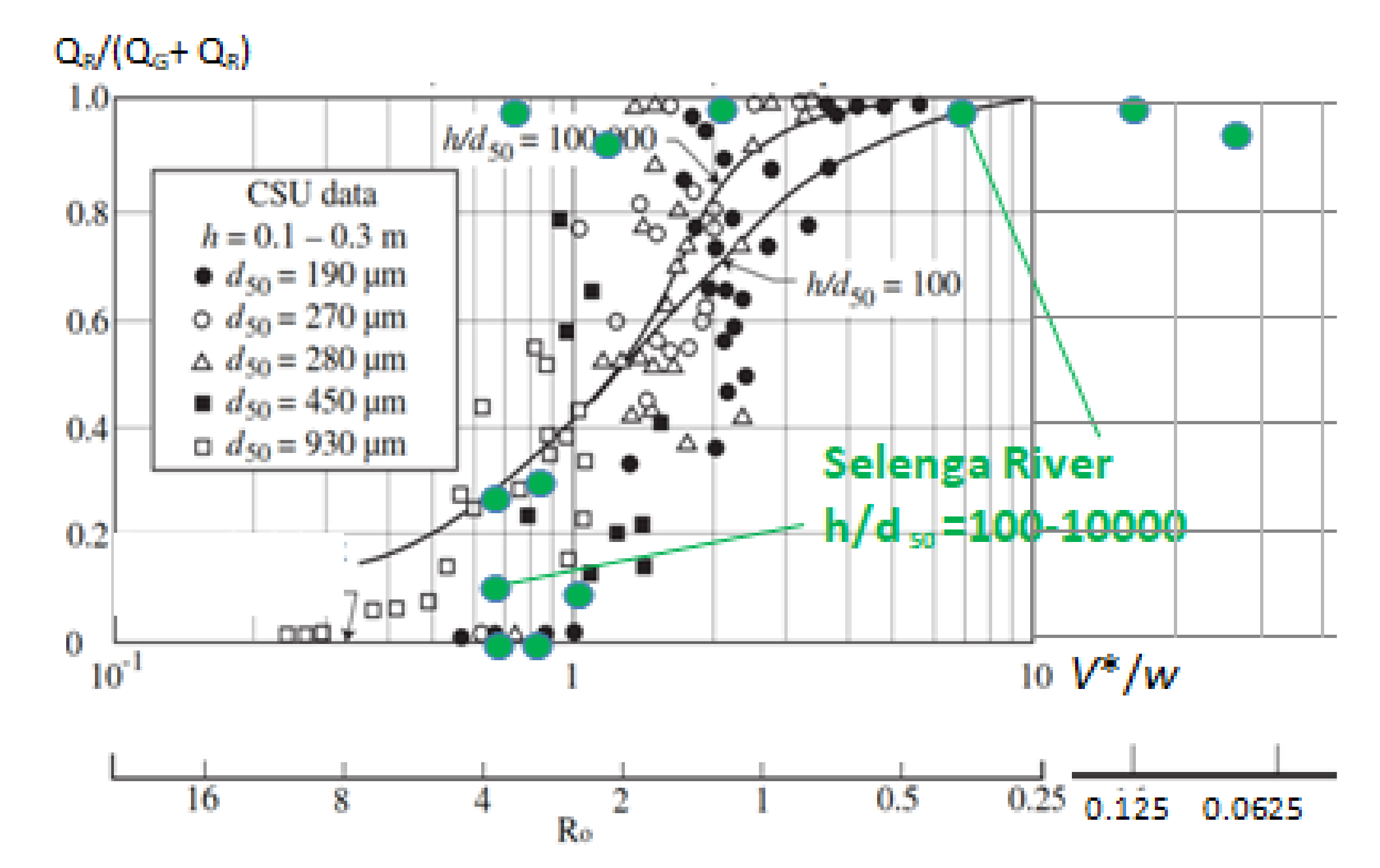
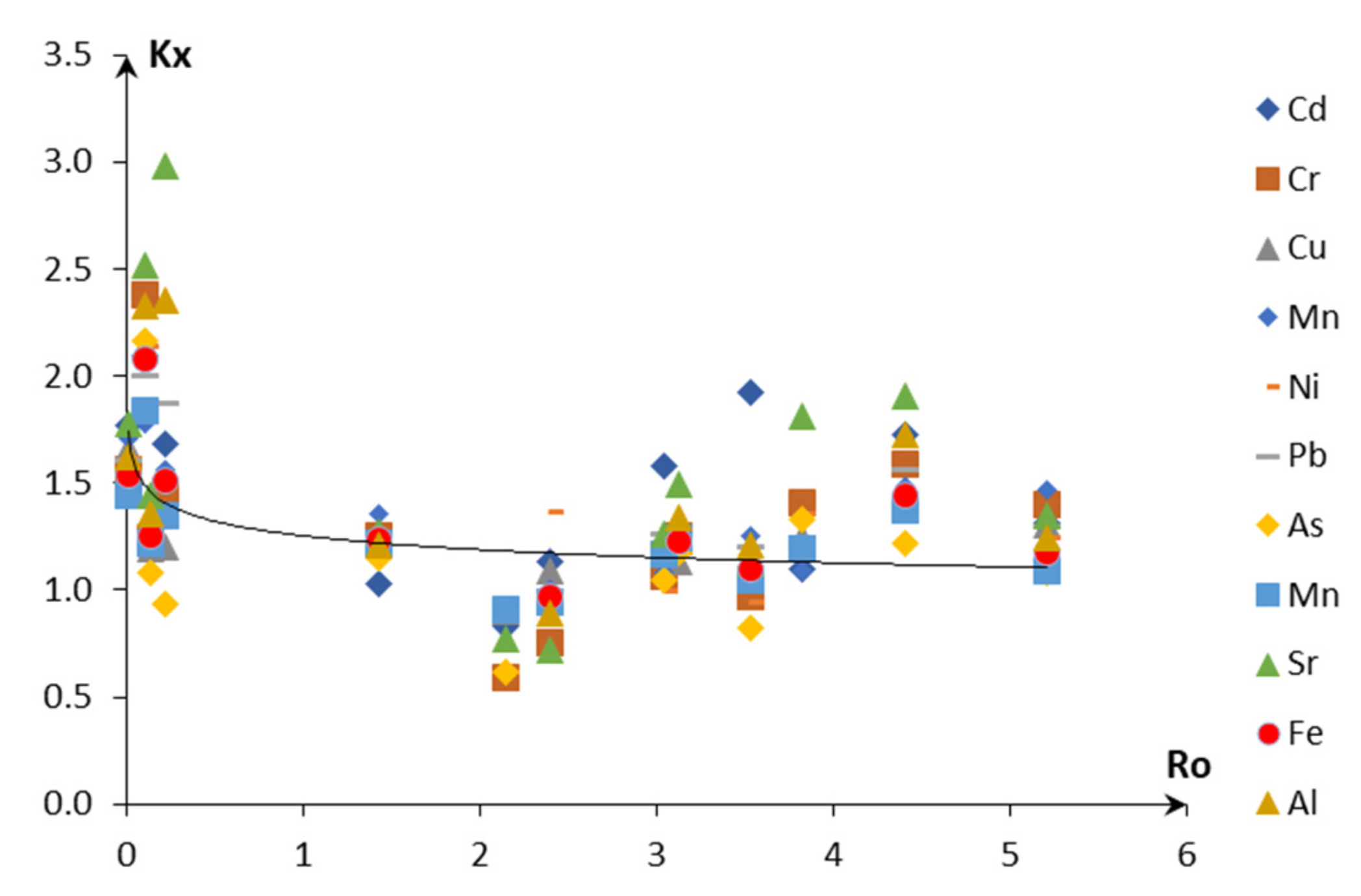
| Metal | Cd | Cu | Zn | Pb | Ni | Mo | As | Sr | Mn | Fe | Al |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Suspended sediments | 0.27 | 33 | 107 | 23.7 | 37.8 | 1.73 | 14.0 | 319 | 1345 | 46811 | 79107 |
| Bottom sediments | 0.08 | 6 | 44 | 12.5 | 7.7 | 0.47 | 2.5 | 338 | 334 | 13422 | 61969 |
| Reach | Layer | V | Cd | Cr | Cu | Mo | Ni | Pb | As | Mn | Sr | Fe | Al |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Main channel | top (n = 5) | mean | 0.02 | 3.62 | 1.90 | 0.10 | 2.36 | 1.30 | 0.89 | 82.0 | 17.0 | 2669 | 4343 |
| ± SD | 0.00 | 0.44 | 0.15 | 0.01 | 0.23 | 0.14 | 0.15 | 6.00 | 3.00 | 221 | 455 | ||
| middle (n = 5) | mean | 0.02 | 3.63 | 2.07 | 0.10 | 2.35 | 1.50 | 0.92 | 89.0 | 21.0 | 3005 | 5132 | |
| ± SD | 0.00 | 0.43 | 0.27 | 0.02 | 0.30 | 0.22 | 0.08 | 10.0 | 4.0 | 343 | 798 | ||
| bottom (n = 5) | mean | 0.02 | 3.38 | 2.07 | 0.10 | 2.45 | 1.43 | 0.81 | 86.0 | 18.0 | 2992 | 5036 | |
| ± SD | 0.01 | 0.74 | 0.17 | 0.01 | 0.63 | 0.17 | 0.13 | 5.00 | 4.00 | 187 | 658 | ||
| Delta | top (n = 9) | mean | 0.02 | 4.67 | 2.74 | 0.14 | 3.02 | 1.96 | 1.16 | 109 | 25.0 | 3787 | 6278 |
| ± SD | 0.01 | 1.21 | 0.66 | 0.04 | 0.69 | 0.44 | 0.24 | 23.0 | 7.00 | 854 | 1658 | ||
| middle (n = 8) | mean | 0.02 | 4.97 | 2.78 | 0.15 | 3.20 | 2.07 | 1.18 | 115 | 28.0 | 4018 | 6821 | |
| ± SD | 0.00 | 1.14 | 0.58 | 0.04 | 0.66 | 0.41 | 0.23 | 23.0 | 8.00 | 803 | 1678 | ||
| bottom (n = 8) | mean | 0.02 | 5.41 | 3.07 | 0.17 | 3.39 | 2.27 | 1.23 | 122 | 32.0 | 4298 | 7516 | |
| ± SD | 0.01 | 1.13 | 0.60 | 0.04 | 0.71 | 0.40 | 0.23 | 24.0 | 8.00 | 853 | 1672 | ||
| Delta edge | top (n = 3) | mean | 0.03 | 6.70 | 3.58 | 0.21 | 4.02 | 2.60 | 1.56 | 145 | 35.0 | 5201 | 8795 |
| ± SD | 0.00 | 1.06 | 0.36 | 0.01 | 0.46 | 0.22 | 0.18 | 15.0 | 6.00 | 610 | 1357 | ||
| middle (n = 3) | mean | 0.04 | 9.75 | 5.28 | 0.29 | 5.92 | 3.66 | 2.17 | 196 | 53.0 | 7207 | 12,704 | |
| ± SD | 0.01 | 0.91 | 0.75 | 0.05 | 0.61 | 0.29 | 0.27 | 15.0 | 6.00 | 543 | 661 | ||
| bottom (n = 3) | mean | 0.05 | 11.75 | 5.88 | 0.35 | 6.74 | 4.71 | 2.32 | 222 | 85.0 | 8763 | 18,172 | |
| ± SD | 0.01 | 1.64 | 1.27 | 0.04 | 1.08 | 0.15 | 0.72 | 23.0 | 21.0 | 769 | 2601 |
| Particle Size Fraction, μm | Al | As | Cd | Cr | Cu | Fe | Mn | Mo | Ni | Pb | Sr | SSC, mg/l |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <0.5 | −13 | −7 | −12 | −9 | −12 | −14 | −12 | −13 | −9 | −13 | −10 | −9 |
| 0.5–1 | 61 | 48 | 40 | 51 | 48 | 61 | 49 | 50 | 51 | 53 | 53 | 57 |
| 1–5 | −30 | −23 | −40 | −31 | −28 | −23 | −31 | −32 | −28 | −33 | −38 | −32 |
| 5–10 | −51 | −37 | −42 | −46 | −41 | −44 | −43 | −46 | −43 | −49 | −55 | −54 |
| 10–50 | 2 | 13 | 23 | 13 | 15 | 2 | 15 | 14 | 11 | 12 | 10 | −1 |
| 50–100 | 62 | 33 | 46 | 47 | 40 | 48 | 44 | 47 | 44 | 53 | 67 | 70 |
| 100–250 | 5 | −9 | −2 | −2 | −7 | −4 | −5 | −2 | −3 | 1 | 11 | 17 |
| 250–500 | −19 | −17 | −14 | −16 | −18 | −21 | −18 | −18 | −16 | −18 | −16 | −15 |
| Location | I | II | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | V | d50 | sand | SSC | |||||||||||
| Cd | Cr | Cu | Mo | Ni | Pb | As | Mn | Se | Fe | Al | |||||
| Delta channels | 1.40 | 1.31 | 1.31 | 1.38 | 1.33 | 1.40 | 1.22 | 1.28 | 1.72 | 1.35 | 1.54 | 0.96 | 1.05 | 1.75 | 1.75 |
| Main channel | 0.93 | 1.09 | 1.09 | 1.07 | 1.04 | 1.10 | 0.91 | 1.04 | 1.08 | 0.84 | 0.87 | 0.94 | 0.9 | 0.43 | 0.99 |
| Whole research area | 1.29 | 1.26 | 1.26 | 1.31 | 1.26 | 1.33 | 1.14 | 1.22 | 1.58 | 1.25 | 1.41 | 0.95 | 0.99 | 1.11 | 1.57 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chalov, S.; Moreido, V.; Sharapova, E.; Efimova, L.; Efimov, V.; Lychagin, M.; Kasimov, N. Hydrodynamic Controls of Particulate Metals Partitioning Along the Lower Selenga River—Main Tributary of The Lake Baikal. Water 2020, 12, 1345. https://doi.org/10.3390/w12051345
Chalov S, Moreido V, Sharapova E, Efimova L, Efimov V, Lychagin M, Kasimov N. Hydrodynamic Controls of Particulate Metals Partitioning Along the Lower Selenga River—Main Tributary of The Lake Baikal. Water. 2020; 12(5):1345. https://doi.org/10.3390/w12051345
Chicago/Turabian StyleChalov, Sergey, Vsevolod Moreido, Ekaterina Sharapova, Lyudmila Efimova, Vasyli Efimov, Mikhail Lychagin, and Nikolay Kasimov. 2020. "Hydrodynamic Controls of Particulate Metals Partitioning Along the Lower Selenga River—Main Tributary of The Lake Baikal" Water 12, no. 5: 1345. https://doi.org/10.3390/w12051345
APA StyleChalov, S., Moreido, V., Sharapova, E., Efimova, L., Efimov, V., Lychagin, M., & Kasimov, N. (2020). Hydrodynamic Controls of Particulate Metals Partitioning Along the Lower Selenga River—Main Tributary of The Lake Baikal. Water, 12(5), 1345. https://doi.org/10.3390/w12051345








