Zonation of Positively Buoyant Jets Interacting with the Water-Free Surface Quantified by Physical and Numerical Modelling
Abstract
:1. Introduction
2. Materials and Methods
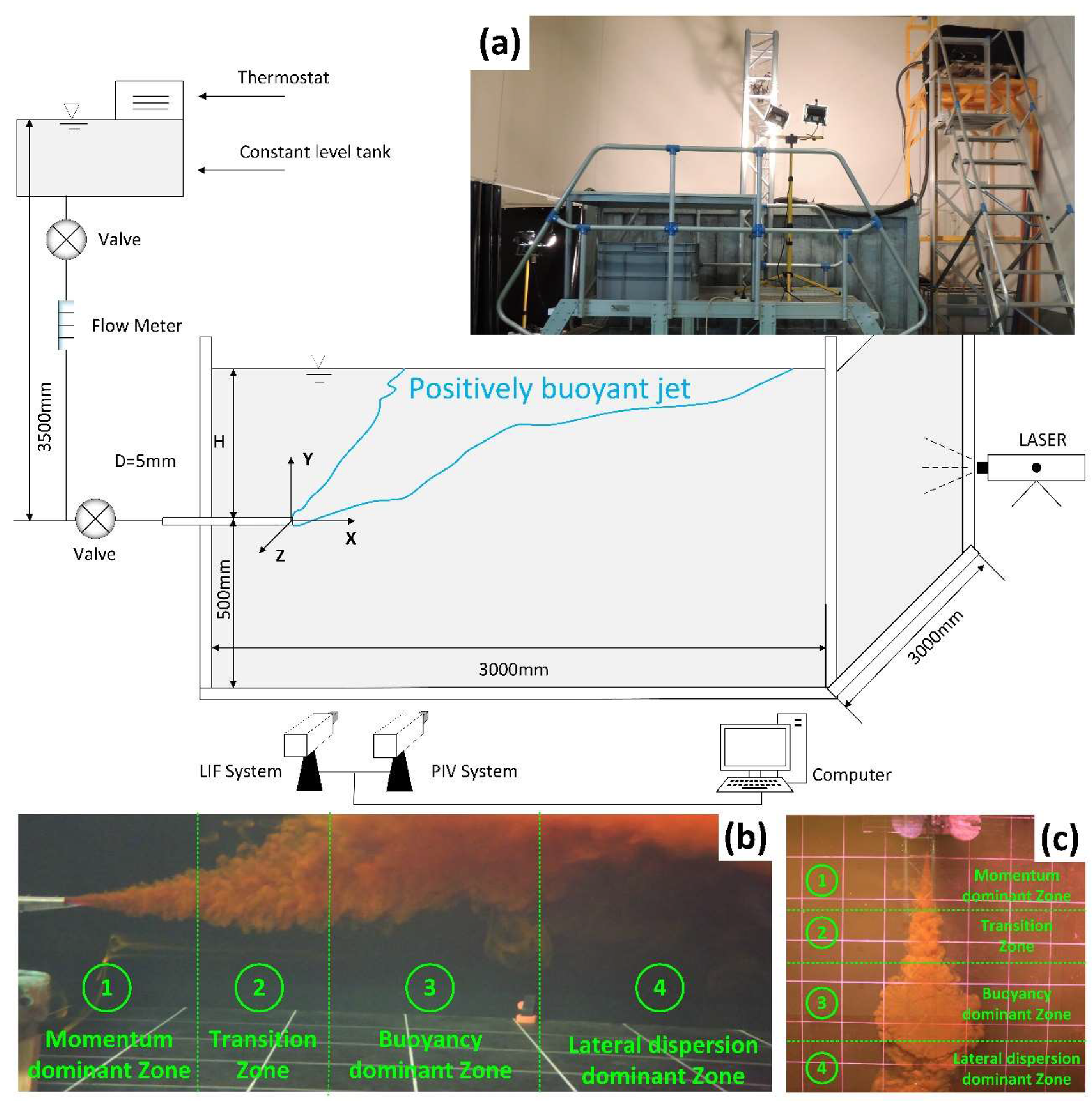
2.1. Physycal Modelling
2.1.1. Description of the PIV and LIF Techniques
2.1.2. Setup of the Physical Modelling
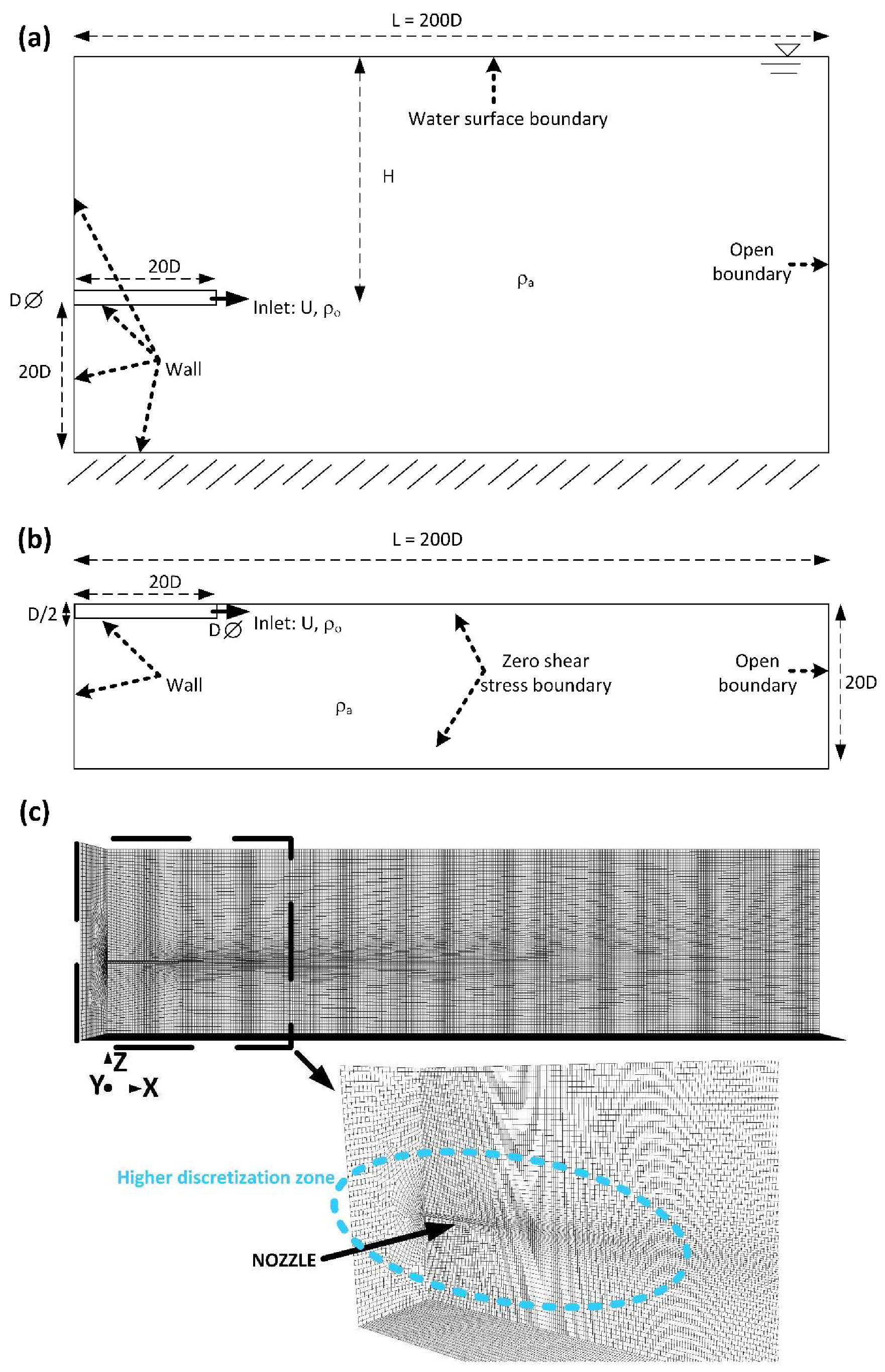
2.2. Numerical Modelling
2.2.1. Description of Numerical Models
2.2.2. Setup of the Computational Fluid Dynamics Model
2.2.3. Setup of the Semiempirical Models
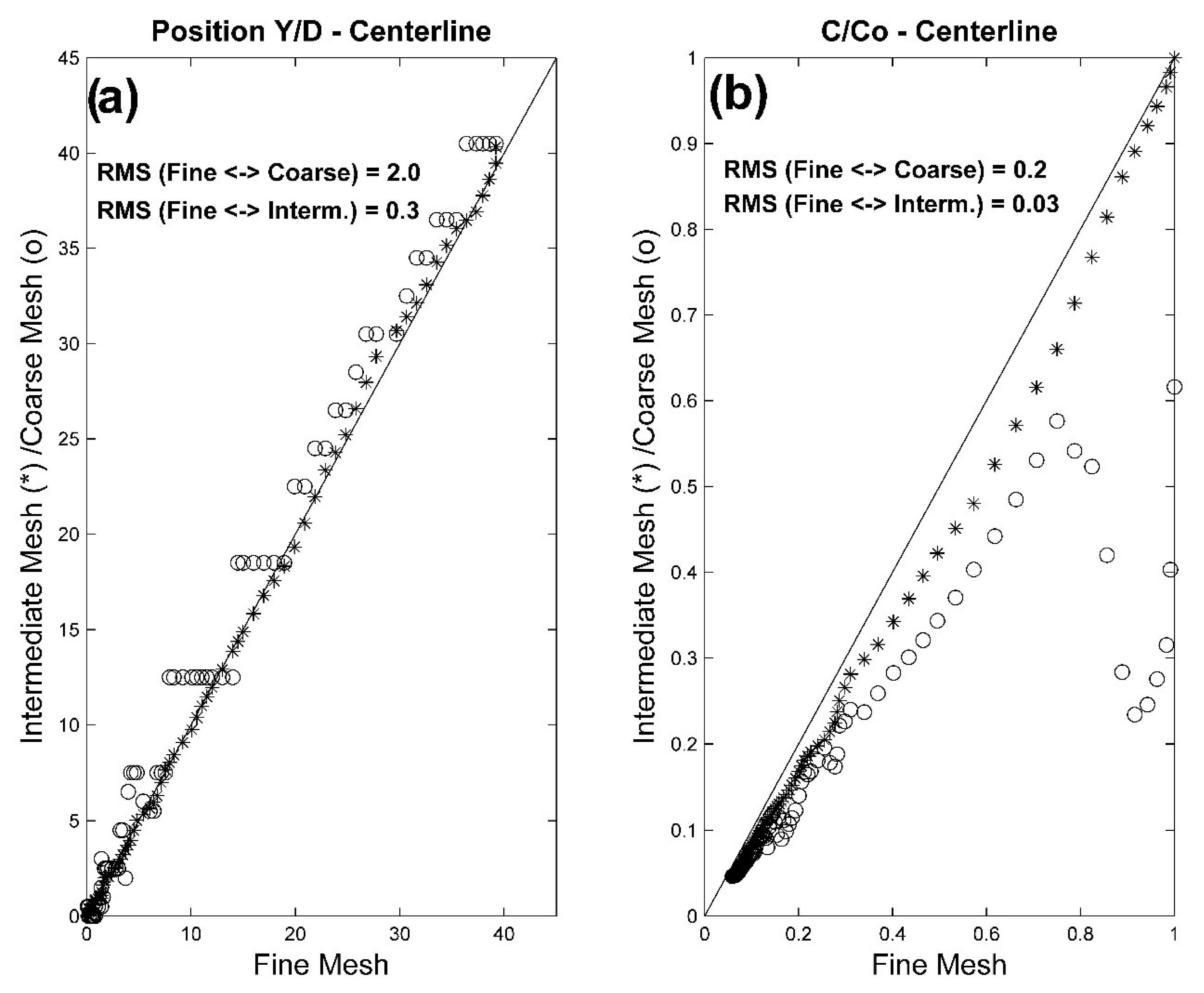
2.2.4. Performance Metrics of Numerical Modelling
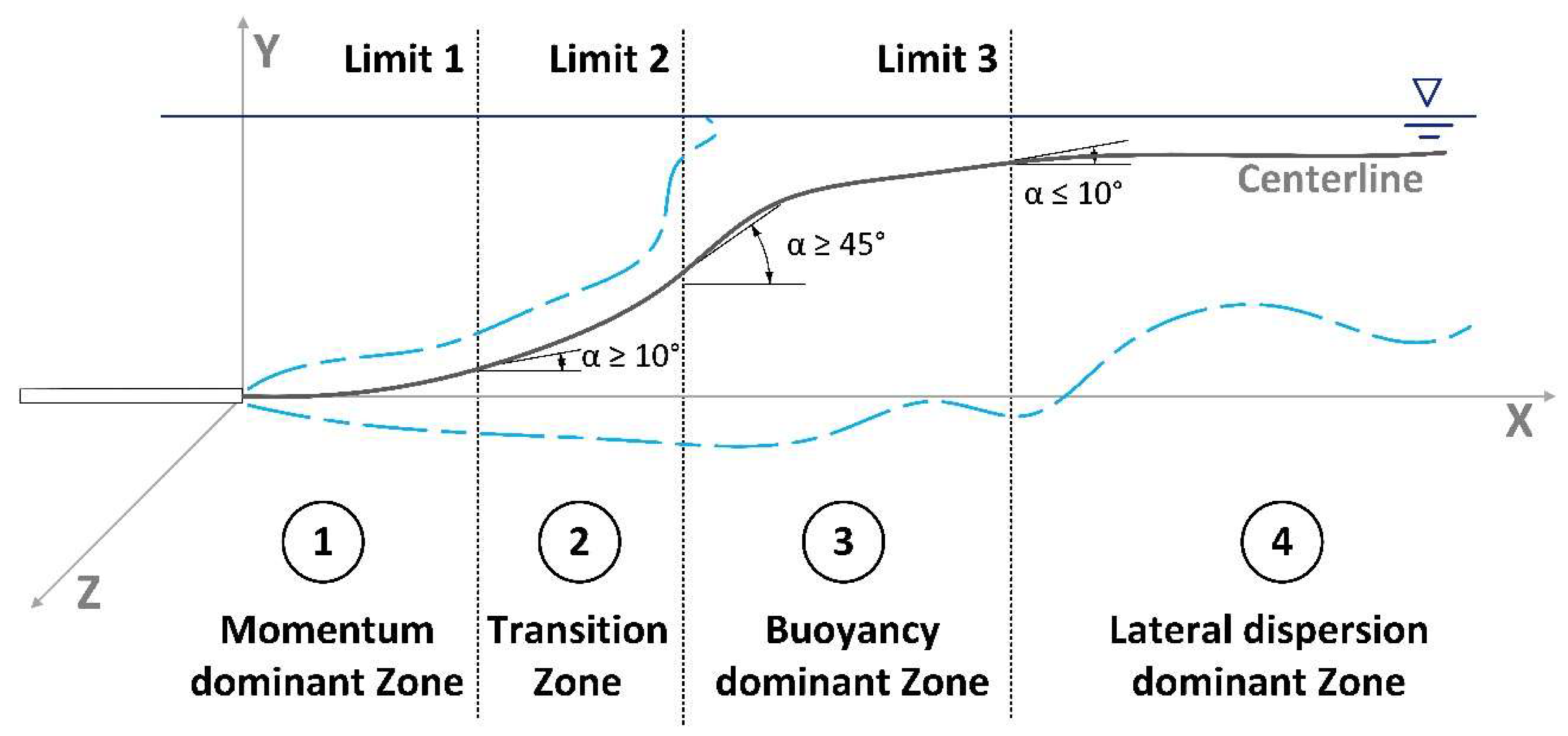
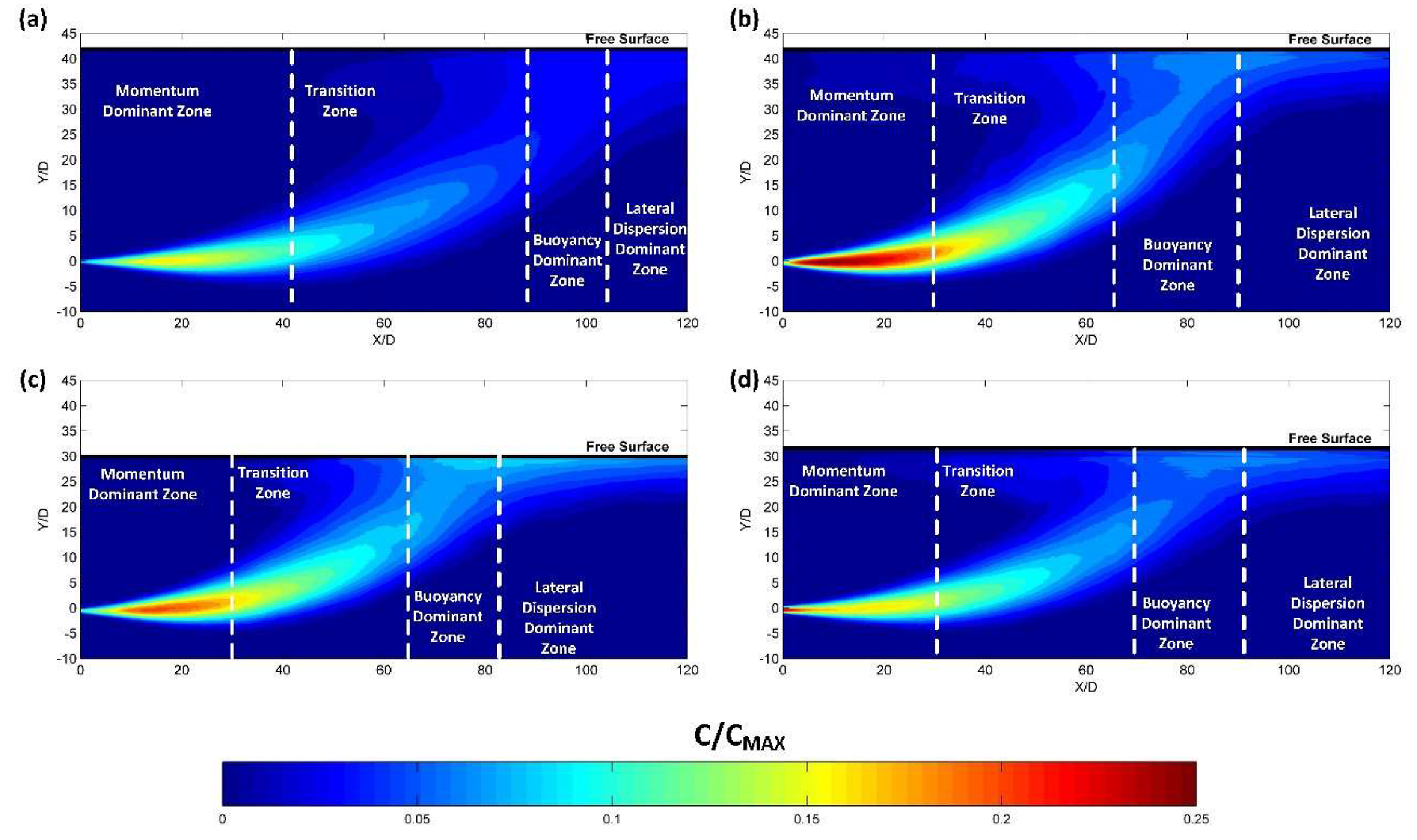
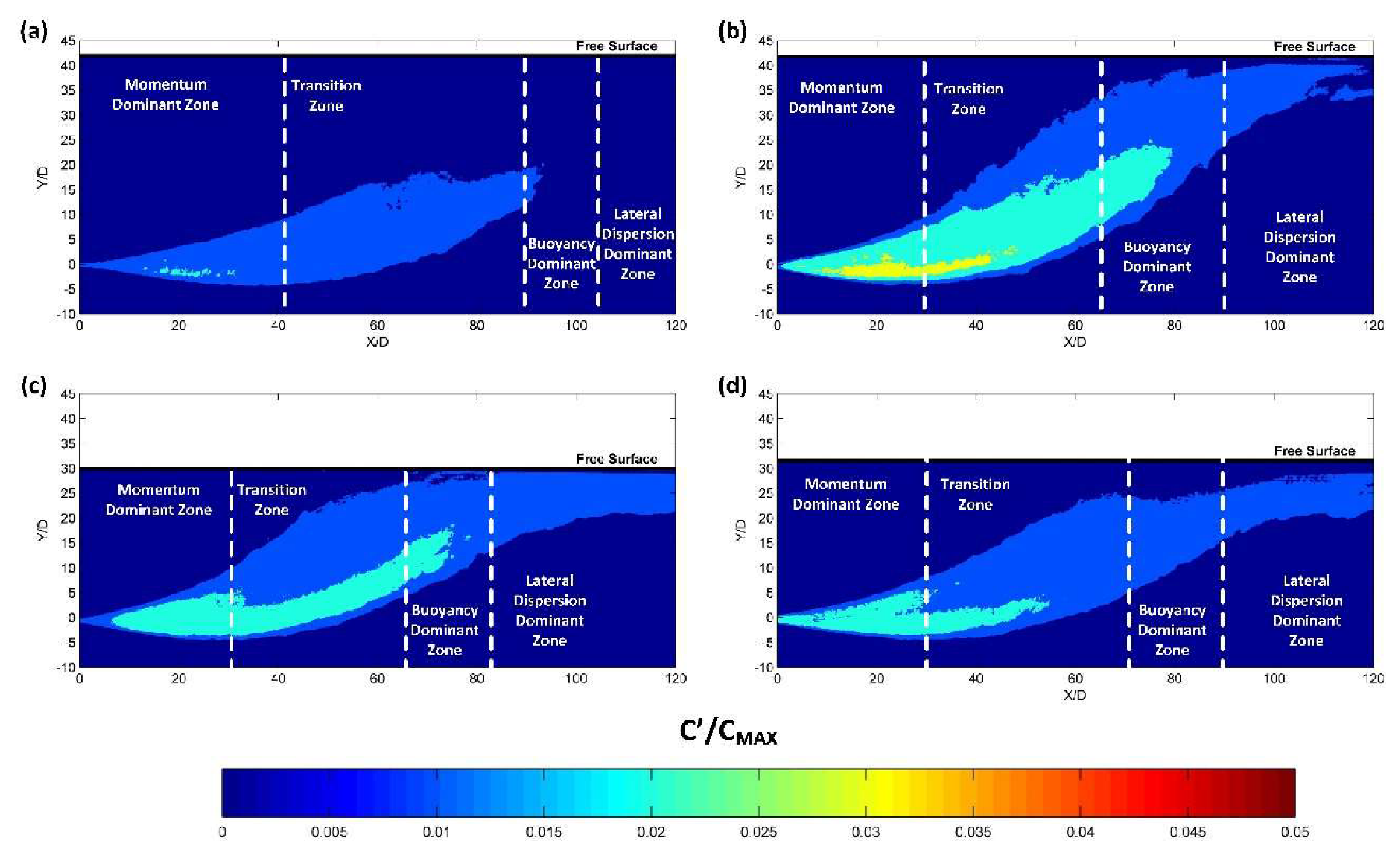
2.3. Zonation of Positively Buoyant Jets
3. Results
3.1. Physycal Modelling
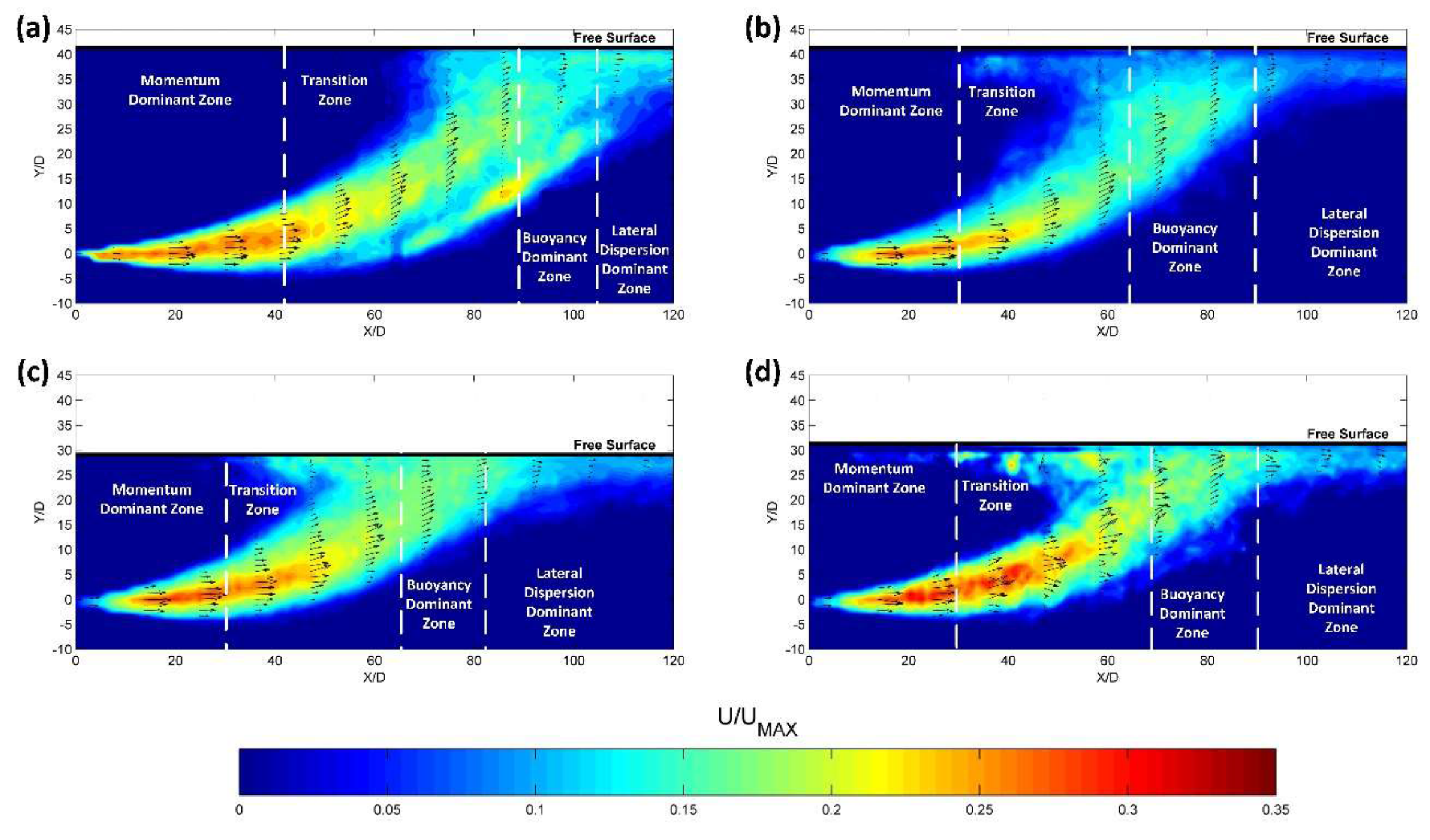
3.1.1. PIV Measurements
3.1.2. LIF Measurements
3.2. Numerical Modelling
3.2.1. Setup of the Computational Fluid Dynamics Model
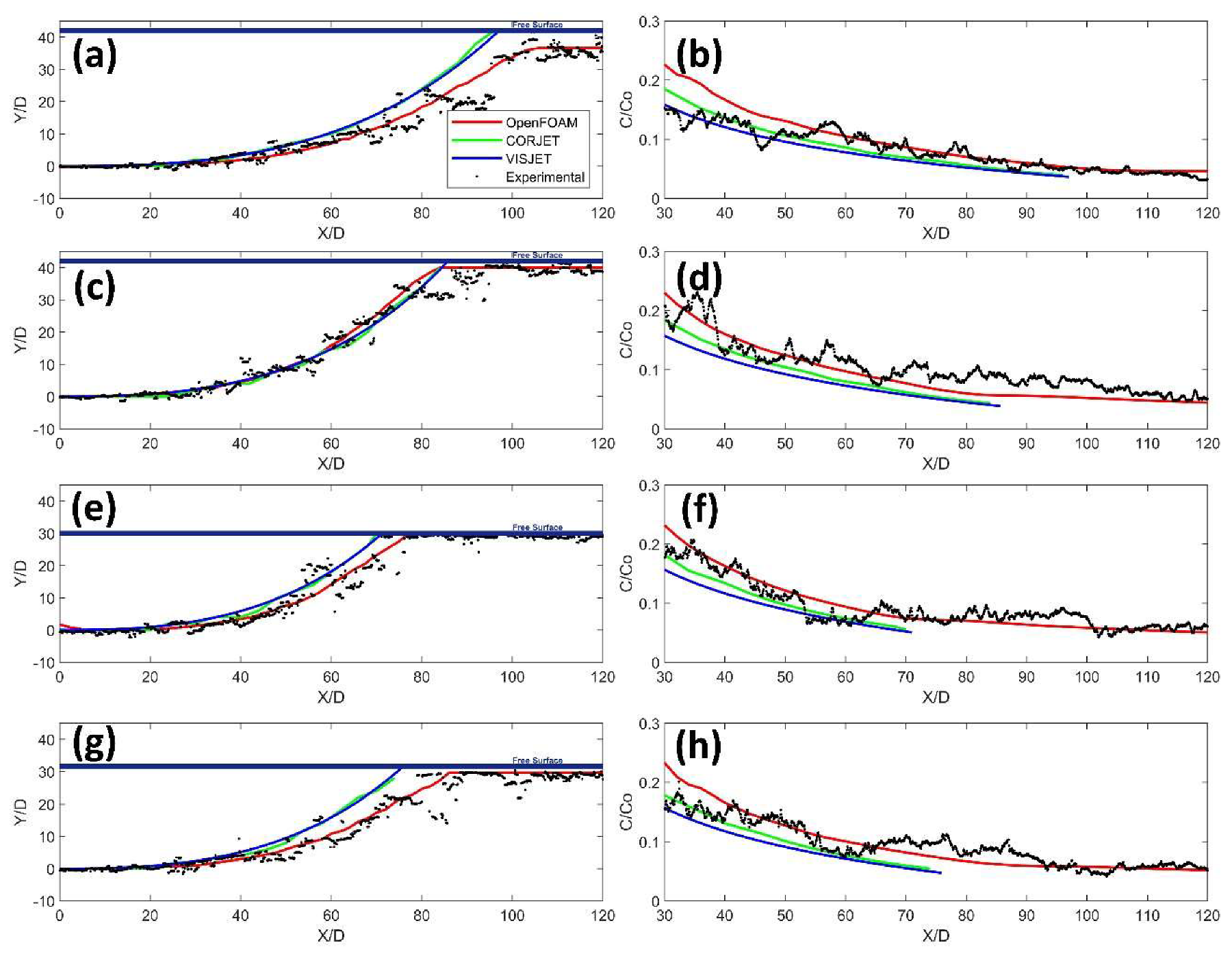
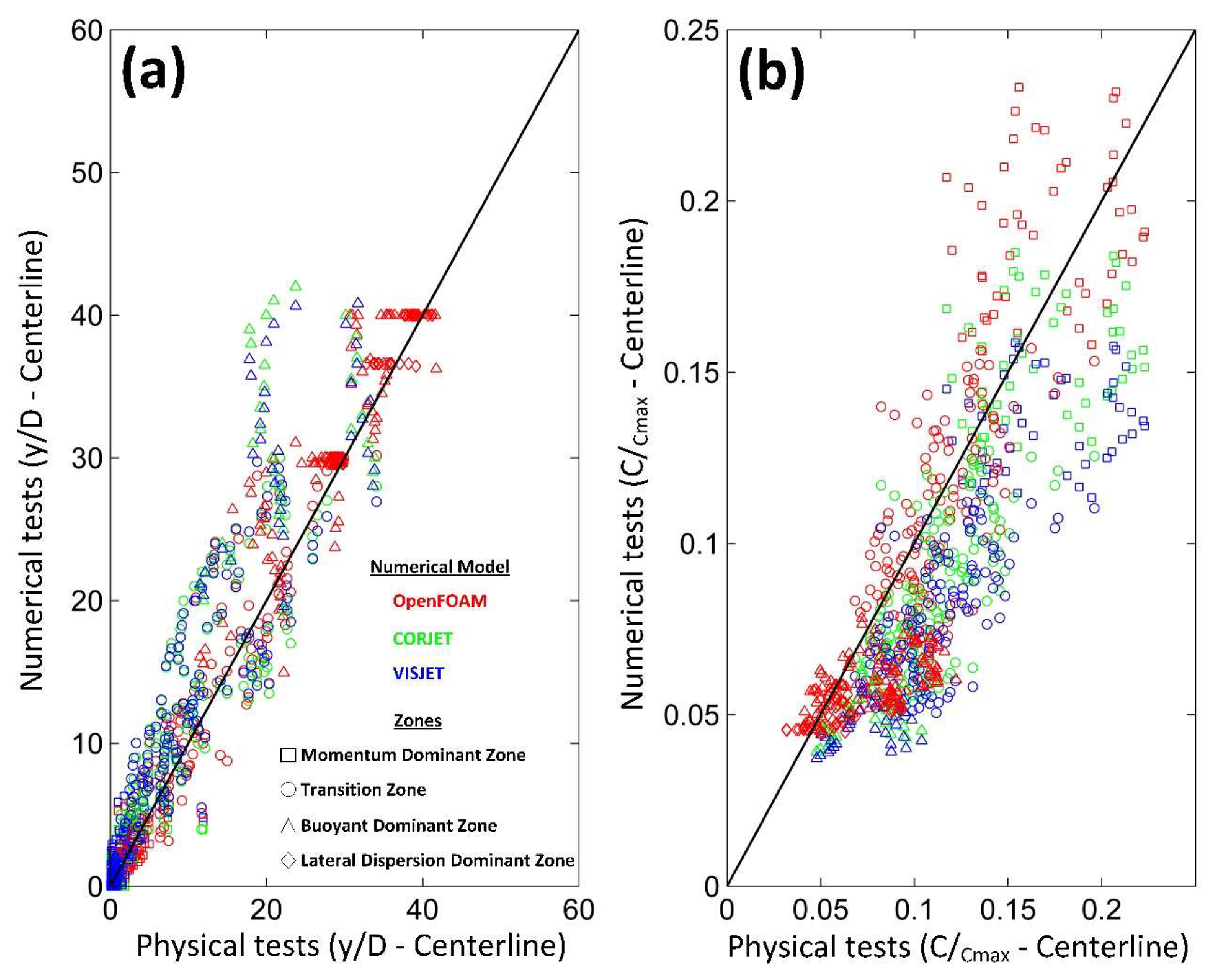
3.2.2. Performance of Numerical Models
3.3. Zonation of Positively Buoyant Jets
4. Discussion
4.1. Physycal Modelling
4.2. Numerical Modelling
4.3. Zonation of Positively Buoyant Jets
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roose, P.; Brinkman, U.A.T. Monitoring Organic Microcontaminants in the Marine Environment: Principles, Programmes and Progress. TrAC Trends Anal. Chem. 2005, 24, 897–926. [Google Scholar] [CrossRef]
- Bárcena, J.F.; Claramunt, I.; García-Alba, J.; Pérez, M.L.; García, A. A Method to Assess the Evolution and Recovery of Heavy Metal Pollution in Estuarine Sediments: Past History, Present Situation and Future Perspectives. Mar. Pollut. Bull. 2017, 124, 421–434. [Google Scholar] [CrossRef] [PubMed]
- Demchenko, N.; He, C.; Rao, Y.R.; Valipour, R. Surface River Plume in a Large Lake under Wind Forcing: Observations and Laboratory Experiments. J. Hydrol. 2017, 553, 1–12. [Google Scholar] [CrossRef]
- Bárcena, J.F.; Gómez, A.G.; García, A.; Álvarez, C.; Juanes, J.A. Quantifying and Mapping the Vulnerability of Estuaries to Point-Source Pollution Using a Multi-Metric Assessment: The Estuarine Vulnerability Index (EVI). Ecol. Indic. 2017, 76, 159–169. [Google Scholar] [CrossRef]
- García, J.; Álvarez, C.; García, A.; Revilla, J.; Juanes, J. Study of a Thermal Brine Discharge Using a 3D Model. In Environmental Hydraulics, Two Volume Set; CRC Press: London, UK, 2010; Volume 1, pp. 553–558. [Google Scholar] [CrossRef]
- Cushman-Roisin, B.; Gačić, M.; Poulain, P.-M.; Artegiani, A. Physical Oceanography of the Adriatic Sea; Springer: Dordrecht, The Netherlands, 2001. [Google Scholar] [CrossRef]
- Koh, R.C.Y.; Brooks, N.H. Fluid Mechanics of Waste-Water Disposal in the Ocean. Annu. Rev. Fluid Mech. 1975, 7, 187–211. [Google Scholar] [CrossRef] [Green Version]
- Ungate, C.D.; Harleman, D.R.F.; Jirka, G.H. Stability and Mixing of Submerged Turbulent Jets at Low Reynolds Numbers; MIT Energy Lab: Cambridge, UK, 1975; Available online: https://dspace.mit.edu/handle/1721.1/27517 (accessed on 23 January 2020).
- Fischer, H.B. Mixing in Inland and Coastal Waters; Academic Press: San Diego, CA, USA, 1979. [Google Scholar] [CrossRef]
- Wallace, R.B.; Wright, S.J. Spreading Layer of Two-Dimensional Buoyant Jet. J. Hydraul. Eng. 1984, 110, 813–828. [Google Scholar] [CrossRef]
- Jirka, G.H.; Domeker, R.L. Hydrodynamic Classification of Submerged Single-Port Discharges. J. Hydraul. Eng. 1991, 117, 1095–1112. [Google Scholar] [CrossRef]
- Lee, J.H.W.; Cheung, V. Generalized Lagrangian Model for Buoyant Jets in Current. J. Environ. Eng. 1990, 116, 1085–1106. [Google Scholar] [CrossRef]
- Akar, P.J.; Jirka, G.H. Buoyant Spreading Processes in Pollutant Transport and Mixing Part 1: Lateral Spreading with Ambient Current Advection. J. Hydraul. Res. 1994, 32, 815–831. [Google Scholar] [CrossRef]
- Alba, J.G.; Gómez, A.G.; del Barrio Fernández, P.; Gómez, A.G.; Álvarez Díaz, C. Hydrodynamic Modelling of a Regulated Mediterranean Coastal Lagoon, the Albufera of Valencia (Spain). J. Hydroinform. 2014, 16, 1062–1076. [Google Scholar] [CrossRef] [Green Version]
- Bárcena, J.F.; García-Alba, J.; García, A.; Álvarez, C. Analysis of Stratification Patterns in River-Influenced Mesotidal and Macrotidal Estuaries Using 3D Hydrodynamic Modelling and K-Means Clustering. Estuar. Coast. Shelf Sci. 2016, 181, 1–13. [Google Scholar] [CrossRef]
- Gogineni, S.; Goss, L.; Roquemore, M. Manipulation of a Jet in a Cross Flow. Exp. Therm. Fluid Sci. 1998, 16, 209–219. [Google Scholar] [CrossRef]
- Pantzlaff, L.; Lueptow, R.M. Transient Positively and Negatively Buoyant Turbulent Round Jets. Exp. Fluids 1999, 27, 117–125. [Google Scholar] [CrossRef]
- Li, C.-T.; Chang, K.-C.; Wang, M.-R. PIV Measurements of Turbulent Flow in Planar Mixing Layer. Exp. Therm. Fluid Sci. 2009, 33, 527–537. [Google Scholar] [CrossRef]
- Wen, Q.; Kim, H.D.; Liu, Y.Z.; Kim, K.C. Dynamic Structures of a Submerged Jet Interacting with a Free Surface. Exp. Therm. Fluid Sci. 2014, 57, 396–406. [Google Scholar] [CrossRef]
- González-Espinosa, A.; Buchmann, N.; Lozano, A.; Soria, J. Time-Resolved Stereo PIV Measurements in the Far-Field of a Turbulent Zero-Net-Mass-Flux Jet. Exp. Therm. Fluid Sci. 2014, 57, 111–120. [Google Scholar] [CrossRef]
- Tian, X.; Roberts, P.J.W.; Daviero, G.J. Marine Wastewater Discharges from Multiport Diffusers. I: Unstratified Stationary Water. J. Hydraul. Eng. 2004, 130, 1137–1146. [Google Scholar] [CrossRef]
- Tian, X.; Roberts, P.J.W.; Daviero, G.J. Marine Wastewater Discharges from Multiport Diffusers. II: Unstratified Flowing Water. J. Hydraul. Eng. 2004, 130, 1147–1155. [Google Scholar] [CrossRef]
- Daviero, G.J.; Roberts, P.J. Marine Wastewater Discharges from Multiport Diffusers. III: Stratified Stationary Water. J. Hydraul. Eng. 2006, 132, 404–410. [Google Scholar] [CrossRef]
- Tian, X.; Roberts, P.J.; Daviero, G.J. Marine Wastewater Discharges from Multiport Diffusers. IV: Stratified Flowing Water. J. Hydraul. Eng. 2006, 132, 411–419. [Google Scholar] [CrossRef]
- Kikkert, G.A.; Davidson, M.J.; Nokes, R.I. Buoyant Jets with Three-Dimensional Trajectories. J. Hydraul. Res. 2010, 48, 292–301. [Google Scholar] [CrossRef]
- Kawanabe, H.; Kondo, C.; Kohori, S.; Shioji, M. Simultaneous Measurements of Velocity and Scalar Fields in a Turbulent Jet Using PIV and LIF. J. Environ. Eng. 2010, 5, 231–239. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Chen, J. Experimental Study of Stratified Jet by Simultaneous Measurements of Velocity and Density Fields. Exp. Fluids 2012, 53, 145–162. [Google Scholar] [CrossRef]
- Grafsrønningen, S.; Jensen, A. Simultaneous PIV/LIF Measurements of a Transitional Buoyant Plume above a Horizontal Cylinder. Int. J. Heat Mass Transf. 2012, 55, 4195–4206. [Google Scholar] [CrossRef]
- Siddiqui, M.I.; Munir, S.; Heikal, M.R.; de Sercey, G.; Aziz, A.R.A.; Dass, S.C. Simultaneous Velocity Measurements and the Coupling Effect of the Liquid and Gas Phases in Slug Flow Using PIV–LIF Technique. J. Vis. 2016, 19, 103–114. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Wing-Keung Law, A. Second-Order Integral Model for a Round Turbulent Buoyant Jet. J. Fluid Mech. 2002, 459, 397–428. [Google Scholar] [CrossRef]
- Tang, H.S.; Paik, J.; Sotiropoulos, F.; Khangaonkar, T. Three-Dimensional Numerical Modeling of Initial Mixing of Thermal Discharges at Real-Life Configurations. J. Hydraul. Eng. 2008, 134, 1210–1224. [Google Scholar] [CrossRef] [Green Version]
- García Alba, J. Estudio de Chorros Turbulentos Con Modelos Cfd: Aplicación En El Diseño de Emisarios Submarinos; Universidad de Cantabria: Santander, Spain, 2011. [Google Scholar]
- Doneker, R.L.; Jirka, G.H. Expert Systems for Mixing-Zone Analysis and Design of Pollutant Discharges. J. Water Resour. Plan. Manag. 1991, 117, 679–697. [Google Scholar] [CrossRef]
- Lee, J.H.W.; Cheung, V.W.L. Inclined Plane Buoyant Jet in Stratified Fluid. J. Hydraul. Eng. 1986, 112, 580–589. [Google Scholar] [CrossRef]
- Roberts, P.J.W.; Snyder, W.H.; Baumgartner, D.J. Ocean Outfalls. I: Submerged Wastefield Formation. J. Hydraul. Eng. 1989, 115, 1–25. [Google Scholar] [CrossRef]
- Roberts, P.J.W.; Snyder, W.H.; Baumgartner, D.J. Ocean Outfalls. II: Spatial Evolution of Submerged Wastefield. J. Hydraul. Eng. 1989, 115, 26–48. [Google Scholar] [CrossRef]
- Roberts, P.J.W.; Snyder, W.H.; Baumgartner, D.J. Ocean Outfalls. III: Effect of Diffuser Design on Submerged Wastefield. J. Hydraul. Eng. 1989, 115, 49–70. [Google Scholar] [CrossRef]
- Palomar, P.; Lara, J.L.; Losada, I.J.; Rodrigo, M.; Alvárez, A. Near Field Brine Discharge Modelling Part 1: Analysis of Commercial Tools. Desalination 2012, 290, 14–27. [Google Scholar] [CrossRef]
- Crimaldi, J.P. Planar Laser Induced Fluorescence in Aqueous Flows. Exp. Fluids 2008, 44, 851–863. [Google Scholar] [CrossRef]
- Martin, J.E.; García, M.H. Combined PIV/PLIF Measurements of a Steady Density Current Front. Exp. Fluids 2009, 46, 265–276. [Google Scholar] [CrossRef]
- Liao, Q.; Cowen, E.A. Relative Dispersion of a Scalar Plume in a Turbulent Boundary Layer. J. Fluid Mech. 2010, 661, 412–445. [Google Scholar] [CrossRef]
- Pérez-Díaz, B.; Palomar, P.; Castanedo, S.; Álvarez, A. PIV-PLIF Characterization of Nonconfined Saline Density Currents under Different Flow Conditions. J. Hydraul. Eng. 2018, 144, 04018063. [Google Scholar] [CrossRef]
- Willert, C. The Fully Digital Evaluation of Photographic PIV Recordings. Appl. Sci. Res. 1996, 56, 79–102. [Google Scholar] [CrossRef]
- Sarpkaya, T. Vorticity, Free Surface, and Surfactants. Annu. Rev. Fluid Mech. 1996, 28, 83–128. [Google Scholar] [CrossRef]
- Ferrier, A.J.; Funk, D.R.; Roberts, P.J.W. Application of Optical Techniques to the Study of Plumes in Stratified Fluids. Dyn. Atmos. Ocean. 1993, 20, 155–183. [Google Scholar] [CrossRef]
- UNESCO. The International Thermodynamic Equation of Seawater-2010: Calculation and Use of Thermodynamic Properties Intergovernmental Oceanographic Commission; UNESCO: Paris, France, 2015; Available online: https://unesdoc.unesco.org/ark:/48223/pf0000193020 (accessed on 4 February 2020).
- Jirka, G.H. Integral Model for Turbulent Buoyant Jets in Unbounded Stratified Flows. Part I: Single Round Jet. Environ. Fluid Mech. 2004, 4, 1–56. [Google Scholar] [CrossRef]
- Jirka, G.H. Integral Model for Turbulent Buoyant Jets in Unbounded Stratified Flows Part 2: Plane Jet Dynamics Resulting from Multiport Diffuser Jets. Environ. Fluid Mech. 2006, 6, 43–100. [Google Scholar] [CrossRef]
- Jirka, G.H. Buoyant Surface Discharges into Water Bodies. II: Jet Integral Model. J. Hydraul. Eng. 2007, 133, 1021–1036. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Realistic Wave Generation and Active Wave Absorption for Navier–Stokes Models. Coast. Eng. 2013, 71, 102–118. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- García Alba, J.; Gómez, A.G.; Tinoco López, R.O.; Sámano Celorio, M.L.; García Gómez, A.; Juanes, J.A. A 3-D Model to Analyze Environmental Effects of Dredging Operations—Application to the Port of Marin, Spain. Adv. Geosci. 2014, 39, 95–99. [Google Scholar] [CrossRef] [Green Version]
- Gómez, A.G.; García Alba, J.; Puente, A.; Juanes, J.A. Environmental Risk Assessment of Dredging Processes—Application to Marin Harbour (NW Spain). Adv. Geosci. 2014, 39, 101–106. [Google Scholar] [CrossRef] [Green Version]
- García-Alba, J.; Bárcena, J.F.; Ugarteburu, C.; García, A. Artificial Neural Networks as Emulators of Process-Based Models to Analyse Bathing Water Quality in Estuaries. Water Res. 2019, 150, 283–295. [Google Scholar] [CrossRef]
- Zapata, C.; Puente, A.; García, A.; García-Alba, J.; Espinoza, J. The Use of Hydrodynamic Models in the Determination of the Chart Datum Shape in a Tropical Estuary. Water 2019, 11, 902. [Google Scholar] [CrossRef] [Green Version]
- Servat, E.; Dezetter, A. Selection of Calibration Objective Fonctions in the Context of Rainfall-Ronoff Modelling in a Sudanese Savannah Area. Hydrol. Sci. J. 1991, 36, 307–330. [Google Scholar] [CrossRef]
- Sobey, R.J.; Johnston, A.J.; Keane, R.D. Horizontal Round Buoyant Jet in Shallow Water. J. Hydraul. Eng. 1988, 114, 910–929. [Google Scholar] [CrossRef]
- Kida, S.; Takaoka, M.; Hussain, F. Collision of Two Vortex Rings. J. Fluid Mech. 1991, 230, 583–646. [Google Scholar] [CrossRef]
| Test | Sa (psu) | Ta (°C) | ρa (kg/m3) | So (psu) | To (°C) | ρo (kg/m3) | Qo (m3/s) | H (m) | Re (-) | Fr (-) |
|---|---|---|---|---|---|---|---|---|---|---|
| V1 | 0.28 | 21.5 | 998.10 | 0.25 | 50 | 988.25 | 0.81 | 0.210 | 3390 | 31.27 |
| V2 | 0.28 | 21.9 | 998.00 | 0.25 | 55 | 985.96 | 0.75 | 0.210 | 3132 | 26.18 |
| V3 | 0.28 | 22.1 | 997.96 | 0.20 | 55 | 985.96 | 0.68 | 0.150 | 2840 | 23.78 |
| V4 | 0.28 | 22.7 | 997.82 | 0.20 | 50 | 985.96 | 0.66 | 0.158 | 2756 | 23.21 |
| Parameter | Numerical Model | Metrics | |||
|---|---|---|---|---|---|
| R2 | RMSE (y/D or C/Cmax) | NRMSE (%) | CE | ||
| y/D - Centerline | CORJET | 0.88 | 3.94 | 11.93 | 0.78 |
| VISJET | 0.88 | 3.87 | 11.54 | 0.79 | |
| OpenFOAM | 0.98 | 1.84 | 4.62 | 0.98 | |
| C/Cmax - Centerline | CORJET | 0.71 | 0.03 | 16.00 | 0.45 |
| VISJET | 0.61 | 0.04 | 20.65 | 0.37 | |
| OpenFOAM | 0.81 | 0.02 | 12.03 | 0.64 | |
| Physical Test | Data Type | x/D | ||
|---|---|---|---|---|
| Limit 1 | Limit 2 | Limit 3 | ||
| V1 | Experimental | 41.5 | 90.0 | 103.9 |
| OpenFOAM | 43.0 | 92.0 | 107.9 | |
| CORJET | 34.0 | 83.3 | * | |
| VISJET | 34.3 | 85.3 | * | |
| V2 | Experimental | 29.0 | 65.0 | 91.0 |
| OpenFOAM | 28.8 | 66.5 | 88.2 | |
| CORJET | 27.0 | 72.9 | * | |
| VISJET | 27.8 | 71.6 | * | |
| V3 | Experimental | 31.8 | 65.0 | 82.5 |
| OpenFOAM | 32.0 | 65.0 | 82.3 | |
| CORJET | 28.0 | 63.0 | * | |
| VISJET | 25.0 | 64.0 | * | |
| V4 | Experimental | 32.5 | 69.0 | 90.3 |
| OpenFOAM | 33.0 | 70.0 | 91.8 | |
| CORJET | 28.0 | 65.0 | * | |
| VISJET | 27.0 | 65.0 | * | |
| Numerical Model | RMSE (x/D) | NRMSE (%) | ||||
|---|---|---|---|---|---|---|
| Limit 1 | Limit 2 | Limit 3 | Limit 1 | Limit 2 | Limit 3 | |
| OpenFOAM | 0.8 | 1.3 | 2.6 | 6.4 | 5.4 | 11.9 |
| CORJET | 4.9 | 5.7 | * | 39.0 | 22.6 | * |
| VISJET | 5.7 | 4.5 | * | 45.6 | 18.2 | * |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Alba, J.; Bárcena, J.F.; García, A. Zonation of Positively Buoyant Jets Interacting with the Water-Free Surface Quantified by Physical and Numerical Modelling. Water 2020, 12, 1324. https://doi.org/10.3390/w12051324
García-Alba J, Bárcena JF, García A. Zonation of Positively Buoyant Jets Interacting with the Water-Free Surface Quantified by Physical and Numerical Modelling. Water. 2020; 12(5):1324. https://doi.org/10.3390/w12051324
Chicago/Turabian StyleGarcía-Alba, Javier, Javier F. Bárcena, and Andrés García. 2020. "Zonation of Positively Buoyant Jets Interacting with the Water-Free Surface Quantified by Physical and Numerical Modelling" Water 12, no. 5: 1324. https://doi.org/10.3390/w12051324
APA StyleGarcía-Alba, J., Bárcena, J. F., & García, A. (2020). Zonation of Positively Buoyant Jets Interacting with the Water-Free Surface Quantified by Physical and Numerical Modelling. Water, 12(5), 1324. https://doi.org/10.3390/w12051324






