How to Account for the Human Motion to Improve Flood Risk Assessment in Urban Areas
Abstract
:1. Introduction
- Pre-emergency evacuation strategies cannot be implemented because of lack of early warnings or Civil Body Protection/First Responders management activities, thus making ineffective coordinated motor vehicles and public transport-based solutions (including, e.g., scenarios in underdeveloped countries);
- Flash flood conditions can exist;
- Flood-affected areas are pedestrian areas and/or the majority of the exposed population is placed outdoors, e.g., along the streets and the public squares;
- The motor vehicle evacuation cannot be performed because of specific conditions, e.g., (a) the urban space configuration (e.g., see compact urban fabric in historical scenarios); (b) critical effects in vehicle use along the evacuation roads, essentially due to vehicle-density related issues, such as traffic jams; (c) prevalence of pedestrian evacuees in respect to motorized ones (e.g., because of socio-economic factors, as for example, in underdeveloped countries);
- Distances to the evacuation areas (or the flood-affected area dimensions) are quite limited, such as in case of shelters in urban areas or “invacuation” strategies (According to PD 25111:2010, this evacuation solution concerns “the movement of people to pre-identified areas inside the building/site in order to protect them from external dangers during an incident”. In flood evacuation, building occupants can remain inside and move towards the higher stories, while individuals placed in the building surrounding try to reach the nearest one and then move upstairs), and they should be reached on foot;
- Disruption of the mobility system can appear as leading people to move on foot;
- The real emergency scenario is quite different from what is expected, thus affecting one of the previous elements;
- Some First Responders activities can imply the movement on foot to support the population in the emergency scenarios.
- Which are the risk-affecting factors in BE, by underlining the population-related contribute (Section 1.1);
- Which tools can be used to merge such two aspects to evaluate the effectiveness of the evacuation (Section 1.2);
- Which models can be used to evaluate man-floodwaters interactions in pedestrian evacuation (Section 1.3).
1.1. BE Risk-Affecting Factors and the Population-Related Contribute
- Location of settlement on floodplains;
- Land use-related issues, by including a lower capacity of absorbing rain by urban surfaces (e.g., low porosity of urban surfaces, especially in high-built up areas) in respect to the ones in rural areas;
- Compact urban areas layout which can increase open-channel related effects in floodwater spreading;
- Insufficient sewer systems, because, e.g., of poor maintenance plans and actions as well as of the variations in functioning conditions (e.g., severity of floods different from the one used in their design) also due to climate-change effects;
- Vulnerability of buildings, suffering damage because of a low resistance level in respect to floodwater strains (e.g., elevations, foundations);
- Low level of control of possible hazard conditions, also in relation to poor flood sensor systems; inadequate management of immediate pre-disaster and disaster conditions, with the possible lack of early warning systems, which can provoke a delay in emergency action starting.
- Emergency planning elements: poor awareness/preparedness levels of the population can bring people to adopt risky behaviors, underestimate the impact of disasters conditions, and delay the starting of safety procedures. Meanwhile, a similar result can be provoked by ineffective early warning systems. Emergency plans can be not well known by the population, hence making impossible to properly identify “safe” areas and gathering points, as well as evacuation paths;
- Surrounding BE elements: people generally try to move towards the nearest areas with lower floodwaters depth and speed (e.g., ground elevations), by looking for direct support of unmovable obstacles to move in floodwaters (e.g., fences, street furniture). Meanwhile, they try to modify their motion direction to avoid all the obstacles dragged by the flood (e.g., cars, debris);
- Other individuals and belongings: social share identity (including phenomena connected to information exchange) and attachment-to-things effects are time-wasting behaviors that can delay or slow down the evacuation process. Such elements can also bring people to move towards “unsafe” areas (e.g., to rescue other individuals, to retrieve some personal belongings, or to guard the properties). People can also prefer to move in a group by sharing evacuation direction and motion speed;
- Floodwaters: “curiosity” effects lead individuals to delay the evacuation starting to observe floodwaters conditions or event recording with smartphones or cameras. Meanwhile, when floodwaters depth and speed increase, the possibility to freely move is reduced and the evacuees’ motion process is slowed down, hence increasing the overall evacuation time.
1.2. Simulation Tools to Risk-Assessment and Risk-Mitigation Strategies Evaluation
1.3. Modelling Pedestrians’ Evacuation in Floodwater: Current Approaches and Limitations
2. Phases, Materials, and Methods
- General characterization of the selected database, according to Section 2.2 methods. The motion speeds in walking and running conditions are compared depending on D and on the individuals’ gender. In this way, it can be possible to respectively trace general relationships depending on floodwater-characterization constraints to motion and to individuals’ main features;
- Modelling of the speed variation (normalized speed and dimensional speed variations) depending on D and in respect of the dry surface motion, according to Section 2.3 methods. In particular, dry surface motion speeds are retrieved according to average literature values depending on the age [43]. The individuals’ height (i.e., the knee height from the ground) is considered in the model because of the related influence assessed by preliminary works on motion and human body stability conditions in floodwaters [9,44];
- Modelling of the normalized speed variation depending on D in respect to the minimum constraint and maximum excitement conditions for the considered database, according to methods in Section 2.4. Such model delves into specific experimental conditions and sample features, to generalize speed estimation data regardless of dry surface motion conditions data.
2.1. Materials: Original Input Database Characterization
2.2. General Methods for Model Definition and Characterization of the Selected Database
- Gender, to evaluate difference among the two excitement conditions and compare them with previous works outcomes (i.e., males generally moves faster than females) [43].
2.3. Methods for Speed Variation Modelling Depending on D and Dry Surface Motion Conditions
- Variation of the normalized speed v* in respect of D experimental classes: the distribution of v* in respect of D experimental classes takes advantages of boxplot analysis and graph to evidence if and how the input data are widespread and if outliers are present. Input data involve the whole sample and male (outlined by subscript M) and female (outlined by subscript F) separate samples to highlight the differences due to gender. In general terms, it is expected that running regression model should involve higher v* values, especially for lower D-related input data;
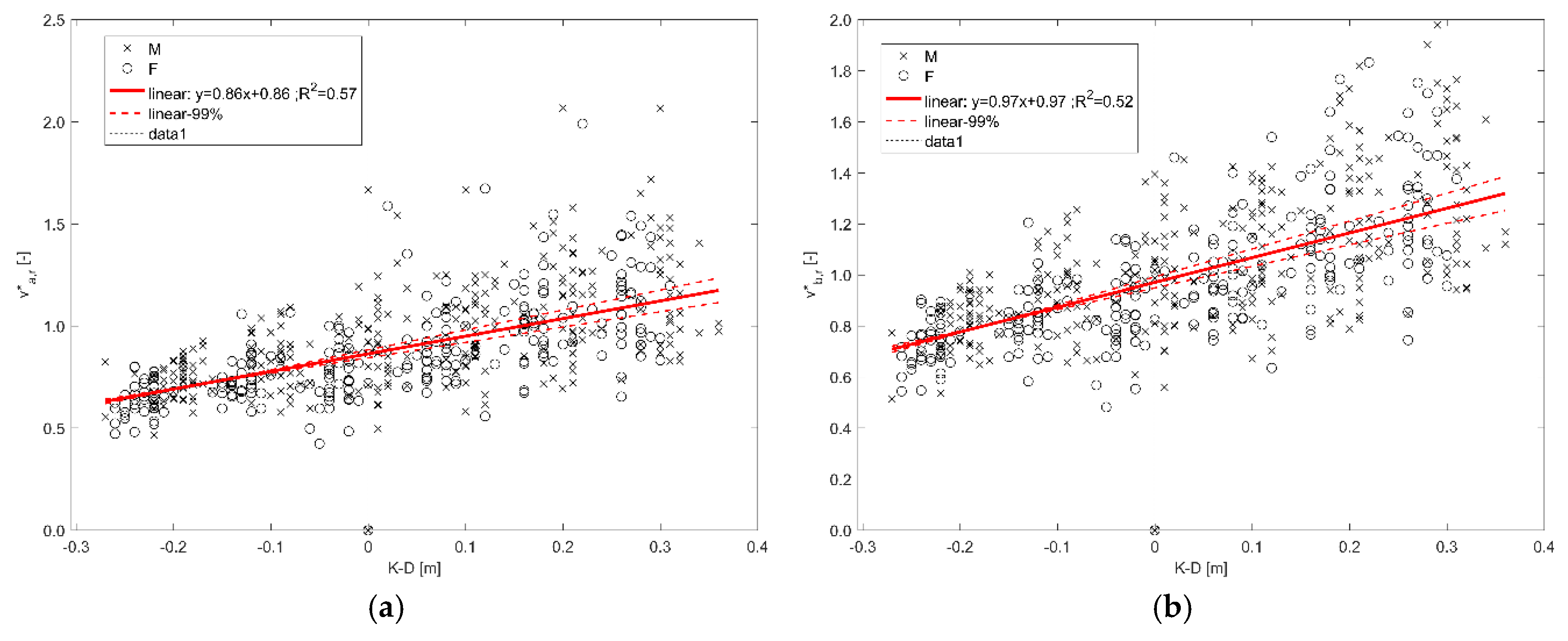
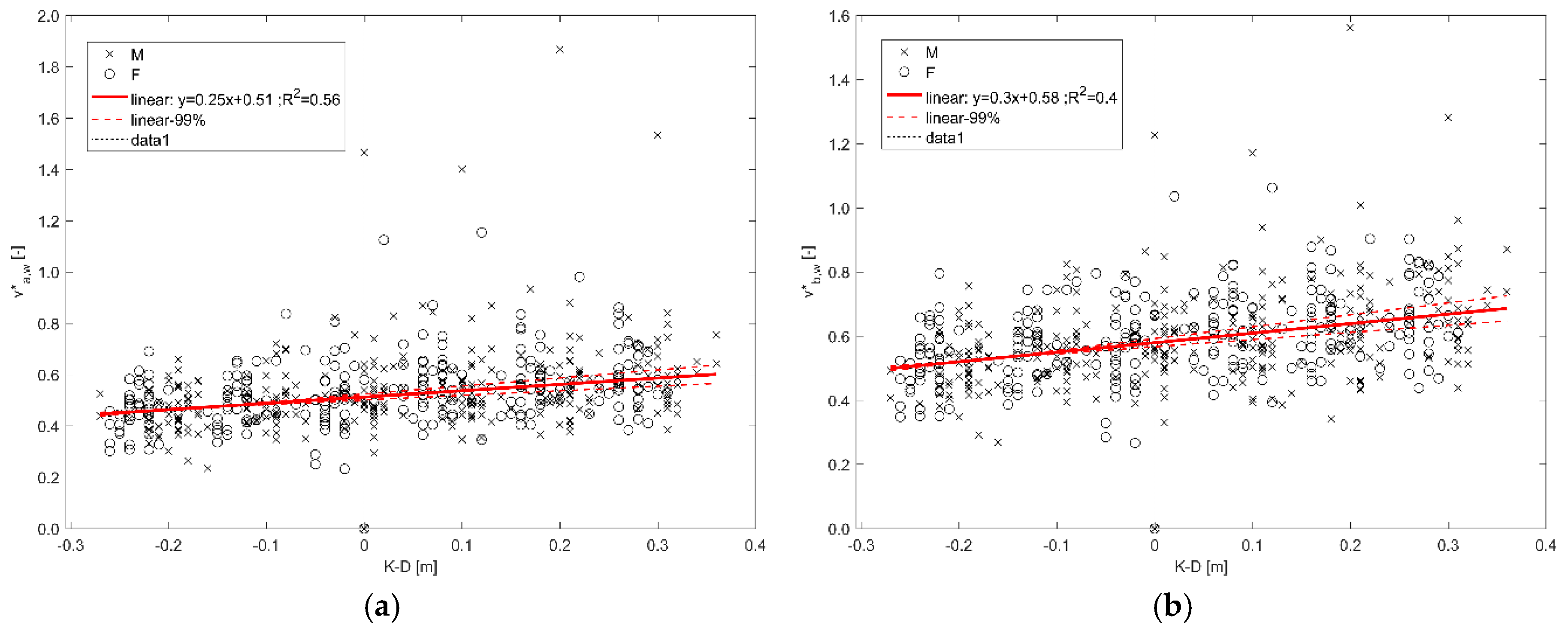
- Variation of the normalized speed v* in respect of K-D: linear regression models are tested. Such modelling approach allows detecting the effects of the reciprocal position of knee and floodwater levels. Male and female samples are shown in the regression model but considered together in the regression model to focus on the main factor influencing human behavior, which is the individuals’ height. It is expected that v* should be equal to or higher than 1 when the knee is placed outside the floodwaters, especially in running conditions.
2.4. Methods for Normalized Speed Variation Modelling Depending on D, Minimum Constraint, and Maximum Excitement Conditions for the Considered Database
3. Results
3.1. Characterization of the Selected Database
3.2. Speed Variation Modelling Depending on D and Dry Surface Motion Conditions
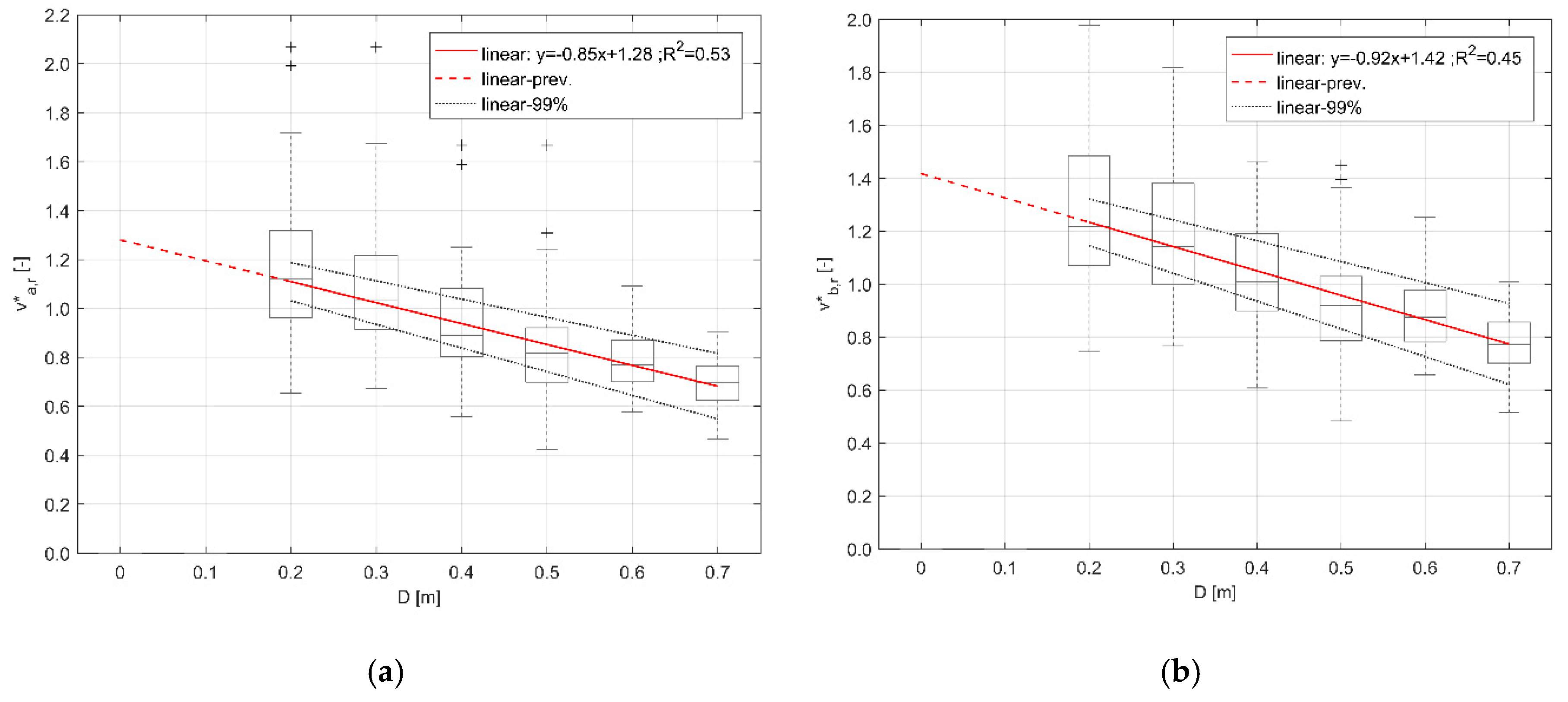
- Motion speed (and so v*) decreases while D increases. Regressions on the curve a-based model show a slighter regression slope, according to the first term in the regression equation (−8% for running conditions and −16% for walking conditions in respect to the curve a-based model). Hence, curve b-based models seem to amplify the v* reduction;
- The speed-D relationship in both the excitement conditions can be properly represented by using speed normalization. In particular, regressions on the curve a [46]-based model show a moderate relationship, according to the R2 value, for both walking and running conditions. R2 values for the curve b [43]-based model are lower than these, suggesting that this model more limitedly represents the effects of D in v* variation. Hence, the adoption of curve a-based model could improve the prediction model capabilities in evacuation simulators;
- In view of the above, differences between running and walking excitement conditions exist. In particular, the effects of D on the variation of speed in walking conditions seem to be less relevant than the ones of running conditions. This result is evidenced by the more significant presence of possible outliers (see Figure 6) and by the lower value of the first coefficient of the linear regression (about −70% in respect to running conditions model). This result confirms the original work outcomes [44] and the outcomes of studies concerning other evacuation typologies [47]. In fact, issues related to the individual’s motion effort and the distance between individual and motion goals seem to be more relevant while people are running towards the motion goal (as in evacuation conditions). In addition, it is worth noting that the assessed v* value in the dry surface for running conditions is about 2 times greater than the one for walking conditions, regardless of the adopted model. Besides, v* in running conditions seems to be equal to about 1 when D is about 0.3 to 0.5m, which corresponds to the D classes for which the individuals’ knee is generally closer to the floodwater level, according to Figure 2 statistics;
- Differences between dry surface motion in literature reference works [43,46] and the adopted database [44] exist (compare the second linear regression coefficient in all the models), by underlining how specific database should be adopted to represent the flood evacuation. Forecasted v* for D < 0.2 m are beyond the lower limit of the tested D conditions and so they could be affected by additional non-linear speed-D interferences [33]. Nevertheless, the importance of this result is shown by the v* values for the minimum tested constraint conditions (D = 0.2 m) in both walking and running conditions.
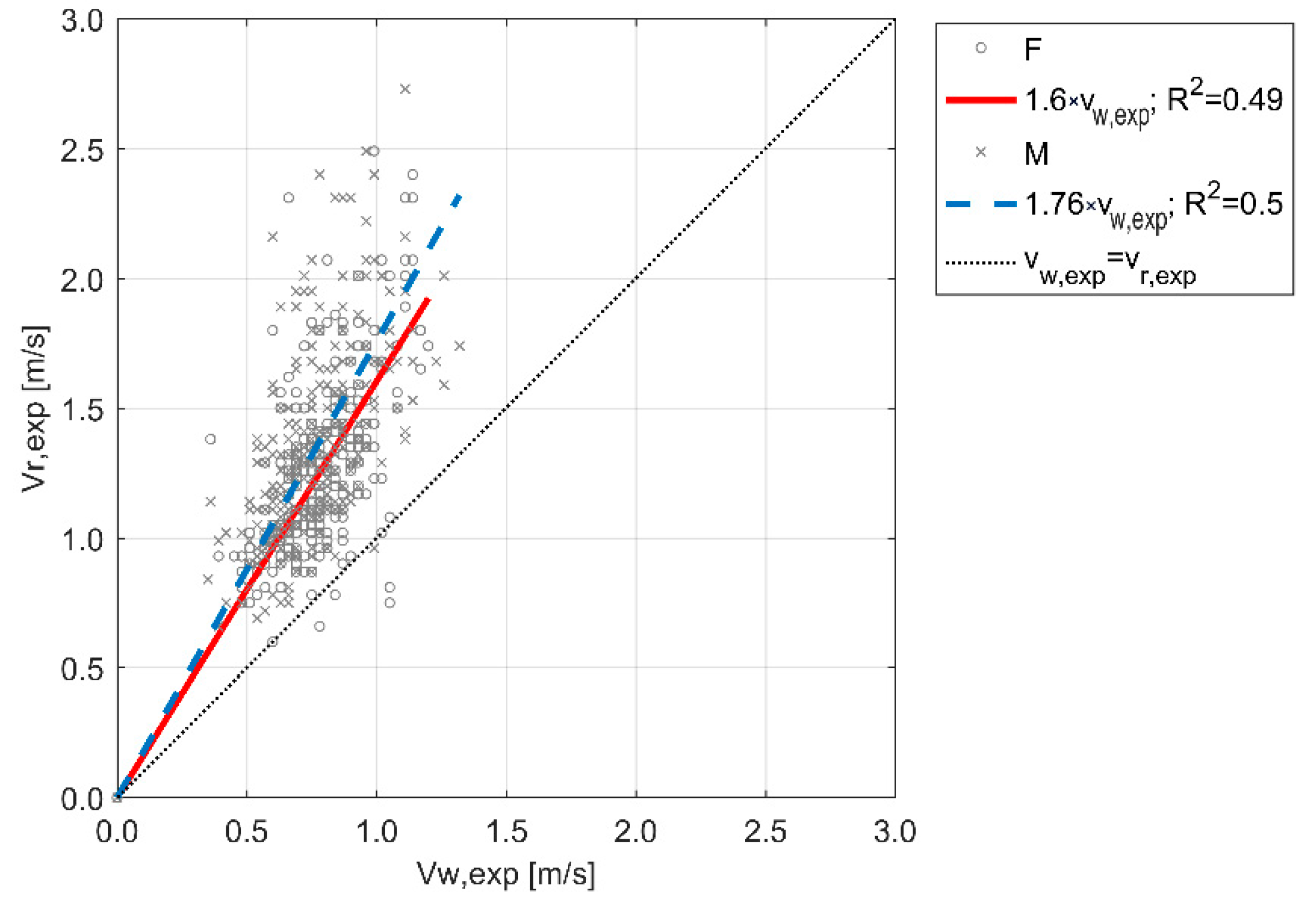
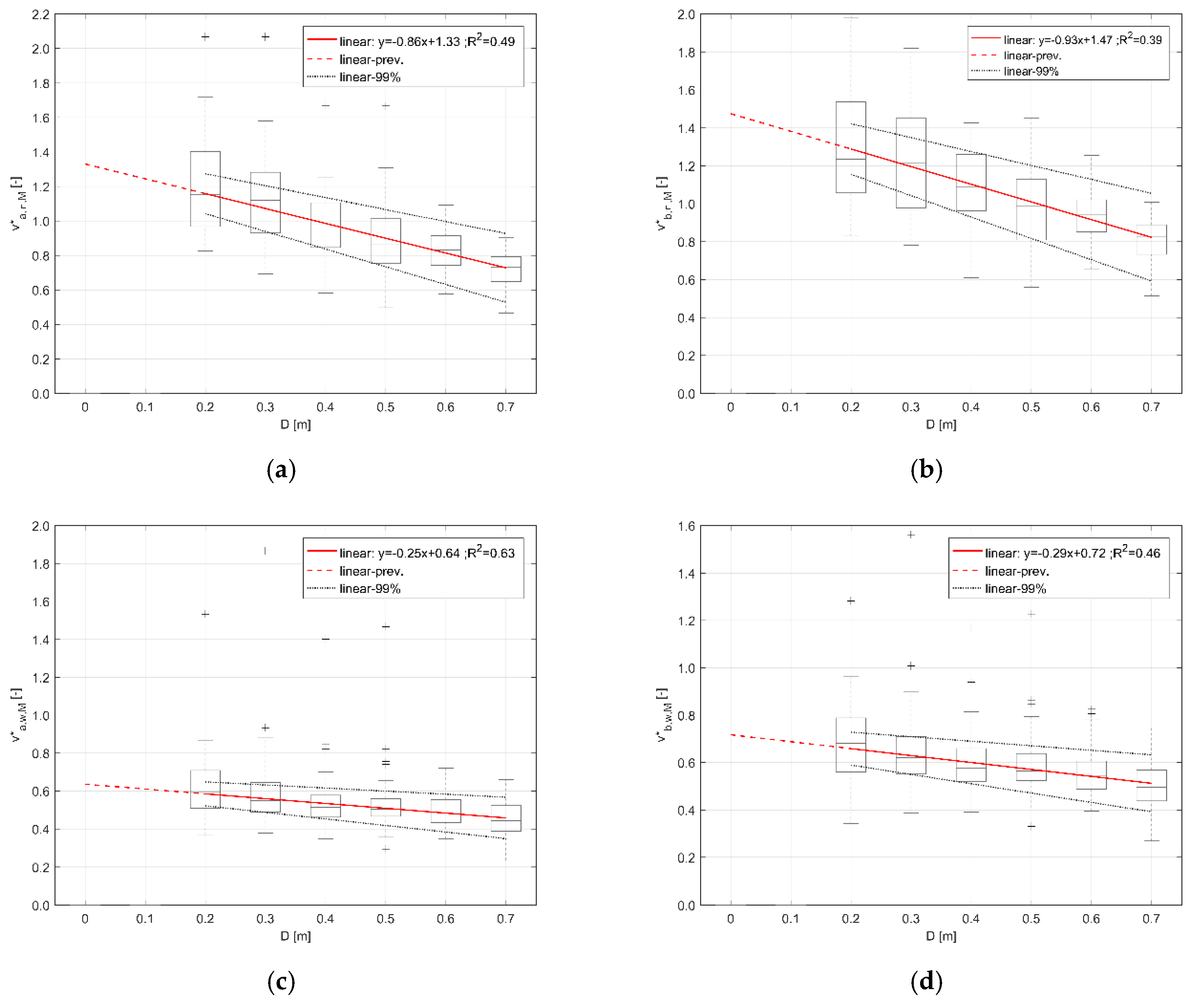
- Males seem to move faster than females in running conditions, confirming previous works outcomes [33,43] and Section 3.1 (i.e., compare with Figure 3) outcomes. This result is evidenced by the second linear regression coefficient in both the models (in curve a-based model: 1.33 for males versus 1.23 for females; in curve b-based model: 1.47 for males versus 1.36 for females). In particular, males seem to move +8% faster (in normalized terms) in dry surface conditions, in both models;
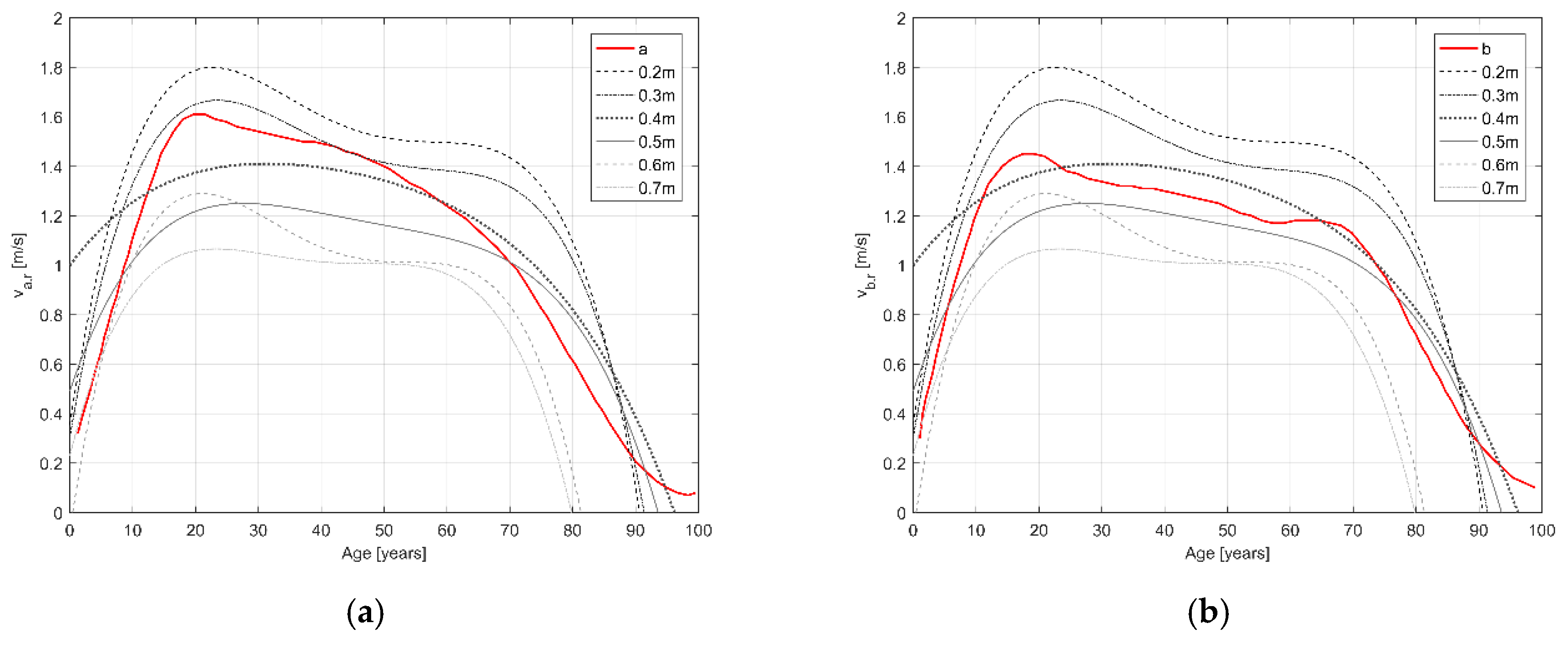
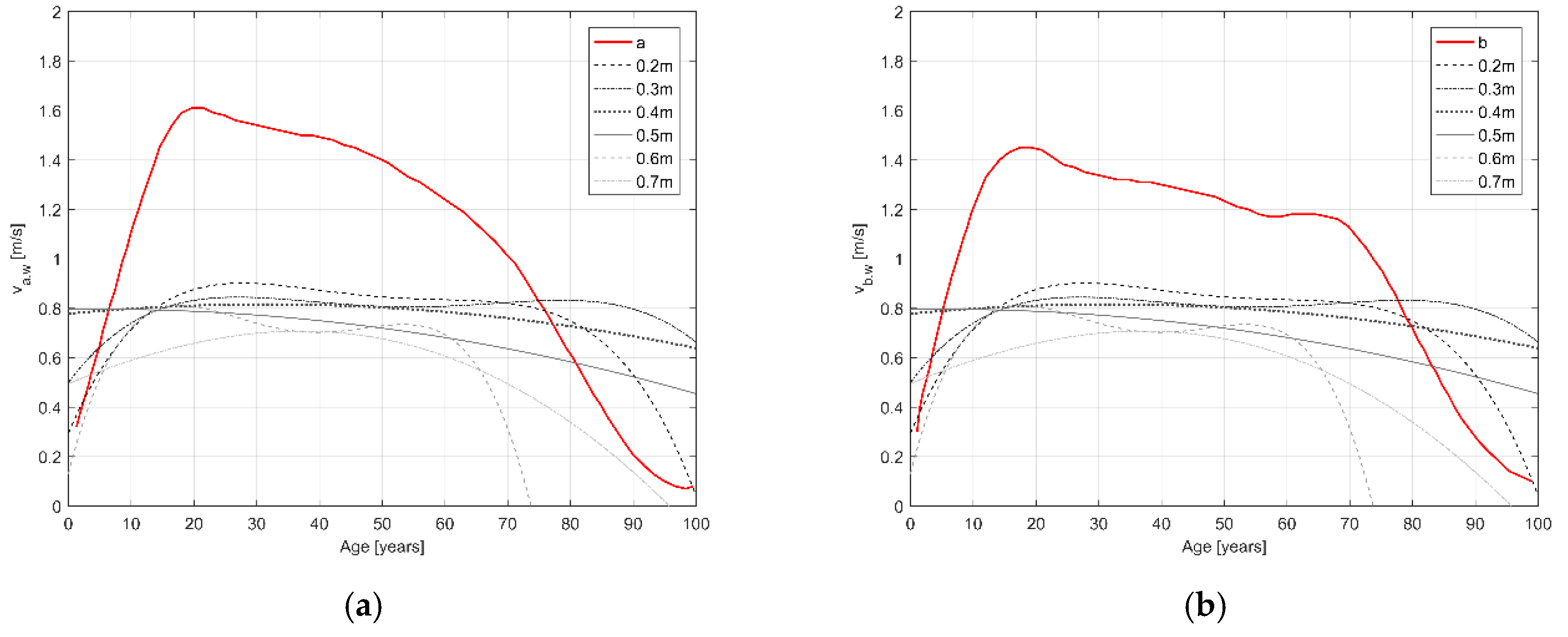
- Considering running conditions, the age-v regression for the overall sample is over the references curves when D ranges from 0.2 m to 0.4 m, regardless of the considered curve in the model; this result confirms the “average” results of Figure 9. Meanwhile, the regression curves on the maximum age-v pairs seem to be always over the reference curves or, at least, equal (i.e., if considering the curve b data);
- On the contrary, walking conditions-related regression on maximum age-v pairs are generally under the reference curves, with similar predicted values for the age range 10 to 30 years. This seems to evidence that younger individuals can generally be less affected in their motion by D conditions, confirming previous results on age-related impact on motion speed [42,43,44]. Average age-v pairs regression in walking speeds seems to evidence no substantial differences, especially for intermediate ranges, confirming the interpretation of outcomes in Figure 6 and Figure 10.
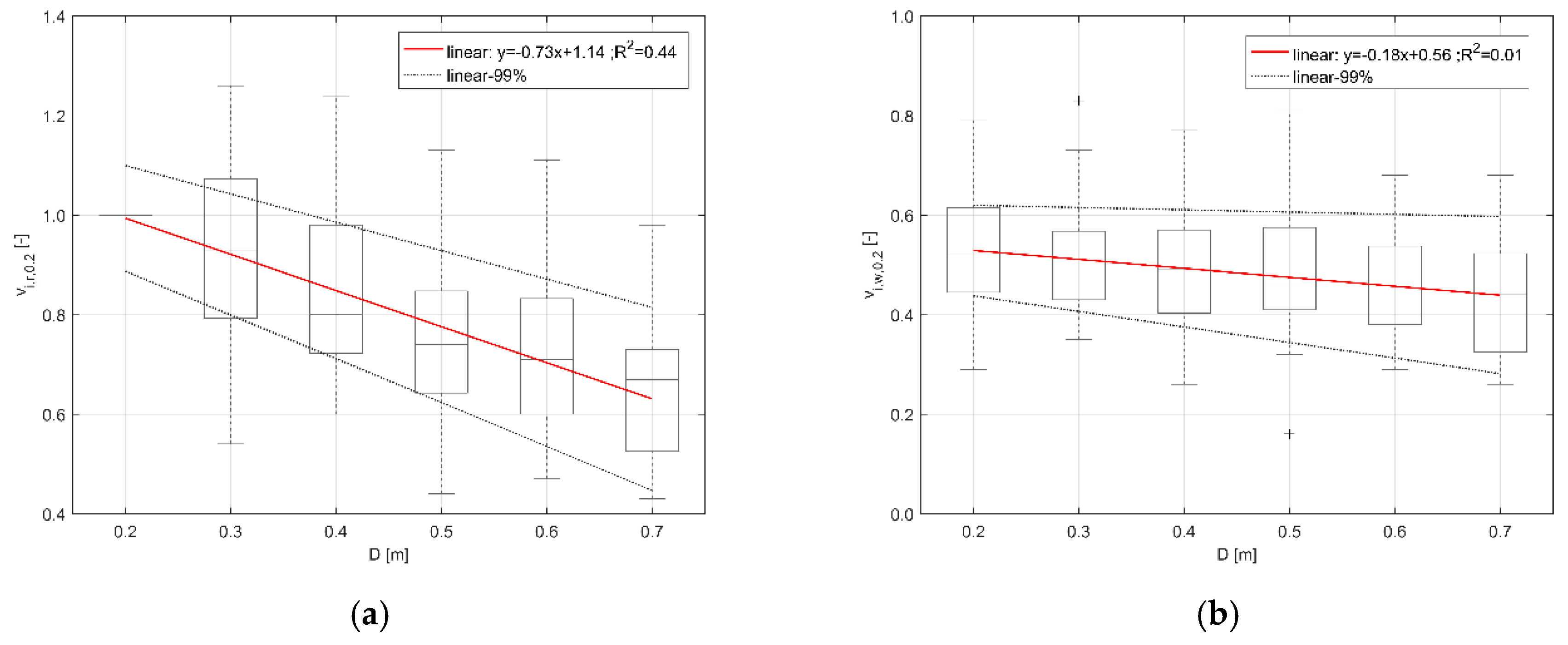
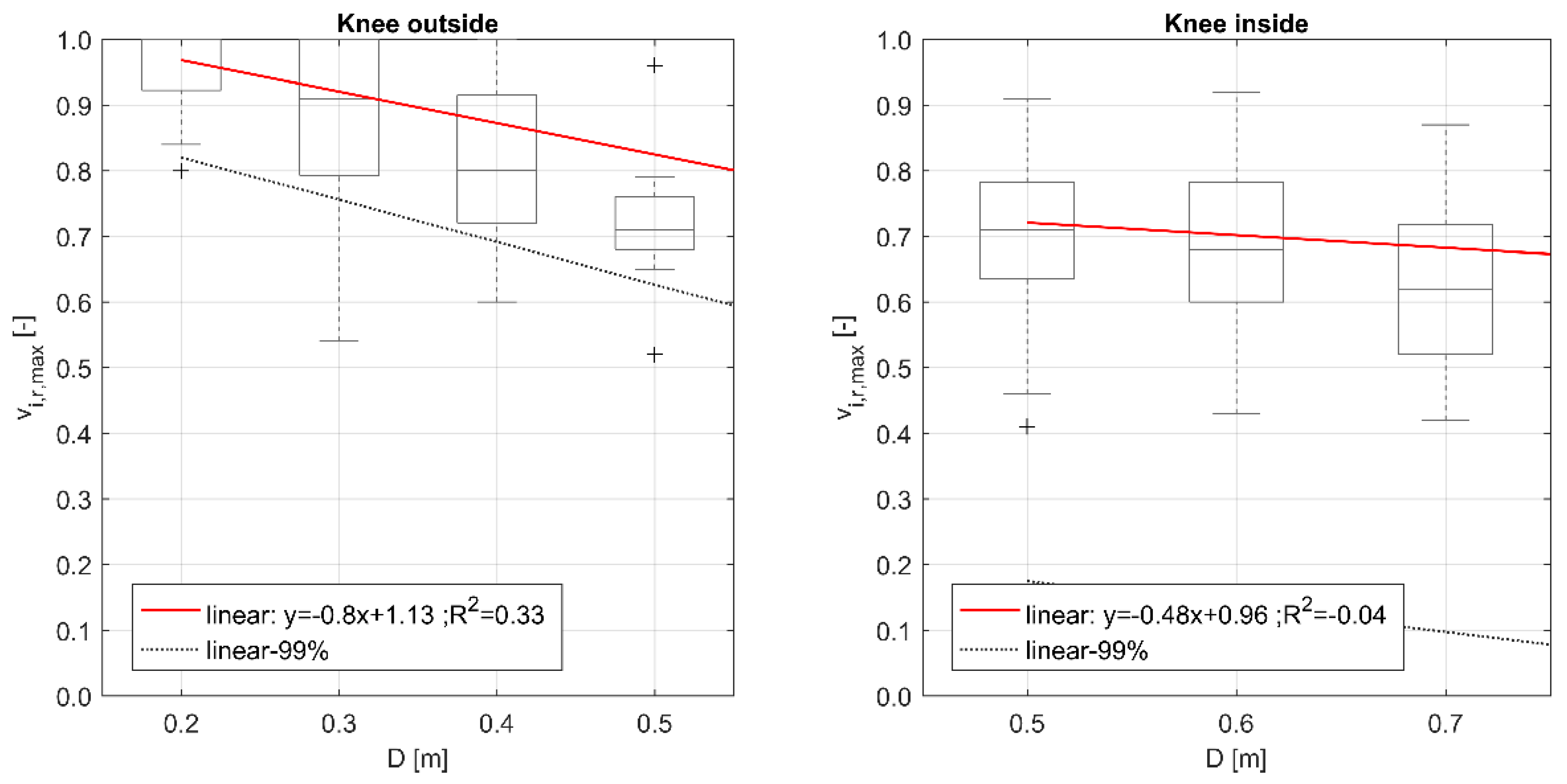
3.3. Normalized Speed Variation Modelling Depending on D, Minimum Constraint, and Maximum Excitement Conditions for the Considered Database
- The effect of D on an individual’s speed is higher while the pedestrian is moving with the knee outside of the floodwater level, especially in running conditions as shown for the sub-sample with the knee inside the floodwater by: (a) the lower R2 value, (b) the wider range for boundary conditions (99%) regression lines, and (c) the lower first regression coefficient value (only for running conditions of Figure 16).
4. Results Discussion in View of Model Implementation in Flood Evacuation Simulators
- Effects due to the presence of other pedestrians: crowd-density effects could reduce the speeds in compact groups; social shared identity factors could lead people to share the same direction and to adjust their individual speeds to remain in group (e.g., waiting for more vulnerable and slow group members);
- Guidance and support elements: they can speed up the process by giving continuous support to the evacuee in terms of direction to be followed and in terms of physical aid (e.g., handrails along the paths);
- Other flood-related phenomena like the attraction towards unmovable obstacles, according to the aforementioned support needs of the evacuees.
- Input running conditions used in this study are similar to the one of excited individual, who, for instance, participate to an evacuation process with a high engagement level (e.g., because of rising floodwater levels or other hazard-increasing evacuation drivers perceived by the individuals);
- Input walking conditions used in this study are similar to the one of normal motion individual, who for instance, participate in an evacuation process in still waters, or under organized circumstances.
- Dimensional models, which are the ones in which the dependent variables are directly expressed in dimensional terms (i.e., the dependent variable is a speed (m/s) (Table 1). These models allow tracing the simplest solutions to predict motion speed in flood evacuation according to a microscopic approach, by directly retrieving evacuation speed values in dimensional terms (m/s) only according to a single motion driver [41,43];
- Normalized models, which are the ones in which the dependent variables are a non-dimensional parameter vnorm (-) (Table 2). To calculate the effective motion speed, vnorm should be multiplied by the isolated individuals’ speed, which can be the one in (a) minimum constraint-maximum excitement conditions in the tested database (vr,0.2) or (b) dry surface motion (vid). Although the validity of the model application can be extended to different isolated pedestrians’ speed databases, the use of reference curves by this work for models development is encouraged especially in the second aforementioned case (i.e., [46], and so to vid,a, due to the higher statistical significance of results).
5. Conclusions and Future Research Remarks
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Paquier, A.; Mignot, E.; Bazin, P.-H. From Hydraulic Modelling to Urban Flood Risk. Procedia Eng. 2015, 115, 37–44. [Google Scholar] [CrossRef]
- Kontokosta, C.E.; Malik, A. The Resilience to Emergencies and Disasters Index: Applying big data to benchmark and validate neighborhood resilience capacity. Sustainable Cities Soc. 2018, 36, 272–285. [Google Scholar] [CrossRef]
- Chen, K.F.; Leandro, J. A Conceptual Time-Varying Flood Resilience Index for Urban Areas: Munich City. Water 2019, 11, 830. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, K.; Peden, A.E.; Pearson, M.; Hagger, M.S. Stop there’s water on the road! Identifying key beliefs guiding people’s willingness to drive through flooded waterways. Saf. Sci. 2016, 89, 308–314. [Google Scholar] [CrossRef] [Green Version]
- Jamrussri, S.; Toda, Y. Available Flood Evacuation Time for High-Risk Areas in the Middle Reach of Chao Phraya River Basin. Water 2018, 10, 1871. [Google Scholar] [CrossRef] [Green Version]
- Chanson, H.; Brown, R.; McIntosh, D. Human body stability in floodwaters: The 2011 flood in Brisbane CBD. In Proceedings of the Hydraulic Structures and Society—Engineering Challenges and Extremes: Proceedings of the 5th IAHR International Symposium on Hydraulic Structures (ISHS2014), Brisbane, Australia, 25–27 June 2014; The University of Queensland: Australia; pp. 1–9. [Google Scholar]
- Xia, J.; Falconer, R.A.; Lin, B.; Tan, G. Numerical assessment of flood hazard risk to people and vehicles in flash floods. Environ. Modell. Softw. 2011, 26, 987–998. [Google Scholar] [CrossRef]
- Milanesi, L.; Pilotti, M.; Ranzi, R. A conceptual model of people’s vulnerability to floods. Water Resour. Res. 2015, 51, 182–197. [Google Scholar] [CrossRef]
- Cox, R.J.; Shand, T.D.; Blacka, M.J. Australian Rainfall and Runoff Revision Project 10: Appropriate Safety Criteria for People; Engineers Australia—Water Engineering: Barton, ATC, Australia, 2010; ISBN 9780858259454. Available online: http://arr.ga.gov.au/__data/assets/pdf_file/0006/40578/ARR_Project_10_Stage1_report_Final.pdf (accessed on 4 May 2020).
- Bernardini, G.; Camilli, S.; Quagliarini, E.; D’Orazio, M. Flooding risk in existing urban environment: From human behavioral patterns to a microscopic simulation model. Energy Procedia 2017, 134, 131–140. [Google Scholar] [CrossRef]
- Hu, P.; Zhang, Q.; Shi, P.; Chen, B.; Fang, J. Flood-induced mortality across the globe: Spatiotemporal pattern and influencing factors. Sci. Total Environ. 2018, 643, 171–182. [Google Scholar] [CrossRef]
- Confederation of Fire Protection Associations Europe. European Guideline—CFPA-E No 1:2012 N Protection against Flood Damage; CFPA Europe: Copehangen, Denmark, 2012; Available online: http://www.cfpa-e.eu/wp-content/uploads/files/guidelines/CFPA_E_Guideline_No_1_2012_N.pdf (accessed on 4 May 2020).
- Arrighi, C.; Pregnolato, M.; Dawson, R.J.; Castelli, F. Preparedness against mobility disruption by floods. Sci. Total Environ. 2019, 654, 1010–1022. [Google Scholar] [CrossRef]
- Melo, R.; Zêzere, J.L.; Oliveira, S.C.; Garcia, R.A.C.; Oliveira, S.; Pereira, S.; Piedade, A.; Santos, P.P.; van Asch, T.W.J. Defining evacuation travel times and safety areas in a debris flow hazard scenario. Sci. Total Environ. 2020, 712, 136452. [Google Scholar] [CrossRef] [PubMed]
- Wood, N.; Jones, J.; Peters, J.; Richards, K. Pedestrian evacuation modeling to reduce vehicle use for distant tsunami evacuations in Hawai‘i. Int. J. Disaster Risk Reduction 2018, 28, 271–283. [Google Scholar] [CrossRef]
- Lin, J.; Zhu, R.; Li, N.; Becerik-Gerber, B. How occupants respond to building emergencies: A systematic review of behavioral characteristics and behavioral theories. Saf. Sci. 2020, 122, 104540. [Google Scholar] [CrossRef]
- Takagi, H.; Li, S.; de Leon, M.; Esteban, M.; Mikami, T.; Matsumaru, R.; Shibayama, T.; Nakamura, R. Storm surge and evacuation in urban areas during the peak of a storm. Coastal Eng. 2016, 108, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Kolen, B.; van Gelder, P.H.A.J.M. Risk-Based Decision-Making for Evacuation in Case of Imminent Threat of Flooding. Water 2018, 10, 1429. [Google Scholar] [CrossRef] [Green Version]
- Kawasaki, A.; Kawamura, G.; Zin, W.W. A local level relationship between floods and poverty: A case in Myanmar. Int. J. Disaster Risk Reduction 2020, 42, 101348. [Google Scholar] [CrossRef]
- Fan, Q.; Tian, Z.; Wang, W. Study on Risk Assessment and Early Warning of Flood-Affected Areas when a Dam Break Occurs in a Mountain River. Water 2018, 10, 1369. [Google Scholar] [CrossRef] [Green Version]
- Bernardini, G.; Postacchini, M.; Quagliarini, E.; Brocchini, M.; Cianca, C.; D’Orazio, M. A preliminary combined simulation tool for the risk assessment of pedestrians’ flood-induced evacuation. Environ. Modell. Softw. 2017, 96, 14–29. [Google Scholar] [CrossRef]
- Ishigaki, T.; Toda, K.; Baba, Y.; Inoue, K.; Nakagawa, H.; Yoshida, Y.; Tagawa, H. Experimental study on evacuation from underground space by using real size models. Proc. Hydraul. Eng. 2006, 50, 583–588. [Google Scholar] [CrossRef]
- Wu, J.; Ye, M.; Wang, X.; Koks, E. Building Asset Value Mapping in Support of Flood Risk Assessments: A Case Study of Shanghai, China. Sustainability 2019, 11, 971. [Google Scholar] [CrossRef] [Green Version]
- Morelli, S.; Segoni, S.; Manzo, G.; Ermini, L.; Catani, F. Urban planning, flood risk and public policy: The case of the Arno River, Firenze, Italy. Appl. Geogr. 2012, 34, 205–218. [Google Scholar] [CrossRef]
- Milman, A.; Warner, B.P. The interfaces of public and private adaptation: Lessons from flooding in the Deerfield River Watershed. Glob. Environ. Chang. 2016, 36, 46–55. [Google Scholar] [CrossRef]
- Hissel, F.; Morel, G.; Pescaroli, G.; Graaff, H.; Felts, D.; Pietrantoni, L. Early warning and mass evacuation in coastal cities. Coastal Eng. 2014, 87, 193–204. [Google Scholar] [CrossRef]
- Wang, Y. Advances in Remote Sensing of Flooding. Water 2015, 7, 6404–6410. [Google Scholar] [CrossRef]
- Bodoque, J.M.; Amérigo, M.; Díez-Herrero, A.; García, J.A.; Cortés, B.; Ballesteros-Cánovas, J.A.; Olcina, J. Improvement of resilience of urban areas by integrating social perception in flash-flood risk management. J. Hydrol. 2016. [Google Scholar] [CrossRef] [Green Version]
- Birkholz, S.; Muro, M.; Jeffrey, P.; Smith, H.M. Rethinking the relationship between flood risk perception and flood management. Sci. Total Environ. 2014, 478, 12–20. [Google Scholar] [CrossRef]
- Haer, T.; Botzen, W.J.W.; Aerts, J.C.J.H. The effectiveness of flood risk communication strategies and the influence of social networks—Insights from an agent-based model. Environ. Sci. Policy 2016, 60, 44–52. [Google Scholar] [CrossRef]
- Opper, S.; Cinque, P.; Davies, B. Timeline modelling of flood evacuation operations. Procedia Eng. 2010, 3, 175–187. [Google Scholar] [CrossRef] [Green Version]
- Jonkman, S.N.; Maaskant, B.; Boyd, E.; Levitan, M.L. Loss of life caused by the flooding of New Orleans after Hurricane Katrina: Analysis of the relationship between flood characteristics and mortality. Risk Anal. 2009, 29, 676–698. [Google Scholar] [CrossRef]
- Ishigaki, T.; Onishi, Y.; Asai, Y.; Toda, K.; Shimada, H. Evacuation criteria during urban flooding in underground space. In Proceedings of the 11th International Conference on Urban Drainage, Scotland, UK, 31 August–5 September 2008; p. 7. [Google Scholar]
- Matsuo, K.; Natainia, L.; Yamada, F. Flood and Evacuation Simulations for Urban Flooding. In Proceedings of the 5th International Conference on Flood Management, Tokyo, Japan, 27–29 September 2011; pp. 391–398. [Google Scholar]
- Veeraswamy, A.; Galea, E.R.; Filippidis, L.; Lawrence, P.J.; Haasanen, S.; Gazzard, R.J.; Smith, T.E.L. The simulation of urban-scale evacuation scenarios with application to the Swinley forest fire. Saf. Sci. 2018, 102, 178–193. [Google Scholar] [CrossRef]
- Zlateski, A.; Lucesoli, M.; Bernardini, G.; Ferreira, T.M. Integrating human behaviour and building vulnerability for the assessment and mitigation of seismic risk in historic centres: Proposal of a holistic human-centred simulation-based approach. Int. J. Disaster Risk Reduction 2020, 43, 101392. [Google Scholar] [CrossRef]
- Ronchi, E.; Uriz, F.N.; Criel, X.; Reilly, P. Modelling large-scale evacuation of music festivals. Case Stud. Fire Saf. 2015, 5, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Pant, P.; Yamashita, E. Integrating travel demand modeling and flood hazard risk analysis for evacuation and sheltering. Int. J. Disaster Risk Reduction 2018, 31, 1177–1186. [Google Scholar] [CrossRef]
- Lämmel, G.; Grether, D.; Nagel, K. The representation and implementation of time-dependent inundation in large-scale microscopic evacuation simulations. Transp. Res. Part C Emerg. Technol. 2010, 18, 84–98. [Google Scholar] [CrossRef] [Green Version]
- Bolia; Lakshay, N.B. Operating strategies of buses for mass evacuation. Saf. Sci. 2019, 111, 167–178. [Google Scholar] [CrossRef]
- Lakoba, T.I.; Kaup, D.J.; Finkelstein, N.M. Modifications of the Helbing-Molnar-Farkas-Vicsek Social Force Model for Pedestrian Evolution. Simulation 2005, 81, 339–352. [Google Scholar] [CrossRef]
- Lee, H.-K.; Hong, W.-H.; Lee, Y.-H. Experimental study on the influence of water depth on the evacuation speed of elderly people in flood conditions. Int. J. Disaster Risk Reduction 2019, 39, 101198. [Google Scholar] [CrossRef]
- Bosina, E.; Weidmann, U. Estimating pedestrian speed using aggregated literature data. Physica A: Stat. Mech. Its Appl. 2017, 468, 1–29. [Google Scholar] [CrossRef]
- Bernardini, G.; Quagliarini, E.; D’Orazio, M.; Brocchini, M. Towards the simulation of flood evacuation in urban scenarios: Experiments to estimate human motion speed in floodwaters. Saf. Sci. 2020, 123, 104563. [Google Scholar] [CrossRef]
- Herman, I.P. Physics of the Human Body. In Biological and Medical Physics, Biomedical Engineering; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-23930-9. [Google Scholar]
- Weidmann, U. Transporttechnik der Fußgänger—Transporttechnische Eigenschaften des Fussgängerverkehrs (Literaturauswertung); Zweite ergänzte Auflage. Schriftenreihe des IVT 90, Institut für Verkehrsplanung, Transporttechnik, Strassen-und Eisenbahnbau, ETH Zürich: Zürich, Switzerland, 1993. [Google Scholar] [CrossRef]
- Lu, X.; Yang, Z.; Cimellaro, G.P.; Xu, Z. Pedestrian evacuation simulation under the scenario with earthquake-induced falling debris. Saf. Sci. 2019, 114, 61–71. [Google Scholar] [CrossRef]
- Parisi, D.R.; Dorso, C.O. Microscopic dynamics of pedestrian evacuation. Phys. A Stat. Mech. Its Appl. 2005, 354, 606–618. [Google Scholar] [CrossRef]







| Independent Variables (unit of measure) | Dependent Variable (unit of measure) | Regression Model (sample) 1,2 | R2 1 | Specific Discussion |
|---|---|---|---|---|
| walking speed vw,exp (m/s); gender (F or M) | running speed vr,exp (m/s) | vr,exp = 1.6vw,exp (F) vr,exp = 1.76vw,exp (M) | ≈0.5 | Figure 3, Section 3.1 |
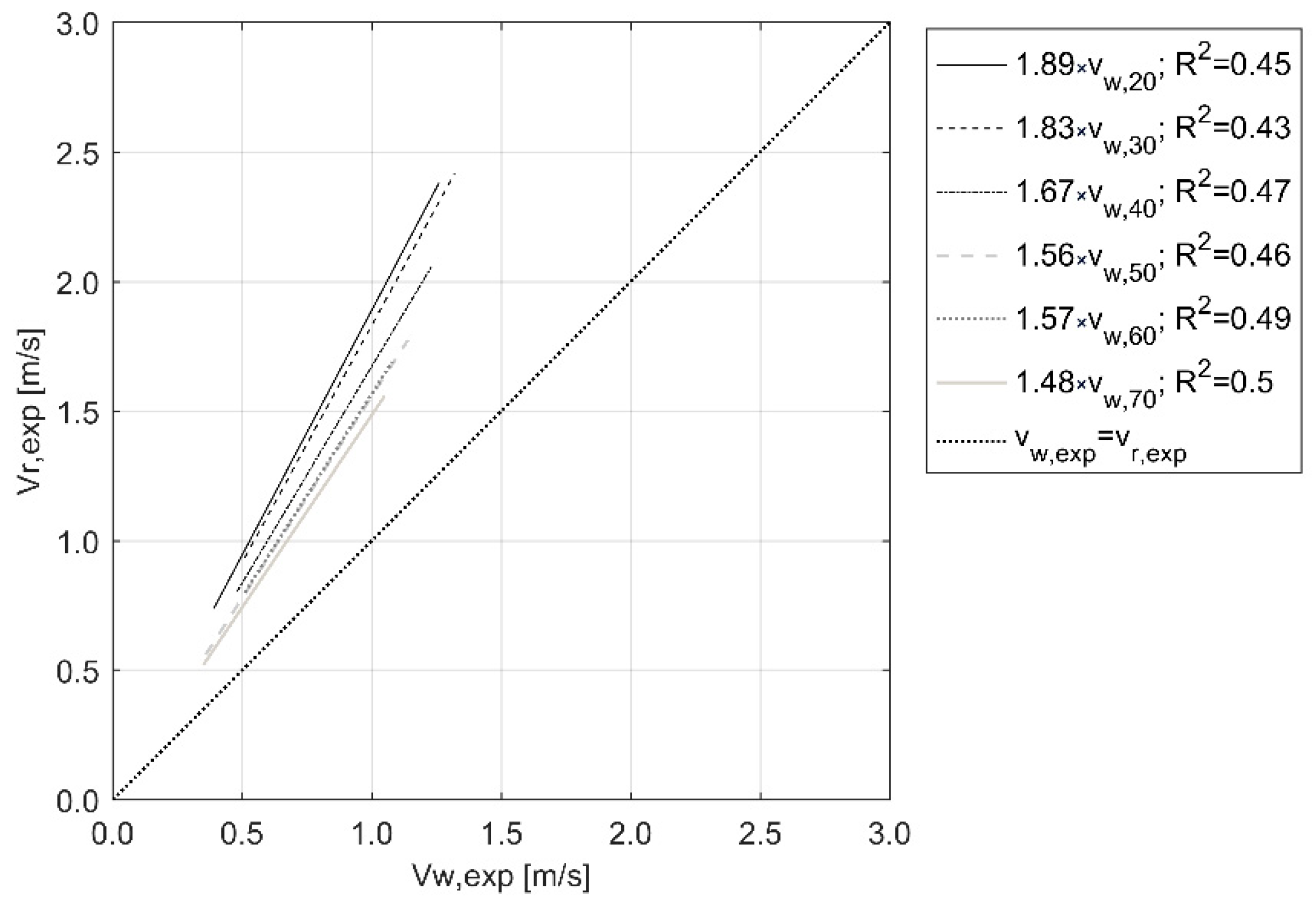
| walking speed vw,exp (m/s); floodwater depth D (m) | running speed vr,exp (m/s) | D = 0.2 m: vr,exp = 1.89vw,exp (A) D = 0.3 m: vr,exp = 1.83vw,exp (A) D = 0.4 m: vr,exp = 1.67vw,exp (A) D = 0.5 m, 0.6 m: vr,exp = 1.56vw,exp (A) D = 0.7 m: vr,exp = 1.48vw,exp (A) | ≈0.5 | Figure 4, Section 3.1 |
| age (years) | “maximum” running speed vr,exp (m/s) | 4th polynomial regression model graphically traced in Figure 13 | >0.7 | Figure 13, Section 3.2 |
| age (years) | “maximum” walking speed vr,exp (m/s) | 4th polynomial regression model graphically traced in Figure 14 | >0.7 | Figure 14, Section 3.2 |
| Independent Variables (Unit of Measure) | Dependent Variable (Unit of Measure) | vnorm Regression Model (Sample) 1,2 | R2 1 | Specific Discussion |
|---|---|---|---|---|
| floodwater depth D (m) | running speed vr (m/s) | vr = (−0.85D + 1.28)vid,a (A) | ≈0.5 | Figure 5a, Section 3.2 |
| floodwater depth D (m) | walking speed vw (m/s) | vw = (−0.25D + 0.64)vid,a (A) | ≈0.6 | Figure 6a, Section 3.2 |
| floodwater depth D (m); gender (F or M) | running speed vr (m/s) | vr = (−0.86D + 1.23)vid,a (F) vr = (−0.86D + 1.33)vid,a (F) | >0.5 | Figure 7a and Figure 8a, Section 3.2 |
| relative position between the knee height and the floodwater level K-D (m) | running speed vr (m/s) | vr = (−0.86D + 0.86)vid,a (A) | ≈0.6 | Figure 9a, Section 3.2 |
| relative position between the knee height and the floodwater level K-D (m) | walking speed vw (m/s) | vw = (−0.25D + 0.51)vid,a (A) | ≈0.6 | Figure 10a, Section 3.2 |
| floodwater depth D (m) | running speed 3 vr (m/s) | vr = (−0.73D + 1.14)vr,0.2 (A) | ≈0.4 | Figure 15a, Section 3.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernardini, G.; Quagliarini, E. How to Account for the Human Motion to Improve Flood Risk Assessment in Urban Areas. Water 2020, 12, 1316. https://doi.org/10.3390/w12051316
Bernardini G, Quagliarini E. How to Account for the Human Motion to Improve Flood Risk Assessment in Urban Areas. Water. 2020; 12(5):1316. https://doi.org/10.3390/w12051316
Chicago/Turabian StyleBernardini, Gabriele, and Enrico Quagliarini. 2020. "How to Account for the Human Motion to Improve Flood Risk Assessment in Urban Areas" Water 12, no. 5: 1316. https://doi.org/10.3390/w12051316





