Evaluation of Satellite-Derived Soil Moisture in Qinghai Province Based on Triple Collocation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Triple Collocation (TC) Method
2.2. Data Sources
2.3. Data Preprocessing
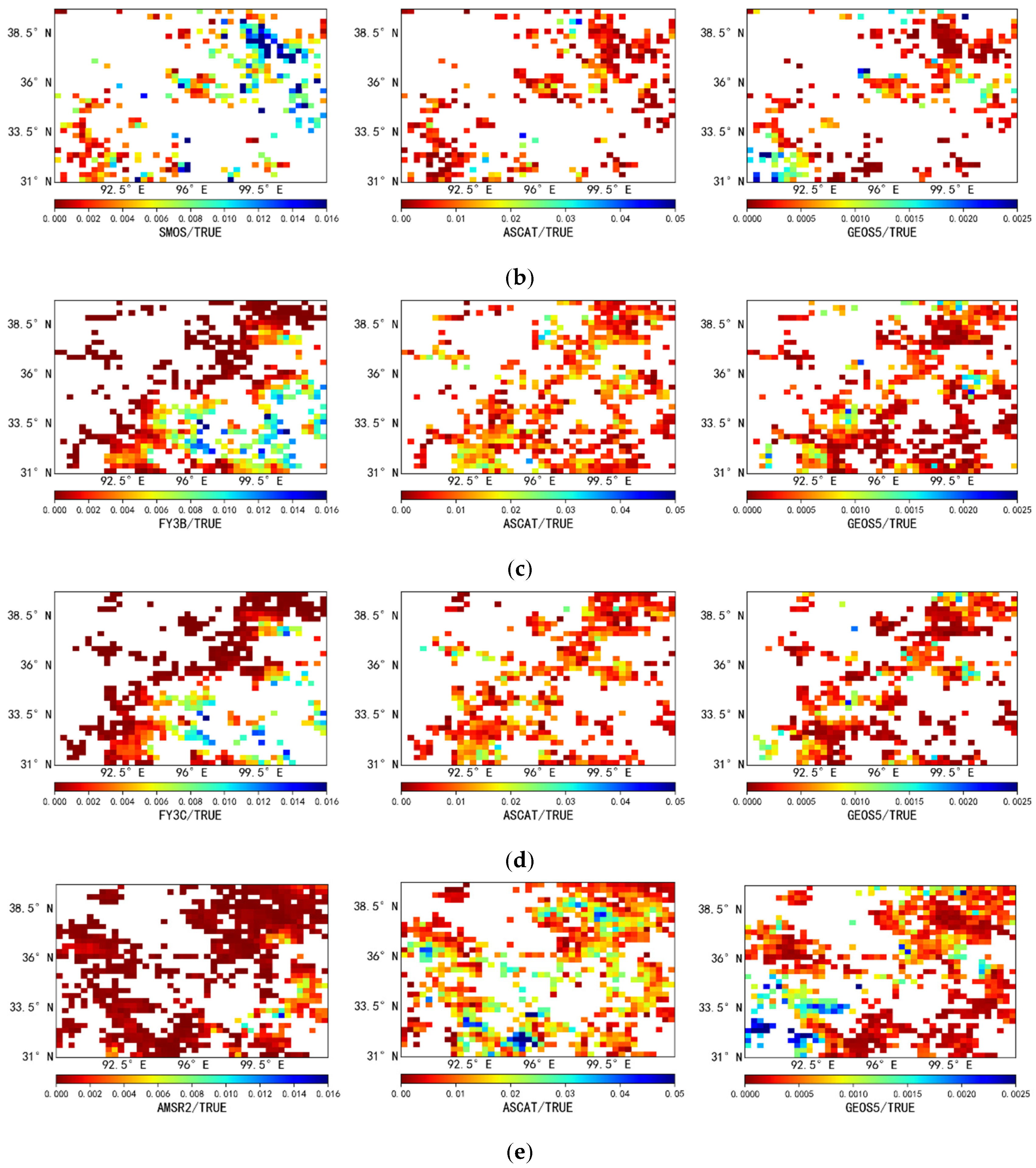
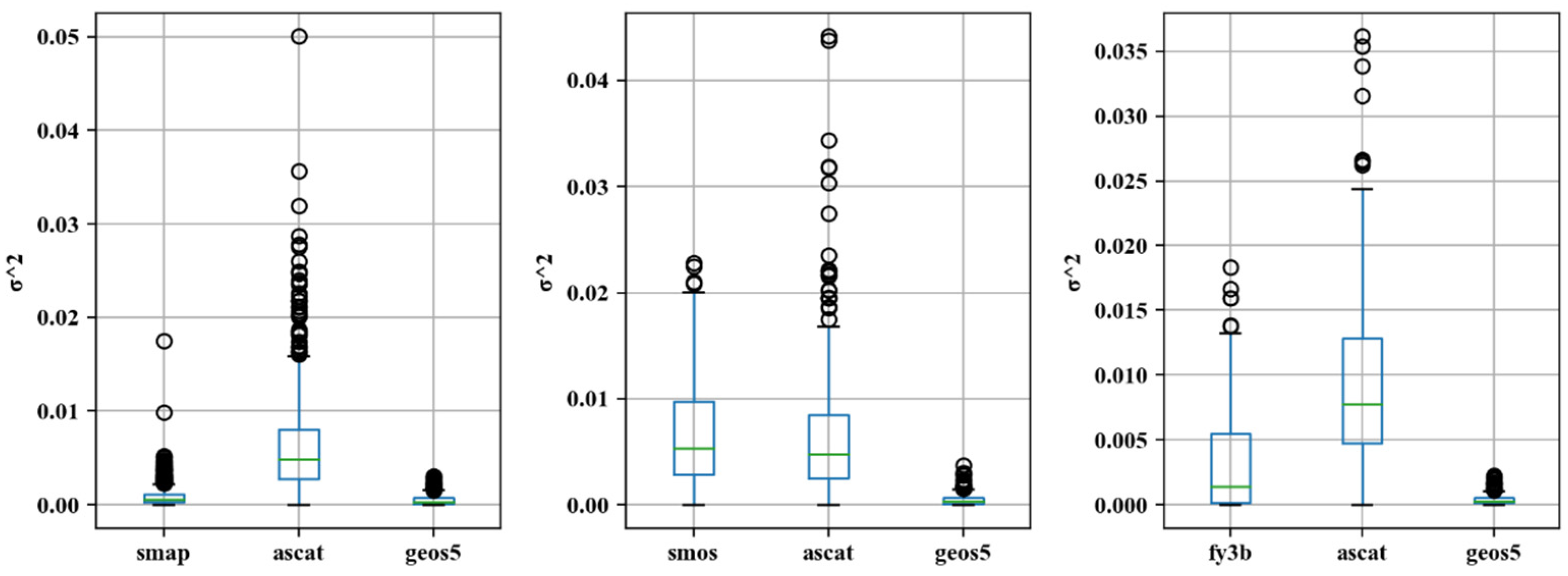
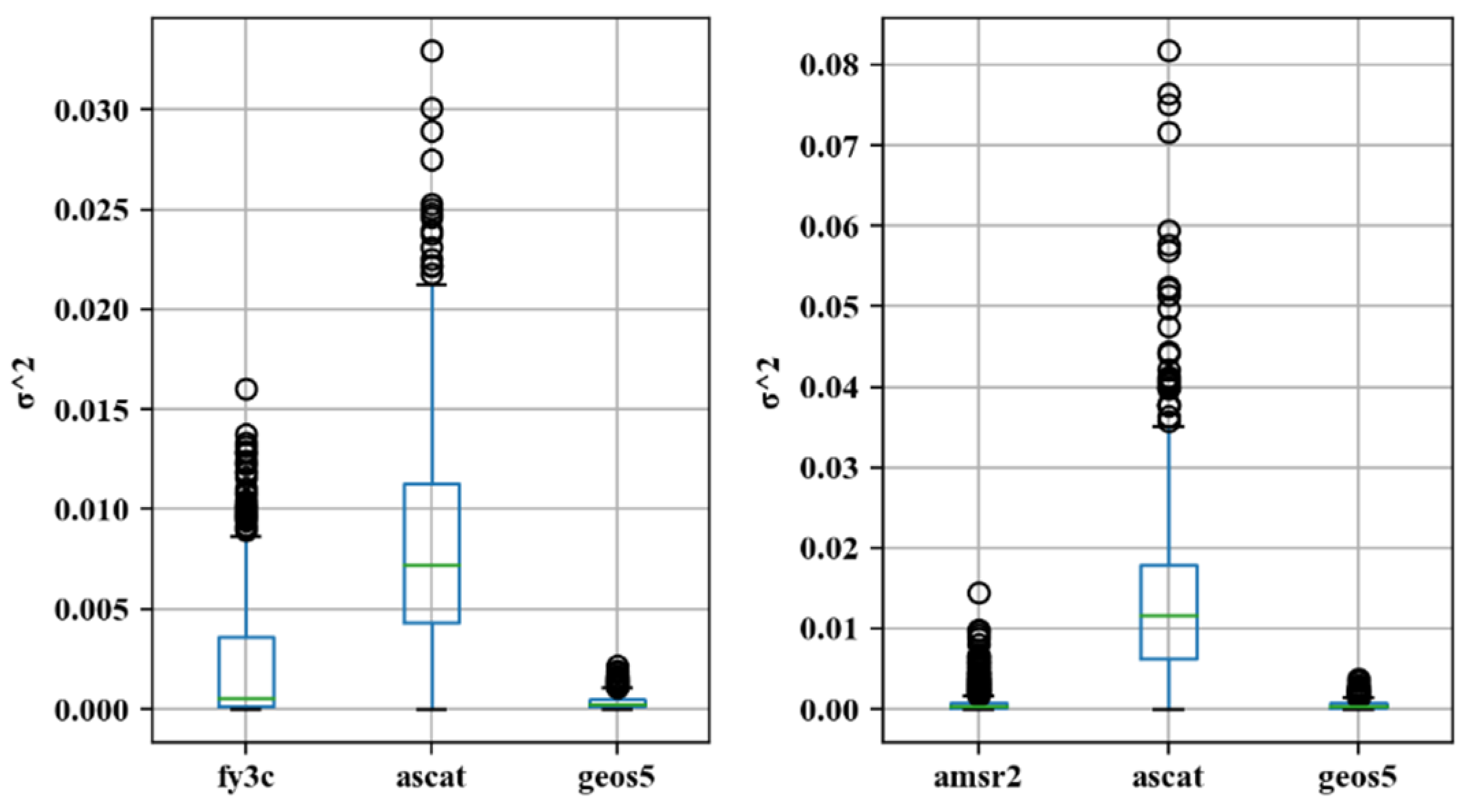
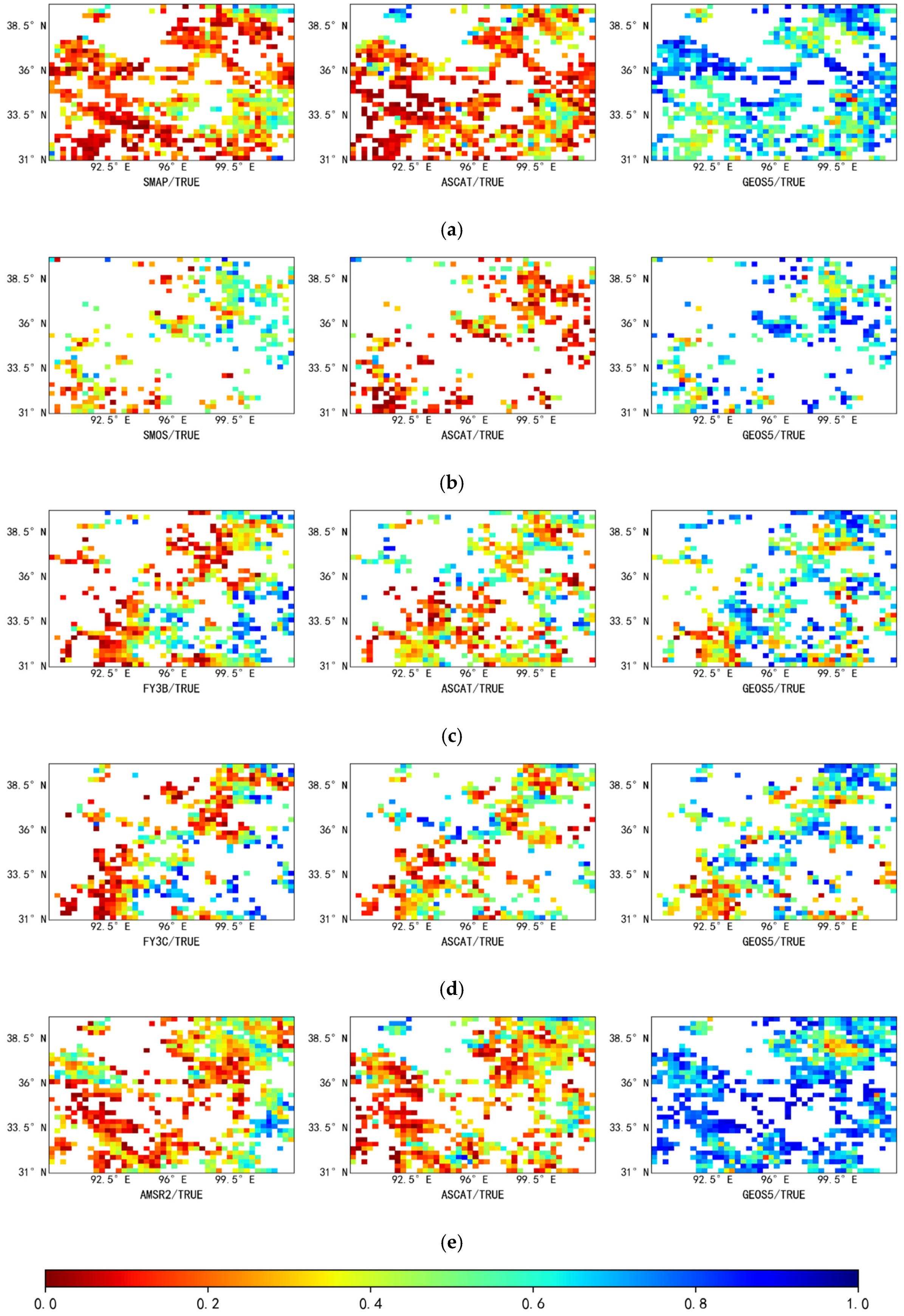
3. Results
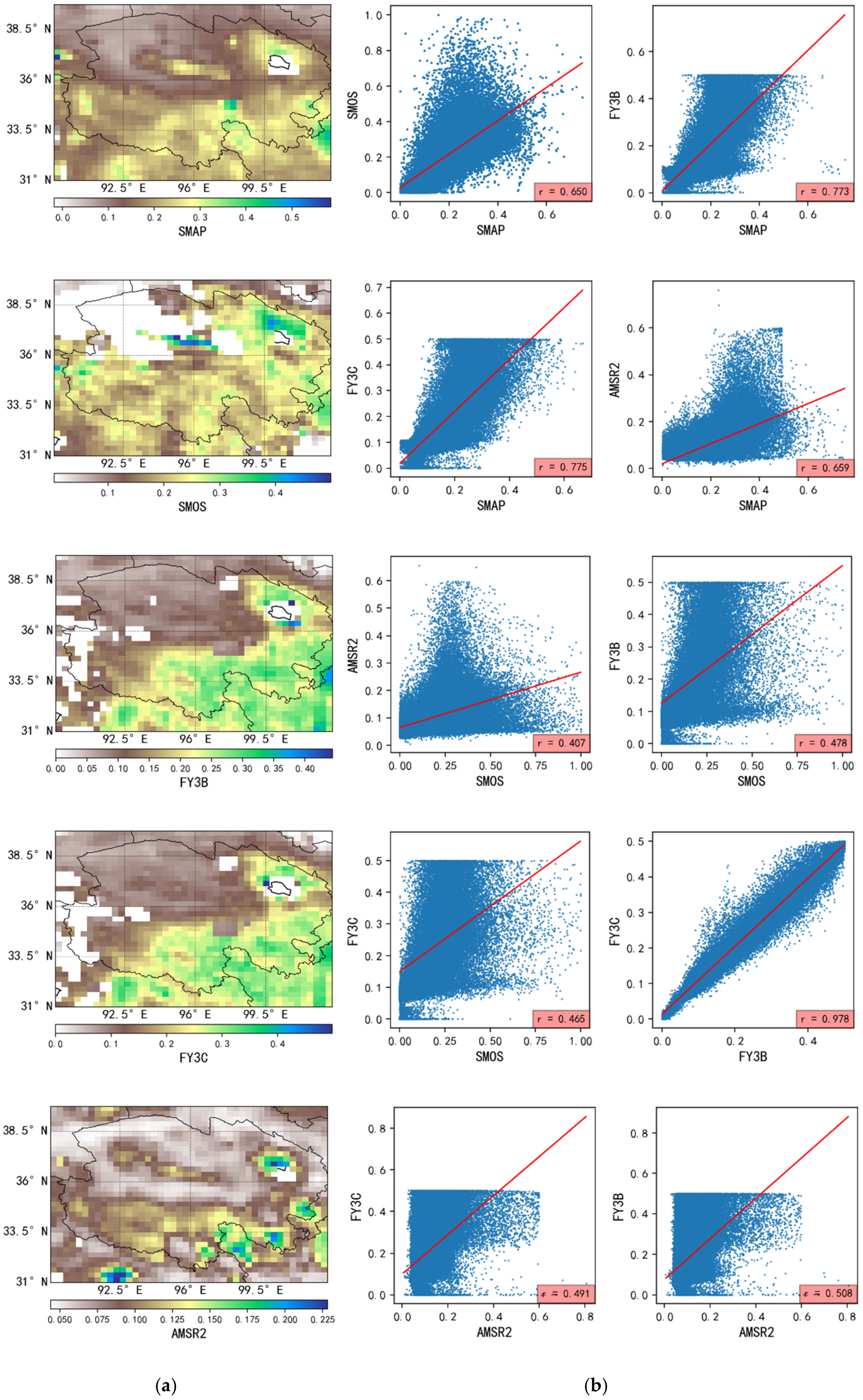
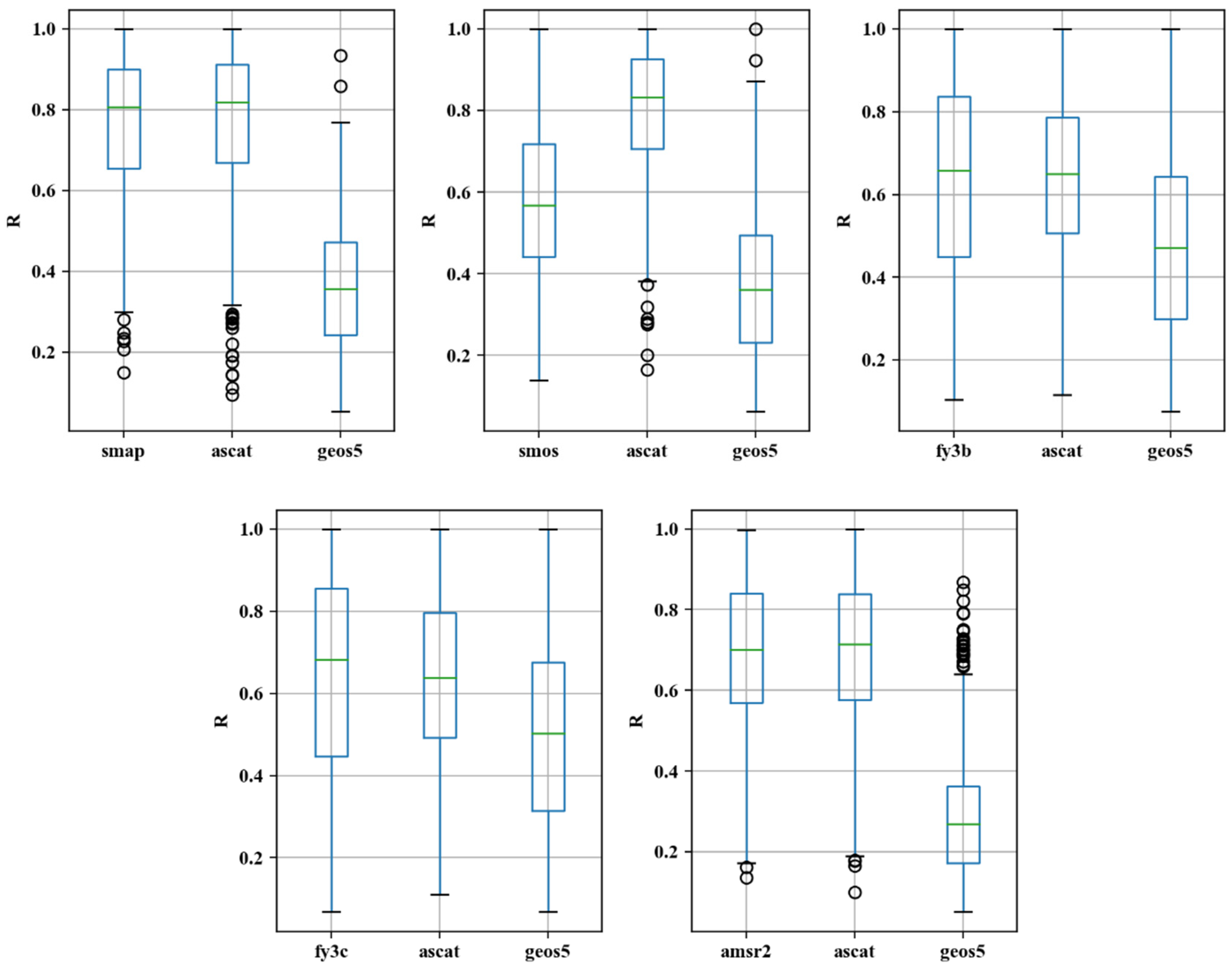
3.1. Correlation between Satellite Soil Moisture Products
3.1.1. Correlation between Passive Satellite Soil Moisture Products
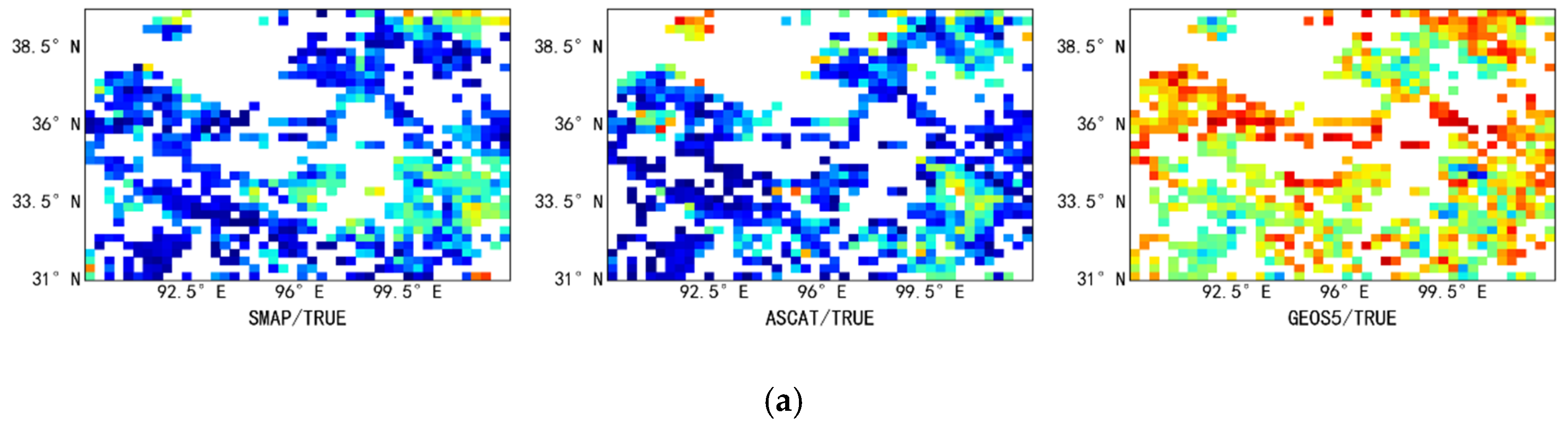
3.1.2. Correlation Analysis between Different Types of Soil Moisture Products
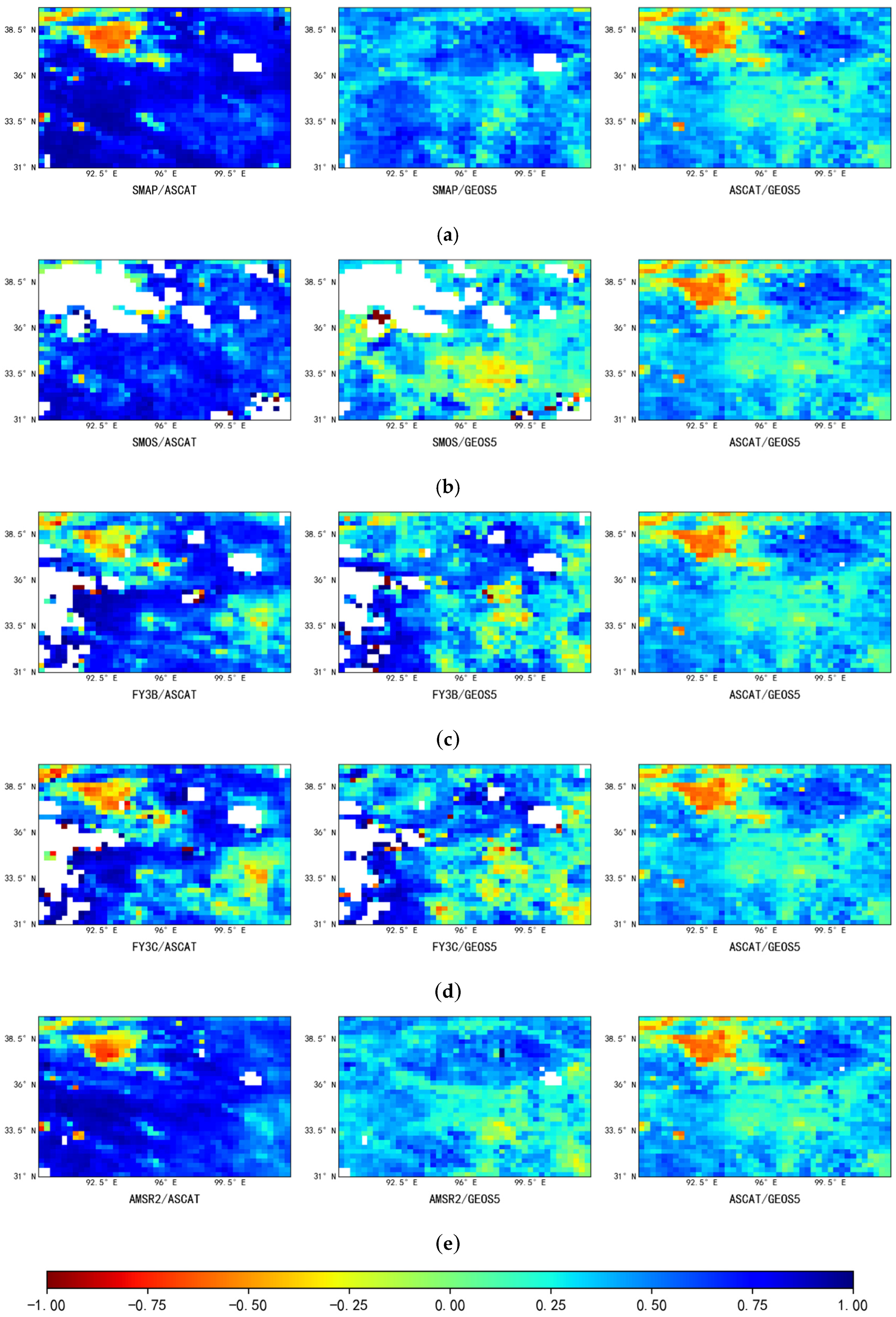
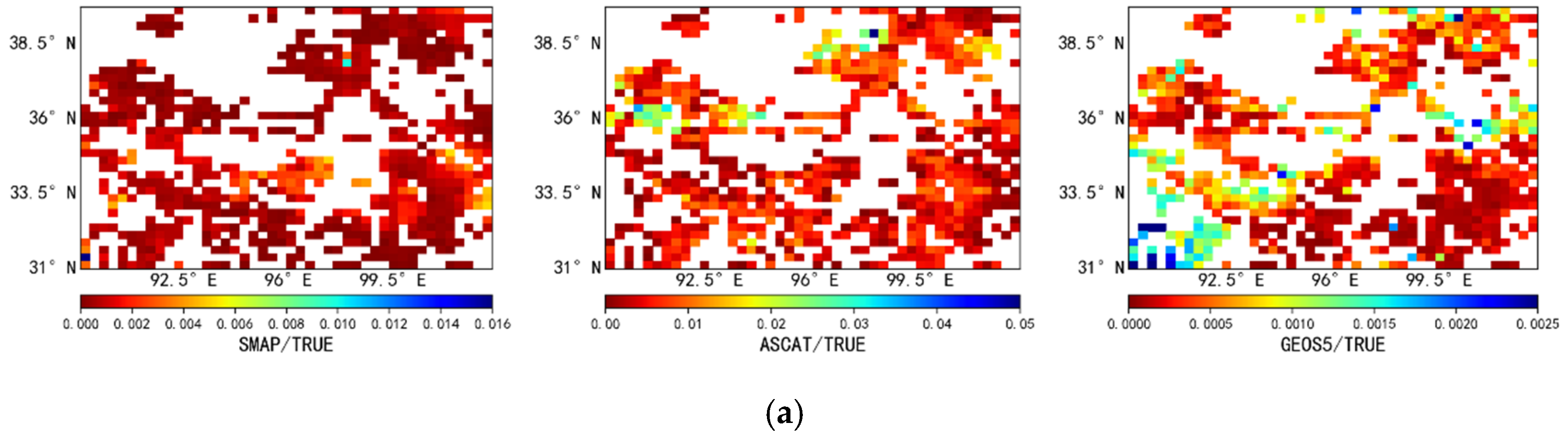
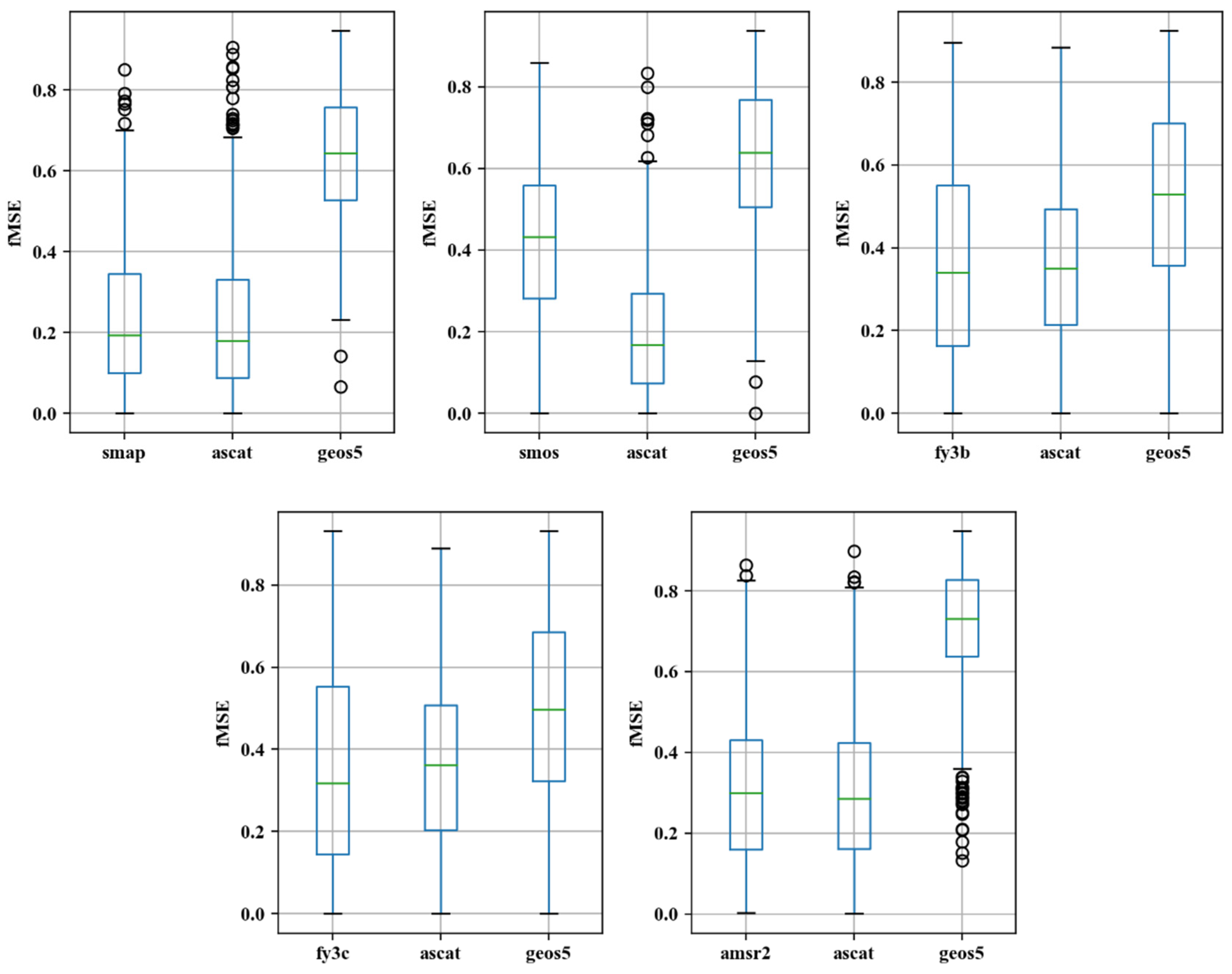
3.2. Analysis of Triple Collocation Results
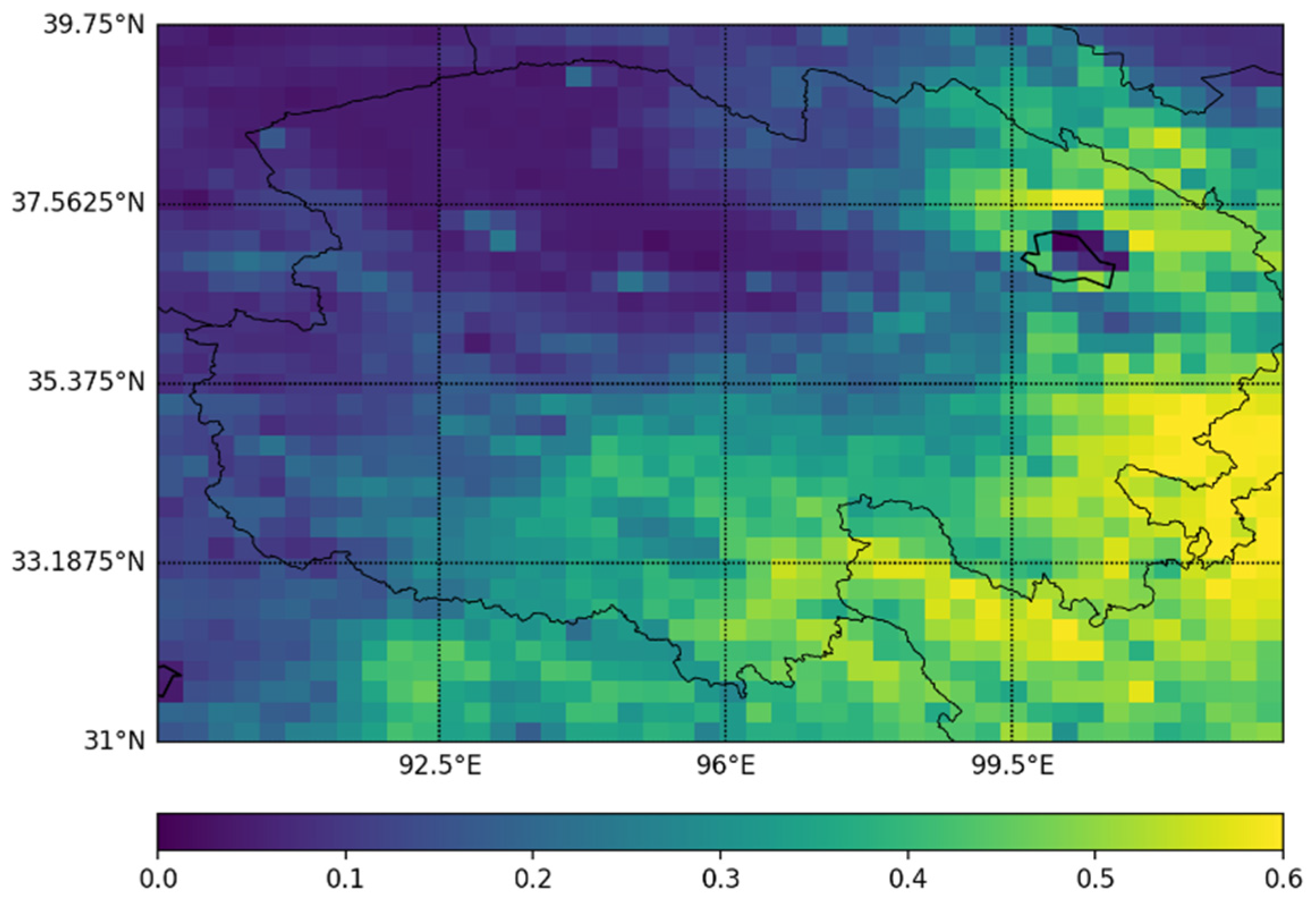
3.3. Correlation between TC Results and Vegetation Coverage
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McColl, K.A.; Alemohammad, S.H.; Akbar, R.; Konings, A.G.; Yueh, S.; Entekhabi, D. The global distribution and dynamics of surface soil moisture. Nat. Geosci. 2017, 10, 100–104. [Google Scholar] [CrossRef]
- Fiifi, D.; Hagan, T.; Parinussa, R.M.; Wang, G. An Evaluation of Soil Moisture Anomalies from Global Model-Based Datasets over the People’s Republic of China. Water 2020, 12, 117. [Google Scholar]
- Manzoni, S.; Schimel, J.P.; Barbara, S. Responses of soil microbial communities to water stress: Results from a Responses of soil microbial communities to water stress: Results from a meta-analysis. Ecology 2017, 93, 930–938. [Google Scholar] [CrossRef] [PubMed]
- Porporato, A.; D’odorico, P.; Laio, F.; Rodriguez-Iturbe, I. Hydrologic Controls on Soil Carbon and nitrogen cycles. Adv. Water Resour. 2016, 26, 45–58. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Tubiello, F.N.; Goldberg, R.; Mills, E.; Bloomfield, J. Increased crop damage in the US from excess precipitation under climate change. Glob. Environ. Chang. 2002, 12, 197–202. [Google Scholar] [CrossRef] [Green Version]
- Fécan, F.; Marticorena, B.; Bergametti, G. Parametrization of the increase of the aeolian erosion threshold wind friction velocity due to soil moisture for arid and semi-arid areas. Ann. Geophys. 1998, 17, 149–157. [Google Scholar] [CrossRef] [Green Version]
- Bomblies, A.; Eltahir, E.A.B. Assessment of the impact of climate shifts on malaria transmission in the Sahel. Ecohealth 2009, 6, 426–437. [Google Scholar] [CrossRef]
- Qiu, J.; Crow, W.T.; Nearing, G.S. The impact of vertical measurement depth on the information content of soil moisture for latent heat flux estimation. J. Hydrometeorol. 2016, 17, 2419–2430. [Google Scholar] [CrossRef]
- Lu, X.D. Methods of soil moisture meteorological observation are introduced. Agric. Technol. 2018, 38, 151–153. [Google Scholar]
- Su, C.-H.; Ryu, D.; Crow, W.T. Beyond triple collocation: Applications to soil moisture monitoring. J. Geophys. Res. Atmos. 2014, 19, 6419–6439. [Google Scholar] [CrossRef]
- McColl, K.A.; Vogelzang, J.; Konings, A.G.; Entekhabi, D.; Piles, M.; Stoffelen, A. Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target. Geophys. Res. Lett. 2014, 41, 6229–6236. [Google Scholar] [CrossRef] [Green Version]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. C Ocean. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Scipal, K.; Holmes, T.; De Jeu, R.; Naeimi, V.; Wagner, W. A possible solution for the problem of estimating the error structure of global soil moisture data sets. Geophys. Res. Lett. 2008, 35, 2–5. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Crow, W.T.; Bindlish, R.; Colliander, A.; Burgin, M.S.; Asanuma, J.; Aida, K. Global-scale evaluation of SMAP, SMOS and ASCAT soil moisture products using triple collocation. Remote Sens. Environ. 2018, 214, 1–13. [Google Scholar] [CrossRef]
- Gruber, A.; Su, C.-H.; Zwieback, S.; Crow, W.; Dorigo, W.; Wagner, W. Recent advances in (soil moisture) triple collocation analysis. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 200–211. [Google Scholar] [CrossRef]
- Dong, J.; Crow, W.T. An Improved Triple Collocation Analysis Algorithm for Decomposing Autocorrelated and White Soil Moisture Retrieval Errors. J. Geophys. Res. Atmos. 2017, 122, 13081–13094. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Shu, H.; Nie, L.; Jiao, Z.H. Error analysis of soil moisture based on Triple Collocation method. Remote Sens. Land Resour. 2018, 30, 68–75. [Google Scholar]
- Medeiros, J. Design and Development of the SMAP Microwave Radiometer Electronics. 2019; pp. 1–17. Available online: http://ntrs.nasa.gov/search.jsp?R=20140005426 (accessed on 30 April 2020).
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS L: New tool for monitoring key elements ofthe global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
- Zabolotskikh, E.V.; Mitnik, L.M.; Chapron, B. New approach for severe marine weather study using satellite passive microwave sensing. Geophys. Res. Lett. 2013, 40, 3347–3350. [Google Scholar] [CrossRef] [Green Version]
- Ducharne, A.; Koster, R.D.; Suarez, M.J.; Stieglitz, M.; Kumar, P. A catchment-based approach to modeling land surface processes in a general circulation model 2. Parameter estimation and model demonstration. J. Geophys. Res. Atmos. 2000, 105, 24823–24838. [Google Scholar] [CrossRef]
- Jia, Y.C.; Xie, M.W.; Jiang, H.T. Daily Estimate of global 36 km grid soil moisture. J. Geo Inf. Sci. 2017, 19, 854–860. [Google Scholar]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; De Rosnay, P.; Jann, A.; Schneider, S.; et al. The ASCAT soil moisture product: A review of its specifications, validation results, and emerging applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef] [Green Version]
- Su, J.L.; Luo, W.Q.; Wang, G.Z. Spatiotemporal Variation of Vegetation and Its Influencing Factors in Xijiang River Basin of Guangxi Based on MODIS-EVI. Res. Soil Water Conserv. 2019, 26, 232–238. [Google Scholar]
- Bo, Z.; Jianxin, M.; Lu, X.; Xinggang, M.; Bureau, L.M. Spatial and Temporal Variation of Vegetation Coverage in Mountain Area of Longnan:Based on MODIS EVI. Chin. Agric. Sci. Bull. 2017, 33, 70–77. [Google Scholar]
- Zhai, Y.Q.; Zhang, C.; Zhou, Q. Spatio-temporal variation and interrelationship of vegetation cover and soil moisture in Qinling-Daba Mountains. J. Geo Inf. Sci. 2018, 20, 967–977. [Google Scholar]



| Dataset Name | Sensor | Retrieval Band | Time of Ascending Pass/Descending Pass | Unit | Spatial Resolution | Time Period | Coverage |
|---|---|---|---|---|---|---|---|
| L3_SM_P | Passive | 1.4 GHz | 06:00/18:00 | m3/m3 | 36 km | 2015–present | Global |
| SMOS-CATDS | Passive | 1.4 GHz | 06:00/18:00 | m3/m3 | 25 km | 2010–present | Global |
| FY3B-MWRI | Passive | 10.7/36.5 GHz | 13:30/01:30 | m3/m3 | 25 km | 2011–present | Global |
| FY3C-MWRI | Passive | 10.7/36.5 GHz | 13:30/01:30 | m3/m3 | 25 km | 2014–present | Global |
| AMSR2_L3 | Passive | 10.7/36.5 GHz | 13:30/01:30 | Saturation (%) | 0.25° | 2012–present | Global |
| ASCAT_L2 | Active | 5.3 GHz | 21:30/09:30 | Saturation (%) | 12.5 km | 2012–present | Global |
| GEOS5 | Fusion | m3/m3 | 0.25° *0.3125° | 2014–present | Global |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Zhang, Z.; Lv, A. Evaluation of Satellite-Derived Soil Moisture in Qinghai Province Based on Triple Collocation. Water 2020, 12, 1292. https://doi.org/10.3390/w12051292
Zhu H, Zhang Z, Lv A. Evaluation of Satellite-Derived Soil Moisture in Qinghai Province Based on Triple Collocation. Water. 2020; 12(5):1292. https://doi.org/10.3390/w12051292
Chicago/Turabian StyleZhu, Hongchun, Zhilin Zhang, and Aifeng Lv. 2020. "Evaluation of Satellite-Derived Soil Moisture in Qinghai Province Based on Triple Collocation" Water 12, no. 5: 1292. https://doi.org/10.3390/w12051292





