Evaluation of a Distributed Streamflow Forecast Model at Multiple Watershed Scales
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hydrologic Model
2.2. Study Area
2.3. Discharge Data
2.4. Model Inputs
2.5. Model Calibration and Validation
2.6. Evaluation Statistics
3. Results
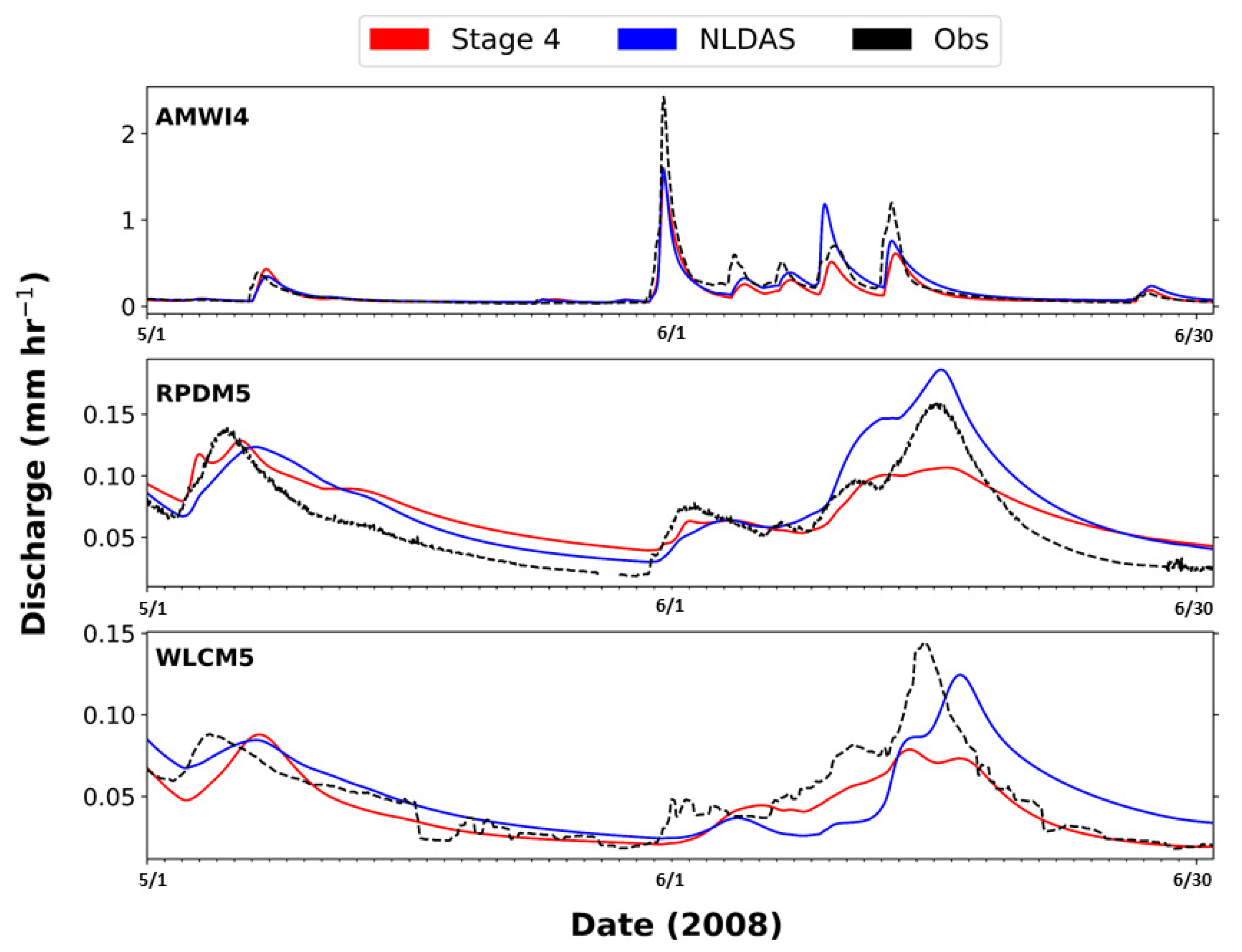
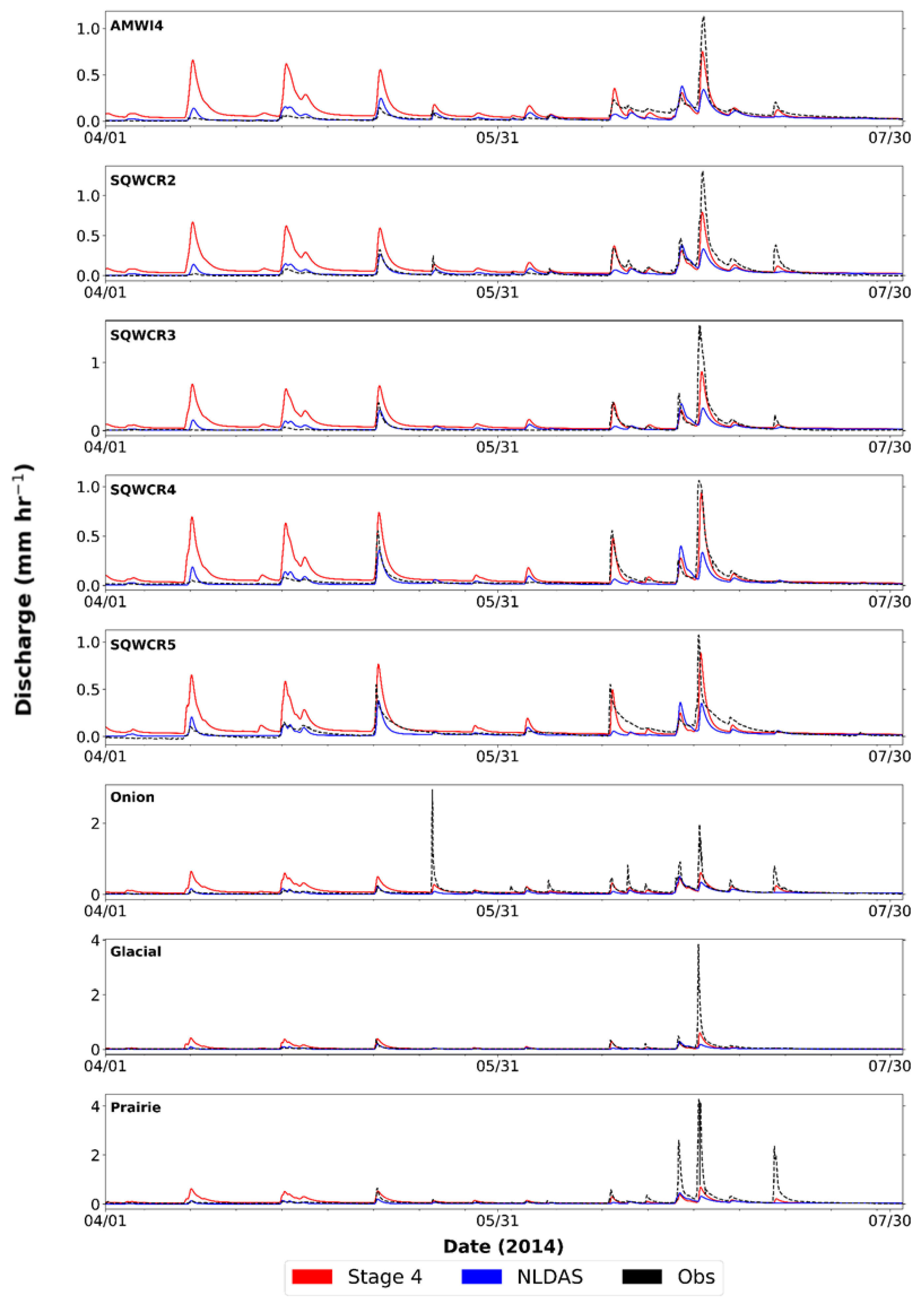
3.1. Model Performance with NLDAS-2 Precipitation
3.2. Model Performances with Stage IV Precipitation
3.3. Comparison of NLDAS-2 and Stage IV Simulations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Koren, V.; Reed, S.; Smith, M.; Zhang, Z.; Seo, D.-J. Hydrology laboratory research modeling system (HL-RMS) of the US national weather service. J. Hydrol. 2004, 291, 297–318. [Google Scholar]
- Koren, V.; Smith, M.; Cui, Z.; Cosgrove, B.; Werner, K.; Zamora, R. Modification of Sacramento Soil Moisture Accounting Heat Transfer Component (SAC-HT) for Enhanced Evapotranspiration. NOAA Tech. Rep. NWS 53; U.S. Dep. Commer. NOAA/NWS: Silver Spring, MD, USA, 2010; 72p.
- Alfieri, L.; Burek, P.; Dutra, E.; Krzeminski, B.; Muraro, D.; Thielen, J.; Pappenberger, F. GloFAS–Global Ensemble Streamflow Forecasting and Flood Early Warning GloFAS–global ensemble streamflow forecasting and flood early warning. Hydrol. Earth Syst. Sci. 2013, 17, 1161–1175. [Google Scholar] [CrossRef] [Green Version]
- Yucel, I.; Onen, A.; Yilmaz, K.K.; Gochis, D.J. Calibration and evaluation of a flood forecasting system: Utility of numerical weather prediction model, data assimilation and satellite-based rainfall. J. Hydrol. 2015, 523, 49–66. [Google Scholar]
- Krajewski, W.F.; Ceynar, D.; Demir, I.; GosKa, R.; Kruger, A.; Langel, C.; Mantilla, R.; Niemeier, J.; Quintero, F.; Seo, B.-C.; et al. Real-time flood forecasting and information system for the state of Iowa. Bull. Am. Meteorol. Soc. 2017, 98, 539–554. [Google Scholar] [CrossRef]
- Salas, F.R.; Somos-valenzuela, M.A.; Dugger, A.; Maidment, D.R.; Gochis, D.J.; David, H.; Yu, W.; Ding, D.; Clark, E.P.; Noman, N. Towards real-time continental scale streamflow simulation in continuous and discrete space. JAWRA J. Am. Water Resour. Assoc. 2018, 54, 7–27. [Google Scholar]
- Beven, K. How far can we go in distributed hydrological modelling? Hydrol. Earth Syst. Sci. 2001, 5, 1–12. [Google Scholar] [CrossRef]
- Koren, V.; Smith, M.; Duan, Q. Use of a Priori parameter estimates in the derivation of spatially consistent parameter sets of rainfall-runoff models. In Calibration of Watershed Models; Duan, Q., Gupta, H.V., Sorooshian, S., Rousseau, A.N., Turcotte, R., Eds.; American Geophysical Union: Washington, DC, USA, 2003; pp. 239–254. [Google Scholar]
- Blöschl, G.; Reszler, C.; Komma, J. A spatially distributed flash flood forecasting model. Environ. Model. Softw. 2008, 23, 464–478. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Wang, Q.J.; Pagano, T.C. A review of advances in flash flood forecasting. Hydrol. Process. 2011, 25, 2771–2784. [Google Scholar]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar]
- Sivapalan, M. Prediction in ungauged basins: A grand challenge for theoretical hydrology. Hydrol. Process. 2003, 17, 3163–3170. [Google Scholar]
- Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Arheimer, B.; Blume, T.; Clark, M.P.; Ehret, U.; et al. A decade of Predictions in Ungauged Basins (PUB)–A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar]
- National Research Council. Challenges and Opportunities in the Hydrologic Sciences; The National Academies Press: Washington, DC, USA, 2012; 200p. [Google Scholar]
- Khakbaz, B.; Imam, B.; Sorooshian, S.; Koren, V.I.; Cui, Z.; Smith, M.B.; Restrepo, P. Modification of the National Weather Service Distributed Hydrologic Model for subsurface water exchanges between grids. Water Resour. Res. 2011, 47, 1–17. [Google Scholar]
- Kauffeldt, A.; Wetterhall, F.; Pappenberger, F.; Salamon, P.; Thielen, J. Technical review of large-scale hydrological models for implementation in operational flood forecasting schemes on continental level. Environ. Model. Softw. 2016, 75, 68–76. [Google Scholar] [CrossRef]
- Fang, X.; Pomeroy, J.W.; Ellis, C.R.; Macdonald, M.K.; Debeer, C.M.; Brown, T. Multi-variable evaluation of hydrological model predictions for a headwater basin in the Canadian Rocky Mountains. Hydrol. Earth Syst. Sci. 2013, 17, 1635–1659. [Google Scholar]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.-J.; DMIP Participants. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Burnash, R.J.C.; Ferral, L.; McGuire, R.A. A Generalized Streamflow Simulation System: Conceptual Models for Digital Computers, Technical Report; Joint Federal and State River Forecast Center: Sacramento, CA, USA, 1973; 204p.
- NWS. Hydrology Laboratory-Research Distributed Hydrologic Model (HL-RDHM) User Manual V.3.5.0; U.S. Dep. Commer. NOAA/NWS: Silver Spring, MD, USA, 2016; 147p.
- Smith, M.B.; Koren, V.I.; Zhang, Z.; Reed, S.M.; Pan, J.-J.; Moreda, F. Runoff response to spatial variability in precipitation: An analysis of observed data. J. Hydrol. 2004, 298, 267–286. [Google Scholar]
- Kavetski, D.; Kuczera, G.; Franks, S.W. Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory. Water Resour. Res. 2006, 42, W03407. [Google Scholar] [CrossRef]
- Koren, V.; Smith, M.; Cui, Z. Physically-based modifications to the Sacramento Soil Moisture Accounting model. Part A: Modeling the effects of frozen ground on the runoff generation process. J. Hydrol. 2014, 519, 3475–3491. [Google Scholar]
- Burnash, R.J.C. The NWS River Forecast System-Catchment Modeling. In Computer Models of Watershed Hydrology; Singh, V., Ed.; Water Resources Publication: Colorado, CO, USA, 1995; pp. 311–366. [Google Scholar]
- Anderson, E. Snow Accumulation and Ablation Model–SNOW-17. In NWSRFS User Documentation; Office of Hydrology, NOAA/NWS: Silver Spring, MD, USA, 2006; p. 44. [Google Scholar]
- Reed, S.M.; Maidment, D.R. Coordinate Transformations for using NEXRAD data in GIS-based hydrologic modeling. J. Hydrol. Eng. 1999, 4, 174–182. [Google Scholar] [CrossRef]
- Spies, R.R.; Franz, K.J.; Hogue, T.S.; Bowman, A.L. Distributed Hydrologic Modeling Using Satellite-Derived Potential Evapotranspiration. J. Hydrometeorol. 2015, 16, 129–146. [Google Scholar] [CrossRef] [Green Version]
- Schilling, K.E.; Libra, R.D. Increased baseflow in Iowa over the second half of the 20th century. J. Am. Water Resour. Assoc. 2003, 39, 851–860. [Google Scholar]
- Schilling, K.E.; Helmers, M. Effects of subsurface drainage tiles on streamflow in Iowa agricultural watersheds: Exploratory hydrograph analysis. Hydrol. Process. 2008, 4506, 4497–4506. [Google Scholar]
- Minnesota Department of Natural Resources (MDNR). Cooperative Stream Gaging (CSG). Available online: www.dnr.state.mn.us/waters/csg (accessed on 16 June 2016).
- Demir, I.; Krajewski, W.F. Towards an integrated Flood Information System: Centralized data access, analysis, and visualization. Environ. Model. Softw. 2013, 50, 77–84. [Google Scholar]
- Rogers, E.; Deaven, D.G.; DiMego, G.J. The Regional analysis system for the operational “Early” Eta model: Original 80-km configuration and recent changes. Weather Forecast. 1995, 10, 810–825. [Google Scholar]
- Xia, Y.; Mitchell, K.; Ek, M.; Cosgrove, B.; Sheffield, J.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; Livneh, B.; et al. Continental-scale water and energy flux analysis and validation for North American Land Data Assimilation System project phase 2 (NLDAS-2): 2. Validation of model-simulated streamflow. J. Geophys. Res. Atmos. 2012, 117, D03110. [Google Scholar]
- Mitchell, K.E. The multi-institution North American Land Data Assimilation System (NLDAS): Utilizing multiple GCIP products and partners in a continental distributed hydrological modeling system. J. Geophys. Res. 2004, 109, 1–32. [Google Scholar]
- Wu, H.; Adler, R.F.; Hong, Y.; Tian, Y.; Policelli, F. Evaluation of Global Flood Detection Using Satellite-Based Rainfall and a Hydrologic Model. J. Hydrometeorol. 2012, 13, 1268–1284. [Google Scholar] [CrossRef]
- Seo, D.; Lakhankar, T.; Mejia, J.; Cosgrove, B.; Khanbilvardi, R. Evaluation of operational national weather service gridded flash flood guidance over the Arkansas Red River basin. J. Am. Water Resour. Assoc. 2013, 49, 1296–1307. [Google Scholar]
- Nan, Z.; Wang, S.; Liang, X.; Adams, T.E.; Teng, W.; Liang, Y. Analysis of Spatial Similarities Between NEXRAD and NLDAS Precipitation Data Products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 371–385. [Google Scholar]
- Prat, O.P.; Nelson, B.R. Evaluation of precipitation estimates over CONUS derived from satellite, radar, and rain gauge data sets at daily to annual scales (2002–2012). Hydrol. Earth Syst. Sci. 2015, 19, 2037–2056. [Google Scholar] [CrossRef] [Green Version]
- Bowman, A.L.; Franz, K.J.; Hogue, T.S. Case studies of a MODIS-based potential evapotranspiration input to the Sacramento Soil Moisture Accounting Model. J. Hydrometeorol. 2016, 18, 151–158. [Google Scholar] [CrossRef] [Green Version]
- Hogue, T.S.; Sorooshian, S.; Gupta, H.; Holz, A.; Braatz, D. A Multistep Automatic Calibration Scheme for River Forecasting Models. J. Hydrometeorol. 2000, 1, 524–542. [Google Scholar]
- Anderson, E. Calibration of Conceptual Hydrologic Models for Use in River Forecasting; U.S. Dep. Commer. NOAA/NWS: Silver Spring, MD, USA, 2002; 300p.
- Ajami, N.K.; Gupta, H.; Wagener, T.; Sorooshian, S. Calibration of a semi-distributed hydrologic model for streamflow estimation along a river system. J. Hydrol. 2004, 298, 112–135. [Google Scholar]
- Tang, Y.; Reed, P.; van Werkhoven, K.; Wagener, T. Advancing the identification and evaluation of distributed rainfall-runoff models using global sensitivity analysis. Water Resour. Res. 2007, 43, 1–14. [Google Scholar] [CrossRef]
- Franz, K.J.; Butcher, P.; Ajami, N.K. Addressing snow model uncertainty for hydrologic prediction. Adv. Water Resour. 2010, 33, 820–832. [Google Scholar] [CrossRef]
- Steffens, K.J.; Franz, K.J. Late 20th-century trends in Iowa watersheds: An investigation of observed and modelled hydrologic storages and fluxes in heavily managed landscapes. Int. J. Climatol. 2012, 32, 1373–1391. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Engel, B.; Storm, D.; White, M.; Arnold, J.; Arabi, M. A hydrologic/water quality model application protocol. J. Am. Water Resour. Assoc. 2007, 43, 1223–1226. [Google Scholar]
- Jackson, E.K.; Roberts, W.; Nelsen, B.; Williams, G.P.; Nelson, E.J.; Ames, D.P. Introductory overview: Error metrics for hydrologic modelling–A review of common practices and an open source library to facilitate use and adoption. Environ. Model. Softw. 2019, 119, 32–48. [Google Scholar] [CrossRef]
- Merz, R.; Parajka, J.; Blöschl, G. Scale effects in conceptual hydrological modeling. Water Resour. Res. 2009, 45, 1–15. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Ricard, S.; Bourdillon, R.; Roussel, D.; Turcotte, R. Global Calibration of Distributed Hydrological Models for Large-Scale Applications. J. Hydrol. Eng. 2013, 18, 719–721. [Google Scholar] [CrossRef]
- Reed, S.M. Deriving flow directions for coarse-resolution (1–4 km) gridded hydrologic modeling. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.F.; Tian, Y.; Gu, G.; Huffman, G.J. Evaluation of Quantitative Precipitation Estimations through Hydrological Modeling in IFloodS River Basins. J. Hydrometeorol. 2017, 18, 529–553. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Hogue, T.S.; Hsu, K.-L.; Sorooshian, S.; Gupta, H.V.; Wagener, T. Intercomparison of Rain Gauge, Radar, and Satellite-Based Precipitation Estimates with Emphasis on Hydrologic Forecasting. J. Hydrometeorol. 2005, 6, 497–517. [Google Scholar] [CrossRef]
- Faurès, J.M.; Goodrich, D.C.; Woolhiser, D.A.; Sorooshian, S. Impact of small-scale spatial rainfall variability on runoff modeling. J. Hydrol. 1995, 173, 309–326. [Google Scholar] [CrossRef]
- Brath, A.; Montanari, A.; Toth, E. Analysis of the effects of different scenarios of historical data availability on the calibration of a spatially-distributed hydrological model. J. Hydrol. 2004, 291, 232–253. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Gourley, J.J.; Huffman, G.J.; Tian, Y.; Cao, Q.; Yong, B.; Kirstetter, P.E.; Hu, J.; Hardy, J.; et al. Evaluation of the successive V6 and V7 TRMM multisatellite precipitation analysis over the Continental United States. Water Resour. Res. 2013, 49, 8174–8186. [Google Scholar] [CrossRef]
- Mantilla, R.; Krajewski, W.F. Pilot Project for a Hybrid Road-Flooding Forecasting System on Squaw Creek, Final Report, IHRB Project TR-642; Iowa Flood Center, University of Iowa: Iowa City, IA, USA, 2014; 42p. [Google Scholar]
- Franz, K.J.; Karsten, L.R. Calibration of a distributed snow model using MODIS snow covered area data. J. Hydrol. 2013, 494, 160–175. [Google Scholar] [CrossRef]
- Rajib, M.A.; Merwade, V.; Yu, Z. Multi-objective calibration of a hydrologic model using spatially distributed remotely sensed/in-situ soil moisture. J. Hydrol. 2016, 536, 192–207. [Google Scholar] [CrossRef] [Green Version]




| Site ID | Location | Period of Record | Area (km2) |
|---|---|---|---|
| AMWI4 * | Ames, IA | 1990–2016 | 542 |
| SQ2 | Ames, IA | 2010–2016 | 531 |
| SQ3 | Gilbert, IA | 2012–2016 | 364 |
| SQ4 | Story City, IA | 2012–2016 | 224 |
| SQ5 | Stanhope, IA | 2012–2016 | 137 |
| Prairie | Gilbert, IA | 2012–2016 | 37 |
| Onion | Ames, IA | 2012–2016 | 46 |
| Glacial | Story City, IA | 2012–2016 | 25 |
| Site ID | Location | Period of Record | Area (km2) |
|---|---|---|---|
| RPDM5 * | Rapidan, MN | 1993–2016 | 2877 |
| LERAP8 | Rapidan, MN | 2006–2016 | 1165 |
| LESTCL | St. Clair, MN | 2007–2016 | 911 |
| MAPRAP | Rapidan, MN | 2003–2016 | 867 |
| MASTER | Sterling Center, MN | 2006–2016 | 779 |
| BIGCOB | Beauford, MN | 2006–2016 | 807 |
| LICOBB | Beauford, MN | 1996–2010 | 337 |
| LBEAUF | Beauford, MN | 2010–2016 | 19 |
| Site ID | Location | Period of Record | Area (km2) |
|---|---|---|---|
| WLCM5 * | Welch, MN | 1993–2016 | 3493 |
| CANORT | Northfield, MN | 2012–2016 | 2429 |
| CAFARI | Faribault, MN | 2013–2016 | 2128 |
| CAMORR | Morristown, MN | 2007–2015 | 588 |
| CASOGN | Sogn, MN | 2007–2010 | 142 |
| LCANNO | Cannon Falls, MN | 2005–2010 | 222 |
| PINECR | Cannon Falls, MN | 2010 | 35 |
| Basin Outlet | NCRFC MAPs (mm) | NLDAS-2 Precip (mm) | Adj Factor (%) | Adjusted NLDAS-2 (mm) | Stage IV Precip (mm) | Adj Factor (%) | Adjusted Stage IV (mm) |
|---|---|---|---|---|---|---|---|
| AMWI4 | 949 | 854 | 10 | 932 | 777 | 18 | 917 |
| RPDM5 | 828 | 742 | 10 | 817 | 724 | 13 | 819 |
| WLCM5 | 773 | 820 | −6 | 783 | 783 | 0 | 783 |
| Site | Pbias (%) | R2 | NSE | MAPD (%) | ||||
|---|---|---|---|---|---|---|---|---|
| cal | val | cal | val | cal | val | cal | val | |
| Squaw Creek basin | ||||||||
| AMWI4 * | −3.0 | −2.8 | 0.75 | 0.67 | 0.75 | 0.67 | 43.77 | 50.4 |
| SQ2 | - | 0.5 | - | 0.58 | - | 0.57 | - | 27.5 |
| SQ3 | - | −2.2 | - | 0.43 | - | 0.43 | - | 36.8 |
| SQ4 | - | −27.1 | - | 0.42 | - | 0.40 | - | 33.4 |
| SQ5 | - | −40.7 | - | 0.30 | - | 0.22 | - | 39.5 |
| Prairie | - | −57.8 | - | 0.33 | - | 0.20 | - | 29.3 |
| Onion | - | −41.8 | - | 0.39 | - | 0.30 | - | 79.3 |
| Glacial | - | −54.1 | - | 0.28 | - | 0.20 | - | 15.8 |
| LeSueur River basin | ||||||||
| RPDM5 * | 28.7 | −8.1 | 0.68 | 0.62 | 0.63 | 0.59 | 57.2 | 52.2 |
| LERAP8 | 17.7 | −2.3 | 0.68 | 0.59 | 0.58 | 0.56 | 50.8 | 56.3 |
| LESTCL | 5.4 | −2.7 | 0.61 | 0.57 | 0.60 | 0.53 | 48.6 | 52.1 |
| MAPRAP | 14.0 | −4.2 | 0.56 | 0.45 | 0.55 | 0.39 | 59.1 | 64.3 |
| MASTER | 3.9 | 0.1 | 0.67 | 0.51 | 0.67 | 0.45 | 52.0 | 62.4 |
| BIGCOB | 9.0 | −3.3 | 0.60 | 0.46 | 0.59 | 0.43 | 53.7 | 61.9 |
| LICOBB | 25.9 | - | 0.57 | - | 0.34 | - | 64.2 | - |
| LBEAUF | - | −33.9 | - | 0.14 | - | 0.11 | - | 86.5 |
| Cannon River basin | ||||||||
| WLCM5 * | 0.2 | −21.4 | 0.60 | 0.53 | 0.57 | 0.50 | 37.6 | 40.0 |
| CANORT | - | −17.5 | - | 0.69 | - | 0.65 | - | 49.3 |
| CAFARI | - | −19.2 | - | 0.70 | - | 0.67 | - | 39.4 |
| CAMORR | 62.4 | 1.7 | 0.65 | 0.60 | 0.35 | 0.57 | 82.1 | 40.2 |
| LCANNO | −27.5 | - | 0.21 | - | 0.18 | - | 43.9 | - |
| CASOGN | −28.9 | - | 0.37 | - | 0.31 | - | 40.8 | - |
| PINECR | - | −19.5 | - | 0.41 | - | 0.24 | - | 107.7 |
| Site | Pbias (%) | R2 | NSE | MAPD (%) | ||||
|---|---|---|---|---|---|---|---|---|
| cal | val | cal | val | cal | val | cal | val | |
| Squaw Creek basin | ||||||||
| AMWI4 * | 11.6 | 46.8 | 0.77 | 0.59 | 0.77 | 0.33 | 47.2 | 65.2 |
| SQ2 | - | 69.7 | - | 0.41 | - | 0.04 | - | 35.2 |
| SQ3 | - | 73.0 | - | 0.35 | - | −0.20 | - | 45.9 |
| SQ4 | - | 29.4 | - | 0.36 | - | −0.78 | - | 38.2 |
| SQ5 | - | 3.5 | - | 0.44 | - | −0.29 | - | 41.9 |
| Prairie | - | −26.2 | - | 0.24 | - | 0.22 | - | 30.6 |
| Onion | - | −0.10 | - | 0.38 | - | 0.38 | - | 77.9 |
| Glacial | - | −19.8 | - | 0.25 | - | −0.05 | - | 15.9 |
| LeSueur River basin | ||||||||
| RPDM5 * | 31.6 | 3.40 | 0.59 | 0.53 | 0.48 | 0.52 | 66.5 | 60.2 |
| LERAP8 | 33.2 | 6.70 | 0.49 | 0.52 | 0.13 | 0.50 | 72.0 | 59.7 |
| LESTCL | 8.7 | −16.90 | 0.47 | 0.32 | 0.46 | 0.30 | 61.2 | 60.2 |
| MAPRAP | 22.8 | −0.70 | 0.46 | 0.39 | 0.42 | 0.33 | 68.1 | 73.6 |
| MASTER | 23.2 | 5.00 | 0.54 | 0.43 | 0.47 | 0.37 | 65.5 | 76.4 |
| BIGCOB | 39.9 | 7.00 | 0.48 | 0.39 | 0.16 | 0.36 | 79.1 | 71.2 |
| LICOBB | 24.8 | - | 0.35 | - | 0.08 | - | 73.1 | - |
| LBEAUF | - | −24.9 | - | 0.14 | - | 0.11 | - | 92.2 |
| Cannon River basin | ||||||||
| WLCM5 * | −6.9 | −15.3 | 0.49 | 0.53 | 0.41 | 0.51 | 42.0 | 42.7 |
| CANORT | - | −3.7 | - | 0.67 | - | 0.67 | - | 59.8 |
| CAFARI | - | −9.2 | - | 0.65 | - | 0.64 | - | 44.0 |
| CAMORR | 62.3 | 5.1 | 0.18 | 0.37 | −2.8 | −0.26 | 101.3 | 45.0 |
| LCANNO | −11 | - | 0.15 | - | 0.09 | - | 52.1 | - |
| CASOGN | −16.7 | - | 0.26 | - | 0.21 | - | 49.8 | - |
| PINECR | - | −51.6 | - | 0.74 | - | 0.21 | - | 92.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madsen, T.; Franz, K.; Hogue, T. Evaluation of a Distributed Streamflow Forecast Model at Multiple Watershed Scales. Water 2020, 12, 1279. https://doi.org/10.3390/w12051279
Madsen T, Franz K, Hogue T. Evaluation of a Distributed Streamflow Forecast Model at Multiple Watershed Scales. Water. 2020; 12(5):1279. https://doi.org/10.3390/w12051279
Chicago/Turabian StyleMadsen, Tyler, Kristie Franz, and Terri Hogue. 2020. "Evaluation of a Distributed Streamflow Forecast Model at Multiple Watershed Scales" Water 12, no. 5: 1279. https://doi.org/10.3390/w12051279
APA StyleMadsen, T., Franz, K., & Hogue, T. (2020). Evaluation of a Distributed Streamflow Forecast Model at Multiple Watershed Scales. Water, 12(5), 1279. https://doi.org/10.3390/w12051279





