Micellar-Enhanced Ultrafiltration to Remove Nickel Ions: A Response Surface Method and Artificial Neural Network Optimization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Dead-End Ultrafiltration Experiments
2.3. Sample and Data Analysis
2.4. Response Surface Modeling
2.4.1. Design of Experiments
2.4.2. RSM Modeling
2.5. Artificial Neural Network (ANN) Modeling
3. Results and Discussion
3.1. Ultrafiltration Experimental Results
3.2. RSM Models
3.3. Effect of Factors on Rejection Rate and Permeate Flux
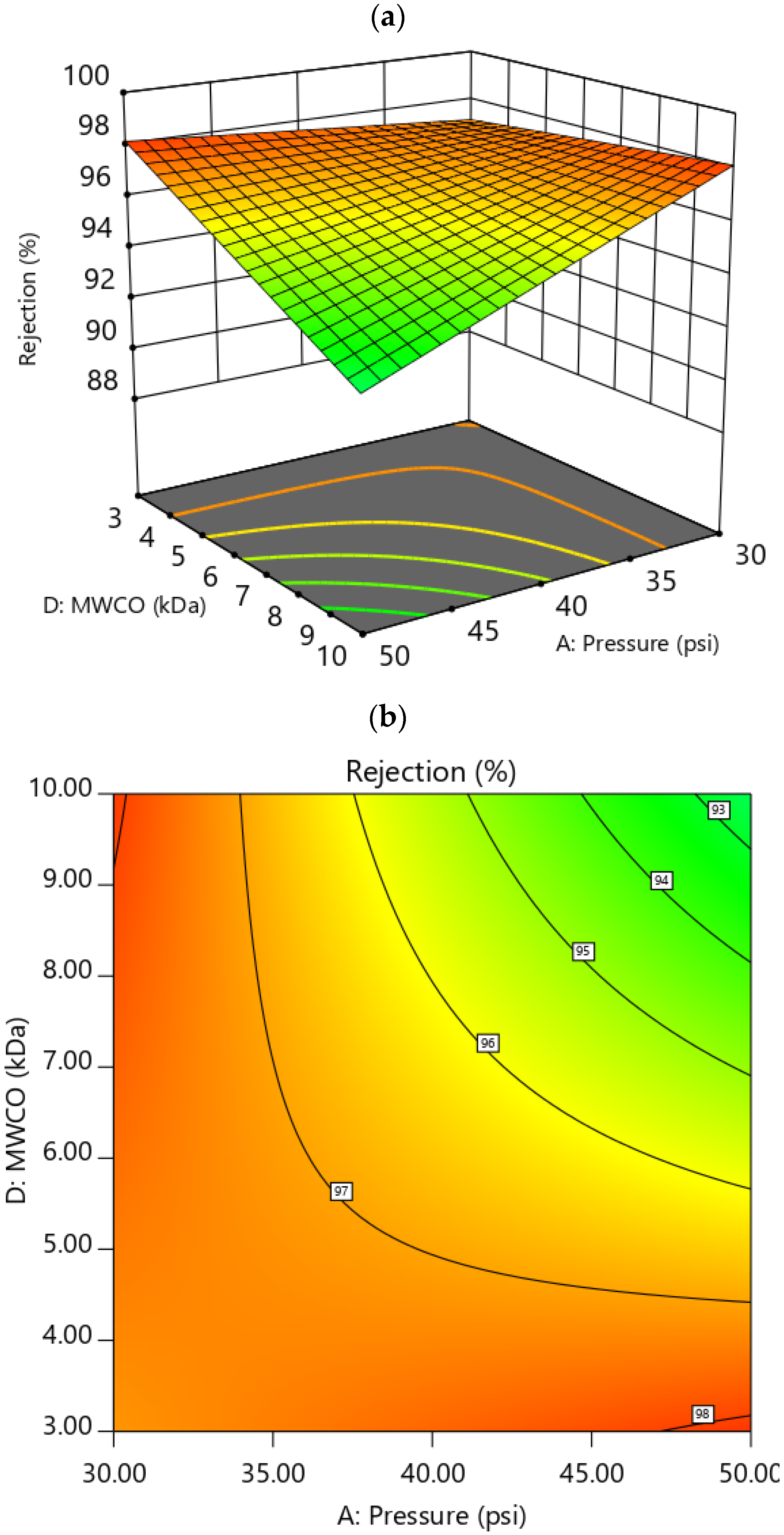
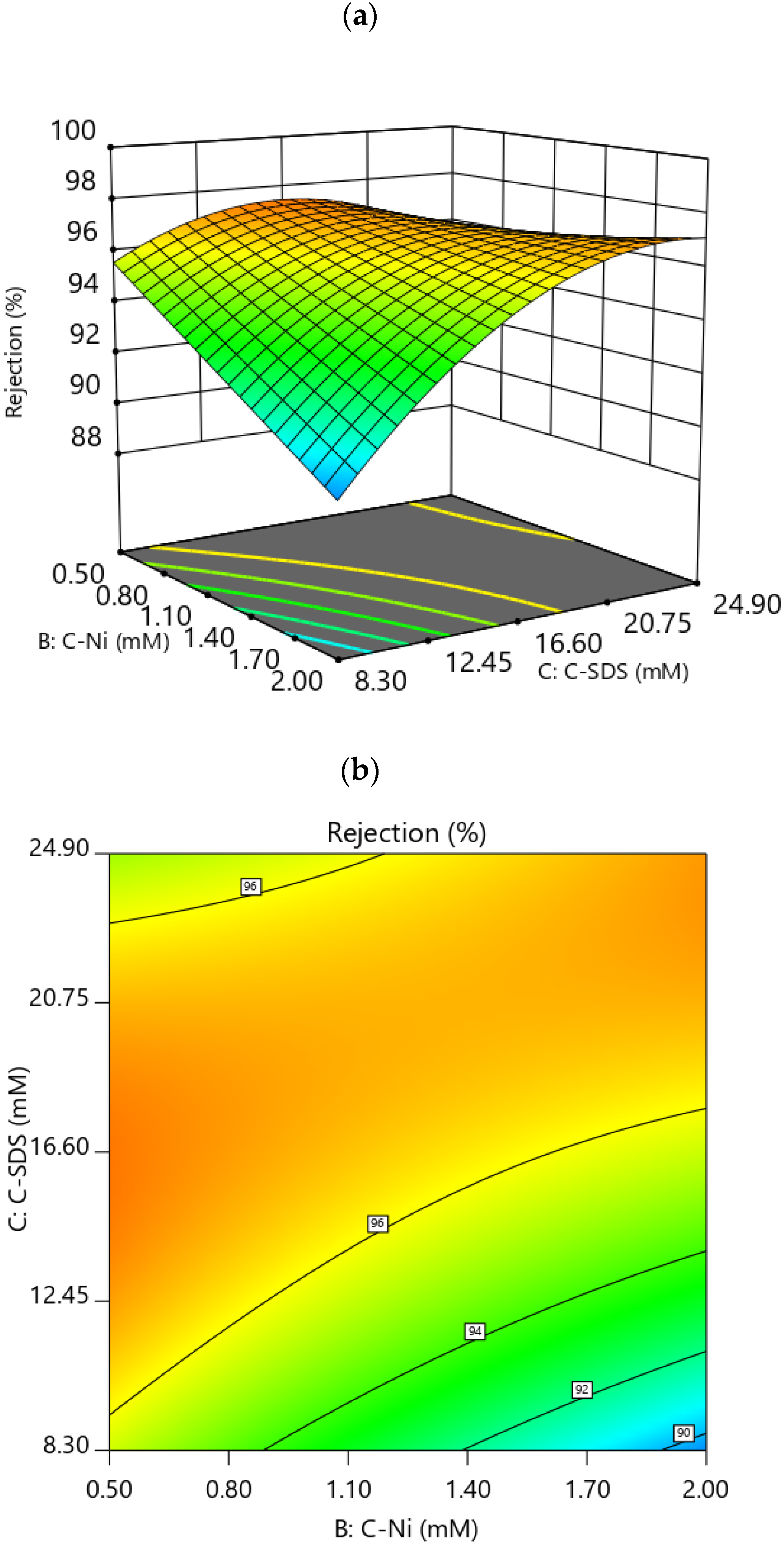
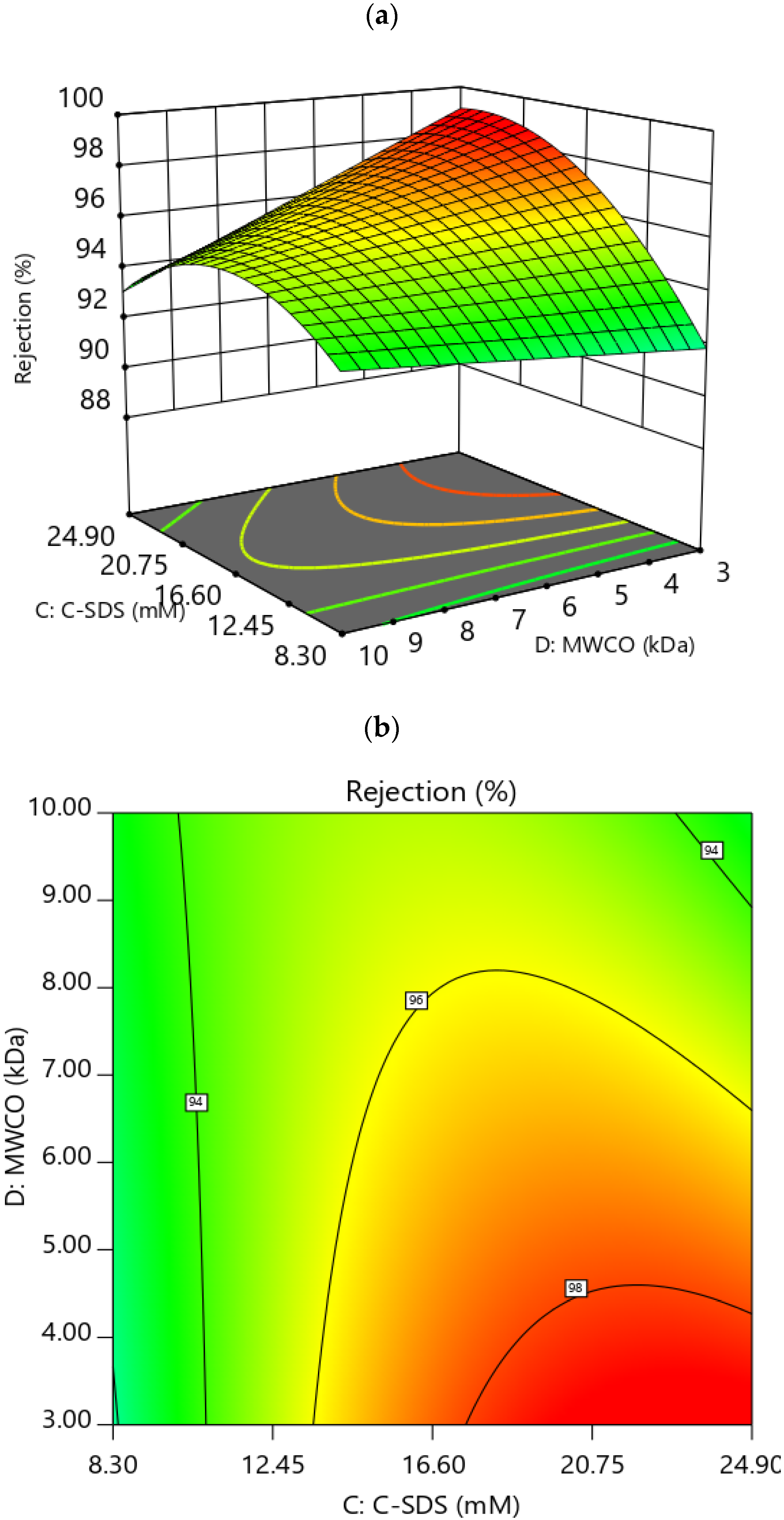
3.3.1. Effect of Factors on Rejection
3.3.2. Effect of Factors on Flux
3.4. RSM Optimization
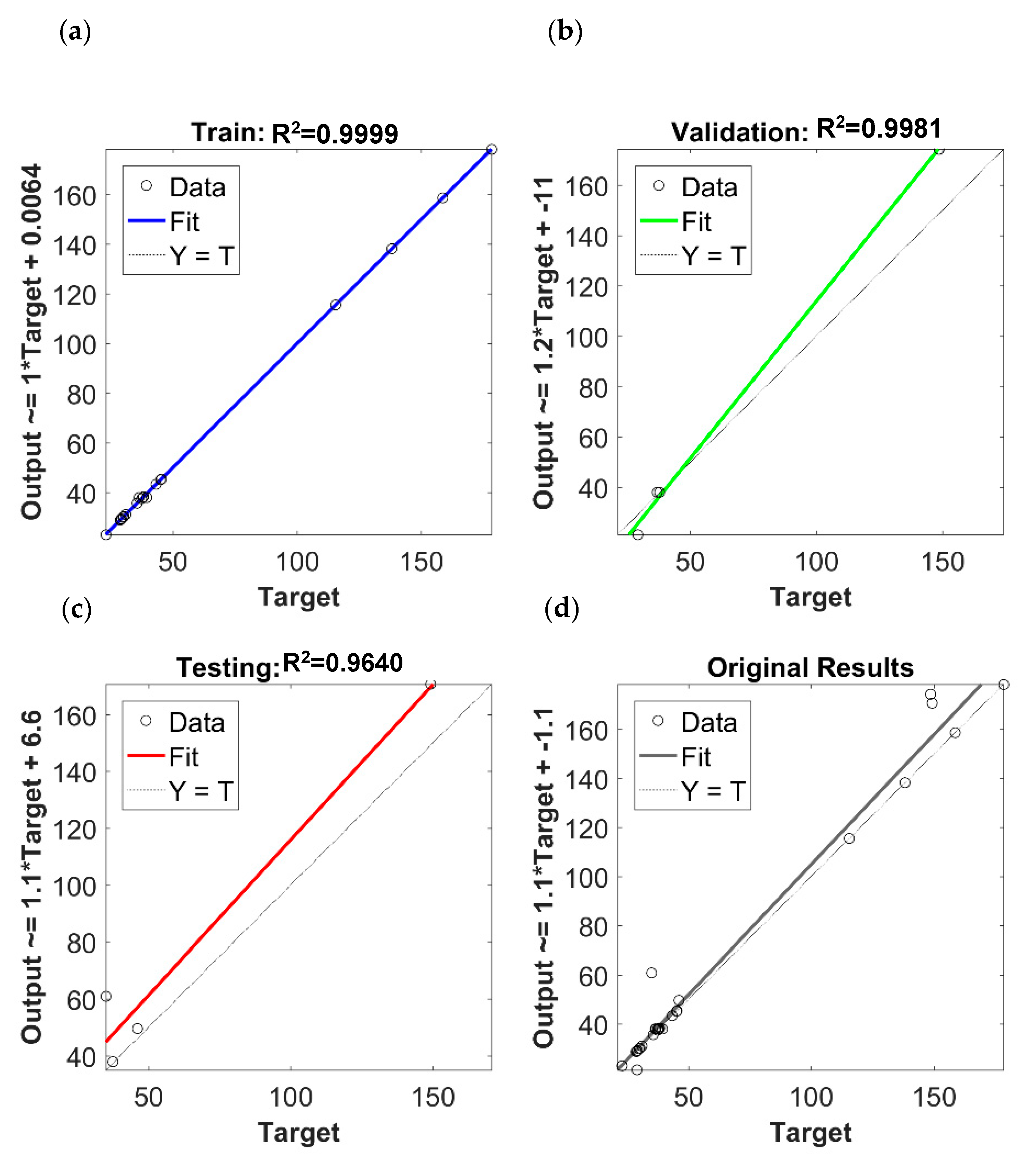
3.5. ANN Modeling
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fu, F.; Wang, Q. Removal of heavy metal ions from wastewaters: A review. J. Environ. Manag. 2011, 92, 407–418. [Google Scholar] [CrossRef]
- Tchounwou, P.B.; Yedjou, C.G.; Patlolla, A.K.; Sutton, D.J. Heavy Metal Toxicity and the Environment; Springer: Basel, Switzerland, 2012; pp. 133–164. [Google Scholar] [CrossRef] [Green Version]
- Xiarchos, I.; Jaworska, A.; Zakrzewska-Trznadel, G. Response surface methodology for the modelling of copper removal from aqueous solutions using micellar-enhanced ultrafiltration. J. Membr. Sci. 2008, 321, 222–231. [Google Scholar] [CrossRef]
- Landaburu-Aguirre, J.; Pongrácz, E.; Perämäki, P.; Keiski, R.L. Micellar-enhanced ultrafiltration for the removal of cadmium and zinc: Use of response surface methodology to improve understanding of process performance and optimisation. J. Hazard. Mater. 2010, 180, 524–534. [Google Scholar] [CrossRef] [PubMed]
- Tung, C.-C.; Yang, Y.-M.; Chang, C.-H.; Maa, J.-R. Removal of copper ions and dissolved phenol from water using micellar-enhanced ultrafiltration with mixed surfactants. Waste Manag. 2002, 22, 695–701. [Google Scholar] [CrossRef]
- Huang, J.; Yuan, F.; Zeng, G.; Li, X.; Gu, Y.; Shi, L.; Liu, W.; Shi, Y. Influence of pH on heavy metal speciation and removal from wastewater using micellar-enhanced ultrafiltration. Chemosphere 2017, 173, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Karate, V.D.; Marathe, K. Simultaneous removal of nickel and cobalt from aqueous stream by cross flow micellar enhanced ultrafiltration. J. Hazard. Mater. 2008, 157, 464–471. [Google Scholar] [CrossRef]
- Tanhaei, B.; Pourafshari Chenar, M.; Saghatoleslami, N.; Hesampour, M.; Kallioinen, M.; Sillanpää, M.; Mänttäri, M. Removal of nickel ions from aqueous solution by micellar-enhanced ultrafiltration, using mixed anionic–non-ionic surfactants. Sep. Purif. Technol. 2014, 138, 169–176. [Google Scholar] [CrossRef]
- Danis, U.; Aydiner, C. Investigation of process performance and fouling mechanisms in micellar-enhanced ultrafiltration of nickel-contaminated waters. J. Hazard. Mater. 2009, 162, 577–587. [Google Scholar] [CrossRef]
- Czitrom, V. One-factor-at-a-time versus designed experiments. Am. Stat. 1999, 53, 126–131. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John wiley & sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Ahmadi, M.; Vahabzadeh, F.; Bonakdarpour, B.; Mofarrah, E.; Mehranian, M. Application of the central composite design and response surface methodology to the advanced treatment of olive oil processing wastewater using Fenton’s peroxidation. J. Hazard. Mater. 2005, 123, 187–195. [Google Scholar] [CrossRef]
- Chavalparit, O.; Ongwandee, M. Optimizing electrocoagulation process for the treatment of biodiesel wastewater using response surface methodology. J. Environ. Sci. 2009, 21, 1491–1496. [Google Scholar] [CrossRef]
- Kiran, B.; Kaushik, A.; Kaushik, C.P. Response surface methodological approach for optimizing removal of Cr (VI) from aqueous solution using immobilized cyanobacterium. Chem. Eng. J. 2007, 126, 147–153. [Google Scholar] [CrossRef]
- Körbahti, B.K.; Aktaş, N.; Tanyolaç, A. Optimization of electrochemical treatment of industrial paint wastewater with response surface methodology. J. Hazard. Mater. 2007, 148, 83–90. [Google Scholar] [CrossRef] [PubMed]
- Sadri Moghaddam, S.; Alavi Moghaddam, M.R.; Arami, M. Coagulation/flocculation process for dye removal using sludge from water treatment plant: Optimization through response surface methodology. J. Hazard. Mater. 2010, 175, 651–657. [Google Scholar] [CrossRef]
- Wang, J.-P.; Chen, Y.-Z.; Ge, X.-W.; Yu, H.-Q. Optimization of coagulation–flocculation process for a paper-recycling wastewater treatment using response surface methodology. Colloids Surf. A Physicochem. Eng. Asp. 2007, 302, 204–210. [Google Scholar] [CrossRef]
- Zhu, X.; Tian, J.; Liu, R.; Chen, L. Optimization of Fenton and electro-Fenton oxidation of biologically treated coking wastewater using response surface methodology. Sep. Purif. Technol. 2011, 81, 444–450. [Google Scholar] [CrossRef]
- Landaburu-Aguirre, J.; García, V.; Pongrácz, E.; Keiski, R.L. The removal of zinc from synthetic wastewaters by micellar-enhanced ultrafiltration: Statistical design of experiments. Desalination 2009, 240, 262–269. [Google Scholar] [CrossRef]
- Desai, K.M.; Vaidya, B.K.; Singhal, R.S.; Bhagwat, S.S. Use of an artificial neural network in modeling yeast biomass and yield of β-glucan. Process Biochem. 2005, 40, 1617–1626. [Google Scholar] [CrossRef]
- Kasiri, M.; Aleboyeh, H.; Aleboyeh, A. Modeling and optimization of heterogeneous photo-fenton process with response surface methodology and artificial neural networks. Environ. Sci. Technol. 2008, 42, 7970–7975. [Google Scholar] [CrossRef]
- Yi, Q.-X.; Huang, J.-F.; Wang, F.-M.; Wang, X.-Z.; Liu, Z.-Y. Monitoring rice nitrogen status using hyperspectral reflectance and artificial neural network. Environ. Sci. Technol. 2007, 41, 6770–6775. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, B.; Chen, B.; Jing, L.; Zhu, Z.; Kazemi, K. Modeling and optimization of Newfoundland shrimp waste hydrolysis for microbial growth using response surface methodology and artificial neural networks. Mar. Pollut. Bull. 2016, 109, 245–252. [Google Scholar] [CrossRef] [PubMed]
- Balkin, S.D.; Lin, D.K. A neural network approach to response surface methodology. Commun. Stat. Theory Methods 2000, 29, 2215–2227. [Google Scholar] [CrossRef]
- Rahmanian, B.; Pakizeh, M.; Mansoori, S.A.A.; Esfandyari, M.; Jafari, D.; Maddah, H.; Maskooki, A. Prediction of MEUF process performance using artificial neural networks and ANFIS approaches. J. Taiwan Inst. Chem. Eng. 2012, 43, 558–565. [Google Scholar] [CrossRef]
- Rahmanian, B.; Pakizeh, M.; Mansoori, S.A.A.; Abedini, R. Application of experimental design approach and artificial neural network (ANN) for the determination of potential micellar-enhanced ultrafiltration process. J. Hazard. Mater. 2011, 187, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Rahmanian, B.; Pakizeh, M.; Esfandyari, M.; Heshmatnezhad, F.; Maskooki, A. Fuzzy modeling and simulation for lead removal using micellar-enhanced ultrafiltration (MEUF). J. Hazard. Mater. 2011, 192, 585–592. [Google Scholar] [CrossRef] [PubMed]
- Jana, D.K.; Roy, K.; Dey, S. Comparative assessment on lead removal using micellar-enhanced ultrafiltration (MEUF) based on a type-2 fuzzy logic and response surface methodology. Sep. Purif. Technol. 2018, 207, 28–41. [Google Scholar] [CrossRef]
- Lin, W.; Jing, L.; Zhu, Z.; Cai, Q.; Zhang, B. Removal of heavy metals from mining wastewater by micellar-enhanced ultrafiltration (MEUF): Experimental investigation and monte carlo-based artificial neural network modeling. Water Air Soil Pollut. 2017, 228, 206. [Google Scholar] [CrossRef]
- Jing, L.; Chen, B.; Zhang, B. Modeling of UV-induced photodegradation of naphthalene in marine oily wastewater by artificial neural networks. Water Air Soil Pollut. 2014, 225, 1–14. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, D.; Wang, X.; Huang, W.; Lawless, D.; Feng, X. Removal of heavy metals from water using polyvinylamine by polymer-enhanced ultrafiltration and flocculation. Sep. Purif. Technol. 2016, 158, 124–136. [Google Scholar] [CrossRef]
- Baek, K.; Yang, T.-W. Competitive bind of anionic metals with cetylpyridinium chloride micelle in micellar-enhanced ultrafiltration. Desalination 2004, 167, 101–110. [Google Scholar] [CrossRef]
- Bade, R.; Lee, S.-H. Chromate removal from wastewater using micellar enhanced ultrafiltration and activated carbon fibre processes; validation of experiment with mathematical equations. Environ. Eng. Res. 2008, 13, 98–104. [Google Scholar] [CrossRef]
- Kamble, S.; Marathe, K. Membrane characteristics and fouling study in MEUF for the removal of chromate anions from aqueous streams. Sep. Sci. Technol. 2005, 40, 3051–3070. [Google Scholar] [CrossRef]


| Solute | UF System (Surfactant and Flow) | RSM Design | Independent Variables | Optimization Model | References |
|---|---|---|---|---|---|
| Pb2+ | SDS, cross-flow | BBD (3 factors and 3 levels, 17 runs) | CSDS (2–6 mM), S/M (5–15), pH (2–12) | ANN and ANFIS | [25] |
| Zn2+ | SDS and Brij-35, cross-flow | FFD (7 factors, 22 runs) | Pressure, pH, CSDS, S/M, L/M, CNaCl, Brij35/SDS ratio | ANN, R2 > 0.91 | [26] |
| Pb2+ | SDS, cross-flow | BBD (3 factors, 3 levels) | CSDS (2–6 mM), S/M (5–15), pH (2–12) | Fuzzy logic models, R > 0.91 | [27] |
| Pb2+ | CTAB, cross-flow | BBD (3 factors, 3 levels) | CSDS (1.61–6.43 mM), S/M (5.64–13.8), pH (2.34–12.1) | Interval type-2 fuzzy logic | [28] |
| Properties | Specifications |
|---|---|
| Name | Sodium dodecyl sulfate (SDS) |
| Chemical structure |  |
| Ionic type | Anionic |
| Molecular weight | 288.38 g/mol |
| Critical micellar concentration (CMC) | 8.2-8.3 mM |
| Factors | Levels | ||
|---|---|---|---|
| Minimum (−1) | Center (0) | Maximum (+1) | |
| (A) Pressure (psi) | 30 | 40 | 50 |
| (B) Ni concentration (mM) | 0.5 | 1.25 | 2 |
| (C) SDS concentration (mM) | 8.3 | 16.6 | 24.9 |
| (D) Molecular weight cut-off, or MWCO (kDa) | 3 | 5* | 10 |
| Std. | Run | Factor Input Variables | Response Variable | ||||
|---|---|---|---|---|---|---|---|
| Factor A Pressure (psi) | Factor B Ni conc. (Mm) | Factor C SDS conc. (Mm) | Factor D MWCO (kDa) | Rejection a (%) | Flux a (L/h∙m2) | ||
| 13 | 1 | 40 | 0.5 | 8.3 | 5 | 94.86 | 37.93 |
| 18 | 2 | 50 | 1.25 | 8.3 | 5 | 92.98 | 45.15 |
| 25 | 3 | 40 | 1.25 | 16.6 | 5 | 98.13 | 36.83 |
| 7 | 4 | 40 | 1.25 | 8.3 | 10 | 94.30 | 158.67 |
| 29 | 5 | 40 | 1.25 | 16.6 | 5 | 97.09 | 37.43 |
| 20 | 6 | 50 | 1.25 | 24.9 | 5 | 98.13 | 43.31 |
| 6 | 7 | 40 | 1.25 | 24.9 | 3 | 97.15 | 29.96 |
| 19 | 8 | 30 | 1.25 | 24.9 | 5 | 98.17 | 28.74 |
| 22 | 9 | 40 | 2 | 16.6 | 3 | 97.98 | 31.03 |
| 23 | 10 | 40 | 0.5 | 16.6 | 10 | 97.76 | 148.64 |
| 14 | 11 | 40 | 2 | 8.3 | 5 | 88.06 | 37.41 |
| 10 | 12 | 50 | 1.25 | 16.6 | 3 | 98.67 | 38.25 |
| 3 | 13 | 30 | 2 | 16.6 | 5 | 96.15 | 29.27 |
| 28 | 14 | 40 | 1.25 | 16.6 | 5 | 96.59 | 39.51 |
| 11 | 15 | 30 | 1.25 | 16.6 | 10 | 97.84 | 115.56 |
| 27 | 16 | 40 | 1.25 | 16.6 | 5 | 96.32 | 37.78 |
| 9 | 17 | 30 | 1.25 | 16.6 | 3 | 98.70 | 23.03 |
| 26 | 18 | 40 | 1.25 | 16.6 | 5 | 96.47 | 36.45 |
| 8 | 19 | 40 | 1.25 | 24.9 | 10 | 80.53 b | 149.23 |
| 4 | 20 | 50 | 2 | 16.6 | 5 | 95.70 | 45.36 |
| 2 | 21 | 50 | 0.5 | 16.6 | 5 | 95.08 | 46.16 |
| 17 | 22 | 30 | 1.25 | 8.3 | 5 | 91.31 | 28.78 |
| 16 | 23 | 40 | 2 | 24.9 | 5 | 98.20 | 35.00 |
| 21 | 24 | 40 | 0.5 | 16.6 | 3 | 98.40 | 29.10 |
| 1 | 25 | 30 | 0.5 | 16.6 | 5 | 90.43 b | 30.19 |
| 12 | 26 | 50 | 1.25 | 16.6 | 10 | 91.83 | 178.28 |
| 15 | 27 | 40 | 0.5 | 24.9 | 5 | 96.94 | 35.67 |
| 24 | 28 | 40 | 2 | 16.6 | 10 | 93.53 | 138.17 |
| 5 | 29 | 40 | 1.25 | 8.3 | 3 | 92.61 | 28.96 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 158.79 | 8 | 19.85 | 12.61 | <0.0001 | significant |
| A-Pressure | 12.24 | 1 | 12.24 | 7.78 | 0.0121 | |
| B-C-Ni | 10.51 | 1 | 10.51 | 6.68 | 0.0187 | |
| C-C-SDS | 17.18 | 1 | 17.18 | 10.92 | 0.0039 | |
| D-MWCO | 13.18 | 1 | 13.18 | 8.37 | 0.0097 | |
| AD | 12.10 | 1 | 12.10 | 7.69 | 0.0125 | |
| BC | 16.26 | 1 | 16.26 | 10.33 | 0.0048 | |
| CD | 7.33 | 1 | 7.33 | 4.66 | 0.0447 | |
| C² | 27.39 | 1 | 27.39 | 17.40 | 0.0006 | |
| Residual | 28.33 | 18 | 1.57 | |||
| Lack of Fit | 26.16 | 14 | 1.87 | 3.46 | 0.1200 | not significant |
| Pure Error | 2.16 | 4 | 0.5409 | |||
| Cor Total | 187.12 | 26 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 10.68 | 4 | 2.67 | 2173.32 | <0.0001 | significant |
| A-Pressure | 0.5914 | 1 | 0.5914 | 481.41 | <0.0001 | |
| C-C-SDS | 0.0033 | 1 | 0.0033 | 2.67 | 0.1151 | |
| D-MWCO | 7.65 | 1 | 7.65 | 6229.95 | <0.0001 | |
| D² | 0.3832 | 1 | 0.3832 | 311.97 | <0.0001 | |
| Residual | 0.0295 | 24 | 0.0012 | |||
| Lack of Fit | 0.0256 | 20 | 0.0013 | 1.31 | 0.4387 | not significant |
| Pure Error | 0.0039 | 4 | 0.0010 | |||
| Cor Total | 10.71 | 28 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.; Jing, L.; Zhang, B. Micellar-Enhanced Ultrafiltration to Remove Nickel Ions: A Response Surface Method and Artificial Neural Network Optimization. Water 2020, 12, 1269. https://doi.org/10.3390/w12051269
Lin W, Jing L, Zhang B. Micellar-Enhanced Ultrafiltration to Remove Nickel Ions: A Response Surface Method and Artificial Neural Network Optimization. Water. 2020; 12(5):1269. https://doi.org/10.3390/w12051269
Chicago/Turabian StyleLin, Weiyun, Liang Jing, and Baiyu Zhang. 2020. "Micellar-Enhanced Ultrafiltration to Remove Nickel Ions: A Response Surface Method and Artificial Neural Network Optimization" Water 12, no. 5: 1269. https://doi.org/10.3390/w12051269
APA StyleLin, W., Jing, L., & Zhang, B. (2020). Micellar-Enhanced Ultrafiltration to Remove Nickel Ions: A Response Surface Method and Artificial Neural Network Optimization. Water, 12(5), 1269. https://doi.org/10.3390/w12051269






