Hydrologic Validation of MERGE Precipitation Products over Anthropogenic Watersheds
Abstract
:1. Introduction
2. Material and Methods
2.1. Study Area
2.2. Evaluation of Satellite Precipitation Data
2.2.1. Precipitation Data Sources and Preparation
2.2.2. Statistical Evaluation
2.3. Hydrologic Validation of Satellite Precipitation Data
2.3.1. Hydrologic Data Sources and Preparation
2.3.2. MGB-IPH
3. Results and Discussion
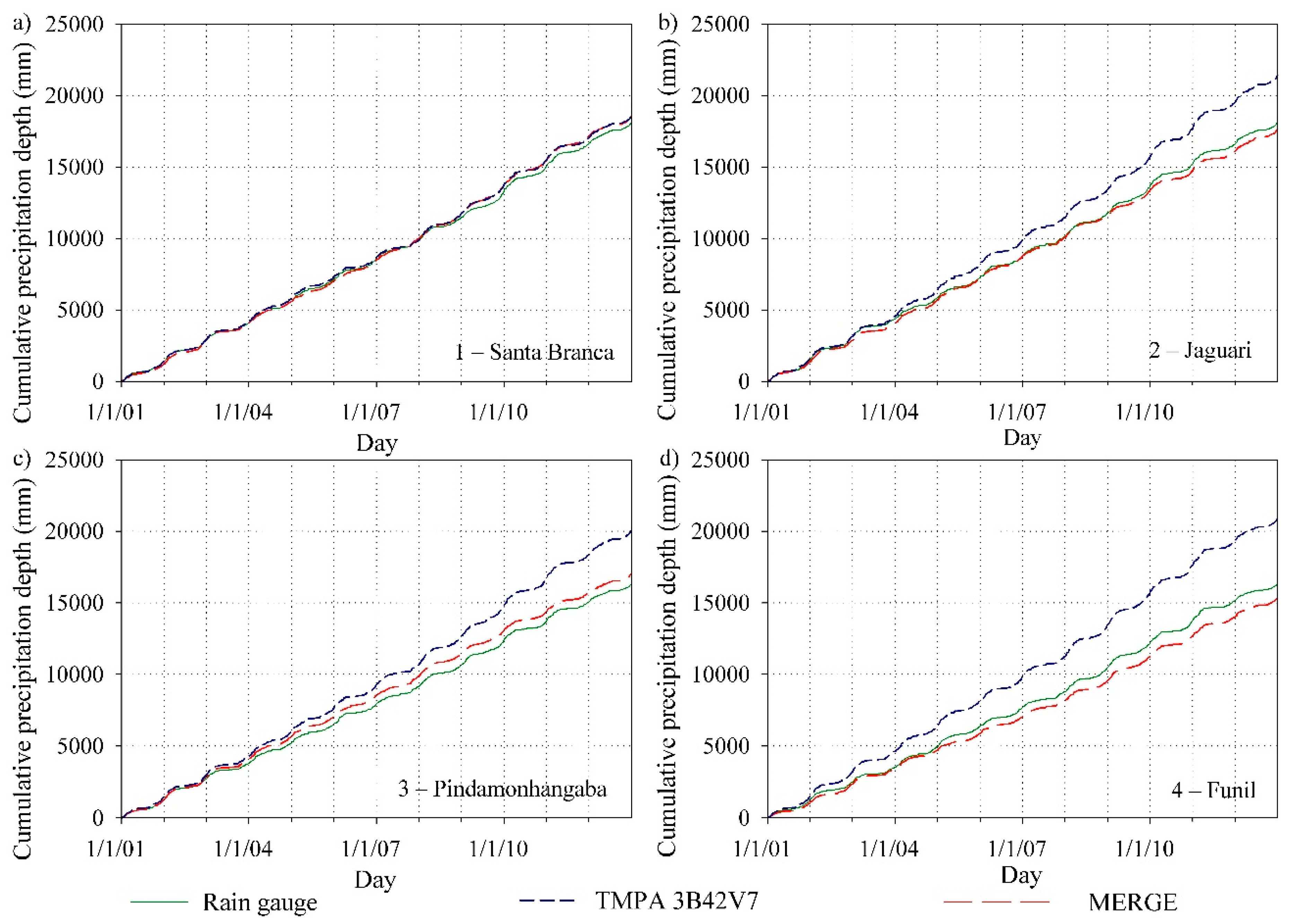
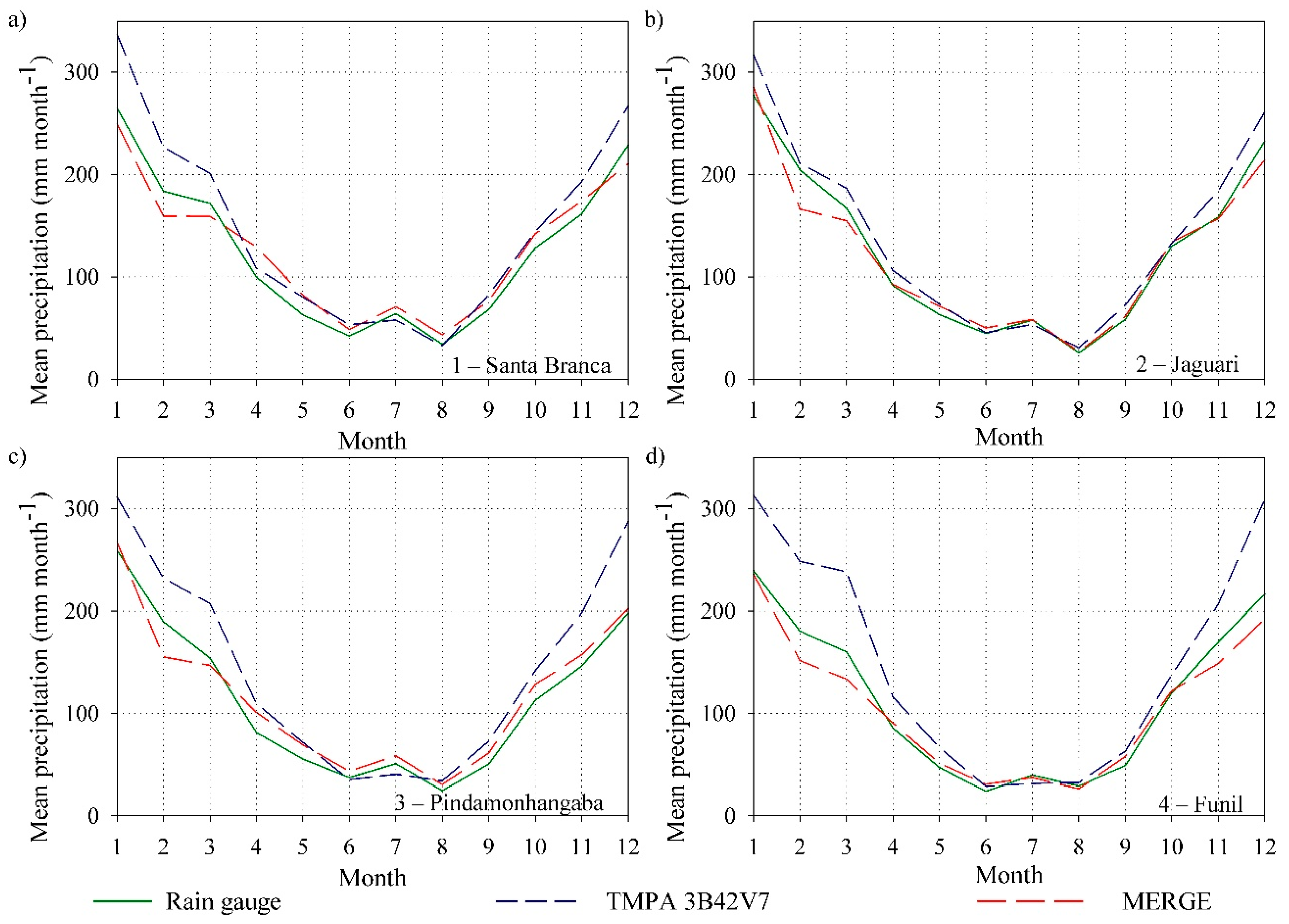
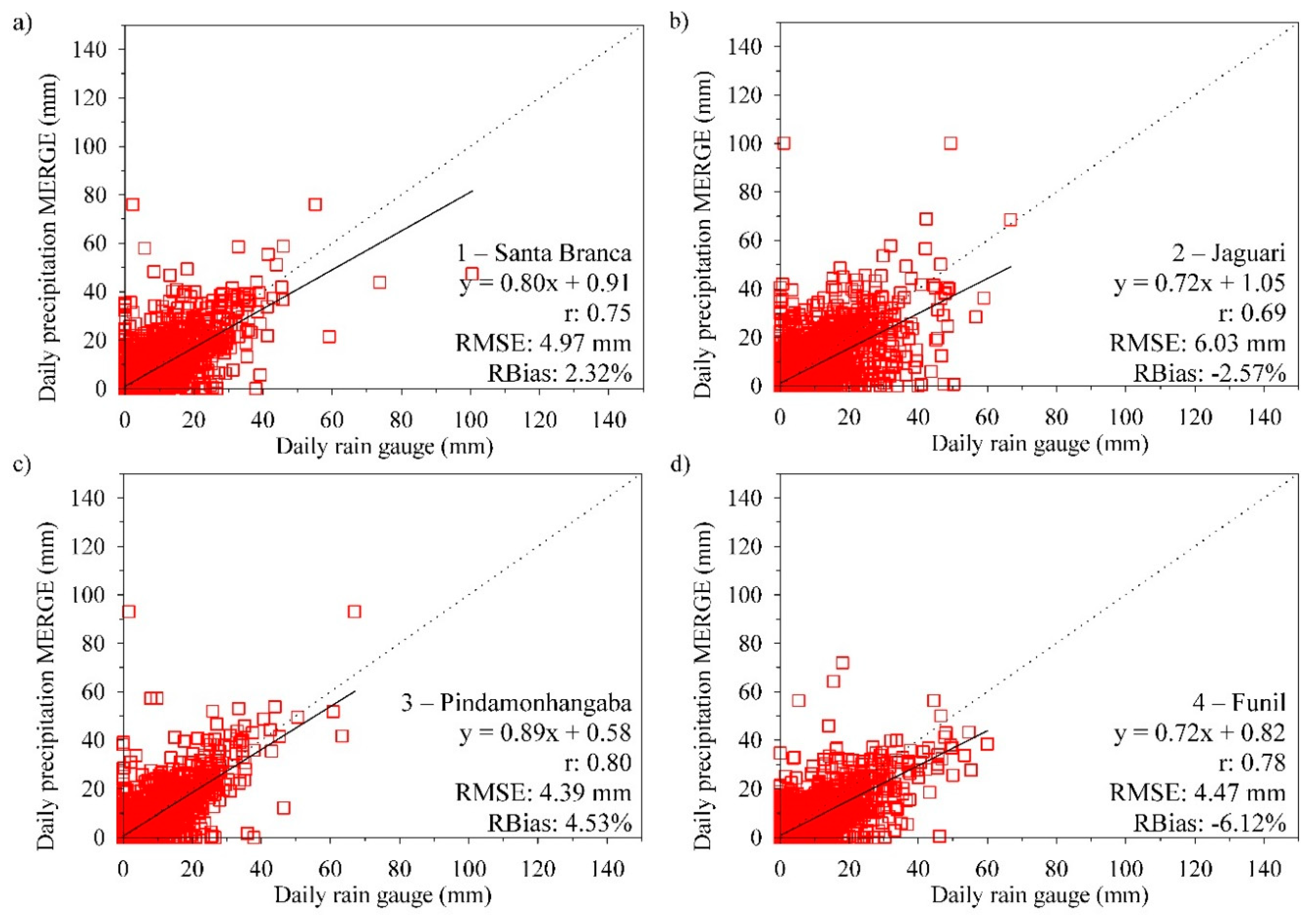
3.1. Statistical Validation of TMPA 3b42v7 and MERGE Products
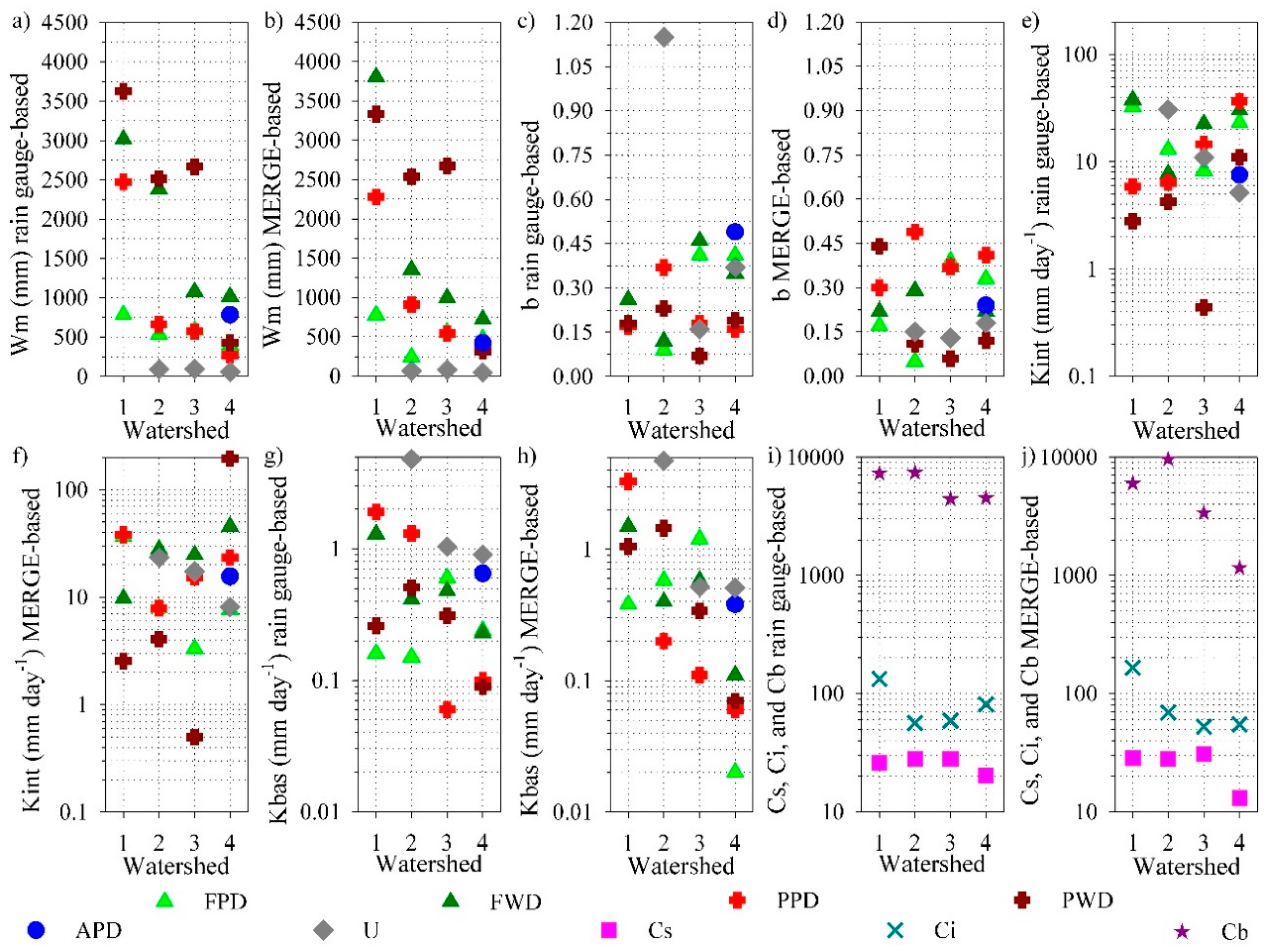
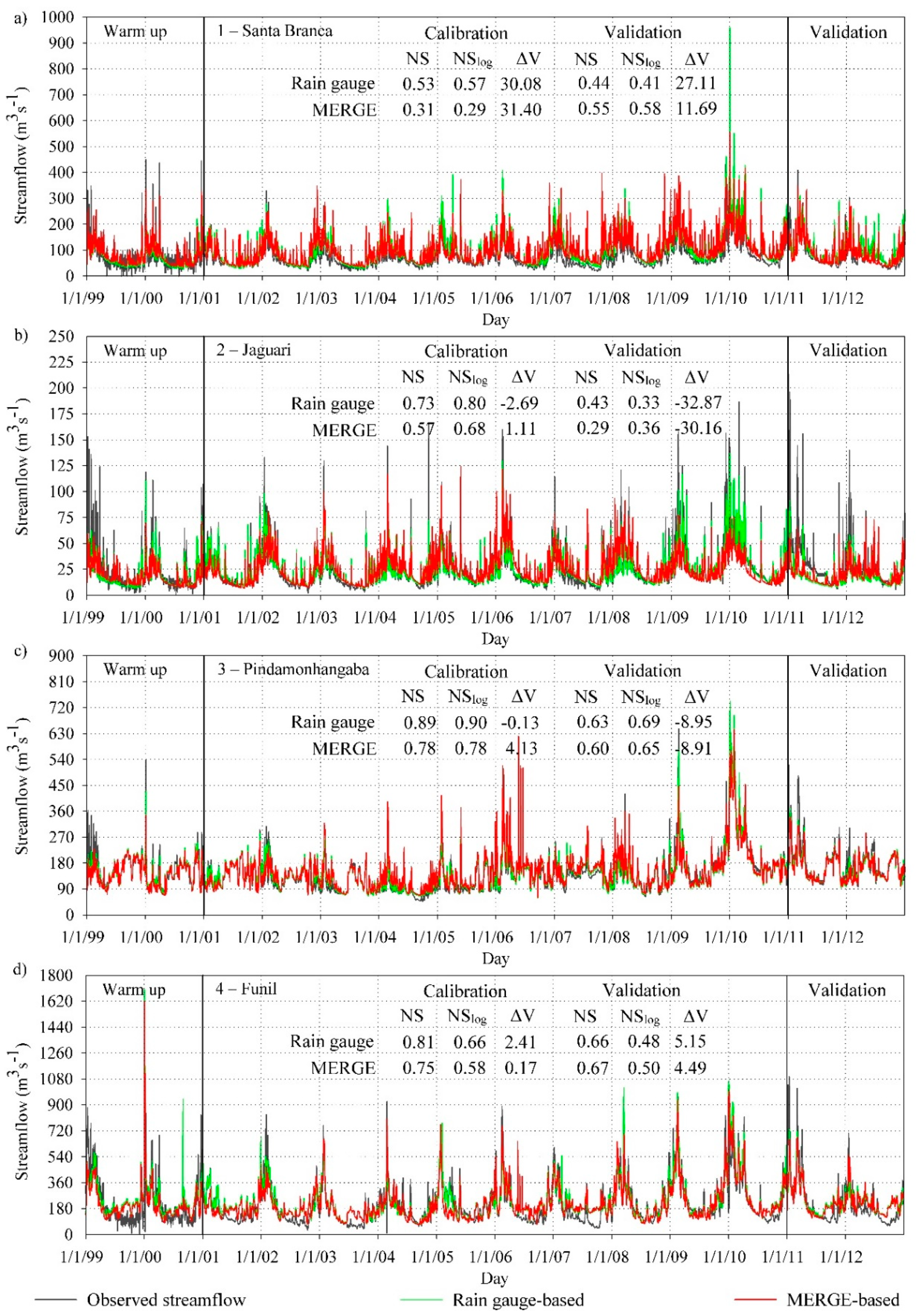
3.2. Hydrologic Validation of MERGE Products
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tong, K.; Fengge, S.; Yang, D.; Hao, Z. Evaluation of satellite precipitation retrievals and their potential utilities in hydrologic modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Maathuis, B.; Adem, A.A.; Demissie, S.S.; Langan, S.; Steenhuis, T.S. Comparison of rainfall estimations by TRMM 3B42, MPEG and CFSR with ground-observed data for the Lake Tana basin in Ethiopia. Hydrol. Earth Syst. Sci. 2014, 18, 4871–4881. [Google Scholar] [CrossRef] [Green Version]
- Shukla, A.K.; Ojha, P.S.C.; Singh, R.P.; Pal, L.; Fu, D. Evaluation of TRMM Precipitation Dataser over Himalayan Catchment: The Upper Ganga Basin, India. Water 2019, 11, 613. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Christakos, G.; Ding, X.; Wu, J. Adequacy of TRMM satellite data in driving the SWAT modeling of Tiaoxi catchment (Taihu lake basin, China). J. Hydrol. 2018, 556, 1139–1152. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Lu, H.; Khem, S.; Yang, K.; Huang, X. Evaluation of Three Satellite-Based Precipitation Products Over the Lower Mekong River Basin Using Rain Gauge Observations and Hydrological Modeling. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2357–2373. [Google Scholar] [CrossRef]
- Scheel, M.L.M.; Rohrer, M.; Huggel, C.; Villar, D.S.; Silvestre, E.; Huffman, G.J. Evaluation of TRMM Multi-satellite Precipitation Analysis (TMPA) performance in the Central Andes region and its dependency on spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2011, 15, 2649–2663. [Google Scholar] [CrossRef] [Green Version]
- Ouma, Y.O.; Owiti, T.; Kipkorir, E.; Kibiiy, J.; Tateishi, R. Multitemporal comparative analysis of TRMM-3B42 satellite-estimated rainfall with surface gauge data at basin scales: Daily, decadal and monthly evaluations. Int. J. Remote Sens. 2012, 33, 7662–7684. [Google Scholar] [CrossRef]
- Młyński, D.; Wałęga, A.; Petroselli, A.; Tauro, F.; Cebulska, M. Estimating Maximum Daily Precipitation in the Upper Vistula Basin, Poland. Atmosphere 2019, 10, 43. [Google Scholar] [CrossRef] [Green Version]
- Moazami, S.; Golian, S.; Kavianpour, M.R.; Hong, Y. Comparison of PERSIANN and V7 TRMM Multi-satellite Precipitation Analysis (TMPA) products with rain gauge data over Iran. Int. J. Remote Sens. 2013, 34, 8156–8171. [Google Scholar] [CrossRef]
- Gilewski, P.; Nawalany, M. Inter-Comparison of Rain-Gauge, Radar, and Satellite (IMERG GPM) Precipitation Estimates Performance for Rainfall-Runoff Modeling in a Mountainous Catchment in Poland. Water 2018, 10, 1665. [Google Scholar] [CrossRef] [Green Version]
- Price, K.; Purucker, S.T.; Kraemer, S.R.; Babendreier, J.E.; Knightes, C.D. Comparison of radar and gauge precipitation data in watershed models across varying spatial and temporal scales. Hydrol. Process. 2014, 28, 3505–3520. [Google Scholar] [CrossRef]
- Tong, K.; Zhao, Y.; Wei, Y.; Hu, B.; Lu, Y. Evaluation and Hydrological Validation of GPM Precipitation Products over the Nanliu River Basin, Beibu Gulf. Water 2018, 10, 1777. [Google Scholar] [CrossRef] [Green Version]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Hossain, F.; Gebremichael, M.; Borga, M. Understanding the Scale Relationships of Uncertainty Propagation of Satellite Rainfall through a Distributed Hydrologic Model. J. Hydrometeor. 2010, 11, 520–532. [Google Scholar] [CrossRef]
- Li, X.H.; Zhang, Q.; Xu, C.Y. Suitability of the TRMM satellite rainfalls in driving a distributed hydrological model for water balance computations in Xinjiang catchment, Poyang lake basin. J. Hydrol. 2012, 426, 28–38. [Google Scholar] [CrossRef]
- Chokngamwong, R.; Chiu, L.S. Thailand Daily Rainfall and Comparison with TRMM Products. J. Hydrometeor. 2008, 9, 256–266. [Google Scholar] [CrossRef]
- Tobin, K.J.; Bennett, M.E. Using SWAT to model streamflow in two river basins with ground and satellite precipitation data. J. Am. Water Resour. Assoc. 2009, 45, 253–271. [Google Scholar] [CrossRef]
- Dinku, T.; Connor, S.J.; Ceccato, P. Comparison of CMORPH and TRMM-3B42 over Mountainous Regions of Africa and South America. In Satellite Rainfall Applications for Surface Hydrology, 1st ed.; Gebremichael, M., Hossain, F., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 193–204. [Google Scholar]
- Bitew, M.M.; Gebremichael, M. Evaluation of satellite rainfall products through hydrologic simulation in a fully distributed hydrologic model. Water Resour. Res. 2011, 47, W06526. [Google Scholar] [CrossRef]
- Liechti, T.C.; Matos, J.P.; Boillat, J.L.; Schleiss, A.J. Comparison and evaluation of satellite derived precipitation products for hydrological modeling of the Zambezi River Basin. Hydrol. Earth Syst. Sci. 2012, 16, 489–500. [Google Scholar] [CrossRef] [Green Version]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; Roo, A.D. Hydrological evaluation of satellite-based rainfall estimates over the Volta and Boro-Akobo Basin. J. Hydrol. 2013, 499, 324–338. [Google Scholar] [CrossRef]
- Maggioni, V.; Meyers, P.C.; Robinson, M.D. A Review of Merged High-Resolution Satellite Precipitation Product Accuracy during the Tropical Rainfall Measuring Mission (TRMM) Era. J. Hydrometeor. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
- Reis, J.B.C.; Rennó, C.D.; Lopes, E.S.S. Validation of Satellite Rainfall Products over a Mountainous Watershed in a Humid Subtropical Climate Region of Brazil. Remote Sens. 2017, 9, 1240. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Tian, J.; Huang, Y.; Chen, X.; Chen, S.; Duan, Z. Hydrologic Evaluation of TRMM and GPM IMERG Satellite-Based Precipitation in a Humid Basin of China. Remote Sens. 2019, 11, 431. [Google Scholar] [CrossRef] [Green Version]
- Nerini, D.; Zulkafli, Z.; Wang, L.P.; Onof, C.; Buytaert, W.; Lavado-Casimiro, W.; Guyot, J.L. A Comparative Analysis of TRMM-Rain Gauge Data Merging Techniques at the Daily Time Scale for Distributed Rainfall-Runoff Modeling Applications. J. Hydrometeor. 2015, 16, 2153–2168. [Google Scholar] [CrossRef] [Green Version]
- Rozante, J.R.; Moreira, D.S.; Gonçalves, L.G.G.; Vila, D.A. Combining TRMM and Surface Observations of Precipitation: Technique and Validation over South America. Weather Forecast 2010, 25, 885–894. [Google Scholar] [CrossRef] [Green Version]
- Nair, S.; Srinivasan, G.; Nemani, R. Evaluation of Multi-Satellite TRMM Derived Rainfall Estimates over a Western State of India. J. Meteorol. Soc. Jpn. 2009, 87, 927–939. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Hong, Y.; Gourley, J.J.; Huffman, G.J.; Tian, Y.; Cao, Q.; Yong, B.; Kirstetter, P.E.; Hu, J.; Hardy, J.; et al. Evaluation of the successive V6 and V7 TRMM multisatellite precipitation analysis over the Continental United States. Water Resour. Res. 2013, 49, 8174–8186. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I. Evaluation of remote-sensing-based rainfall products through predictive capacity in hydrological runoff modelling. Hydrol. Process. 2010, 24, 879–891. [Google Scholar] [CrossRef]
- Kahn, J.R.; Vásquez, W.F.; Rezende, C.E. Choice modeling of system-wide or large scale environmental change in a developing country context: Lessons from Paraíba do Sul River. Sci. Total Environ. 2017, 598, 488–496. [Google Scholar] [CrossRef]
- Marques, J.S.J.; Dittmar, T.; Niggemann, J.; Almeida, M.G.; Gomez-Saez, G.V.G.; Rezende, C.E. Dissolved Black Carbon in the Headwaters-to-Ocean Continuum of Paraíba Do Sul River, Brazil. Front. Earth Sci. 2017, 5, 11. [Google Scholar] [CrossRef] [Green Version]
- Marengo, J.A.; Alves, L.M. Tendências Hidrológicas da Bacia do Rio Paraíba do Sul. Rev. Bras. Meteorol. 2005, 2, 215–226. [Google Scholar]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; Gonçalves, J.L.M.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef]
- Projeto RADAMBRASIL—Folhas SF. 23/24, Rio de Janeiro/Vitória: Geologia, Geomorfologia, Pedologia, Vegetação, uso Potencial da Terra. 1983. Available online: https://biblioteca.ibge.gov.br/index.php/bibliotecacatalogo?view=detalhes&id=217129 (accessed on 1 April 2019).
- MapBiomas Project—Collection [Version 3.1] of the Annual Land Use Land Cover Maps of Brazil. Available online: http://mapbiomas.org/en (accessed on 25 March 2019).
- ANA—Agência Nacional de Águas, Sistema Nacional de Informações sobre Recursos Hídricos, Portal Hidroweb. Available online: http://www.snirh.gov.br/hidroweb/publico/apresentacao.jsf (accessed on 5 April 2019).
- Viessman, G.; Lewis, G.L. Introduction to Hydrology, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2003; p. 624. [Google Scholar]
- Xue, X.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of TRMM-based Multi-satellite Precipitation Analysis over the Wangchu Basin of Bhutan: Ate the latest satellite precipitation products 3B42V7 ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
- CPTEC—MERGE, Centro de Previsão de Tempo e Estudos Climáticos. Available online: http://ftp.cptec.inpe.br/modelos/io/produtos/MERGE/ (accessed on 12 April 2019).
- NASA—National Aeronautics and Space Administration, TRMM. Available online: https://pmm.nasa.gov/data-access/downloads/trmm (accessed on 2 May 2019).
- Franchito, S.H.; Rao, V.B.; Vasques, A.C.; Santo, C.M.E.; Conforte, J.V. Validation of TRMM precipitation radar monthly rainfall estimates over Brazil. J. Geophys. Res. 2009, 144, D02105. [Google Scholar] [CrossRef] [Green Version]
- Collischonn, W.; Allasia, D.; Silva, B.C.; Tucci, E.M. The MGB-IPH model for large-scale raingall-runoff modelling. Hydrol. Sci. J. 2007, 52, 878–895. [Google Scholar] [CrossRef] [Green Version]
- Pontes, P.R.M.P.; Fan, F.M.; Fleischmann, A.S.; Paiva, R.C.D.; Buarque, D.C.; Siqueira, V.A.; Jardim, P.F.; Sorribas, M.V.; Collischonn, W. MGB-IPH model for hydrological and hydraulic simulations of large floodplain river systems coupled with open source GIS. Environ. Model. Softw. 2017, 94, 1–20. [Google Scholar] [CrossRef]
- Guilhon, L.G.F.; Rocha, V.F.; Moreira, J.C. Comparação de Métodos de Previsão de Vazões Naturais Afluentes a Aproveitamentos Hidroelétricos. Rev. Bras. Recur. Hídricos 2007, 12, 13–20. [Google Scholar]
- ONS—Operador Nacional do Sistema Elétrico. Available online: https://www.ana.gov.br/sar/sin/b_paraiba-do-sul (accessed on 1 August 2019).
- Oliveira, V.A.; Mello, C.R.; Viola, M.R.; Srinivasan, R. Assessment of climate change impacts on streamflows and hydrolpower potential in the headwater region of the Grande river basin, Southeastern Brazil. Int. J. Climatol. 2017, 37, 5005–5023. [Google Scholar] [CrossRef]
- Medeiros, M.S.; Fleischmann, A.S.; Oliveira, A.M.; Corati, B.K.; Fan, F.M.; Martinbiacho, G.K.; Jargim, P.F.; Correa, S.W.; Siqueira, V.A.; Collischonn, W. Personal Communication, Manual de Exemplo de Aplicação do Modelo MGB 2018 Utilizando o IPH-Hydro Tools; Hidrologia de Grande Escala-Instituto de Pesquisas Hidráulicas UFRGS: Porto Alegre, Brazil, 2018. [Google Scholar]
- INMET—Instituto Nacional de Meteorologia, Normais Climatológicas do Brasil 1961–1990. Available online: http://www.inmet.gov.br/portal/index.php?r=clima/normaisClimatologicas (accessed on 14 May 2019).
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar]
- Van Liew, M.W.; Arnold, J.G.; Garbrecht, J.D. Hydrologic simulations on agricultural watersheds: Choosing between two models. Trans. ASABE 2003, 46, 1539–1551. [Google Scholar] [CrossRef]
- Falck, A.S.; Maggioni, V.; Tomasella, J.; Vila, D.A.; Diniz, F.L.R. Propagation of satellite precipitation uncertainties through a distributed hydrologic model: A case study in the Tocantins-Araguaia Basin in Brazil. J. Hydrol. 2015, 527, 943–957. [Google Scholar] [CrossRef]
- Collischonn, W. Simulação Hidrológica de Grandes Bacias. Ph.D. Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, December 2001. [Google Scholar]
- Silva, B.C. Previsão Hidroclimática de Vazão para a Bacia do Rio São Francisco. Ph.D. Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, October 2005. [Google Scholar]
- Viola, M.R.; Mello, C.R.; Chow, S.C.; Yanagi, S.C.; Gomes, J.L. Assessing climate change impacts on Upper Grande River Basin hydrology, Southeastern Brazil. Int. J. Climatol. 2015, 35, 1054–1068. [Google Scholar] [CrossRef]
- Nippgen, F.; McGlynn, B.L.; Emanuel, R.E.; Vose, J.M. Watershed memory at the Coweeta Hydrology Laboratory: The effect of past precipitation and storage on hydrologic response. Water Resour. Res. 2016, 52, 1673–1695. [Google Scholar] [CrossRef] [Green Version]
- Klemeš, V. Operational testing of hydrological simulation. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Foy, C.; Arabi, M.; Yen, H.; Gironás, J.; Bailey, R.T. Multisite Assessment of Hydrologic Processes in Snow-Dominated Mountainous River Basins in Colorado Using a Watersheds Model. J. Hydrol. Eng. 2015, 20, 04015017. [Google Scholar] [CrossRef]
- Weedon, G.P.; Prudhomme, C.; Crooks, S.; Ellis, R.J.; Folwell, S.S.; Best, M.J. Evaluating the Performance of Hydrological Models via Cross-Spectral Analysis: Case Study of the Thames Basin, United Kingdom. J. Hydrometeor. 2015, 16, 214–231. [Google Scholar] [CrossRef] [Green Version]
- Bui, H.T.; Ishidaira, H.; Shaowei, N. Evaluation of the use of global satellite-gauge and satellite-only precipitation products in stream flow simulations. Appl. Water Sci. 2019, 9, 1–15. [Google Scholar] [CrossRef] [Green Version]



| Data | Variable (Unit) | Spatial Resolution | Agency |
|---|---|---|---|
| SRTM—DEM | Altitude (m) | 30 m | USGS |
| MapBiomas | Land cover class (-) | 30 m | MapBiomas |
| RADAMBRASIL | Soil class (-) | 1:250,000 | IBGE |
| Rain gauge network | Precipitation (mm day−1) | Point | ANA |
| TMPA 3B42 | Precipitation (mm day−1) | ~25 km | NASA |
| MERGE | Precipitation (mm day−1) | 20 km | CPTEC |
| Observed streamflow | Streamflow (m3 s−1) | Point | ANA |
| Naturalized streamflow | Streamflow (m3 s−1) | Point | ONS |
| Meteorological variables | Temperature (°C), relative humidity (%), insolation (h day−1), wind speed (m s−1) e atmospheric pressure (kPa) | Point | INMET |
| Watershed | HRU (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| FPD | FWD | PPD | PWD | APD | AWD | R | U | W | |
| 1 | 20.64 | 17.99 | 27.33 | 30.57 | 0.01 | 0.00 | 0.01 | 0.24 | 3.21 |
| 2 | 3.33 | 43.46 | 1.22 | 47.87 | 0.00 | 0.00 | 0.03 | 0.91 | 3.17 |
| 3 | 4.05 | 24.65 | 10.06 | 53.02 | 0.05 | 0.01 | 0.07 | 7.53 | 0.55 |
| 4 | 16.97 | 14.02 | 14.69 | 50.17 | 0.75 | 0.10 | 0.06 | 2.69 | 0.55 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cassalho, F.; Daleles Rennó, C.; Bosco Coura dos Reis, J.; Cláudio da Silva, B. Hydrologic Validation of MERGE Precipitation Products over Anthropogenic Watersheds. Water 2020, 12, 1268. https://doi.org/10.3390/w12051268
Cassalho F, Daleles Rennó C, Bosco Coura dos Reis J, Cláudio da Silva B. Hydrologic Validation of MERGE Precipitation Products over Anthropogenic Watersheds. Water. 2020; 12(5):1268. https://doi.org/10.3390/w12051268
Chicago/Turabian StyleCassalho, Felício, Camilo Daleles Rennó, João Bosco Coura dos Reis, and Benedito Cláudio da Silva. 2020. "Hydrologic Validation of MERGE Precipitation Products over Anthropogenic Watersheds" Water 12, no. 5: 1268. https://doi.org/10.3390/w12051268
APA StyleCassalho, F., Daleles Rennó, C., Bosco Coura dos Reis, J., & Cláudio da Silva, B. (2020). Hydrologic Validation of MERGE Precipitation Products over Anthropogenic Watersheds. Water, 12(5), 1268. https://doi.org/10.3390/w12051268





