Tendency of Runoff and Sediment Variety and Multiple Time Scale Wavelet Analysis in Hongze Lake during 1975–2015
Abstract
:1. Introduction
2. Materials and Methods
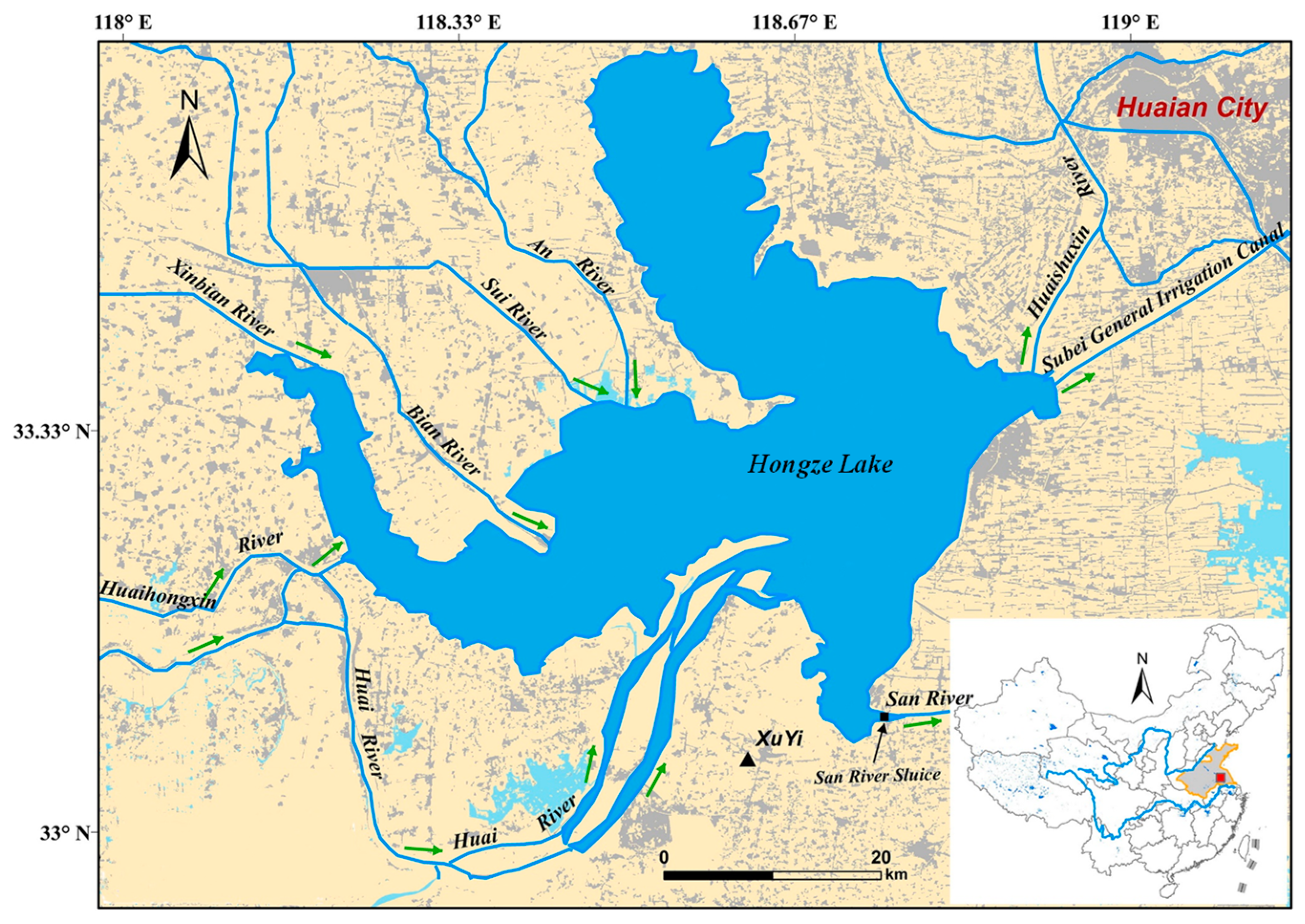
2.1. Research Areas and Data
2.2. Combinatorial Mutation Test Method
2.2.1. M–K Test
2.2.2. Pettitt Test
2.2.3. Combinatorial Test
2.3. Wavelet Analysis Method
2.3.1. Wavelet Function
2.3.2. Wavelet Transform
2.3.3. Wavelet Variance
3. Results and Discussion
3.1. Spatial and Temporal Distribution of Runoff and Sediment
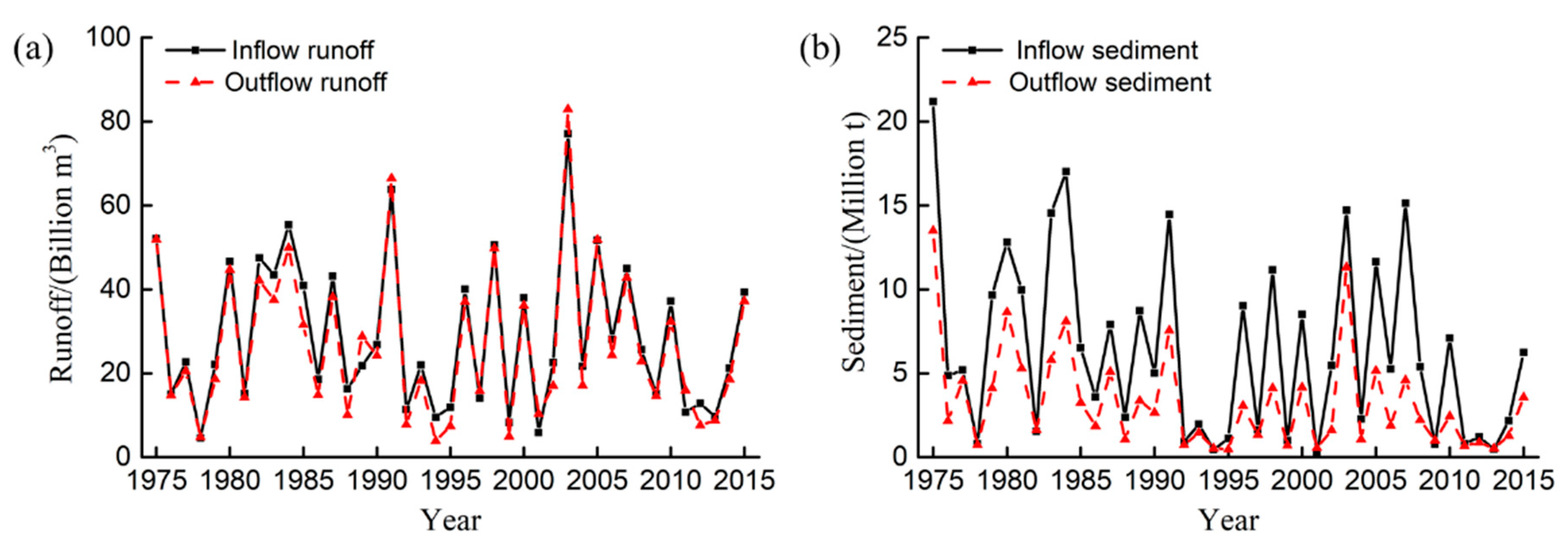
3.1.1. Runoff and Sediment Trend Analysis
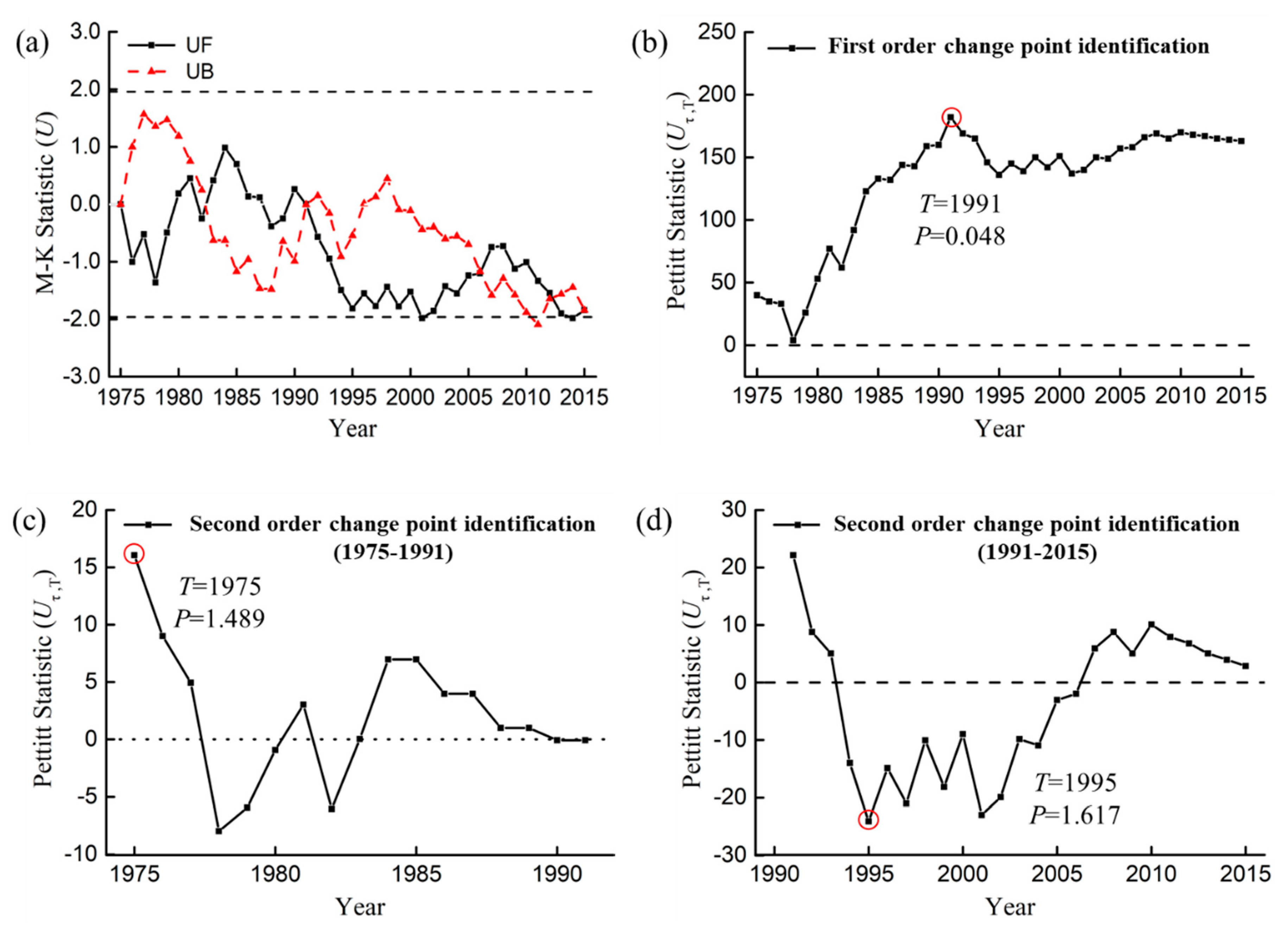
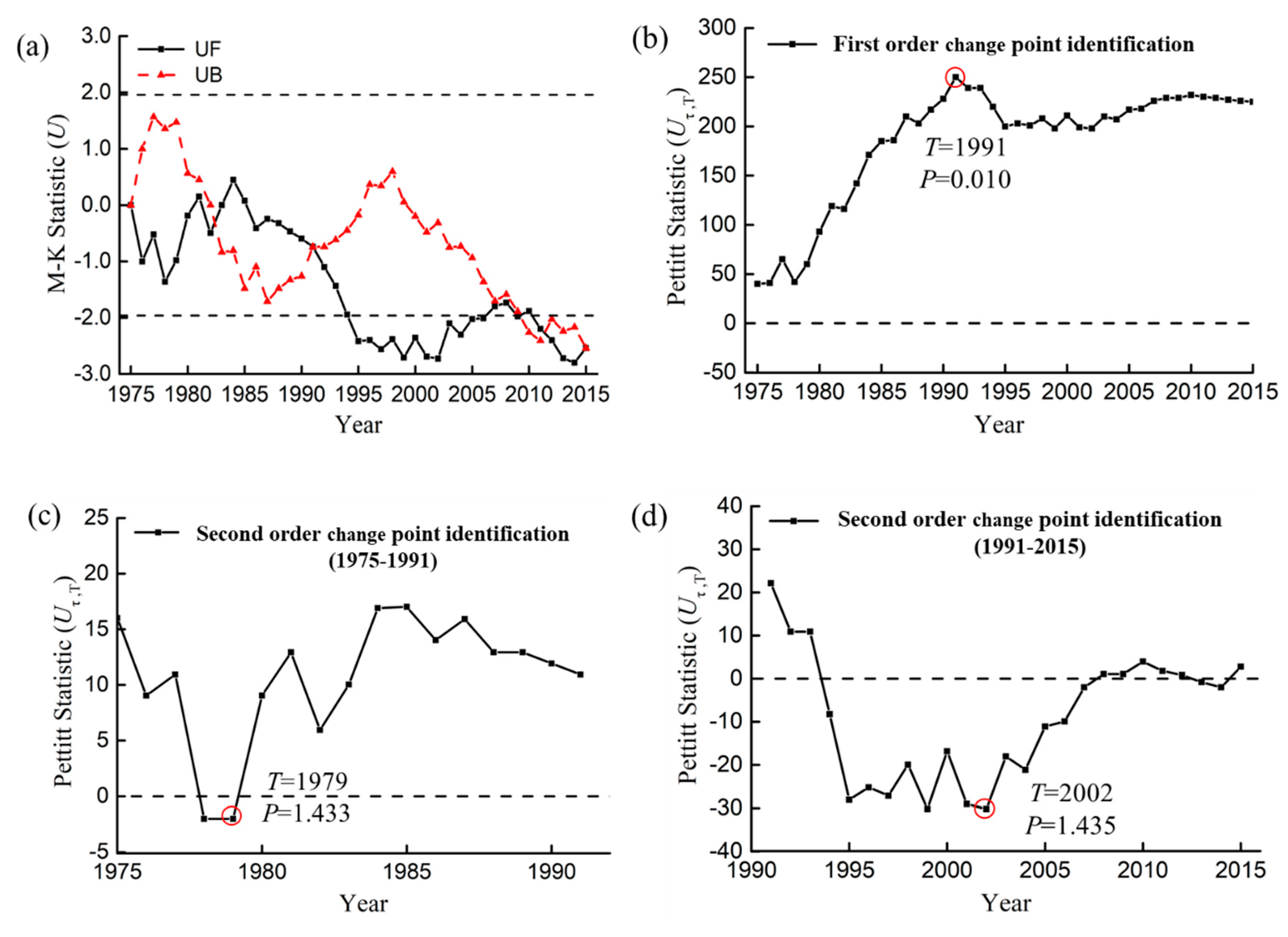
3.1.2. Analysis of Runoff and Sediment Change Point
3.2. Wavelet Analysis
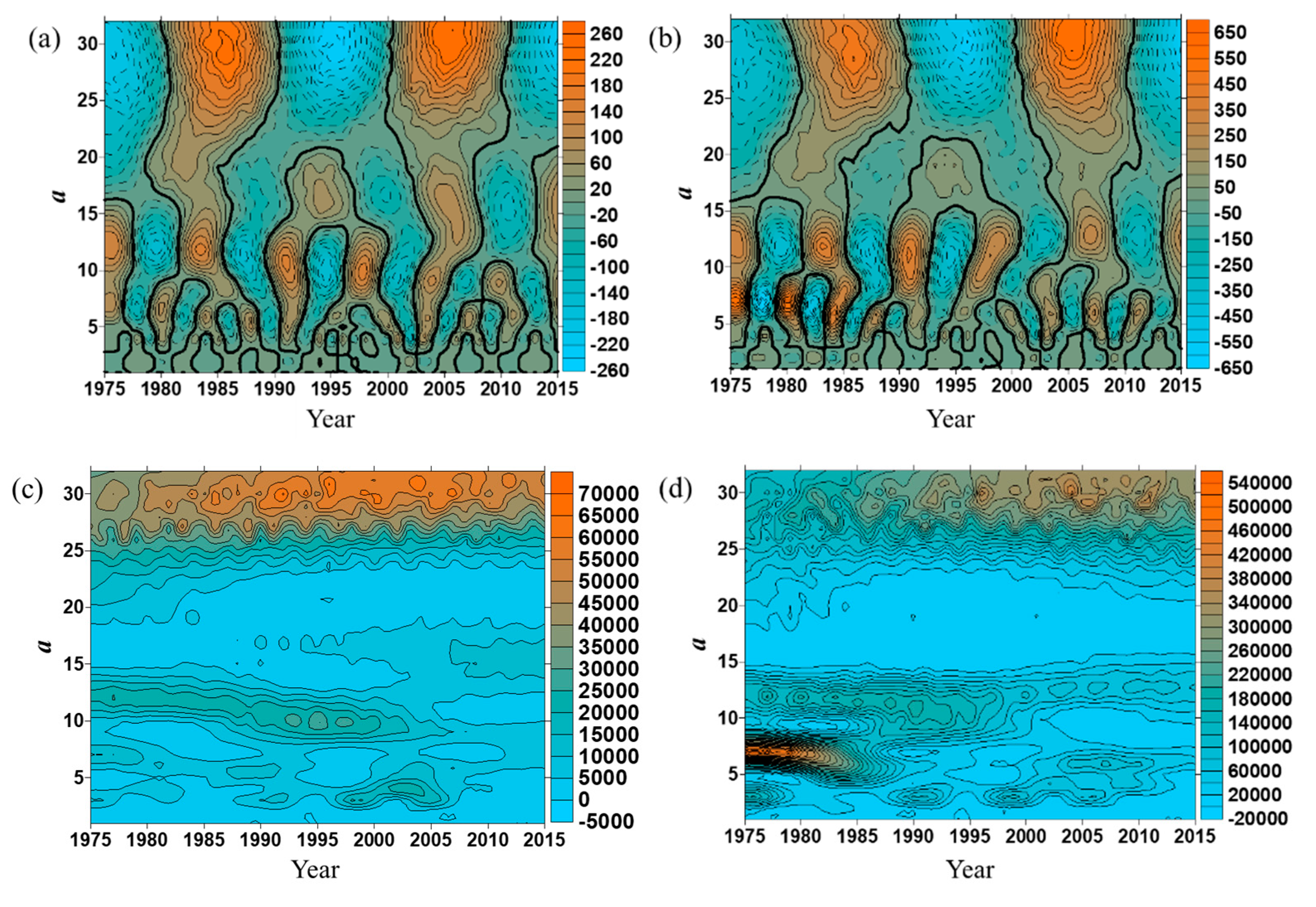
3.2.1. Analysis of Wavelet Transform
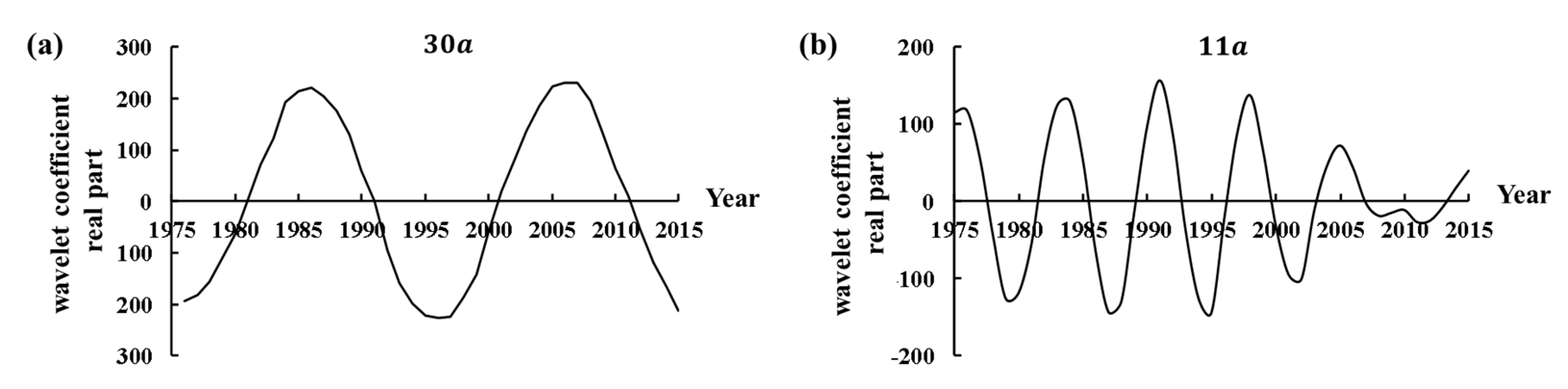
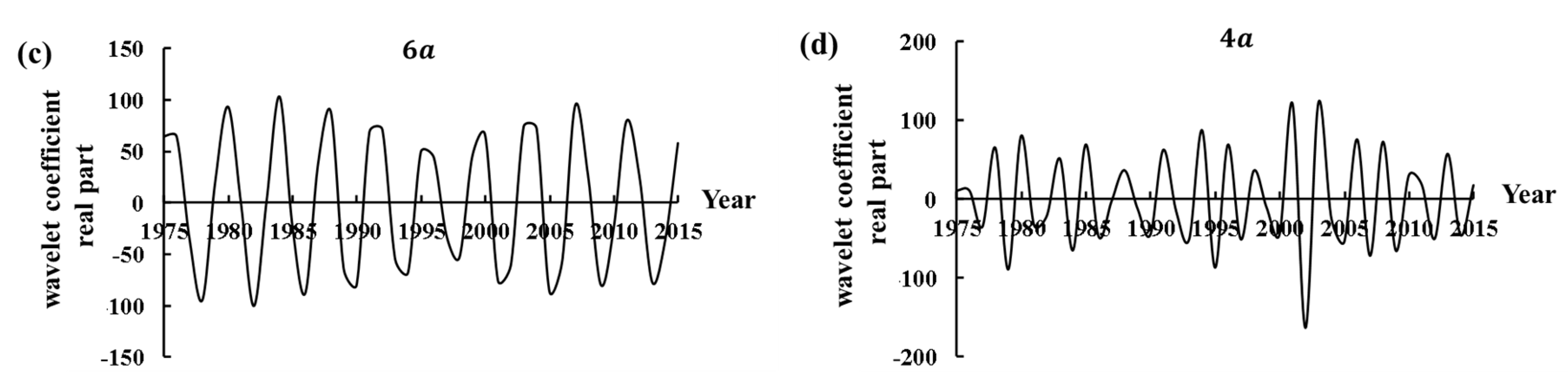
3.2.2. Analysis of Wavelet Variance and Periodic Characteristic
3.3. Cause Analysis of Runoff and Sediment Variation
3.3.1. Cause Analysis of Runoff Trend Variation
3.3.2. Trend Variation of Sediment and Cause Analysis of Change Point
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rice, J.S.; Emanuel, R.E.; Vose, J.M.; Nelson, S. Continental U.S. Streamflow trends from 1940 to 2009 and their relationships with watershed spatial characteristics. Water Resour. Res. 2015, 51, 6262–6275. [Google Scholar] [CrossRef]
- Lins, H.F.; Slack, J.R. Streamflow trends in the United States. Geophys. Res. Lett. 1999, 26, 227–230. [Google Scholar] [CrossRef] [Green Version]
- Lettenmaier, D.P.; Wood, E.F.; Wallis, J.R. Hydro-Climatological Trends in the Continental United States, 1948–1988. J. Climate. 1994, 7, 586–607. [Google Scholar] [CrossRef] [Green Version]
- Kalra, A.; Ahmad, S.; Nayak, A. Increasing Streamflow Forecast Lead Time for Snowmelt Driven Catchment Based on Large Scale Climate Patterns. Adv. Water Resour. 2013, 53, 150–162. [Google Scholar] [CrossRef]
- Zhou, Y.; Ma, Z.; Wang, L. Chaotic dynamics of the flood series in the Huaihe River Basin for the last 500 years. J. Hydrol. 2002, 258, 100–110. [Google Scholar] [CrossRef]
- Lin, C.A.; Wen, L.; Lu, G.; Wu, Z.; Zhang, J.Y.; Yang, Y.; Zhu, Y.F.; Tong, L.Y. Atmospheric-hydrological modeling of severe precipitation and floods in the Huaihe River Basin, China. J. Hydrol. 2006, 330, 249–259. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, W.; Liu, Y.; Wang, H.J. Runoff changes and their potential links with climate variability and anthropogenic activities: A case study in the upper Huaihe River Basin, China. Hydrol. Res. 2015, 2015, 1019–1036. [Google Scholar] [CrossRef]
- Ye, Z.W.; Li, Z.H. Spatiotemporal Variability and Trends of Extreme Precipitation in the Huaihe River Basin, a Climatic Transitional Zone in East China. Adv. Meteorol. 2017, 2017, 1–15. [Google Scholar] [CrossRef]
- Yu, Z.; Yan, D.; Ni, G.; Do, P.; Yan, D.; Cai, S.; Qin, T.; Weng, B.; Yang, M. Variability of Spatially Grid-Distributed Precipitation over the Huaihe River Basin in China. Water 2017, 9, 489. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.H.; Yuan, J.X. Analysis on the historical flood of Hongze Lake (1736–1992). J. Lake Sci. 1997, 1997, 231–236. [Google Scholar] [CrossRef]
- Yin, Y.; Chen, Y.; Yu, S.; Xu, W.; Wang, W.; Xu, Y. Maximum water level of Hongze Lake and its relationship with natural changes and human activities from 1736 to 2005. Quatern. Int. 2013, 304, 85–94. [Google Scholar] [CrossRef]
- Duan, H.; Cao, Z.; Shen, M.; Liu, D.; Xiao, Q. Detection of illicit sand mining and the associated environmental effects in China’s fourth largest freshwater lake using daytime and nighttime satellite images. Sci. Total Environ. 2019, 647, 606–618. [Google Scholar] [CrossRef] [PubMed]
- Milly, P.C.D.; Wetherald, R.T.; Dunne, K.A.; Delworth, T.L. Increasing risk of great floods in a changing climate. Nature (London) 2002, 415, 514–517. [Google Scholar] [CrossRef] [PubMed]
- Tamaddun, K.A.; Kalra, A.; Ahmad, S. Patterns and Periodicities of the Continental U.S. Streamflow Change. World Environ. Water Resour. Congr. 2016, 2016, 658–667. [Google Scholar] [CrossRef]
- Mann, H.B. Non-Parametric Test Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar] [CrossRef]
- Mondal, A.; Kundu, S.; Mukhopadhyay, A. Rainfall trend analysis by Mann-Kendall test: A case study of north-eastern part of Cuttack district, Orissa. Int. J. Earth Sci. 2012, 2, 70–78. [Google Scholar]
- Nourani, V.; Mehr, A.D.; Azad, N. Trend analysis of hydroclimatological variables in Urmia lake basin using hybrid wavelet Mann–Kendall and Sen tests. Environ. Earth Sci. 2018, 77, 207. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE T. Inform. Tteory. 1990, 36, 961–1005. [Google Scholar] [CrossRef] [Green Version]
- Tamaddun, K.A.; Kalra, A.; Ahmad, S. Wavelet analyses of western US streamflow with ENSO and PDO. J. Water Clim. Chang. 2017, 8, 26–39. [Google Scholar] [CrossRef] [Green Version]
- Thakur, B.; Pathak, P.; Kalra, A.; Ahmad, S.; Bernardez, M. Using Wavelet to Analyze Periodicities in Hydrologic Variables. World Environ. Water Resour. Congr. 2017, 2017, 499–510. [Google Scholar] [CrossRef]
- Chong, K.L.; Lai, S.H.; El-Shafie, A. Wavelet Transform Based Method for River Stream Flow Time Series Frequency Analysis and Assessment in Tropical Environment. Water Resour. Manag. 2019, 33, 2015–2032. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, A.W. Use of ranks in one-criterion variance analysis. J. Am. Stat. Asso. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. C Appl. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Chandler, R.E.; Scott, M. Statistical Methods for Trend Detection and Analysis in the Environmental Sciences; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Conte, L.C.; Débora, M.B.; Fábio, M.B. Bootstrap Pettitt test for detecting change points in hydroclimatological data: Case study of Itaipu Hydroelectric Plant, Brazil. Hydrolog. Sci. J. 2019, 64, 1312–1326. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A. Flood peak distributions for the eastern United States. Water Resour. Res. 2010, 46, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Shao, Q.; Yang, T.; Peng, S.; Xing, W.; Sun, F.; Luo, Y. Quantitative assessment of the impact of climate variability and human activities on runoff changes: A case study in four catchments of the Haihe River basin, China. Hydrol. Process. 2013, 27, 1158–1174. [Google Scholar] [CrossRef]
- Suhaila, J.; Yusop, Z. Trend analysis and change point detection of annual and seasonal temperature series in Peninsular Malaysia. Meteorol. Atmos. Phys. 2017, 130, 565–581. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Liang, K.; Bai, P.; Li, J.J.; Liu, C. Variability of temperature extremes in the Yellow River basin during 1961–2011. Quat. Int. 2014, 336, 52–64. [Google Scholar] [CrossRef]
- Klaus, S.; Christian, D.; Matthias, H.; Stötter, J. Assessing potential climate change impacts on the seasonality of runoff in an Alpine watershed. J. Water Clim. Chang. 2015, 6, 263–277. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H.L.; Bao, A.M.; Pan, X.L.; Chen, X. Estimating the sensitivity of runoff to climate change in an alpine-valley watershed of Xinjiang, China. Hydrol. Sci. J. 2016, 61, 1069–1079. [Google Scholar] [CrossRef] [Green Version]
- Walling, D.E.; Fang, D. Recent trends in the suspended sediment loads of the world’s rivers. Glob. Planet. Chang. 2003, 39, 111–126. [Google Scholar] [CrossRef]
- Vorosmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [Green Version]
- Carlson, T.N.; Arthur, S.T. The impact of land use-land cover changes due to urbanization on surface microclimate and hydrology: A satellite perspective. Glob. Planet. Chang. 2000, 25, 49–65. [Google Scholar] [CrossRef]
- Ervinia, A.; Huang, J.; Zhang, Z. Land-use changes reinforce the impacts of climate change on annual runoff dynamics in a southeast China coastal watershed. Hydrol. Earth Syst. Sci. 2015, 12, 6305–6325. [Google Scholar] [CrossRef]
- Dao, N.K.; Tadashi, S. Impact of climate and land-use changes on hydrological processes and sediment yield-A case study of the Be River catchment, Vietnam. Hydrol. Sci. J. 2014, 59, 1095–1108. [Google Scholar] [CrossRef]
- Apollonio, C.; Balacco, G.; Novelli, A.; Tarantino, E.; Piccinni, A.F. Land Use Change Impact on Flooding Areas: The Case Study of Cervaro Basin (Italy). Sustainability 2016, 8, 996. [Google Scholar] [CrossRef] [Green Version]
- Bussi, G.; Dadson, S.J.; Prudhomme, C.; Whitehead, P.G. Modelling the future impacts of climate and land-use change on suspended sediment transport in the River Thames (UK). J. Hydrol. 2016, 542, 357–372. [Google Scholar] [CrossRef] [Green Version]
- Cao, Z.; Duan, H.; Feng, L.; Ma, R.; Xue, K. Climate- and human-induced changes in suspended particulate matter over Lake Hongze on short and long timescales. Remote Sens. Environ. 2017, 192, 98–113. [Google Scholar] [CrossRef]
- Xing, L.; Huang, L.; Chi, G.; Yang, L.; Li, C.; Hou, X. A Dynamic Study of a Karst Spring Based on Wavelet Analysis and the Mann-Kendall Trend Test. Water 2018, 10, 698. [Google Scholar] [CrossRef] [Green Version]
- Li, W.W.; Fu, X.D.; Wu, W.Q.; Wu, B.S. Study on runoff and sediment process variation in the lower Yellow River. J. Hydroelectr. Eng. 2014, 33, 108–113. [Google Scholar]
- Labat, D. Recent advances in wavelet analyses: Part 1. A review of concepts. J. Hydrol. 2008, 314, 275–288. [Google Scholar] [CrossRef]
- Kovács, J.; Hatvani, I.G.; Korponai, J.; Kovács, I.S. Morlet wavelet and autocorrelation analysis of long-term data series of the Kis-Balaton water protection system (KBWPS). Ecol. Eng. 2010, 36, 1469–1477. [Google Scholar] [CrossRef]
- Hermida, L.; López, L.; Merino, A.; Berthet, C.; Gercía-Ortega, E.; Sánchez, J.L.; Dessens, J. Hailfall in southwest France: Relationship with precipitation, trends and wavelet analysis. Atmos. Res. 2015, 156, 174–188. [Google Scholar] [CrossRef]
- Oloruntade, A.J.; Mohammad, T.A.; Ghazali, A.H.; Wayayok, A. Analysis of meteorological and hydrological droughts in the Niger-South Basin, Nigeria. Glob. Planet. Chang. 2017, 155, 225–233. [Google Scholar] [CrossRef]
- Guignard, F.; Mauree, D.; Kanevski, M.; Telesca, L. Wavelet variance scale-dependence as a dynamics discriminating tool in high-frequency urban wind speed time series. Phys. A Stat. Mech. Its Appl. 2019, 525, 771–777. [Google Scholar] [CrossRef] [Green Version]
- Sun, P.; Sun, Y.Y.; Zhang, Q.; Wen, Q.Z. Temporal and spatial variation characteristics of runoff processes and its causes in Huaihe Basin. J. Lake Sci. 2018, 30, 497–508. [Google Scholar] [CrossRef] [Green Version]
- Mario, V.S.; Le, B.Y.; Moussa, R.; Bruno, R. Temporal dynamics of runoff and soil loss on a plot scale under a coffee plantation on steep soil (Ultisol), Costa Rica. J. Hydrol. 2015, 523, 409–426. [Google Scholar] [CrossRef]
- Jiang, Y.; Peng, Q.D.; Luo, H.H.; Ma, W. Analysis of spatial and temporal variation of water quality in Huaihe River Basin. J. Hydraul. Eng. 2011, 42, 1283–1288. [Google Scholar] [CrossRef]
- Cai, T.; Li, Q.F.; Yu, M.X.; Lu, G.B.; Cheng, L.P.; Wei, X. Investigation into the impacts of land-use change on sediment yield characteristics in the upper Huaihe River basin, China. Phys. Chem. Earth 2012, 53, 1–9. [Google Scholar] [CrossRef]
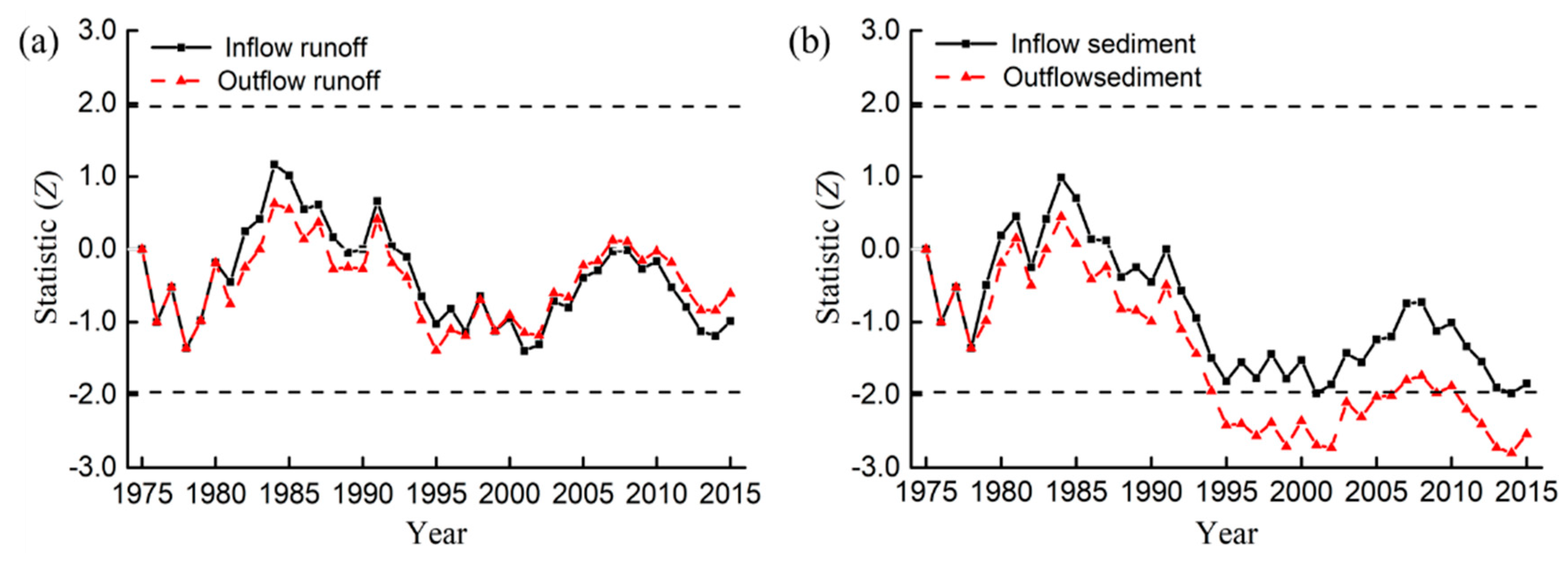


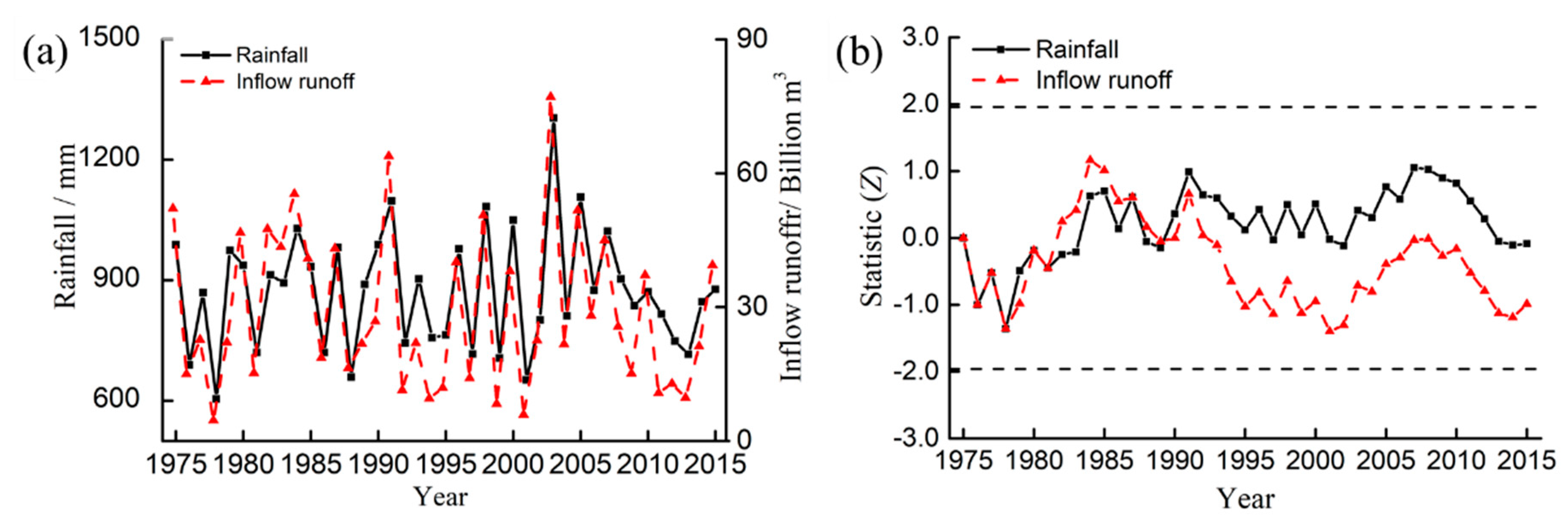
| M–K test | Inflow Runoff | Outflow Runoff | Inflow Sediment | Outflow Sediment |
|---|---|---|---|---|
| Statistic | −0.98 | −0.60 | −1.83 | −2.53 |
| Inspection criterion | −1.96 ≤ Z ≤ 1.96 | −1.96 ≤Z ≤ 1.96 | −1.96 ≤ Z ≤ 1.96 | −1.96 ≤ Z ≤ 1.96 |
| Significance level | No significant downtrend | No significant downtrend | Slightly downtrend | Significantly downtrend |
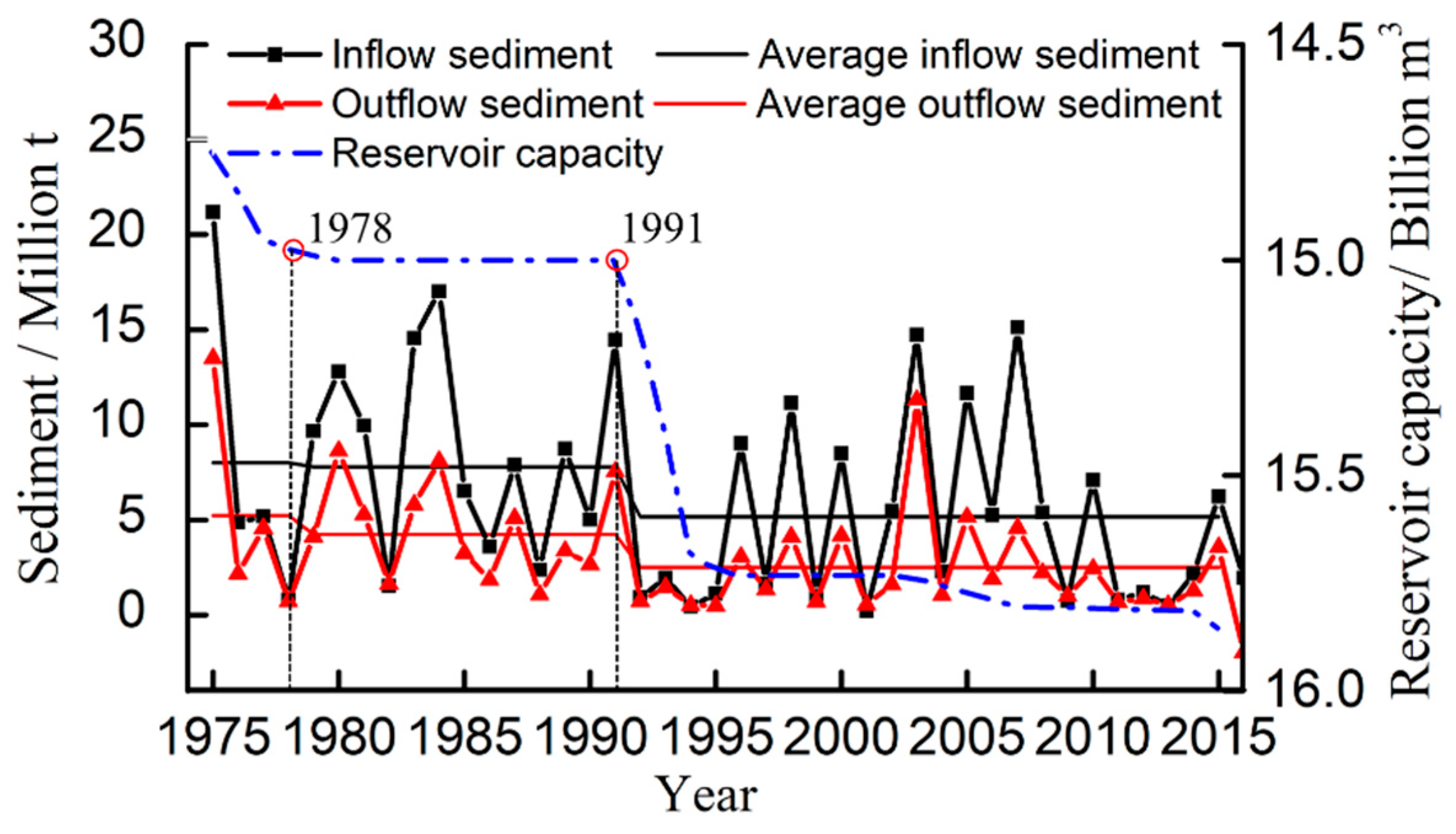
| Sediment | Change Point | Former Mutation | After Mutation | Mean Difference/t | |||||
|---|---|---|---|---|---|---|---|---|---|
| Year | Significant | Mean/t | Standard Deviation/t | Coefficient of Variation | Mean/t | Standard Deviation/t | Coefficient of Variation | ||
| Inflow | 1991 | 0.05 | 860 | 546 | 0.64 | 442 | 406 | 0.92 | 418 |
| Outflow | 1991 | 0.05 | 467 | 321 | 0.69 | 205 | 187 | 0.91 | 262 |
| Time Scale | Variation Period /Year | Cycle Times | Runoff Variation Trend after 2015 | |
|---|---|---|---|---|
| 30 | 20 | 2 | Maintain in a low water period and will reach the valley floor value | Figure 8a |
| 11 | 8 | 5 | Enter into a relatively rich water period | Figure 8b |
| 6 | 4 | 10 | Enter into a relatively rich water period | Figure 8c |
| 4 | The distribution characteristics are not obvious | Figure 8d | ||
| Time Scale | Variation Period/Year | Cycle Times | Sediment Variation Trend after 2015 | |
|---|---|---|---|---|
| 30 | 20 | 2 | Maintain in a low sediment period and will reach the valley floor value | Figure 9a |
| 12 | 8 | 5 | Enter into a relatively rich sediment period | Figure 9b |
| 7 | The distribution characteristics are not obvious | Figure 9c | ||
| 3 | The distribution characteristics are not obvious | Figure 9d | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, Y.; Xu, G.; Liu, Y.; Liu, Y.; Zhao, S.; Fan, X. Tendency of Runoff and Sediment Variety and Multiple Time Scale Wavelet Analysis in Hongze Lake during 1975–2015. Water 2020, 12, 999. https://doi.org/10.3390/w12040999
Duan Y, Xu G, Liu Y, Liu Y, Zhao S, Fan X. Tendency of Runoff and Sediment Variety and Multiple Time Scale Wavelet Analysis in Hongze Lake during 1975–2015. Water. 2020; 12(4):999. https://doi.org/10.3390/w12040999
Chicago/Turabian StyleDuan, Yu, Guobin Xu, Yuan Liu, Yijun Liu, Shixiong Zhao, and Xianlu Fan. 2020. "Tendency of Runoff and Sediment Variety and Multiple Time Scale Wavelet Analysis in Hongze Lake during 1975–2015" Water 12, no. 4: 999. https://doi.org/10.3390/w12040999




