Pulsating Flow of an Ostwald—De Waele Fluid between Parallel Plates
Abstract
:1. Introduction
2. Analytical Solution
2.1. Flow Enhancement
2.2. Dispersion Coefficient
3. Numerical Solution of the Velocity Distribution
4. Results
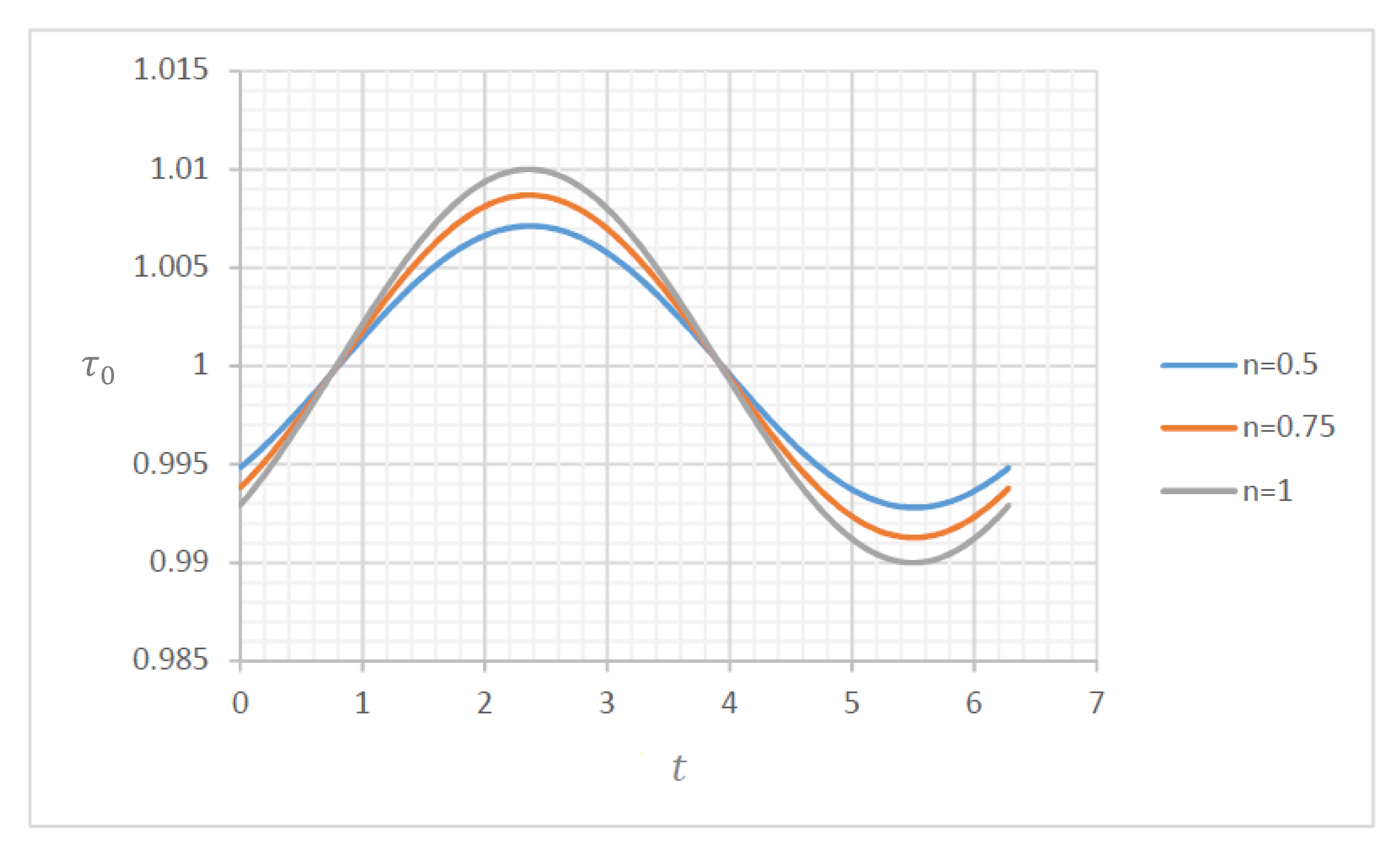
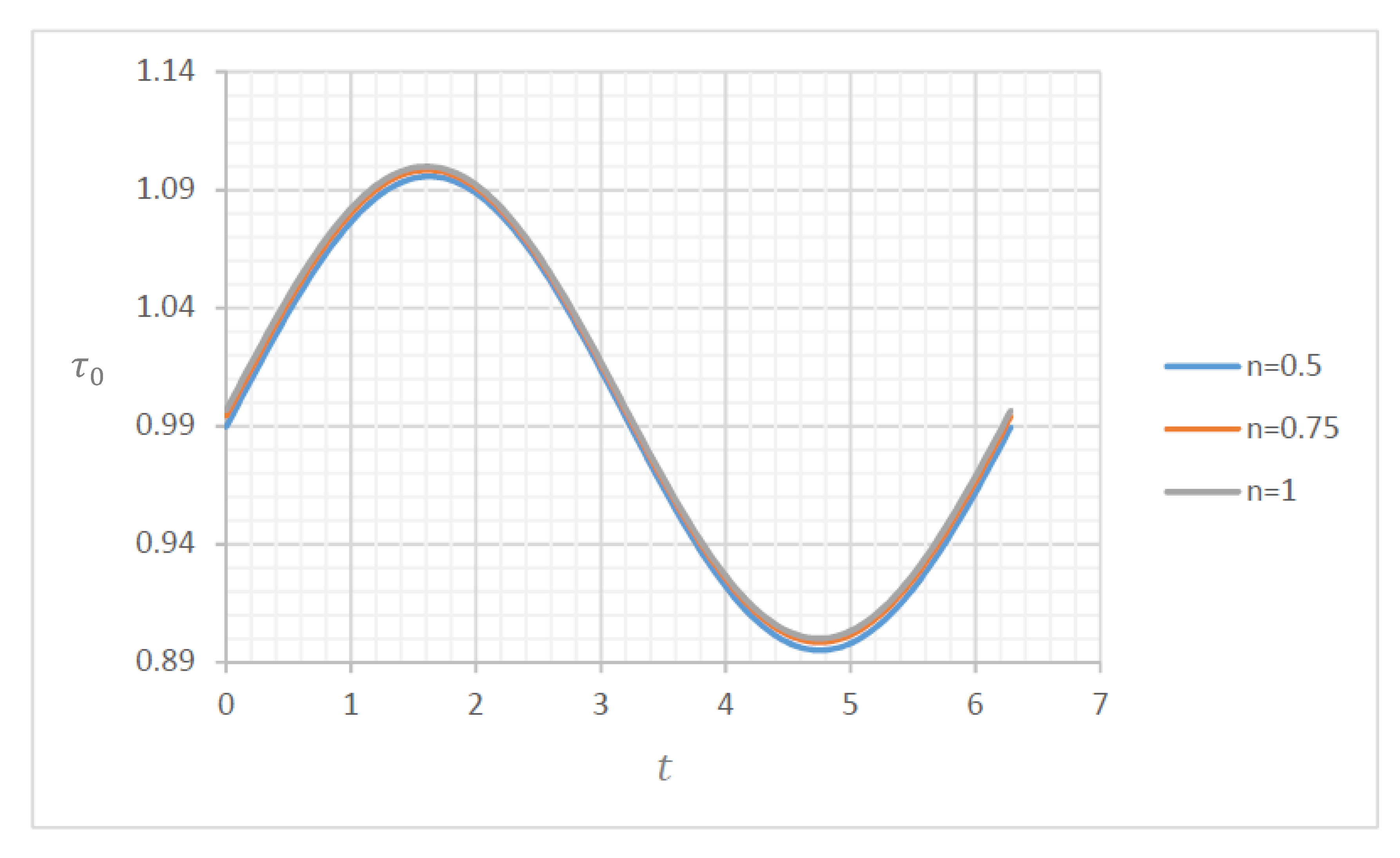
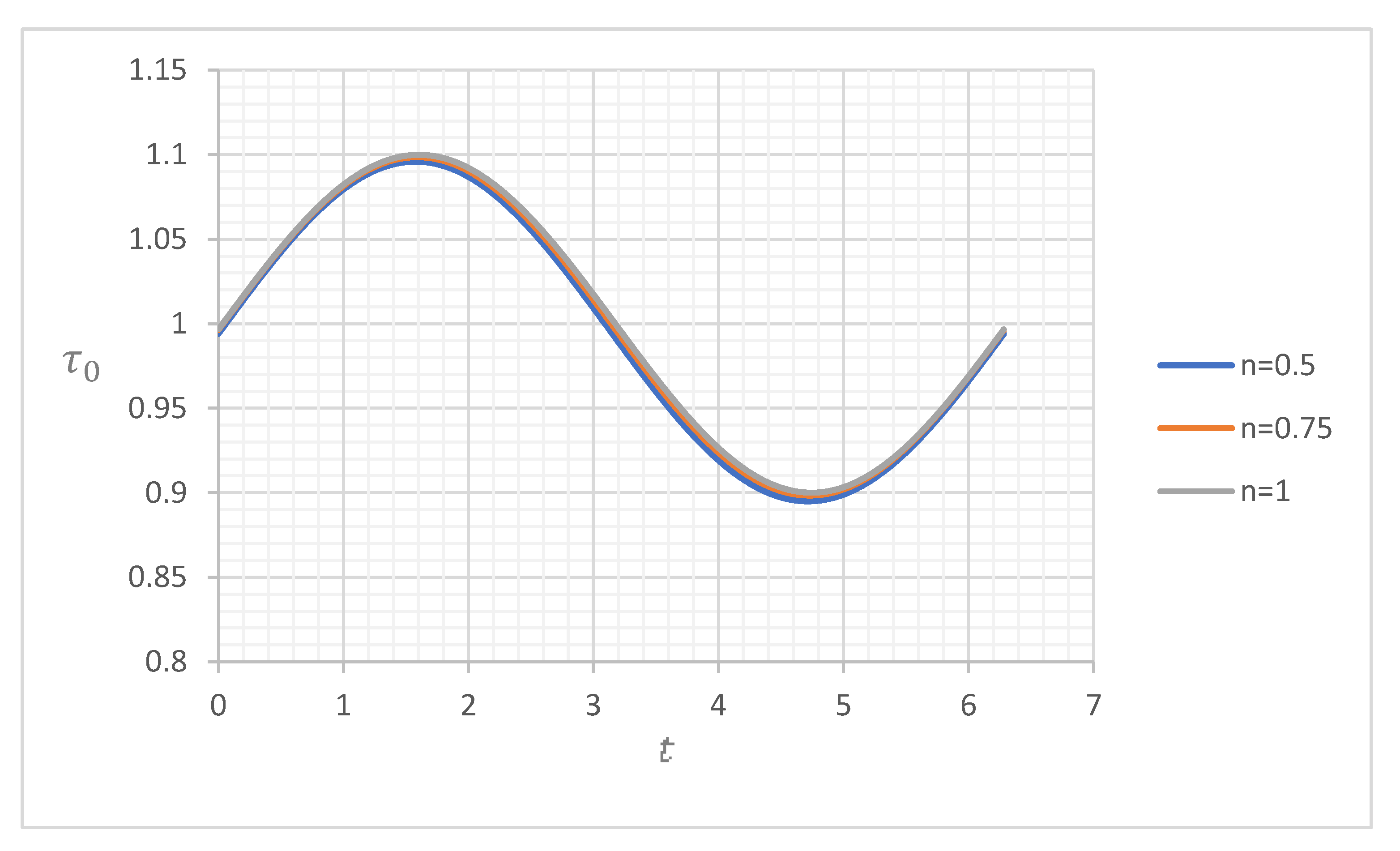
4.1. Wall Shear Stress
4.1.1. Wall Shear Stress for and
4.1.2. Wall Shear Stress for and
4.1.3. Wall Shear Stress for and
4.1.4. Wall Shear Stress for and
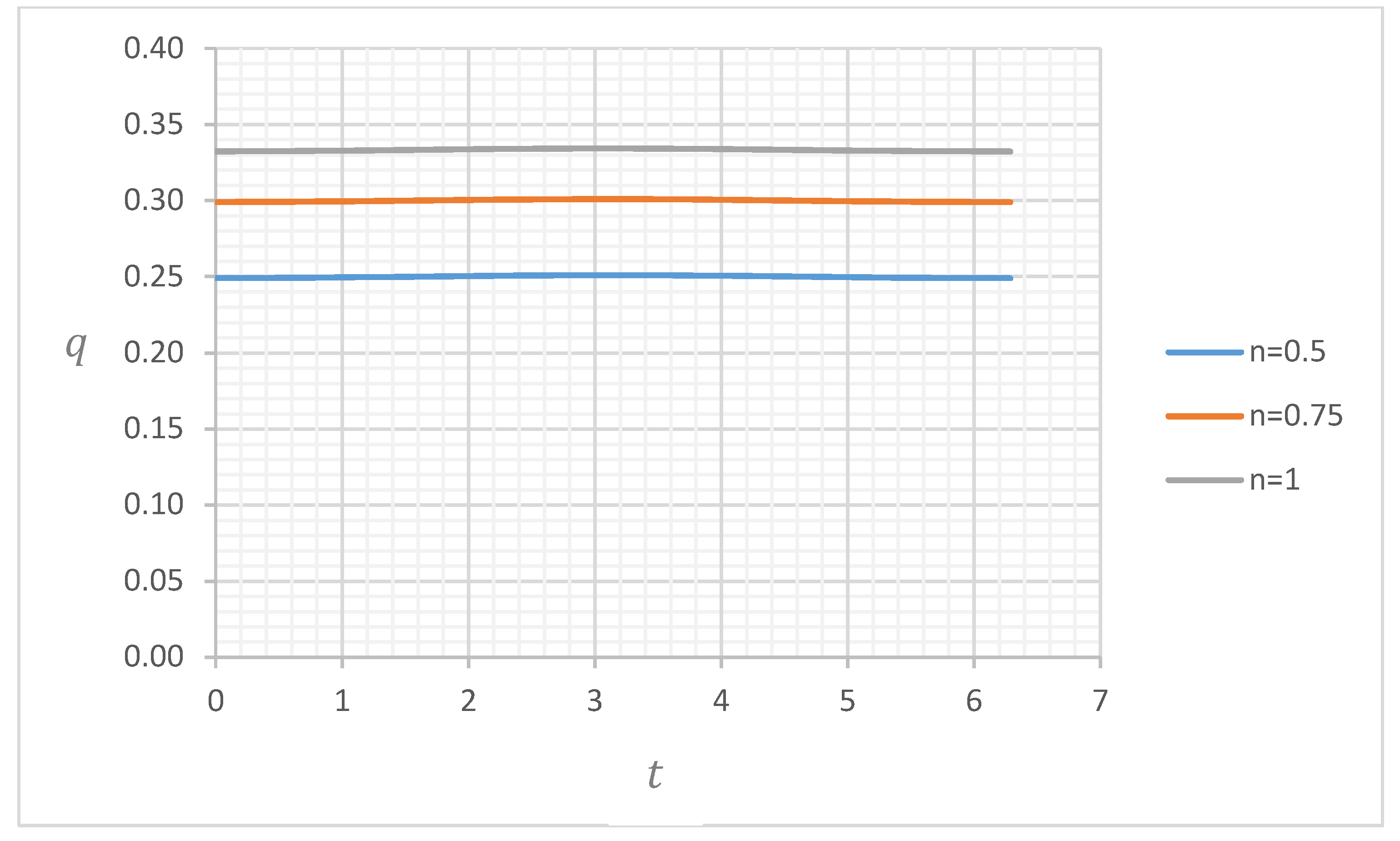
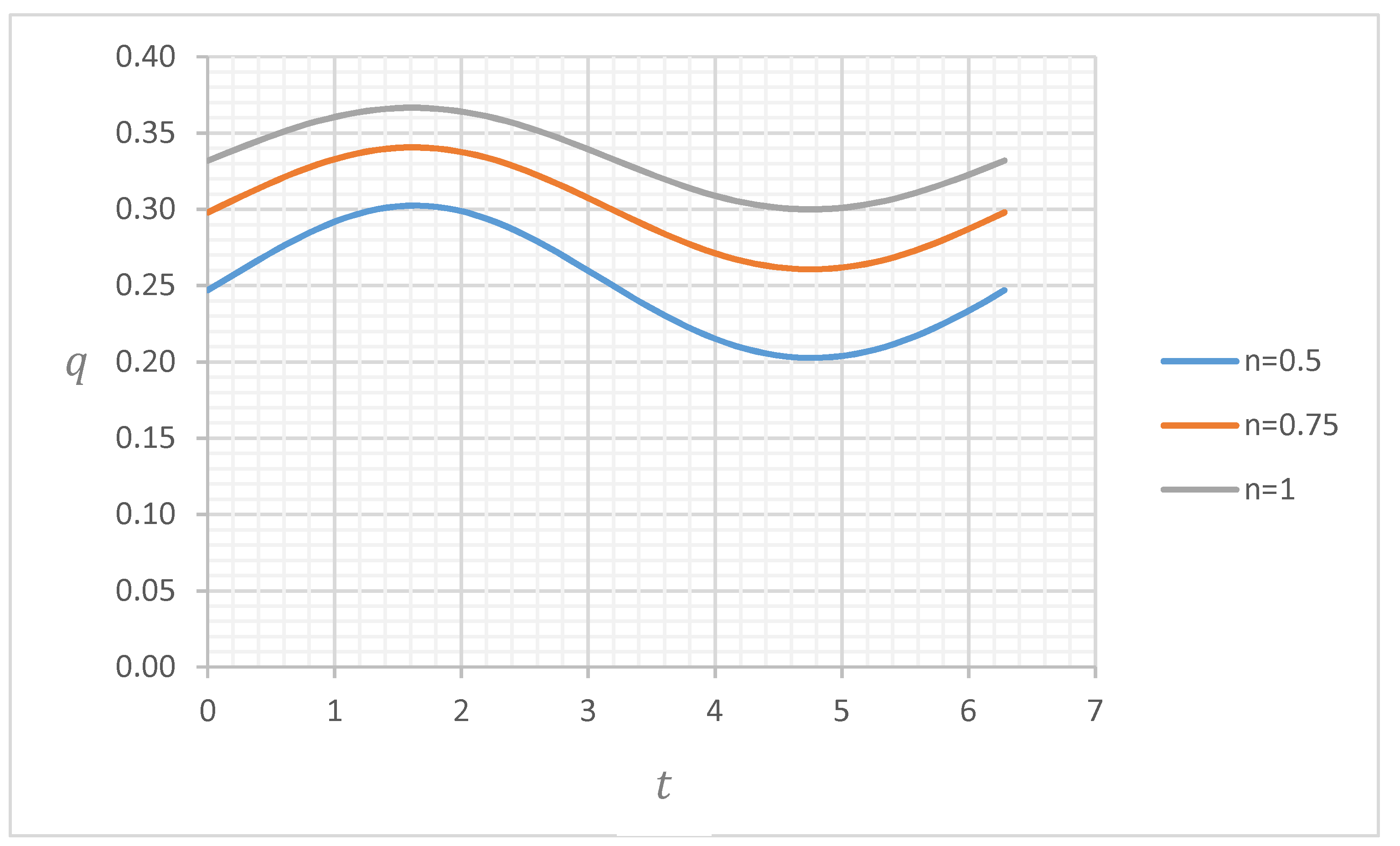
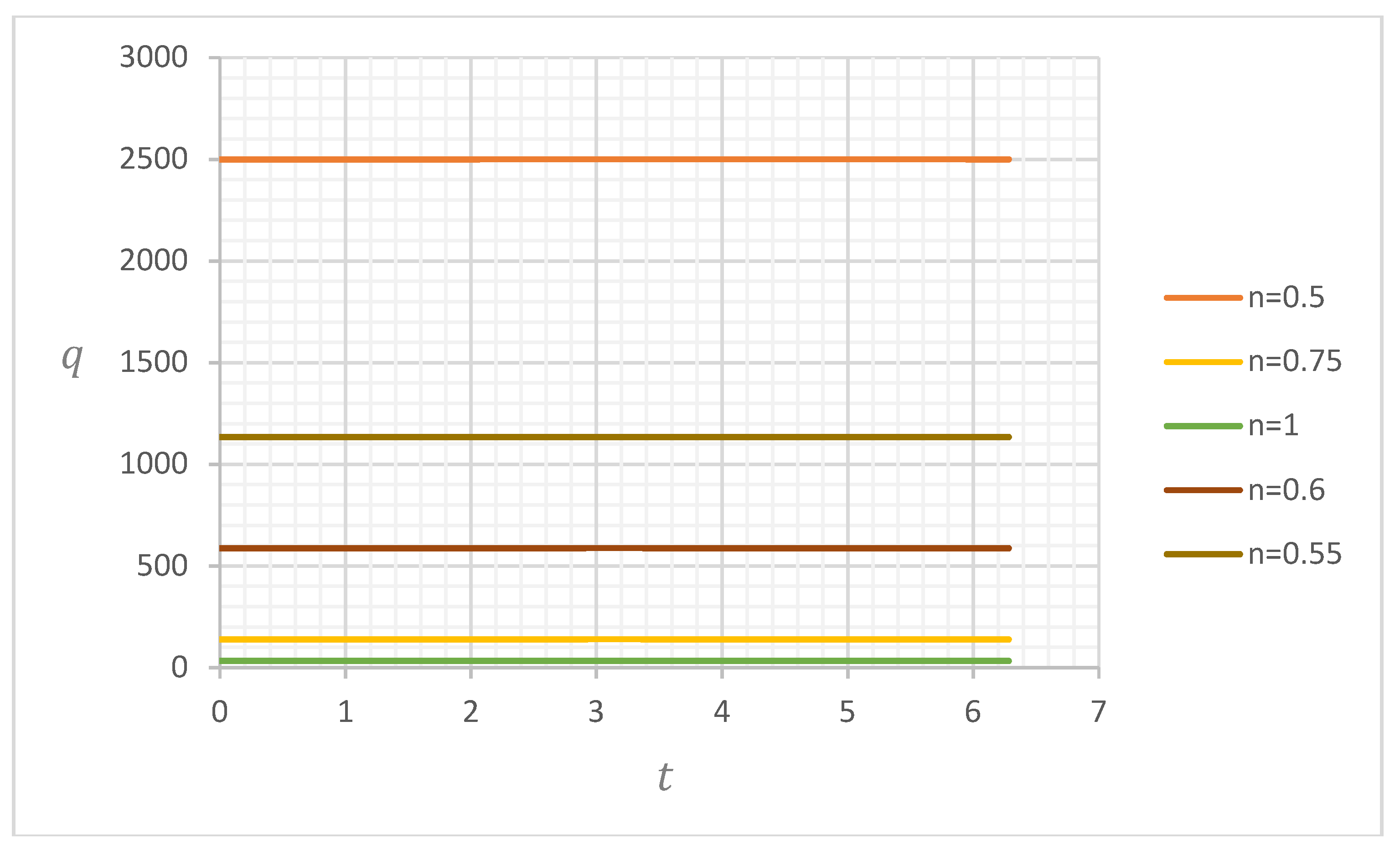
4.2. Discharge
4.2.1. Discharge for and
4.2.2. Discharge for and
4.2.3. Discharge for and
4.2.4. Discharge for and
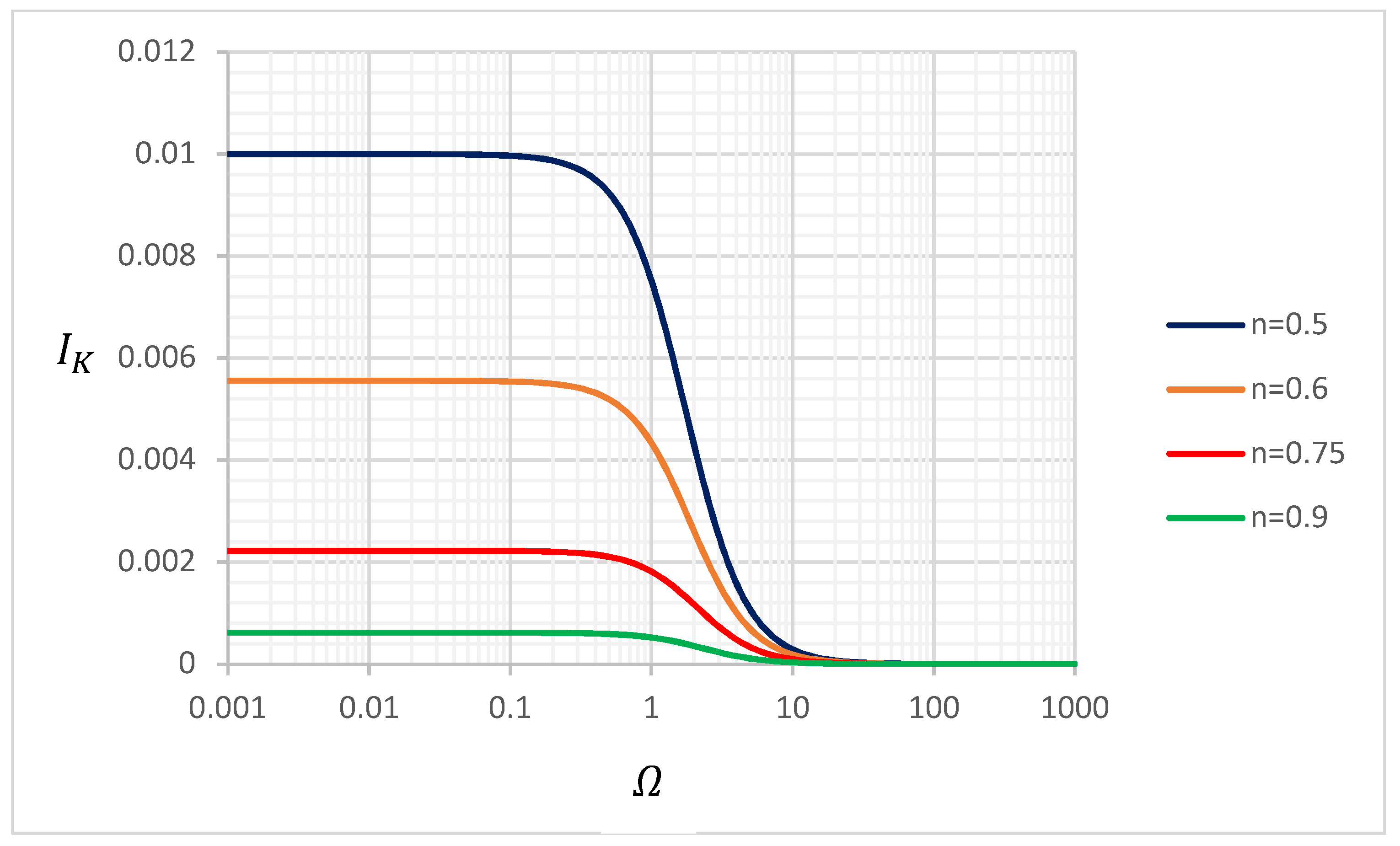
4.3. Flow Enhancement
4.4. Dispersion Enhancement
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sexl, T.; Ueber den von, E.G. Richardson entdeckten Annulareffect. Z. Phys. 1930, 61, 349–362. [Google Scholar] [CrossRef]
- Lambossy, P. Oscillations forcees d’un liquide incompressible et visqueux dans un tuve rigide et horizontal. Calcul de la force de frottement. Helv. Phys. Acta 1952, 25, 371–386. [Google Scholar]
- Womersley, J. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef] [PubMed]
- Womersley, J. Oscillatory motion of a viscous liquid in a thin-walled elastic tube-I: The linear approximation for long waves. Proc. R. Soc. Ser. 1955, 46, 199–221. [Google Scholar] [CrossRef]
- Pipkin, A.C. Alternating flow of non-Newtonian Fluids in tubes of arbitrary cross-section. Arch. Rat. Mech. Anal. 1964, 15, 1–13. [Google Scholar] [CrossRef]
- Etter, I.; Schowalter, W.R. Unsteady flow of an Oldroyd fluid in a circular tube. Trans. Soc. Rheol. 1965, 9, 351–369. [Google Scholar] [CrossRef]
- Rahaman, K.D.; Ramkissoon, H. Unsteady axial viscoelastic pipe flows. J. Non Newton. Fluid Mech. 1995, 57, 27–38. [Google Scholar] [CrossRef]
- Uchida, S. Pulsating viscous flow superposed on the steady laminar motion. Z. Angew. Math. Phys.(ZAMP) 1956, 5, 403–422. [Google Scholar] [CrossRef]
- Barnes, H.A.; Townsend, P.; Walters, K. On pulsatile flow of non-Newtonian liquids. Rheol. Acta 1971, 10, 517–527. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Dudek, J. Pulsating flow revisited. J. Non Newton. Fluid Mech. 1982, 11, 147–161. [Google Scholar] [CrossRef]
- Phan-Thien, N. Flow enhancement mechanisms of a pulsating flow of non-Newtonian liquids. Rheol. Acta 1980, 19, 285–290. [Google Scholar] [CrossRef]
- Steller, R. A new approach to the pulsating oscillating flows of viscoelastic liquid in channels. Rheol. Acta 1993, 32, 192–205. [Google Scholar] [CrossRef]
- Davies, J.M.; Bhumiratana, S.; Bird, R.B. Elastic and inertial effects in pulsatile flow of polymeric liquids in circular tubes. J. Non Newton. Fluid Mech. 1978, 3, 237–259. [Google Scholar] [CrossRef]
- Mai, T.-Z.; Davis, A.M.J. Laminar pulsatile two-phase non-Newtonian flow through a pipe. Comput. Fluids 1996, 25, 77–93. [Google Scholar] [CrossRef]
- Daprà, I.; Scarpi, G. Pulsatile pipe flow of pseudoplastic fluids. Meccanica 2006, 41, 501–508. [Google Scholar] [CrossRef]
- Merril, E.W. Rheology of blood. Physiol. Rev. 1969, 49, 863–888. [Google Scholar]
- Prakash, J.; Ogulu, A. A study of pulsatile blood flow modelled as a power law fluid in a constricted tube. Int. Commun. Heat Mass. Transfer. 2007, 34, 762–768. [Google Scholar] [CrossRef]
- Sankar, D.S.; Lee, U. Mathematical modelling of pulsatile flow of non-Newtonian fluid in stenosed arteries. Commun. Nonlinear Sci. Numer. Simulat. 2009, 14, 2971–2981. [Google Scholar] [CrossRef]
- Herrera-Valencia, E.E.; Calderas, F.; Medina-Torres, L.; Pérez-Camacho, M.; Moreno, L.; Manero, O. On the pulsating flow behavior of a biological fluid: Human blood. Rheol. Acta 2017, 56, 387–407. [Google Scholar] [CrossRef]
- Siginer, A. On the pulsating pressure gradient driven flow of viscoelastic liquids. J. Rheol. 1991, 35, 271–311. [Google Scholar] [CrossRef]
- McGInty, S.; McKee, S.; McDermont, R. Analytic solutions of Newtonian and non-Newtonian pipe flows subject to a general time-dependent pressure gradient. J. Non Newton. Fluid Mech. 2009, 162, 54–77. [Google Scholar] [CrossRef]
- Daprà, I.; Scarpi, G. Pulsatile Poiseuille flow of a viscoplastic fluid in the gap between coaxial cylinders. J. Fluids Eng. 2011, 133, 081203. [Google Scholar] [CrossRef]
- Letelier, M.F.; Siginer, D.A.; Caceres, C. Pulsating flow of viscoelastic fluids in straight tubes of arbitrary cross-section—Part I: Longitudinal Field. Int. J. Non Linear Mech. 2002, 37, 369–393. [Google Scholar] [CrossRef]
- Daprà, I.; Scarpi, G. Perturbation solution for pulsatile flow of a non-Newtonian Williamson fluid in a rock fracture. Int. J. Rock Mech. Min. Sci. 2007, 44, 271–278. [Google Scholar] [CrossRef]
- Nandakumar, N.; Sahu, K.C.; Anand, M. Pulsatile flow of a shear thinning model for blood through a two-dimensional stenosed channel. Eur. J. Mech. B Fluids 2015, 49, 29–35. [Google Scholar] [CrossRef]
- Edwards, M.F.; Nellist, D.A.; Wilkinson, W.L. Unsteady, laminar flows of non-Newtonian fluids in pipes. Chem. Eng. Sci. 1972, 27, 295–306. [Google Scholar] [CrossRef]
- Balmer, R.T.; Fiorina, M.A. Unsteady flow of an inelastic power law fluid in a circular tube. J. Non Newton. Fluid Mech. 1980, 7, 89–198. [Google Scholar] [CrossRef]
- Adusumilli, R.S.; Hill, G.A. Transient Laminar Flows of Truncated Power Law Fluids in Pipes. Can. J. Chem. Eng. 1984, 62, 594–601. [Google Scholar] [CrossRef]
- Nakamura, M.; Sawada, T. Numerical study on the laminar pulsatile flow of slurries. J. Non Newton. Fluid Mech. 1987, 22, 191–206. [Google Scholar] [CrossRef]
- Warsi, Z.U.A. Unsteady flow of power-law fluids through circular pipes. J. Non Newton. Fluid Mech. 1994, 55, 197–202. [Google Scholar] [CrossRef]
- Javadzadegan, A.; Esmaeili, M.; Majidi, S.; Fakhimghanbarzadeh, B. Pulsatile flow of viscous and viscoelastic fluids in constricted tubes. J. Mech. Sci. Technol. 2009, 23, 2456–2467. [Google Scholar] [CrossRef]
- Yakhot, A.; Arad, M.; Ben-Dor, G. Numerical investigation of a laminar pulsating flow in a rectangular duct. Int. J. Numer. Meth. Fluids 1999, 29, 935–950. [Google Scholar] [CrossRef]
- Tu, C.; Deville, M. Pulsatile flow of non-newtonian fluids through arterial stenoses. J. Biomech. 1996, 29, 899–908. [Google Scholar] [CrossRef]
- Pontrelli, G. Pulsatile blood flow in a pipe. Comput. Fluids 1998, 27, 367–380. [Google Scholar] [CrossRef] [Green Version]
- Harris, J.; Maheshwari, R. Oscillatory pipe flow: A comparison between predicted and observed displacement profiles. Rheol. Acta 1975, 14, 162–168. [Google Scholar] [CrossRef]
- Thurston, G. Elastic Effects in Pulsatile Blood Flow. Microvasc. Res. 1975, 9, 145–157. [Google Scholar] [CrossRef]
- Davies, J.; Chakrabarti, A. A modified pulsatile flow apparatus for measuring flow enhancement in combined steady and oscillatory shear flow. In Rheology, 1st ed.; Astarita, G., Marruci, G., Nicolais, L., Eds.; Springer Science + Business Media: New York, NY, USA, 1980. [Google Scholar]
- Kajiuchi, T.; Saito, A. Flow enhancement of laminar pulsating flow of Bingham plastic fluids. J. Chem. Eng. Jpn. 1984, 17, 34–38. [Google Scholar] [CrossRef]
- Lin, Y.; Tan, G.; Phan-Thien, N.; Khoo, B. Flow enhancement in pulsating flow of non-colloidal suspensions in tubes. J. Non Newton. Fluid Mech. 2014, 212, 13–17. [Google Scholar] [CrossRef]
- Watson, G. A Treatise on the Theory of Bessel Functions, 1st ed.; Cambridge University Press: Cambridge, UK, 1922. [Google Scholar]
- Fischer, H.B.; List, E.J.; Koh, R.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press Inc.: Cambridge, MA, USA, 1979. [Google Scholar]
- Thomas, G.; Finney, R. Calculus and Analytic Geometry, 9th ed.; Addison-Wesley: Boston, MA, USA, 1996. [Google Scholar]
- Patera, A.T. A spectral element method for fluid dynamics: Laminar flow in a channel expansion. J. Comput. Phys. 1984, 54, 468–488. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P.; Moser, R. Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef] [Green Version]
- Manna, M.; Vacca, A.; Deville, M. Preconditioned spectral multi-domain discretization of the incompressible Navier-Stokes equations. J. Comp. Phys. 2004, 201, 204–223. [Google Scholar] [CrossRef]
- Huang, L.; Chen, Q. Spectral Collocation Model for Solitary Wave Attenuation and Mass Transport over Viscous Mud. J. Eng. Mech. 2009, 135, 881–891. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Q.S. Non-modal instability in plane Couette flow of a power-law fluid. J. Fluid Mech. 2011, 676, 145–171. [Google Scholar] [CrossRef] [Green Version]
- Niu, J.; Zheng, L.; Yang, Y.; Shu, C.-W. Chebyshev spectral method for unsteady axisymmetric mixed convection heat transfer of power law fluid over a cylinder with variable transport properties. Int. J. Numer. Anal. Mod. 2014, 11, 525–540. [Google Scholar]
- Canuto, C.; Hussaini, M.; Quarteroni, A.; Zang, T. Spectral Methods in Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Manna, M.; Vacca, A. An efficient method for the solution of the incompressible Navier-Stokes equations in cylindrical geometries. J. Comput. Phys. 1999, 151, 563–584. [Google Scholar] [CrossRef]
- Pascal, J.P.; D’Alessio, J.D.; Hasan, M. Instability of gravity-driven flow of a heated power-law fluid with temperature dependent consistency. AIP Adv. 2018, 8, 105215–105226. [Google Scholar] [CrossRef]
- Iervolino, M.; Pascal, J.P.; Vacca, A. Instabilities of a power–law film over an inclined permeable plane: A two–sided model. J. Non Newton. Fluid Mech. 2018, 259, 111–124. [Google Scholar] [CrossRef]
- Iervolino, M.; Pascal, J.P.; Vacca, A. Thermocapillary instabilities of a shear-thinning fluid falling over a porous layer. J. Non Newton. Fluid Mech. 2019, 270, 36–50. [Google Scholar] [CrossRef]







| −1.6% | −1.8% | −2.0% | −1.9 | |
| −0.4% | −0.4% | −0.4% | −0.4% | |
| −0.7% | −0.7% | −0.7% | −0.7% |
| 0.4% | −0.1% | 0.6% | −0.1% | |
| 0.6% | 0.6% | −0.3% | −0.3% | |
| Less than 0.1% | Less than 0.1% | Less than 0.1% | Less than 0.1% |
| Discharge | −14.9% | −19.7% | −84.9% | −42.8% |
| Wall shear stress | 6.7% | −1.9% | 30.9% | −3.5% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, R.; Tamburrino, A.; Vacca, A.; Iervolino, M. Pulsating Flow of an Ostwald—De Waele Fluid between Parallel Plates. Water 2020, 12, 932. https://doi.org/10.3390/w12040932
González R, Tamburrino A, Vacca A, Iervolino M. Pulsating Flow of an Ostwald—De Waele Fluid between Parallel Plates. Water. 2020; 12(4):932. https://doi.org/10.3390/w12040932
Chicago/Turabian StyleGonzález, Rodrigo, Aldo Tamburrino, Andrea Vacca, and Michele Iervolino. 2020. "Pulsating Flow of an Ostwald—De Waele Fluid between Parallel Plates" Water 12, no. 4: 932. https://doi.org/10.3390/w12040932
APA StyleGonzález, R., Tamburrino, A., Vacca, A., & Iervolino, M. (2020). Pulsating Flow of an Ostwald—De Waele Fluid between Parallel Plates. Water, 12(4), 932. https://doi.org/10.3390/w12040932






