1. Introduction
Gully erosion is a global problem, particularly in the southeastern United States, where erodible soils, high relief, and climatic and meteorological factors encourage soil erosion. Gully erosion is one of the most dangerous forms of soil degradation, which is caused by natural and anthropogenic activities. Gullies are composed of several continuous or discontinuous channels and rills with varying slopes, which may later develop into deep trenches, inhibiting effective remediation by tillage. Gully erosion can initiate from anthropogenic factors like farming or grazing on susceptible soils, increased runoff from land-use changes due to logging or construction, and poor vegetative cover from wildfire or high soil salinity. Additionally, natural drivers for soil erosion are meteorological variables, topography, and soil type and texture [
1,
2].
Changes in land use can increase soil erosion. Vast regions of the United States experienced soil erosion when forested lands were converted to croplands in the late 19th century and the early 20th century [
3]. Estimates of the volume of soil erosion in the United States caused by both sheet and rill erosion combined is 6.7 Mg/ha/y in cultivated cropland, 0.90 Mg/ha/y on federal lands, and 1.55 Mg/ha/y in pasture lands [
3]. Considerable land area in the southeastern US was converted from forest to agriculture to support cotton farming in the 1800s and pasture for animal grazing [
4,
5]. Land cover change due to logging and conversion of forest to crop and pasture was linked to nineteenth-century European settlement in the southern Blue Ridge Mountains and Appalachian hillslopes [
6,
7,
8,
9]. Harvesting on the steep Appalachian hillslopes has been identified as one potential cause of soil erosion [
10]. After recognizing the problem as early as 1933, soil conservation programs were implemented in the United States. As part of present soil conservation efforts, afforestation on the reclaimed land has partially halted erosion, but severe erosional areas from the past cotton farming era are still prominent [
4]. Some researchers have described a multi-stage formation of severe soil erosion [
11,
12], i.e., a process for gully development in the Appalachian Piedmont: (i) rills and gullies are initiated along existing paths, tracks, ditches, or animal burrows, where runoff is concentrated due to reduced infiltration; (ii) head scarp erosion begins as runoff gains energy and is concentrated in steeply sloped land; (iii) gully downcutting eventually stabilizes when weathered bedrock and the shallow groundwater zone are encountered; (iv) erosion continues laterally along channel sidewalls and headwalls by slumping and under caving, inhibiting effective control by tillage. Hence, reclamation can be expensive.
Sidewalls (or midslopes), gully channels (or valleys), and interfluves (or gully divides) are major topographical factors that influence soil erosion [
7,
8,
13]. Soil erosion increases with slope steepness, which is more relevant to gully sidewall erosion and less relevant to interfluves. Gully channels are dynamic and can serve as intermittent sediment sinks and sources, transporting sediment to the gully outlet [
14].
In addition to land cover change and topographic variation, water-induced soil erosion from severe precipitation events erodes fertile soil, mainly in areas with poor agricultural management, land degradation from mining, road construction, or wild fires [
2]. Unique climatic conditions in the humid subtropical climate (Köppen Cfa) of the southeastern United States are a major contributing factor in gully erosion [
15]. Cold periods in the south are short and winters are mild, inhibiting deeper ground freezing. The thin surface layer (5–10 cm) of frost-heaved soil becomes loose after a few freeze-thaw cycles, and can erode easily from subsequent heavy rain or snow-melt runoff [
13]. During warm periods, intensive rainfall that falls on steep, sparsely vegetated slopes contributes to erosion. General precipitation trends in the Appalachian hillslopes indicate that high-intensity events occur more during summer months, while higher accumulation low-intensity storms are more prevalent in winter months. Seasonal variability in precipitation characteristics impacts erosion, but the extent and nature of this relationship are not well understood in this region.
A short-term study of hillslope erosion in the Appalachians found that duration and accumulation of precipitation were more important than storm intensity as drivers for gully erosion [
13]. The same study also found antecedent precipitation is a stronger predictor of erosion and discrete precipitation events alone may not result in measurable erosion. Antecedent precipitation along with successive precipitation events can saturate the soil, reduce shear strength, and cause erosion. To examine inter-annual variability and longer-term effects from antecedent precipitation, as well as the influence of seasonal events on soil erosion, a more extensive time series of precipitation and corresponding erosion data is necessary [
16], however, it will be important to retain a high temporal resolution in the data to assess seasonal scale patterns.
In this context, the Appalachian hillslopes in the southern US are representative of a region of historic and modern land degradation from unique meteorological conditions, variable topography, and land use/land cover change. Therefore, the objective of the present study is to examine the effect of meteorological parameters, specifically precipitation, on soil erosion through long term high-resolution monitoring. This paper summarizes six years of comprehensive weekly monitoring of precipitation events and soil erosion in an Appalachian hillslope paying particular attention to seasonal effect. An understanding of the seasonal pattern of soil erosion with respect to precipitation-related drivers of erosion will improve the potential to achieve conservation measures.
2. Materials and Methods
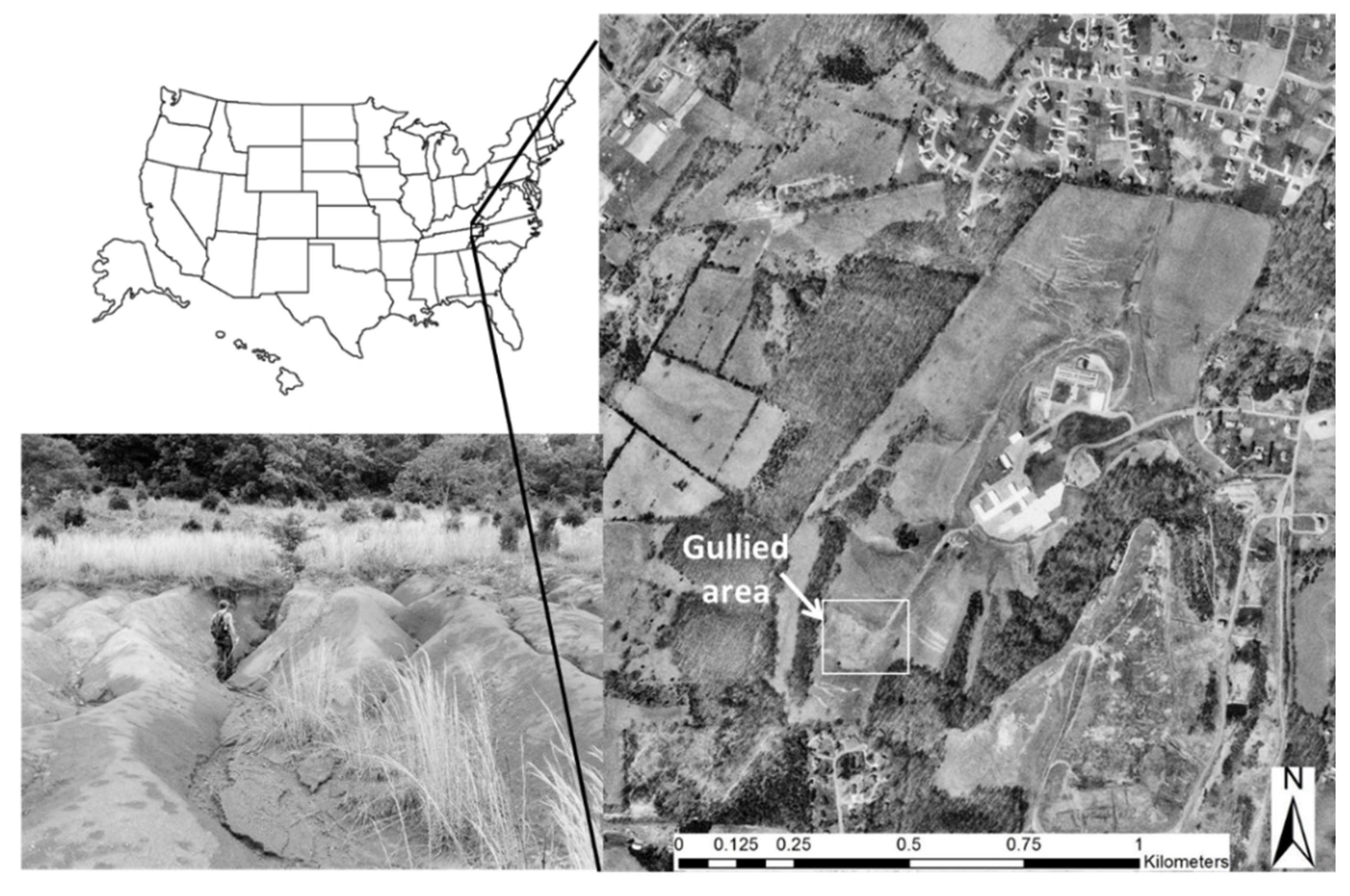
The study site was a system of branching gullies located on a hillslope at the East Tennessee State University Valleybrook research facility in northeast Tennessee, USA (+36°25′36.77″, −82°32′10.63″) at an elevation of 530 m (
Figure 1). The site was within the Appalachian Valley and Ridge physiographic province and consisted of northeast-southwest trending parallel limestone valleys (Maynardville Formation) and sandstone or shale ridges (Nolichucky Formation) [
17]. The 1.5 ha study area was located on a grass and shrub hillslope surrounded by forest (on the ridges) and pasture (in the valleys). Soils were highly erodible fine-grained silt and clay Ultisols (Collegedale-Etowah complex (CeD3)) with an average erodibility factor (RUSLE K-factor) of 0.28, indicating susceptibility to raindrop impact and transport by surface runoff [
18]. The region has a humid subtropical climate (Köppen Cfa) with year-round precipitation of 1070 mm (42 in) annually and an average annual temperature range from 1.1 °C (34 °F) in January to 23.3 °C (74 °F) in July. The National Oceanic and Atmospheric Administration describe Tennessee’s winter precipitation as dominated by the polar front and summer precipitation that results from convectional systems. September and October are the driest months.
A detailed description of the site setup can be found in [
13,
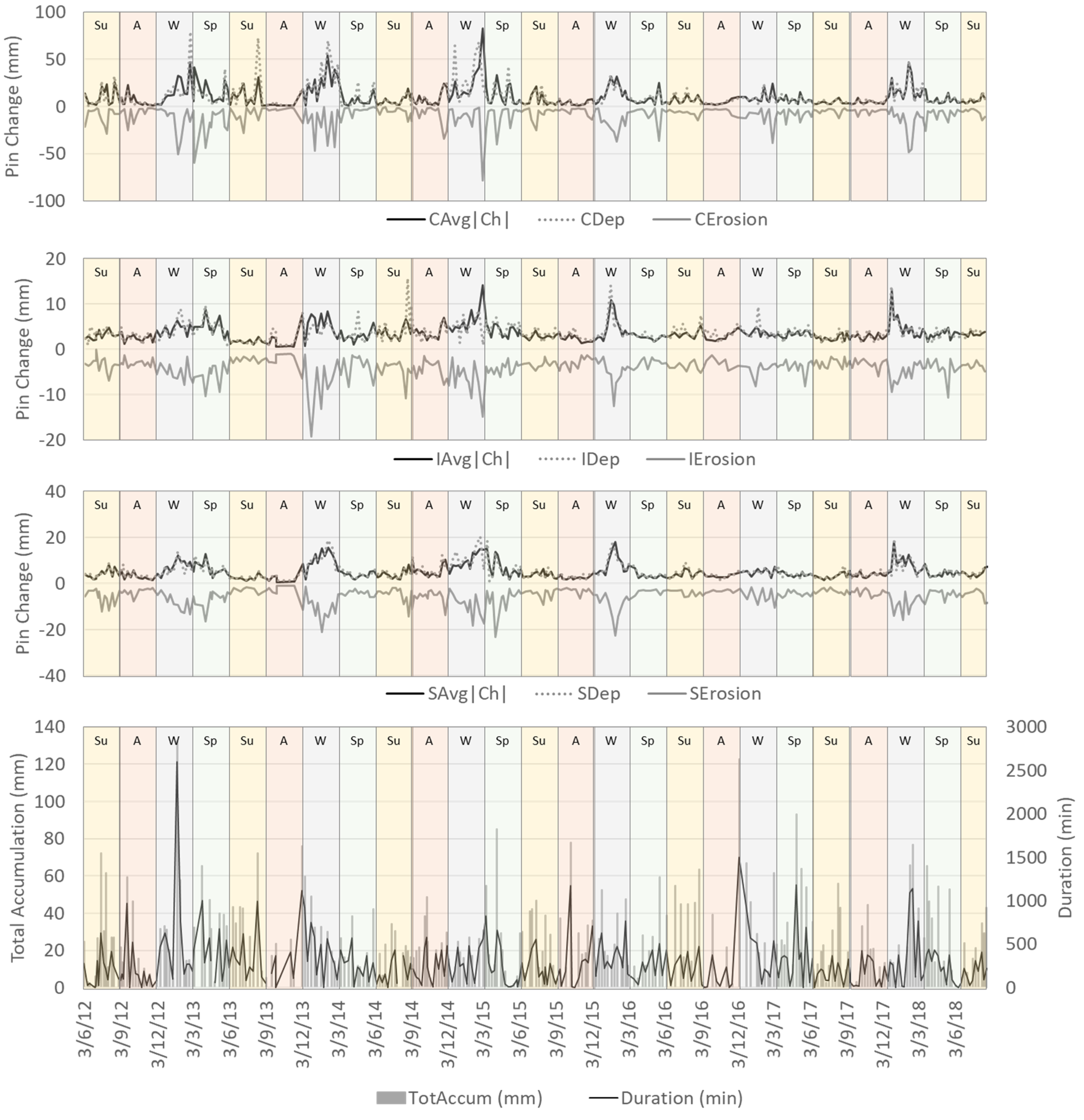
19] and is summarized as following. Steel erosion pins were installed in transects throughout the 100 m × 100 m gullied zone. Each transect spanned interfluves, sidewalls, and the gully channel to assess erosion in these three morphological settings. In total, 105 erosion pins were installed, 34 (1 m × 5 mm) pins in channels, and the remaining (0.5 m × 5 mm) pins in interfluves (29 pins) and sidewalls (42 pins). From 23 May 2012 to 22 August 2018, pin length was recorded approximately weekly for each pin using a folding ruler. Pin attrition occurred periodically over the study period, such that some pins were eroded, damaged, or dislodged by animals. Therefore, in May 2015, 43 new pins were installed and 3 damaged pins were replaced, bringing the total number of pins to 105. The nature of the site surface limited access during and immediately after rain events, and over the six-year period, pin length was recorded 294 times. The difference between the exposed lengths of each pin was calculated between one measurement period and the next, and this dataset of pin change was compared to precipitation data to identify important drivers for erosion in each morphological setting.
For each setting, we created three erosion variables: (1) average of the absolute value of change (Avg|Ch|); (2) average of only positive changes in pin lengths (deposition) from one measurement period to the next (AvgDep), and; (3) average of only negative changes in pin lengths (erosion) from one measurement period to the next (AvgErosion). In prior research, a fourth variable, average change, was generated, however, because of a balance of erosion and deposition, especially in channels, the average change remained near zero and was not a useful parameter to capture weekly and longer-term erosion on-site [
13,
14,
19,
20,
21]. Therefore, in this study, we have retained the three variables described above.
A Davis Vantage Pro wireless weather station (KTNJONES12, data available at
https://www.wunderground.com/dashboard/pws/KTNJONES12) was located 350 m from the research site, and recorded precipitation, pressure, temperature, and wind data at five-minute intervals. Occasional data gaps were filled with data from a neighboring station 1.6 km away (KTNJONES7, data available at
https://www.wunderground.com/dashboard/pws/KTNJONES7), with only 21 of 2282 study days missing weather data. See [
19] for a detailed list of weather data gaps and coverage.
From these data, four precipitation parameters were generated for each measurement period: (1) Duration (total minutes of rainfall); (2) Total Accumulation (total precipitation in mm); (3) Average Intensity in mm/min (Total Accumulation/Duration), and; (4) Maximum Intensity in mm/min (the greatest station-reported rain rate during the measurement period). The rain rate is a smoothed function of rain accumulation over time that is calculated using the ratio of the tipping bucket depth-adjusted volume to the time between tips. As rainfall tapers off, the rate drops but does not reach zero immediately upon cessation of precipitation. Instead, it smooths the rate to more accurately represent how precipitation naturally tapers over an area at the end of a rain storm [
22].
Prior research has shown that antecedent precipitation may be an important factor in erosion, and therefore a series of antecedent precipitation parameters were generated for the prior eleven measurement periods, for each of Duration, Total Accumulation (TotAcc), Average Intensity (AvgInt), and Maximum Intensity (MaxInt). These antecedent lagged variables were named Duration-1, Duration-2 ... Duration-11, TotAcc-1, TotAcc-2 … and so-on, a total of 48 precipitation parameters, which we refer to as lagged precipitation parameters.
The relationship between erosion variables and all precipitation parameters was assessed with Spearman correlation coefficients. Ordinary Least Squares (OLS) regression models were created for the nine erosion variables using the set of current and lagged precipitation parameters. Further, because seasonal variability in erosion was observed in prior studies [
13,
19], the data were partitioned by season: winter (December, January, February); spring (March, April, May); summer (June, July, August); and autumn (September, October, November). OLS regression models were generated for the erosion variables using the precipitation parameters for each of the seasonal datasets.
5. Conclusions
This study examined the effect of precipitation parameters on soil erosion through six years of high-resolution weekly monitoring in an Appalachian hillslope paying particular attention to seasonal effect. The long-term data provided an understanding of the seasonal pattern of soil erosion in a humid sub-tropical environment, which was not noticeable in other studies in the region using an annual dataset.
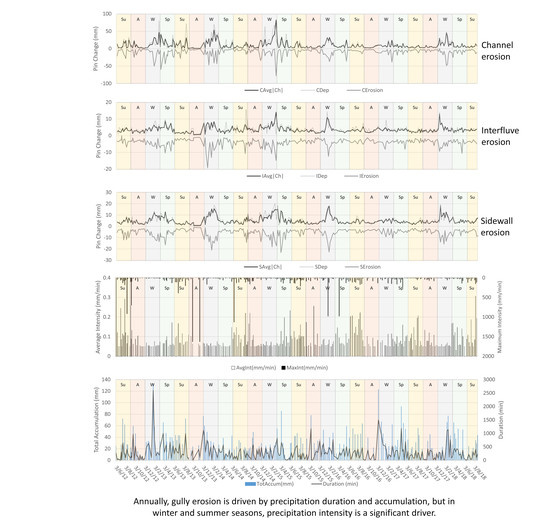
Different gully morphologies responded differently to long-term erosion. Channels were most active, showed a wide range of variability, and responded most dynamically, whereas the interfluves were least disturbed by erosion. Sidewalls were prone to erosion but were not as dynamic as channels. To explore the reason behind varied gully erosion patterns in the different geomorphic settings, further studies are recommended to evaluate how erosion fluctuates with soil cover thickness, soil types, moisture contents, slope aspect, and slope angle.
Precipitation duration was the most important factor in initiating and continuing erosion year-round, yet seasonality played a significant role in the severity of gully erosion. Erosion was most pronounced in winter months, followed by spring, indicating the influence of high-intensity precipitation from frontal systems and repeated freeze-thaw cycles. Erosion in summer was driven by high-intensity precipitation from convectional storms. Soils in the study area were least prone to erosion during the moderate months of autumn. In channels, precipitation duration was the dominant driver for erosion due to runoff-related erosion, while in sidewalls and interfluves, intensity parameters were equally important as duration, likely related to rain splash erosion. This research shows that soil erosion is seasonally variable and an understanding of the seasonal pattern of soil erosion with respect to precipitation-related drivers improves the potential to achieve strategic conservation measures.