1. Introduction
While saline groundwater systems in semi-arid and arid environments are generally considered a problem for water resource managers, the occurrence of shallow (<100 m) brackish to saline groundwater promotes the development of localized accumulations of subsurface freshwater referred to as inland freshwater lenses (IFLs) [
1,
2,
3]. IFLs serve as alternative freshwater resources for drinking water, livestock management, and micro-oasis agriculture in several arid and semi-arid regions including the Middle East (e.g., Kuwait, Oman, United Arab Emirates (UAE), Saudi Arabia), Australia (e.g., Murray Basin, Queensland), Central South America (e.g., Paraguay), Central Asia (e.g., Turkmenistan), Africa (e.g., Zambia, Namibia), and elsewhere with similar environmental settings [
2,
3,
4,
5,
6,
7,
8,
9,
10].
IFLs form and are sustained by runoff from infrequent, high-intensity rainfall events (>20 mm/h), which occur between every one to three years based on a correlation between the El Niño-Southern Oscillation and rainfall anomalies [
11,
12]. Runoff collects in low elevation geomorphic features (e.g., depressions, gullies, interdune swales) and infiltrates vertically and laterally through highly permeable sediments towards the saline groundwater [
13,
14]. The resultant variable-density condition forms a boundary surface or freshwater-saltwater interface, above which a freshwater lens forms [
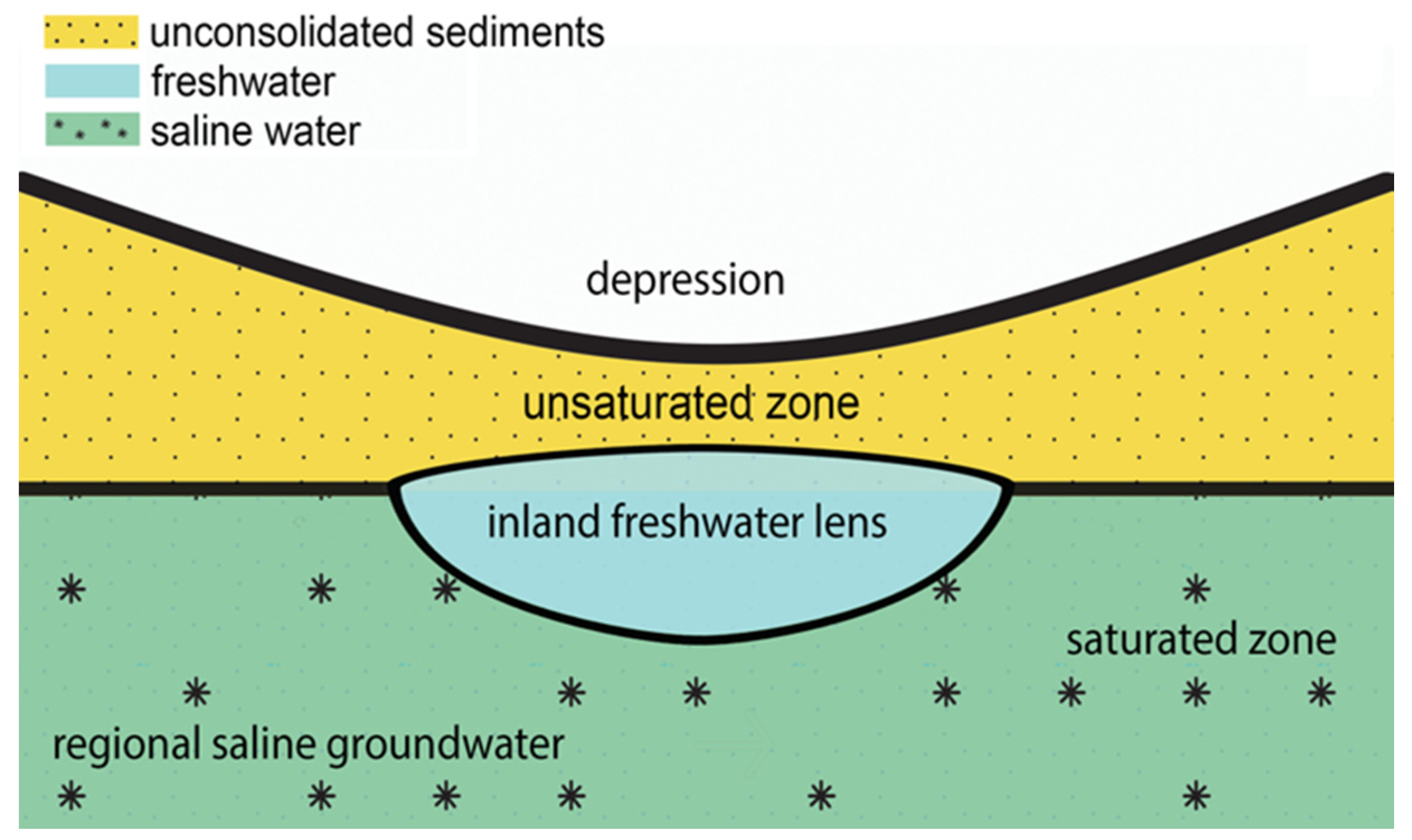
15] (
Figure 1). Unlike coastal and oceanic island freshwater lenses, which are stabilized by bounding seawater on one or more sides, IFLs migrate atop the saline groundwater in the direction of the regional gradient changing in geometry and position through time [
1,
16].
Investigations into IFLs are limited likely due to their sporadic nature and smaller scale relative to the larger-scale freshwater aquifers commonly exploited in populous regions. However, Bedouin communities likely once utilized these resources along with other ancient irrigation techniques (i.e., runoff harvesting), but abandoned these systems due to changes in the governing authority, modern agricultural practices, and inadequate drainage [
17]. Recent studies have identified more than 100 potential locations throughout the Arabian Peninsula with conditions favorable (e.g., climatic, geomorphic, hydrogeologic) for the development and sustainability of IFLs [
18]. Investigations into the formation and transient evolution of IFLs offer freshwater resources sustainability and development opportunities throughout the Arabian Peninsula and elsewhere with similar environmental settings. Novel solutions for the management of freshwater resources in these regions are critical as the overreliance on desalinization and non-renewable fossil water has created risks for environmental, political, economic, and social conditions [
19,
20,
21,
22].
Freshwater lens studies typically occur in coastal settings where the lenses are surrounded by seawater [
23,
24,
25,
26]. Physical models [
27], analytical solutions [
23,
24,
28], and numerical models have demonstrated the relationships between recharge rate, hydraulic conductivity, differences in fluid densities, and coastal freshwater lens geometry. IFL investigations using geophysical techniques [
5,
7], analytical methods [
8,
14,
29], and physical laboratory models [
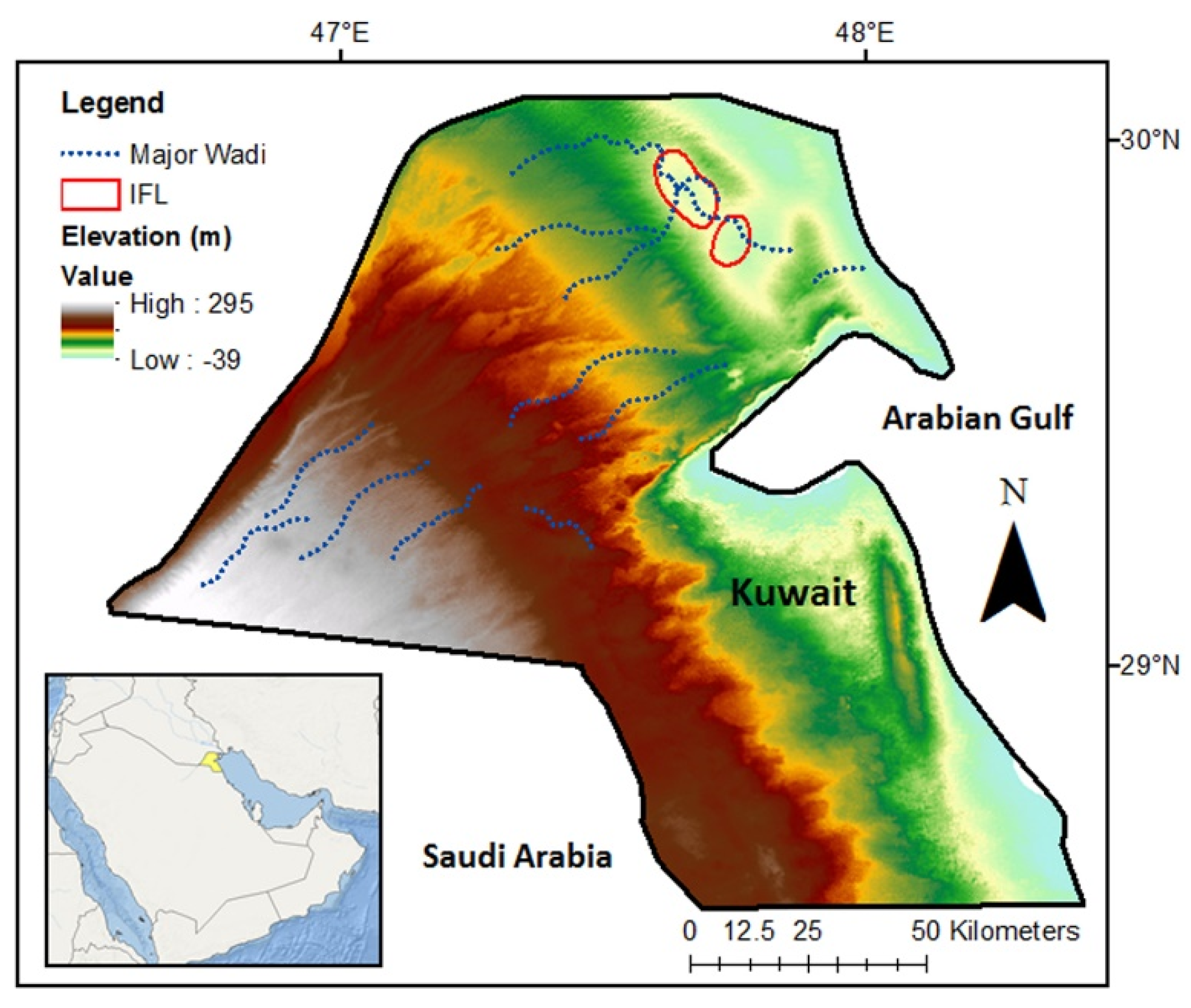
1] highlight IFL relationships between the physical and chemical properties (i.e., salinity, age) and geometry. However, none of these studies address the transient nature of IFLs over varying temporal and spatial scales. A three-dimensional, numerical model of the Raudhatain and Umm Al-Aish IFLs in Kuwait by Al-Weshah and Yihdego [
30] used MODLFOW-SURFACT code to predict water table elevations over 22 years but does not account for the freshwater extent in the vertical or horizontal direction as it migrates laterally through space and time. Research into the geometry of IFLs is needed to adequately predict the position and sustainability of exploitable freshwater resources. The purpose of this research is to presents a variable-density, finite-difference numerical model that considers geometry (i.e., thickness, length) calibrated by and compared with shared results from physical model observations by Rotz and Milewski [
1].
2. Materials and Methods
The goal of this study is to investigate the development and transient evolution of a topographically induced IFL over varying recharge rates by comparing three simulations from a newly developed numerical model with three corresponding simulations from a previously conducted physical model in Rotz and Milewski [
1]. The physical model simulations conducted in Rotz and Milewski [
1] represent the formation, migration, and degradation of IFLs using an acrylic sandbox model inspired by the Raudhatain IFL in northern Kuwait (
Figure 2). The previous study investigated the effect of recharge on IFL development and compared results to the Dupuit–Ghyben–Herzberg analytical solution by Vacher [
24]. The statistical analyses in Rotz and Milewski [
1] showed the analytical solution overestimated IFL thickness (
D) and had no correlation with the recharge rate (
R) (Δ
D = 278.57
R + 0.0872,
R2 = 0.34,
p = 0.1304). The study concluded that the differences in lens geometry between the physically modeled lenses and the analytical solution were due to the transient nature of IFLs, subsequently motivating the need for numerical studies that could address IFL changes in geometry through time.
For this study, the numerical model was designed by using the physical model dimensions, porous medium, boundary conditions, and initial conditions from Rotz and Milewski [
1]. In addition, numerical model calibration and comparative analyses used the observational data from three physical model simulations. The observational data (i.e., water table elevation, thickness, length) was obtained from still photographic images generated during the previous study (
Figure 3). Uranine tracer-dye added to the freshwater during the physical model simulations allowed for the digital measurement of IFL geometry (i.e., thickness, length) using ImageJ software. Results from the numerical model were then compared to the results from the previously conducted physical model simulations to determine if the numerical model adequately simulated the observed IFLs.
The numerical model was developed using the SEAWAT programming code to simulate saturated, variable-density groundwater flow and solute transport. The SEAWAT program is a density-dependent groundwater flow model utilized for the modeling of groundwater in aquifers with fresh and saline groundwater interaction [
31]. SEAWAT couples MODFLOW-2000 [
32] and the Modular Three-Dimensional Multispecies Transport Model (MT3DMS) to solve the three-dimensional groundwater flow and solute transport numerically with finite difference approximations [
32,
33,
34,
35]. The shell program is Visual Modflow. The numerical model was designed in a two-dimensional manner to represent a cross-sectional slice of the hydrogeological system of a topographically induced IFL simulated with the physical model.
SEAWAT solves the fluid flow equation in terms of the hydraulic head by combining a general form of Darcy’s law for variable density conditions [
36] with a hydraulic conductivity tensor [
37], and vertical flow components [
38,
39] (Equation (1)):
where
is the divergence operator,
is fluid density (ML
−3),
K is hydraulic conductivity tensor (LT
−1),
h is the freshwater head (L),
ρf is the freshwater density (ML
−3),
z is elevation,
Ss is the freshwater specific storage (L
−1),
θ is porosity (1), and
qs is a source or sink (T
−1) of fluid with density
ρs.
SEAWAT uses the MT3DMS model to solve the general form of the solute transport equation [
34] (Equation (2)):
where
C is the solute concentration (ML
−3),
D is the solute dispersion tensor,
v is the advective velocity (LT
−1), and
Cs is the source or sink concentration (ML
−3). The linking of Equations (1) and (2) requires a function to relate concentration and fluid density.
2.1. Numerical Model Design and Parameters
The transient flow model was developed with SEAWAT to assess IFL geometry and transience for 200 h. The domain of the numerical model encompasses a space of 2.0 m (L) × 0.5 m (H) × 0.10 m (W) (
Figure 4). The numerical model did not include the upper 0.5 m of the unsaturated zone of the physical model, as these were considered inactive cells within SEAWAT. The bottom left side elevation of the domain is at 0 m. The grid consists of 100 columns to represent the length (
x-axis), 25 rows to represent the height (
z-axis), and one layer to represent the width (
y-axis). The parameters of hydraulic conductivity (
Kx,
Ky,
Kz), were used from measurements taken during the previously conducted physical laboratory model study with a constant head permeameter during the laboratory experiments from sediments comprised of medium to fine sand (
d50 = 0.55 mm) to represent the highly permeable gravel sediments in the upper layer of the Kuwait Group Aquifer [
36]. The porosity (
) was calculated during the previous study using the sum of solid and pore volumes. Additional representative properties of variable-density values through porous media were selected after Konikow, et al. [
40] and others, as shown in
Table 1.
2.2. Boundary and Initial Conditions
The boundary conditions of the numerical model corresponded to the physical laboratory model conditions (
Figure 4). The base of the domain included a no-flux boundary. The left side of the domain included a constant head boundary of 0.41 m (
h1) with a constant concentration of 35,700 mg/L for the full duration of the model (200 h). The right side of the domain included a general-head boundary with a general-head elevation at 0.405 m (
h2) and boundary-head elevation at 0.40 m for a distance of 2 m, which generated a slope of 0.25% to represent the gentle gradient. The top layer of the domain included a recharge boundary with a width (
wr) of 0.42 m. The initial condition of the freshwater head (
hf) was calculated to 0.4075 m based on the change in water table elevation between the left and right boundaries of the domain. The initial saltwater concentration (
Cs) of 35,700 mg/L was selected for the brackish to saline water from the Raudhatain Depression (7000–50,000 mg/L) and used with the physical model simulations. Evaporation, similar to the previously conducted physical laboratory simulations, was considered negligible. A summary of the boundary conditions is shown in
Table 2.
2.3. Observation Wells and Geometry Data
Observation wells for water table elevations were used within the numerical model. Measurements from the physical model simulations at four static locations along the cross-section provided data for the wells. Water table elevation measurements were obtained from the physical laboratory model simulations from the previous study when the lens reached a maximum thickness and then every hour until ten hours, which was the time observed for the physical simulations where the tank wall did not interfere with the lens geometry. Wells 1–3 were located beneath the recharge zone, and Well 4 was assigned on the right side or down gradient end of the model (
Figure 4). The elevation of the well screens within the numerical model was set directly below the initial water table elevation of 0.40 m. IFL thickness and length measurements from the physical model were taken to compare with the numerical model.
2.4. Numerical Settings
The simulation scenario selections for the SEAWAT numerical engine are described here. The explicitly coupled or “one-time step lag” option was selected where the flow equation is calculated using the fluid density from the previous transport time step, as solute concentrations are not expected to change rapidly. Due to the transient nature of IFLs, the upstream-weighting algorithm was selected to calculate the density value based on the flow direction of a particular iteration. For the viscosity calculations, a single species was used with no temperature dependence.
The Preconditioned Conjugate Gradient (PCG2) solver package was selected for the flow calculations with the maximum inner and outer iterations set to 100 each. The head change criterion was set to 1 × 10−5 m because of the small range of measurement values from the physical laboratory model. The flow solver used the incomplete Cholesky preconditioning method.
The implicit finite-difference method was used with the Generalized Conjugate Gradient (GCG) package to solve the transport equation. An upstream finite difference method was used to solve the advection term. The maximum number of outer and inner iterations was set to 1 and 50, respectively. A modified incomplete Cholesky preconditioner was also used for the transport solver. The relative convergence criterion was set to 1 × 10−8. The lengths of transport time steps were calculated using a Courant number of 0.75. The time steps for the flow calculations for stress periods 1, 2, and 3 are 10, 50, and 50, respectively. The maximum number of transport steps was set at 3000 with a maximum step size set at 0.125 h. Simulation results were saved at every time step for both flow and transport calculations to use for analyses.
2.5. Simulations
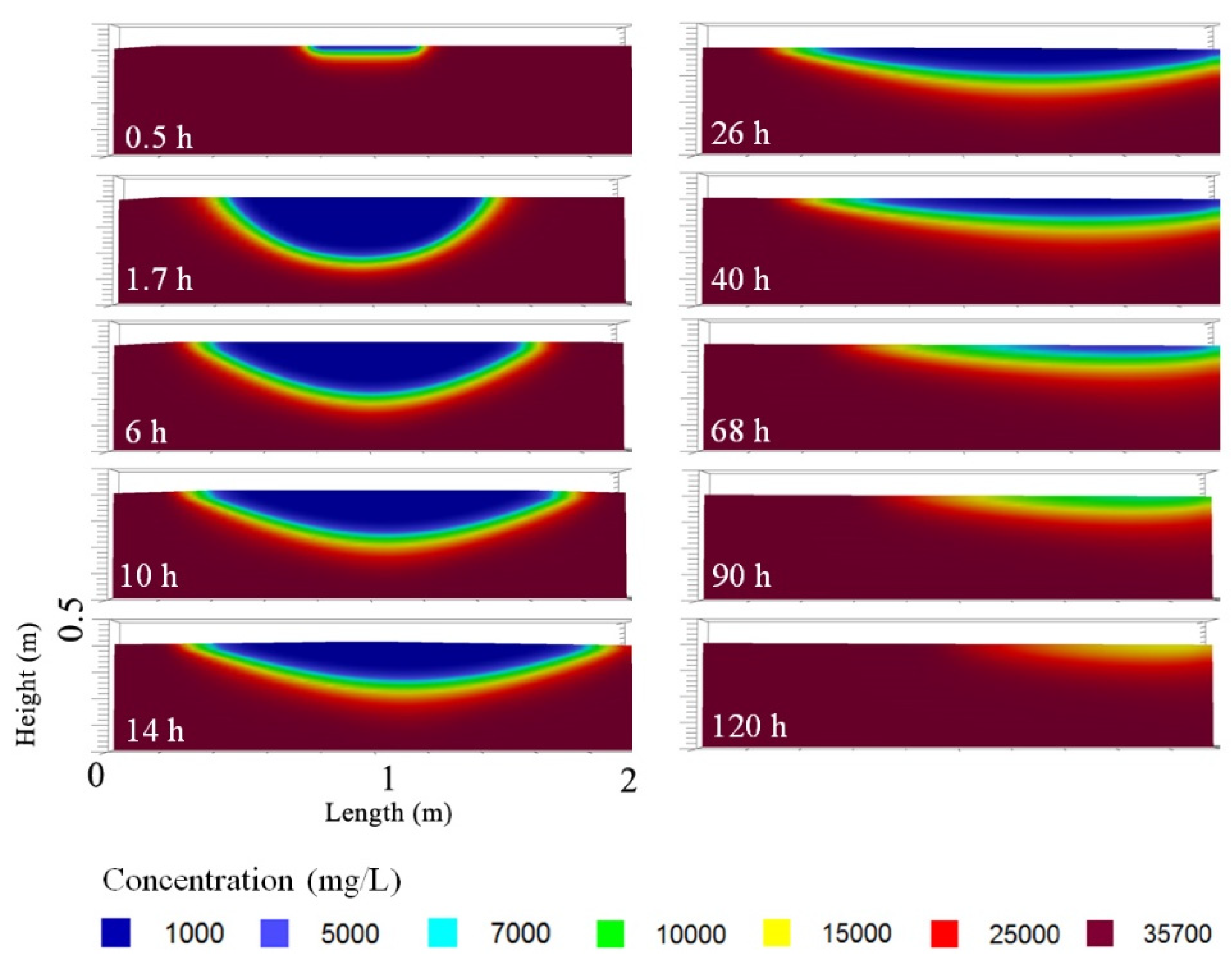
Three physical laboratory simulations at varying recharge rates were selected to reproduce three numerical simulations (
Table 3). An example of Simulation 2 from the previously conducted physical laboratory simulations is shown in
Figure 5. For the physical model simulations, recharge was applied at varying rates for 1 hour. For the numerical model, the recharge rates were adjusted to account for the infiltration travel time through the unsaturated zone (
Table 3). Observations made of the time passed for the freshwater to initially flux across the water table (
Tq) were recorded and subtracted from the time observed for each simulated lens to reach a maximum thickness (
Tmax). The initial recharge rates (
Ri) used in physical experiments were divided by the calculated time differences to equal the adjusted recharge rates (
Ra). The beginning of the second stress period was set to the observed time of initial flux, and the end of the second stress period was set at the time of the observed maximum thickness to match the maximum thickness times of the physical model to the numerical model. Three stress periods were assigned to each simulation to apply the recharge and represent (1) a period of no recharge, (2) a period of freshwater recharge applied across the recharge boundary, and (3) a period of no recharge for a total duration of 200 h. The duration of each stress period was set accordingly (
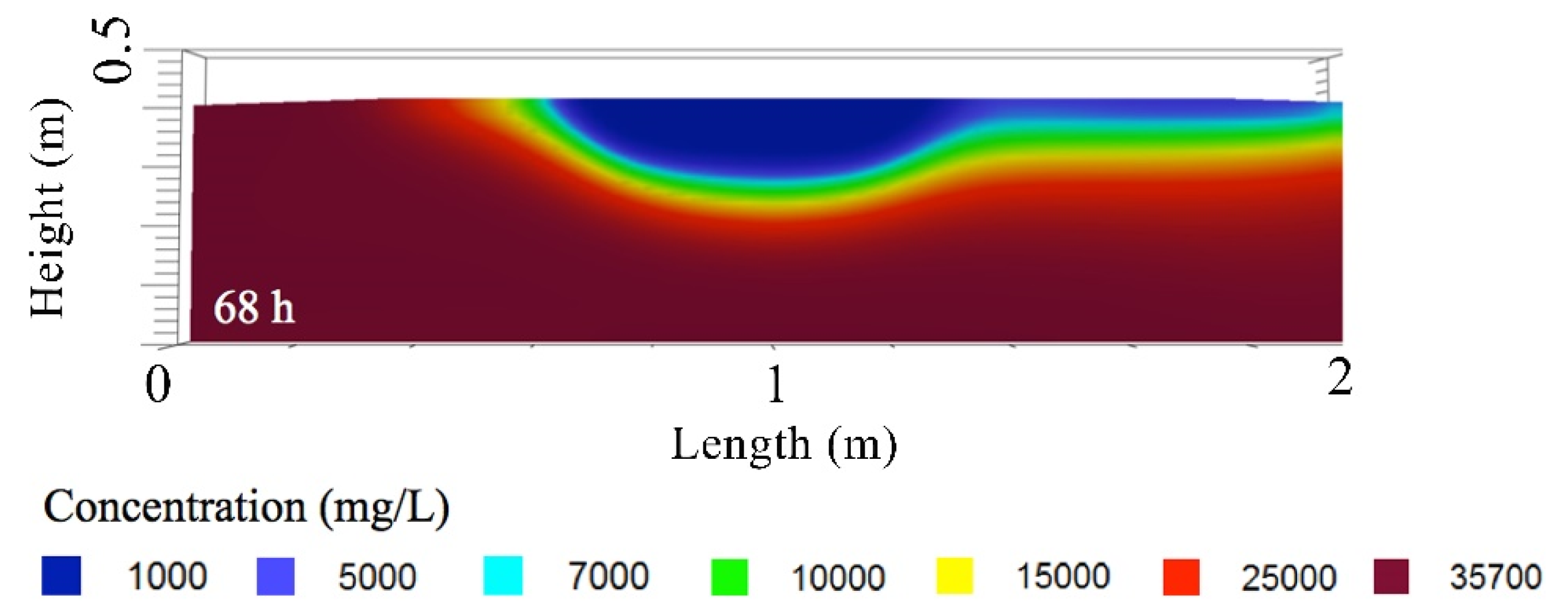
Table 3). Freshwater was infused with uranine, which is a tracer dye that allowed for the measurements of IFL thicknesses and lengths for ten hours for each simulation before the tank wall interfered with the lens geometry, which was compared to the numerical model using concentration data exported from the software. Statistical model evaluation techniques were used to determine the accuracy of the simulated data [
41].
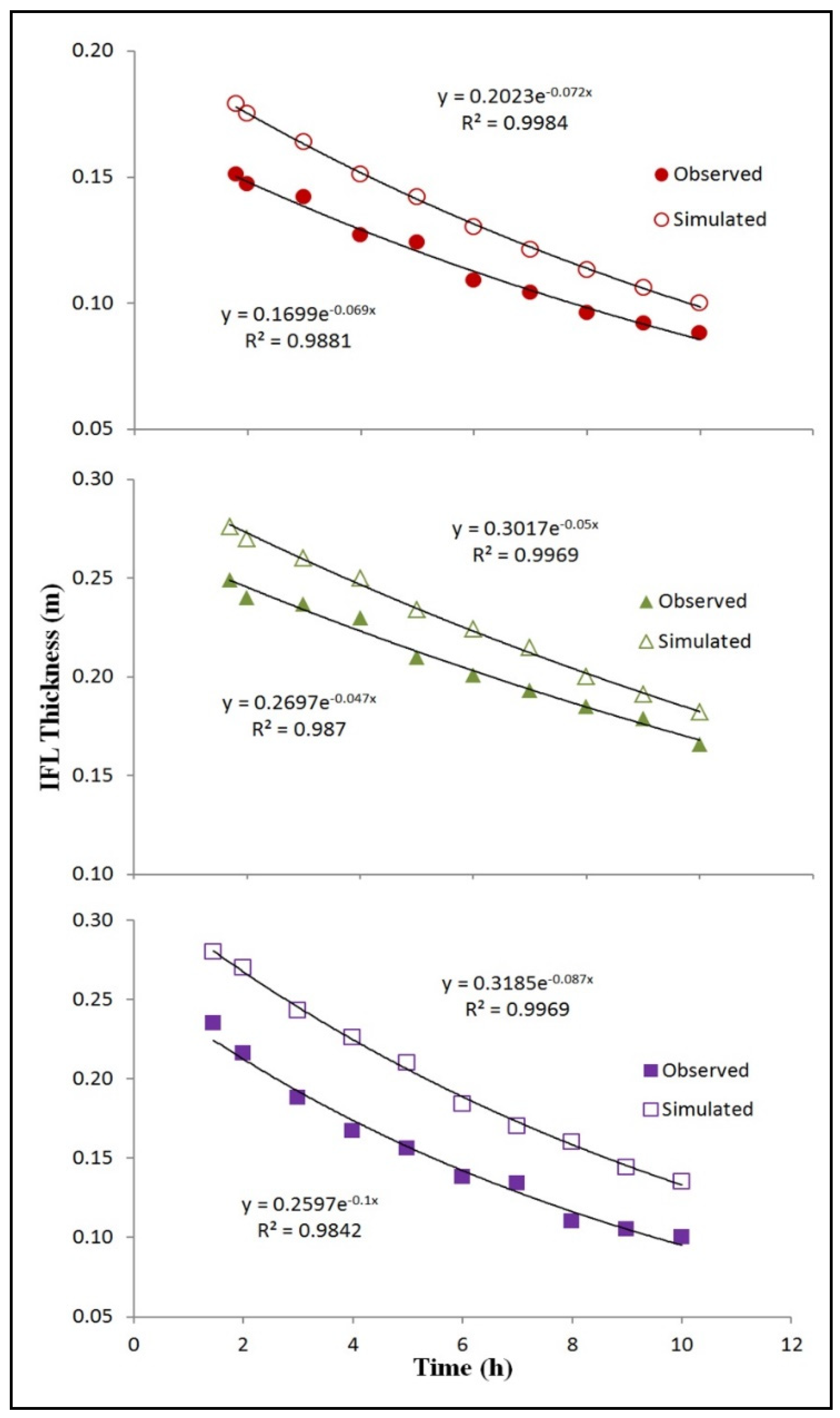
4. Discussion
The numerical model using the SEAWAT programming code successfully modeled the development and transient evolution of three IFLs produced with a physical laboratory model [
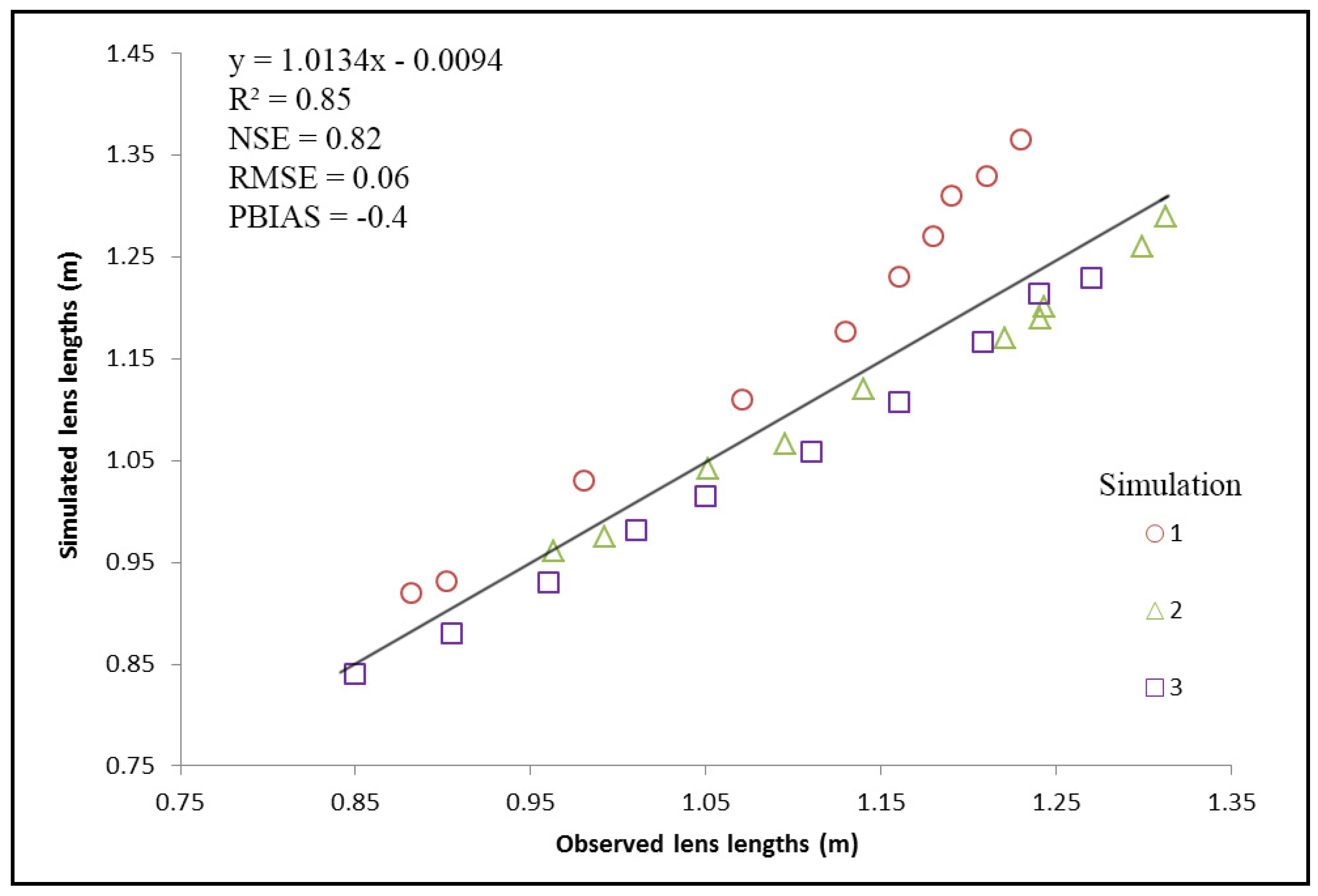
1]. Although SEAWAT does not model variable-saturated conditions, the adjusted recharge rates were sufficient to adequately simulate water table elevations, thicknesses, and lengths based on the physical laboratory model observations. In all cases, the model evaluation statistics indicated that the numerical model over-predicted thicknesses and lengths under the assumption that the error variance occurs within the simulated values.
The numerical model parameters of hydraulic conductivity were refined with the PEST calibration tool, which estimated hydraulic conductivities within an acceptable range for fine to medium unconsolidated, heterogeneous sand. The initial laboratory measurement of hydraulic conductivity at 0.0015 m/s likely did not consider the heterogeneity and anisotropy present in the physical model sand due to the systematic, horizontal packing of sand during the model setup. However, the statistical evaluations of the water table elevations, thicknesses, and lengths show that the numerical model adequately reproduced the magnitudes of the measured data.
The average velocities estimated by the numerical model aligned with velocities measured from the physical model, as well as the average velocities reported by Al-Weshah and Yihdego [
30] of 6.34 × 10
−7–2.85 × 10
−6 m/s. The numerical model showed an increase in average velocity during the recharge stress period by an order of magnitude (10
−5 m/s), which aligns with the range of recharge rates used in the physical and numerical model simulations 3.33 × 10
−6–6.67 × 10
−6 m/s. Based on these values, freshwater recharge that entered the center of the Raudhatain depression is estimated to travel 4000 meters towards the periphery between 20 and 200 years, depending on the hydraulic conductivity. This estimate aligns with those by Yihdego and Al-Weshah [
43] and Parsons Engineering and Construction Corporation [
44] who reported an inferred flow velocity between 11 and 245 m/year based on
14C and
3H age dating, as well as an estimated groundwater velocity of 20–90 m/year based on a hydraulic conductivity range of 40–80 m/day. Estimates such as these inform geochemical studies that aim to approximate IFL water age, such as the study by Kuldzhayev [
45], which determined the onset of freshwater accumulation of an IFL in the Karakum desert to be 3400 years. Investigations into the formation, geometry, and extent of freshwater lenses over long temporal scales are needed for inland and coastal environments to quantify the supply of drinking water and the effects of external changes such as precipitation and sea-level rise [
13,
30], but also geomorphological [
46] and anthropogenic impacts [
47,
48].
Errors from the measurements taken from the physical model simulations were likely produced from multiple sources. The water table elevation or top of the IFL was challenging to estimate due to the capillary fringe. Preferential flow paths or heterogeneities of hydraulic conductivity likely developed from the packing of the sand during the setup of the physical model simulations, which required careful consideration when determining IFL length. The numerical model did not account for these heterogeneities or water retained in the pore space of the unsaturated area, which likely further contributes to errors in the numerical simulations.
Physical and numerical models are helpful tools to understand the stochastic relationships for subsurface flow and transport in variable-density aquifers in naturally and artificially recharged aquifers [
49,
50]. Numerical models such as SEAWAT and others (e.g., MODFLOW-SURFACT, SUTRA (Saturated-Unsaturated Transport)) allow for the incorporation of variable-density conditions and parameters such as recharge volume, recharge location, concentration, temperature, multiple species, and other variables in terms of solute transport and subsurface flow. Although freshwater lens geometry, including transience, can be determined with these models, additional tools and optimization approaches to automate the monitoring of lens geometry are needed to improve the understanding of IFL sustainability. Models should be developed to consider the freshwater extent in the vertical and horizontal directions to predict volume, location, and residence time. Numerical simulations that include concentration data may use PEST to improve model calibration, which in turn improves the position and shape of the lens. These advancements will be useful for studying the dependence of periodic recharge on IFL degradation for water resources management.
Figure 11 shows a conceptual example of IFL sustainability after a second recharge pulse is applied during IFL degradation.
5. Conclusions
The purpose of this study was to create a conceptual framework for topographically induced IFL transient evolution using a numerical model and demonstrate the utility of IFL geometric analyses for resource management. We employed the SEAWAT programming code with Visual Modflow to simulate variable-density groundwater flow and solute transport within an inland setting based on observations made during physical laboratory model simulations [
1]. The numerical model was calibrated against the observed water table elevations measured in the laboratory by adjusting the values of hydraulic conductivity. The numerical model simulated IFL transient evolution and demonstrated the usefulness of predicting IFL geometry over time for water resource management.
As the demand for water resources in arid environments intensifies in conjunction with climate change, novel approaches for water resources development are needed [
51,
52,
53,
54,
55]. Desert communities have historically used inland and coastal freshwater lenses combined with ancient irrigation techniques (e.g., runoff harvesting, subsurface canals) for access to freshwater because the methods were uncomplicated and technologically inexpensive [
56,
57,
58]. Similar systems have been identified within the deserts of the Middle East, Asia, Australia, South America, and Africa but have declined in use. A return to these systems with a focus on the interplay between meteoric recharge and the underlying saline groundwater offers development opportunities through modern and traditional methods to meet the growing demand for water resources in arid environments [
18,
57].
This study provides a useful example for investigating IFL dynamics for the discovery of new resources [
18], adjustment of pumping schemes [
47], and artificial recharge applications [
50]. The SEAWAT programming code serves as an effective tool for investigating the complexity of IFL transient evolution over long temporal scales for the prediction of available water resources in drylands.