Shear-Thinning Fluid Flow in Variable-Aperture Channels
Abstract
1. Introduction
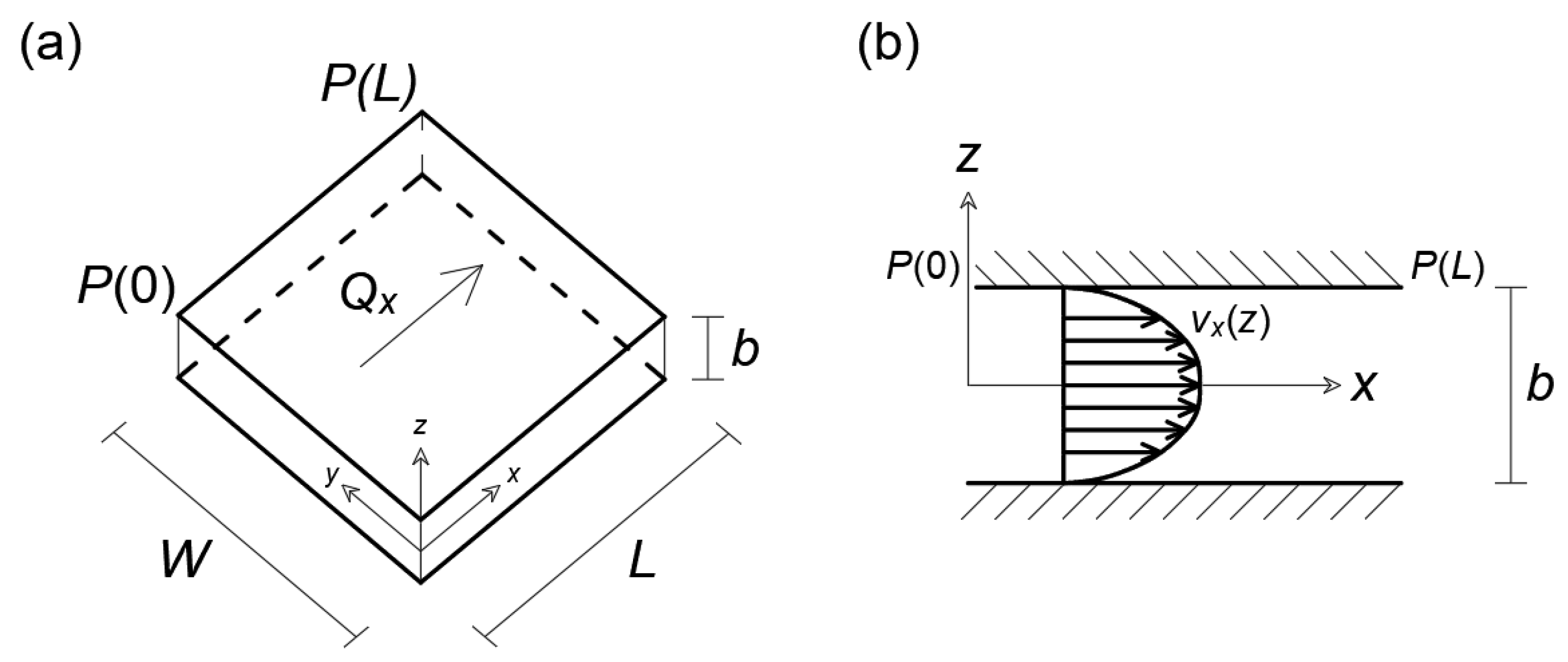
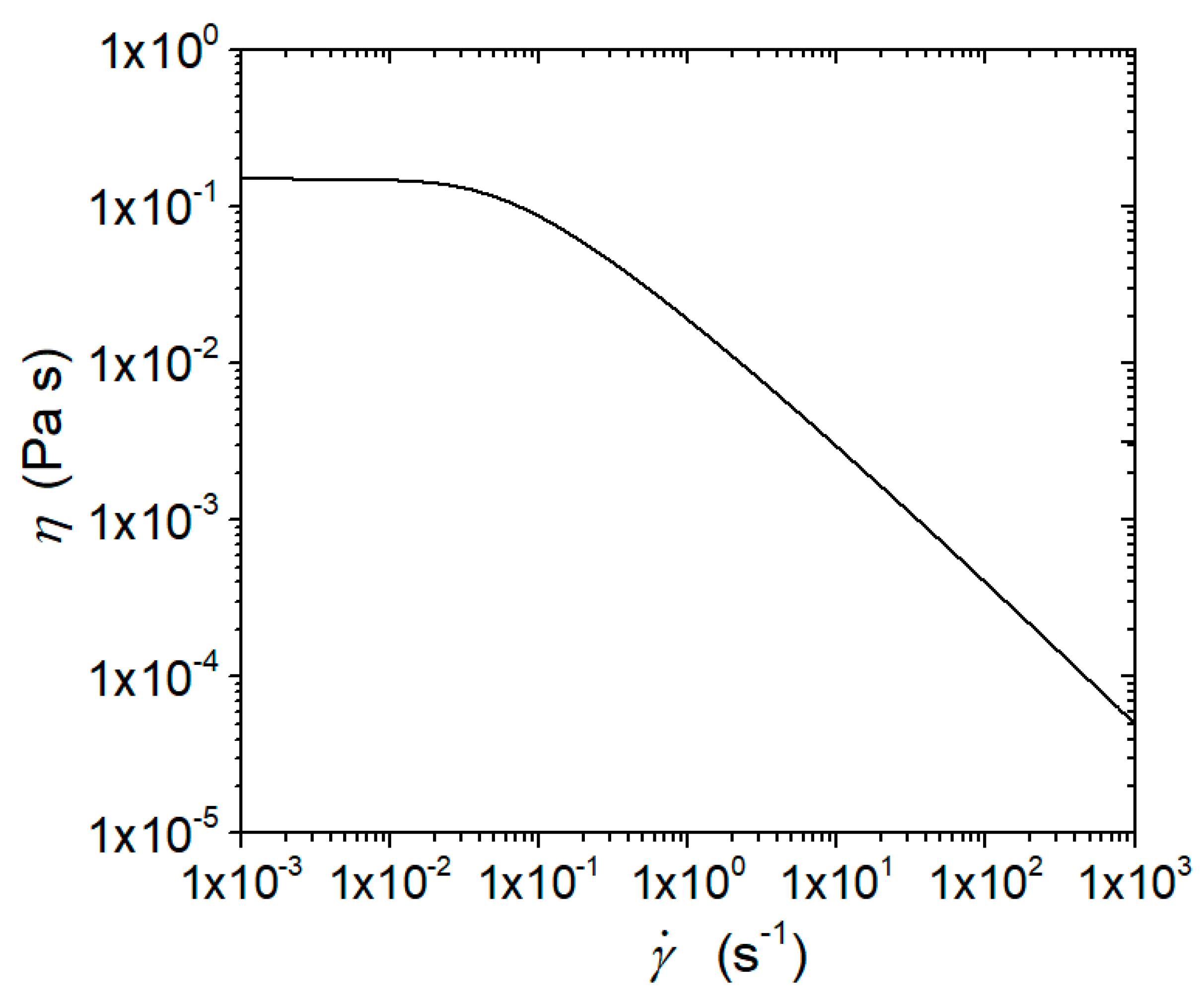
2. Prandtl–Eyring Fluid Flow in Constant-Aperture Fracture
3. Flow in Variable-Aperture Channels
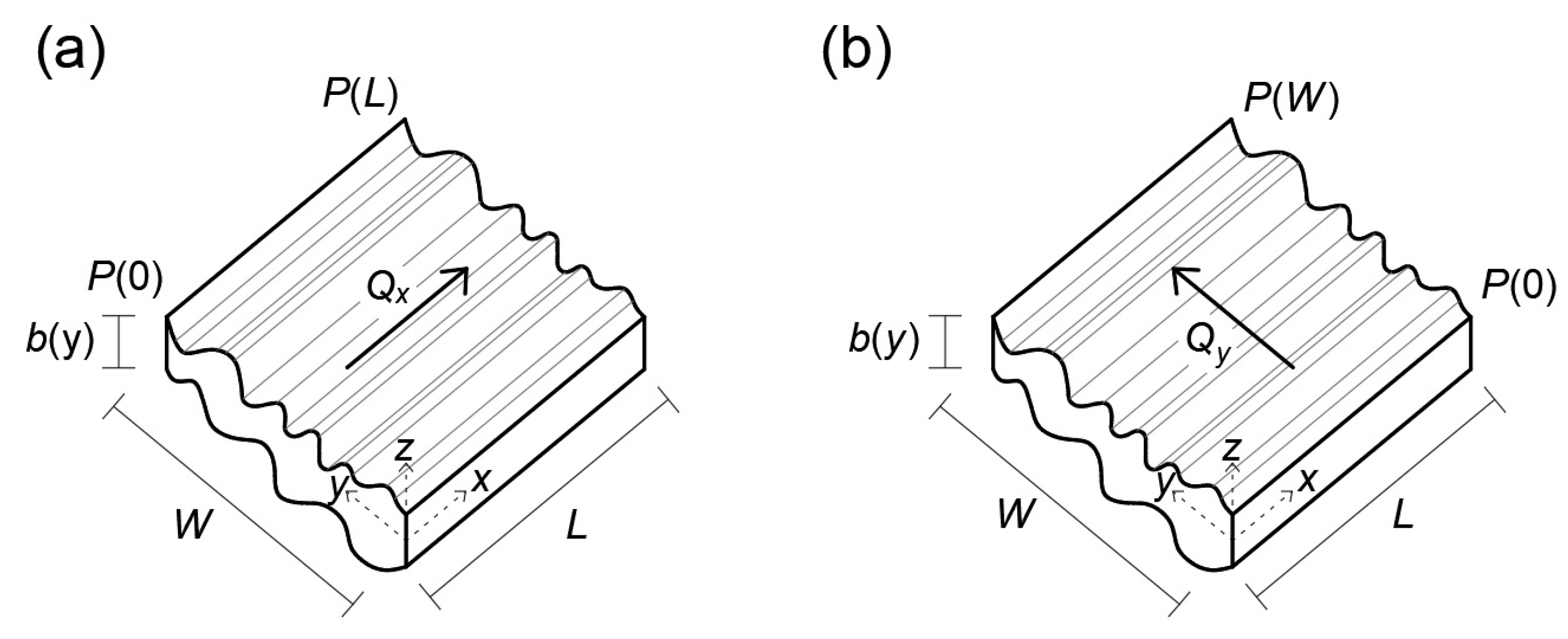
3.1. Channels in Parallel
3.2. Channels in Series
3.3. Flow in 2-D Isotropic Aperture Field
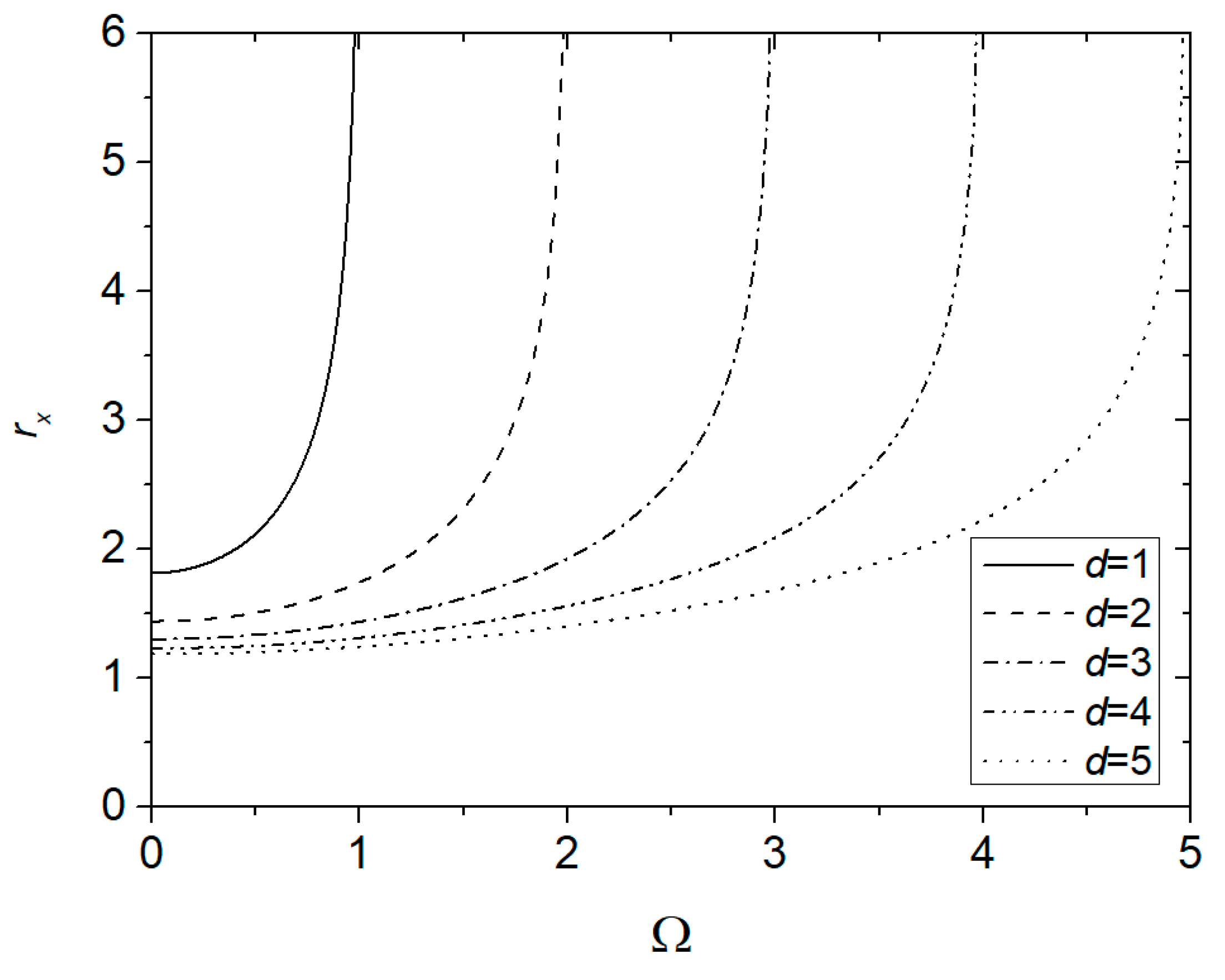
4. Estimates of Hydraulic Aperture
4.1. Aperture Probability Distribution
4.2. Channels in Parallel
4.3. Channels in Series
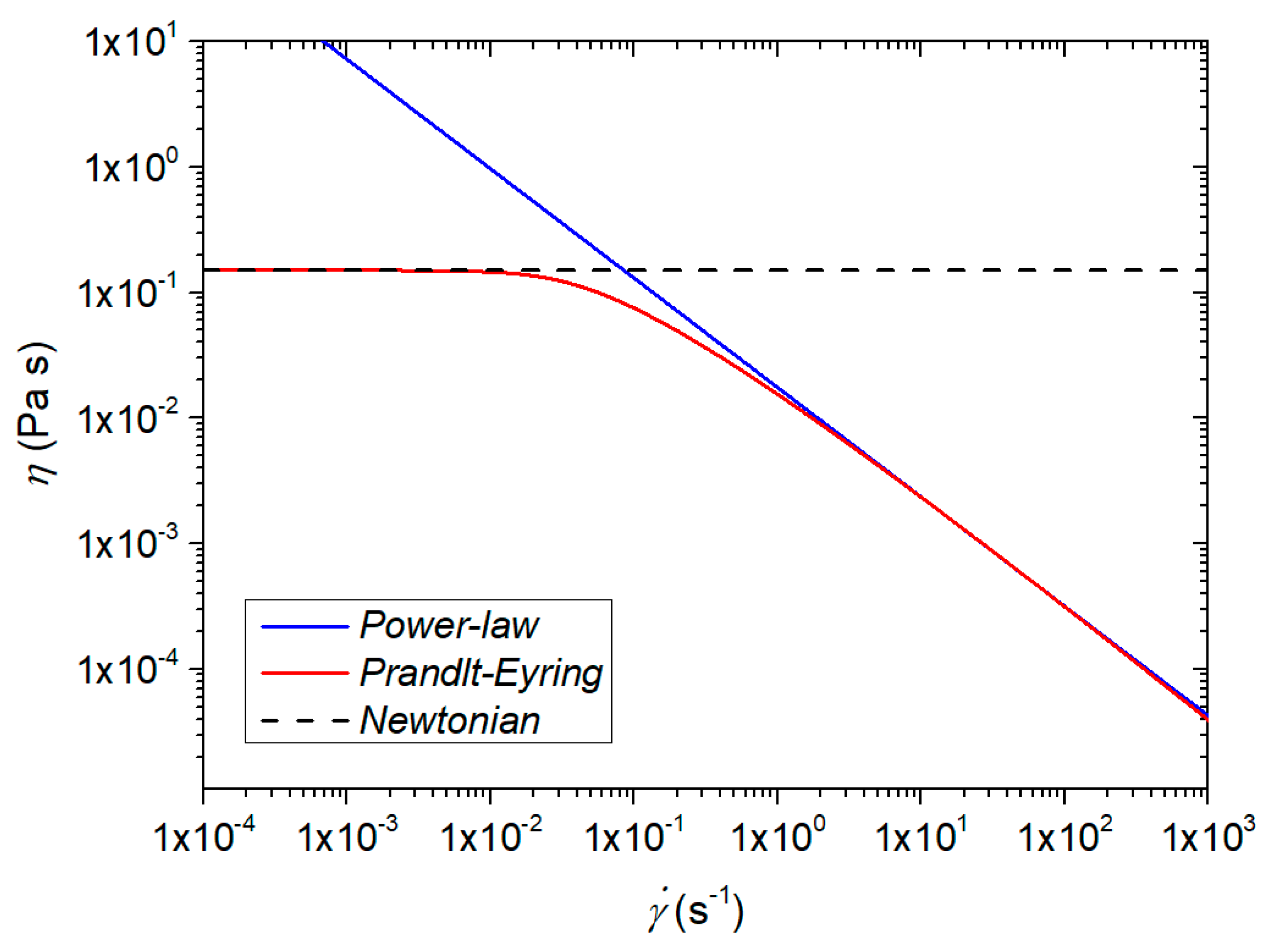
5. Comparison with Power-Law Fluid Flow
5.1. Results for a Power-Law Fluid
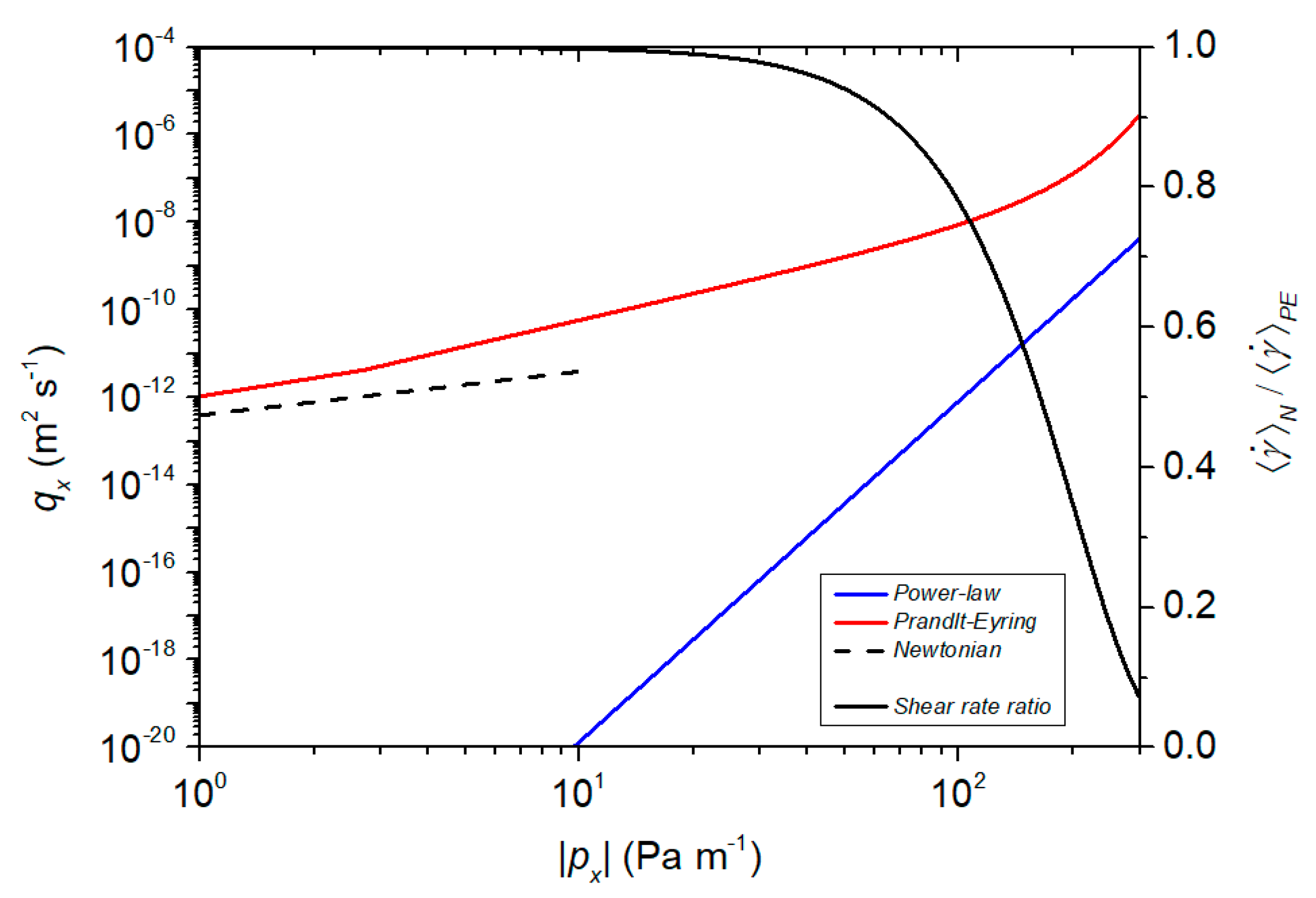
5.2. Comparison between Power-Law and Prandtl–Eyring Models
6. Conclusions
- Values of the flow rate are extremely sensitive to the applied pressure gradient and to the shape of the distribution; in particular, a more skewed distribution entails larger values of the dimensionless flow rate;
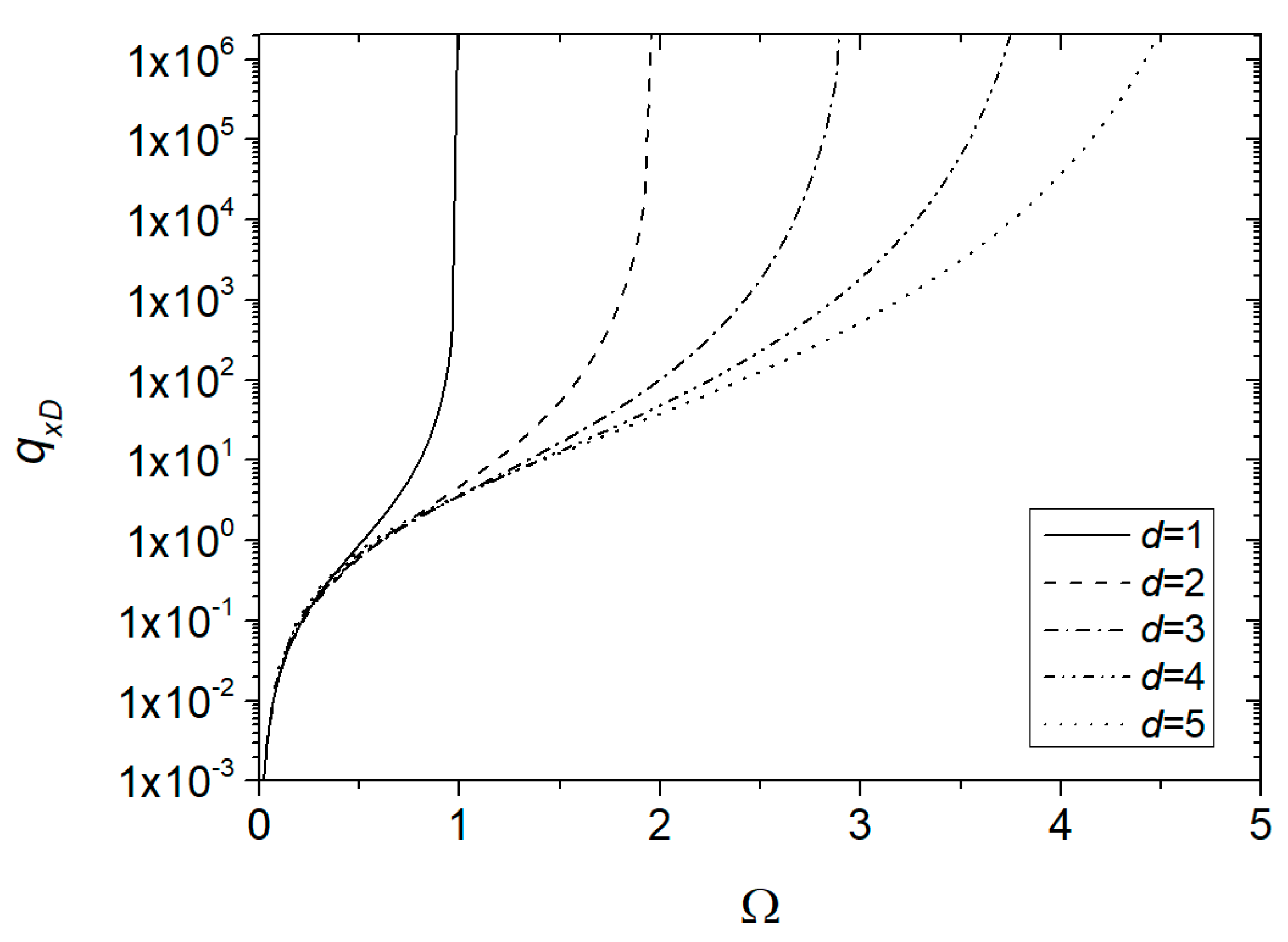
- A comparison was drawn between the Prandtl–Eyring (PE) and the power-law (PL) model having equal apparent viscosity for a wide range of shear rates. For channels in parallel, the absence of a shear stress plateau for low shear rates, associated with power-law rheology, implies an underestimation of the fracture flow rate with respect to the Prandtl–Eyring case. For the latter fluid, low-pressure gradients are characterized by a flow regime dominated by the plateau viscosity , with a behavior similar to a Newtonian (N) fluid, while for sufficiently high-pressure gradients, as the ratio between the two average fracture flow rates (PE to N) increases, the effect of the falling limb of the Prandtl–Eyring model, associated with a lower apparent viscosity, becomes evident.
- the incorporation of drag effects, local losses, and slip in the simplified 1-D models;
- the adoption of truncated and correlated distributions to represent more realistically the spatial variability;
- further refinements of the fluid rheology (e.g., Powell–Eyring, Cross, or Carreau–Yasuda model [7]).
Author Contributions
Funding
Conflicts of Interest
References
- Adler, P.M.; Thovert, J.F.; Mourzenko, V.M. Fractured Porous Media; Oxford University Press: Oxford, UK, 2002; p. 184. [Google Scholar]
- Wang, L.; Cardenas, M.B. Analysis of permeability change in dissolving rough fractures using depth-averaged flow and reactive transport models. Int. J. Greenh. Gas Control 2019, 91, 102824. [Google Scholar] [CrossRef]
- Meheust, Y.; Schmittbuhl, J. Geometrical heterogeneities and permeability anisotropy of rock fractures. J. Geophys. Res. 2001, 106, 2089–2102. [Google Scholar] [CrossRef]
- Silliman, S. An interpretation of the difference between aperture estimates derived from hydraulic and tracer tests in a single fracture. Water Resour. Res. 1989, 25, 2275–2283. [Google Scholar] [CrossRef]
- Lavrov, A. Redirection and channelization of power-law fluid flow in a rough walled fracture. Chem. Eng. Sci. 2013, 99, 81–88. [Google Scholar] [CrossRef]
- de Castro, A.R.; Radilla, G. Flow of yield stress and Carreau fluids through rough walled rock fractures: Prediction and experiments. Water Resour. Res. 2017, 53, 6197–6217. [Google Scholar] [CrossRef]
- Bechtel, S.; Youssef, N.; Forest, M.; Zhou, H.; Koelling, K.W. Non-Newtonian viscous oscillating free surface jets, and a new strain-rate dependent viscosity form for flows experiencing low strain rates. Rheol. Acta 2001, 40, 373–383. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Kumar, S.; Bodvarsson, G.S. Lubrication theory analysis of the permeability of rough-walled fractures. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1991, 28, 325–331. [Google Scholar] [CrossRef]
- Yoon, H.K.; Ghajar, A.J. A note on the Powell-Eyring fluid model. Int. Commun. Heat Mass 1967, 14, 381–390. [Google Scholar] [CrossRef]
- Rehman, K.U.; Awais, M.; Hussain, A.; Kousar, N.; Malik, M.Y. Mathematical analysis on MHD Prandtl-Eyring nanofluid new mass flux conditions. Math. Methods Appl. Sci. 2019, 42, 24–38. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier: New York, NY, USA, 1972; p. 764. [Google Scholar]
- Di Federico, V. Estimates of equivalent aperture for Non-Newtonian flow in a rough-walled fracture. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1997, 34, 1133–1137. [Google Scholar] [CrossRef]
- Brown, S.R. Transport of fluid and electric current through a single fracture. J. Geophys. Res. 1989, 94, 9429–9438. [Google Scholar] [CrossRef]
- Di Federico, V. Non-Newtonian flow in a variable aperture fracture. Transp. Porous Med. 1998, 30, 75–86. [Google Scholar] [CrossRef]
- Felisa, G.; Lenci, A.; Lauriola, I.; Longo, S.; Di Federico, V. Flow of truncated power-law fluid in fracture channels of variable aperture. Adv. Water Resour. 2018, 122, 317–327. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Bodvarsson, G.S. Hydraulic conductivity of rock fractures. Transp. Porous Med. 1996, 23, 1–30. [Google Scholar] [CrossRef]
- Dagan, G. Flow and Transport in Porous Formations; Springer: Berlin/Heidelberg, Germany, 1989; p. 658. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: New York, NY, USA, 1994; p. 1204. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenci, A.; Longo, S.; Di Federico, V. Shear-Thinning Fluid Flow in Variable-Aperture Channels. Water 2020, 12, 1152. https://doi.org/10.3390/w12041152
Lenci A, Longo S, Di Federico V. Shear-Thinning Fluid Flow in Variable-Aperture Channels. Water. 2020; 12(4):1152. https://doi.org/10.3390/w12041152
Chicago/Turabian StyleLenci, Alessandro, Sandro Longo, and Vittorio Di Federico. 2020. "Shear-Thinning Fluid Flow in Variable-Aperture Channels" Water 12, no. 4: 1152. https://doi.org/10.3390/w12041152
APA StyleLenci, A., Longo, S., & Di Federico, V. (2020). Shear-Thinning Fluid Flow in Variable-Aperture Channels. Water, 12(4), 1152. https://doi.org/10.3390/w12041152






