1. Introduction
The range of fluid and tracer dynamics in aquatic systems extends from basin scale, up to approximately 10,000 km in the ocean, to turbulence scale, approximately 1 mm, which is related to the dissipation of Turbulent Kinetic Energy (m
2/s
3 or Watt/kg) [
1,
2,
3]. Turbulent Kinetic Energy has a critical effect in transporting and changing the local concentration of ocean tracers such as dissolved oxygen, carbon dioxide, nutrients, plankton, and pollutants. Processes at the air–water interface can influence the transport and transformation of tracers in the water column. For instance, wind-driven waves can affect tracer concentration and distribution through advection and diffusion. In particular, diffusive processes should be dominated by turbulence, which may be biased by waves because of their overlap in frequency and scale. Thus, the study of diffusion and turbulence in the water column, and its identification from waves’ influence, should allow an understanding of vertical exchange processes that determine the fate of tracers in aquatic environments. It follows that estimating Turbulent Kinetic Energy, including its transport, production, and dissipation, is obscured by the presence of surface waves because, as mentioned above, waves and turbulence share spectral energy bands. A reliable approach for velocity measurements is needed to distinguish the signal related to waves and to turbulence.
Most fluid motions in nature and engineering are turbulent [
4]. Measurements of turbulence in the coastal environment can bolster our understanding of vertical exchange of momentum, energy, heat, and any tracer (e.g., nutrients), and they can help us parameterize turbulence in boundary layers [
5,
6,
7,
8]. Microstructure measurements have been used to estimate turbulence in the marine environment with devices that either fall, rise, or move horizontally (on an AUV). However, these microstructure measurements are labor intensive and require a dedicated platform [
9,
10]. Although this approach can produce reliable results, it is logistically and financially unfeasible to collect continuous long-term spatial—in the water column—series of turbulence [
11]. The use of anchored shipboard or bottom-mounted Acoustic Doppler Current Profilers (ADCPs) has allowed measurements of time series of turbulent parameters in the water column [
9,
12,
13].
Estimates of tracer transport under turbulent conditions in shallow coastal regions throughout the world may be contaminated by wave action. Turbulence properties may be confused by velocity fluctuations that include orbital velocities generated by multi-scale and multi-directional waves. Unless the effects of wave orbital velocities are eliminated from turbulence assessments, descriptions of tracer transport will be overestimated by at least one order of magnitude. Therefore, in studies of tracer transport, it is essential to implement a reliable approach to eliminate, remove, or at least reduce wave bias.
2. Previous Methods for Removing Wave Bias
Direct turbulence measurements can be overwhelmed by wave motion in coastal and ocean environments [
14,
15,
16]. Observational studies have recognized that velocity covariance produced by waves can be one order of magnitude larger even than the covariance generated by an instrument tilt [
16,
17]. Several methods have been introduced to remove wave contamination from turbulent velocity measurements. The Velocity Differencing method, introduced by Lohrmann et al. (1990), is based on the assumption that the correlation scale of wave-induced velocity is larger than that of the turbulence. Wave contamination can be reduced by contrasting measurements between two velocimeters that are separated by a distance where the turbulent fluctuations are uncorrelated [
17]. This differencing method was extended to ADCPs and named the Variance Fit method [
13].
The Variance Fit method [
13,
14] assumes that the wave-induced velocities along ADCP beams are in phase and that velocities at two different vertical positions are scaled by a constant. An adaptive filtering method was introduced by Shaw and Trowbridge (2001) [
15] assuming the wave-induced fluctuations are 100% coherent in space. Rosman et al. (2008) [
18] applied the adaptive filtering method to ADCP measurements. Vertical Adaptive Filtering (VAF) and Horizontal Adaptive Filtering (HAF) methods relax the assumptions of the Variance Fit method [
18]. These adaptive filtering methods assume that the velocities at a position are a linear function of the velocities at another position rather than a constant [
18]. Both of these methods reduce wave bias to an acceptable level in relatively “mild” wave climates [
16] by differencing velocities measured by two sensors. Gerbi et al. (2008) [
19] proposed an alternative approach showing that the cospectra of the Reynolds stress (
, where
and
are fluctuating parts of horizontal and vertical velocity, respectively) are approximately constant at low frequencies and roll off with a −7/3 slope in the inertial subrange [
16]. This method was later extended to ADCP observations by Kirincich et al. (2010) [
16]. Scannell et al. (2017) [
20] introduced a method to remove the wave bias in the Turbulent Kinetic Energy Dissipation Rate (
), which is estimated by a modified structure function. From ADCP data at three depths, they demonstrated that the modified structure function is effective in removing wave bias, compared to the standard structure function [
10]. However, this method is limited to the estimation of a structure function.
Free fall profilers recording at high frequencies (>100 Hz) have been developed to observe turbulence. However, data collection is labor-intensive and limits observational periods (Williams and Simpson, 2004). While ADCPs were not ideal to measure turbulence in coastal environments because of their coarse sampling frequency, they have been used widely to derive Reynolds stresses
and
[
12,
13]. The variance method for extracting Reynolds stresses from ADCP observations has been applied by different researchers [
13,
16,
18]. In the absence of instrument misalignment and waves, the Reynolds stresses can be computed from the difference of beam velocity variance along opposing beams [
12,
21]:
where
is the demeaned along-beam velocity of 4 beams which are positive toward the transducer, and
is the angle formed by the beam and the vertical. By comparing with results from Acoustic Doppler Velocimeters (ADVs), the variance method was validated in Souza and Howarth (2005) [
22] and Nidzieko et al. (2006) [
23]. However, the variance method failed in the presence of surface waves, because their orbital velocities are orders of magnitude larger than turbulent velocities and bias the estimates [
16].
In the presence of surface waves, the velocity components can be decomposed as:
where an overbar denotes a temporal mean value, and tilde and prime are orbital velocities and turbulent fluctuations, respectively. Substituting Equation (3) into Equation (2) yields
with the corresponding expression for Equation (1), where
and
are instrument tilts, which are commonly referred to as pitch and roll, respectively. The derivation of wave-induced bias is illustrated in detail by Rosman et al. (2008) [
18] and Trowbridge (1998) [
17]. On the right-hand side of Equation (4), the first term is the unbiased Reynolds stress [
18], which is the quantity of interest. The second term
is the error due to wave stresses. The third term
includes errors of the interaction between waves and the instrument misalignment. The fourth term, the turbulence bias
, is insignificant if the sensor misalignment is small [
17]. For tilts <3°, the proposed
is less than 50% of the true Reynolds stress in the absence of waves [
18]. The wave-induced errors,
and
, are one order of magnitude larger than the Reynolds stresses even if the tilt is small.
can be removed by rotating the principal axis where waves propagate [
17]. To reduce the error to 10% of the Reynolds stress, one must be able to establish the principal axis, which is not feasible [
17] in an open coastal area. Therefore, it is essential to remove wave contamination from the beam velocities before applying the variance method.
The bias produced by surface waves can be reduced to an acceptable level by differencing velocities measured by two sensors [
17]. In order to be effective, the two sensors must be separated by a distance shorter than the predominant wavelength and longer than the distance at which the turbulent fluctuations are correlated [
15,
17]. Hereafter, this method is referred to as the Differencing method. An extension of the Differencing method to ADCP measurements [
13] consists of vertically differencing beam velocities (
) at two locations. One of the velocities is scaled by a parameter
that accounts for wave attenuation, in accordance with linear wave theory.
where
and
denote the demeaned beam velocities, and
A and
B are two different vertical positions with
A being farther from the transducer than
B. The scaling parameter
can be chosen to minimize the difference of wave orbital velocity variance between two levels:
where wave variances
and
are computed from linear wave theory. Wave height (
, frequency (
), and wave number (
) are determined by fitting a model variance vertical profile,
, to the observations of velocity variance (Whipple et al., 2006)
where
is the vertical coordinate (zero at the water surface and positive upward), and
is the angle formed by the beam and the vertical (approximately 20°).
Assuming
is the same for opposing beams, the variance of the remainder yields:
If the distance between
A and
B is chosen to be such that the turbulent fluctuations are uncorrelated, the third terms on the right hand side of Equations (9) and (10) are zero. The application of the variance method of Equation (2) gives:
Therefore, an average value of the Reynolds stress between positions
A and
B is:
with the corresponding equation along beams 1 and 2.
Under “high wave energy”, the Differencing method in Equations (5) and (6) can fail to reduce the wave bias to an acceptable level due to the differences of amplitude and phase between two locations [
15]. To minimize the wave-induced differences in Equations (5) and (6), Shaw and Trowbridge (2001) [
15] used linear filtering techniques. Based on the Differencing method with linear filtering, Rosman et al. (2008) [
18] developed vertical and horizontal Differencing methods with Adaptive Filtering, which are henceforth referred to as VAF and HAF, respectively. Instead of using the constant parameter
, Rosman et al. (2008) [
18], and Shaw and Trowbridge (2001) [
15] described the wave velocity at
as a linear function (
) of the wave velocity at
by assuming that wave-induced velocities are spatially coherent.
where
is time,
is an integration variable, and
is a continuous function that relates
to
. The VAF and HAF method are explained in detail by Rosman et al. (2008) [
18].
The Cospectra-Fit (CF) method [
16] assumes that the momentum and heat in the bottom boundary layer of the atmosphere are transported in the upper ocean with similar turbulence scales as predicted by Kaimel et al. (1972) [
24]. Based on observations of the atmospheric boundary layer, Kaimel et al. (1972) [
24] determined that the cospectra of Reynolds stress are approximately constant at low frequencies but roll off as a
power law in the inertial subrange. According to Gerbi et al. (2008) [
19], the spectral shape of turbulence cospectral energy
can be expressed as a function of wave number
, where
and
is a turbulence length scale, as follows:
where the cospectra are denoted by an asterisk. The model turbulence cospectrum
[
16] can be described as the integral of the cospectrum (
), the covariances of two signals
and
, and a “roll off” wave number
(a measurement of the dominant length scale of turbulent fluctuations). The CF method involves fitting the model cospectrum (Equation (14)) to the observed cospectrum at frequencies below those of surface gravity waves [
16]. If the observed cospectra are integrated in the entire frequency range, the resulting covariance
is one or two orders of magnitude larger than the expected covariance, which is likely caused by a combination of instrument misalignment and waves [
19]. From ADV data obtained at 1–3 m below the sea surface, Gerbi et al. (2008) [
19] successfully estimated the unbiased Reynolds stress with the CF method.
By applying the CF method to ADCP data, unbiased Reynolds stresses were also computed by Kirincich et al. (2010) [
16]. The variance method for one-side cospectra of horizontal and vertical velocities can be expressed as
where
is the velocity spectra of
th beam velocities. Integration of Equations (15) and (16) in the entire frequency range, i.e., the covariances, yields the Reynolds stresses
and
. The wave-band cut-off frequency (
) for fitting to the below-wave band cospectra was estimated [
16] by comparing the beam velocity spectrum to the vertical velocity spectrum derived by linear wave theory. Kirincich et al. (2010) [
16] showed that the CF method minimizes wave-induced errors and yields more realistic estimates of near-bottom Reynolds stress than the VAF method. The method introduced here, the Harmonic Analysis (HA) method, relaxes the assumptions (turbulence scales < wave scales) that are used in the Differencing methods and the VAF method. The method also overcomes the assumptions of constant phase and linearity. Without considering correlation and coherence, the HA method is likely to preserve the wave-induced turbulence, which may be correlated between two locations. The HA method is tested by using a 1200 kHz RDI workhorse ADCP dataset from the northeastern Gulf of Mexico, in the Florida Big Bend region and by using a 1000 kHz RDI Sentinel V dataset from a shoal off Cape Canaveral, Florida.
3. Harmonic Analysis (HA) Method
Wave bias is only partially removed with simple filtering approaches because waves often overlap in frequency range with turbulence [
18]. The approach proposed here, the HA method, identifies wave harmonics from ADCP measurements by using Power Spectral Density (PSD) analysis and then fitting, via least squares [
25], those harmonics identified from the PSD distribution to the ADCP measurements. The HA method is illustrated with a synthetic signal (
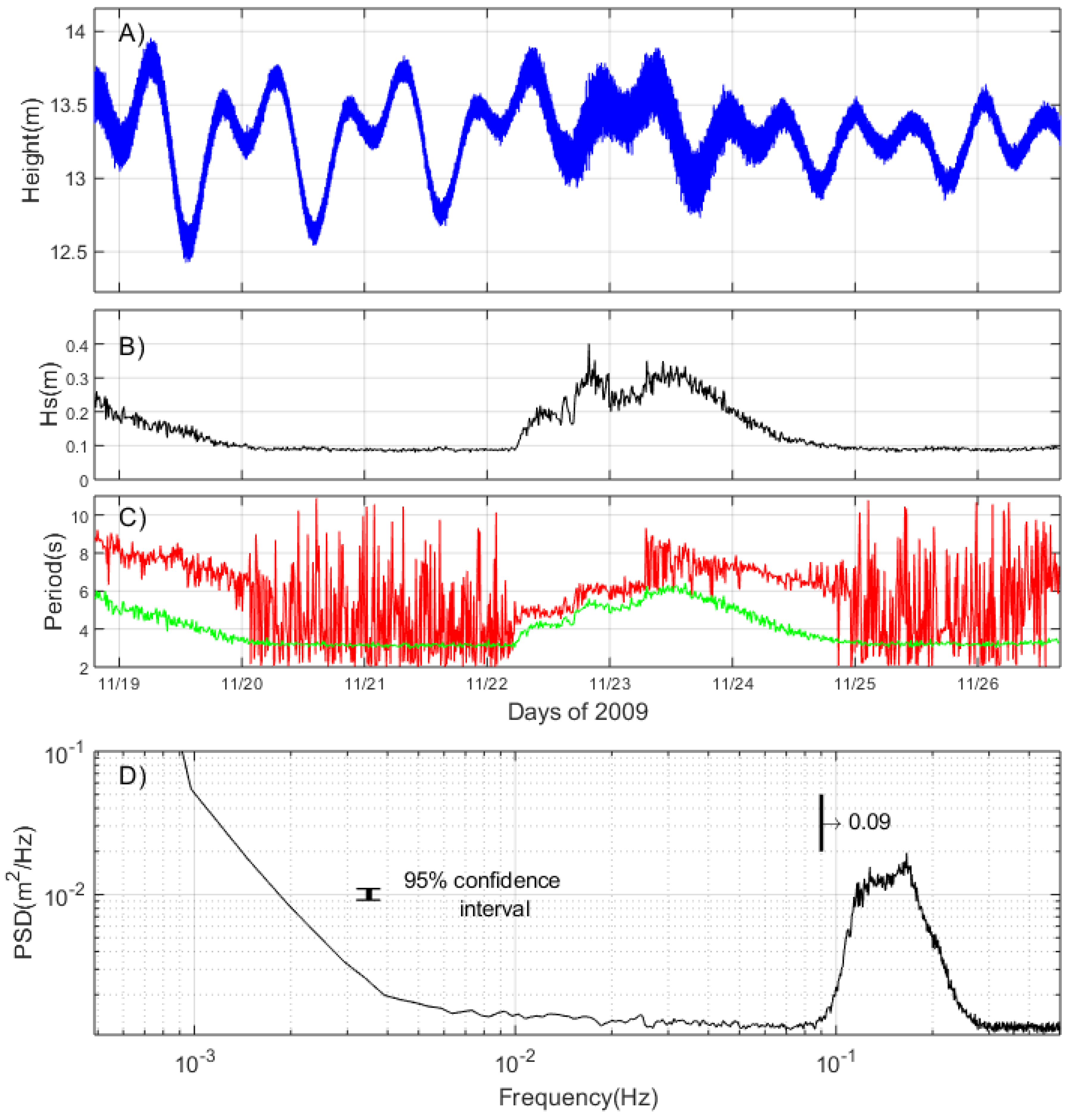
Supplementary Material, Section 2) and with an approximately 8-day time series of sea surface height (m) and its PSD (m
2/Hz) (
Figure 1A,D). Wave energy is mostly distributed at frequencies higher than 0.09 Hz (
Figure 1D). The highest significant wave height (
Figure 1B) is approximately 0.4 m with a dominant period of 6 s at 20:00, on 22 November 2009. The dominant periods of the waves vary from 2 to 10 s, and the average periods change from 3 to 6.4 s (
Figure 1C).
Frequencies associated with wave energy are identified from the PSD of the four beam velocities at the bin closest to the surface (top bin, 0.5 m thick). All wave frequencies identified from each PSD are then fitted to each of the four beam velocities for the top bin. This fit provides the amplitude and phase of the wave orbital velocities that are then reconstructed and subtracted from the beam velocities recorded by the ADCP.
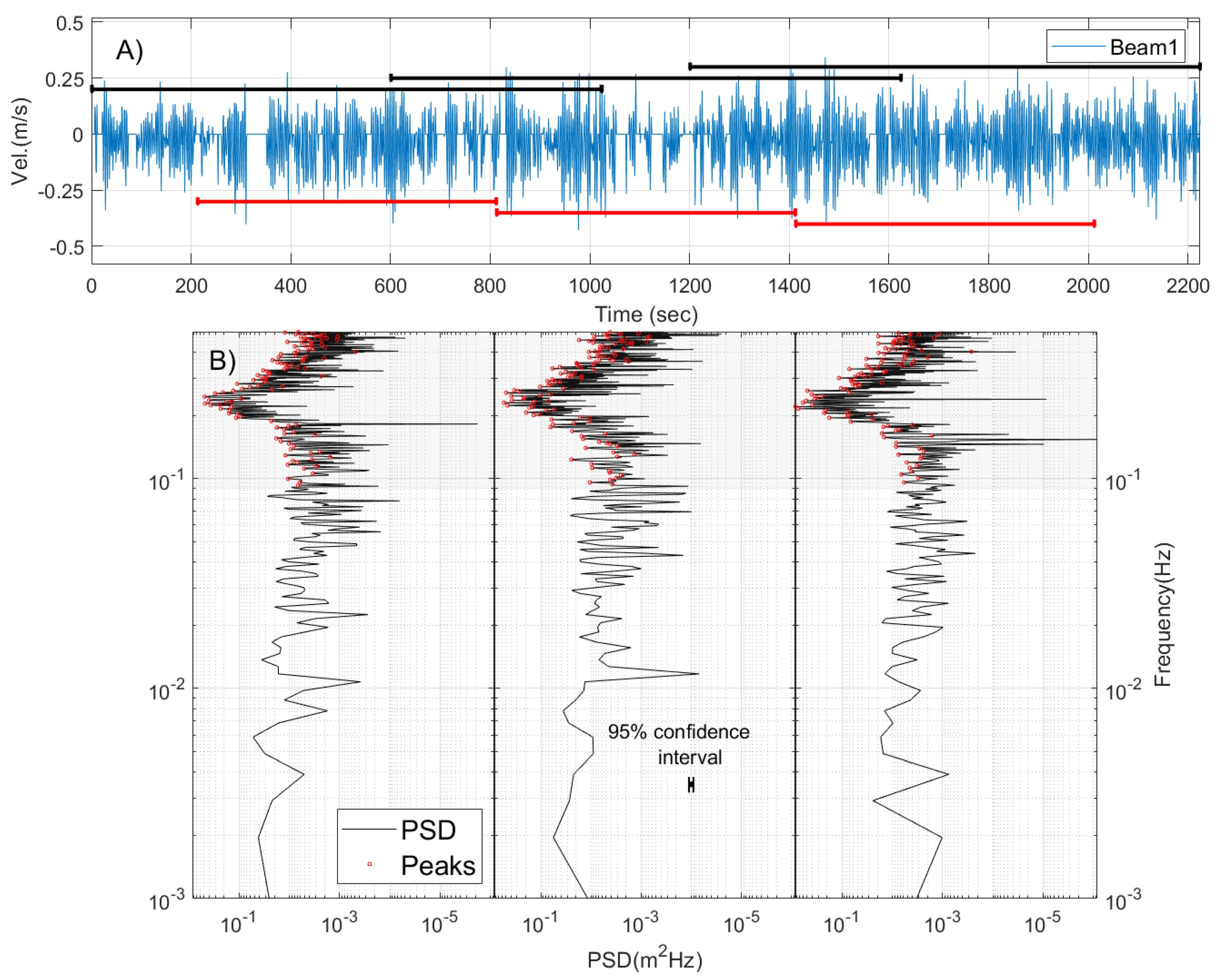
The HA method is applied to beam velocities because they resolve the rapidly changing orbital velocities better than the surface height. Details of the HA method are now illustrated with a segment (approximately 40 min) of the top-bin Beam1 velocity data (
Figure 2A). The blue line is the top-bin Beam1 velocity measured at 1 Hz and the red lines delimit 600-s ensembles used to calculate turbulence parameters. Absolute values of pitch and roll tilts remained below 3 degrees throughout the deployment.
The HA method works under the assumption that turbulence is stationary for 10 min. Although PSDs can be estimated with 10-min ensembles, the actual PSDs are calculated with ensembles of 1024 samples (approximately 17 min or 1024 s) to avoid padding with zeros. Each PSD ensemble has overlaps of 424 s with each other, extending 212 s before and after each 10-min ensemble (e.g.,
Figure 2A). The black solid lines in
Figure 2A indicate the window or ensemble size for the PSD calculation. The PSD for each black-line window of
Figure 2A appears in
Figure 2B. The shaded area in
Figure 2B (frequencies > 0.09 Hz) denotes the wave-energy frequency band, which is the portion in need of wave-bias removal.
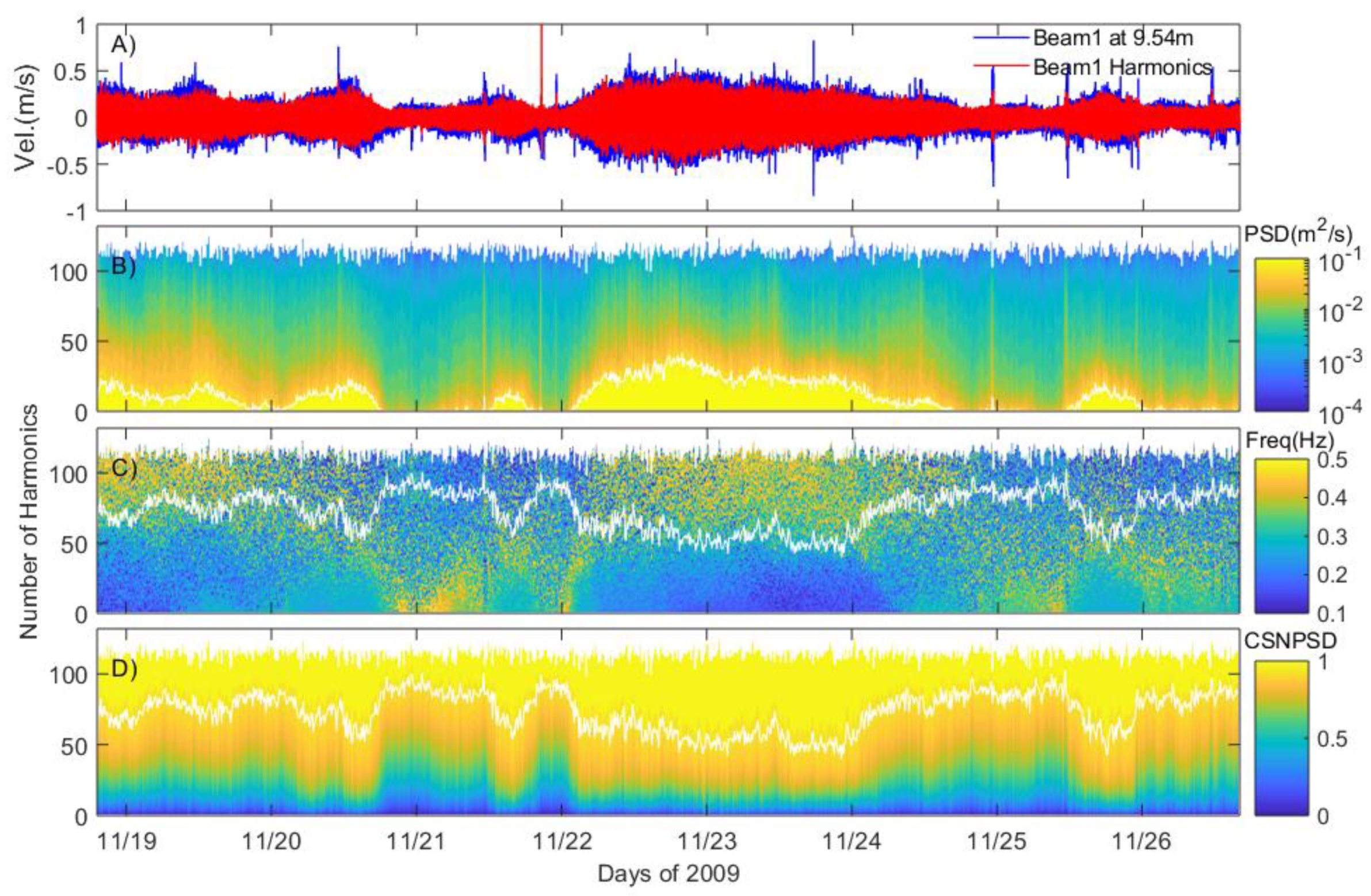
Subsequently, approximately 8 days of top-bin beam velocities (
Figure 3A for Beam1) are used to calculate PSDs for all 10-min segments, as explained in
Figure 2. The first step, after PSD calculation of each ensemble, is to find spectral peaks (red circles in
Figure 2B) in the frequency range between 0.09 and 0.5 Hz. Each peak is assumed to be related to wave orbital velocities and identified as having larger spectral density than two neighboring values (please also see the
Supplementary Material, Section 2). The next step is to sort the spectral peaks by descending order of spectral value (
Figure 3B). This is done to identify X% of the wave energy, e.g., 95%, and remove it from the beam velocity. The vertical axis in
Figure 3B–D indicates the number of peaks, or harmonics, identified in each 10-min ensemble. The shaded contour plot of sorted spectral peaks (
Figure 3B) shows increased spectral energy at times with more harmonics containing the highest PSD (yellow-shaded areas). Increased spectral energies should appear at times of largest Beam1 velocity fluctuations (e.g., between 11/22 and 11/24; between 11/19 and 11/20; in the middle of 11/20; and in the second half of 11/25). The frequency corresponding to each sorted spectral peak is presented in
Figure 3C. The largest spectral peaks between 11/22 and 11/24 correspond to frequencies between 0.1 and 0.2 Hz (blue regions in the contour plot). Similar frequency values are observed during other periods with largest variability in Beam1 velocity.
The following step is to remove X% of wave energy (e.g., 95%) from each 10-min ensemble. For this purpose, the PSDs are normalized with the sum of all spectral peaks (between 0.09 and 0.5 Hz) of that ensemble. In other words, each normalized PSD represents the ratio of each PSD value to the sum of all spectral peaks between 0.09 and 0.5 Hz. Then, normalized PSD values are integrated throughout all peaks of each 10-min ensemble to represent the Cumulative Normalized Power Spectral Density (CNPSD,
Figure 3D). Thus, a value of 1 denotes 100% of the wave energy related to each ensemble. The white contour line in
Figure 3C,D shows the number of peaks (or harmonics) representing 95% of the total wave energy from each ensemble (95% of the largest peaks in the PSDs of each ensemble). Overall, around 75 peaks represent 95% of the total energy of the peaks (
Figure 3C,D). This number of peaks changes over time according to wave conditions. Relatively fewer spectral peaks contain 95% of the wave energy when the beam velocities are relatively higher. The crux of this method is to fit all harmonic frequencies, up to the white line, to each 10-min ensemble and thus obtain the amplitude and phase of each oscillatory harmonic, the wave signal. The fitted wave signal is finally subtracted from each 10-min beam velocity ensemble. This final procedure is as follows.
The wave orbital velocity may be represented by the sum of M harmonics plus a mean (
):
where
is an approximation to the wave orbital velocity of each 10-min ensemble.
,
, and
are the amplitude, angular frequency, and phase, respectively, associated with the spectral peaks. Values of
are gleaned from the PSD peaks of the beam velocity 10-min ensemble
(
Figure 3C). Values of
u0,
, and
are obtained by fitting the harmonics
to
. For a more in-depth explanation of the least squares fit to Equation (17), see the
Supplementary Material, Section 1. The harmonic orbital velocities are reconstructed with
u0,
, and
from Equation (17) (red line in
Figure 3A). This signal is taken as the wave orbital velocities
, and then subtracted from the
, i.e.,
The remaining signal (
, or the difference between red and blue lines in
Figure 3A) is assumed to be related predominantly to turbulent fluctuations and noise.
4. Comparison between VAF and HA Method
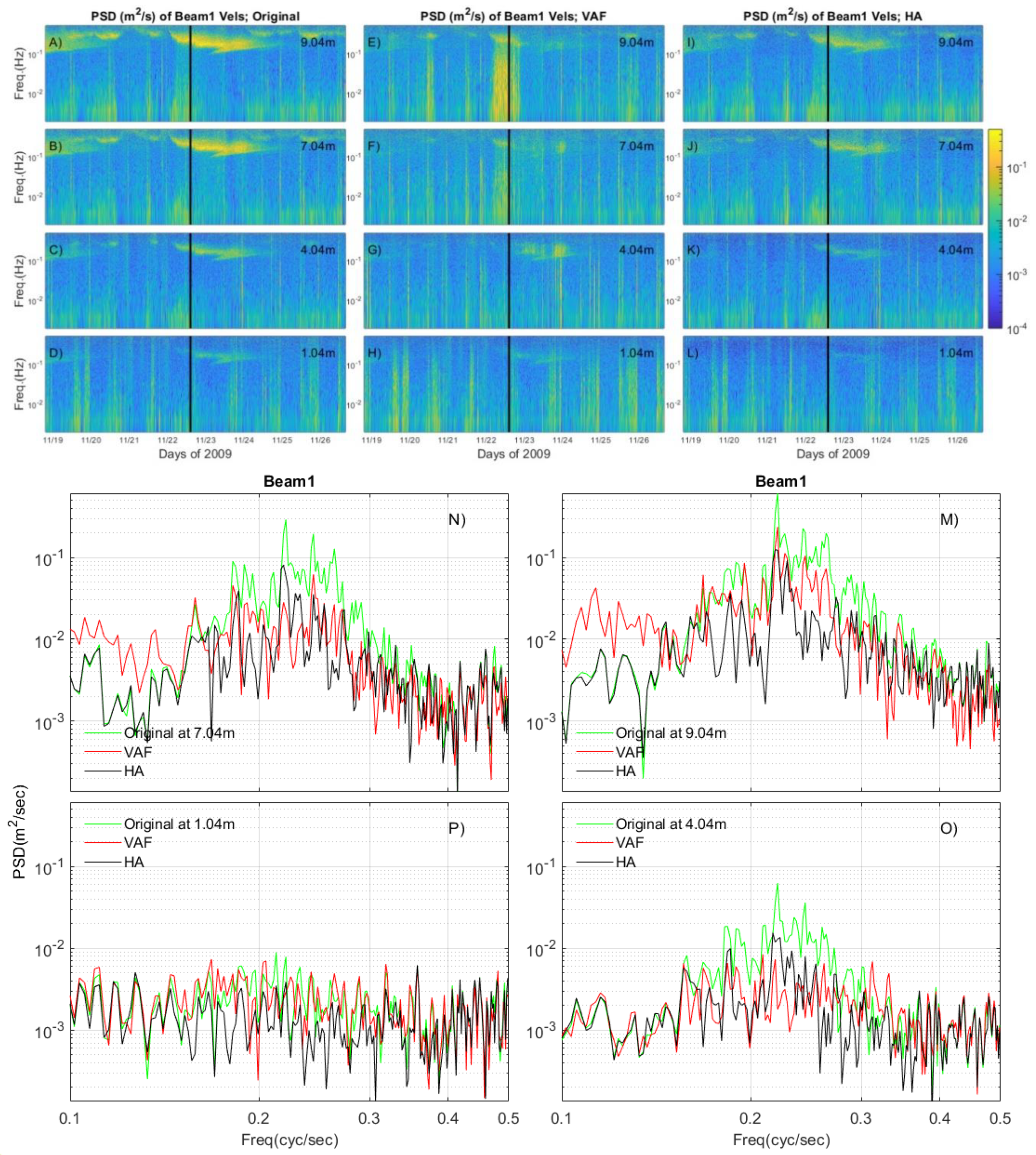
Power Spectral Densities derived from the VAF and HA methods are compared to the PSDs of original velocities over the entire water column for all 8 days of measurements (
Figure 4). To evaluate the methods, PSDs are computed for every 10-min ensemble of the Beam1 velocities. The PSDs of original Beam1 velocities are shown in
Figure 4A–D for different distances from the bottom. As shown in
Figure 1B, surface gravity wave energy is predominantly distributed between 0.09 and 0.5 Hz, and it decreases with depth (
Figure 4A–D). Surface gravity waves are evident between 11/19 and 11/21, evolving from low to high frequencies, and between 11/22 and 11/24, evolving from high to low frequencies. The shortest waves (>0.3 Hz) do not reach the bin closest to the bottom, while the longest waves (near 0.1 Hz) do reach those depths. This is expected from linear wave theory [
26].
The PSDs corrected by VAF are shown in
Figure 4E–H. A 2 m vertical separation is chosen to determine the continuous function in Equation (13), together with a 10-s window length for the weight function. Near the surface (9.04 m from the bottom, i.e., at the top bin) the VAF performs well at frequencies > 0.1 Hz. However, longer period waves are artificially amplified, especially between 11/22 and 11/23, when significant wave heights reach approximately 0.4 m (
Figure 1B). The amplification of longer period waves also occurs at a distance of 7.04 m, although it is less prominent than near the surface. This artifact is caused by the least squares fit of the VAF method. Least squares Adaptive Filters amplify or generate signals, especially in longer period waves, to minimize the sum of squared residuals between two locations. Rosman et al. (2008) [
18] explained that the linear transform does not sufficiently resolve the abrupt change of wave directions and phase difference between two locations during a 10-min averaging period. As a result, the VAF method does not perform well near the surface.
While the VAF method performs unreliably near the surface, the HA method removes most of the wave bias in the beam velocities (
Figure 4I). The wave energy is drastically reduced between 0.09 and 0.5 Hz. Moreover, the VAF method loses vertical resolution at the surface because of its requirement to relate beam velocities at two locations. In this case, 2 m is used as the vertical separation to compute the linear function. Therefore, unbiased beam velocities are unattainable at 2 m below the surface. The wave energy is successfully removed at 1.04 m above the bottom (
Figure 4L), but the VAF method generates pseudo-longer period waves in
Figure 4H because VAF depends on the quality of the linear function [
18] in Equation (13).
The wave signal removal by VAF and HA methods is illustrated on specific PSD plots (
Figure 4M–P) corresponding to the black vertical lines of
Figure 4A through L. Wave biases do not seem to be removed entirely between 11/22 and 11/24. However, the HA method reduces wave energies in the dominant peaks by approximately one order of magnitude relative to the original data. In addition, the wave energy resulting from the HA method is not amplified at low frequencies (<0.15 Hz), in contrast to the VAF method. This is particularly conspicuous in the signals at 7.04 m (
Figure 4N) and 9.04 m (
Figure 4M).
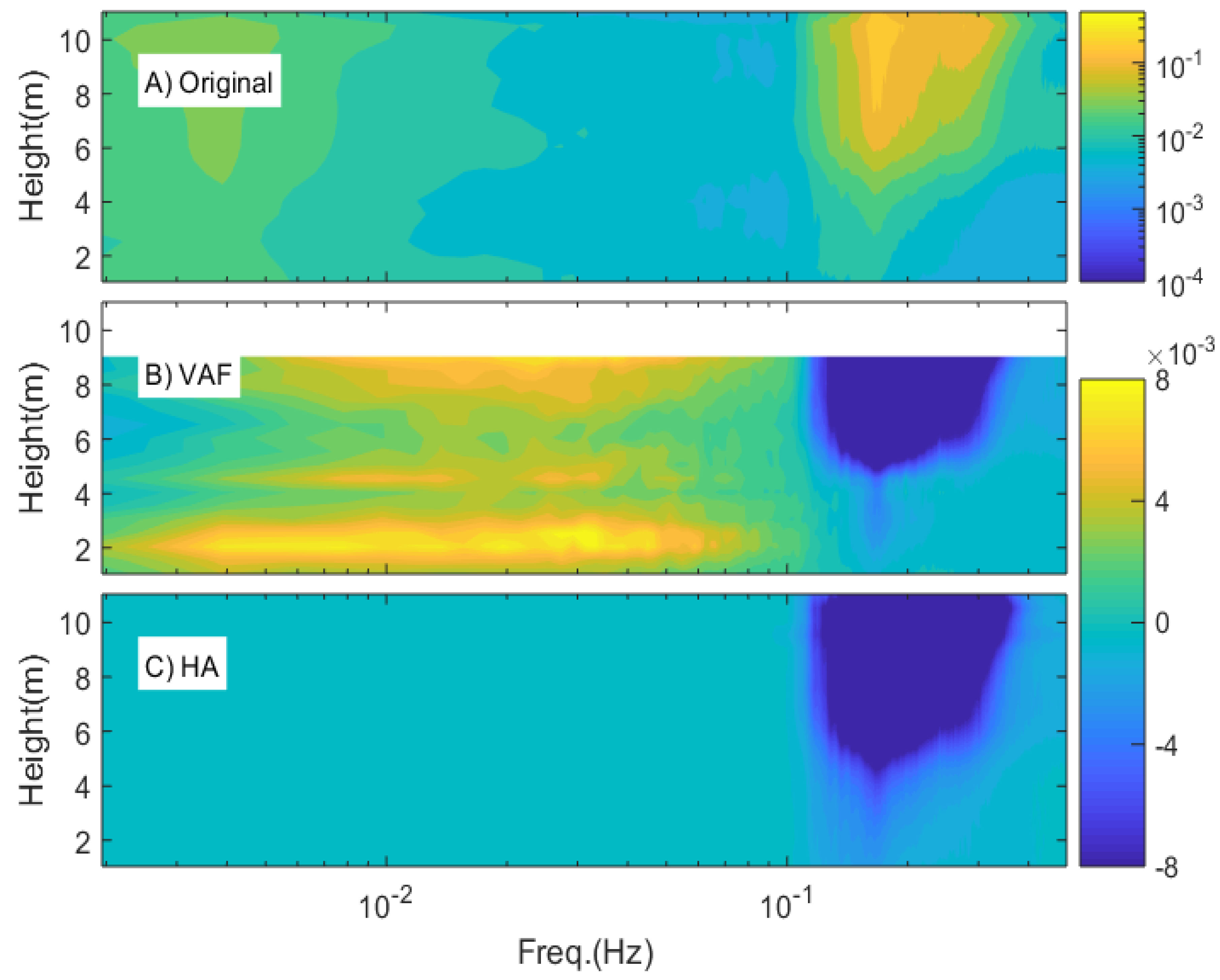
One way to evaluate the performance of the methods is to generate average PSD contours (
Figure 5A) of all 10-min ensembles at each depth (
Figure 4). The original average PSDs show wave energy predominantly at 0.17 Hz and at heights from the bottom above 5 m (
Figure 5A). Deviations of the VAF and HA method from original ensemble-averaged PSDs are shown in
Figure 5B,C, respectively. The deviations show that both VAF and HA methods remove the predominant wave energy at frequencies > 0.1 Hz. However, low-frequency wave energy is amplified with the VAF approach, especially at the surface and the bottom (
Figure 5B). This is caused by the assumption that the wave velocity at A is a linear function of the wave velocity at B (Equation (13)). Wave velocities are unlikely to decay linearly with depth. The wave bias at frequencies > 0.1 Hz is approximately 10% less marked with the HA method than with the VAF. Moreover, spurious low frequency waves are not present in results obtained with the HA method (
Figure 5C).
Another indicator of wave-bias removal is the cospectra of the beam velocities. Rosman et al. (2008) [
18] indicated that the cospectra of
and
can be computed as
where
and
are the Power Spectral Densities of Beam1 and Beam2, respectively. The cospectra of original beam velocities have increased energy at the surface and in the middle of the water column at frequencies > 0.1 Hz (
Figure 6A). As expected, the wave energy is highest at the surface and decreases with depth. In addition, increased wave energy appears at an approximately 5 m height. The VAF method performs well at frequencies > 0.1 Hz (
Figure 6B) but loses vertical resolution as it relates velocities between two vertical positions to obtain the linear function described in
Section 3. The cospectra computed by the HA method provides reasonable estimates at the surface (
Figure 6C). Decreased cospectra indicated that the peaks where
and
have the same frequencies are largely removed. The magnitude of the HA method cospectra is approximately 64% and 36% smaller than the original cospectra at the surface and bottom, respectively.
5. Discussion
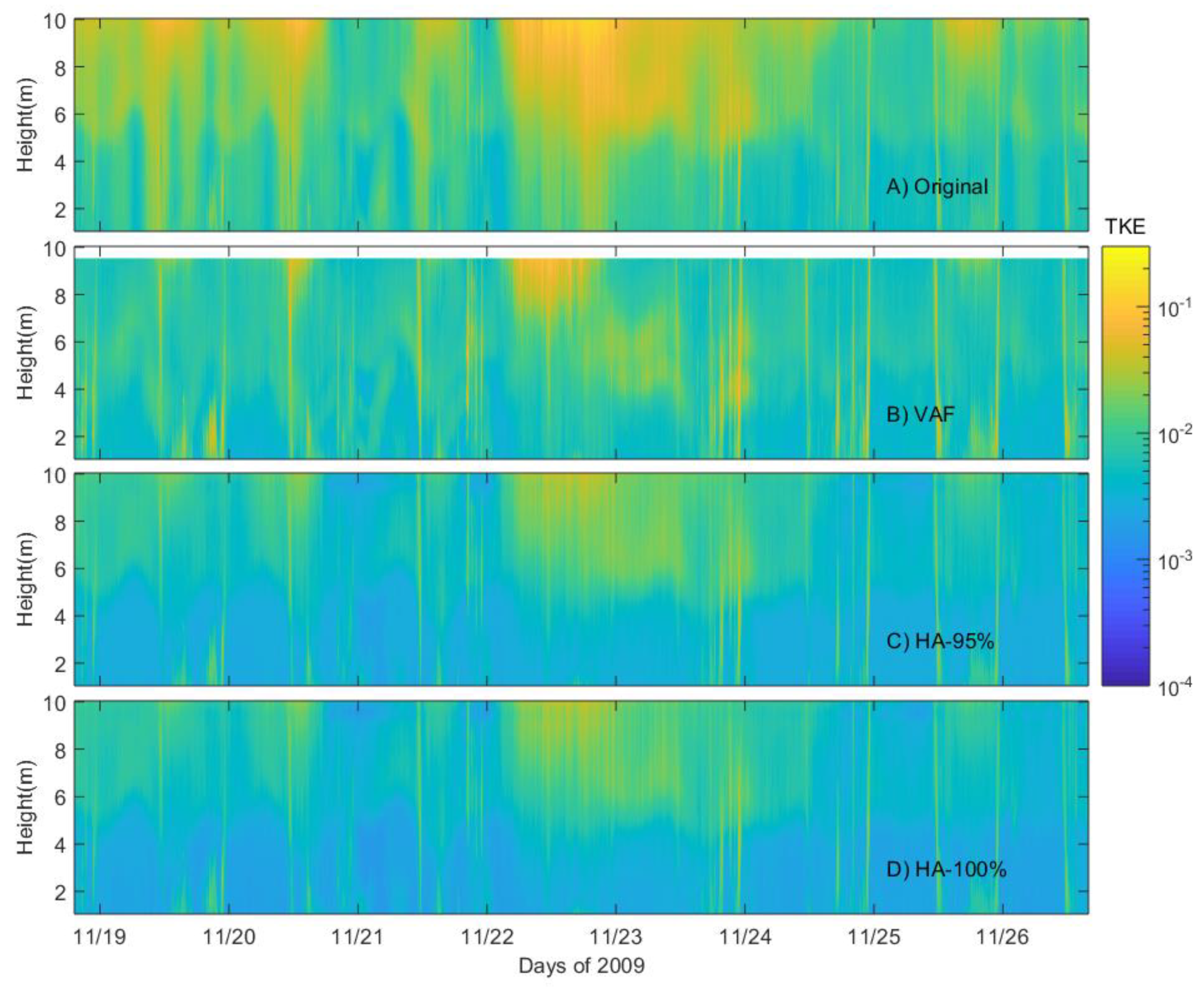
Turbulent Kinetic Energy was calculated with the original data and with the VAF and HA methods (
Figure 7). The HA method was now applied by removing 95% and also 100% of the wave harmonics obtained from the PSD. The labels “HA-95%” and “HA-100%” in
Figure 7C,D denote the Harmonic Analysis method that removes 95% and 100% of the wave energy. The sum of Turbulent Kinetic Energy (TKE) at 9.04 m was approximately 60% lower with the VAF method (
Figure 7B) and approximately 67% lower with HA-95% (
Figure 7C) relative to the original data. At 1.04 m, the TKE sum was approximately 24% less with the VAF method and approximately 55% less with the HA-95% method than with the original data. At 5.04 m, the TKE sum was approximately 34% less with the VAF method and approximately 63% less with the HA-95% method than that calculated with the original data (see also
Table 1). The result of the TKE sum indicated that the HA method reduced more wave energy throughout the water column than the VAF method. Looking at the HA-100% approach, the TKE sum with HA-95% was approximately 15% more than the TKE sum with HA-100%. This shows a small change in the TKE budgets.
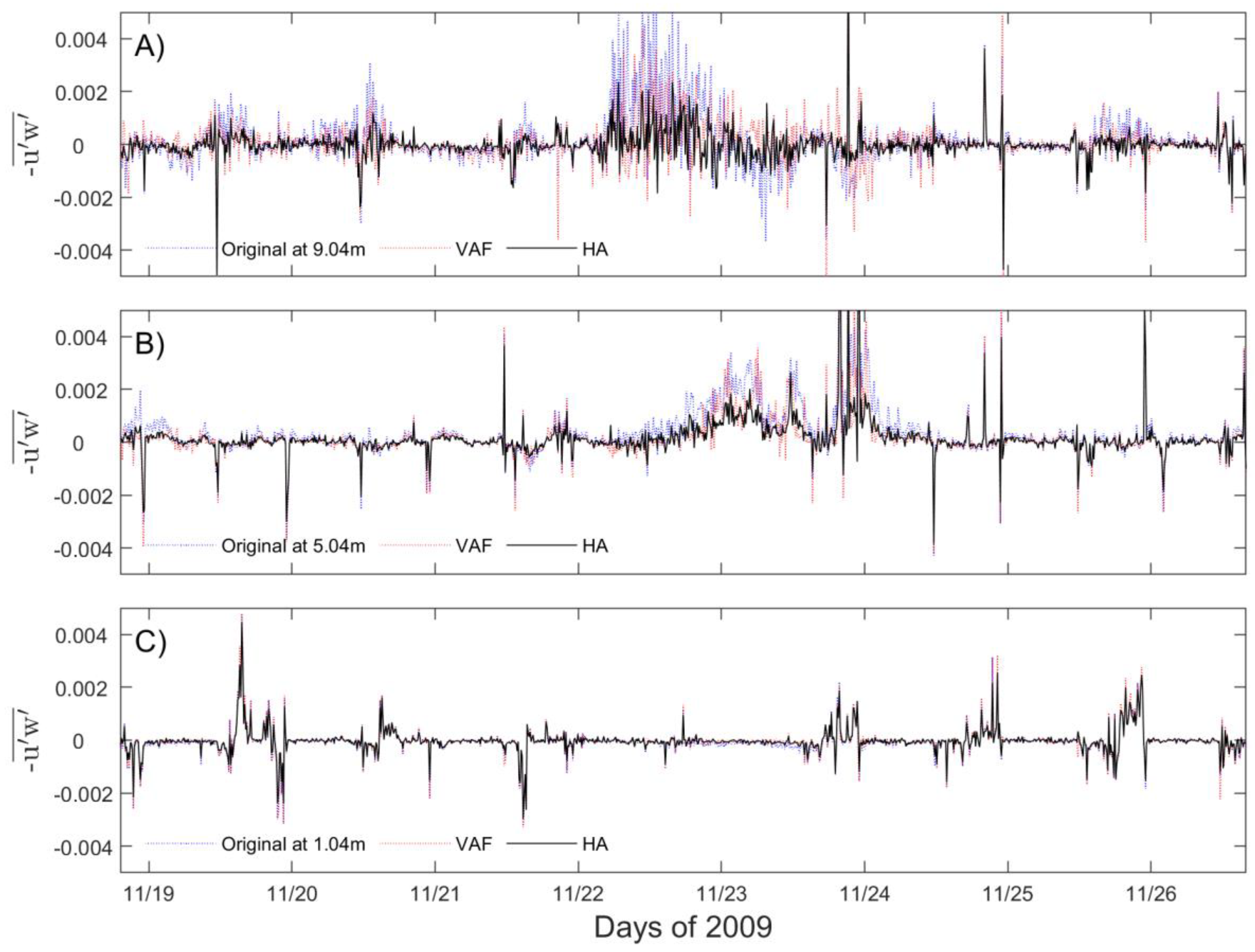
In addition, Reynolds stresses (
) were calculated with original velocities, with the VAF method and with the HA method at 3 different heights above the bottom (
Figure 8). Compared to the original estimates and the VAF methods, the HA method gives the smallest standard deviation of Reynolds stresses at all depths. The standard deviation of Reynolds stresses for the HA method is approximately
at 9.04 m (close to the surface) and
at 1.04 m (closest to the bottom). Comparatively, the standard deviation of Reynolds stresses for the VAF method is approximately
and
at the same depths (
Table 1). In other words, the Reynolds stresses standard deviation of the VAF method tends to be 50% greater than that of the HA method near the surface.
Furthermore, an estimate of the variance of Reynolds stresses (
) with the VAF method [
18] is given by:
where
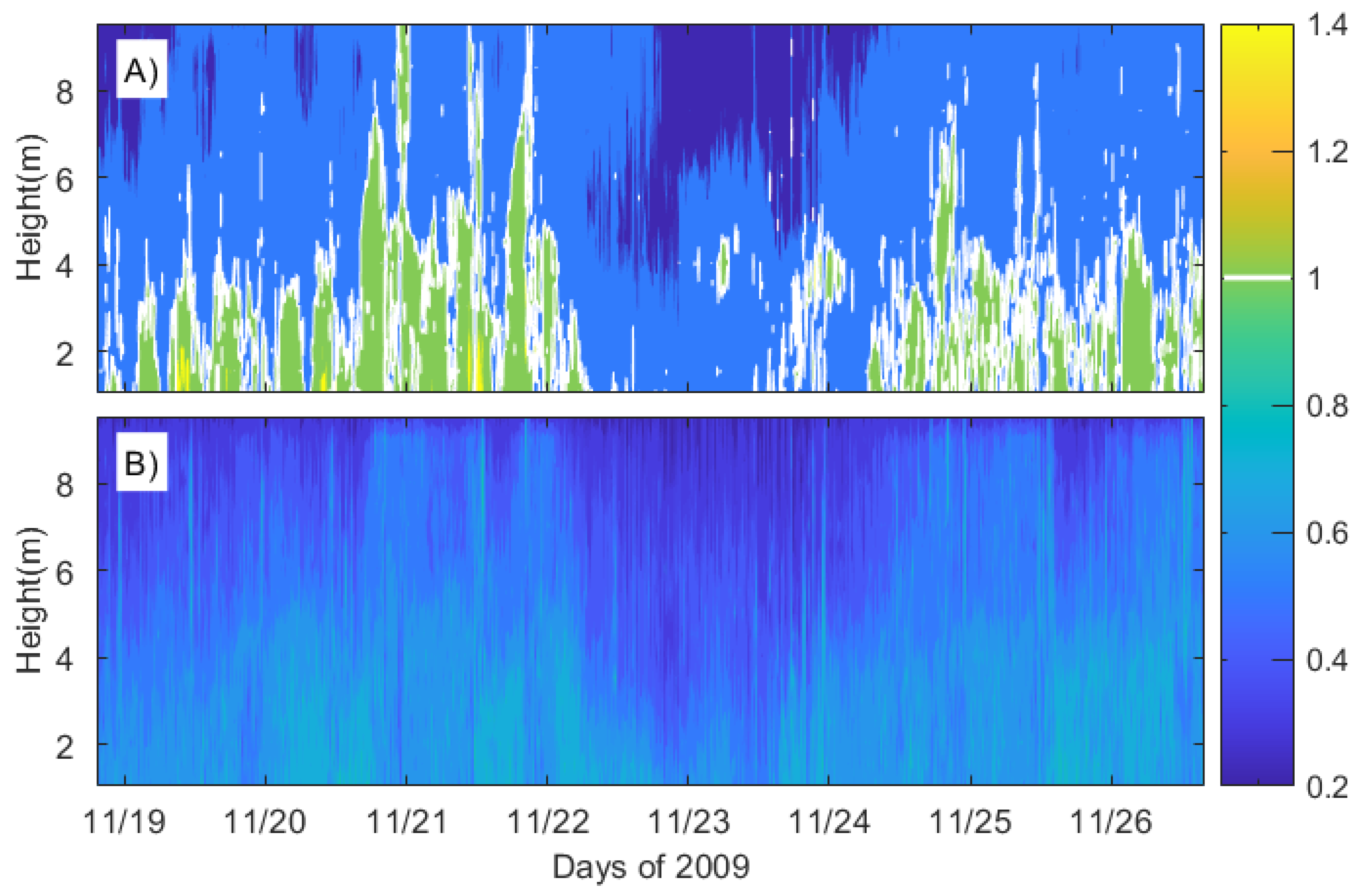
denotes the estimator of the Reynolds stress. For comparison, the variance of Reynolds stresses can be estimated for the original velocity perturbations, for the VAF method, and for the HA method following Equation (20). In particular, standard deviations of Reynolds stresses derived from the VAF and HA methods are normalized with those obtained from the original velocities to compare the reliability of the VAF method with that of the HA method (
Figure 9). Contour values >1 indicate that the estimator (
) of the VAF method is more broadly distributed than that of the original data (
Figure 9A). Values > 1 from the VAF method are mostly found in the lower water column. This trend is caused by the difference between the velocity variance of the original beam velocities and the VAF method. As shown in
Figure 4D,H, the Power Spectral Density for the original beam velocities is smaller than the Power Spectral Density for the VAF estimates. Based on the normalized standard deviation, the reliability in Reynolds stress estimates for the VAF method decreases toward the bottom of the water column. In contrast, contours of normalized standard deviations for the HA method are <1 everywhere (
Figure 9B). This indicates that the reliability of the HA method increases in the entire water column, relative to the original estimates. The normalized standard deviations of the HA method are smallest at the top of the water column because the wave energy decreases with depth. Thus, the reliability of the Reynolds stresses is greater under relatively strong wave conditions (between 11/22 and 11/24) than under relatively weak wave conditions, as also noted in
Figure 3A.
Rosman et al. (2008) [
18] and Kirincich et al. (2010) [
16] indicated that the VAF method is limited to mild wave climates, which would explain the difference with the HA method. To further evaluate the HA method in relatively more energetic wave conditions, the HA method is tested with a 4+ days, 2 Hz frequency dataset (
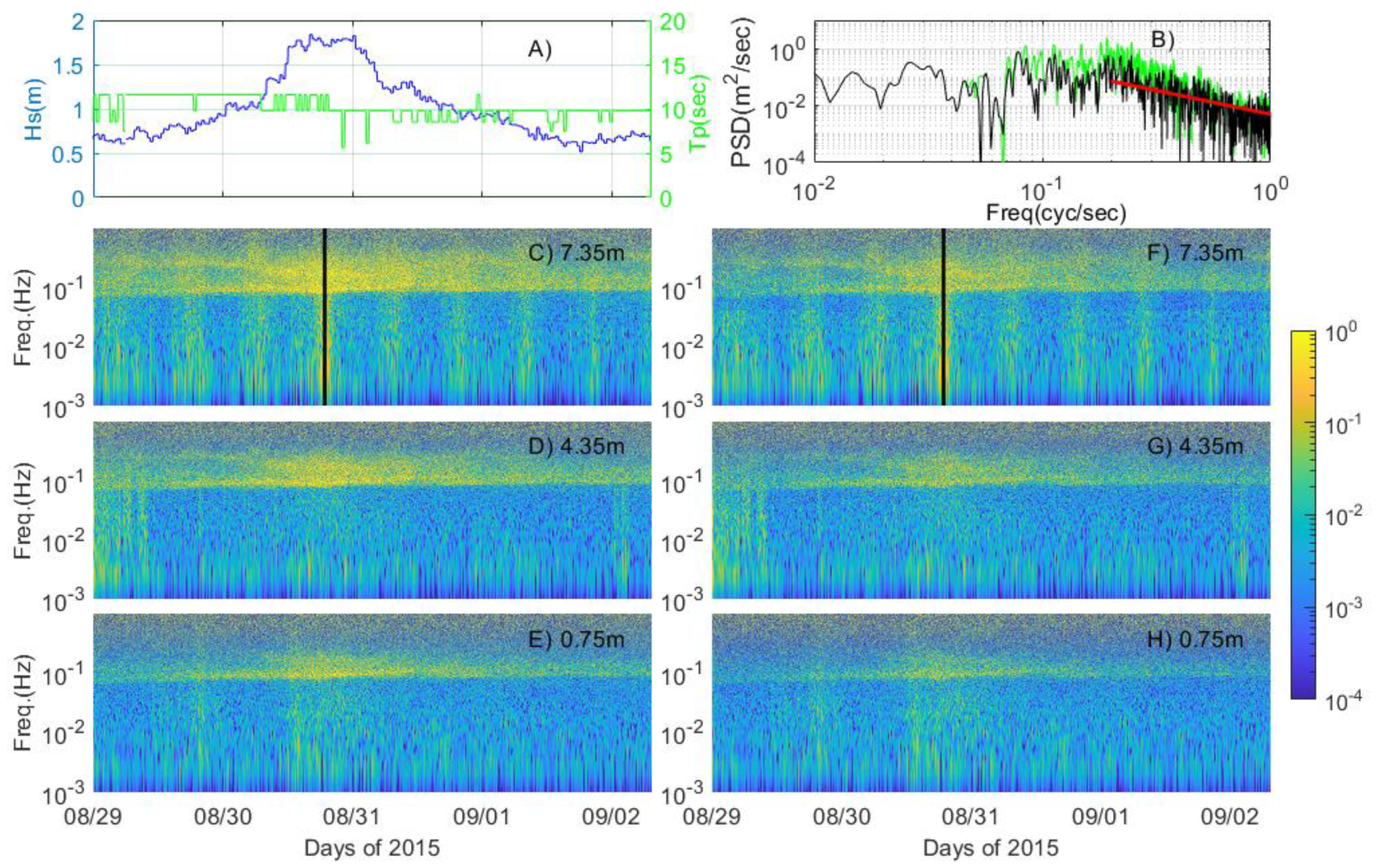
Figure 10) over an approximately 8.5 m-depth water column near Cape Canaveral, Florida. The mean significant wave height (
Hs) was approximately 1.0 m with a 10.2 s period. The highest significant wave height was 1.84 m with an approximately 12 s period at 16:05, August 30, 2015 (
Figure 10A). The highest waves
Hs > 1.5 m were steadily recorded from 11:30 on August 30 to 4:00 on August 31. The PSD of Beam1 velocity was estimated with a 10-min ensemble during the highest
Hs (
Figure 10B). The PSD of 95% wave-removed data (black line) decreases by approximately one order of magnitude at each peak identified, compared to the PSD of original data (green line). Moreover, the energy spectrum of the 95% wave-removed data cascades down with Kolmogorov’s −5/3 slope (red line, consistent with turbulence dissipation). Contours of PSD with 95% of waves removed show energy reduction at all depths (
Figure 10F–H).
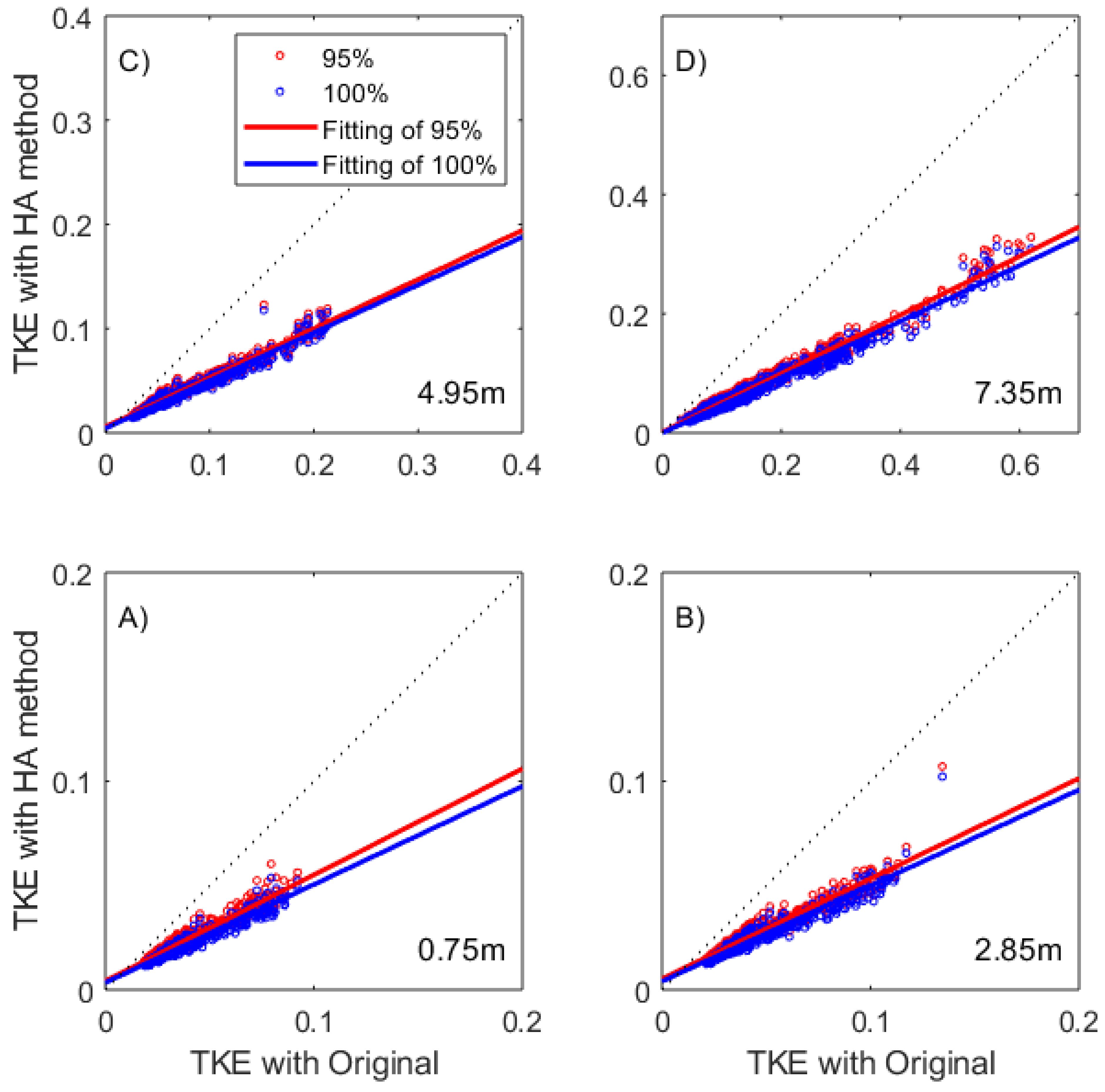
Turbulent Kinetic Energy estimated with 95% and 100% wave removal (for all depths) indicates the sensitivity of the method to the percentage of wave removal. This is assessed through a rough TKE budget (
Figure 11). The black dotted line has a slope of 1. Data falling on that line would indicate no wave elimination from the total TKE budget. The red and blue circles denote that the HA method reduces wave energy from the total TKE because they fall below the straight line. Turbulent Kinetic Energy with corrected data is reduced by approximately 50% for every 10-min ensemble, compared with original data (
Figure 11). The difference between a 95% and a 100% wave removal is determined by the linear fit lines (red and blue). The mean slope is approximately 0.02 larger for the 95% removal (red line) than the 100% removal (blue line). This indicates that the HA method of 100% wave removal reduces 2% more wave energy than the 95% wave removal. However, the time to reconstruct harmonics with HA-100% was 10.5 times longer than the time taken by HA-95%. In this study, the difference between HA-95% and 100% was barely noticeable. The user of the HA approach may determine the most convenient implementation of wave percentage to remove. From these results, the HA method performs well under energetic wave conditions and in the surface boundary layer, where the VAF method would be inadequate.