Clustering Groundwater Level Time Series of the Exploited Almonte-Marismas Aquifer in Southwest Spain
Abstract
:1. Introduction
2. Materials and Methods
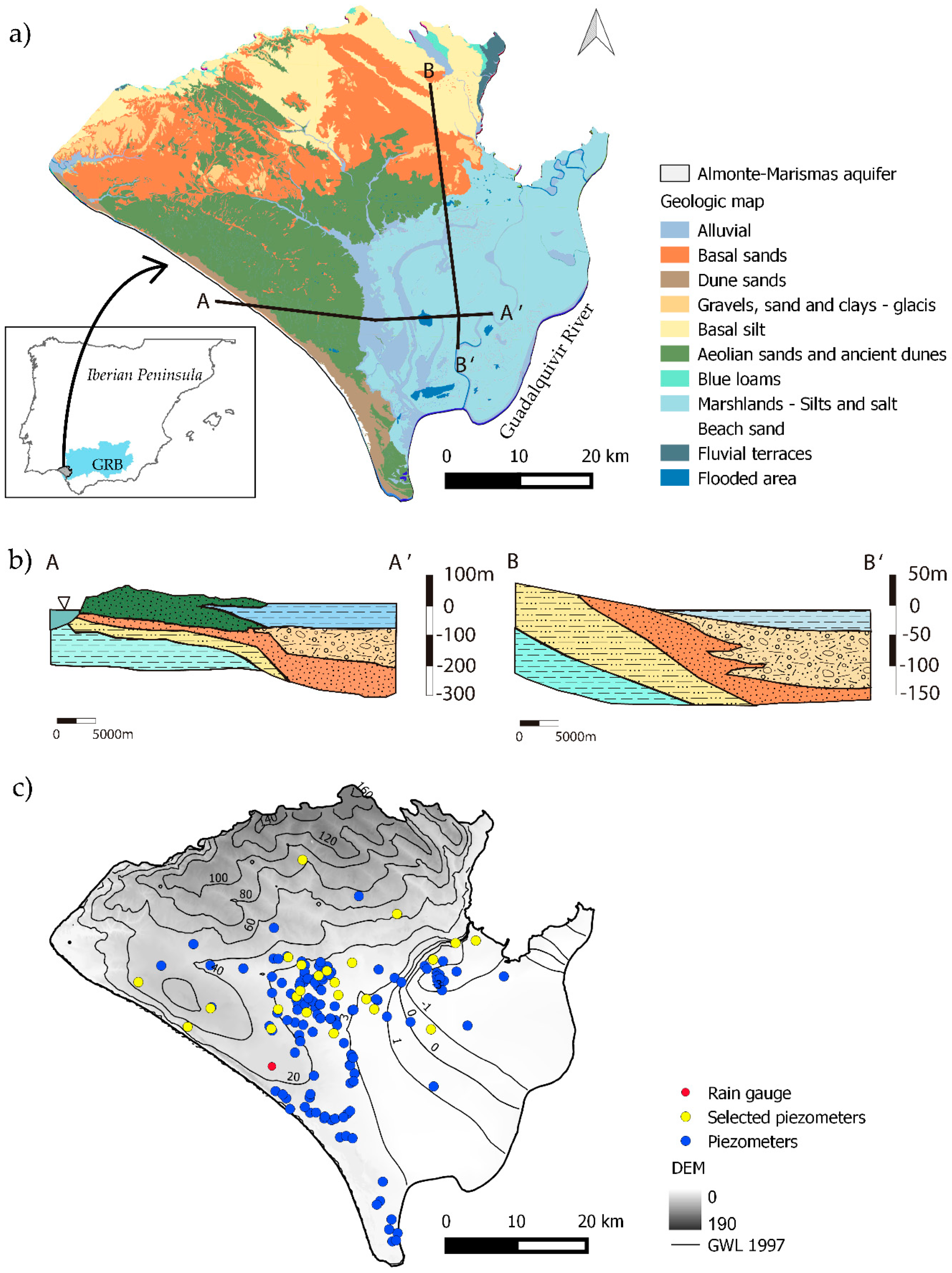
2.1. Study Site
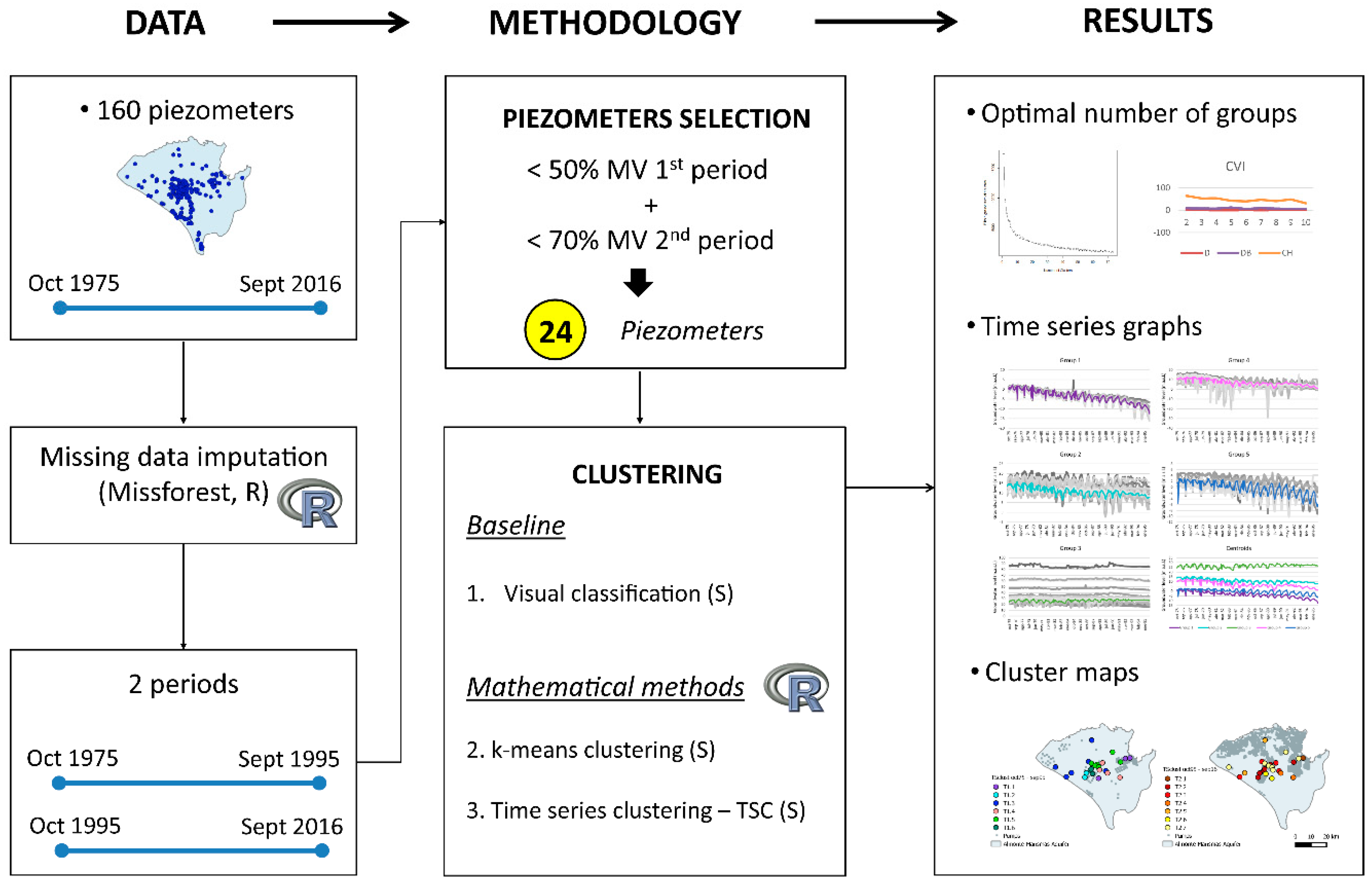
2.2. Data Collection and Pre-Treatment
2.3. K-Means Clustering
2.4. Time Series Clustering (TSC)
3. Results and Discussion
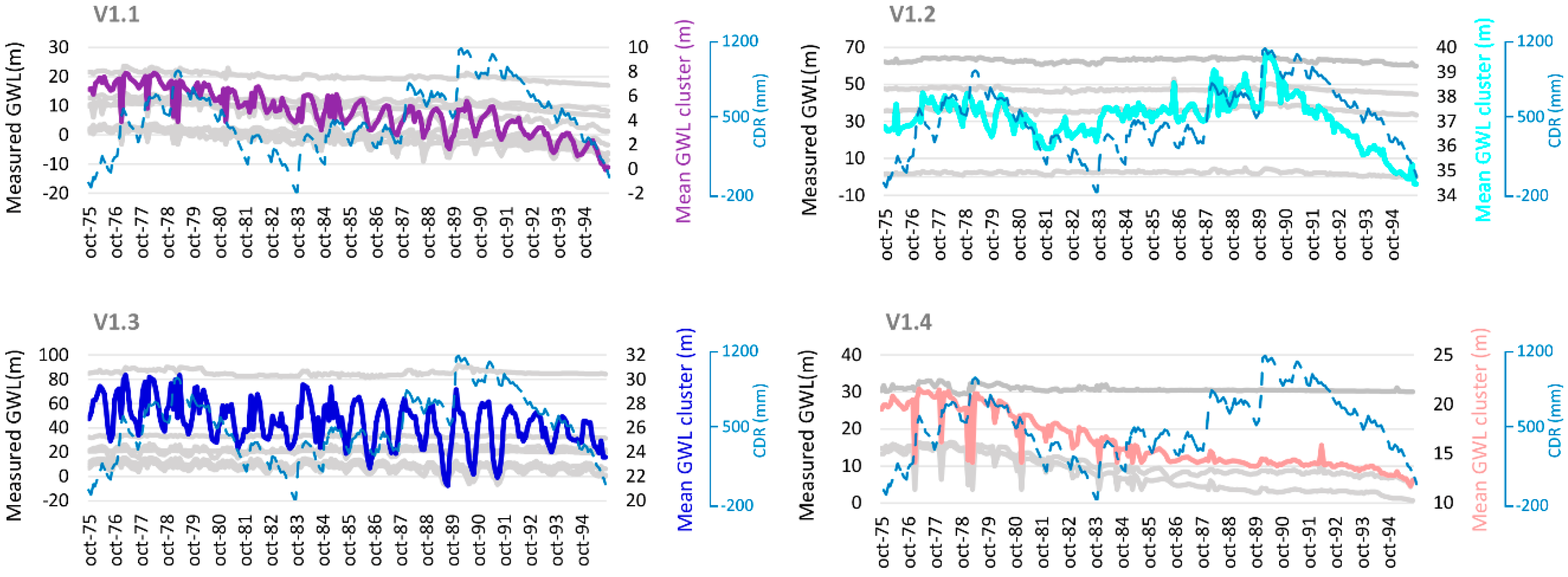
3.1. Imputation Piezometry and Visual Classification
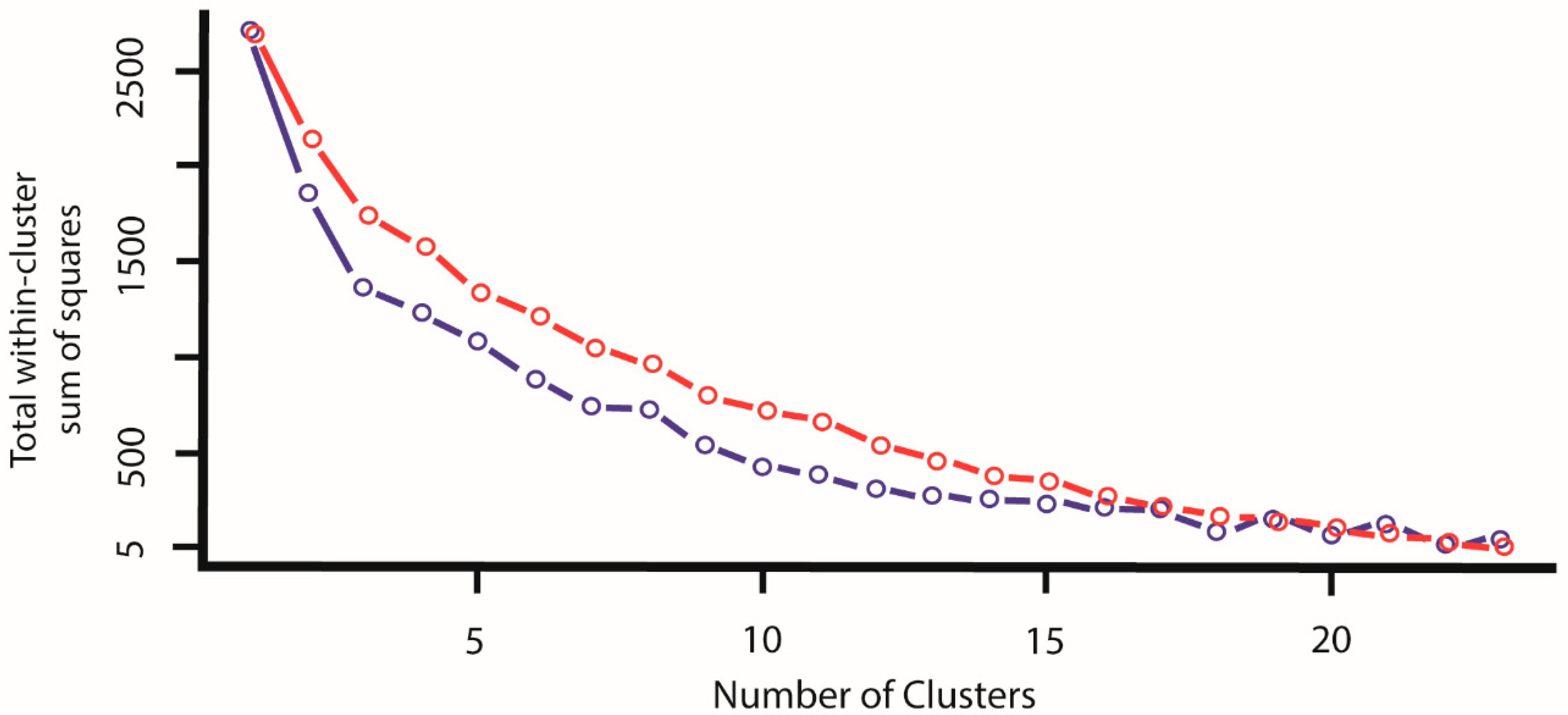
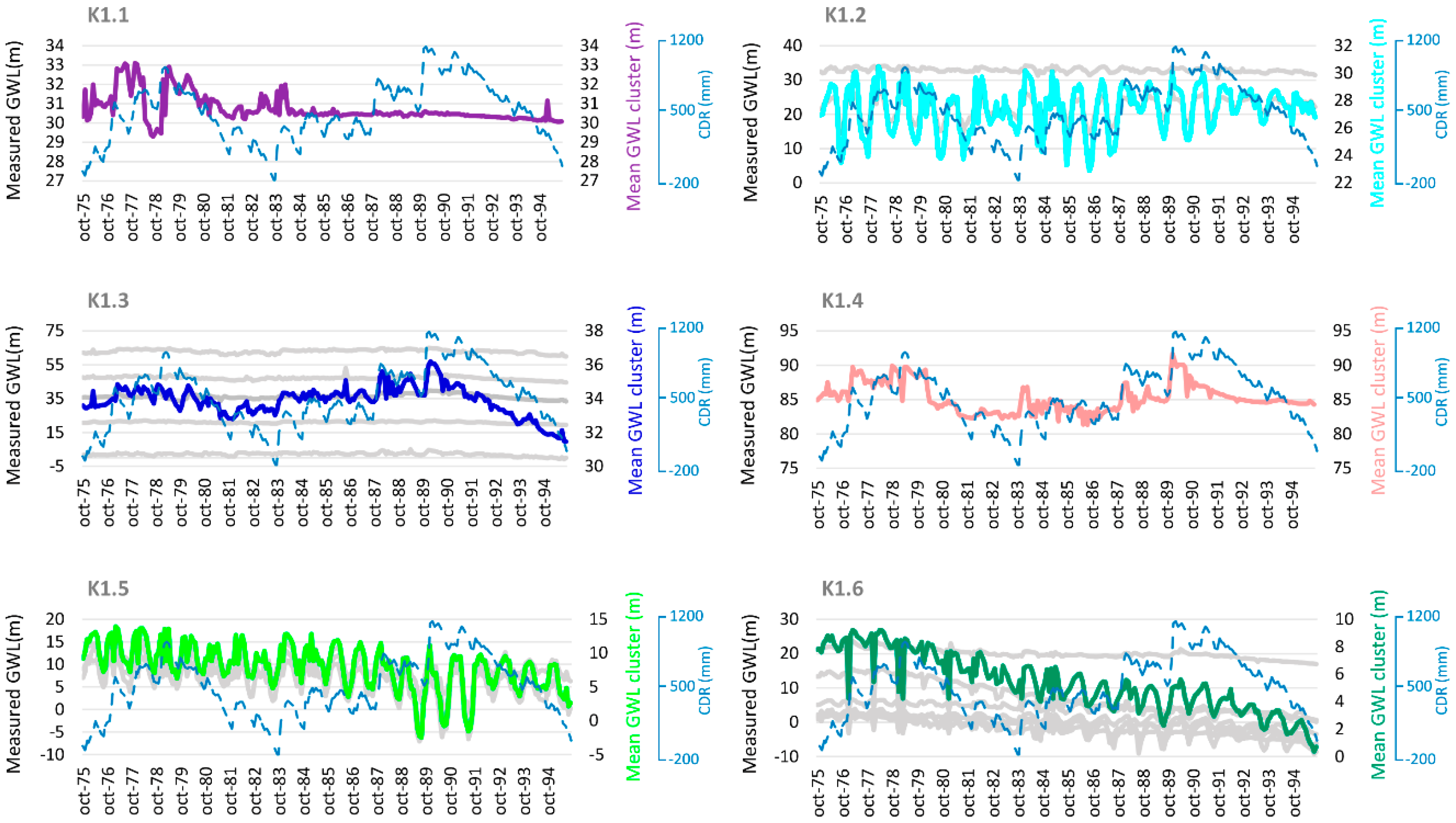
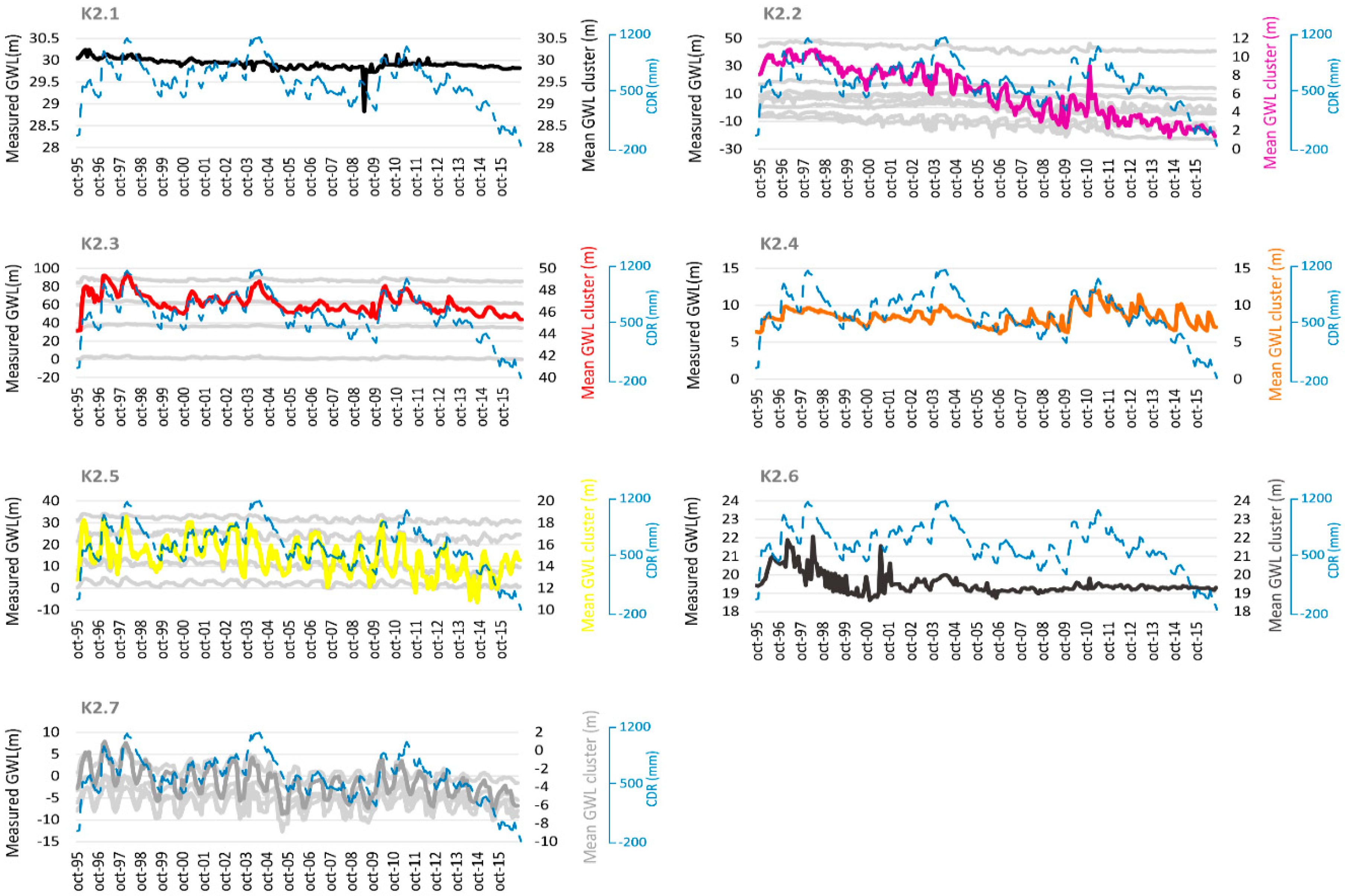
3.2. K-Means Clustering
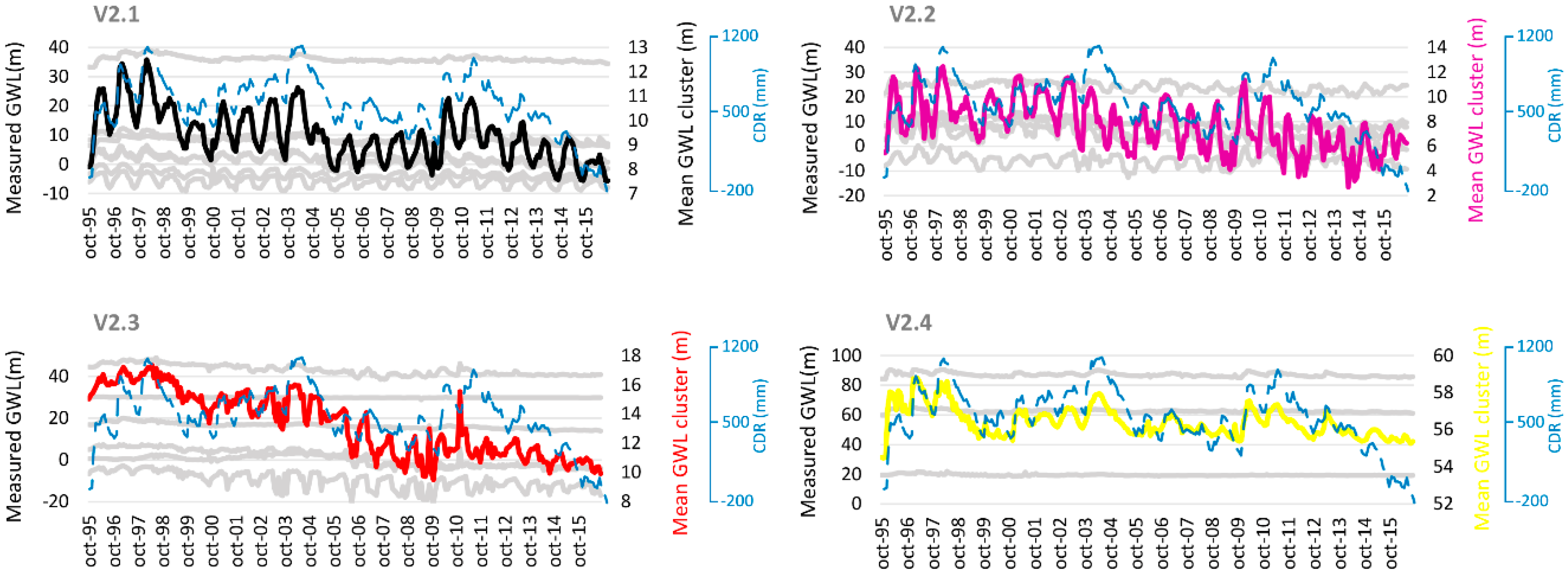
3.3. Time Series Clustering
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Code | N | Mean | Med. | Max. | Min. | St. Dev | % MV |
|---|---|---|---|---|---|---|---|
| 104140047 | 377 | 86.34 | 86.27 | 91.64 | 81.33 | 2.02 | 23.37 |
| 104180012 | 234 | 20.57 | 20.81 | 22.11 | 18.62 | 0.90 | 52.44 |
| 104180021 | 422 | 18.07 | 17.88 | 23.63 | 13.88 | 2.36 | 14.23 |
| 104210004 | 252 | 46.41 | 46.78 | 53.04 | 38.56 | 2.08 | 48.78 |
| 104220006 | 253 | 36.30 | 36.13 | 39.74 | 33.19 | 1.42 | 48.58 |
| 104230003 | 261 | 62.94 | 62.97 | 65.05 | 59.80 | 1.09 | 46.95 |
| 104240033 | 321 | 10.28 | 10.39 | 15.47 | 0.39 | 2.64 | 34.76 |
| 104240058 | 431 | 23.10 | 23.71 | 27.92 | 14.46 | 2.78 | 12.40 |
| 104240066 | 335 | 32.08 | 32.26 | 34.21 | 28.88 | 1.18 | 31.91 |
| 104240082 | 431 | 5.01 | 5.41 | 12.09 | −5.48 | 3.81 | 12.40 |
| 114150046 | 343 | 8.75 | 8.97 | 11.98 | 6.03 | 1.30 | 30.28 |
| 114150065 | 404 | 2.37 | 1.94 | 15.50 | −5.36 | 5.10 | 17.89 |
| 114160012 | 392 | 30.27 | 30.02 | 33.10 | 28.83 | 0.68 | 20.33 |
| 114170034 | 350 | −7.95 | −5.54 | 4.73 | −23.19 | 7.59 | 28.86 |
| 114170040 | 335 | −6.51 | −5.36 | 3.89 | −21.29 | 5.75 | 31.91 |
| 114180059 | 327 | −4.35 | −4.56 | 3.55 | −12.66 | 3.31 | 33.54 |
| 114210031 | 235 | 5.45 | 7.87 | 16.44 | −4.15 | 6.86 | 52.24 |
| 114210051 | 379 | 6.60 | 6.64 | 14.23 | −7.06 | 3.87 | 22.97 |
| 114210076 | 356 | 2.67 | 2.47 | 6.60 | −0.54 | 1.71 | 27.64 |
| 114210094 | 243 | 5.06 | 4.87 | 12.64 | −2.82 | 3.54 | 50.61 |
| 114210114 | 338 | 9.65 | 9.50 | 14.20 | 5.98 | 1.98 | 31.30 |
| 114220007 | 390 | 1.66 | 1.65 | 5.00 | −0.78 | 1.03 | 20.73 |
| 114220013 | 428 | −1.49 | −1.83 | 2.62 | −5.52 | 2.50 | 13.01 |
| 114230024 | 359 | −3.87 | −3.88 | 0.86 | −9.21 | 2.96 | 27.03 |
References
- Álvarez-Cobelas, M.; Cirujano, S.; Sánchez-Carrillo, S. Hydrological and botanical man-made changes in the Spanish wetland of Las Tablas de Daimiel. Biol. Conserv. 2001, 97, 89–98. [Google Scholar] [CrossRef]
- Castellazzi, P.; Martel, R.; Rivera, A.; Huang, J.; Pavlic, G.; Calderhead, A.I.; Chaussard, E.; Garfias, J.; Salas, J.; Goran, P. Groundwater depletion in Central Mexico: Use of GRACE and InSAR to support water resources management. Water Resour. Res. 2016, 52, 5985–6003. [Google Scholar] [CrossRef]
- Lubis, R.F. Urban hydrogeology in Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2018, 118, 012022. [Google Scholar] [CrossRef]
- Custodio, E. Aquifer overexploitation: What does it mean? Hydrogeol. J. 2002, 10, 254–277. [Google Scholar] [CrossRef]
- Díaz-Paniagua, C.; Zamudio, R.F.; Florencio, M.; Murillo, P.G.; Rodríguez, C.G.; Portheault, A.; Martín, L.S.; Siljestrom, P. Temporay ponds from Doñana National Park: A system of natural habitats for the preservation of aquatic flora and fauna. Limnetica 2010, 29, 41–58. [Google Scholar]
- Green, A.J.; Alcorlo, P.; Peeters, E.T.; Morris, E.; Espinar, J.L.; Bravo-Utrera, M.A.; Bustamante, J.; Díaz-Delgado, R.; Koelmans, A.; Mateo, R.; et al. Creating a safe operating space for wetlands in a changing climate. Front. Ecol. Environ. 2017, 15, 99–107. [Google Scholar] [CrossRef] [Green Version]
- Irawan, D.E.; Puradimaja, D.J.; Notosiswoyo, S.; Soemintadiredja, P. Hydrogeochemistry of volcanic hydrogeology based on cluster analysis of Mount Ciremai, West Java, Indonesia. J. Hydrol. 2009, 376, 221–234. [Google Scholar] [CrossRef]
- Bloomfield, J.; Marchant, B.; Bricker, S.H.; Morgan, R.B. Regional analysis of groundwater droughts using hydrograph classification. Hydrol. Earth Syst. Sci. 2015, 19, 4327–4344. [Google Scholar] [CrossRef] [Green Version]
- Nakagawa, K.; Yu, Z.-Q.; Berndtsson, R.; Kagabu, M. Analysis of earthquake-induced groundwater level change using self-organizing maps. Environ. Earth Sci. 2019, 78. [Google Scholar] [CrossRef]
- Rinderer, M.; Van Meerveld, I.; McGlynn, B.L. From Points to Patterns: Using Groundwater Time Series Clustering to Investigate Subsurface Hydrological Connectivity and Runoff Source Area Dynamics. Water Resour. Res. 2019, 55, 5784–5806. [Google Scholar] [CrossRef]
- Yuan, R.; Wang, M.; Wang, S.; Song, X. Water transfer imposes hydrochemical impacts on groundwater by altering the interaction of groundwater and surface water. J. Hydrol. 2020, 583, 124617. [Google Scholar] [CrossRef]
- Asgharinia, S.; Petroselli, A. A comparison of statistical methods for evaluating missing data of monitoring wells in the Kazeroun Plain, Fars Province, Iran. Groundw. Sustain. Dev. 2020, 10, 100294. [Google Scholar] [CrossRef]
- Celestino, A.M.; Cruz, D.M.; Otazo-Sánchez, E.; Reyes, F.G.; Soto, D.V. Groundwater Quality Assessment: An Improved Approach to K-Means Clustering, Principal Component Analysis and Spatial Analysis: A Case Study. Water 2018, 10, 437. [Google Scholar] [CrossRef] [Green Version]
- Bottou, L.; Bengio, Y. Convergence properties of the k-mean algorithms. In Neural Information Processing Systems 7 (NIPS 1994); MIT Press: Denver, CO, USA, 1995; pp. 585–592. [Google Scholar]
- Sardá-Espinosa, A. Time-Series Clustering in R Using the Dtwclust Package. Available online: https://journal.r-project.org/archive/2019/RJ-2019-023/RJ-2019-023.pdf (accessed on 2 November 2019).
- UPC. Regional Groundwater Flow in the Almonte-Marismas Aquifer; Groundwater Hydrology Group of the Technical University of Catalonia and Geological Institute of Spain: Madrid, Spain, 1999; p. 114. [Google Scholar]
- Olías Álvarez, M.; Rodríguez Rodríguez, M. Evolución de los niveles en la red de control piezométrica del acuífero Almonte-Marismas (periodo 1994–2012). In Proceedings of the X Simposio de Hidrogeología, Hidrogeología y Recursos Hidráulicos, Granada, Spain, 16–18 October 2013; Volume 30, pp. 1.121–1.130. [Google Scholar]
- CHG. Informe De Seguimiento Del Plan Hidrológico De La Demarcación Hidrográfica Del Guadalquivir; Ciclo de Planificación 2015–2021; Ministerio de Transición Ecológica: Madrid, Spain, 2019.
- Nguyen, T.T.; Kawamura, A.; Tong, T.N.; Nakagawa, N.; Amaguchi, H.; Gilbuena, R. Clustering spatio–seasonal hydrogeochemical data using self-organizing maps for groundwater quality assessment in the Red River Delta, Vietnam. J. Hydrol. 2015, 522, 661–673. [Google Scholar] [CrossRef]
- Guardiola-Albert, C.; Jackson, C.R. Potential Impacts of Climate Change on Groundwater Supplies to the Doñana Wetland, Spain. Wetlands 2011, 31, 907–920. [Google Scholar] [CrossRef] [Green Version]
- WWF. Salvemos Doñana. Del Peligro a la Prosperidad. 2016. Available online: http://awsassets.wwf.es/downloads/wwf_informe_salvemos_donana__2016.pdf?_ga=2.266321487.1975888914.1579078039-1333755382.1573218666 (accessed on 15 January 2020).
- Erostate, M.; Huneau, F.; Garel, E.; Ghiotti, S.; Vystavna, Y.; Garrido, M.; Pasqualini, V. Groundwater dependent ecosystems in coastal Mediterranean regions: Characterization, challenges and management for their protection. Water Res. 2020, 172, 115461. [Google Scholar] [CrossRef]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; Volume 1, pp. 281–297. Available online: http://projecteuclid.org:443/euclid.bsmsp/1200512992 (accessed on 10 January 2020).
- Custodio, E.; Manzano, M.; Montes, C. Las Aguas Subterráneas En Doñana; Aspectos Ecológicos y Sociales; Junta de Andalucía: Sevilla, Spain, 2009; p. 244. ISBN 978-84-92807-19-2.
- Guardiola-Albert, C.; García-Bravo, N.; Mediavilla, C.; Martín Machuca, M. Gestión de los recursos hídricos subterráneos en el entorno de Doñana con el apoyo del modelo matemático del acuífero Almonte-Marismas. Bol. Geol. y Min. 2009, 120, 361–376, ISSN 0366-0176. [Google Scholar]
- Salvany, J.M.; Custodio, E. Características litoestratigráficas de los depósitos pliocuaternarios del bajo Guadalquivir en el área de Doñana: Implicaciones hidrogeológicas. Rev. de la Soc. Geol. de Esp. 1995, 8, 21–31. [Google Scholar]
- Salvany, J.M.; Larrasoaña, J.C.; Mediavilla, C.; Rebollo, A. Chronology and tectono-sedimentary evolution of the Upper Pliocene to Quaternary deposits of the lower Guadalquivir foreland basin, SW Spain. Sediment. Geol. 2011, 241, 22–39. [Google Scholar] [CrossRef] [Green Version]
- CHG. Propuesta para la Declaración de la Masa de Aagua Subterránea de la Rocina en Riesgo de no Aalcanzar uun Buen Estado Cuantitativo y Guímico; Ministerio de Transición Ecológica: Madrid, Spain, 2019.
- Carnicer i Cols, J. Species richness, interaction networks, and diversification in bird communities: A synthetic ecological and evolutionary perspective. Bellaterra: Universitat Autònoma de Barcelona, 2008. ISBN 9788469139042. Tesis doctoral - Universitat Autònoma de Barcelona, Facultat de Ciències, Departament de Biologia Animal, Biologia Vegetal i Ecologia. 2007. Available online: https://ddd.uab.cat/record/36713 (accessed on 10 December 2019).
- Diaz-Paniagua, C.; Fernández-Zamudio, R.; Florencio, M.; García-Murillo, P.; Gómez-Rodríguez, J.M.; Siljeström, P.; Serrano, L. The temporary ponds of Doñana: Conservation value and present tretas. Eur. Pond Conserv. Netw. Newsl. 2008, 1, 5–685. [Google Scholar]
- Stekhoven, D.J.; Bühlmann, P. Miss-Forest? Non parametric missing value imputation for mixed-type data. Bioinformatics 2011, 28, 112–118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Aguilera, H.; Guardiola-Albert, C.; Naranjo-Fernández, N.; Kohfahl, C. Towards flexible groundwater-level prediction for adaptive water management: Using Facebook’s Prophet forecasting approach. Hydrol. Sci. J. 2019, 64, 1504–1518. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. Appl. Stat. 1979, 28, 100. [Google Scholar] [CrossRef]
- Ketchen, D.J.; Shook, C.L. The application of cluster analysis in Strategic Management Research: An analysis and critique. Strateg. Manag. J. 1996, 17, 441–458. [Google Scholar] [CrossRef]
- Kassambara, A.; Mundt, F. Factoextra: Extract and Visualize the Results of Multivariate Data Analyses. 2017. Available online: http://www.sthda.com/english/rpkgs/factoextra (accessed on 12 December 2019).
- Paparrizos, J.; Gravano, L. k-Shape: Efficient and Accurate Clustering of Time Series. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data—SIGMOD ’15, Portland, OR, USA, 14–19 June 2020; Association for Computing Machinery (ACM): New York, NY, USA, 2015; pp. 1855–1870, ISBN 978-1-4503-2758-9. [Google Scholar] [CrossRef]
- Maulik, U.; Bandyopadhyay, S. Performance evaluation of some clustering algorithms and validity indices. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1650–1654. [Google Scholar] [CrossRef] [Green Version]
- Kryszczuk, K.; Hurley, P. Estimation of the Number of Clusters Using Multiple Clustering Validity Indices. In Multiple Cassifier Systems; El Gayar, N., Kittler, J., Roli, F., Eds.; MSC 2010. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 5997, pp. 114–123. [Google Scholar]
- Dunn, J.C. A fuzzy relative of the ISODARA process and its use in detecting compact well-separated clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [CrossRef]
- Calinski, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar]
- Manzano, M.; Custodio, E.; Montes, C.; Mediavilla, C. Groundwater Quality and Quantity Assessment through a Dedicated Monitoring Network: The Doñana Aquifer Experience (SW Spain). Groundwater Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 273–287. [Google Scholar]
- Manzano, M.; Borja, F.; Montes, C. Metodología de tipificación hidrología de los humedales españoles con vistas a su valoración funcional y a su gestión. Aplicación a los humedales de Doñana. Bol. Geol. Min. 2002, 113, 313–330, ISSN 0366-0176. [Google Scholar]
- Naranjo-Fernández, N.; Guardiola-Albert, C.; Aguilera, H.; Serrano-Hidalgo, C.; Rodríguez-Rodríguez, M.; Fernández-Ayuso, A.; Ruiz-Bermudo, F.; Montero-González, E. Relevance of spatio-temporal rainfall variability regarding groundwater management challenges under global change: Case study in Doñana (SW Spain). Stoch. Environ. Res. Risk Assess. 2020. [Google Scholar] [CrossRef]
- Fundación Doñana 21. Bases estratégicas para una agricultura sostenible en Doñana. Área de agricultura. 2003. Available online: http://donana.es/source/BASES%20ESTRATEGICAS%20PARA%20UNA%20AGRICULTURA%20SOSTENIBLE%20EN%20DO%C3%91ANA.pdf (accessed on 20 February 2020).
- Fernández-Ayuso, A.; Aguilera, H.; Guardiola-Albert, C.; Rodríguez-Rodríguez, M.; Heredia, J.; Naranjo-Fernández, N. Unraveling the Hydrological Behavior of a Coastal Pond in Doñana National Park (Southwest Spain). Groundwater 2019, 57, 895–906. [Google Scholar] [CrossRef]
- Guijo-Rubio, D.; Rosal, A.M.D.; Gutiérrez, P.A.; Troncoso, A.; Hervas-Martínez, C. Time series clustering based on the characterisation of segment typologies. arXiv 2018, arXiv:1810.11624v1. [Google Scholar]
- Lorenzo-Lacruz, J.; Garcia, C.; Morán-Tejeda, E. Groundwater level responses to precipitation variability in Mediterranean insular aquifers. J. Hydrol. 2017, 552, 516–531. [Google Scholar] [CrossRef]
- Shapoori, V.; Peterson, T.J.; Western, A.; Costelloe, J. Top-down groundwater hydrograph time-series modeling for climate-pumping decomposition. Hydrogeol. J. 2015, 23, 819–836. [Google Scholar] [CrossRef]
- Van Dijk, W.M.; Densmore, A.L.; Jackson, C.R.; Mackay, J.D.; Joshi, S.K.; Sinha, R.; Shekhar, S.; Gupta, S. Spatial variation of groundwater response to multiple drivers in a depleting alluvial aquifer system, northwestern India. Prog. Phys. Geogr. Earth Environ. 2019, 44, 94–119. [Google Scholar] [CrossRef] [Green Version]
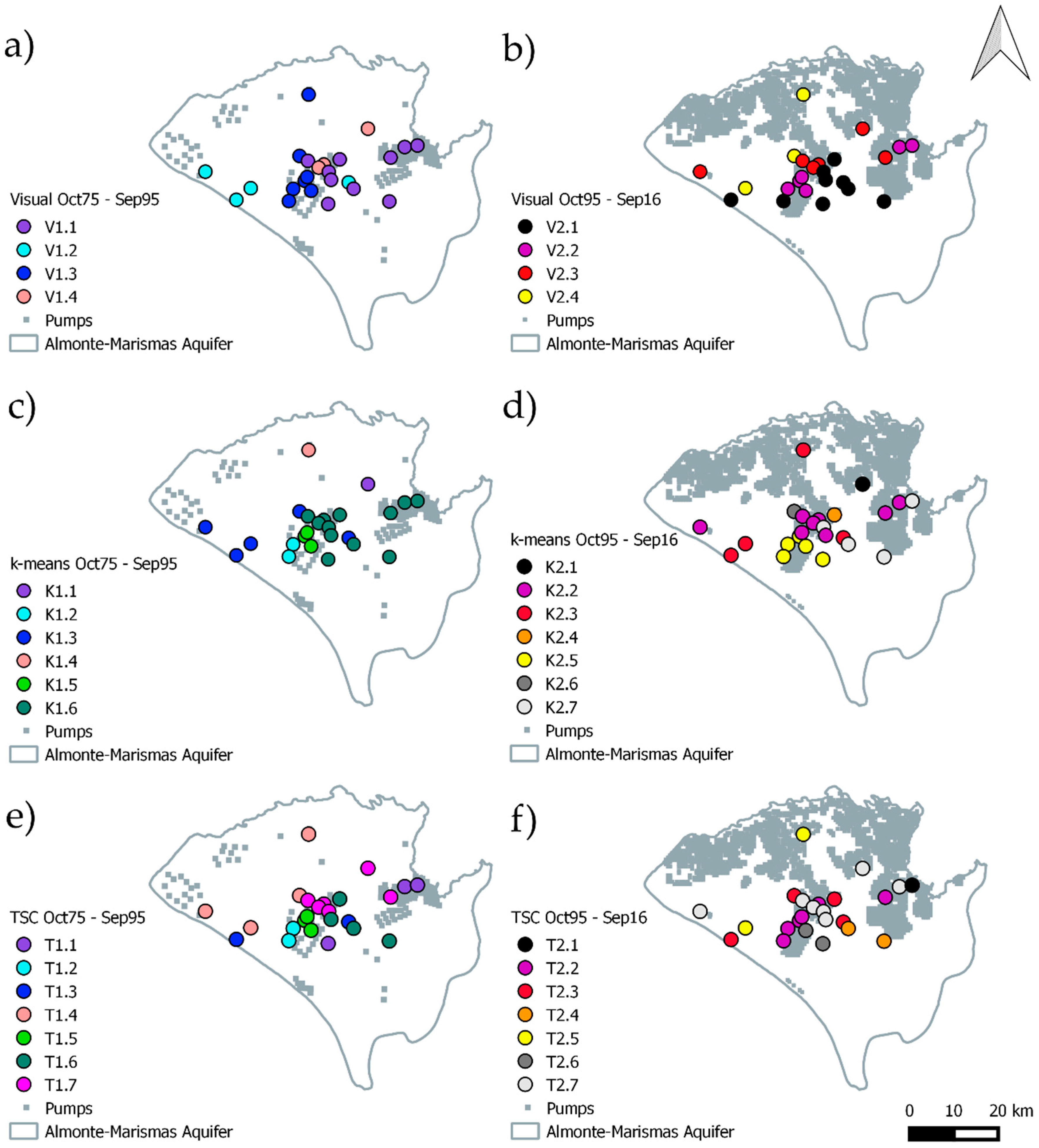
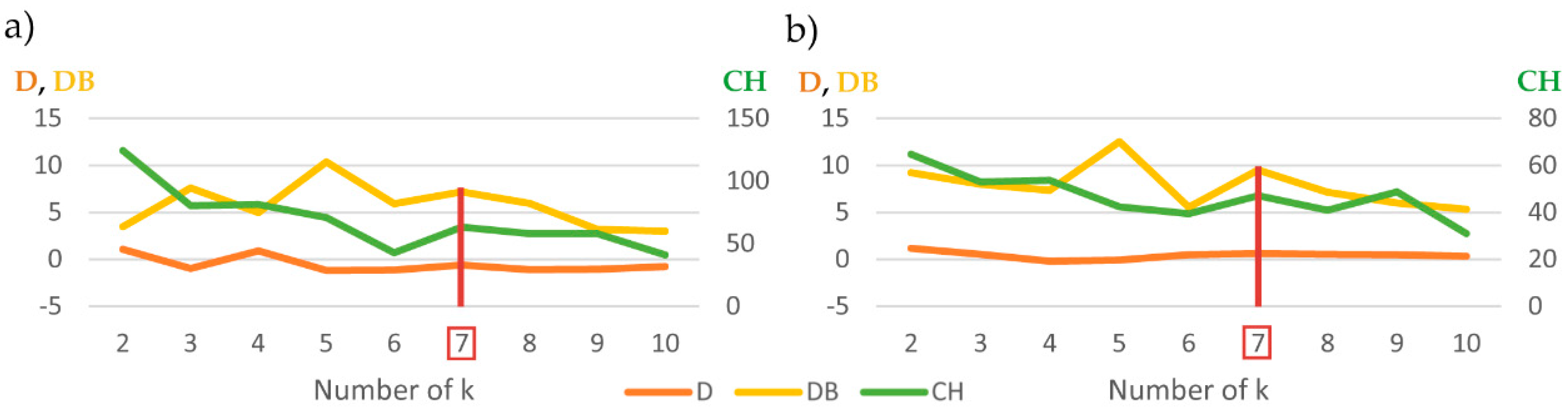

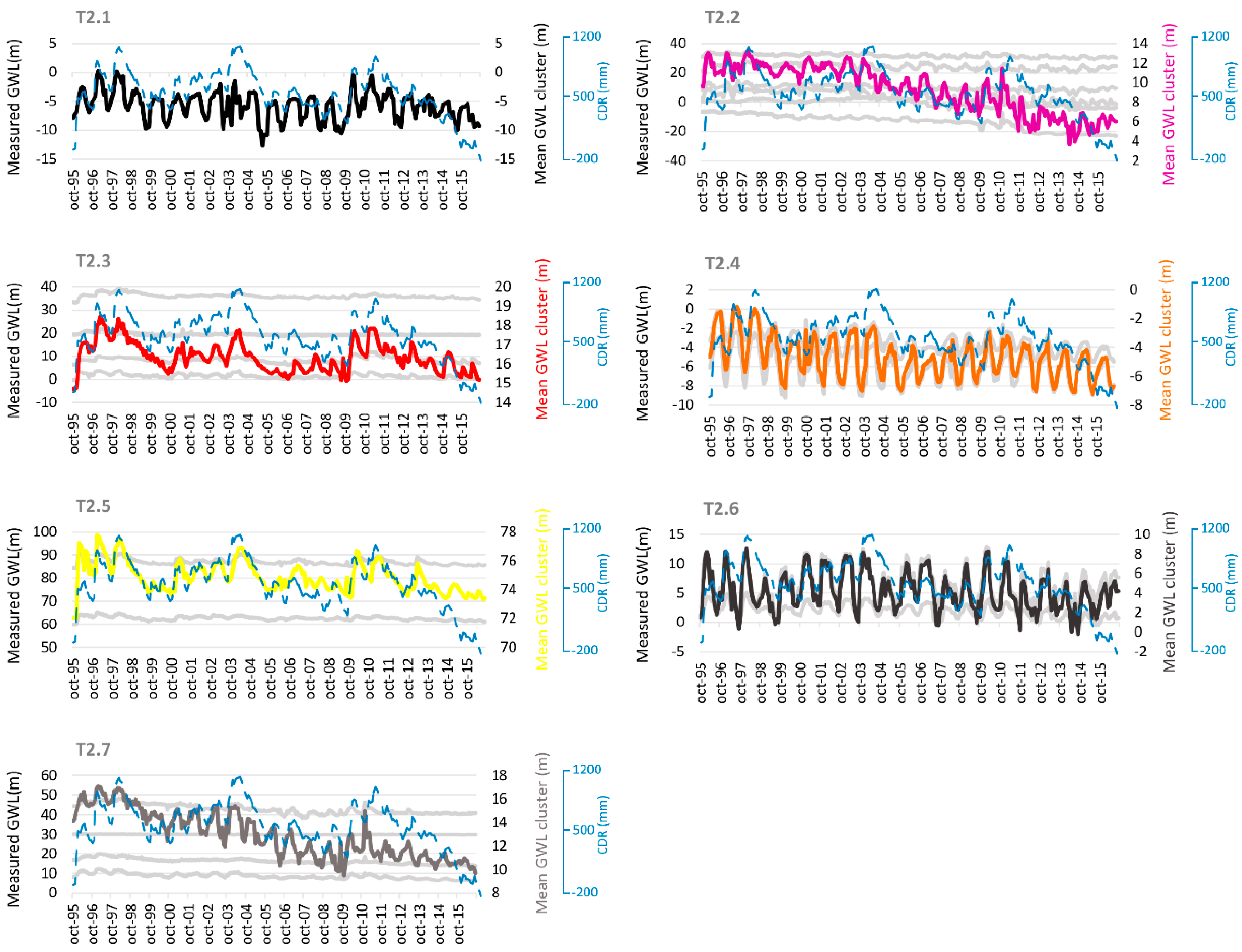
| Method | Sub-Period | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | Cluster 6 | Cluster 7 |
|---|---|---|---|---|---|---|---|---|
| Visual | 1 | 10 | 4 | 7 | 3 | - | - | - |
| 2 | 10 | 5 | 6 | 3 | - | - | - | |
| k-means | 1 | 1 | 2 | 5 | 1 | 3 | 12 | - |
| 2 | 1 | 8 | 4 | 1 | 5 | 1 | 4 | |
| TSC | 1 | 3 | 2 | 2 | 3 | 4 | 6 | 4 |
| 2 | 1 | 6 | 4 | 2 | 2 | 7 | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naranjo-Fernández, N.; Guardiola-Albert, C.; Aguilera, H.; Serrano-Hidalgo, C.; Montero-González, E. Clustering Groundwater Level Time Series of the Exploited Almonte-Marismas Aquifer in Southwest Spain. Water 2020, 12, 1063. https://doi.org/10.3390/w12041063
Naranjo-Fernández N, Guardiola-Albert C, Aguilera H, Serrano-Hidalgo C, Montero-González E. Clustering Groundwater Level Time Series of the Exploited Almonte-Marismas Aquifer in Southwest Spain. Water. 2020; 12(4):1063. https://doi.org/10.3390/w12041063
Chicago/Turabian StyleNaranjo-Fernández, Nuria, Carolina Guardiola-Albert, Héctor Aguilera, Carmen Serrano-Hidalgo, and Esperanza Montero-González. 2020. "Clustering Groundwater Level Time Series of the Exploited Almonte-Marismas Aquifer in Southwest Spain" Water 12, no. 4: 1063. https://doi.org/10.3390/w12041063





