Assessing Inhomogeneities in Extreme Annual Rainfall Data Series by Multifractal Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Source
2.2. Methodology
2.2.1. Homogeneity Tests
- (1)
- Buishand Range testThis test is based on the adjusted partial sums or cumulative derivations from the mean of the n data points, :For a homogeneous record, values fluctuate around zero. The values of can be rescaled by the sample standard deviation, :withThe Q, which is sensitive to departures from homogeneity, can then be obtained as:For different significance levels, the critical values for the test statistics (Qc) depend on the number of data and can be found in [30].
- (2)
- Standard Normal Homogeneity testThis test [31] compares the mean of the first k years of data with the last (n − k) years by using the Tk of the statistics:whereThe year k shows a break if the value of Tk is the maximum. If the is greater than the critical values [32], the null hypothesis is rejected.
- (3)
- Pettitt testThe Pettitt test [33] is based on the ranking ri of the yi values. The ranks ri are obtained by ordering the data in crescent order, so that the smallest one gets ranked 1 and the highest gets the n-rank. The Uk is then obtained as:If a break occurs in the year K, then the Uk is:The statistical significance of the break point is checked by comparing the value of (Equation (7)) to its theoretical value:with α the significance level.
- (4)
- Sequential Mann–Kendall testThis test is usually applied to evaluate trends in data series and also to check the moment when they start being significant [34,35,36]. It calculates two series of statistic values: one (U(t)) for the progressive temporal data set (y1, y2, …, yn) and the other (U’(t)) for the corresponding regressive data set (yn, yn−1, …, y1), both with an average value of zero and a standard deviation of one. Usually, the ranks of the yi values are preferred.The tk has to be obtained by:with ni being the number of cases for whichUnder the null hypothesis, it is assumed that no trend exists, and tk follows a normal distribution with average and variance values given by:The sequential values of U(tk) are finally obtained as:A positive value of U(tk) shows a positive trend, whereas a negative trend appears if the U(tk) value is negative.The null hypothesis is rejected if where is the critical value of the typified normal distribution with a probability higher than . For a significance level α = 5%, the critical value of is 1.9604.The values of U’() are also obtained from regressive temporal data series, tk’, E[tk’], Var[tk’] by using Equations (9)–(11), and finally:By plotting the curves of the U(t) and U’(t) as a function of the year, a break point is detected where the curves cross and diverge.
- (5)
- Mann–Whitney U testThis test can detect a step change in a time series by assessing the difference in the means of two sub-series arising from splitting the complete data series. The original time series (yi, i = 1, 2, …, n) is broken into two subseries, one from y1 to yn1 and the other from yn1+1 to yn, of sizes n1 and n2 (n − n1 + 1), respectively. A new data series, zt (t = 1, …, n) is obtained by rearranging the original time series yi in increasing order of magnitude. The Mann–Whitney test statistic is obtained by:where R(yi) is the rank of observation yi in the series zt. If the hypothesis of equal means in both subseries is rejected, being the (1 − α/2) quantile of the normal distribution.
- (6)
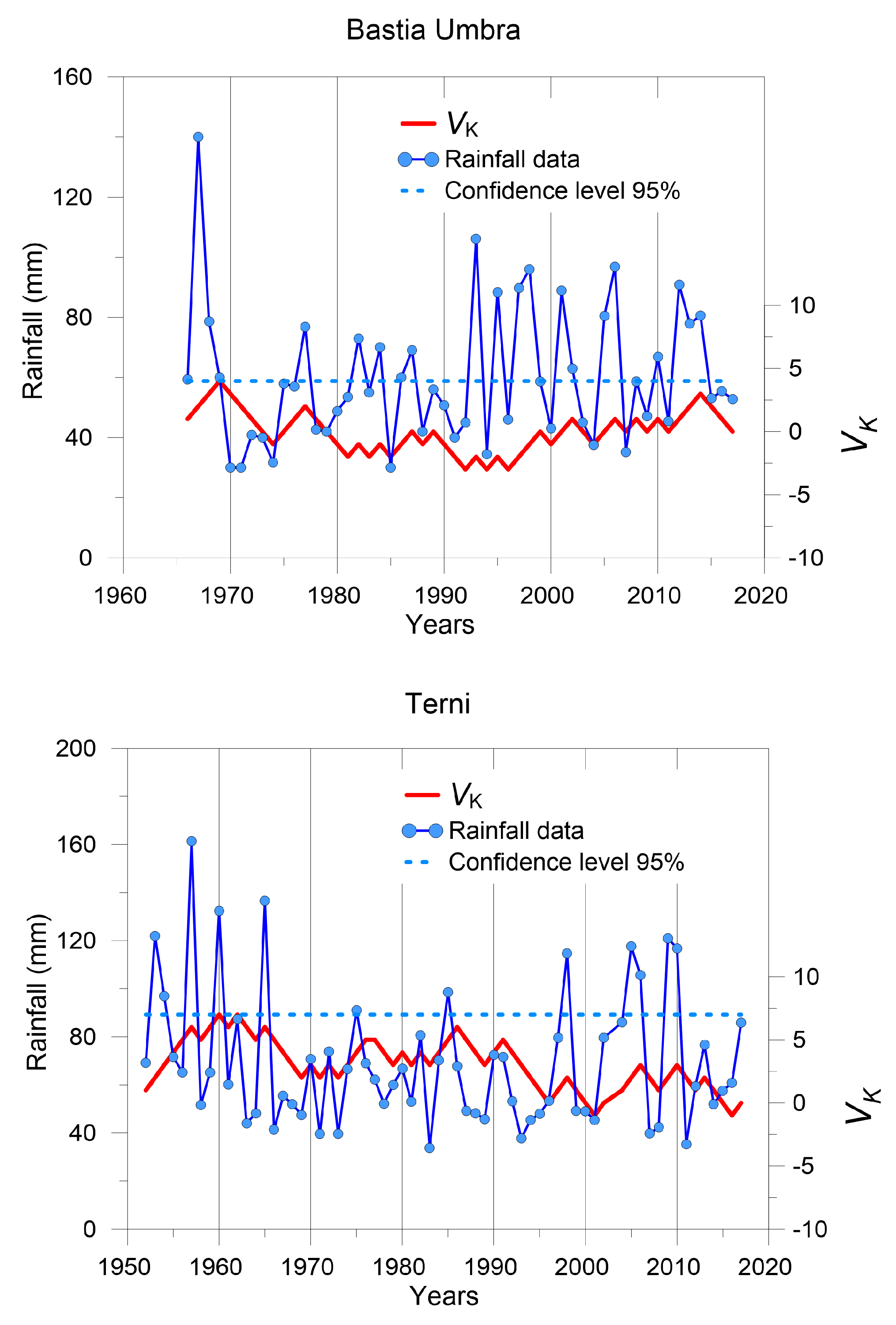
- Cumulative Sum testThe distribution-free cumulative sum technique was proposed by [37] to detect if a significant step change occurred in a given time series at a significance level α = 0.05 [38]. The null hypothesis considers that no step change exists. For the given data series yi (i = 1, …, n), the test statistics Vk is obtained as:where k = 1, 2, …, n; ymedian is the median of the time series, and the sign function is:A step-change point consists of any year when the maximal or minimal Vk falls outside the 95% confidence limit of ±1.36 [38].
2.2.2. Multifractal Characterization
3. Results
3.1. Break Point Detection
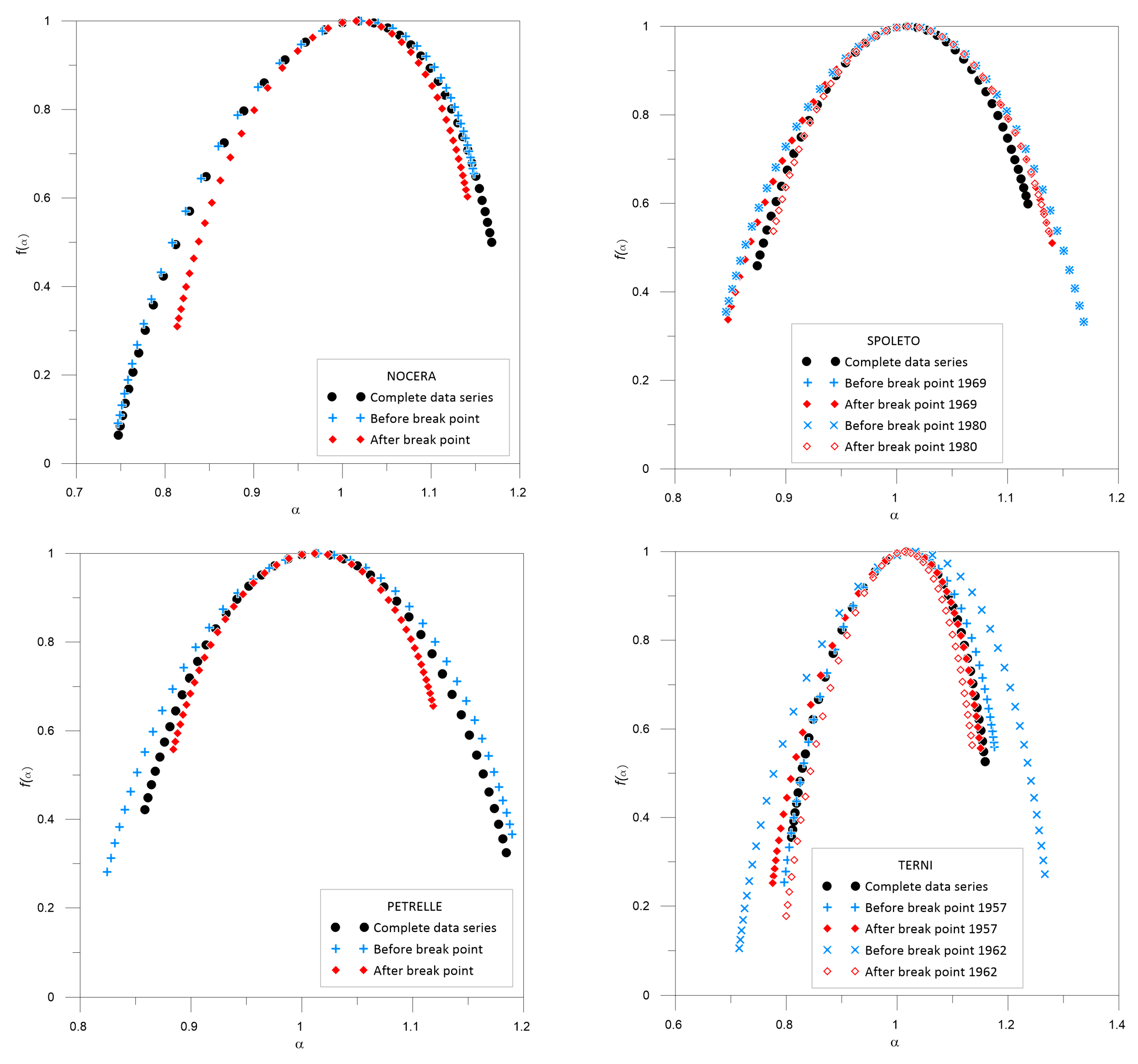
3.2. Multifractal Behavior
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haktanir, T.; Citakoglu, H. Trend, Independence, Stationarity, and Homogeneity Tests on Maximum Rainfall Series of Standard Durations Recorded in Turkey. J. Hydrol. Eng. 2014, 19, P05014009. [Google Scholar] [CrossRef]
- Wijngaard, J.B.; Klein Tank, A.M.G.; Können, G.P. Homogeneity of 20th century European daily temperature and precipitation series. Int. J. Climatol. 2003, 23, 679–692. [Google Scholar] [CrossRef]
- Hoerling, M.; Kumar, A.; Eischeid, J.; Jha, B. What is causing the variability in global mean land temperature? Geophys. Res. Lett. 2008, 35, L23712. [Google Scholar] [CrossRef] [Green Version]
- Martínez, M.D.; Serra, C.; Burgueño, A.; Lana, X. Time trends of daily maximum and minimum temperatures in Catalonia (NE Spain) for the period 1975–2004. Int. J. Climatol. 2010, 30, 267–290. [Google Scholar]
- Geng, Q.; Wu, P.; Zhao, X. Spatial and temporal trends in climatic variables in arid areas of northwest China. Int. J. Climatol. 2016, 36, 4118–4129. [Google Scholar] [CrossRef]
- Swanson, K.L.; Tsonis, A.A. Has the climate recently shifted? Geophys. Res. Lett. 2009, 36, L06711. [Google Scholar] [CrossRef] [Green Version]
- Morozova, A.L.; Valente, M.A. Homogenization of Portuguese long-term temperature data series: Lisbon, Coimbra and Porto. Earth Syst. Sci. Data 2012, 4, 187–213. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y. Updating Rainfall IDF Relationships to Maintain Urban Drainage Design Standards. J. Hydrol. Eng. 2006, 11, 506–509. [Google Scholar] [CrossRef]
- Hassan, H.W.; Nile, B.K.; Al-Masody, B.A. Study the climate change effect on storm drainage networks by storm water management model [SWMM]. Environ. Eng. Res. 2017, 22, 393–400. [Google Scholar] [CrossRef]
- Adamowski, K.; Bougadis, J. Detection of trends in annual extreme rainfall. Hydrol. Process. 2003, 17, 3547–3560. [Google Scholar] [CrossRef]
- Fujibe, F.; Yamazaki, N.; Katsuyama, M.; Kobayashi, K. The increasing trend of intense precipitation in Japan based on four-hourly data for a hundred years. Sci. Online Lett. Atmos. SOLA 2005, 1, 41–44. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Ding, Q.; Jhun, J.G. Trends in Seoul (1778–2004) summer precipitation. Geophys. Res. Lett. 2006, 33, L15803. [Google Scholar] [CrossRef] [Green Version]
- Burn, D.H.; Mansour, R.; Zhang, K.; Whitfield, P.H. Trends and variability in extreme rainfall events in British Columbia. Can. Water Resour. J. 2011, 36, 67–82. [Google Scholar] [CrossRef]
- Douglas, E.M.; Fairbank, C.A. Is precipitation in northern New England becoming more extreme? Statistical analysis of extreme rainfall in Massachusetts, New Hampshire, and Maine and updated es- timates of the 100-year storm. J. Hydrol. Eng. 2011, 16, 203–217. [Google Scholar] [CrossRef] [Green Version]
- Nandargi, S.; Dhar, O.N. Extreme rainfall events over the Himalayas between 1871 and 2007. Hydrol. Sci. J. 2011, 56, 930–945. [Google Scholar] [CrossRef] [Green Version]
- Yavuz, H.; Erdogan, S. Spatial analysis of monthly and annual precipitation trends in Turkey. Water Resour. Manag. 2012, 26, 609–621. [Google Scholar] [CrossRef]
- Xu, Z.X.; Takeuchi, K.; Ishidaira, H. Monotonic trend and step changes in Japanese precipitation. J. Hydrol. 2003, 279, 144–150. [Google Scholar] [CrossRef]
- Shadmani, M.; Marofiand, S.; Roknian, M. Trend analysis in reference evapotranspiration using Mann–Kendall and Spear- man’s Rho tests in Arid Regions of Iran. Water Resour. Manag. 2012, 26, 211–224. [Google Scholar] [CrossRef] [Green Version]
- Piccarreta, M.; Lazzari, M.; Pasini, A. Trends in daily temperature extremes over the Basilicata region (southern Italy) from 1951 to 2010 in a Mediterranean climatic context. Int. J. Climatol. 2015, 35, 1964–1975. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Climatic change, the hurst phenomenon, and hydrological statistics. Hydrol. Sci. J. 2003, 48, 3–24. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Nonstationarity versus scaling in hydrology. J. Hydrol. 2006, 324, 239–254. [Google Scholar] [CrossRef] [Green Version]
- Haddad, O.B.; Moravej, M. Discussion of “Trend, Independence, Stationarity, and Homogeneity Tests on Maximum Rainfall Series of Standard Durations Recorded in Turkey” by Tefaruk Haktanir and Hatice Citakoglu. J. Hydrol. Eng. 2015, 20, 07015016. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The Mann–Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Baranowski, P.; Krzyszczak, J.; Slawinski., C.; Hoffmann, H.; Kozyra, J.; Nierόbca, A.; Siwek, K.; Gluza, A. Multifractal analysis of me- teorological time series to assess climate impacts. Clim. Res. 2015, 65, 39–52. [Google Scholar] [CrossRef] [Green Version]
- Krzyszczak, J.; Baranowski, P.; Zubik, M.; Kazandjiev, V.; Georgieva, V.; Sławiński, C.; Siwek, K.; Kozyra, J.; Nierόbca, A. Multifractal characterization and comparison of meteorological time series from two climatic zones. Theor. Appl. Climatol. 2018, 137, 1811–1824. [Google Scholar] [CrossRef] [Green Version]
- García-Marín, A.P.; Jiménez-Hornero, F.J.; Ayuso, J.L. Applying multifractality and the self-organized criticality theory to describe the temporal rainfall regimes in Andalusia (southern Spain). Hydrol. Process. 2008, 22, 295–308. [Google Scholar] [CrossRef]
- García-Marín, A.P.; Estévez, J.; Jiménez-Hornero, F.J.; Ayuso-Muñoz, J.L. Multifractal analysis of validated wind speed time series. Chaos 2013, 23, 13133–21505. [Google Scholar] [CrossRef]
- Jiménez-Hornero, F.J.; Jiménez-Hornero, J.E.; de Ravé, E.G.; Pavon-Dominguez, P. Exploring the relationship between nitrogen dioxide and ground-level ozone by applying the joint multifractal analysis. Environ. Monit. Assess. 2010, 167, 675–684. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Corradini, C.; Wilkinson, S.M.; Fowler, H.J. Influence of temporal data aggregation on trend estimation for intense rainfall. Adv. Water Resour. 2018, 122, 304–316. [Google Scholar] [CrossRef]
- Buishand, T.A. Some methods for testing the homogeneity of rainfall records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
- Alexandersson, H. A homogeneity test applied to precipitation data. Int. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J. On the critical values of the standard normal homogeneity test (SNHT). Int. J. Climatol. 2007, 27, 681–687. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Nanni, T. Variations of temperature and precipitation in Italy from 1866 to 1995. Theor. Appl. Climatol. 2000, 65, 165–174. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend Analysis in Turish Precipitation Data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Karpouzos, D.K.; Kavalieratou, S.; Babajimopoulos, C. Trend Analysis of Precipitation Data in Pieria Region (Greece). Eur. Water 2010, 30, 31–40. [Google Scholar]
- McGilchrist, C.C.; Woodyer, K.D. Note on a Distribution-Free CUSUM Technique. Technometrics 1975, 17, 321–325. [Google Scholar] [CrossRef]
- Wang, X.; Yang, X.; Liu, T.; Li, F.; Gao, R.; Duan, L.; Luo, Y. Trend and extreme occurrence of precipitation in a midlatitude Eurasian steppe watershed at various time scales. Hydrol. Process. 2014, 28, 5547–5560. [Google Scholar] [CrossRef]
- Casas-Castillo, M.C.; Rodríguez-Solá, R.; Navarro, X.; Russo, B.; Lastra, A.; González, P.; Redaño, A. On the consideration of scaling properties of extreme rainfall in Madrid (Spain) for developing a generalized intensity-duration-frequency equation and assessing probable maximum precipitation estimates. Theor. Appl. Climatol. 2018, 131, 573–580. [Google Scholar] [CrossRef]
- García-Marín, A.P.; Morbidelli, R.; Saltalippi, C.; Cifrodelli, M.; Estévez, J.; Flammini, A. On the choice of the optimal frequency analysis of annual extreme rainfall by multifractal approach. J. Hydrol. 2019, 575, 1267–1279. [Google Scholar] [CrossRef]
- Carmona-Cabezas, R.; Ariza-Villaverde, A.B.; Gutiérrez de Ravé, E.; Jiménez-Hornero, F.J. Visibility graphs of ground-level ozone time series: A multifractal analysis. Sci. Total Environ. 2019, 661, 138–147. [Google Scholar] [CrossRef] [PubMed]
- Feder, J. Fractals; Plenum: New York, NY, USA, 1988. [Google Scholar]
- Davis, A.; Marshak, A.; Wiscombe, W.; Cahalan, R. Multifractal characterization of non stationarity and intermittency in geophysical fields: Observed, retrieved or simulated. J. Geophys. Resour. 1994, 99, 8055–8072. [Google Scholar] [CrossRef]
- Herrera-Grimaldi, P.; García-Marín, A.P.; Estévez, J. Multifractal analysis of diurnal temperature range over Southern Spain using validated datasets. Chaos 2019, 29, 063105. [Google Scholar] [CrossRef] [PubMed]
- Ding, M.; Grebogi, C.; Ott, E.; Sauer, T.; Yorke, J.A. Estimating correlation dimension from a chaotic time series: When does plateau onset occur? Physica D 1993, 69, 404–424. [Google Scholar] [CrossRef]


| Station. | Period (Years) Considered |
|---|---|
| Bastia Umbra | from 1966 to 2017 |
| Bevagna | from 1967 to 2017 |
| Nocera Umbra | from 1961 to 2017 |
| Petrelle | from 1951 to 2017 |
| Ponte Nuovo di Torgiano | from 1954 to 2017 |
| Spoleto | from 1949 to 2017 |
| Terni | from 1952 to 2017 |
| Todi | from 1948 to 2017 |
| Station | BRT | SNHT | ||
|---|---|---|---|---|
| Q | Qc | T0 | T0c | |
| Bastia Umbra | 0.862 | 1.271 | 6.689 | 8.480 |
| Bevagna | 0.746 | 1.270 | 2.626 | 8.456 |
| Nocera | 0.650 | 1.273 | 3.094 | 8.586 |
| Petrelle | 0.978 | 1.277 | 3.970 | 8.768 |
| Ponte | 0.615 | 1.276 | 2.182 | 8.717 |
| Spoleto | 1.295 | 1.277 | 7.546 | 8.784 |
| Terni | 1.088 | 1.276 | 7.505 | 8.735 |
| Todi | 0.739 | 1.278 | 3.794 | 8.814 |
| Station | Pettitt Test | |
|---|---|---|
| K | K0.05 | |
| Bastia Umbra | 213.0 | 267.5 |
| Bevagna | 170.0 | 259.9 |
| Nocera | 194.0 | 306.7 |
| Petrelle | 322.0 | 390.4 |
| Ponte | 152.0 | 356.1 |
| Spoleto | 435.0 | 399.1 |
| Terni | 276.0 | 373.1 |
| Todi | 237.0 | 461.8 |
| Station | Parametric Tests | Non-Parametric Tests | ||||
|---|---|---|---|---|---|---|
| BR | SNH | PT | SQMK | MWU | CUSUM | |
| Bastia Umbra | - | - | - | - | - | - |
| Bevagna | - | - | - | - | - | - |
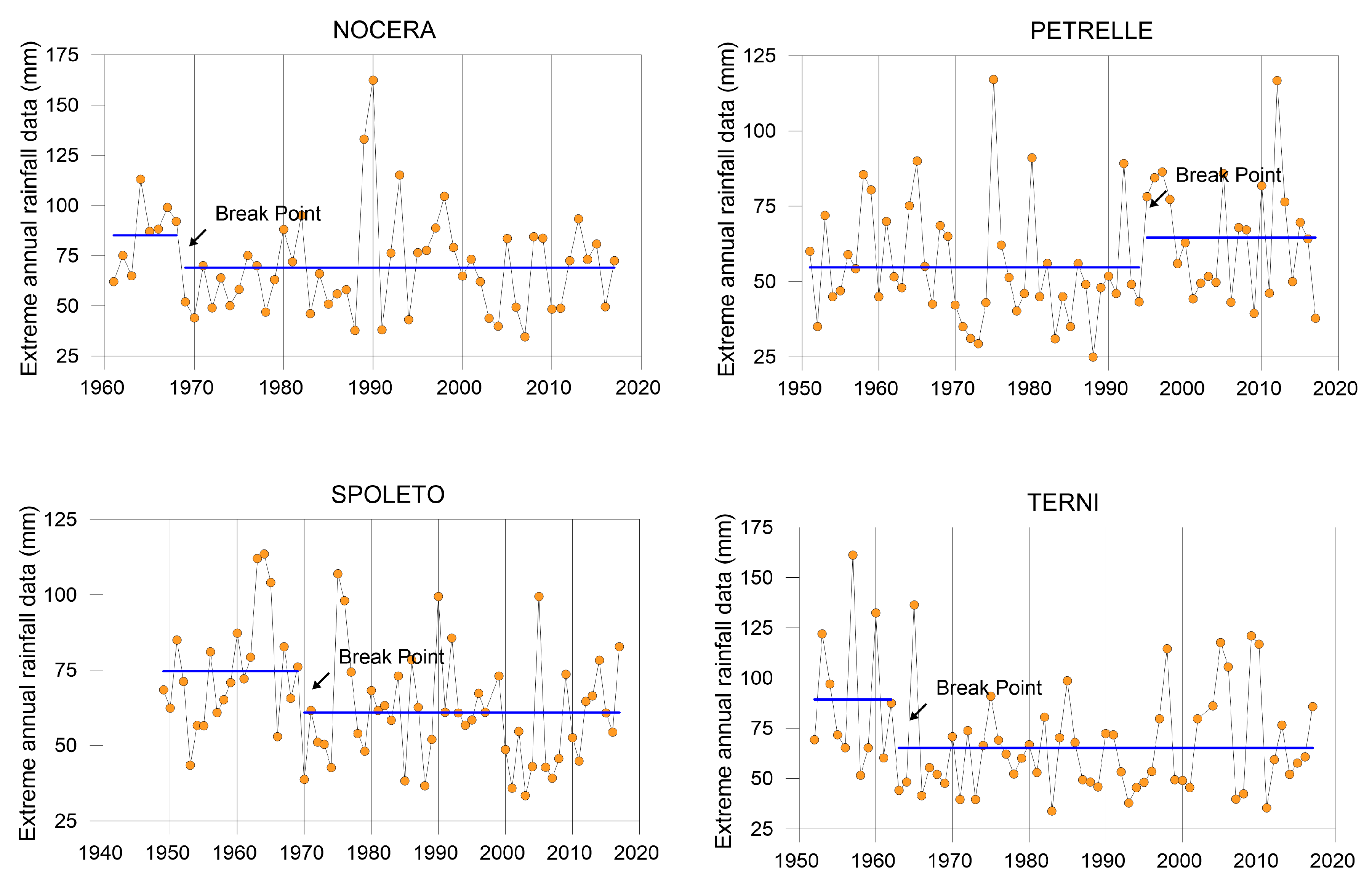
| Nocera Umbra | - | - | - | - | 1968 | - |
| Petrelle | - | - | - | - | 1994 | - |
| Ponte | - | - | - | - | - | - |
| Spoleto | 1977 | - | 1969 | 1980 | 1969 | - |
| Terni | - | - | - | 1957 | 1962 | - |
| Todi | - | - | - | - | - | - |
| Station | Complete Data Series | Before Break Point Series | After Break Point Series | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D1 | D2 | D0-D1 | D0-D2 | D1 | D2 | D0-D1 | D0-D2 | D1 | D2 | D0-D1 | D0-D2 | ||
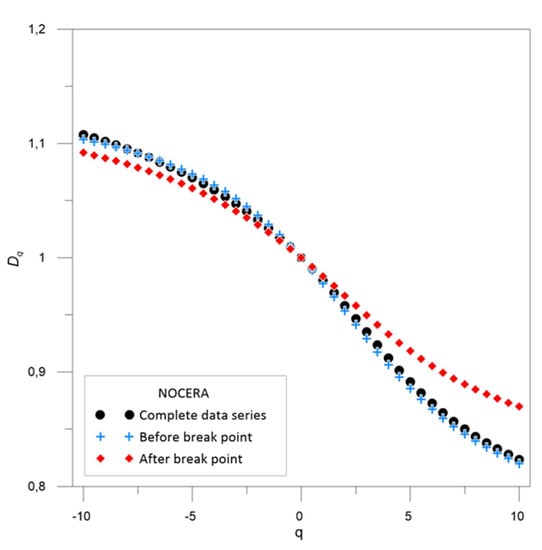
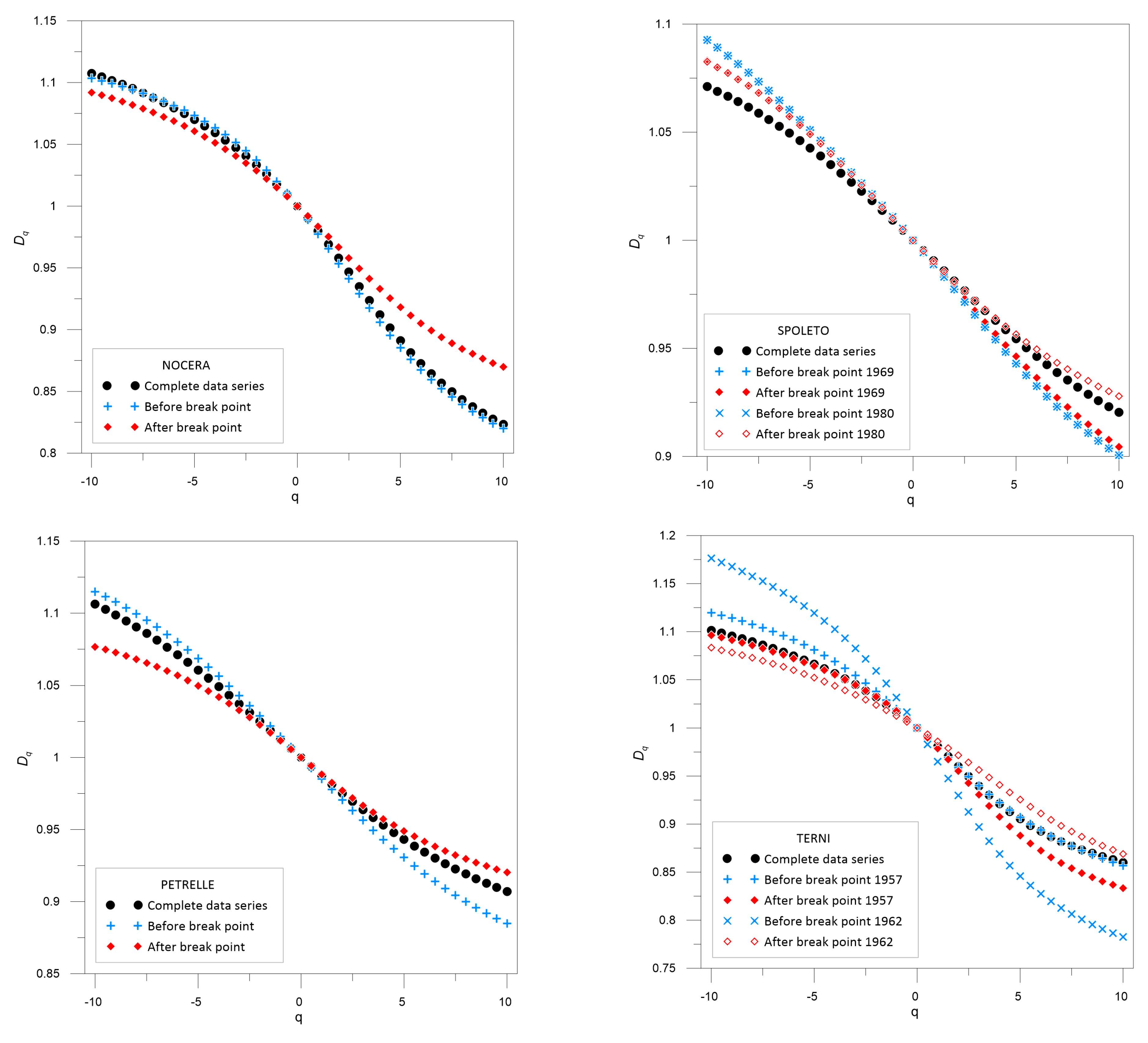
| Nocera Umbra | 1968 | 0.980 | 0.958 | 0.020 | 0.042 | 0.977 | 0.953 | 0.023 | 0.047 | 0.984 | 0.967 | 0.016 | 0.033 |
| Petrelle | 1994 | 0.988 | 0.975 | 0.012 | 0.025 | 0.985 | 0.971 | 0.015 | 0.029 | 0.988 | 0.977 | 0.012 | 0.023 |
| Terni | 1957 | 0.980 | 0.960 | 0.020 | 0.040 | 0.980 | 0.959 | 0.020 | 0.041 | 0.979 | 0.955 | 0.021 | 0.045 |
| 1962 | 0.965 | 0.930 | 0.035 | 0.070 | 0.986 | 0.972 | 0.014 | 0.028 | |||||
| Spoleto | 1969 | 0.991 | 0.981 | 0.009 | 0.019 | 0.989 | 0.977 | 0.011 | 0.023 | 0.989 | 0.978 | 0.011 | 0.022 |
| 1980 | 0.989 | 0.977 | 0.011 | 0.023 | 0.990 | 0.981 | 0.010 | 0.019 | |||||
| Station | Complete Data Series | Before Break Point Series | After Break Point Series | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| αmin | αmax | as | w | αmin | αmax | as | w | αmin | αmax | as | w | ||
| Nocera Umbra | 1968 | 0.74731 | 1.16829 | −0.43561 | 0.42098 | 0.74697 | 1.14838 | −0.56416 | 0.40142 | 0.81372 | 1.14083 | −0.29407 | 0.32712 |
| Petrelle | 1994 | 0.85847 | 1.18429 | 0.09650 | 0.32581 | 0.82446 | 1.18982 | −0.08529 | 0.36536 | 0.88417 | 1.11864 | −0.09868 | 0.23448 |
| Terni | 1957 | 0.80952 | 1.15864 | −0.17081 | 0.34913 | 0.79642 | 1.17564 | −0.30561 | 0.37922 | 0.77523 | 1.15035 | −0.30485 | 0.37513 |
| 1962 | 0.71493 | 1.26671 | −0.16686 | 0.55178 | 0.79981 | 1.13520 | −0.38638 | 0.33539 | |||||
| Spoleto | 1969 | 0.87427 | 1.11828 | −0.13999 | 0.24401 | 0.84608 | 1.16869 | 0.02276 | 0.32261 | 0.84776 | 1.14035 | −0.17251 | 0.29258 |
| 1980 | 0.84608 | 1.16869 | 0.02276 | 0.32261 | 0.88881 | 1.13704 | −0.00022 | 0.24823 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Marín, A.P.; Estévez, J.; Morbidelli, R.; Saltalippi, C.; Ayuso-Muñoz, J.L.; Flammini, A. Assessing Inhomogeneities in Extreme Annual Rainfall Data Series by Multifractal Approach. Water 2020, 12, 1030. https://doi.org/10.3390/w12041030
García-Marín AP, Estévez J, Morbidelli R, Saltalippi C, Ayuso-Muñoz JL, Flammini A. Assessing Inhomogeneities in Extreme Annual Rainfall Data Series by Multifractal Approach. Water. 2020; 12(4):1030. https://doi.org/10.3390/w12041030
Chicago/Turabian StyleGarcía-Marín, Amanda P., Javier Estévez, Renato Morbidelli, Carla Saltalippi, José Luis Ayuso-Muñoz, and Alessia Flammini. 2020. "Assessing Inhomogeneities in Extreme Annual Rainfall Data Series by Multifractal Approach" Water 12, no. 4: 1030. https://doi.org/10.3390/w12041030
APA StyleGarcía-Marín, A. P., Estévez, J., Morbidelli, R., Saltalippi, C., Ayuso-Muñoz, J. L., & Flammini, A. (2020). Assessing Inhomogeneities in Extreme Annual Rainfall Data Series by Multifractal Approach. Water, 12(4), 1030. https://doi.org/10.3390/w12041030