Modification of the MONERIS Nutrient Emission Model for a Lowland Country (Hungary) to Support River Basin Management Planning in the Danube River Basin
Abstract
1. Introduction
1.1. The Nutrient Problem
1.2. Aims of the Study
- determine the degree to which the model system MONERIS is capable of estimating nutrient fluxes in a lowland country such as Hungary;
- identify the model components (equations, parameters) that had to be adjusted to better describe processes in the study area;
- give country-wide, waterbody scale estimates for nitrogen and phosphorus loads of various pathways.
2. Materials and Methods
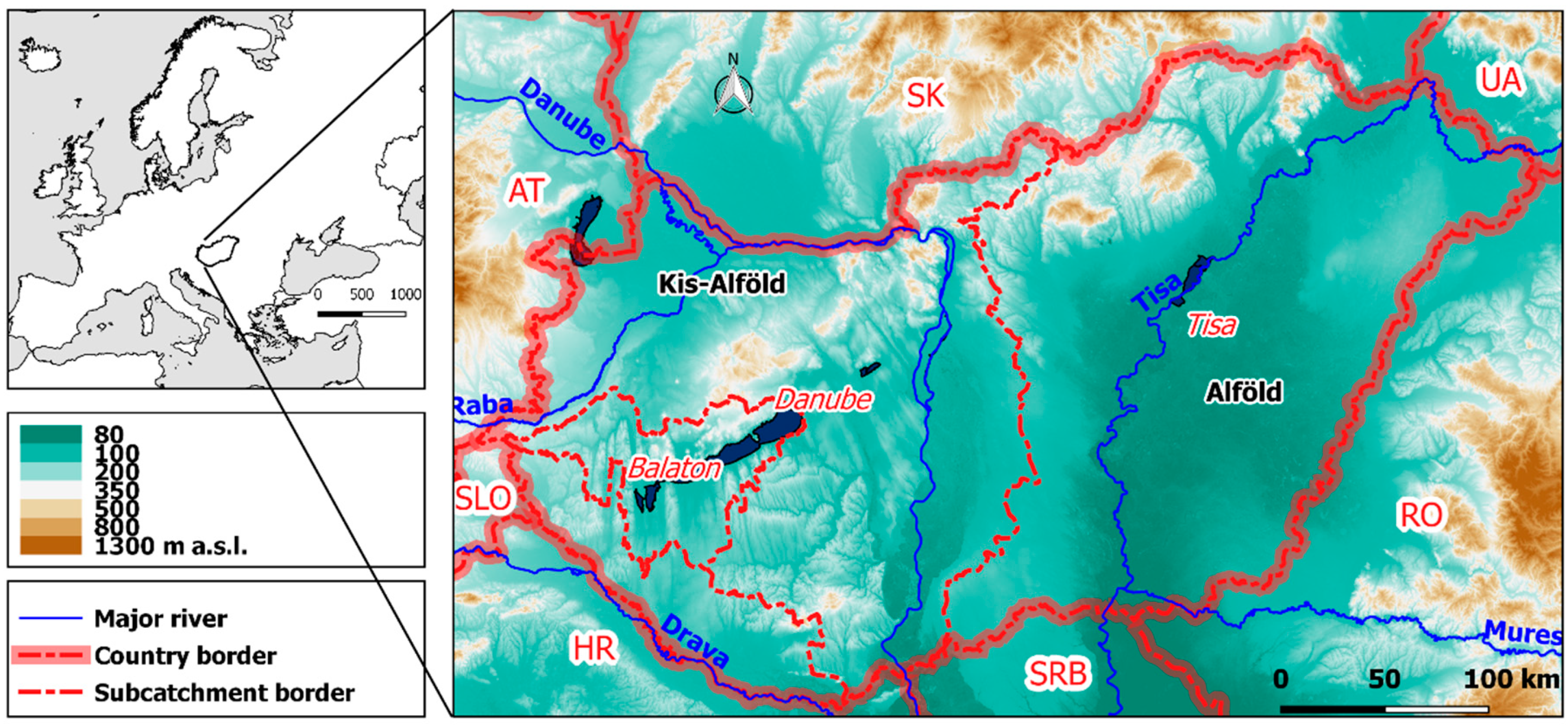
2.1. Study Area
2.2. Model Description
2.2.1. Flow Components/Water Balance
2.2.2. Subsurface Pathway of Nitrogen and Phosphorus
2.2.3. Nutrient Retention in Tributaries
2.2.4. Modeling Environment
2.3. Preparation of Model Input Data
2.3.1. Delineation of AUs and Calculation of Their Basic Characteristics
2.3.2. Runoff
2.3.3. Soil Loss and Nutrient Surplus
2.3.4. Nutrient Emission Pathways
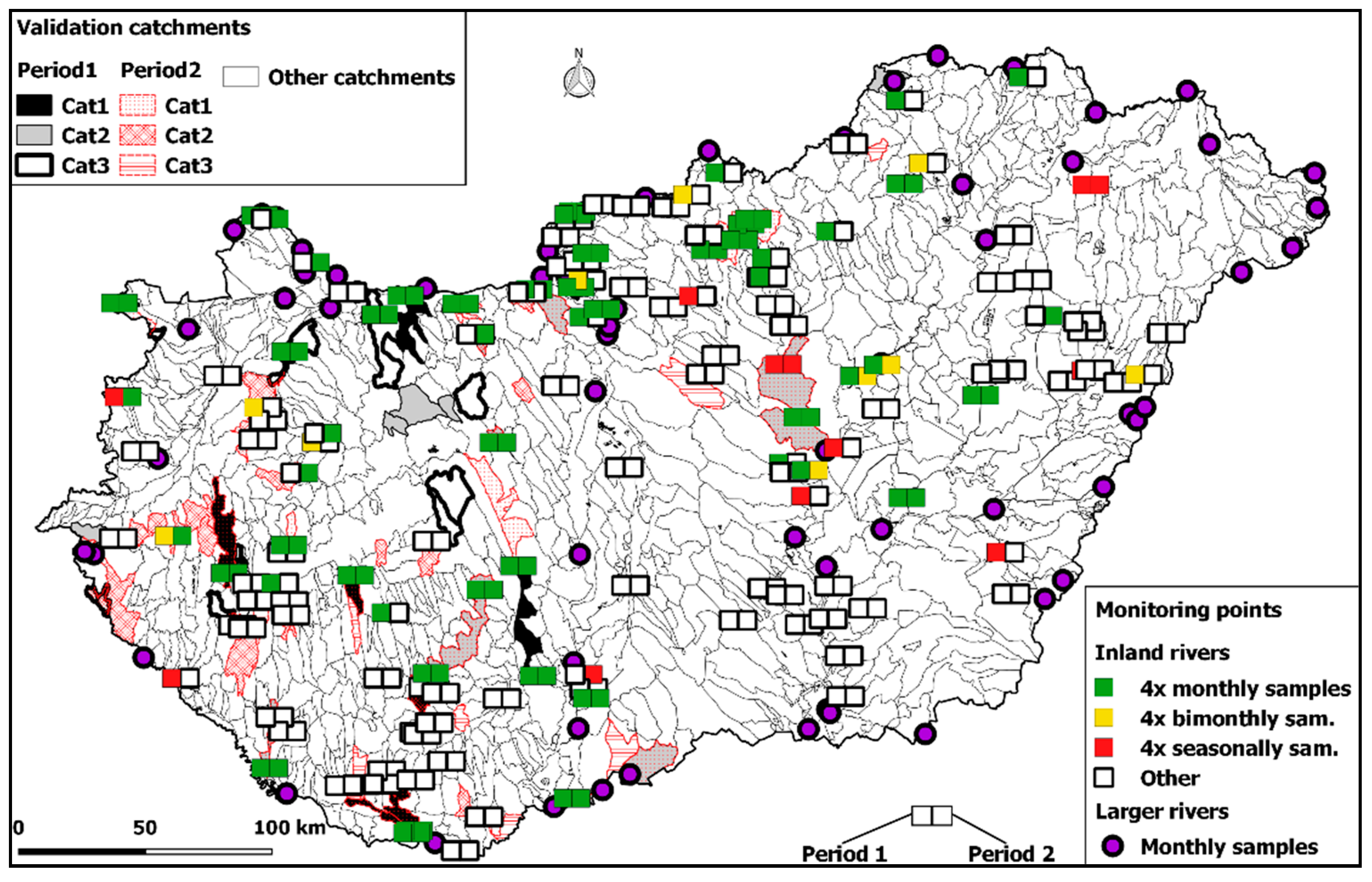
2.4. Water Quality Data Used for Calibration and Validation Purposes
2.4.1. Groundwater Well Data
2.4.2. Surface Water Quality
2.5. Adjustments of the Model Parameters and Structure
2.5.1. Runoff Separation with Digital Filter
2.5.2. Groundwater Nitrogen Concentration
2.5.3. River Retention
2.6. Model Validation
3. Results
3.1. Flow Components/Water Balance
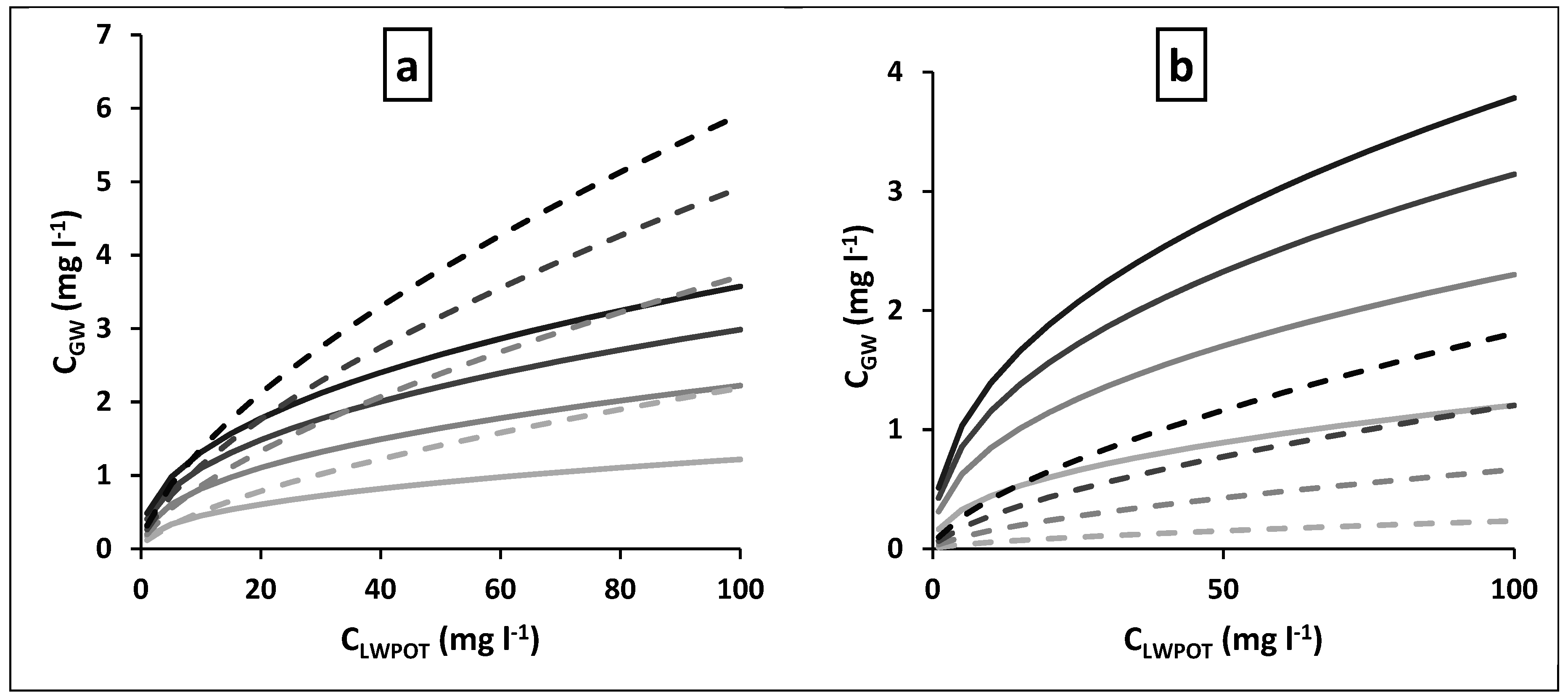
3.2. Groundwater Pathway of Nutrients
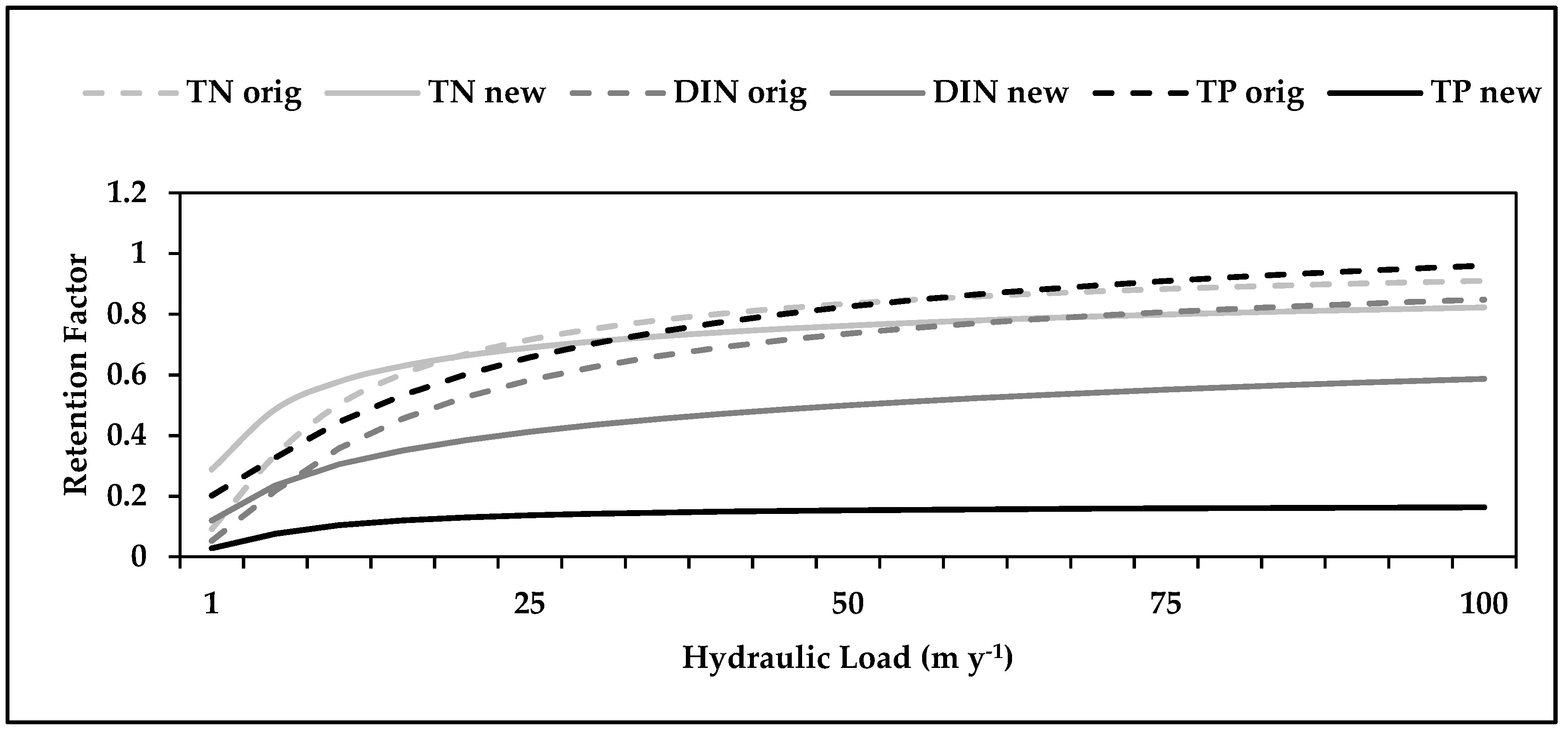
3.3. River Nutrient Retention
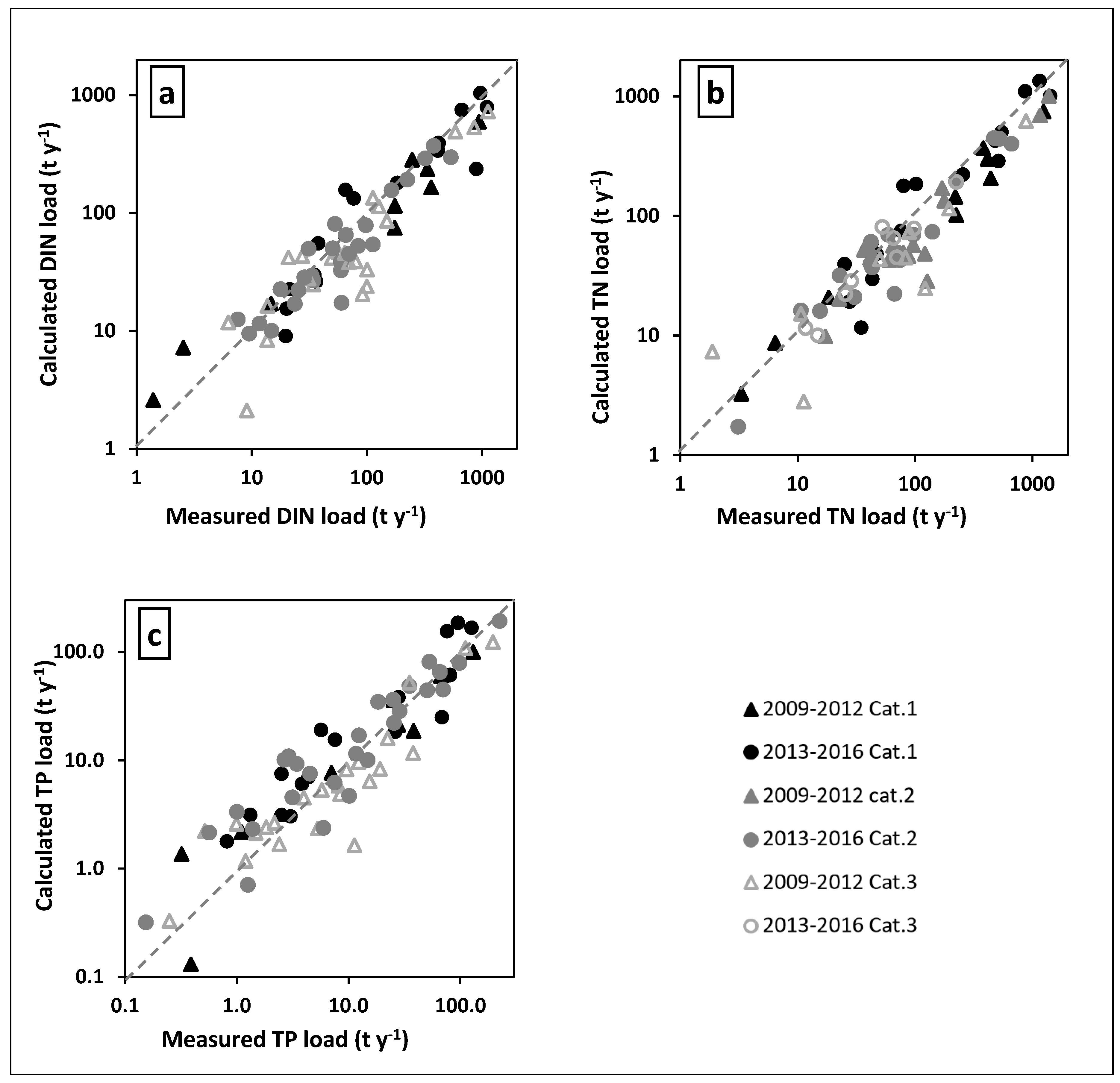
3.4. Model Validation
4. Discussion
4.1. Comparison of Nutrient Load Estimation Results on Gauged Catchments with Different Baseflow Separation Methods, Using the MONERIS Model
4.2. Subsurface Processes
4.3. River Retention
4.4. Model Validation in Context of the Literature
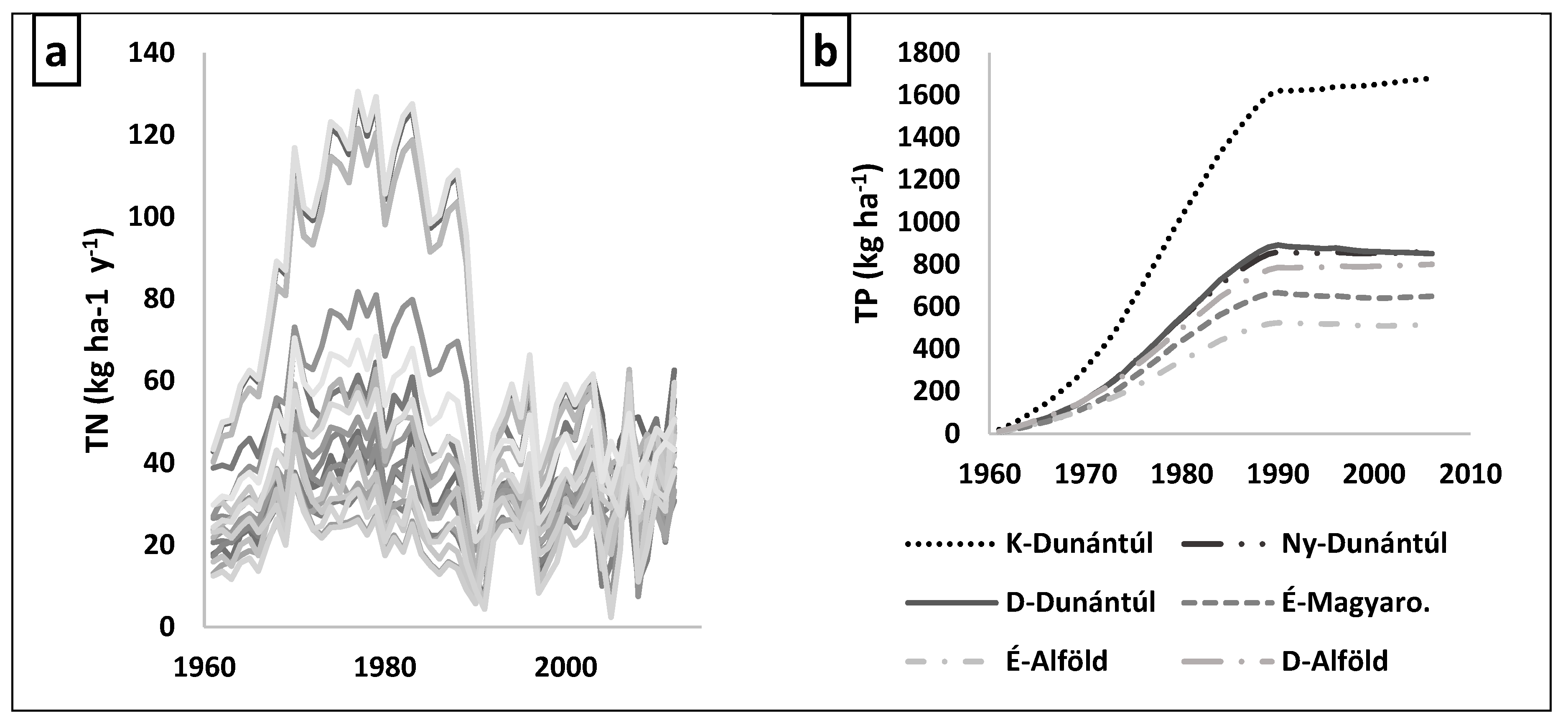
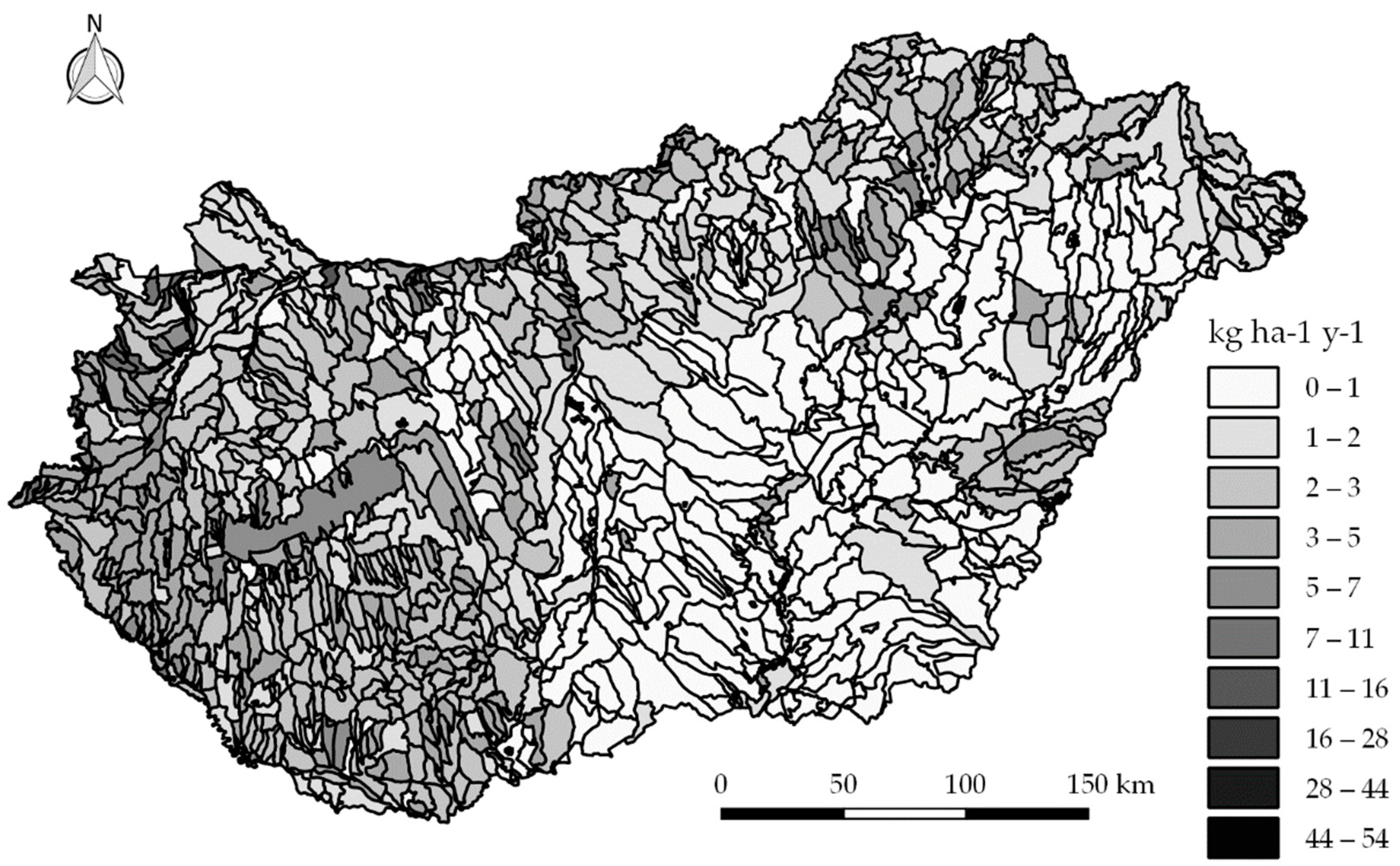
4.5. Local Emissions
4.6. Comparing Nutrient Emission Results with Results from Previous Studies
5. Conclusions
- the water balance equation with regard to the ratio of surface and subsurface runoff,
- the nitrogen retention parameters of the subsurface pathways (excluding the tile drainage),
- phosphorus concentrations in shallow groundwater,
- retention parameters for the retention in surface waters (rivers and lakes).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Input Data Tables
| Data Class | Detail | Data Source and Method | Source/Comment |
|---|---|---|---|
| Catchment area | GIS data for RBMP 2015 | [27] | |
| Land use data | Urban area, arable land areas in slope classes, grassland, woodland, shrubland, water surface area, mines, open areas, wetlands | Spatial statistics based on GIS analysis of CORINE LAND COVER grid | [28] |
| Soil classification | Sandy agricultural soils | The classification made based on national soil texture database | [33] |
| Loamy agricultural soils | |||
| Silty agricultural soils | |||
| Clayey agricultural soils | |||
| Fen agricultural soils | Agrotopo fen type | [27] | |
| Bog agricultural soils | Agrotopo bog type | ||
| Underlying geology | Unconsolidated rock areas near groundwater | Statistics were based on raster data, combining Agrotopo database and groundwater table depth from RBMP 1 in 2009 | [29] |
| Unconsolidated rock areas far groundwater | |||
| Solid rock areas with good porosity | Agrotopo based statistics | ||
| Solid rock areas with poor porosity | Agrotopo based statistics | [29] | |
| Average elevation | Based on a 50 m resolution hydrodem raster | [26] | |
| Average slope | Based on a 50 m resolution hydrodem raster | [26] |
| Data Class | Detail | Input Data and Method | Comment |
|---|---|---|---|
| Net total runoff | Average riverbed runoff in the modeled period | GDWM long term average runoff data | Corrected by rainfall ratios and measured discharge values, where available |
| Average temperature | Average water temperature for the modeled period | FEVISZ database [57] | |
| Yearly precipitation current | Average yearly precipitation in the model period | Precipitation monitoring network data operated by GDWM | Precipitation distribution by Thiessen polygon method. |
| Summer half-yearly precipitation current | Average summer half-year precipitation in the modeled period | Precipitation monitoring network data operated by GDWM | |
| Summer half-yearly precipitation long term | Average summer half-year precipitation in between 1981–2010 | Precipitation monitoring network data operated by GDWM | |
| Evapotranspiration | Mean annual evapotranspiration of the catchments | Country scale evapotranspiration distribution map 2001–2009 | Data source: [22] |
| Measured yearly TN load | Product of yearly average water quality data and yearly average of measured discharge data | FEVI database [57] | |
| Measured yearly DIN load | |||
| Measured yearly TP load | |||
| NH4-N, NO3-N deposition rate-current | Yearly average deposition rates of nutrients in different forms. (mg m−2 y−1) | EMEP European air quality data maps for each component | [38] |
| NH4-N, NO3-N deposition rate-long term | |||
| TP deposition rate | Default value by MONERIS | ||
| Soil loss from agricultural areas, grasslands and natural covered land | Average annual soil loss per land use (t ha−1 y−1) | JRC maps & USLE method [30] | K factor [58] K factor (2013–2016) [32] R Factor [59] |
| N-content of topsoil | Total N content of the topsoil (mg kg−1) | AGROTOPO [29] & DOSOREMI [60] databases | Calculated based on soil organic carbon content |
| N-surplus-current | Nitrogen surplus in the topsoil for the 2009–2012 and 2013–2016 periods (kg ha−1 y−1) | County scale statistics of N balance (average of 2009–2012 and 2013–2016 periods) [36] | |
| N-surplus-residence time | Nitrogen surplus in the topsoil for the average groundwater residence time of the catchments (kg ha−1 y−1) | County scale statistics of N balance for the 1961 to 2016 period [36] | |
| Accumulated P-surplus | Phosphorus surplus in the topsoil from 1961 to 2016 (kg ha−1 y−1) | Large regional, later county scale statistics of P balance for the entire country | Catchment average is calculated based on the country scale raster |
| External discharge | Yearly average river Q data at the upper boundary of a river transboundary sub-catchment Period: 2009–2012 and 2013–2016 | Data derived from the discharge data of the national river monitoring network | Some large rivers lack satisfactory Q and/or WQ data (Vág, Garam, Ipoly tributaries etc.) TNMN is used [61] |
| External TN load | Yearly average TN load at the upper boundary of a transboundary sub-catchment | FEVI database [57] | Some large rivers lack satisfactory Q and/or WQ data (Vág, Garam, Ipoly tributaries etc.), TNMN is used [61] |
| External DON load | Yearly average DON load at the upper boundary of a transboundary sub-catchment | FEVI database [57] | Some large rivers lack satisfactory Q and/or WQ data (Vág, Garam, Ipoly tributaries etc.) [61] |
| External TP load | Yearly average TN load at the upper boundary of a transboundary sub-catchment | FEVI database [57] | Some large rivers lack satisfactory Q and/or WQ data (Vág, Garam, Ipoly tributaries etc.) [61] |
References
- GDWM Hungarian Part of the Danube River Basin—River Basin Management Plan. Hungarian: A Duna-vízgyűjtő magyarországi része; Vízgyűjtőgazdálkodási Terv; General Directorate of Water Management: Budapest, Hungary, 2015; pp. 1–666. [Google Scholar]
- Kardos, M.K.; Clement, A. Prediciting small water courses ’ physico-chemical status with two multivariate statistical methods. Open Geosci. 2020, 12, 71–84. [Google Scholar] [CrossRef]
- Kardos, M.K.; Koncsos, L. A stochastic approach for regional-scale surface water quality modeling. Pollack Period. 2017, 12, 17–27. [Google Scholar] [CrossRef][Green Version]
- Jolánkai, G.; Bíró, I. Basis of Water Quality Protection with Special Regard of Systematic Ecohidrological Approaches (In Hungarian: Vízminőségvédelem alapjai különös tekintettel a rendszerszemléletű ökohidrológiai módszerekre); University Press, Eotvos Lorant Sci. Uni.: Budapest, Hungary, 1999. [Google Scholar]
- Borah, D.K.; Bera, M. Watershed-scale hydrologic and nonpoint-source pollution models: Review of mathematical bases. Trans. Am. Soc. Agric. Eng. 2003, 46, 1553–1566. [Google Scholar] [CrossRef]
- Novotny, V. Water Quality: Diffuse Pollution and Watershed Management, 2nd ed.; Novotny, V., Ed.; Wiley: Hoboken, NJ, USA, 2002; ISBN 978-0-471-39633-8. [Google Scholar]
- Radcliffe, D.E.; Freer, J.; Schoumans, O. Diffuse phosphorus models in the United States and Europe: Their usages, scales, and uncertainties. J. Environ. Qual. 2009, 38, 1956–1967. [Google Scholar] [CrossRef]
- Silgram, M.; Anthony, S.G.; Collins, A.L.; Stromqvist, J.; Bouraoui, F.; Schoumans, O.; Lo Porto, A.; Groenendijk, P.; Arheimer, B.; Mimikou, M.; et al. Evaluation of diffuse pollution model applications in EUROHARP catchments with limited data. J. Environ. Monit. 2009, 11, 554–571. [Google Scholar] [CrossRef]
- Malagó, A.; Venohr, M.; Vigiak, O.; Bouraoui, F.; Kovacs, A. Modelling Nutrient Pollution in the Danube River Basin : A Comparative Study of SWAT, MONERIS and GREEN Models; JRC Technical Reports EUR 27676 EN; JRC: Ispra, Italy, 2015; ISBN 9789279542398. [Google Scholar]
- Venohr, M.; Hirt, U.; Hofmann, J.; Opitz, D.; Gericke, A.; Wetzig, A.; Natho, S.; Neumann, F.; Hürdler, J.; Matranga, M.; et al. Modelling of nutrient emissions in river systems—MONERIS—Methods and background. Int. Rev. Hydrobiol. 2011, 96, 435–483. [Google Scholar] [CrossRef]
- Behrendt, H.; Kornmilch, M.; Opitz, D.; Schmoll, O.; Scholz, G. Estimation of the nutrient inputs into river systems—Experiences from German rivers. J. Mater. Cycles Waste Manag. 2002, 3, 107–117. [Google Scholar] [CrossRef]
- Behrendt, H.; Dannowski, R.; Deumlich, D.; Dolezal, F.; Kajewski, I.; Kornmilch, M.; Korol, R.; Mioduszewski, W.; Opitz, D.; Steidl, J.; et al. Point and Diffuse Emissions of Pollutants, Their Retention in the River System of the Odra and Scenario Calculations on Possible Changes; UBA Research report; Weißensee Verlag: Berlin, Germany, 2001; Project 298-28-299. [Google Scholar]
- De Lima Barros, A.M.; Do Carmo Sobral, M.; Gunkel, G. Modelling of point and diffuse pollution: Application of the Moneris model in the Ipojuca river basin, Pernambuco State, Brazil. Water Sci. Technol. 2013, 68, 357–365. [Google Scholar] [CrossRef]
- Schreiber, H.; Behrendt, H.; Constantinescu, L.T.; Cvitanic, I.; Drumea, D.; Jabucar, D.; Juran, S.; Pataki, B.; Snishko, S.; Zessner, M. Nutrient emissions from diffuse and point sources into the River Danube and its main tributaries for the period of 1998–2000—Results and problems. Water Sci. Technol. 2005, 51, 283–290. [Google Scholar] [CrossRef]
- Venohr, M.; Gericke, A. Further Development of the MONERIS Model with Particular Focus on the Application in the Danube Basin; Technical Report, JOINTISZA Project, Project Code: DTP1-152-2.1; International Commission for the Protection of the Danube River: Vienna, Austria, 2015. [Google Scholar]
- Kovács, Á.; Honti, M. Estimation of diffuse phosphorus emissions at small catchment scale by GIS-based pollution potential analysis. Desalination 2008, 226, 72–80. [Google Scholar] [CrossRef]
- Zessner, M.; Kovács, Á.; Schilling, C.; Hochedlinger, G.; Gabriel, O.; Natho, S.; Thaler, S.; Windhofer, G. Enhancement of the MONERIS Model for Application in Alpine Catchments in Austria. Int. Rev. Hydrobiol. 2011, 96, 541–560. [Google Scholar] [CrossRef]
- Stelczer, K. Hydrological Basics of Water Resource Management (In Hungarian: A vízkészletgazdálkodás hidrológiai alapjai); ELTE Eötvös Kiadó: Budapest, Hungary, 2000; ISBN 9634632491. [Google Scholar]
- Clement, A.; Somlyódy, L. Vízminőség-szabályozás. In Magyarország vízgazdálkodása: Helyzetkép és stratégiai feladatok; Somlyódy, L., Ed.; MTA: Budapest, Hungary, 2011; pp. 169–206. ISBN 978-963-508-608-5. [Google Scholar]
- Bihari, Z.; Babolcsai, G.; Bartholy, J.; Ferenczi, Z. Climate. In The National Atlas of Hungary—Natural Environment; Kocsis, K., Ed.; MTA CSFK Geographical Institute: Budapest, Hungary, 2018; ISBN 978-963-9545-56-4. [Google Scholar]
- Mozsgai, K.; Podmaniczky, L.; Skutai, J.; Deák, J.; Clement, A.; Simonffy, Z. Assessing Achievements and Impacts on Water Quality of Hungarian Rural Development Program; Mechanical Engineering Letters, Szent István University: Gödöllö, Hungary, 2019. [Google Scholar]
- Venohr, M.; Hirt, U.; Opitz, D.; Gericke, A.; Wetzig, A.; Ortelbach, K.; Natho, S.; Neumann, F. The Model System MONERIS—Version 2.14.1vba—Manual; Leibniz-Institute of Freshwater Ecology and Inland Fisheries: Berlin, Germany, 2009; pp. 1–118. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 1 January 2019).
- Szilagyi, J.; Kovacs, A. A calibration-free evapotranspiration mapping technique for spatially-distributed regional-scale hydrologic modeling. J. Hydrol. Hydromech. 2011, 59, 118–130. [Google Scholar] [CrossRef]
- Szilágyi, J.; Kovács, Á. Complementary-relationship-based evapotranspiration mapping (cremap) technique for Hungary. Period. Polytech. Civ. Eng. 2010, 54, 95–100. [Google Scholar] [CrossRef]
- GDWM. HydroDEM—Hydrologically Corrected Digital Elevation Model of Hungary; Digital Data; General Directorate of Water Management: Budapest, Hungary, 2014. [Google Scholar]
- GDWM. Spatial Database of River Water Bodies, Lake Water Bodies and Their Watershed Areas (In Hungarian: Víztestek és víztest-vízgyűjtők téradat állománya. Az OVGT digitális melléklete); General Directorate of Water Management: Budapest, Hungary, 2015. [Google Scholar]
- Copernicus Land Monitoring Service Corine Land Cover (CLC) 2012, Version 18. Available online: https://land.copernicus.eu/pan-european/corine-land-cover/clc-2012 (accessed on 1 January 2018).
- Research Institute for Soil and Agricultural Chemistry(RIISAC). Agrotopo Database (In Hungarian: Agrotopográfiai Adatbázis); RIISAC: Budapest, Hungary, 1991. [Google Scholar]
- Pásztor, L.; Laborczi, A.; Takács, K.; Szatmári, G.; Dobos, E.; Illés, G.; Bakacsi, Z.; Szabó, J. Compilation of novel and renewed, goal oriented digital soil maps using geostatistical and data mining tools. Hung. Geogr. Bull. 2015, 64, 49–64. [Google Scholar] [CrossRef]
- Szalay, M. Quantitative Characterization of Surface Waters—Small Water Courses. RBMP Background Document No 2.3 (In Hungarian: A felszíni vizek mennyiségi jellemzése—Kisvízi készlet—OVGT 2.3 háttéranyag); National Water Directorate (OVF): Budapest, Hungary, 2009. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting rainfall erosion losses—A guide to conservation planning. USDA Agric. Handb. 1978, 537, 1. [Google Scholar]
- Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]
- Pásztor, L.; Waltner, I.; Centeri, C.; Belényesi, M.; Takács, K. Soil erosion of Hungary assessed by spatially explicit modelling. J. Maps 2016, 12, 407–414. [Google Scholar] [CrossRef]
- Jolánkai, Z.; Muzelák, B.; Kardos, M.K. RBMP Background Document No 3-1: Modeling of Nutrient Loads in Surface Water Bodies—Application of the MONERIS Model to Estimate Diffuse Nutrient Emissions to Water Bodies in Hungary (In Hungarian: Felszíni víztestek tápanyagterhelésének modellezése); General Directorate of Water Management: Budapest, Hungary, 2015. [Google Scholar]
- Deák, J. Assessment of the RDP Impact Indicators on National Level in the Field of Water Quality. In Ex-Post Revision of the Rural Development Programme; Final Report; Consortium of AAM-AKI-Collectivo: Budapest, Hungary, 2016. (In Hungarian) [Google Scholar]
- Kremer, A.M. Methodology and Handbook Eurostat/OECD Nutrient Budgets; Version 1.02; European Comission Eurostat: Luxemburg, 2013; pp. 1–112. [Google Scholar]
- EMEP The European Environmental Monitoring and Evaluation Programme. Available online: https://www.emep.int/mscw/index.html (accessed on 15 March 2015).
- GDWM Wastewater Load Data. Supplement No. 3-1 to the Hungarian River Basin Management Plan. (In Hungarian: 3.1 melléklet az Országos Vízgyűjtőgazdálkodási Tervek 2015. évi felülvizsgálatához: Szennyvízterhelés jellemzői: Kommunális és ipari szennyvízkibocsátás. Available online: https://www.vizugy.hu/vizstrategia/documents/10B9EE2E-D889-4C94-815D-5CB2D53C846A/3_1_melleklet_szennyvizterheles.xls (accessed on 1 June 2018).
- Ács, T.; Simonffy, Z. A new deterministic method for groundwater mapping using a digital elevation model. Water Sci. Technol. Water Supply 2013, 13, 1146–1153. [Google Scholar] [CrossRef]
- Jolánkai, Z.; Koncsos, L. Base flow index estimation on gauged and ungauged catchments in Hungary using digital filter, multiple linear regression and artificial neural networks. Period. Polytech. Civ. Eng. 2018, 62, 363–372. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and ground water recharge from streamflow records. J. Am. Water Resour. Assoc. 1999, 35, 13353–13366. [Google Scholar] [CrossRef]
- Ladson, L.S.; Fox, R.L.; Ratner, M.W. Nonlinear optimization using the generalized reduced gradient method. Rev. française d’automatique, informatique, Rech. opérationnelle. Rech. opérationnelle 1974, 8, 73–104. [Google Scholar]
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A trust region method based on interior point techniques for nonlinear programming. Math. Program. Ser. B 2000, 89, 149–185. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, USA, 1988. [Google Scholar]
- Vadas, P.A.; Kleinman, P.J.A.; Sharpley, A.N.; Turner, B.L. Relating soil phosphorus to dissolved phosphorus in runoff: A single extraction coefficient for water quality modeling. J. Environ. Qual. 2005, 34, 572–580. [Google Scholar] [CrossRef] [PubMed]
- Søndergaard, M.; Jensen, J.P.; Jeppesen, E. Role of sediment and internal loading of phosphorus in shallow lakes. Hydrobiologia 2003, 506–509, 135–145. [Google Scholar] [CrossRef]
- Clement, A. Modeling the trophic response of a shallow lake following external load reduction: A case study. In Proceedings of the International Association of Theoretical and Applied Limnology; Williams, W., Ed.; E Schweizerbart’sche Verlagsbuchhandlung: Stuttgart, Germany, 2001; Volume 27, pp. 819–822. [Google Scholar]
- Reddy, K.R.; Kadlec, R.H.; Flaig, E.; Gale, P.M. Phosphorus retention in streams and wetlands: A review. Crit. Rev. Environ. Sci. Technol. 1999, 29, 83–146. [Google Scholar] [CrossRef]
- Clement, A.; Somlyódy, L.; Koncsos, L. Modeling the phosphorus retention of the Kis-Balaton upper reservoir. Water Sci. Technol. 1998, 37, 113–120. [Google Scholar] [CrossRef]
- Rode, M.; Suhr, U. Uncertainties in selected surface water quality data. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 2991–3021. [Google Scholar] [CrossRef]
- Horowitz, A.J. An evaluation of sediment rating curves for estimating suspended sediment concentrations for subsequent flux calculations. Hydrol. Process. 2003, 17, 3387–3409. [Google Scholar] [CrossRef]
- Moatar, F.; Meybeck, M. Compared performances of different algorithms for estimating annual nutrient loads discharged by the eutrophic River Loire. Hydrol. Process. 2005, 19, 429–444. [Google Scholar] [CrossRef]
- Webb, B.W.; Phillips, J.M.; Walling, D.E.; Littlewood, I.G.; Watts, C.D.; Leeks, G.J.L. Load estimation methodologies for British rivers and their relevance to the LOIS RACS(R) programme. Sci. Total Environ. 1997, 194–195, 379–389. [Google Scholar] [CrossRef]
- Walling, D.E.; Webb, B.W.; Woodward, J.C. Some sampling considerations in the design of effective strategies for monitoring sediment-associated transport. Eros. Sediment Monit. Program. River Basins. Proc. Int. Symp. Oslo 1992, 1992, 279–288. [Google Scholar]
- Behrendt, H.; Dannowski, R. Nutrients and Heavy Metals in the Odra River System; Behrendt, H., Dannowski, R., Eds.; Weissensee Verlag Ökologie: Stuttgart, Germany, 2005. [Google Scholar]
- Agricultural Ministry of Hungary. Surface Water Quality Database of Hungary (In Hungarian: OKIR-FEVISz: Országos Környezetvédelmi Információs Rendszer, Felszíni Vízminőség Szakmodul); Agricultural Ministry of Hungary: Budapest, Hungary, 2015. [Google Scholar]
- Panagos, P.; Meusburger, K.; Alewell, C.; Montanarella, L. Soil erodibility estimation using LUCAS point survey data of Europe. Environ. Model. Softw. 2012, 30, 143–145. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadić, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef] [PubMed]
- Pásztor, L.; Laborczi, A.; Takács, K.; Szatmári, G.; Fodor, N.; Illés, G.; Farkas-Iványi, K.; Bakacsi, Z.; Szabó, J. Compilation of Functional Soil Maps for the Support of Spatial Planning and Land Management in Hungary; Elsevier Inc.: Amsterdam, The Netherlands, 2017; ISBN 9780128052013. [Google Scholar]
- ICPDR Transnational Monitoring Network Data. Available online: https://www.icpdr.org/main/activities-projects/tnmn-transnational-monitoring-network (accessed on 15 March 2015).


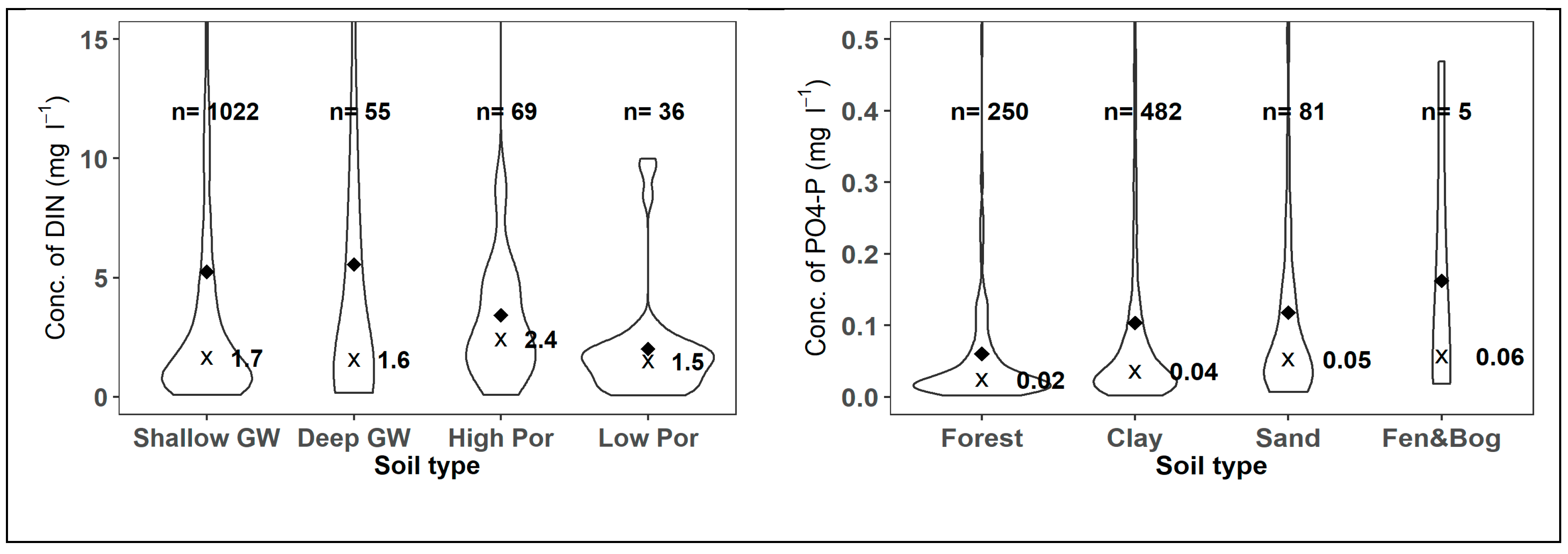
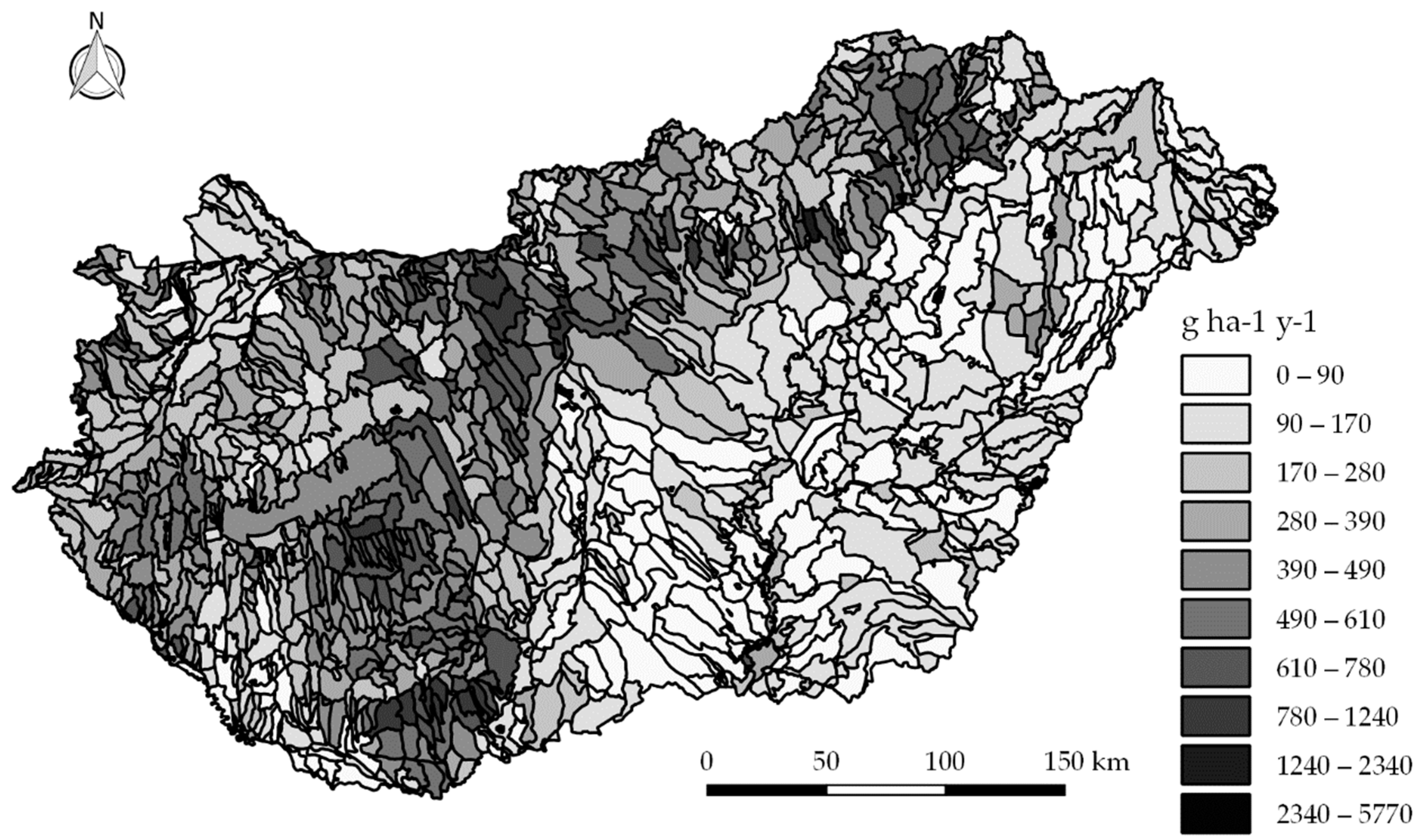
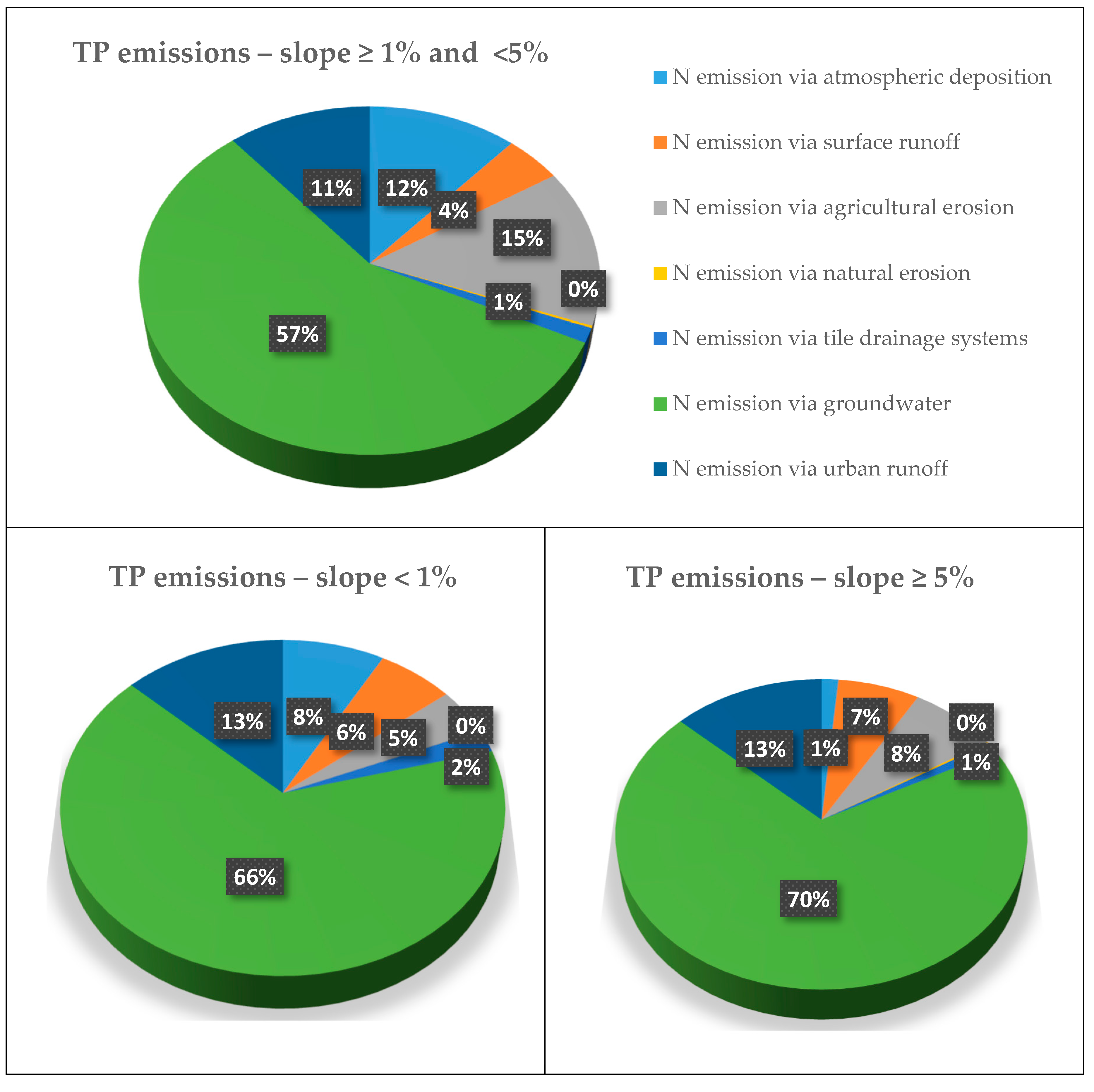
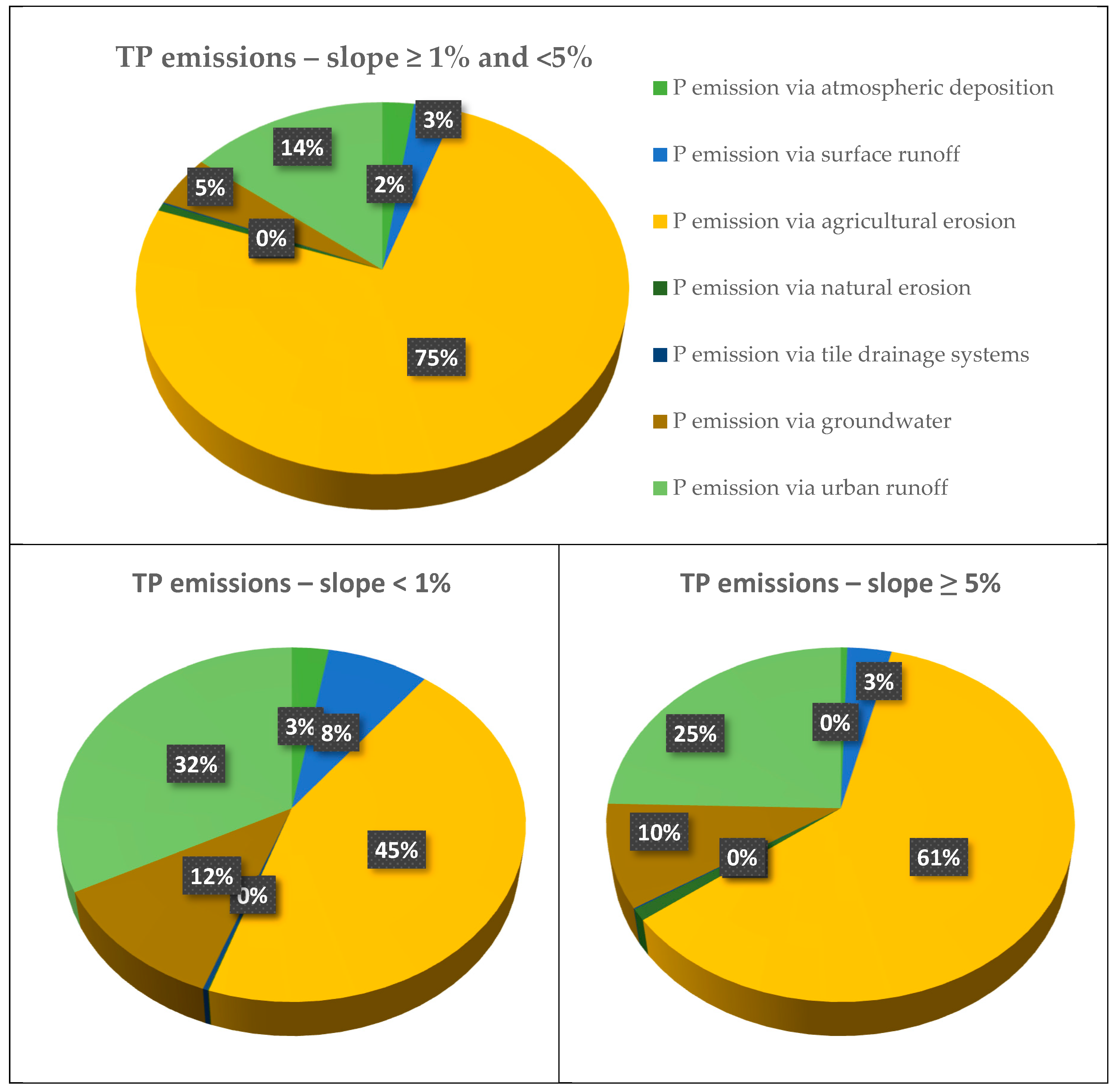
| Well Category for Nitrogen | Groundwater Depth | Soil Geology | Number of Wells |
|---|---|---|---|
| Unconsolidated rock, shallow groundwater | <3 m * | any other | 1022 |
| Unconsolidated rock, deep groundwater | >3 m * | any other | 55 |
| Solid rock, high porosity | any | limestone | 69 |
| Solid rock, impermeable | any | granite, andesite | 36 |
| Well Category for Phosphorus | Land Cover | Soil Texture | Soil Physical Category | Number of Wells |
|---|---|---|---|---|
| Sandy soils | agricultural | SL, LS, or sand | not peat or mull | 81 |
| Clayey soils | agricultural | any other | not peat or mull | 482 |
| Fen & bog soils | any | any | peat or mull | 5 |
| Woodland & open land | forest & seminatural | any | not peat or mull | 250 |
| Category | Yearly Sample Number | Per. 1 | Per. 2 | Total (w/o Overlap) |
|---|---|---|---|---|
| Cat. 1 | 10+ | 8 | 16 | 20 |
| Cat. 2 | 6–9 | 16 | 18 | 32 |
| Cat. 3 | 4–5 | 9 | 9 | 18 |
| Cat. 1–3 | 33 | 43 | 62 |
| Catchment | Total | Surface Runoff | GW Flow Share | ||||
|---|---|---|---|---|---|---|---|
| Catchment Name | Area | Slope | Runoff | MON | DF | MON | DF |
| (km2) | (%) | (m3 s−1) | (m3 s−1) | (m3 s−1) | (-) | (-) | |
| Arany Creek | 36 | 1.9 | 0.33 | 0.022 | 0.043 | 0.85 | 0.70 |
| Kenyérmezei Creek | 125 | 11.3 | 0.15 | 0.000 | 0.000 | 0.79 | 0.76 |
| Kígyós Channel | 594 | 0.8 | 0.25 | 0.010 | 0.002 | 0.73 | 0.78 |
| Tapolca Creek | 51 | 4.1 | 0.28 | 0.061 | 0.000 | 0.84 | 0.85 |
| Tetves Creek | 88 | 8.2 | 0.18 | 0.022 | 0.034 | 0.84 | 0.69 |
| Torna Creek | 176 | 7.2 | 0.56 | 0.099 | 0.035 | 0.84 | 0.82 |
| Únyi Creek | 172 | 9.2 | 0.29 | 0.019 | 0.077 | 0.73 | 0.62 |
| Villány–Pogányi c. | 202 | 5.6 | 0.26 | 0.054 | 0.077 | 0.80 | 0.62 |
| Zagyva Creek (upper) | 168 | 14.1 | 0.94 | 0.112 | 0.439 | 0.84 | 0.48 |
| Average | 179 | 6.9 | 0.36 | 0.04 | 0.08 | 0.81 | 0.70 |
| Process/Constant Name | Soil Category | Units | Original | Adjusted |
|---|---|---|---|---|
| Subsurface Nitrogen | ||||
| Nitrogen constant 1 (kn1) | UC rock, shallow GW | - | 2752 | 84.24 |
| UC rock, deep GW | - | 68,560 | 7917 | |
| Solid rock, high porosity | - | 60.23 | 67.33 | |
| Solid rock, poor porosity | - | 78.54 | 99,787 | |
| Nitrogen constant 2 (kn2) | UC rock, shallow GW | - | −1.540 | −1.216 |
| UC rock, deep GW | - | −1.959 | −3.750 | |
| Solid rock, high porosity | - | −0.903 | −1.124 | |
| Solid rock, poor porosity | - | −0.662 | −2.747 | |
| Denitrification in topsoil (kn3) | any | - | 0.6368 | 0.4340 |
| Subsurface Phosphorus | ||||
| P conc. in groundwater | Sandy agricultural soils | mg L−1 | 0.10 | 0.05 |
| Clayey agricultural soils | mg L−1 | 0.03 | 0.03 | |
| Fen agricultural soils | mg L−1 | 0.10 | 0.10 | |
| Bog agricultural soils | mg L−1 | 0.50 | 0.50 | |
| Woodland and open areas | mg L−1 | 0.02 | 0.02 | |
| River Retention | ||||
| TN constant 1 (kr1) | - | 4.74 | 78.8 | |
| TN constant 2 (kr2) | - | 0.067 | −0.31 | |
| TN constant 3 (kr3) | - | −1 | −0.53 | |
| DIN constant 1 (kr4) | - | 8.58 | 14.39 | |
| DIN constant 2 (kr5) | - | 0.067 | −0.06 | |
| DIN constant 3 (kr6) | - | −1 | −0.51 | |
| TP constant 1 (kr7) | - | 5.07 | 200 | |
| TP constant 2 (kr8) | - | −1 | −9.69 | |
| TP constant 3 (kr9) | - | 25.74 | 4.87 | |
| TP constant 4 (kr10) | - | −1 | −0.89 |
| R2 | Absolute Relative Error | |||
|---|---|---|---|---|
| Original | Adjusted | Original | Adjusted | |
| Cat. 1 | 0.78 | 0.95 | 52% | 21% |
| Cat. 2 | 0.74 | 0.92 | 23% | 31% |
| Cat. 3 | 0.86 | 0.98 | 82% | 17% |
| Cat. 1–3 | 0.48 | 0.95 | 46% | 25% |
| Per. 1 | Per. 2 | Per. 1 + Per. 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Category | DIN | TN | TP | DIN | TN | TP | DIN | TN | TP |
| Square of Pearson correlation coefficient (R2) | |||||||||
| Cat. 1 | 0.93 | 0.94 | 0.95 | 0.77 | 0.89 | 0.78 | 0.79 | 0.85 | 0.74 |
| Cat. 2 | 0.99 | 0.98 | 0.93 | 0.89 | 0.94 | 0.85 | 0.96 | 0.97 | 0.89 |
| Cat. 3 | 0.98 | 0.99 | 0.85 | 0.94 | 0.94 | 0.66 | 0.97 | 0.98 | 0.72 |
| Cat. 1–3 | 0.96 | 0.97 | 0.91 | 0.86 | 0.92 | 0.76 | 0.9 | 0.93 | 0.78 |
| Mean relative error | |||||||||
| Cat. 1 | 0.76 | 0.35 | 1.18 | 0.49 | 0.48 | 1.04 | 0.6 | 0.44 | 1.09 |
| Cat. 2 | 0.48 | 0.39 | 1.01 | 0.41 | 0.35 | 1.41 | 0.44 | 0.37 | 1.25 |
| Cat. 3 | 3.13 | 1.07 | 4.36 | 0.37 | 0.26 | 1.14 | 2.23 | 0.78 | 3.19 |
| Cat. 1–3 | 1.45 | 0.6 | 2.18 | 0.43 | 0.36 | 1.2 | 1.09 | 0.53 | 1.84 |
| Surface Runoff | Groundwater | Total Diffuse | |||
|---|---|---|---|---|---|
| (t y−1) | Ratio to Total (%) | (t y−1) | Ratio to Total (%) | (t y−1) | |
| Total nitrogen | |||||
| Original | 16 | 3.4 | 242 | 52 | 468 |
| Adjusted | 52 | 12 | 185 | 41 | 447 |
| Difference (%) | 69 | 31 | 4.7 | ||
| Total phosphorus | |||||
| Original | 1.6 | 2.6 | 5.7 | 9.0 | 63 |
| Adjusted | 5.4 | 8.3 | 4.1 | 6.3 | 65 |
| Difference (%) | 70 | 36 | 3.5 | ||
| AD | SR | AE | NE | TD | GW | UR | Total Diffuse | Point Source | Total | |
|---|---|---|---|---|---|---|---|---|---|---|
| Total nitrogen loads (1000 t y−1) | ||||||||||
| ICPDR Per. 1 | 1605 | 3403 | 1006 | 483 | 16,142 | 2527 | 25,168 | 7852 | 33 | |
| HUN Per. 1 | 1646 | 894 | 3535 | 12 | 555 | 13,332 | 1876 | 21,849 | 10,314 | 32.2 |
| HUN Per. 2 | 1701 | 980 | 4597 | 18 | 314 | 11,053 | 2147 | 20,809 | 8629 | 29.5 |
| Differences (%) | ||||||||||
| HUN–ICPDR | 3 | −74 | 253 | 15 | −17 | −26 | −13 | 31 | −2 | |
| Per. 2–Per. 1 | 3 | 10 | 30 | 50 | −43 | −17 | 14 | −5 | −16 | −8 |
| Total phosphorus loads (t y−1) | ||||||||||
| ICPDR Per. 1 | 0 | 19.1 | 773 | 3.5 | 585 | 541 | 1922 | 1062 | 2986 | |
| HUN Per. 1 | 60 | 127 | 1083 | 7 | 4 | 270 | 460 | 2010 | 1253 | 3264 |
| HUN Per. 2 | 60 | 123 | 1279 | 11 | 5 | 282 | 534 | 2294 | 1066 | 3360 |
| Differences (%) | ||||||||||
| HUN–ICPDR | 565 | 41 | 14 | −54 | −15 | 5 | 18 | 9 | ||
| Per. 2–Per. 1 | 0 | −3 | 18 | 57 | 25 | 4 | 16 | 14 | −15 | 3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jolánkai, Z.; Kardos, M.K.; Clement, A. Modification of the MONERIS Nutrient Emission Model for a Lowland Country (Hungary) to Support River Basin Management Planning in the Danube River Basin. Water 2020, 12, 859. https://doi.org/10.3390/w12030859
Jolánkai Z, Kardos MK, Clement A. Modification of the MONERIS Nutrient Emission Model for a Lowland Country (Hungary) to Support River Basin Management Planning in the Danube River Basin. Water. 2020; 12(3):859. https://doi.org/10.3390/w12030859
Chicago/Turabian StyleJolánkai, Zsolt, Máté Krisztián Kardos, and Adrienne Clement. 2020. "Modification of the MONERIS Nutrient Emission Model for a Lowland Country (Hungary) to Support River Basin Management Planning in the Danube River Basin" Water 12, no. 3: 859. https://doi.org/10.3390/w12030859
APA StyleJolánkai, Z., Kardos, M. K., & Clement, A. (2020). Modification of the MONERIS Nutrient Emission Model for a Lowland Country (Hungary) to Support River Basin Management Planning in the Danube River Basin. Water, 12(3), 859. https://doi.org/10.3390/w12030859





