Assessment of Flood Inundation by Coupled 1D/2D Hydrodynamic Modeling: A Case Study in Mountainous Watersheds along the Coast of Southeast China
Abstract
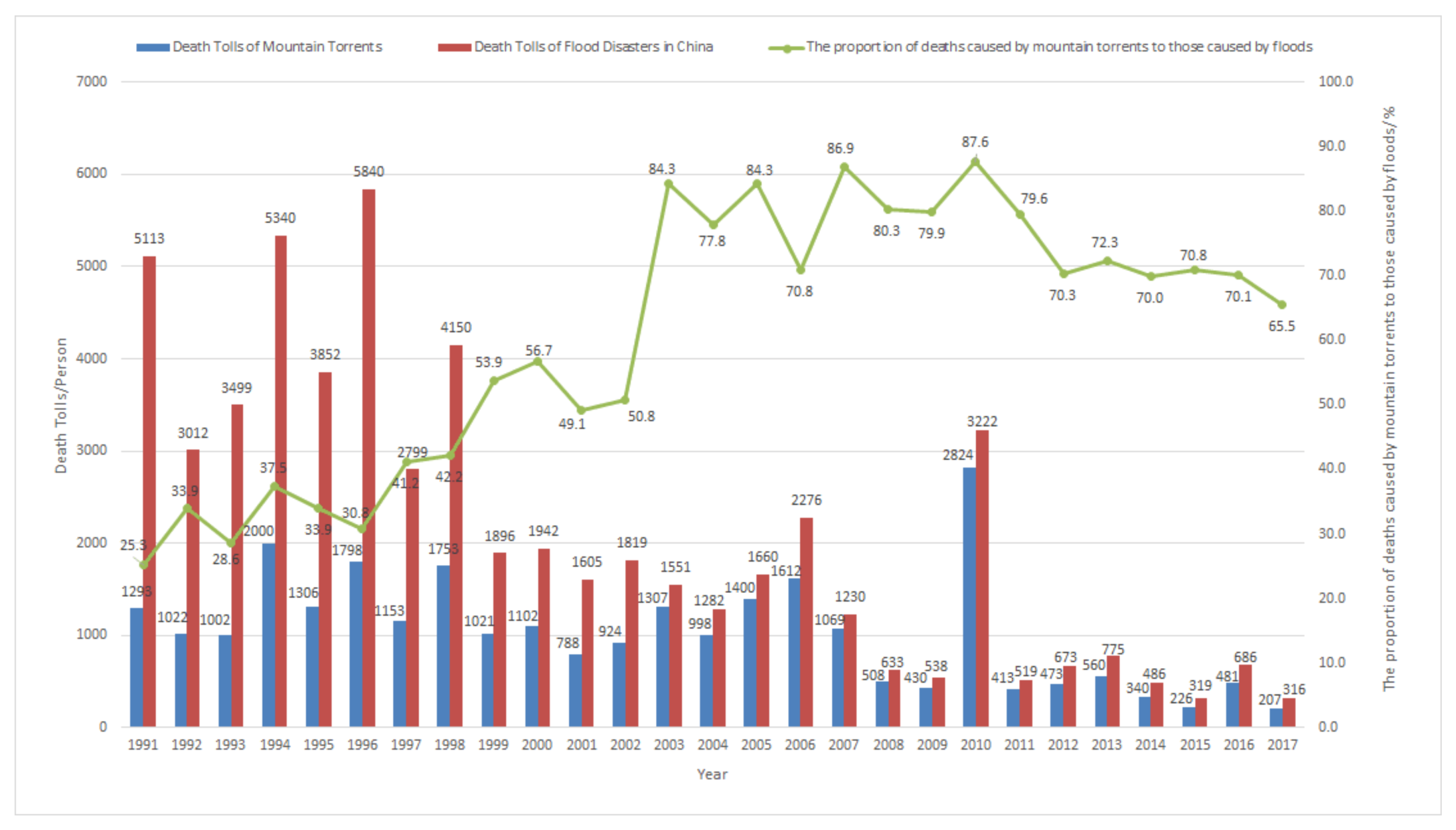
1. Introduction
2. 1D/2D Real-Time Dynamic Coupling Flood Model
2.1. 1D River Hydraulic Model
2.2. 2D Flood-Routing Hydraulic Model
2.3. Modified Models of Dry Water Depth and Wet Water Depth Theory
2.4. Coupling of 1D and 2D Hydraulic Models
2.4.1. Time Coupling of 1D and 2D Hydraulic Models
2.4.2. Spatial Coupling of 1D and 2D Hydraulic Models
3. Data and Methods
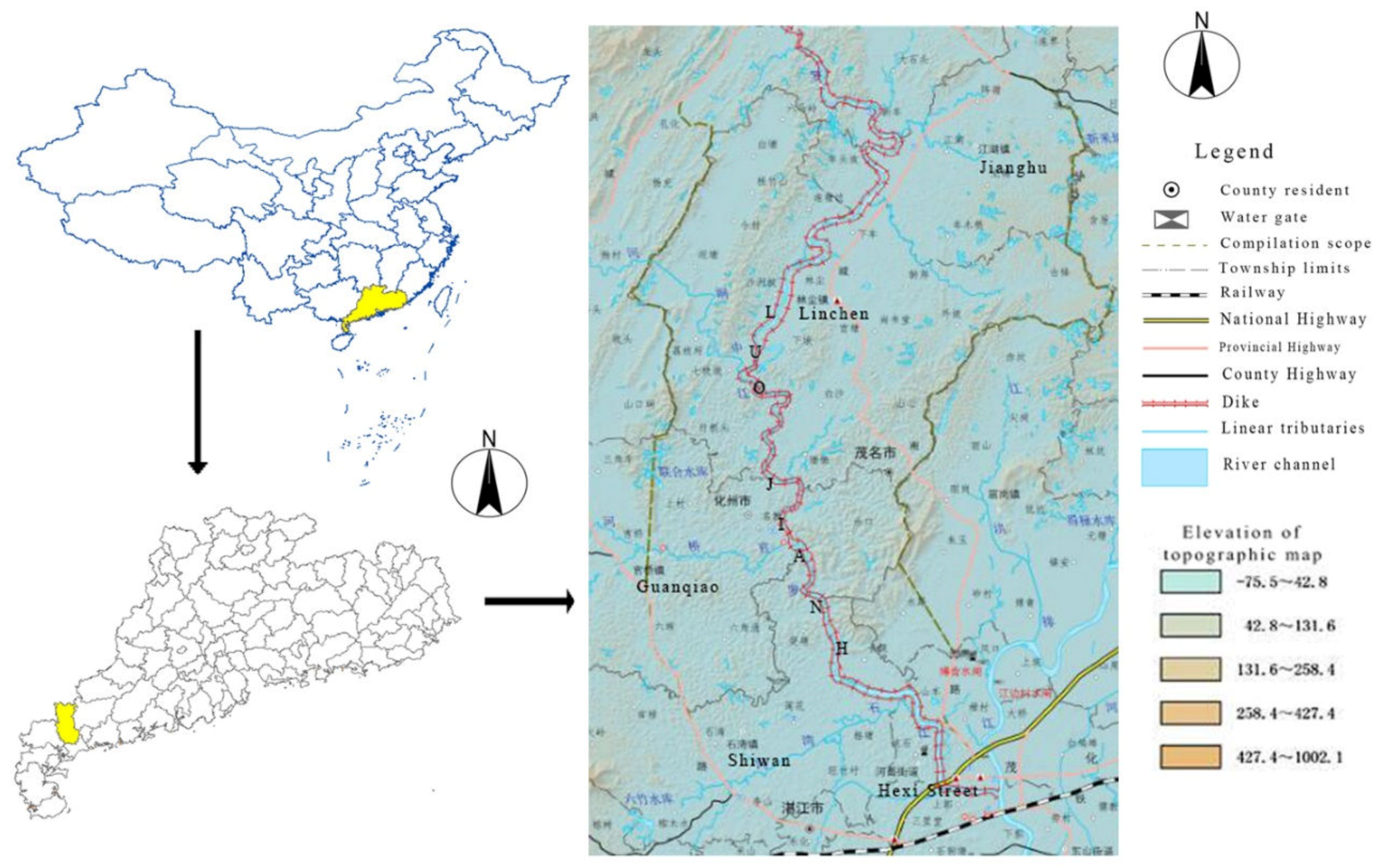
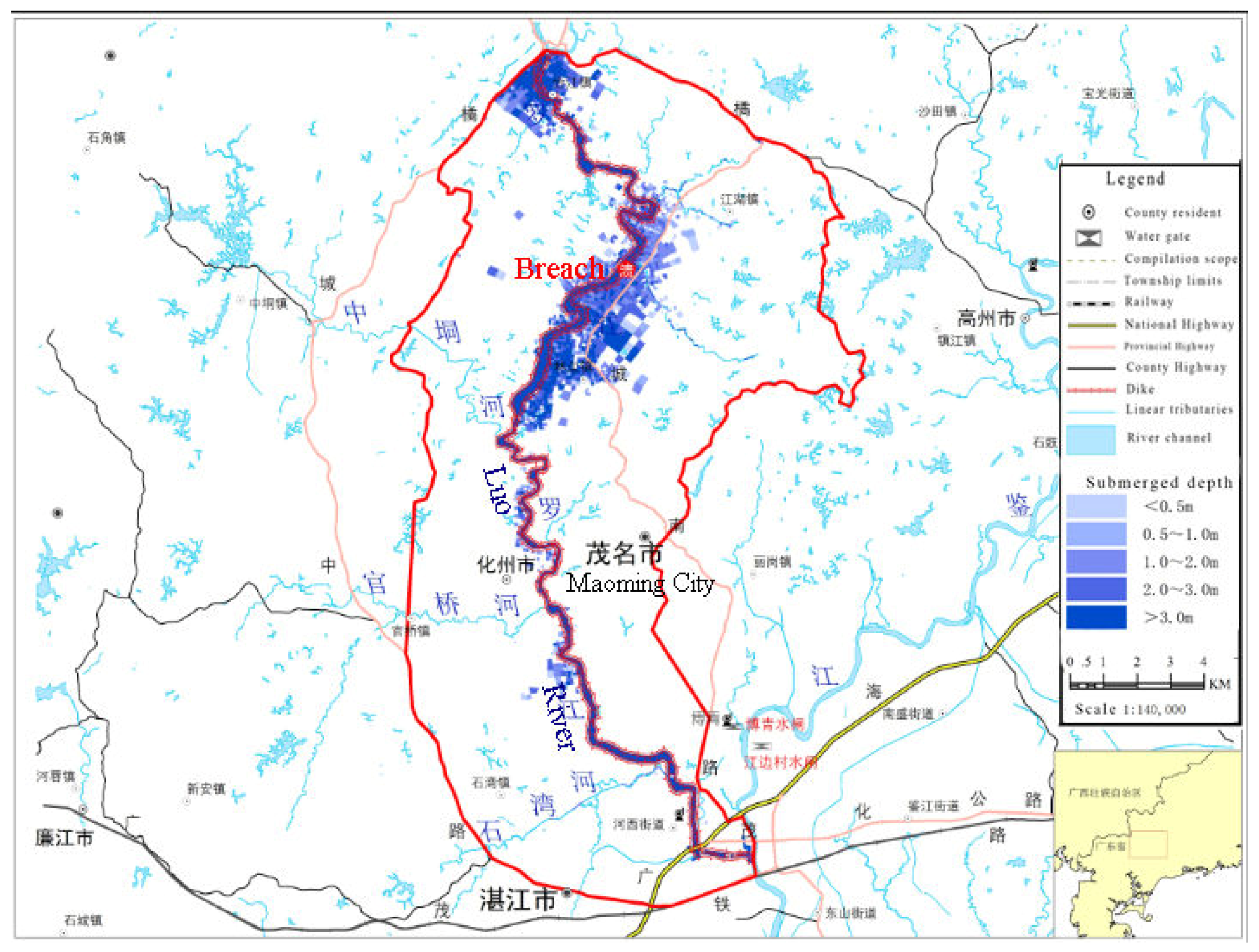
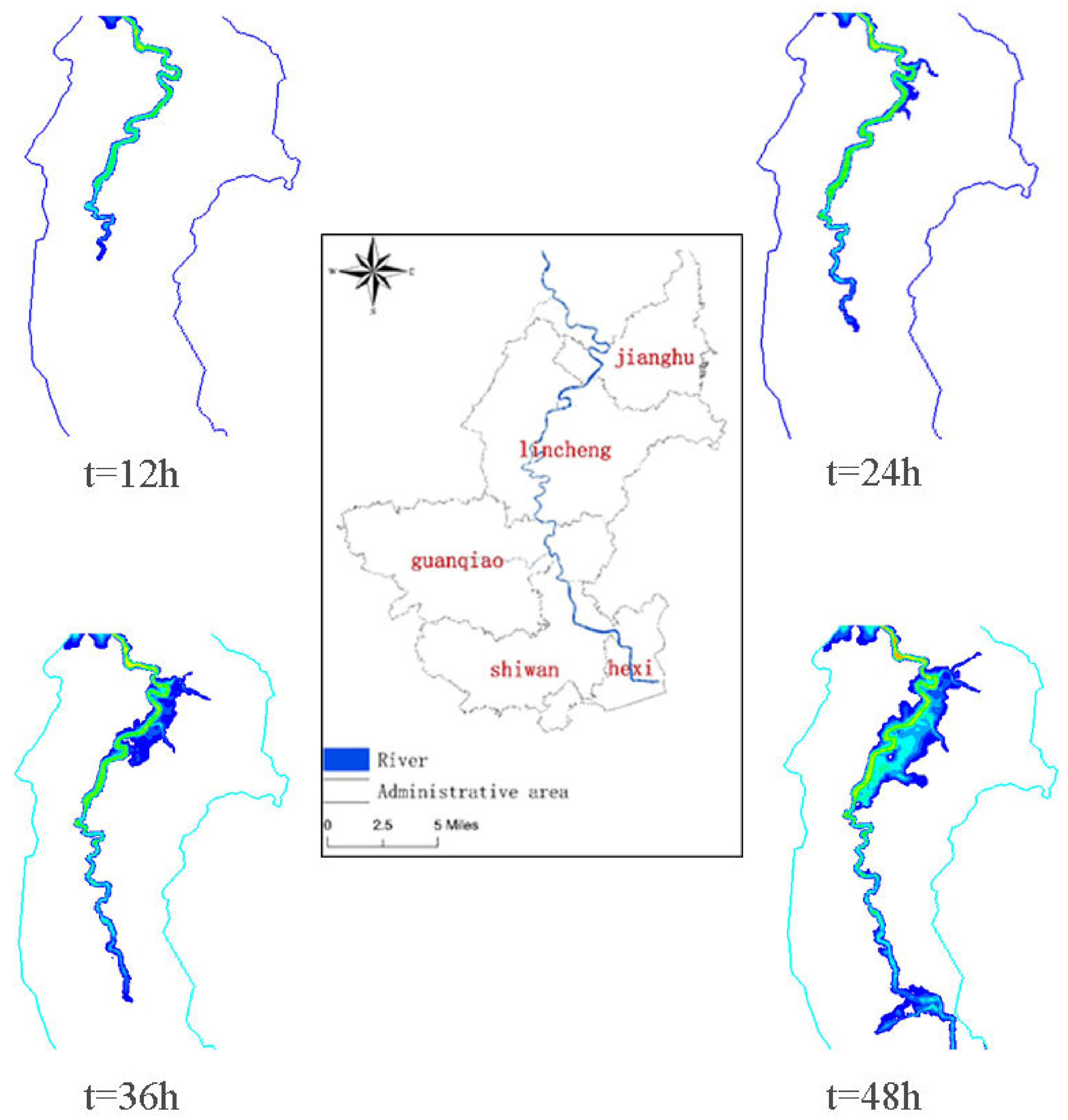
3.1. Research Domain
3.2. Data
3.3. Model Pre-Simulation Processing
3.3.1. Boundary Condition
3.3.2. Selection of Roughness Value
3.3.3. 2D Computation Mesh Construction
4. Results and Analysis
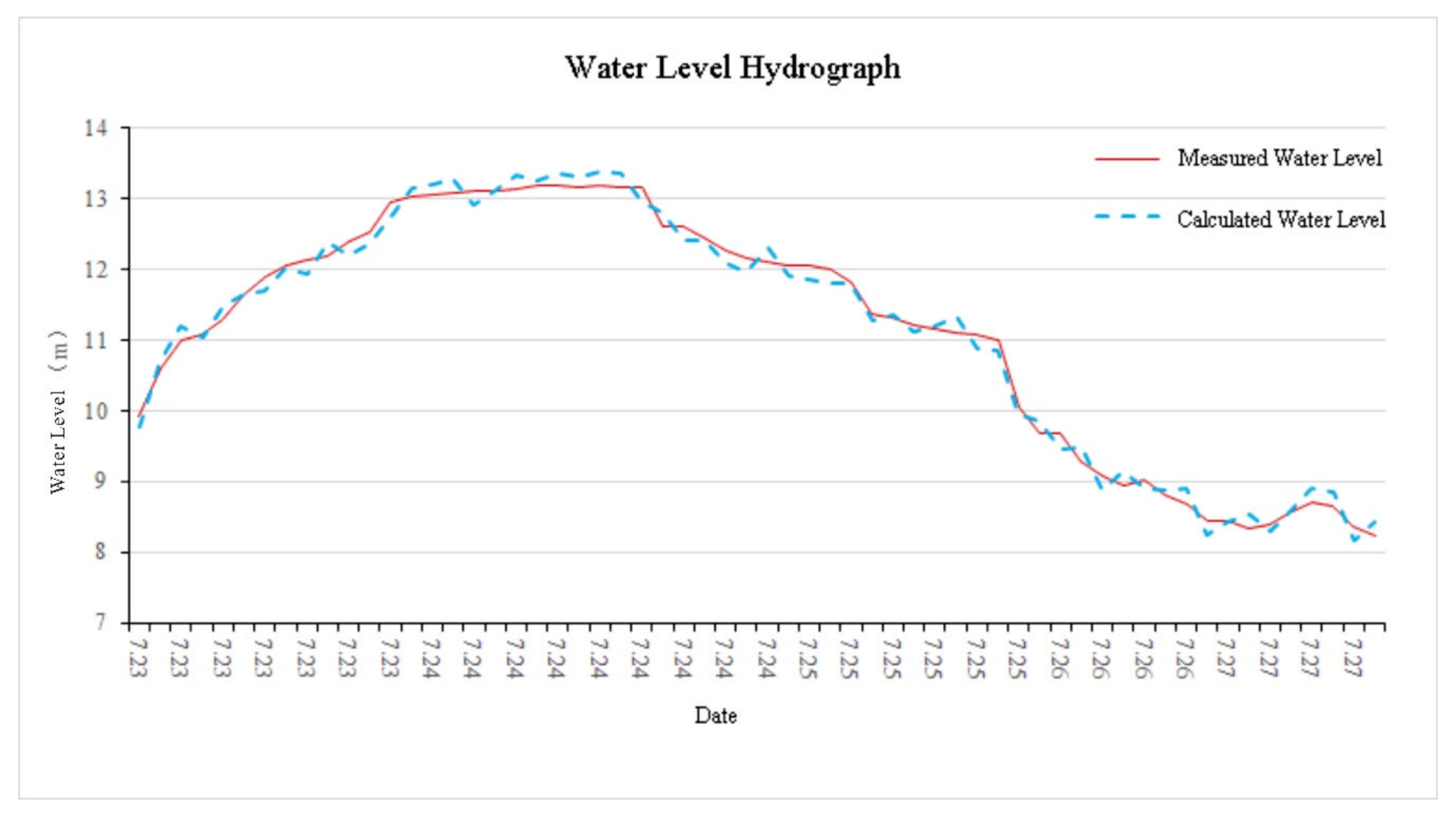
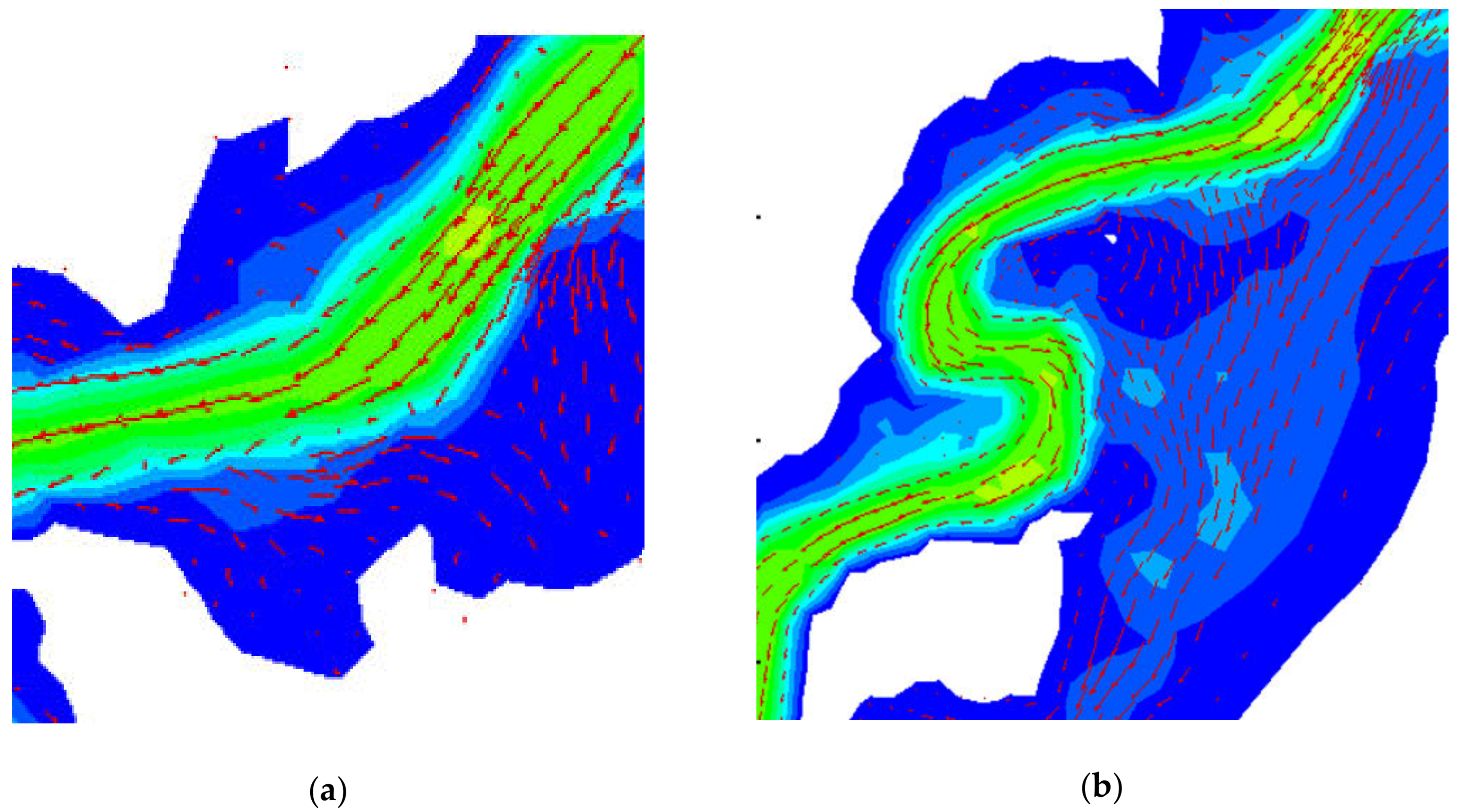
4.1. Flood Simulation under Typhoon ‘Chanthu’ in 2010
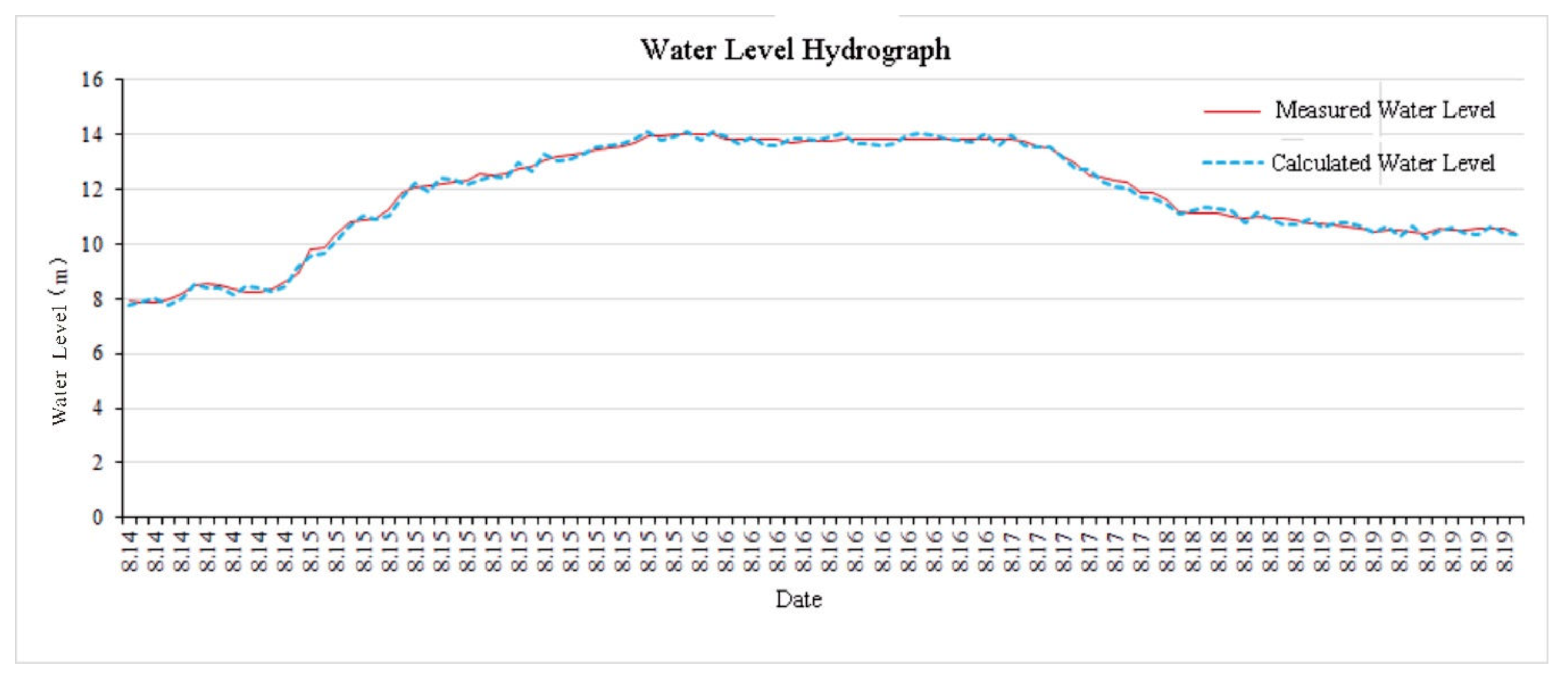
4.2. Flood Simulation under Typhoon ‘Utor’ in 2013
4.3. Simulation Prediction under Different Frequency Flood Conditions
4.4. Flood Inundation Characteristics under Dike Conditions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gourley, J.J.; Hong, Y.; Flamig, Z.L.; Arthur, A.; Clark, R.; Calianno, M.; Ruin, I.; Ortel, T.; Wieczorek, M.E.; Kirstetter, P.-E.; et al. A unified flash flood database across the United States. Bull. Am. Meteorol. Soc. 2013, 94, 799–805. [Google Scholar] [CrossRef]
- Jonkman, S.N.; Kelman, I. An analysis of the causes and circumstances of flood disaster deaths. Disasters 2005, 29, 75–97. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Wang, Q.J.; Pagano, T.C. A review of advances in flash flood forecasting. Hydrol. Process. 2011, 25, 2771–2784. [Google Scholar] [CrossRef]
- Huang, P.N.; Li, Z.J.; Li, Q.L.; Zhang, K.; Zhang, H.C. Application and comparison of coaxial correlation diagram and hydrological model for reconstructing flood series under human disturbance. J. Mt. Sci. 2016, 13, 1245–1264. [Google Scholar] [CrossRef]
- He, B.; Huang, X.; Ma, M.; Chang, Q.; Tu, Y.; Li, Q.; Zhang, K.; Hong, Y. Analysis of flash flood disaster characteristics in china from 2011 to 2015. Nat. Hazards 2018, 90, 407–420. [Google Scholar] [CrossRef]
- Guo, L.; He, B.; Ma, M.; Chang, Q.; Li, Q.; Zhang, K.; Hong, Y. A comprehensive flash flood defense system in China: Overview, achievements, and outlook. Nat. Hazards 2018, 92, 727–740. [Google Scholar] [CrossRef]
- Guo, K.; Liang, G.; He, B. Dynamic critical precipitation flash flood warning method and its application based on API Hydrologic Model. Water Resour. Power 2016, 34, 74–78. [Google Scholar]
- National Flood Control and Drought Relief Headquarters Ministry of Water Resources of the People’s Republic of China. Bulletin of Flood and Drought Disasters in China, 1st ed.; China Map Publishing House: Beijing, China, 2018; pp. 19–25. [Google Scholar]
- Jonkman, S.N.; Kok, M.; Ledden, M.V.; Vrijling, J.K. Risk-based design of flood defence systems: A preliminary analysis of the optimal protection level for the New Orleans metropolitan area. J. Flood Risk Manag. 2009, 2, 170–181. [Google Scholar] [CrossRef]
- Jonkman, S.N.; Kok, M.; Vrijling, J.K. Flood risk assessment in the Netherlands: A case study for dike ring South Holland. Risk Anal. Int. J. 2008, 28, 1357–1374. [Google Scholar] [CrossRef]
- Chiang, Y.; Hsu, K.; Chang, F.; Hong, Y.; Sorooshian, S. Merging multiple precipitation sources for flash flood forecasting. J. Hydrol. 2007, 340, 183–196. [Google Scholar] [CrossRef]
- Norbiato, D.; Borga, M.; Esposti, S.; Gaume, E.; Anquetin, S. Flash flood warning based on rainfall thresholds and soil moisture conditions: An assessment for gauged and ungauged basins. J. Hydrol. 2008, 362, 274–290. [Google Scholar] [CrossRef]
- Lamichhane, N.; Sharma, S. Effect of input data in hydraulic modeling for flood warning systems. Hydrol. Sci. J. 2018, 63, 938–956. [Google Scholar] [CrossRef]
- Khaleghi, M.R.; Gholami, V.; Ghodusi, J.; Hosseini, H. Efficiency of the geomorphologic instantaneous unit hydrograph method in flood hydrograph simulation. Catena 2011, 87, 163–171. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, R.; Guo, L.; Tian, J.; Zhang, X.; Ding, L.; Wang, C.; Shang, Y. Forecasting and Providing Warnings of Flash Floods for Ungauged Mountainous Areas Based on a Distributed Hydrological Model. Water 2017, 9, 776. [Google Scholar] [CrossRef]
- Jasper, K.; Gurtz, J.; Lang, H. Advanced flood forecasting in Alpine watersheds by coupling meteorological observations and forecasts with a distributed hydrological model. J. Hydrol. 2002, 267, 40–52. [Google Scholar] [CrossRef]
- Chen, Y.B.; Li, J.; Wang, H.Y.; Qin, J.M.; Dong, L.M. Large-watershed flood forecasting with high-resolution distributed hydrological model. Hydrol. Earth Syst. Sci. 2017, 21, 735–749. [Google Scholar] [CrossRef]
- Jia, P.; Liu, R.; Ma, M.; Liu, Q.; Wang, Y.; Zhai, X.; Xu, S.; Wang, D. Flash Flood Simulation for Ungauged Catchments Based on the Distributed Hydrological Model. Water 2019, 11, 76. [Google Scholar] [CrossRef]
- Timbadiya, P.; Patel, P.; Porey, P. One-dimensional hydrodynamic modelling of flooding and stage hydrographs in the lower Tapi River in India. Curr. Sci. 2014, 105, 708–716. [Google Scholar]
- Rahmati, O.; Zeinivand, H.; Besharat, M. Flood hazard zoning in Yasooj region, Iran, using GIS and multi-criteria decision analysis. Geomat. Nat. Hazards Risk 2016, 7, 1000–1017. [Google Scholar] [CrossRef]
- Masood, M.; Takeuchi, K. Assessment of flood hazard, vulnerability and risk of mid-eastern Dhaka using DEM and 1D hydrodynamic model. Nat. Hazards 2012, 61, 757–770. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J. Experimental validation of two-dimensional depth-averaged models for forecasting rain-fall-runoff from precipitation data in urban areas. J. Hydrol. 2010, 382, 88–102. [Google Scholar] [CrossRef]
- John, F.E.J.; Mark, L.V.; Pierre, Y.J. Two-dimensional simulations of extreme floods on a large watershed. J. Hydrol. 2007, 347, 229–241. [Google Scholar]
- Gallegos, H.A.; Schubert, J.E.; Sanders, B.F. Two-dimensional, high-resolution modeling of urban dambreak flooding: A case study of Baldwin Hills, California. Adv. Water Resour. 2009, 32, 1323–1335. [Google Scholar] [CrossRef]
- Quiroga, V.M.; Popescu, I.; Solomatine, D.; Bociort, L. Cloud and cluster computing in uncertainty analysis of integrated flood models. J. Hydroinform. 2013, 15, 55–70. [Google Scholar] [CrossRef]
- Quiroga, V.M.; Kure, S.; Udo, K.; Mano, A. Application of 2D numerical simulation for the analysis of the February 2014 Bolivian Amazonia flood: Application of the new HEC-RAS version 5. Ribagua 2016, 3, 25–33. [Google Scholar] [CrossRef]
- Zhou, H.P.; Wei, Y.S.; Li, J.J. Optimal Model of Hydrodynamic Controlling on Pumps and Slice Gates for Water Quality Improvement. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa, Zurich, Switzerland, 2013; Volume 316, pp. 732–740. [Google Scholar]
- Martins, R.; Leandro, J.; Djordjevic, S. Influence of sewer network models on urban flood damage assessment based on coupled 1D/2D models. J. Flood Risk Manag. 2018, 11, S717–S728. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Niu, S.; Zhang, W.T.; Xu, J. Integrated Modeling and Calculation of Urban Surface and Underground Flooding. Ekoloji 2018, 106, 703–711. [Google Scholar]
- Zhang, W.T.; Liu, Y.Z. Comprehensive risk assessment of the Luojiang River basin water environment in Western Guangdong Province. Desalin. Water Treat. 2018, 125, 171–178. [Google Scholar] [CrossRef]
- Luo, B.Y.; Zhang, C.H.; Li, Y.F.; Li, S.A. Rainfall Contrast betewwn Typhoon Bills and Kaemi 2006. Adv. Mar. Sci. 2009, 27, 74–80. [Google Scholar]
- Qi, P.N.; Shen, F.F.; Kou, L.L.; Chu, Z.G.; Xu, D.M. Experiments of assimilating Doppler radar data in forecast of Typhoon Chanthu. J. Trop. Oceanogr. 2019, 38, 20–31. [Google Scholar]
- Zhang, X.L.; Xia, J.Q.; Li, N. Impacts of mesh scale and village region roughness on predictions of flood inundation over complex floodplains. J. Hydroelectr. Eng. 2016, 35, 48–57. [Google Scholar]
- Casas, A.; Lane, S.N.; Yu, D.; Benito, G. A method for parameterizing roughness and topographic sub-grid scale effects in hydraulic modelling from LiDAR data. Hydrol. Earth Syst. Sci. 2010, 14, 1567–1579. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Cui, X.M.; Zhang, W.T. Research and application of reservoir flood emergency operation system. Disaster Adv. 2012, 5, 712–716. [Google Scholar]
- Zhang, J.; Feng, W.Z.; Li, G.M.; Xu, W.M. Analysis and numerical simulation of the storm surge caused by the typhoon “Chanthu”. Mar. Sci. Bull. 2011, 30, 367–370. [Google Scholar]
- Lang, X.B. Analysis of 201003 typhoon “Chanthu”. Mar. Forecast. 2011, 3, 26–31. [Google Scholar]
- Zhao, X.T.; Zhao, Y.C.; Cui, C.G. Analysis on track and intensity changes of STC Utor before and after its landing. Torrential Rain Disaster 2015, 34, 197–205. [Google Scholar]
- Xiong, Y.; Li, L.; Wu, X.; Guo, Y.T. Analysis of the process of severe typhoon “Youte” in 2013 affecting the heavy rainfall in Shaoguan. J. Meteorol. Res. Appl. 2014, S2, 156–158. [Google Scholar]
- Wang, S.F.; He, L.Y. Comprehensive Analysis of Heavy Rainfall Process of Super Typhoon “Utor” No. 1311. J. Meteorol. Res. Appl. 2016, 37, 20–21. [Google Scholar]

| Partial Roughness Values of Riverbed | ||
|---|---|---|
| River Features | ||
| Type | Riverbed Morphology and Characteristics | Roughness Value |
| I | The riverbed is made up of sand and its surface is smooth. | 0.020–0.024 |
| II | The riverbed is a slab consisting of sand and gravel with a flat surface. | 0.022–0.026 |
| III | The riverbed is sandy and the bottom of the river fluctuates greatly. | 0.025–0.029 |
| IV | The smooth riverbed is composed of gravel. its terrain is relatively flat. | 0.025–0.029 |
| V | The riverbed is composed of fine sand with a small amount of vegetation at the bottom. | 0.030–0.034 |
| VI | The riverbed is composed of gravel and it is undulating. | 0.030–0.034 |
| VII | There are pebbles and boulders at the bottom of the river, and the riverbed fluctuates greatly. | 0.035–0.040 |
| VIII | The riverbed is pebble, the bottom of the river fluctuates greatly and its shape is irregular. | 0.04–0.10 |
| Serial Number | Section | Measured Water Level (m) | Model Calculation of Water Level (m) | Absolute Difference of Water Level (m) |
|---|---|---|---|---|
| 1 | Luojiang Estuary | 13.18 | 13.11 | 0.07 |
| Serial Number | Section | Measured Water Level (m) | Model Calculation of Water Level (m) | Absolute Difference of Water Level (m) |
|---|---|---|---|---|
| 1 | Luojiang Estuary | 14.19 | 14.08 | 0.11 |
| Flood Frequency | Maximum Flooded Area (km2) | Maximum Flooded Depth (m) | Average Maximum Flooded Depth (m) |
|---|---|---|---|
| 20-year flood | 56.58 | 7.617 | 2.58 |
| 50-year flood | 66.34 | 8.487 | 2.976 |
| 100-year flood | 79.24 | 9.511 | 3.39 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhang, X.; Liu, Y.; Tang, W.; Xu, J.; Fu, Z. Assessment of Flood Inundation by Coupled 1D/2D Hydrodynamic Modeling: A Case Study in Mountainous Watersheds along the Coast of Southeast China. Water 2020, 12, 822. https://doi.org/10.3390/w12030822
Zhang W, Zhang X, Liu Y, Tang W, Xu J, Fu Z. Assessment of Flood Inundation by Coupled 1D/2D Hydrodynamic Modeling: A Case Study in Mountainous Watersheds along the Coast of Southeast China. Water. 2020; 12(3):822. https://doi.org/10.3390/w12030822
Chicago/Turabian StyleZhang, Wenting, Xingnan Zhang, Yongzhi Liu, Wenwen Tang, Jan Xu, and Zhimin Fu. 2020. "Assessment of Flood Inundation by Coupled 1D/2D Hydrodynamic Modeling: A Case Study in Mountainous Watersheds along the Coast of Southeast China" Water 12, no. 3: 822. https://doi.org/10.3390/w12030822
APA StyleZhang, W., Zhang, X., Liu, Y., Tang, W., Xu, J., & Fu, Z. (2020). Assessment of Flood Inundation by Coupled 1D/2D Hydrodynamic Modeling: A Case Study in Mountainous Watersheds along the Coast of Southeast China. Water, 12(3), 822. https://doi.org/10.3390/w12030822





