A New Method for the Evaluation of Well Rehabilitation from the Early Portion of a Pumping Test
Abstract
1. Introduction
2. Materials and Methods
2.1. Real Wells
- (a)
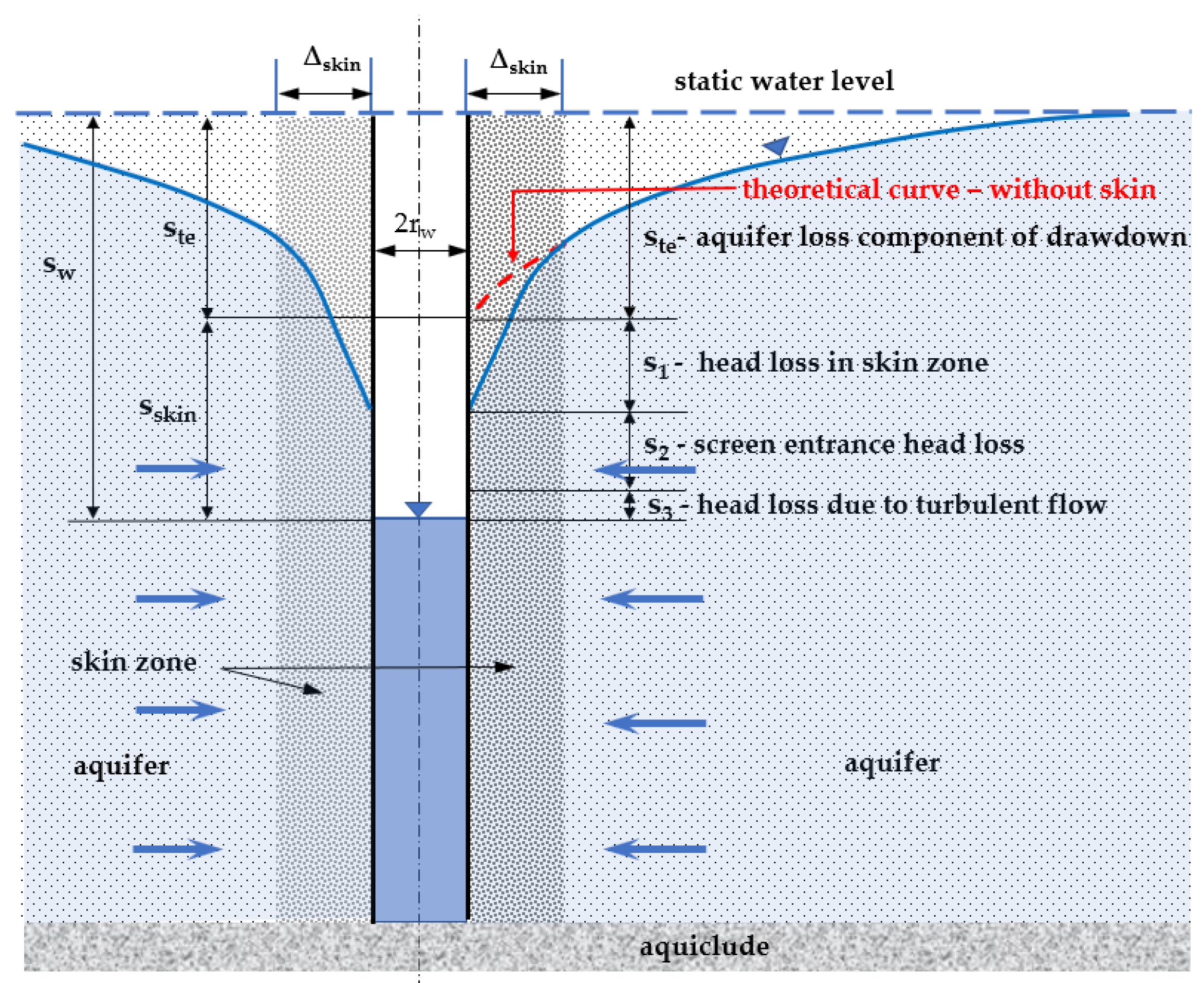
- By the clogging of pores (s1) with, e.g., a fine material, which reduces the flow rate of the porous environment or disrupts the original internal structure of the porous environment in the vicinity of the wellbore during digging and equipping (it decreases the porous environment’s permeability) in rotary drilling, the result of which is so-called sludge bark; in the case of impact drilling, the porous environment in the vicinity of the well is compacted, thereby reducing throughput [52,53,54].
- (b)
- Through a reduction in the wellbore wall cross-section (s2) for the water inflow where the borehole wall is formed by a filter, perforated casing, etc., by trapping rock particles or backfill in filter openings, including chemical incrustation and the blockage of filter openings by microorganisms and bacteria [55,56,57].
- (c)
- Via the friction (s3) of water on the borehole walls and its internal friction (this group also includes the additional resistance arising from the turbulent flow regime of the water inside the borehole and the turbulent flow in the aquifer, especially in the vicinity of the pumping well.
- (d)
- Where appropriate, other types of additional resistance occur.
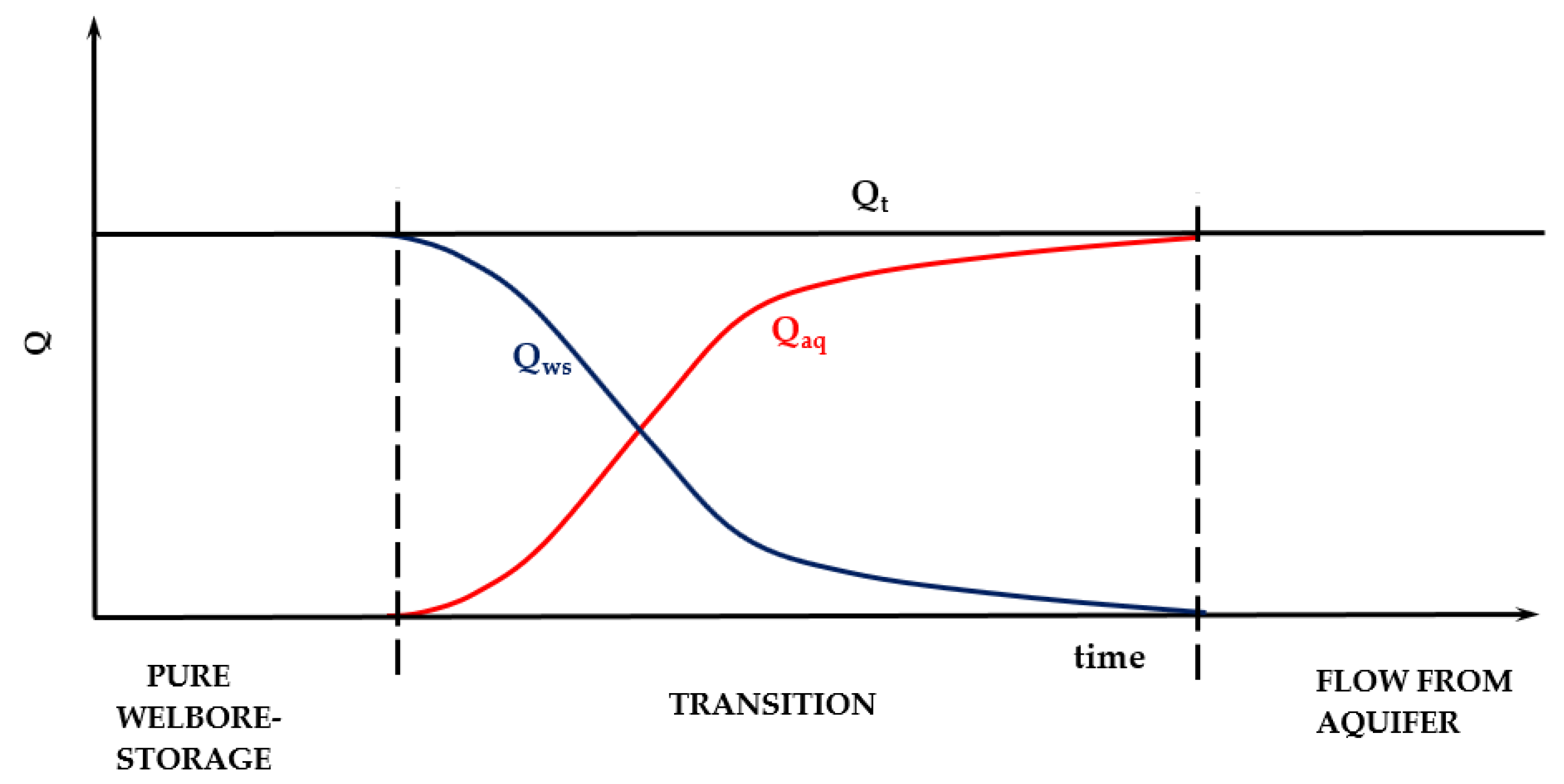
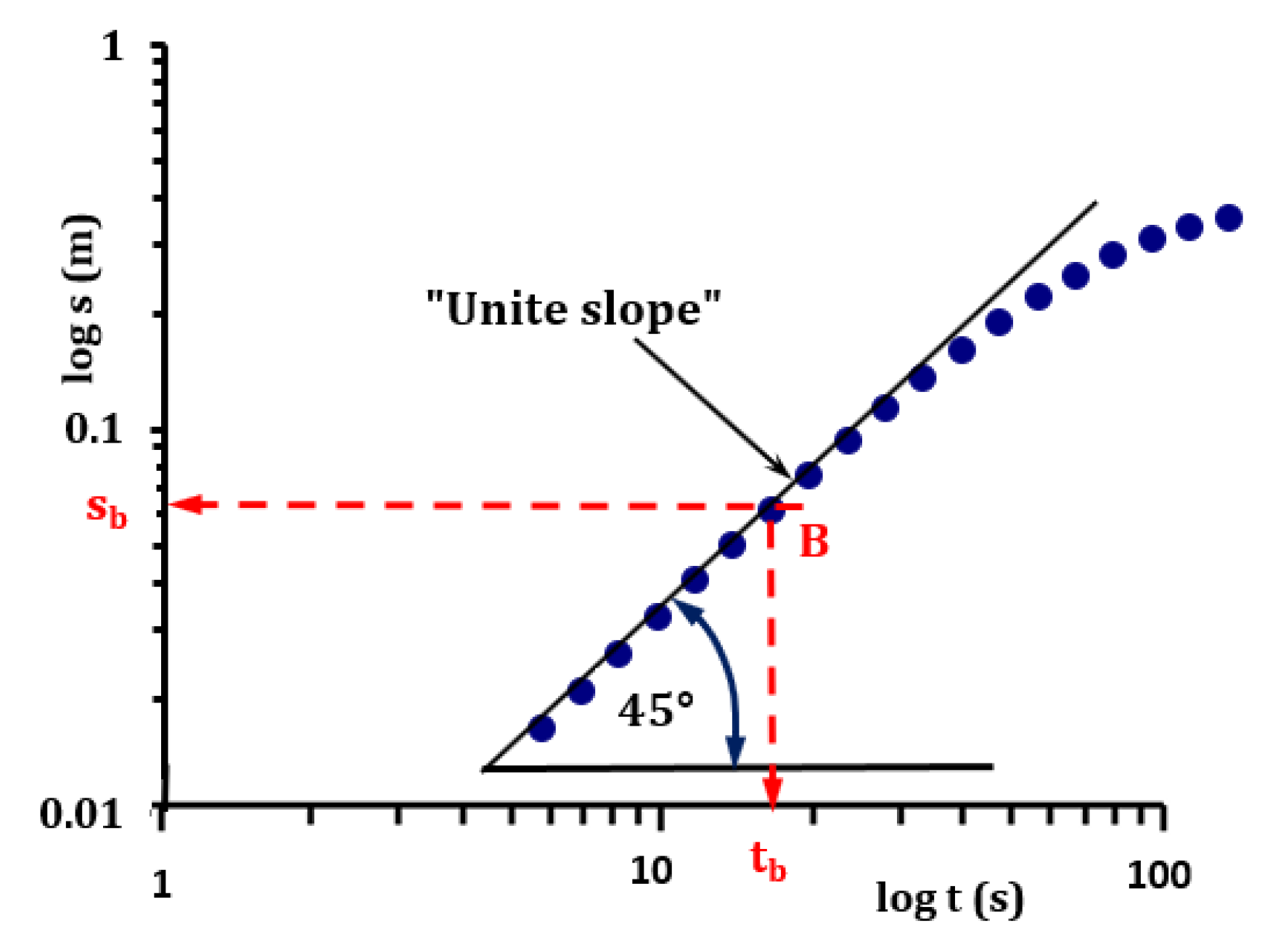
2.2. Deriving the New Correlation to Evaluate the Skin Factor from the First Straight Line
- The gravitational forces are negligible;
- A constant density and viscosity of water;
- The aquifer has an infinite areal extent;
- The pumping well penetrates the full thickness of the aquifer;
- The flow to the pumping well is horizontal;
- The flow is unsteady;
- The diameter of a pumping well is very small (negligible), allowing the storage in the well to be neglected;
- The well is pumped with constant rate Q;
- The aquifer is horizontal and bounded on the bottom and top by impermeable layers (a confined aquifer);
- The aquifer flow to the pumped well is radial and laminar, so Darcy’s law is applied;
- The confined aquifer is homogeneous and isotropic;
- The height of an aquifer (where the flow to the well is constant and has a size b transmissivity, T, and storability (aquifer storage), S) is constant over time and space;
- The water supply from the aquifer to the well changes during the pumping test from Qaq = 0 to the final inflow, Qaq = Q = const.;
- Before pumping begins (i.e., for t = 0), the hydraulic head is constant in all points of the aquatic environment and equals H; this also applies to the water level at a well.
- The well possesses its final volume, and, at the beginning of pumping, the effect of the water volume in the wellbore influences the drawdown and must be considered;
- The wellbore storage coefficient is constant and does not change during pumping;
- The influence of additional resistance occurring in the wellbore itself and in its immediate vicinity is considered (the width of the perpendicular zone can reach up to about 2–7 m).
3. Results
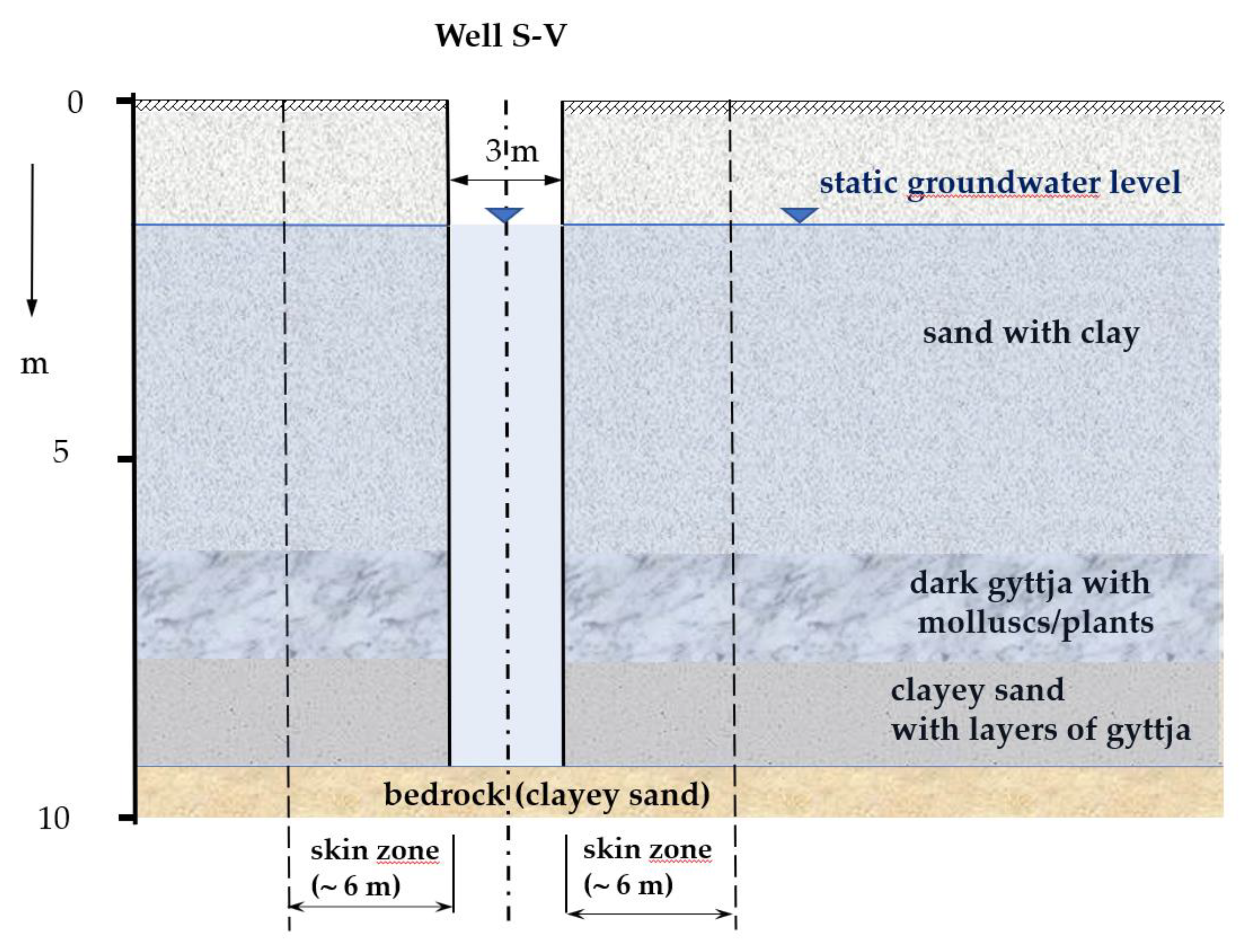
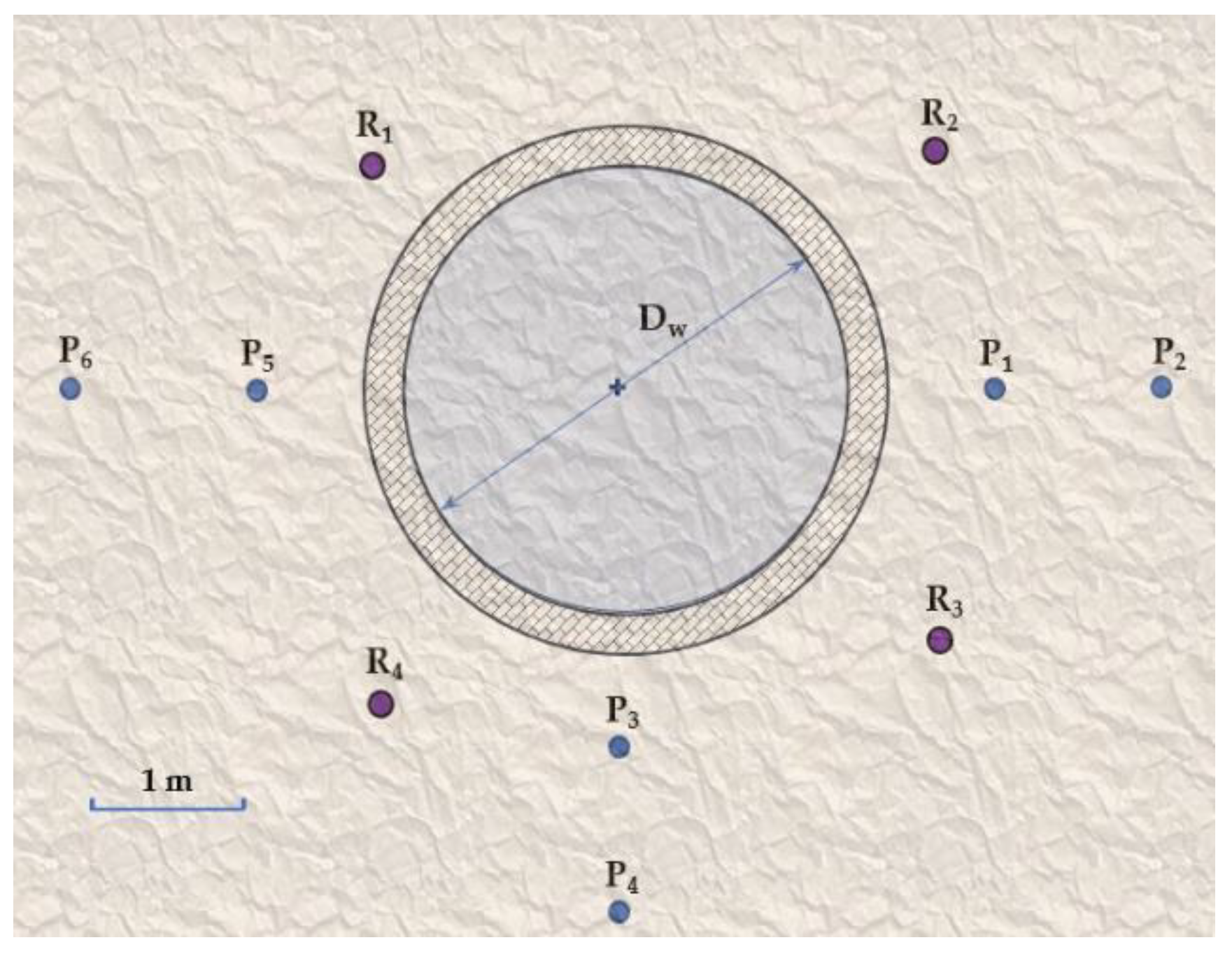
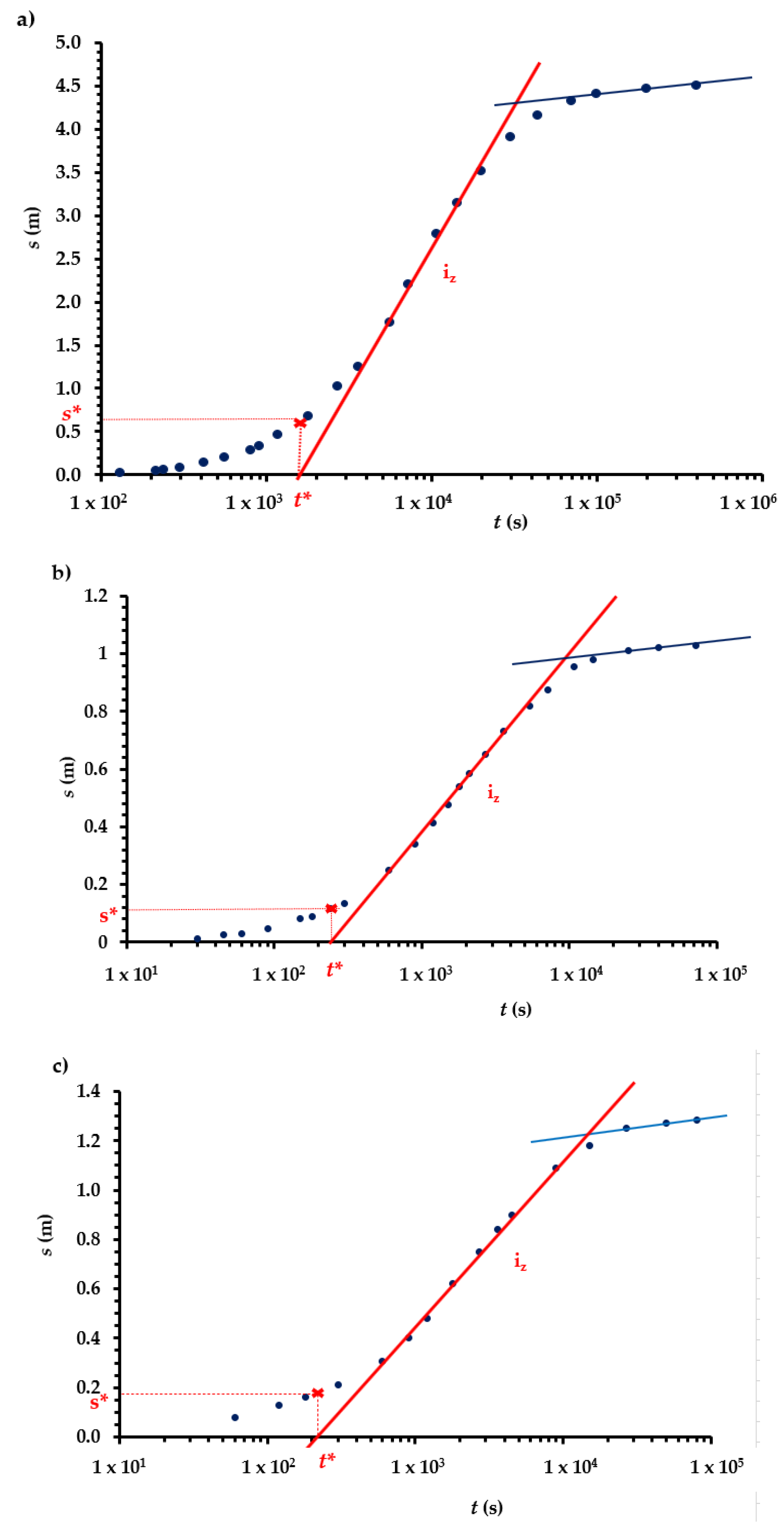
Field Test: Rehabilitation of the Dug S-V well—Veselí Nad Lužnicí
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Theis, C.V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage. Trans. Am. Geophys. Union 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Cooper, H.H.; Jacob, C.E. A generalized graphical method for evaluating formation constants and summarizing well-field history. Trans. Am. Geophys. Union 1946, 27, 526–534. [Google Scholar] [CrossRef]
- Bourdet, D. Well test analysis: The use of advanced interpretation models. Handb. Pet. Explor. Prod. 2002, 3, 1–426. [Google Scholar] [CrossRef]
- Lee, J. Well Testing. In SPE Textbook Series Vol. 1; Society of Petroleum Engineers: Richardson, TX, USA, 1982; p. 159. ISBN 978-089520-317-5. [Google Scholar]
- Horne, R.N. Modern Well Test Analysis: A Computer Aided Approach, 4th ed.; Alto, P., Ed.; Petroway, Inc.: Palo Alto, CA, USA, 1995; p. 185. ISBN -0-9626992-09. [Google Scholar]
- Kresic, N. Hydrogeology and Groundwater Modeling, 2nd ed.; CRC Press, Taylor and Francis: Boca Raton, FL, USA, 2007; ISBN 13 978-0849333484. [Google Scholar]
- Watlton, W.C. Aquifer Test Modeling, 1st ed.; CRC Press: Boca Ralton, FL, USA, 2007; p. 240, ISBN-13: 978-1-4200-4292-4. [Google Scholar]
- Batu, V. Aquifer Hydraulics: A Comprehensive Guide to Hydrogeologic Data Analysis; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Kruseman, G.P.; de Ridder, N.A. Analysis and Evaluation of Pumping Test Data, 2nd ed.; IILRI: Wageningen, The Netherlands, 2008; pp. 1–372. [Google Scholar]
- Tongpenyai, Y.; Raghavan, R. The effect of wellbore storage and skin on interference test data. J. Pet. Technol. 1981, 33, 151–160. [Google Scholar] [CrossRef]
- Novakowski, K.S. A Composite analytical model for analysis of pumping tests affected by well bore storage and finite thickness skin. Water Resour. Res. 1989, 25, 1937–1946. [Google Scholar] [CrossRef]
- Pasandi, M.; Samani, N.; Barry, D.A. Effect of wellbore and finite thickness skin on flow to a partially penetrating well in a phreatic aquifer. Adv. Water Resour. 2008, 31, 383–398. [Google Scholar] [CrossRef]
- Papadopulos, I.S.; Cooper, H.H. Drawdown in a well of large diameter. Water Resour. Res. 1967, 3, 241–244. [Google Scholar] [CrossRef]
- Moench, A.F. Transient flow to a large-diameter well in an aquifer with storative semiconfining layers. Water Resour. Res. 1985, 21, 1121–1131. [Google Scholar] [CrossRef]
- Chen, C.; Lan, C. A simple data analysis method for a pumping test with skin and wellbore storage effect. Terr. Atmos. Ocean. Sci. 2009, 20, 557–562. [Google Scholar] [CrossRef]
- Ramey, H.H., Jr. Short-time well test data interpretation in the presence of skin effect and wellbore storage. J. Pet. Technol. 1970, 22, 97–104. [Google Scholar] [CrossRef]
- Yeh, H.D.; Yang, S.Y.; Peng, H.Y. A new closed-form solution for a radial two-layer drawdown equation for groundwater under constant-flux pumping in a finite-radius well. Adv. Water Resour. 2003, 26, 747–757. [Google Scholar] [CrossRef]
- McKinley, R.M. Wellbore transmissibility from afterflow-dominated pressure buildup data. J. Pet. Technol. 1971, 23, 863. [Google Scholar] [CrossRef]
- Kabala, Z.J. Sensitivity analysis of a pumping test on a well with wellbore storage and skin. Adv. Water Resour. 2001, 24, 483–504. [Google Scholar] [CrossRef]
- Ramey, H.J.; Agarwal, R.G. Annulus unloading rates as influenced by wellbore storage and skin effect. Soc. Pet. Eng. J. 1972, 12, 453–462. [Google Scholar] [CrossRef]
- Van Everdingen, A.F. The skin effect and its influence on the productive capacity of a well. J. Pet. Technol. 1953, 5, 171–176. [Google Scholar] [CrossRef]
- Hurst, W. Establishment of skin effect and its impediment to fluid flow into a well bore. Pet. Eng. 1953, 25, B6–B16. [Google Scholar]
- Hawkins, M.F., Jr. A note on the skin effect. Trans. Am. Inst. Min. Met. Eng. 1956, 8, 356–357. [Google Scholar] [CrossRef]
- Park, E.; Zhan, H.B. Hydraulics of a finite-diameter horizontal well with wellbore storage and skin effect. Adv. Water Resour. 2002, 25, 389–400. [Google Scholar] [CrossRef]
- Barua, G.; Bora, S.N. Hydraulics of a partially penetrating well with skin zone in a confined aquifer. Adv. Water Resour. 2010, 33, 1575–1587. [Google Scholar] [CrossRef]
- Jargon, J.R. Effect of wellbore storage and wellbore damage at the active well on interference test analysis. J. Pet. Technol. 1976, 28, 851–858. [Google Scholar] [CrossRef]
- Yang, S.Y.; Yeh, H.D. Solution for flow rates across the wellbore in a two-zone confined aquifer. J. Hydraul. Eng. ASCE 2002, 128, 175–183. [Google Scholar] [CrossRef]
- Chen, C.S.; Chang, C.C. Theoretical evaluation of non-uniform skin effect on aquifer response under constant rate pumping. J. Hydrol. 2006, 317, 190–201. [Google Scholar] [CrossRef]
- Basak, P. Steady non-Darcian seepage through embankments closure. J. Irrig. Drain. Div. ASCE 1979, 102, 435–443. Available online: http://cedb.asce.org/CEDBsearch/record.jsp?dockey=0007101 (accessed on 4 September 2019).
- Sen, Z. Nonlinear flow toward wells. J. Hydraul. Eng. ASCE 1989, 115, 193–209. [Google Scholar] [CrossRef]
- Chu, W.C.; Garcia-Rivera, J.; Raghavan, R. Analysis of interference test data influenced by wellbore storage and skin at the flowing well. J. Pet. Technol. 1980, 32, 623–630. [Google Scholar] [CrossRef]
- Agarwal, R.G.; Al-Hussainy, R.; Ramey, H.J. An investigation of wellbore storage and skin effect in unsteady liquid flow: I. Analytical treatment. Soc. Pet. Eng. J. 1970, 10, 279–291. [Google Scholar] [CrossRef]
- Earlougher, R.C., Jr.; Kersch, K.H. Analysis of short-time transient test data by type-curve matching. J. Pet. Technol. 1974, 26, 793–800. [Google Scholar] [CrossRef]
- Earlougher, R.C., Jr. Advances in well test analysis. Monogr. Ser. Soc. Pet. Eng. AIME 1977, 5, 264. Available online: https://trove.nla.gov.au/version/13397770 (accessed on 24 August 2019).
- Bourdet, D.; Whittle, T.M.; Douglas, A.A.; Pirard, Y.M. A new set of type curves simplifies well test analysis. World Oil 1983, 196, 95–106. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Bourdet, D.P.; Landel, P.A.; Kniazeff, V.J. A comparison between different skin and wellbore storage type-curves for early–time transient analysis. Soc. Pet. Eng. SPE Ann. Technol. C Exh. 1979, 1–16. [Google Scholar] [CrossRef]
- Yeh, H.D.; Chang, Y.C. Recent advances in modeling of well hydraulics. Adv. Water Resour. 2013, 51, 27–51. [Google Scholar] [CrossRef]
- Yeh, H.D.; Chen, Y.H. Determination of skin and aquifer parameters for a slug test with wellbore-skin effect. J. Hydrol. 2007, 342, 283–294. [Google Scholar] [CrossRef]
- Mashayekhizadeh, M.D.; Ghazanfari, M.H. The application of numerical Laplace inversion methods for type curve development in well testing: A comparative study. Pet. Sci. Technol. 2011, 29, 695–707. [Google Scholar] [CrossRef]
- Kuchuk, F.J.; Kirwan, P.A. New skin and wellbore storage type curves for partially penetrated wells. SPE Eval. 1987, 2, 546–554. [Google Scholar] [CrossRef]
- Wattenbarger, R.A.; Ramey, H.J. An investigation of wellbore storage and skin effect in unsteady liquid flow: II. Finite difference treatment. Soc. Pet. Eng. J. 1970, 10, 291–297. [Google Scholar] [CrossRef]
- Moench, A.F. Specific yield as determined by type-curve analysis of aquifer-test data. Ground Water 1994, 32, 949–957. [Google Scholar] [CrossRef]
- Wen, Z.; Huang, H.G.; Zhan, H.B. Non-Darcian flow in a single confined vertical fracture toward a well. J. Hydrol. 2006, 330, 698–708. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Van Everdingen, A.F.; Hurst, W. The application of the Laplace transformation to flow problems in reservoirs. J. Pet. Technol. 1949, 1, 305–324. [Google Scholar] [CrossRef]
- Pech, P.; Novotny, R. Analytical solutions for well drawdown with well losses: 1. Multiple well system near a boundary. J. Environ. Hydrol. 2005, 13, 1–10. Available online: http://www.hydroweb.com/journal-hydrology-2005-paper-27.html (accessed on 5 November 2019).
- Novotny, R.; Pech, P. Analytical solutions for well drawdown with well losses: 2. Real well near boundary—solution by image well. J. Environ. Hydrol. 2005, 13, 1–7. Available online: http://www.hydroweb.com/jeh/jeh2005/pech2.pdf (accessed on 5 November 2019).
- Pech, P. Estimation of a well damage or stimulation. Sci. Agric. Bohem. 2004, 35, 131–134. Available online: https://sab.czu.cz/en/r-8044-archive/r-8064-older-issues/r-11689-04-2004#i-28f1287e11d0452b811e7a4937989a20 (accessed on 22 September 2019).
- Holub, J.; Pech, P.; Kuraz, M.; Maca, P.; Kahuda, D. Evaluation of a pumping test with skin effect and wellbore storage on a confined aquifer in the Bela Crkva, Serbia. Int. J. Water 2019, 13, 1–11. [Google Scholar] [CrossRef]
- Raghavan, R. Well Test Analysis, 1st ed.; PTR Prentice Hall: Englewood Cliffs, NJ, USA, 1993; p. 554. [Google Scholar]
- Houben, G.; Treskatis, C. Water Well Rehabilitation and Reconstruction, 3rd ed.; McGraw Hill Professional: Two Penn Plaza, NY, USA, 2007; ISBN 0-07-148651-8. [Google Scholar]
- Adebayo, A.R.; Bageri, B.S. A simple NMR methodology for evaluating filter cake properties and drilling fluid-induced formation damage. J. Pet. Explor. Prod. Technol. 2019, 9. [Google Scholar] [CrossRef]
- Elkatatny, S.; Jafarov, T.; Al-Majed, A.; Mahmoud, M. Formation Damage Avoidance by Reducing Invasion with Sodium Silicate-ModifiedWater-Based Drilling Fluid. Energies 2019, 12, 485. [Google Scholar] [CrossRef]
- Iscan, A.G.; Kok, M.V.; Bagci, A.S. Permeability Reduction Due to Formation Damage by Drilling Fluids. Energy Sources 2007, 29, 851–859. [Google Scholar] [CrossRef]
- Ralph, D.E.; Stevenson, J.M. The role of bacteria in well clogging. Water Res. 1995, 29, 365–369. [Google Scholar] [CrossRef]
- Houben, G.J. Iron oxide incrustations in Wells—Part 1: Genesis, mineralogy and geochemistry. Appl. Geochem. 2003, 18, 927–939. [Google Scholar] [CrossRef]
- Patel, M.C.; Singh, A. Near Wellbore Damage and Types of Skin Depending on Mechanism of Damage. In Proceedings of the Society of Petroleum Engineers SPE International Conference and Exhibition on Formation Damage Control, Lafayette, LA, USA, 24–26 February 2016. [Google Scholar] [CrossRef]
- Pech, P. Determination of the skin factor in the early portion of an aquifer test. J. Environ. Hydrol. 2003, 11, 1–9. Available online: http://www.hydroweb.com/jeh/jeh2002/pech.pdf (accessed on 5 November 2019).
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, 10th ed.; Government Printing: Wahington, DC, USA, 1972; p. 470.
- Yang, S.Y.; Yeh, H.D. Laplace-domain solutions for radial two-zone flow equations under the conditions of constant-head and partially penetrating well. J. Hydraul. Eng. ASCE 2005, 131, 209–216. [Google Scholar] [CrossRef]
- Hošek, J.; Pokorný, P.; Prach, J.; Šída, P.; Křížek, M. Fossil thermokarst in South Bohemia (Czech Republic). Geosci. Res. Rep. 2018, 51, 131–139. Available online: http://www.geology.cz/img/zpravyvyzkum/fulltext/27_Hosek_180903.pdf (accessed on 5 September 2019).
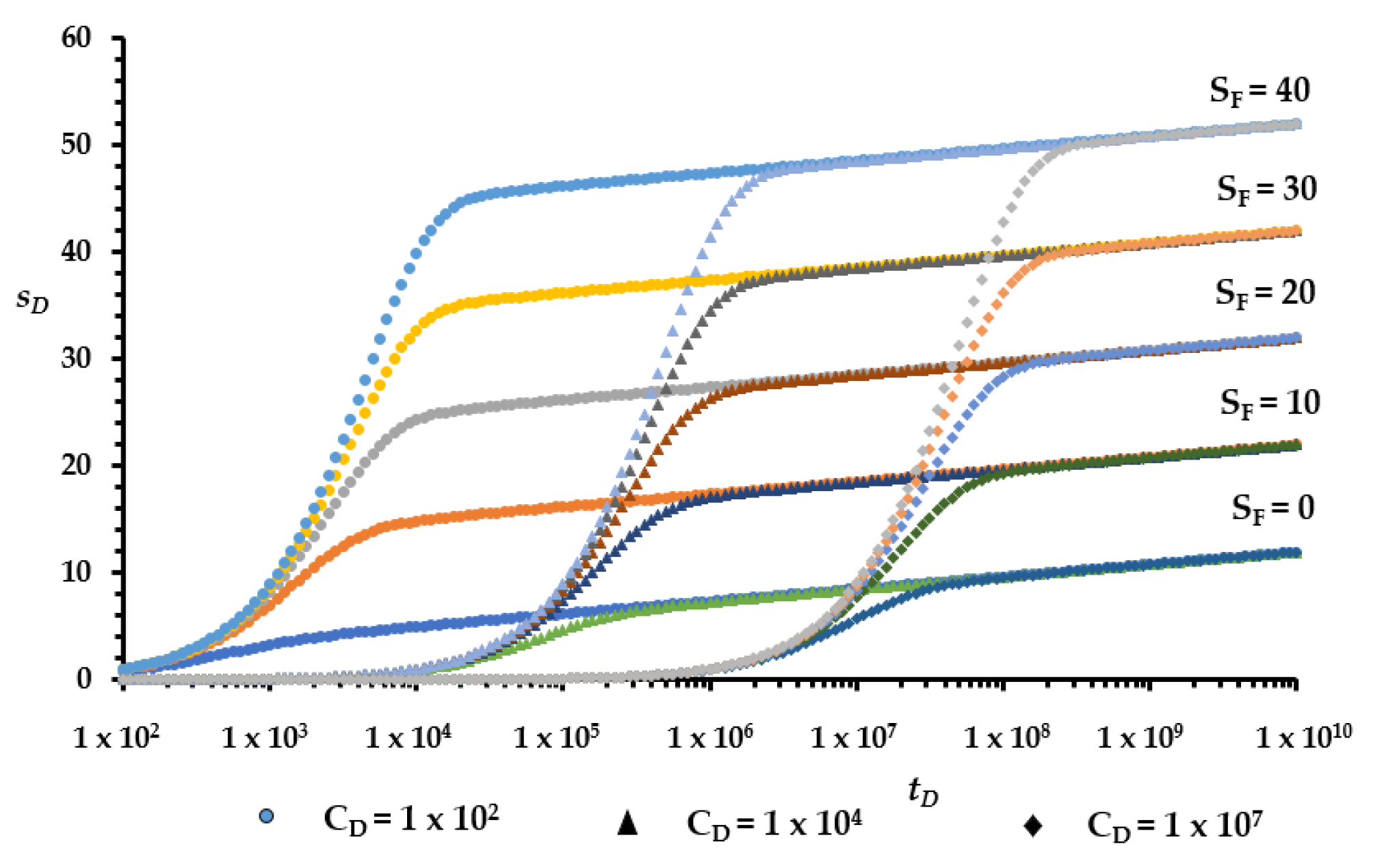
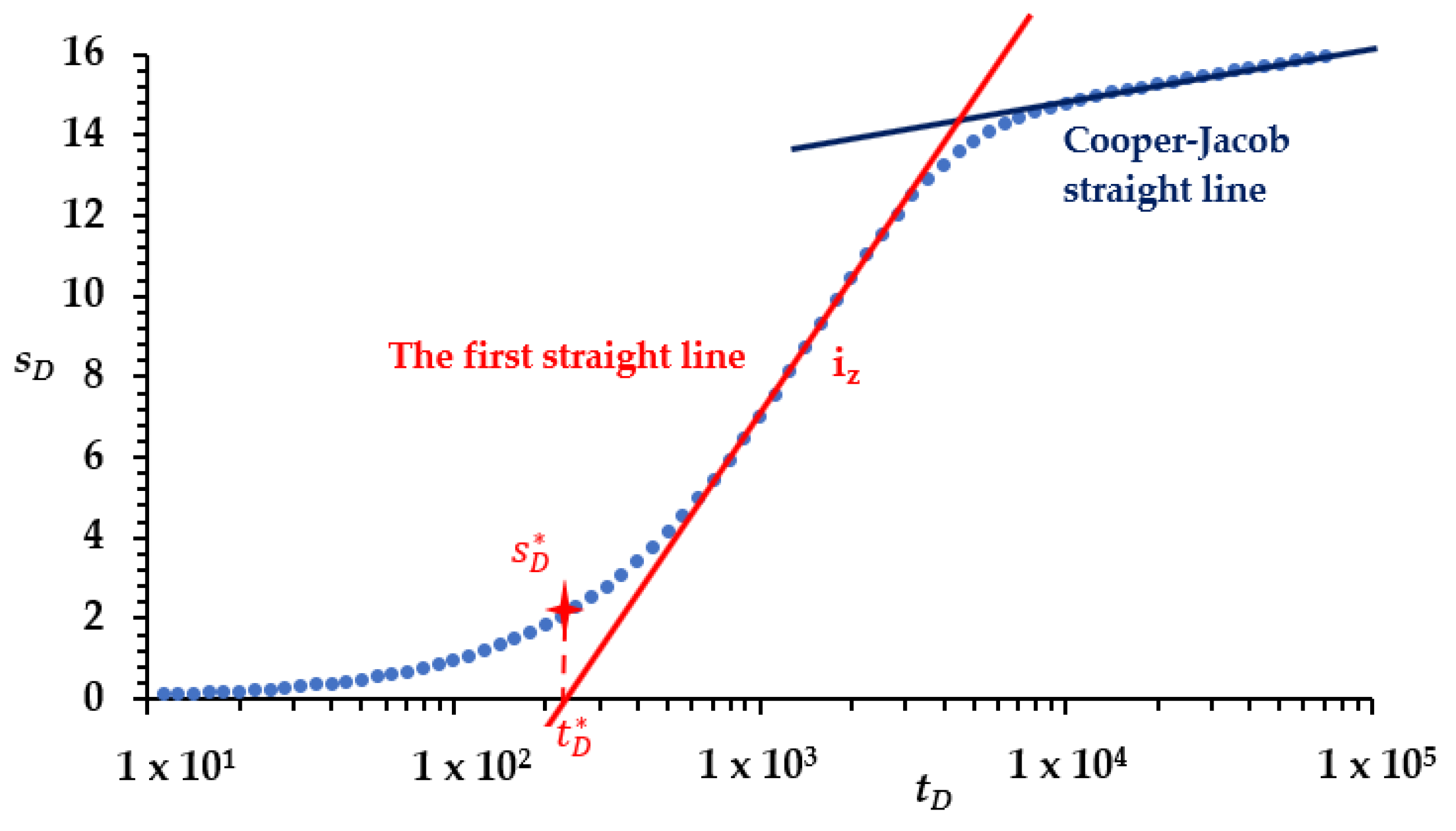
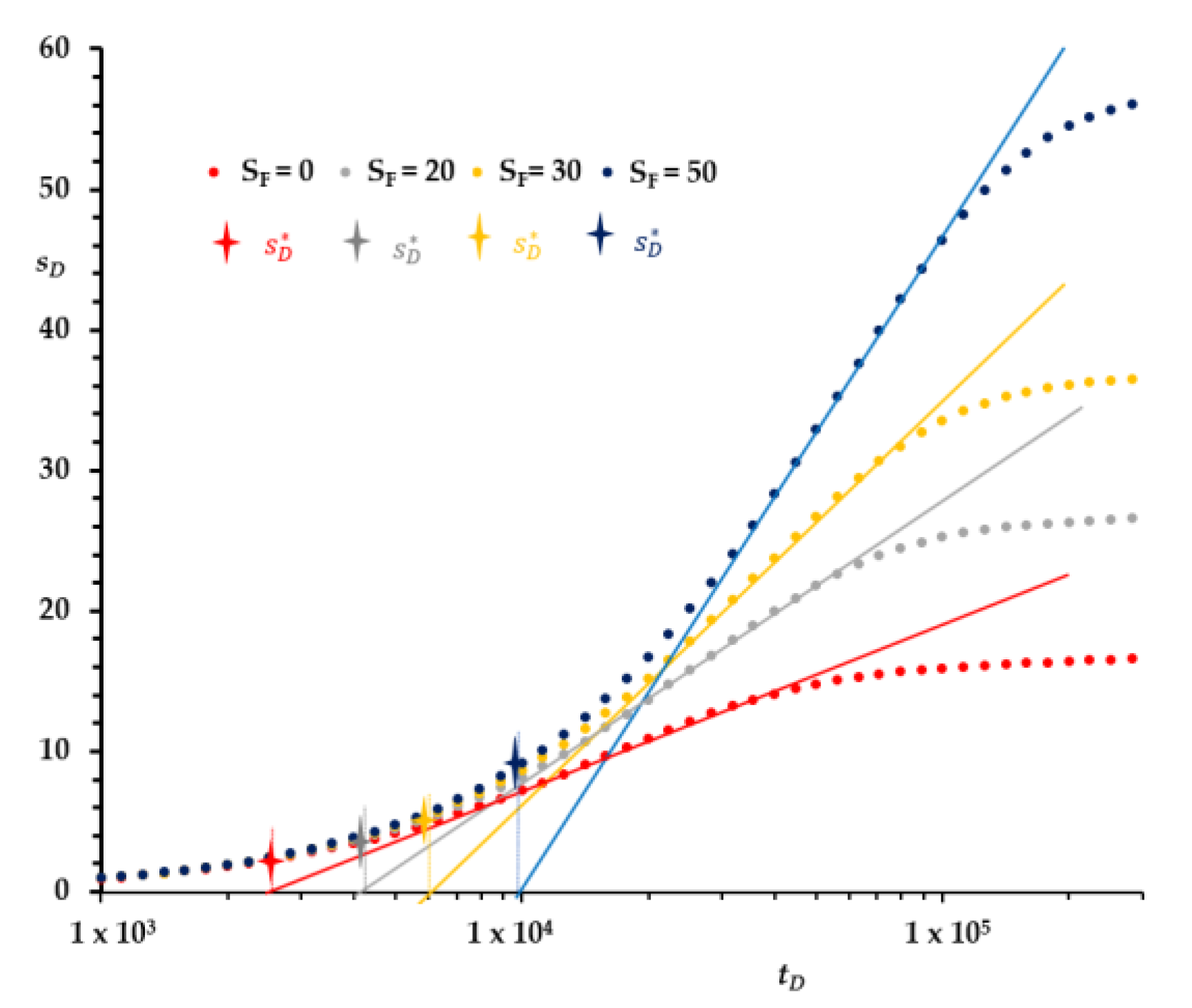
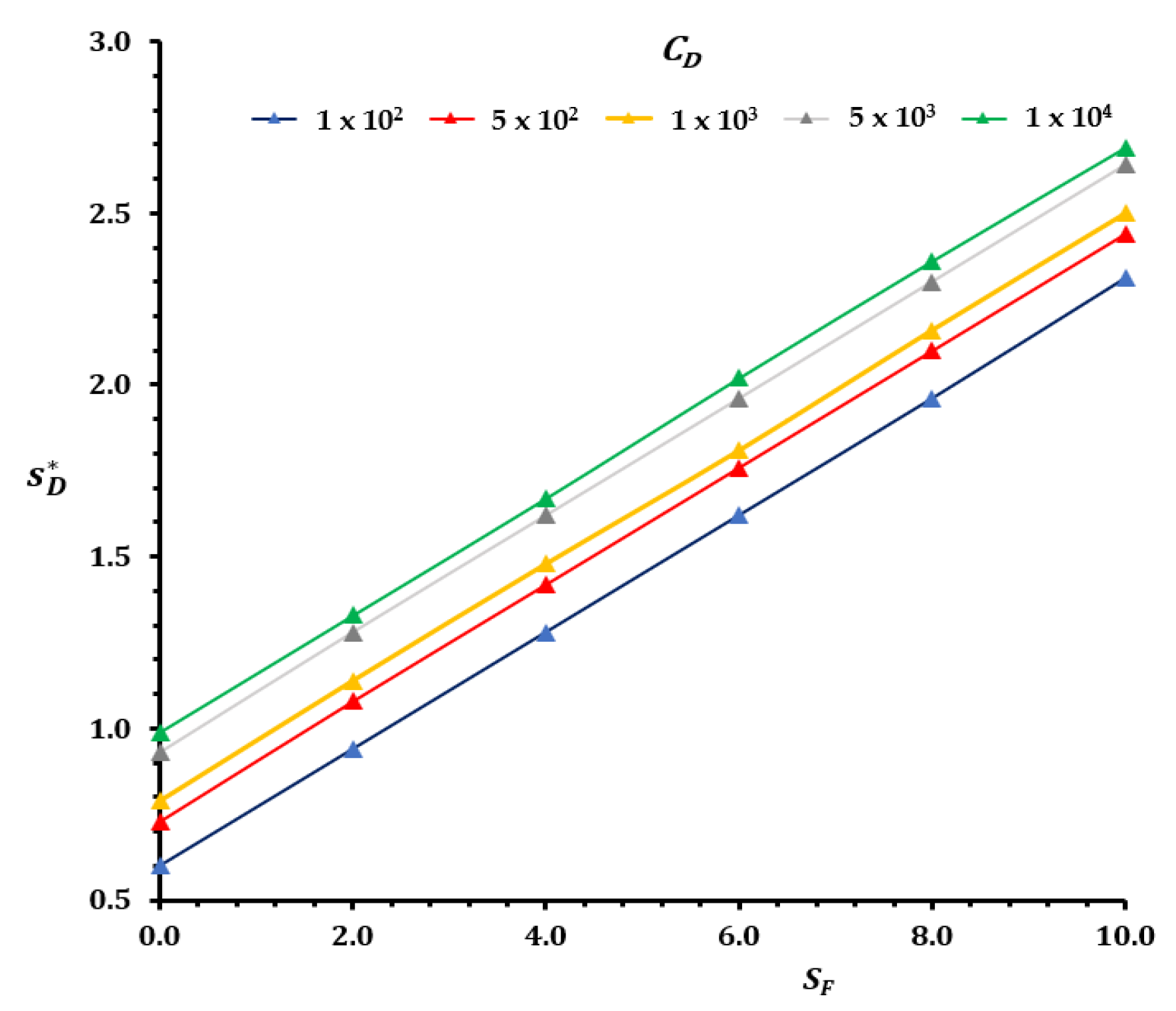
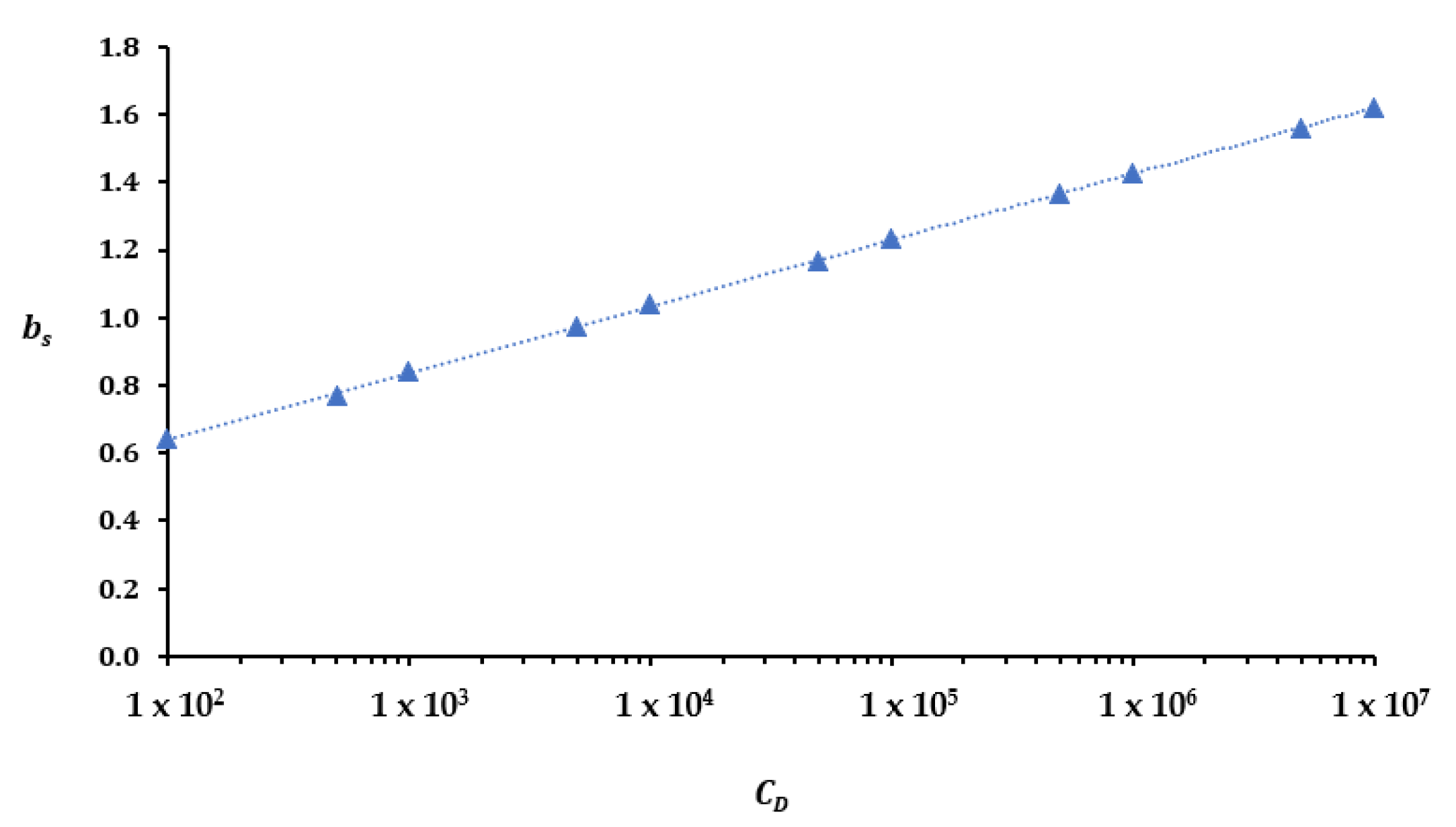
| CD | 1 × 102 | 5 × 102 | 1 × 103 | 5 × 103 | 1 × 104 | 5 × 104 | 1 × 105 | 5 × 105 | 1 × 106 | 5 × 106 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SF | |||||||||||
| 0 | 0.6 | 0.73 | 0.79 | 0.93 | 0.99 | 1.13 | 1.19 | 1.33 | 1.39 | 1.52 | |
| 2 | 0.94 | 1.08 | 1.14 | 1.28 | 1.33 | 1.47 | 1.53 | 1.67 | 1.73 | 1.87 | |
| 4 | 1.28 | 1.42 | 1.48 | 1.62 | 1.67 | 1.82 | 1.86 | 2.01 | 2.07 | 2.20 | |
| 6 | 1.62 | 1.76 | 1.81 | 1.96 | 2.02 | 2.15 | 2.21 | 2.35 | 2.41 | 2.54 | |
| 8 | 1.96 | 2.10 | 2.16 | 2.30 | 2.36 | 2.49 | 2.55 | 2.69 | 2.74 | 2.88 | |
| 10 | 2.31 | 2.44 | 2.50 | 2.64 | 2.69 | 2.83 | 2.89 | 3.02 | 3.08 | 3.21 | |
| 15 | 3.14 | 3.26 | 3.34 | 3.47 | 3.53 | 3.66 | 3.73 | 3.84 | 3.92 | 4.05 | |
| 20 | 3.98 | 4.12 | 4.18 | 4.31 | 4.37 | 4.50 | 4.56 | 4.70 | 4.76 | 4.89 | |
| 25 | 4.82 | 4.95 | 5.01 | 5.14 | 5.20 | 5.34 | 5.40 | 5.53 | 5.58 | 5.71 | |
| 30 | 5.64 | 5.78 | 5.84 | 5.98 | 6.04 | 6.17 | 6.22 | 6.35 | 6.40 | 6.54 | |
| 35 | 6.47 | 6.61 | 6.67 | 6.81 | 6.87 | 7.00 | 7.05 | 7.18 | 7.23 | 7.37 | |
| 40 | 7.30 | 7.44 | 7.50 | 7.64 | 7.70 | 7.83 | 7.88 | 8.01 | 8.06 | 8.20 | |
| 45 | 8.12 | 8.27 | 8.33 | 8.46 | 8.52 | 8.66 | 8.71 | 8.84 | 8.90 | 9.03 | |
| 50 | 8.96 | 9.09 | 9.14 | 9.28 | 9.34 | 9.48 | 9.54 | 9.68 | 9.73 | 9.86 | |
| 60 | 10.62 | 10.76 | 10.82 | 10.95 | 11.00 | 11.13 | 11.19 | 11.32 | 11.37 | 11.49 | |
| 70 | 12.28 | 12.41 | 12.46 | 12.59 | 12.65 | 12.77 | 12.82 | 12.95 | 13.01 | 13.15 | |
| 80 | 13.93 | 14.06 | 14.11 | 14.24 | 14.29 | 14.42 | 14.47 | 14.60 | 14.66 | 14.80 | |
| 90 | 15.58 | 15.71 | 15.76 | 15.89 | 15.94 | 16.07 | 16.12 | 16.25 | 16.30 | 16.43 | |
| 100 | 17.13 | 17.36 | 17.33 | 17.55 | 17.54 | 17.73 | 17.74 | 17.91 | 17.93 | 18.09 | |
| N. | CD | bs |
|---|---|---|
| 1 | 1.0 × 102 | 0.6448 |
| 2 | 5.0 × 102 | 0.7690 |
| 3 | 1.0 × 103 | 0.8420 |
| 4 | 5.0 × 103 | 0.9754 |
| 5 | 1.0 × 104 | 1.0375 |
| 6 | 5.0 × 104 | 1.1689 |
| 7 | 1.0 × 105 | 1.2325 |
| 8 | 5.0 × 105 | 1.3644 |
| 9 | 1.0 × 106 | 1.4272 |
| 10 | 5.0 × 106 | 1.5581 |
| 11 | 1.0 × 107 | 1.6195 |
| (a) | (b) | (c) | |||||
|---|---|---|---|---|---|---|---|
| N. | Time t(s) | Drawdown s (m) | Time t(s) | Drawdown s(m) | N. | Time t(s) | Drawdown s(m) |
| 1. | 130 | 0.02 | 30 | 0.01 | 1. | 60 | 0.08 |
| 2. | 215 | 0.04 | 45 | 0.025 | 2. | 120 | 0.13 |
| 3. | 240 | 0.05 | 60 | 0.03 | 3. | 180 | 0.16 |
| 4. | 300 | 0.08 | 90 | 0.045 | 4. | 300 | 0.21 |
| 5. | 420 | 0.14 | 150 | 0.08 | 5. | 600 | 0.305 |
| 6. | 560 | 0.20 | 180 | 0.09 | 6. | 900 | 0.4 |
| 7. | 800 | 0.28 | 240 | 0.115 | 7. | 1200 | 0.47 |
| 8. | 900 | 0.33 | 300 | 0.135 | 8. | 1800 | 0.62 |
| 9. | 1180 | 0.46 | 600 | 0.25 | 9. | 2700 | 0.75 |
| 10. | 1800 | 0.67 | 900 | 0.34 | 10. | 3600 | 0.84 |
| 11 | 2700 | 1.02 | 1200 | 0.415 | 11 | 4500 | 0.9 |
| 12. | 3600 | 1.25 | 1500 | 0.475 | 12. | 9000 | 1.09 |
| 13. | 5600 | 1.76 | 1800 | 0.54 | 13. | 15,000 | 1.18 |
| 14. | 7200 | 2.20 | 2100 | 0.585 | 14. | 27,000 | 1.25 |
| 15. | 10,800 | 2.78 | 2700 | 0.65 | 15. | 50,000 | 1.27 |
| 16. | 14,200 | 3.14 | 3600 | 0.72 | 16. | 80,000 | 1.285 |
| 17. | 20,000 | 3.51 | 5400 | 0.82 | |||
| 18. | 30,000 | 3.91 | 7200 | 0.875 | |||
| 19. | 44,000 | 4.15 | 10,800 | 0.955 | |||
| 20. | 70,000 | 4.32 | 14,400 | 0.98 | |||
| 21. | 100,000 | 4.41 | 25,000 | 1.01 | |||
| 22. | 200,000 | 4.47 | 40,000 | 1.02 | |||
| 23. | 400,000 | 4.50 | 72,000 | 1.03 | |||
| Before Rehabilitation | After Rehabilitation | 1 Year after Rehabilitation | |
|---|---|---|---|
| Pumping rate, Q (m3·s−1) | 0.00335 | 0.0037 | 0.00352 |
| Pumping test duration (s) | 400,000 | 72,000 | 80,000 |
| s* (m) | 0.62 | 0.135 | 0.18 |
| New method (Equation (34)) | 47 | 6.8 | 10.8 |
| Cooper–Jacob method (Equation (16)) | 51 | 7.9 | 12 |
| Difference (%) | 8.4 | 15 | 11.1 |
| Additional drawdown sskin (Equation (12)) | 3.51 | 0.56 | 0.85 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kahuda, D.; Pech, P. A New Method for the Evaluation of Well Rehabilitation from the Early Portion of a Pumping Test. Water 2020, 12, 744. https://doi.org/10.3390/w12030744
Kahuda D, Pech P. A New Method for the Evaluation of Well Rehabilitation from the Early Portion of a Pumping Test. Water. 2020; 12(3):744. https://doi.org/10.3390/w12030744
Chicago/Turabian StyleKahuda, Daniel, and Pavel Pech. 2020. "A New Method for the Evaluation of Well Rehabilitation from the Early Portion of a Pumping Test" Water 12, no. 3: 744. https://doi.org/10.3390/w12030744
APA StyleKahuda, D., & Pech, P. (2020). A New Method for the Evaluation of Well Rehabilitation from the Early Portion of a Pumping Test. Water, 12(3), 744. https://doi.org/10.3390/w12030744





