Estimation and Mapping of the Transmissivity of the Nubian Sandstone Aquifer in the Kharga Oasis, Egypt
Abstract
1. Introduction
2. Methods
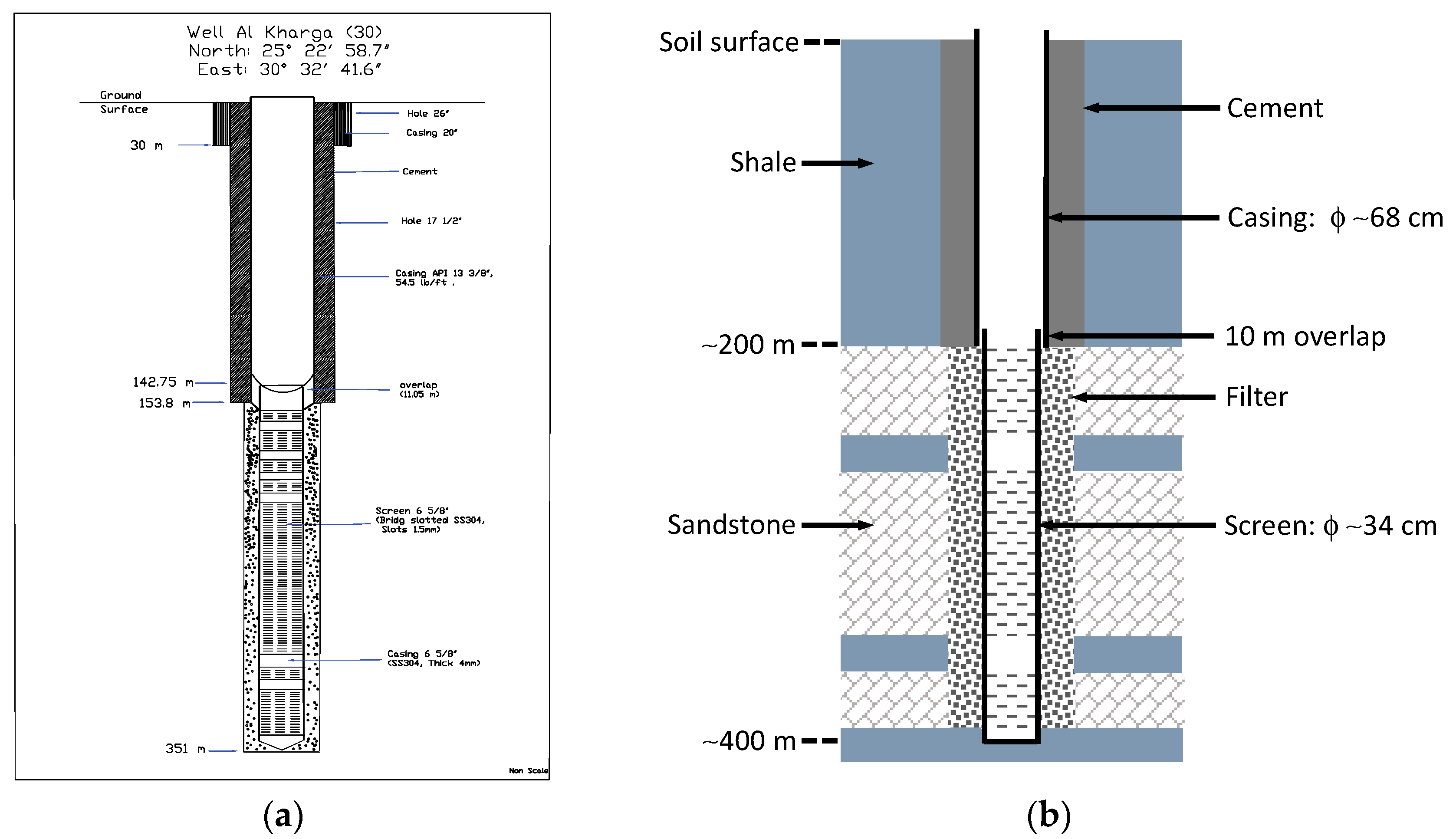
2.1. Study Area and Data
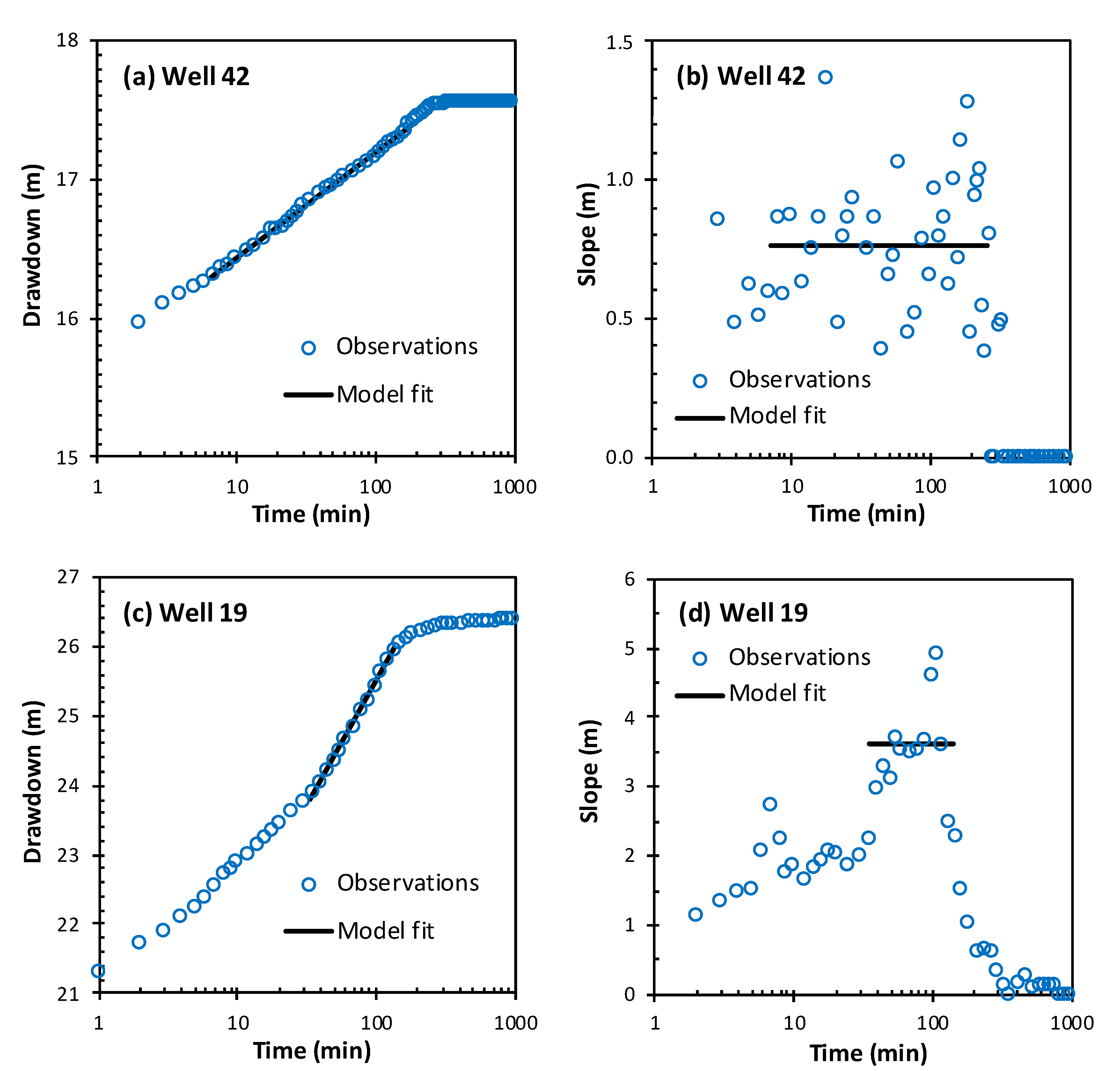
2.2. Pumping Test Analysis
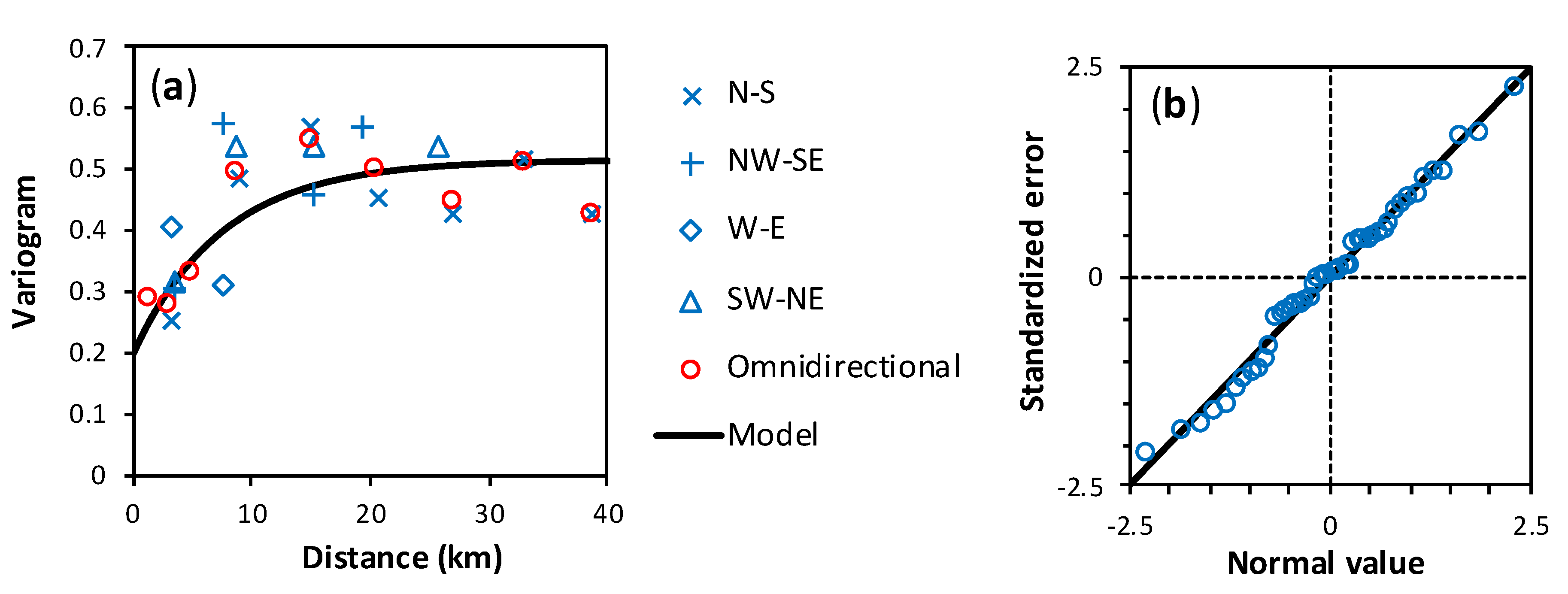
2.3. Geostatistical Analysis
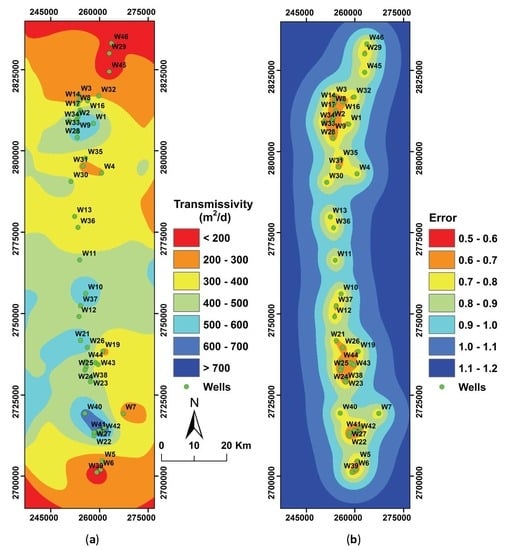
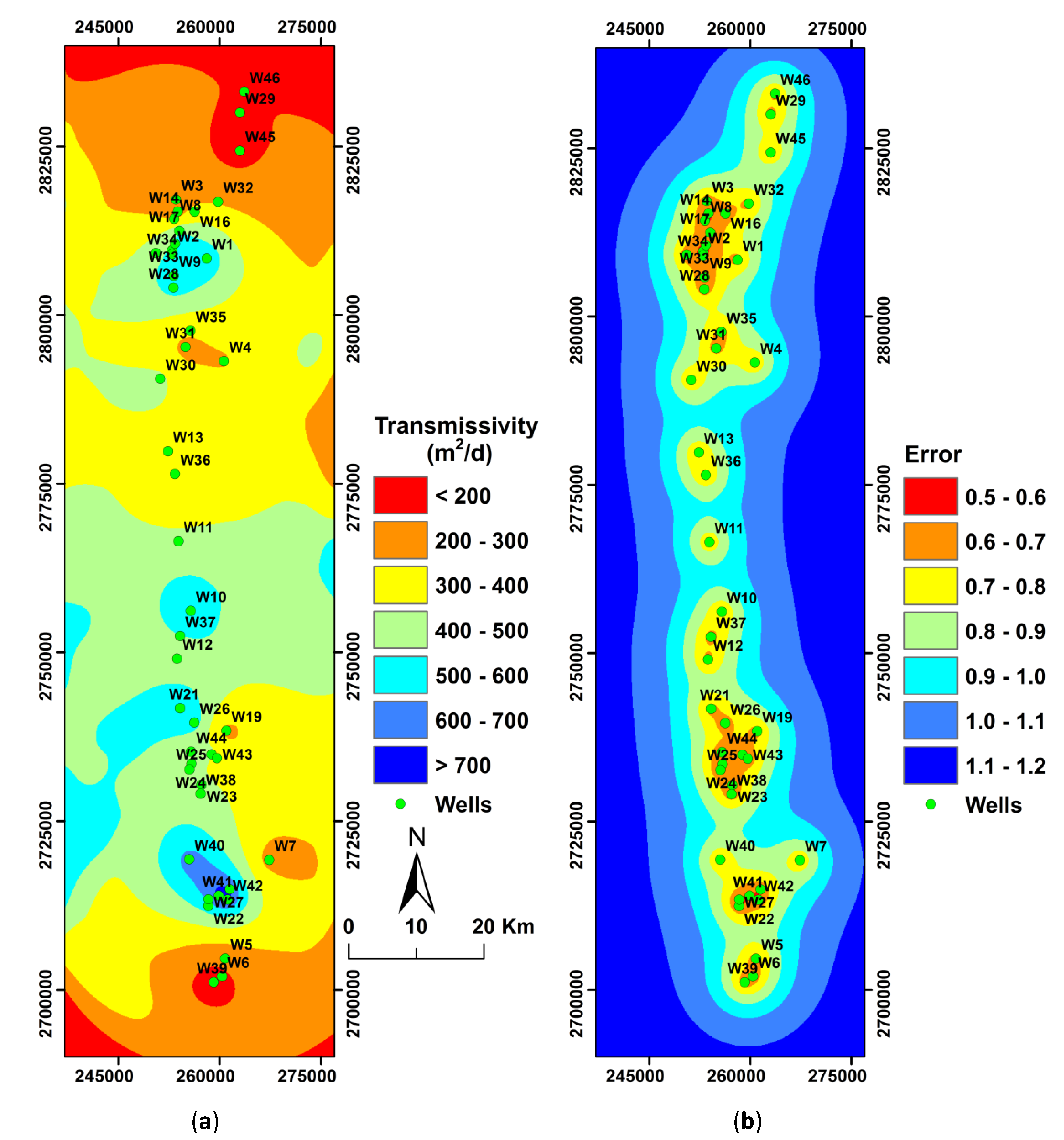
3. Results
3.1. Pumping Test Analyses
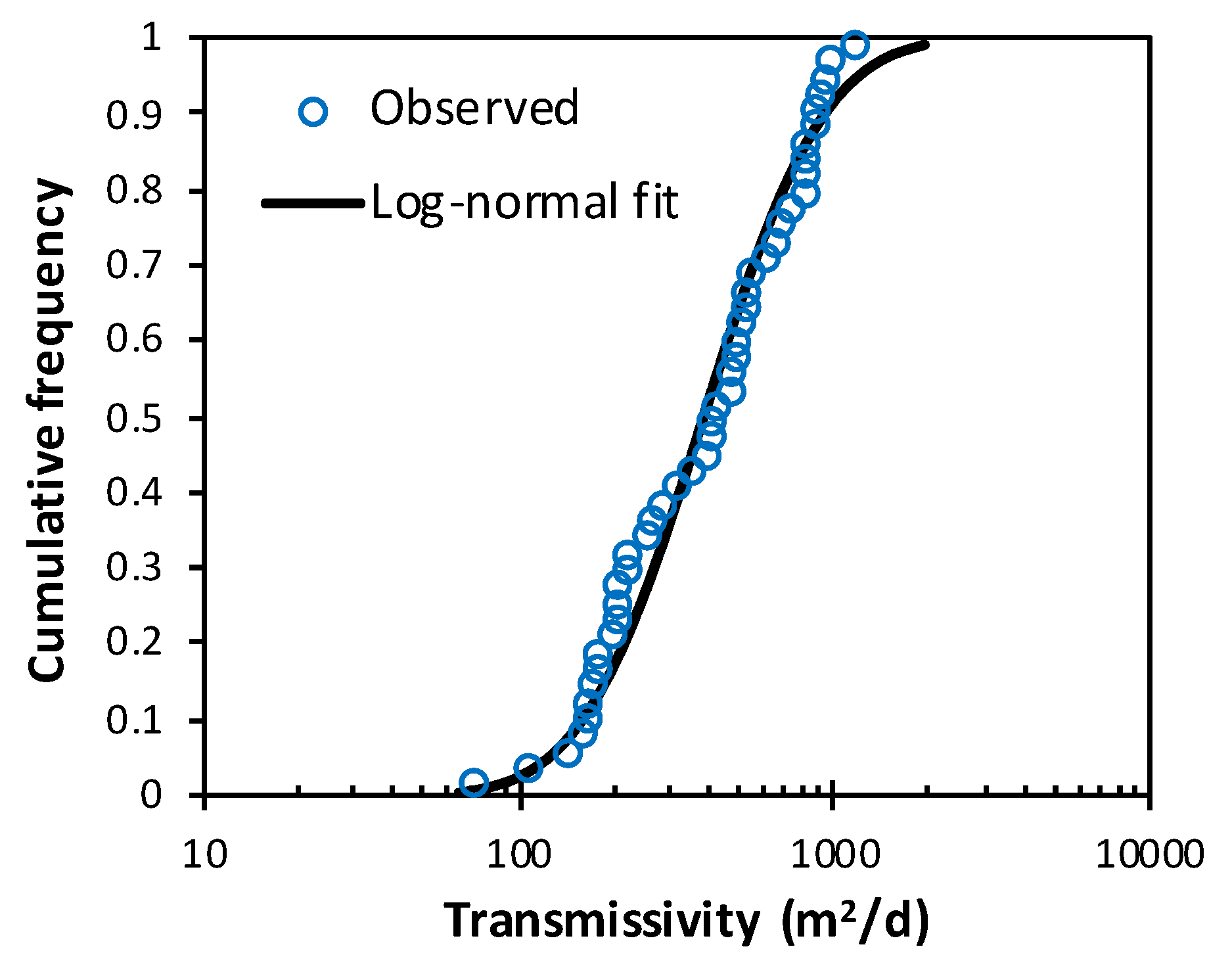
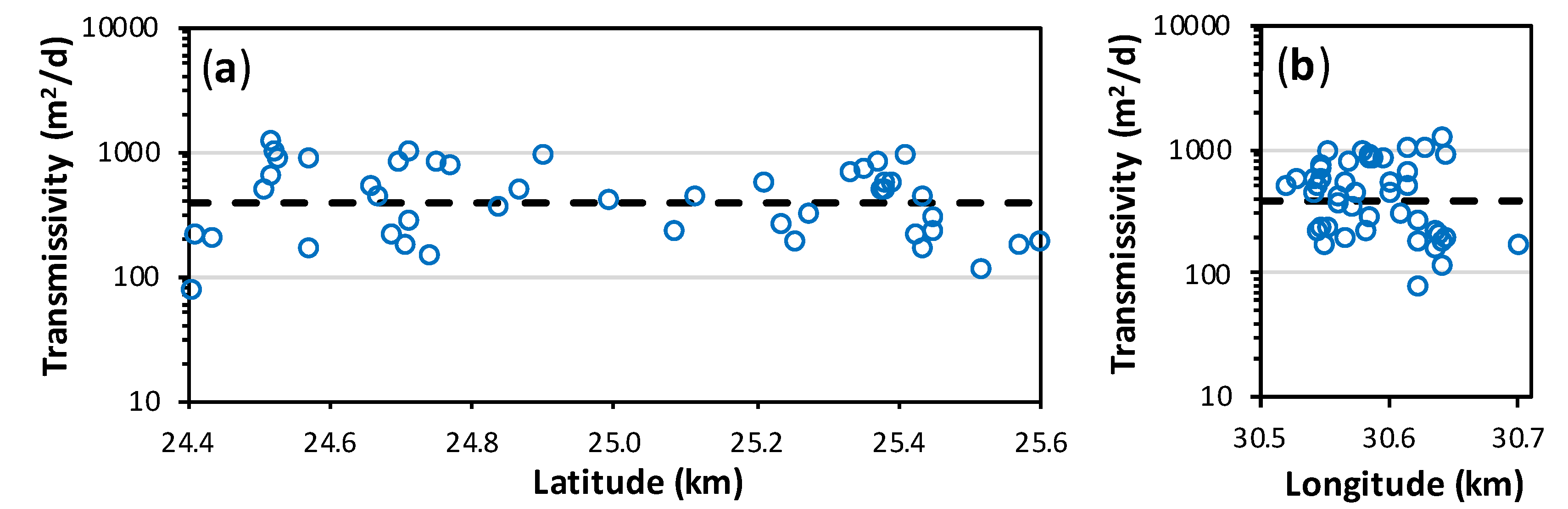
3.2. Statistical Analysis of Transmissivity
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- El-Rawy, M.; Abdalla, F.; El Alfy, M. Water Resources in Egypt. In The Geology of Egypt; Hamimi, Z., El-Barkooky, A., Martínez Frías, J., Fritz, H., Abd El-Rahman, Y., Eds.; Regional Geology Reviews, Springer Nature: Cham, Switzerland, 2020; pp. 687–711. [Google Scholar] [CrossRef]
- CEDARE. Nubian Sandstone Aquifer System (NSAS) M&E Rapid Assessment Report; Monitoring & Evaluation for Water in North Africa (MEWINA) Project, Water Resources Management Program; CEDARE: Cairo Governorate, Egypt, 2014; p. 95. [Google Scholar]
- Shata, A.A. Hydrogeology of the Great Nubian Sandstone basin, Egypt. Q. J. Eng. Geol. 1982, 15, 127–133. [Google Scholar] [CrossRef]
- Mohamed, A.; Sultan, M.; Ahmed, M.; Yan, E.; Ahmed, E. Aquifer recharge, depletion, and connectivity: Inferences from GRACE, land surface models, and geochemical and geophysical data. Geol. Soc. Am. Bull. 2017, 129, 534–546. [Google Scholar] [CrossRef]
- MWRI. National Water Resources Plan 2017; Ministry of Water Resources and Irrigation Planning Sector; Arab Republic of Egypt: Cairo, Egypt, 2005; p. 268. [Google Scholar]
- Heinl, M.; Thorweihe, U. Groundwater Resources and Management in SW Egypt. In Geopotential and Ecology: Analysis of a Desert Region; Meissner, B., Wycisk, P., Eds.; Catena Suppl. 26: Reiskirchen, Germany, 1993; pp. 99–122. [Google Scholar]
- Salman, A.B.; Howari, F.M.; El-Sankary, M.M.; Wali, A.M.; Saleh, M.M. Environmental impact and natural hazards on Kharga Oasis monumental sites, Western Desert of Egypt. J. Afr. Earth Sci. 2010, 58, 341–353. [Google Scholar] [CrossRef]
- Lamoreaux, P.E.; Memon, B.A.; Idris, H. Groundwater development, Kharga Oases, Western Desert of Egypt: A long-term environment concern. Environ. Geol. Water Sci. 1985, 7, 129–149. [Google Scholar] [CrossRef]
- Ebraheem, A.M.; Riad, S.; Wycisk, P.; Seif El-Nasr, A.M. Simulation of impact of present and future groundwater extraction from the non-replenished Nubian Sandstone Aquifer in southwest Egypt. Environ. Geol. 2002, 43, 188–196. [Google Scholar]
- Younis, A.; Soliman, M.; Moussa, S.; Massoud, U.; Abd ElNabi, S.; Attia, M. Integrated geophysical application to investigate groundwater potentiality of the shallow Nubian aquifer at northern Kharga, Western Desert, Egypt. NRIAG J. Astron. Geophys. 2016, 5, 186–198. [Google Scholar] [CrossRef]
- Assaad, F.A. Hydrogeological aspects and environmental concerns of the New Valley Project, Western Dessert, Egypt, with special emphasis on the southern area. Envir. Geol. Water Sci. 1988, 12, 142–161. [Google Scholar] [CrossRef]
- Mahmod, W.E.; Watanabe, K.; Zahr-Eldeen, A.A. Analysis of groundwater flow in arid areas with limited hydrogeological data using the Grey Model: A case study of the Nubian Sandstone, Kharga Oasis, Egypt. Hydrogeol. J. 2013, 21, 1021–1034. [Google Scholar] [CrossRef]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology; John Wiley & Sons: New York, NY, USA, 1990; p. 824. [Google Scholar]
- Mahmod, W.E.; Watanabe, K. Modified Grey Model and its application to groundwater flow analysis with limited hydrogeological data: A case study of the Nubian Sandstone, Kharga Oasis, Egypt. Environ. Monit. Assess. 2014, 186, 1063–1081. [Google Scholar] [CrossRef] [PubMed]
- Elewa, H.; Fathy, R.G.; Qaddah, A. The contribution of geographic information systems and remote sensing in determining priority areas for hydrogeological development, Darb el-Arbain area, Western Desert, Egypt. Hydrogeol. J. 2010, 18, 1157–1171. [Google Scholar] [CrossRef]
- Hamdan, A.M.; Sawires, R.F. Hydrogeological studies on the Nubian sandstone aquifer in El-Bahariya Oasis, Western Desert, Egypt. Arab. J. Geosci. 2013, 6, 1333–1347. [Google Scholar] [CrossRef]
- Masoud, M.H.; El Osta, M.M. Evaluation of groundwater vulnerability in El-Bahariya Oasis, Western Desert, Egypt, using modelling and GIS techniques: A case study. J. Earth. Syst. Sci. 2016, 125, 1139–1155. [Google Scholar] [CrossRef]
- Kehl, H.; Bornkamm, R. Landscape ecology and vegetation units of the Western Desert of Egypt. In Geopotential and Ecology: Analysis of a Desert Region; Meissner, B., Wycisk, P., Eds.; Catena Suppl. 26: Reiskirchen, Germany, 1993; pp. 155–178. [Google Scholar]
- Zahran, M.A.; Willis, A.J. The Vegetation of Egypt; Chapman & Hall: London, UK, 2009; p. 424. [Google Scholar]
- Kruseman, G.P.; de Ridder, N.A. Analysis and Evaluation of Pumping Test Data; International Institute for Land Reclamation and Improvement, Publication 47: Wageningen, The Netherlands, 1991; p. 377. [Google Scholar]
- Nielsen, K.A. Fractured Aquifers-Formation Evaluation by Well Testing; Trafford Publishing: Victoria, BC, Canada, 2008; p. 230. [Google Scholar]
- Batu, V. Aquifer Hydraulics: A Comprehensive Guide to Hydrogeologic Data Analysis; John Wiley & Sons Inc.: New York, NY, USA, 1998; p. 727. [Google Scholar]
- Theis, C.V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground water storage. Eos Trans. Am. Geophys. Union 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997; p. 483. [Google Scholar]
- Ribeiro, P.J., Jr.; Diggle, P.J. geoR: A package for geostatistical analysis. R News 2001, 1, 15–18. [Google Scholar]
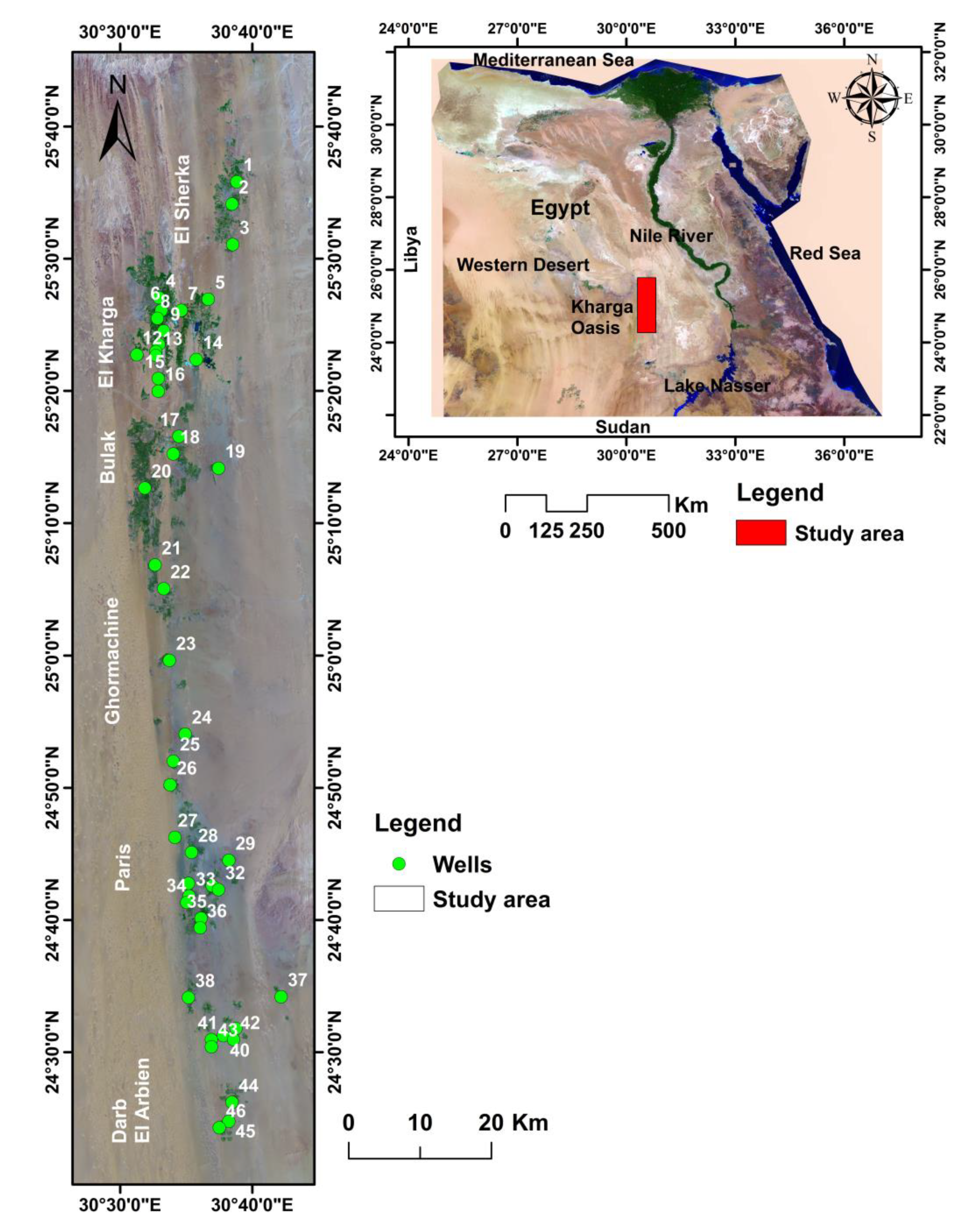
| Well | Location | Latitude | Longitude | Depth (m) | h (m) | Q (m3/h) | s1 (m) | sm (m) | (m2/d) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | El-Sherka | 25.597 | 30.647 | 405 | 54.40 | 120 | 30.80 | 53.60 | 180 |
| 2 | El-Sherka | 25.569 | 30.641 | 712 | 78.24 | 200 | 16.58 | 24.80 | 171 |
| 3 | El-Sherka | 25.518 | 30.642 | 349 | 63.50 | 80 | 22.30 | 36.45 | 109 |
| 4 | El-Kharga | 25.451 | 30.549 | 312 | 45.38 | 180 | 6.46 | 11.58 | 222 |
| 5 | El-Kharga | 25.449 | 30.611 | 784 | 66.00 | 200 | 9.70 | 20.52 | 294 |
| 6 | El-Kharga | 25.435 | 30.552 | 307 | 40.03 | 200 | 15.22 | 21.95 | 163 |
| 7 | El-Kharga | 25.435 | 30.577 | 412 | 89.35 | 200 | 9.56 | 13.44 | 422 |
| 8 | El-Kharga | 25.425 | 30.547 | 315 | 62.80 | 200 | 7.33 | 18.88 | 207 |
| 9 | El-Kharga | 25.409 | 30.555 | 304 | 29.16 | 200 | 7.02 | 12.91 | 932 |
| 10 | El-Kharga | 25.392 | 30.549 | 313 | 25.00 | 200 | 3.50 | 11.60 | 553 |
| 11 | El-Kharga | 25.383 | 30.545 | 351 | 24.20 | 200 | 5.61 | 8.74 | 537 |
| 12 | El-Kharga | 25.379 | 30.521 | 640 | 72.00 | 202 | 1.95 | 10.80 | 473 |
| 13 | El-Kharga | 25.378 | 30.545 | 737 | 22.50 | 220 | 8.04 | 11.54 | 477 |
| 14 | El-Kharga | 25.373 | 30.596 | 358 | 11.78 | 200 | 18.72 | 23.02 | 826 |
| 15 | Genah | 25.349 | 30.548 | 327 | 26.65 | 200 | 10.47 | 13.95 | 687 |
| 16 | Port Said | 25.333 | 30.548 | 357 | 30.33 | 200 | 9.12 | 11.97 | 668 |
| 17 | Genah | 25.276 | 30.574 | 750 | 39.00 | 230 | 15.40 | 22.34 | 317 |
| 18 | Bulaq | 25.254 | 30.567 | 485 | 23.70 | 220 | 23.30 | 39.10 | 181 |
| 19 | Bulaq | 25.236 | 30.624 | 421 | 26.78 | 200 | 21.30 | 26.37 | 260 |
| 20 | Bulaq | 25.211 | 30.531 | 430 | - | 220 | 11.70 | 15.73 | 542 |
| 21 | Ghormachine | 25.114 | 30.544 | 470 | 25.34 | 300 | 36.76 | 49.21 | 417 |
| 22 | Ghormachine | 25.084 | 30.555 | 495 | 43.00 | 207 | 8.35 | 22.50 | 221 |
| 23 | Ghormachine | 24.994 | 30.562 | 574 | 39.36 | 220 | 18.89 | 25.07 | 407 |
| 24 | Ghormachine | 24.901 | 30.582 | 588 | 36.50 | 200 | 18.30 | 21.40 | 898 |
| 25 | Ghormachine | 24.867 | 30.567 | 732 | 36.00 | 220 | 13.20 | 20.91 | 497 |
| 26 | Ghormachine | 24.837 | 30.563 | 673 | 28.40 | 200 | 17.60 | 23.80 | 354 |
| 27 | Paris | 24.771 | 30.569 | 434 | 30.38 | 220 | 18.71 | 22.91 | 749 |
| 28 | Paris | 24.752 | 30.590 | 447 | 28.00 | 225 | 20.50 | 23.90 | 821 |
| 29 | Paris | 24.742 | 30.637 | 444 | - | 150 | 19.10 | 21.48 | 147 |
| 30 | Paris, Ain Ramah | 24.713 | 30.586 | 534 | 37.20 | 230 | 7.40 | 19.79 | 270 |
| 31 | Paris | 24.710 | 30.616 | 435 | 38.15 | 180 | 12.90 | 15.17 | 975 |
| 32 | Paris, Ain Alhajjar | 24.705 | 30.624 | 469 | 47.00 | 225 | 9.22 | 28.92 | 173 |
| 33 | Paris | 24.697 | 30.587 | 434 | 35.73 | 220 | 18.75 | 21.80 | 827 |
| 34 | Paris | 24.689 | 30.584 | 385 | 39.00 | 200 | 23.33 | 33.18 | 212 |
| 35 | Paris, El-Balad | 24.669 | 30.602 | 475 | 45.00 | 200 | 20.90 | 26.23 | 432 |
| 36 | Paris | 24.657 | 30.601 | 384 | 37.50 | 210 | 16.02 | 24.08 | 521 |
| 37 | Dosh | 24.570 | 30.703 | 298 | 38.60 | 220 | 23.49 | 34.50 | 166 |
| 38 | Paris | 24.569 | 30.586 | 403 | - | 260 | 19.95 | 25.36 | 883 |
| 39 | Paris | 24.530 | 30.646 | 420 | 34.12 | 150 | 17.20 | 20.01 | 841 |
| 40 | Paris | 24.521 | 30.630 | 424 | 30.10 | 210 | 14.57 | 16.70 | 957 |
| 41 | Paris | 24.516 | 30.615 | 427 | 33.60 | 210 | 11.60 | 17.55 | 625 |
| 42 | Paris | 24.516 | 30.643 | 348 | 33.54 | 220 | 20.27 | 24.13 | 1201 |
| 43 | Paris, El-Kasr | 24.507 | 30.615 | 325 | 39.50 | 215 | 14.87 | 19.56 | 494 |
| 44 | Darb El-Arbaien | 24.437 | 30.641 | 280 | 41.96 | 150 | 15.14 | 21.20 | 200 |
| 45 | Darb El-Arbaien | 24.413 | 30.637 | 235 | 55.25 | 150 | 18.75 | 27.88 | 212 |
| 46 | Paris, Zaynab El-Deeb | 24.405 | 30.625 | 225 | 53.00 | 170 | 11.50 | 25.82 | 73 |
| Parameter | Symbol | Units | Value |
|---|---|---|---|
| Mean | - | 5.95 | |
| Variance | - | 0.472 | |
| Nugget | - | 0.199 | |
| Sill | - | 0.517 | |
| Range | km | 22.58 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Rawy, M.; De Smedt, F. Estimation and Mapping of the Transmissivity of the Nubian Sandstone Aquifer in the Kharga Oasis, Egypt. Water 2020, 12, 604. https://doi.org/10.3390/w12020604
El-Rawy M, De Smedt F. Estimation and Mapping of the Transmissivity of the Nubian Sandstone Aquifer in the Kharga Oasis, Egypt. Water. 2020; 12(2):604. https://doi.org/10.3390/w12020604
Chicago/Turabian StyleEl-Rawy, Mustafa, and Florimond De Smedt. 2020. "Estimation and Mapping of the Transmissivity of the Nubian Sandstone Aquifer in the Kharga Oasis, Egypt" Water 12, no. 2: 604. https://doi.org/10.3390/w12020604
APA StyleEl-Rawy, M., & De Smedt, F. (2020). Estimation and Mapping of the Transmissivity of the Nubian Sandstone Aquifer in the Kharga Oasis, Egypt. Water, 12(2), 604. https://doi.org/10.3390/w12020604