Hydraulic Optimization of Double Chamber Surge Tank Using NSGA-II
Abstract
1. Introduction
2. Material and Methods
2.1. Governing Equations
2.2. Method of Characteristics
2.3. Boundary Conditions
2.3.1. Surge Tank
2.3.2. Valve in Line
2.4. Modeling
2.5. Objective Functions
2.5.1. Upsurge
2.5.2. Downsurge
2.5.3. Damping
2.6. Variables and Constraints
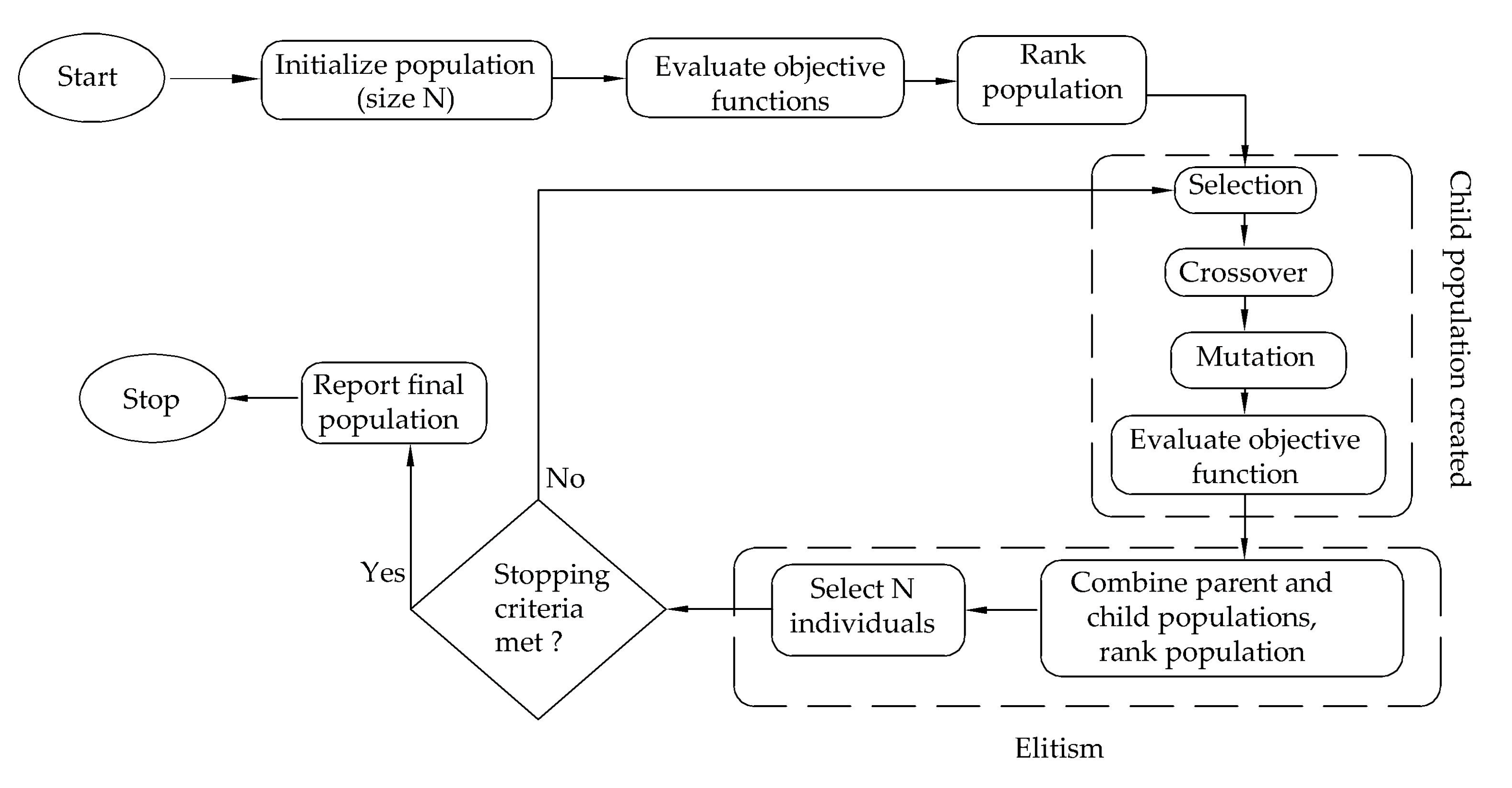
2.7. NSGA-II
3. Results and Discussions
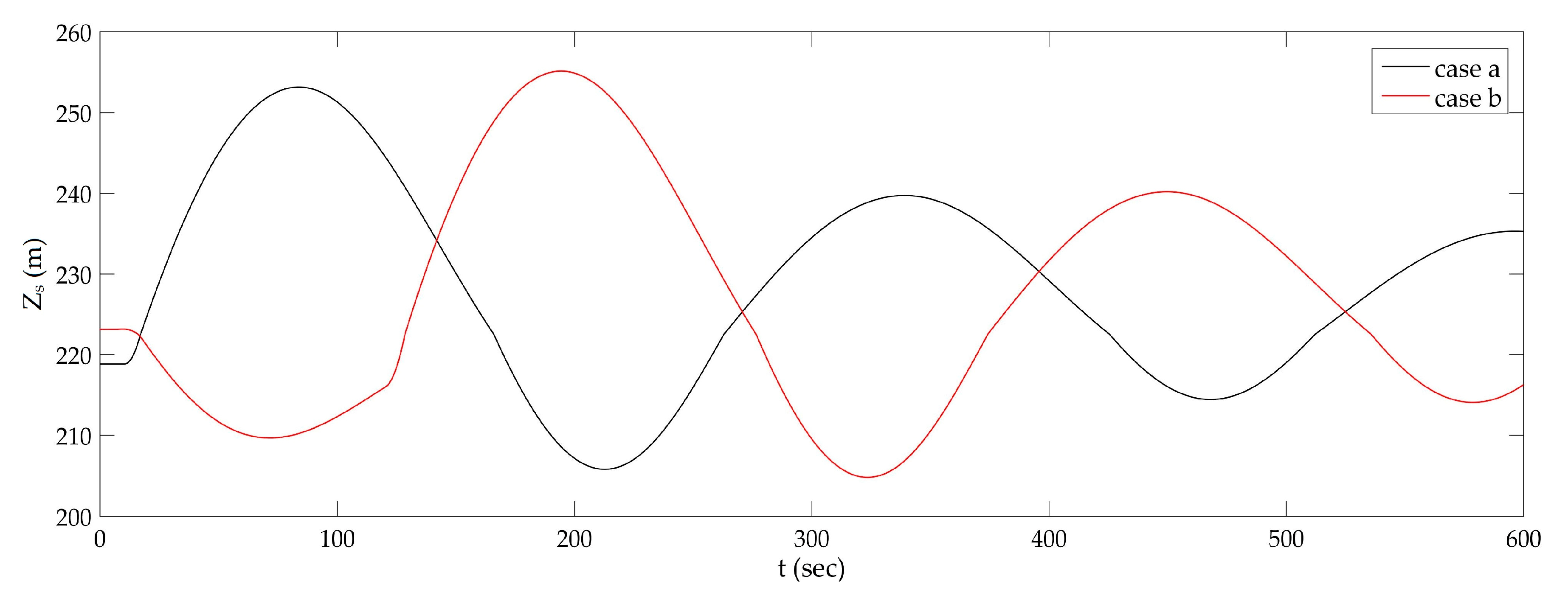
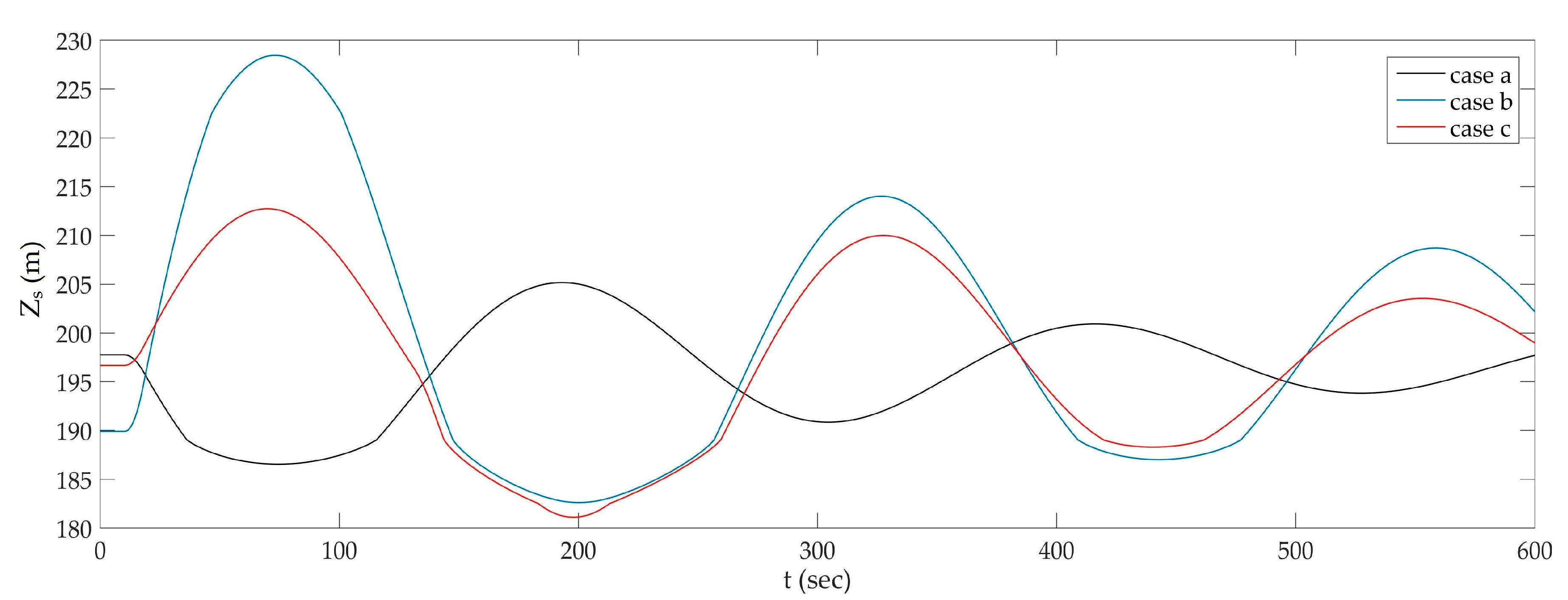
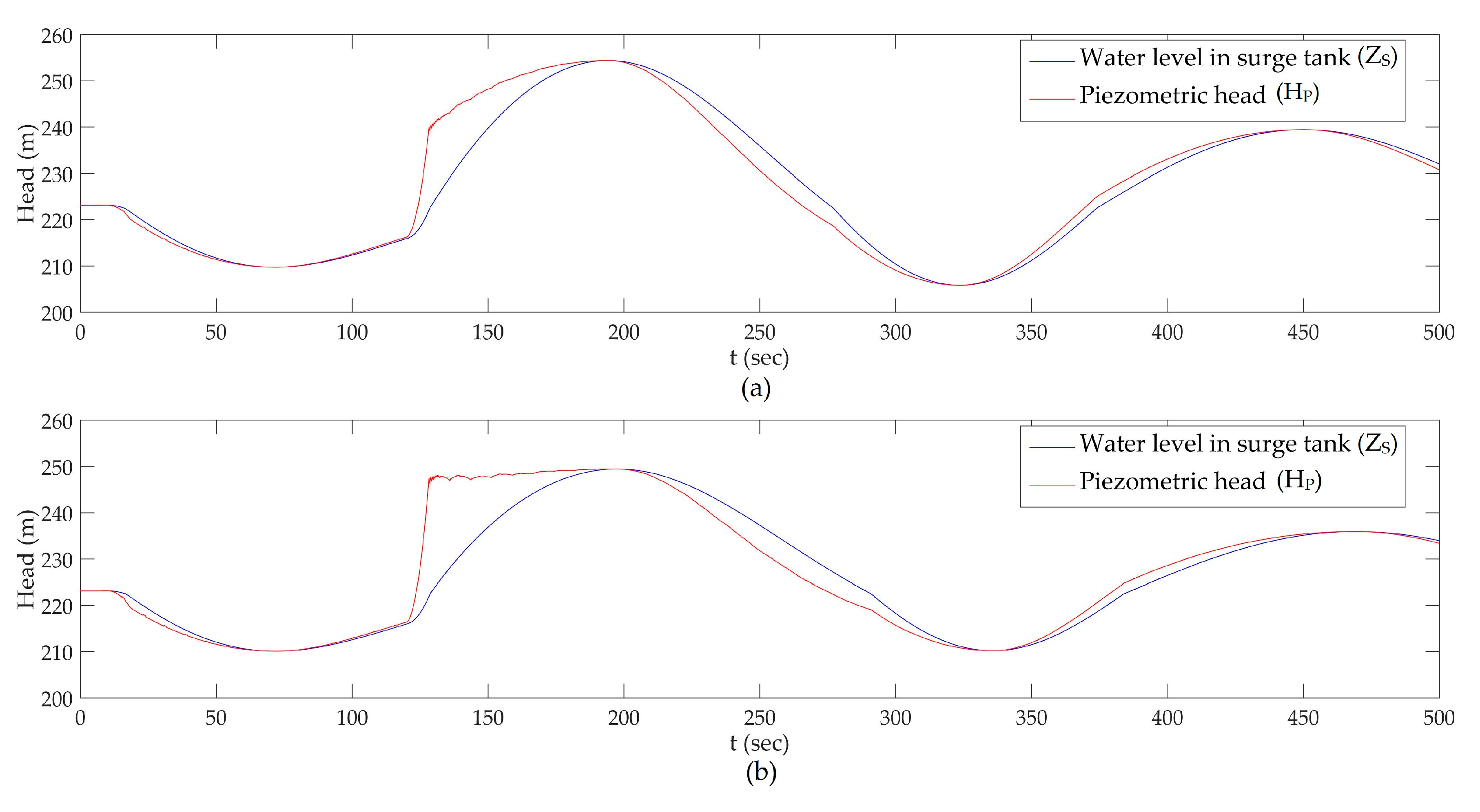
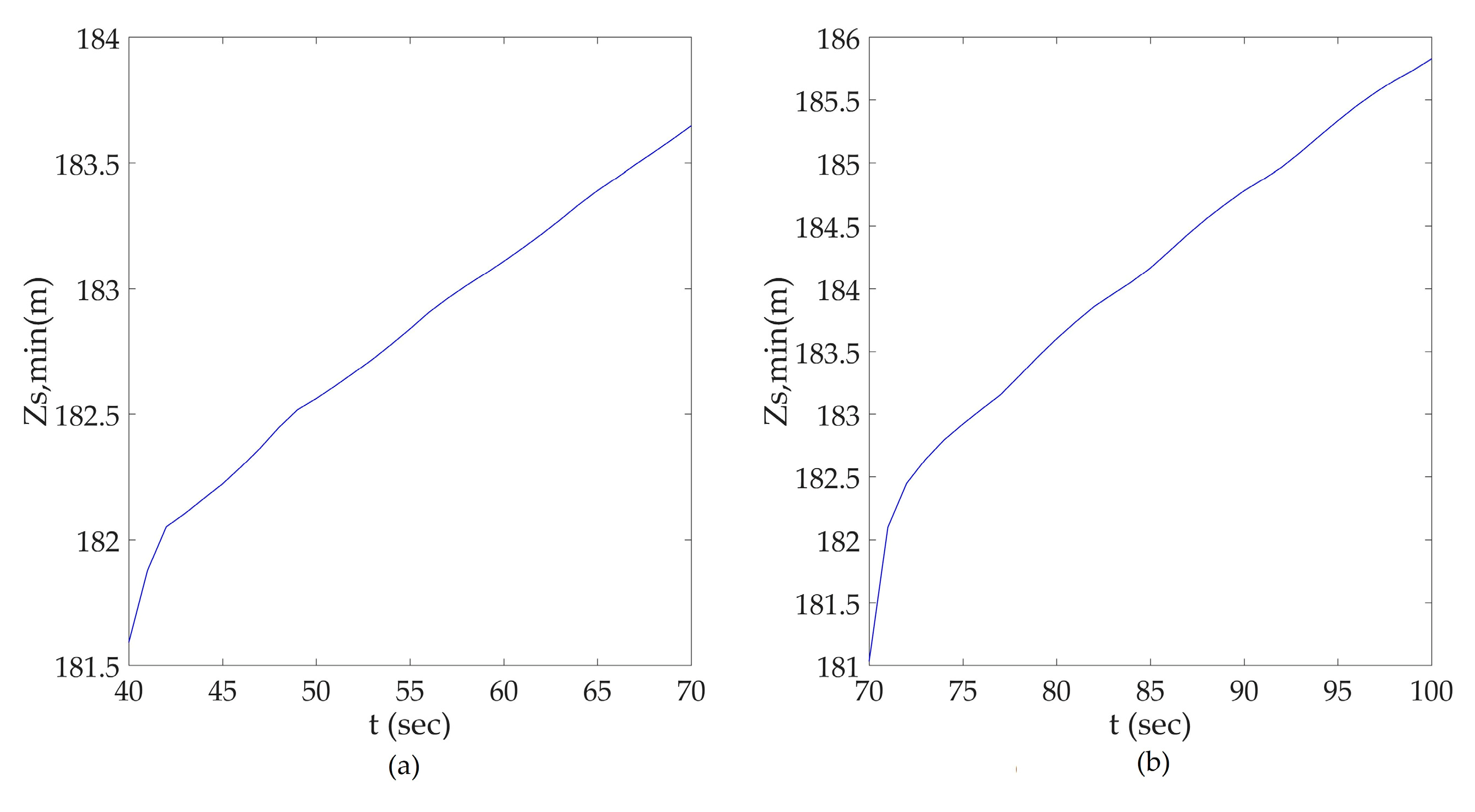
3.1. Surge Analysis
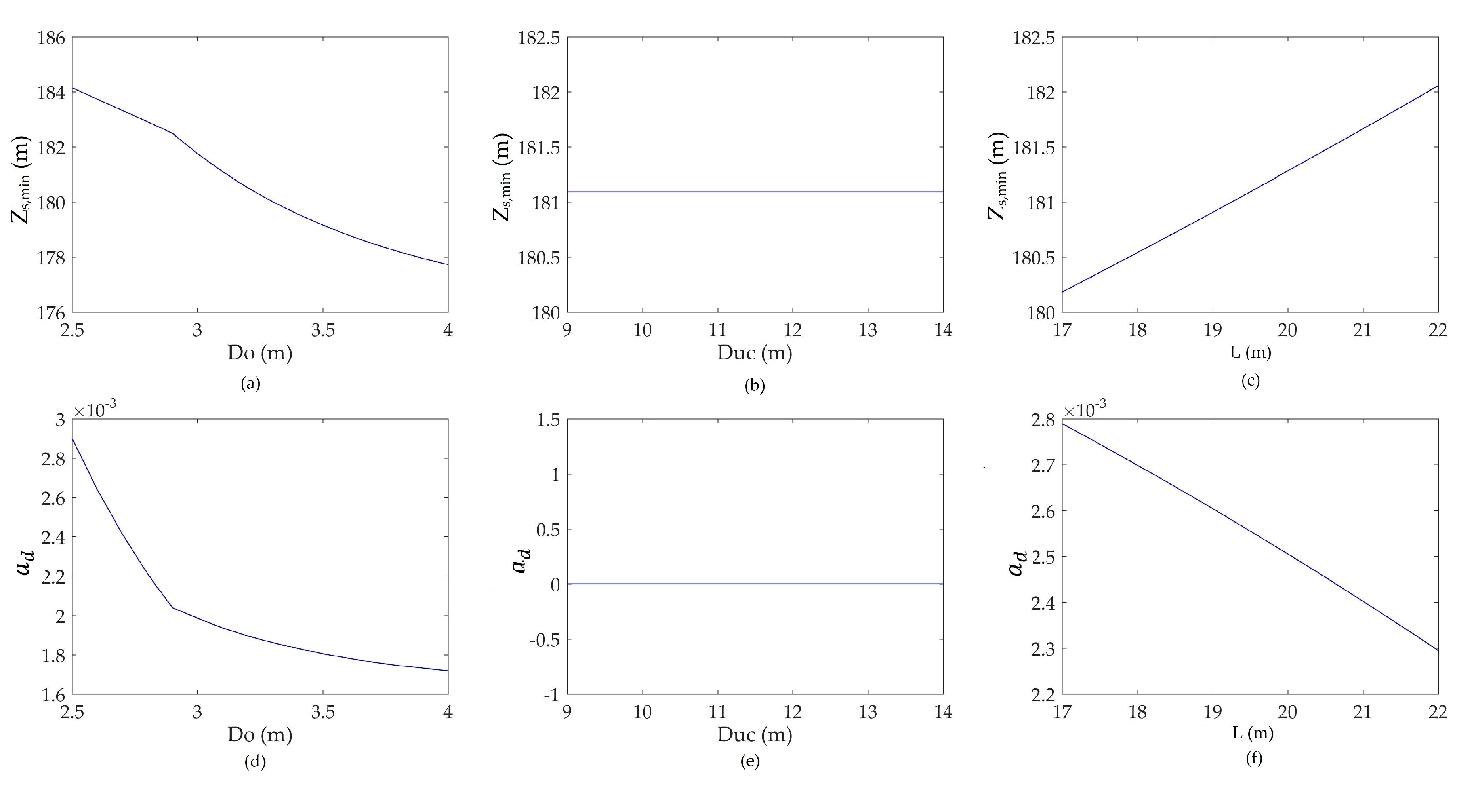
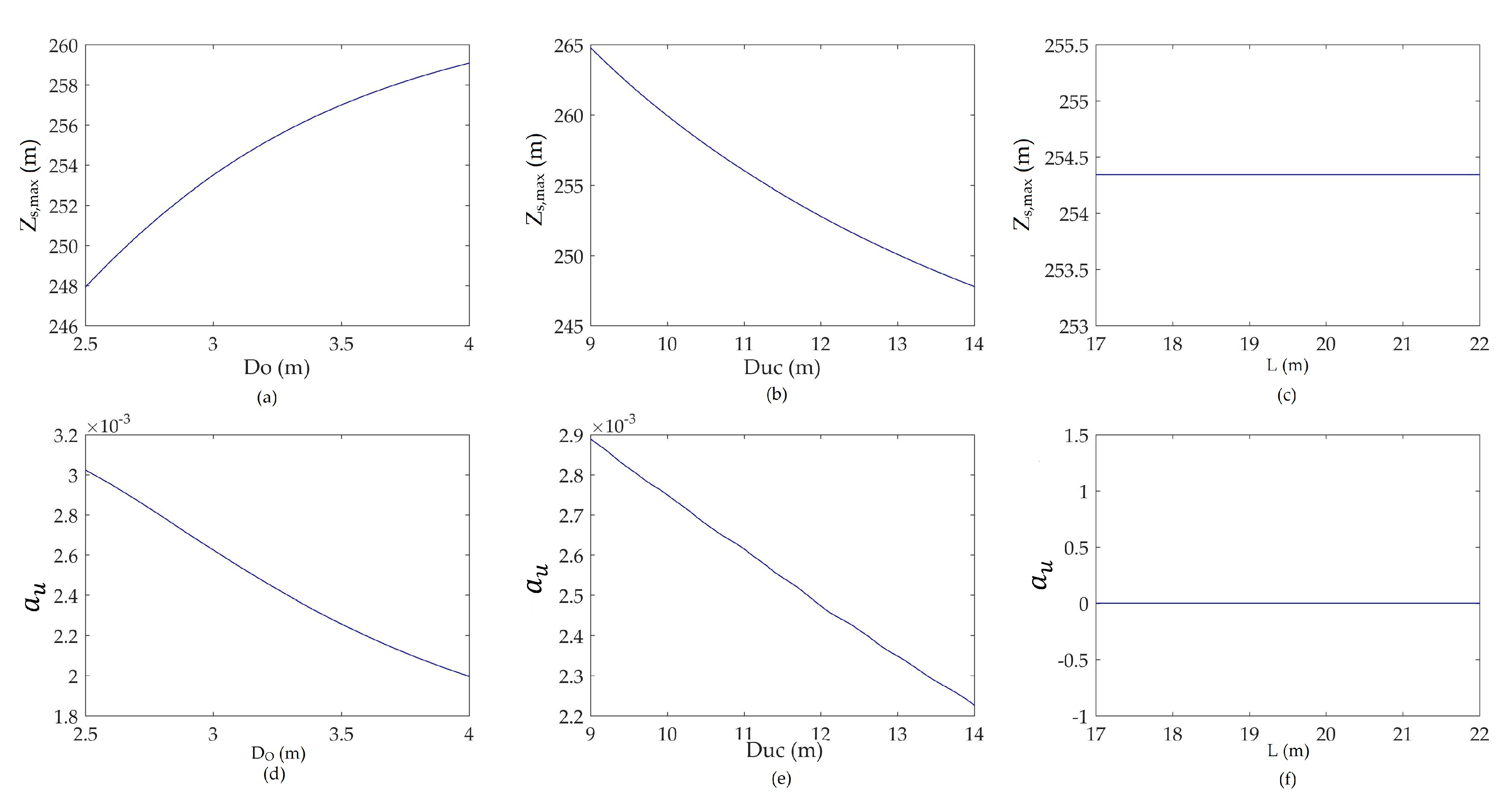
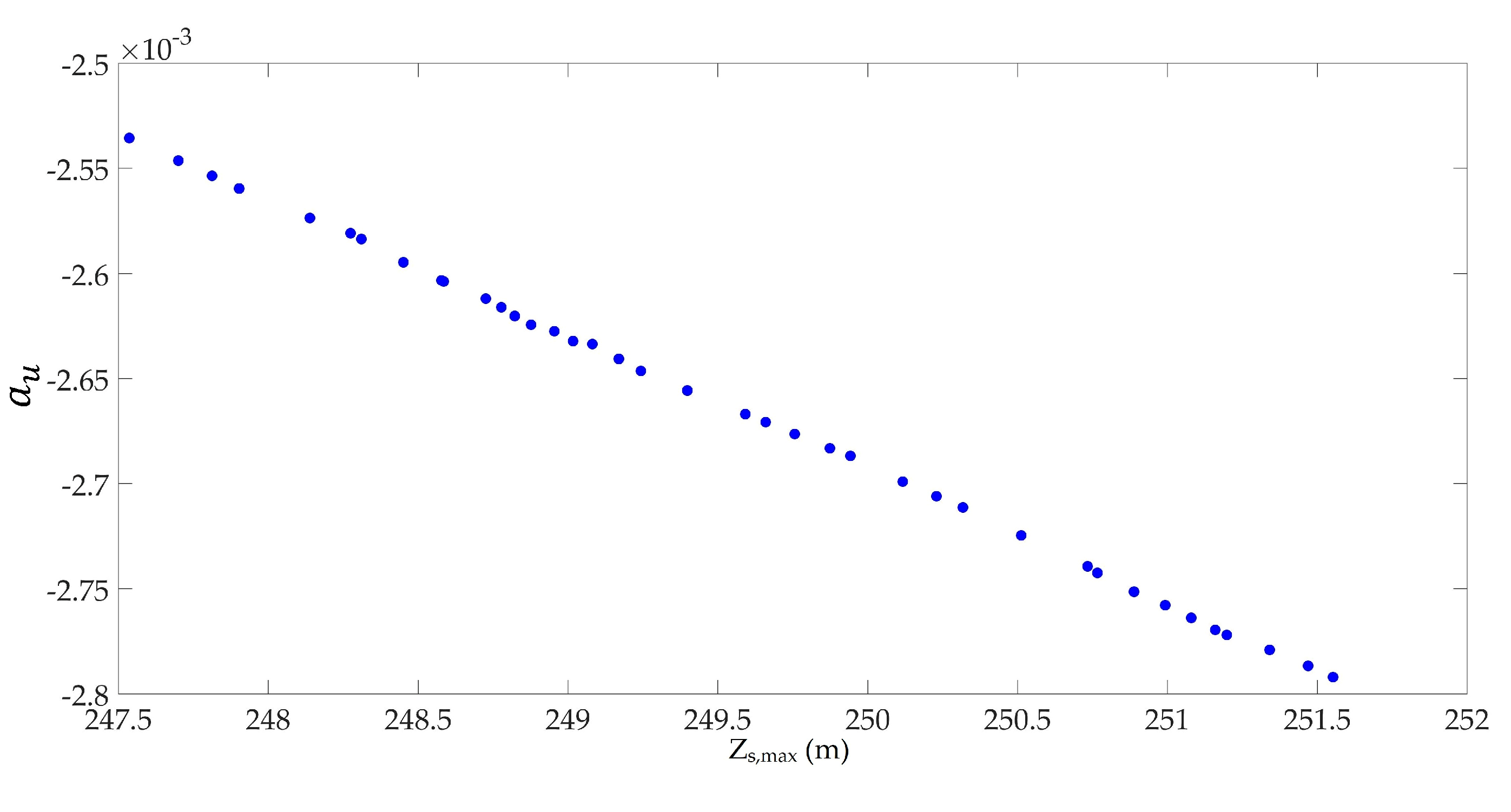
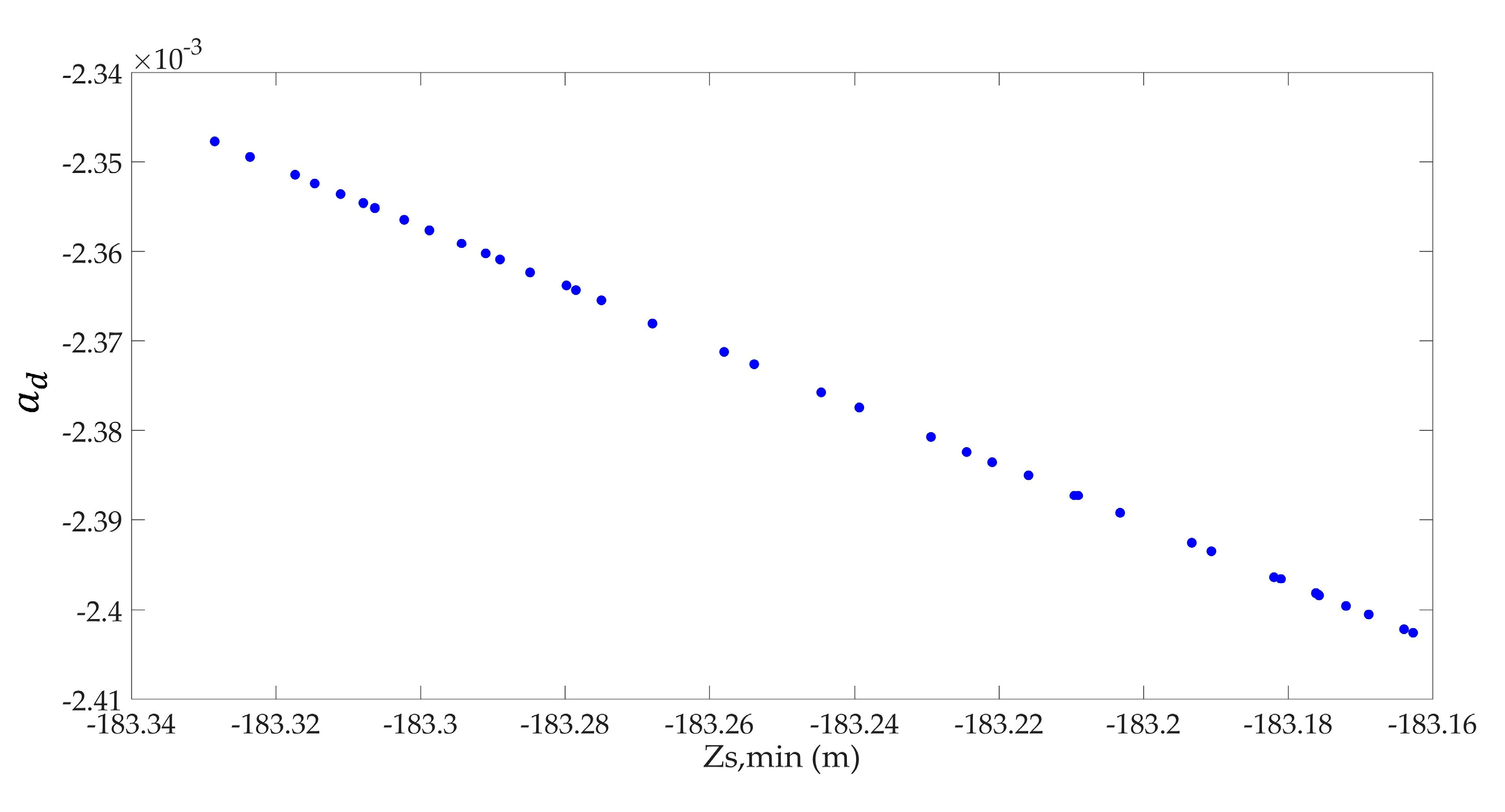
3.2. Sensitivity Analysis
3.3. Optimization
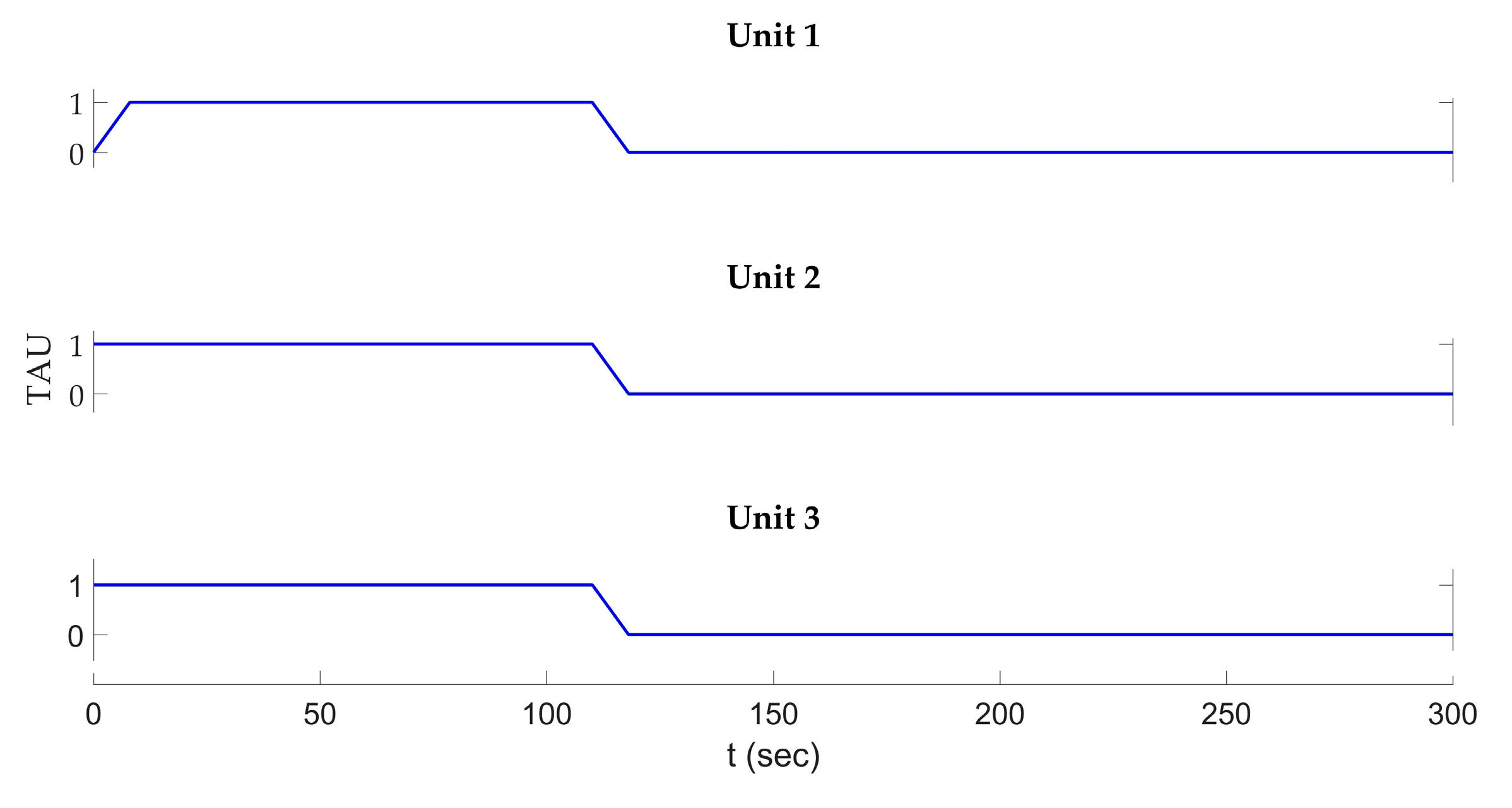
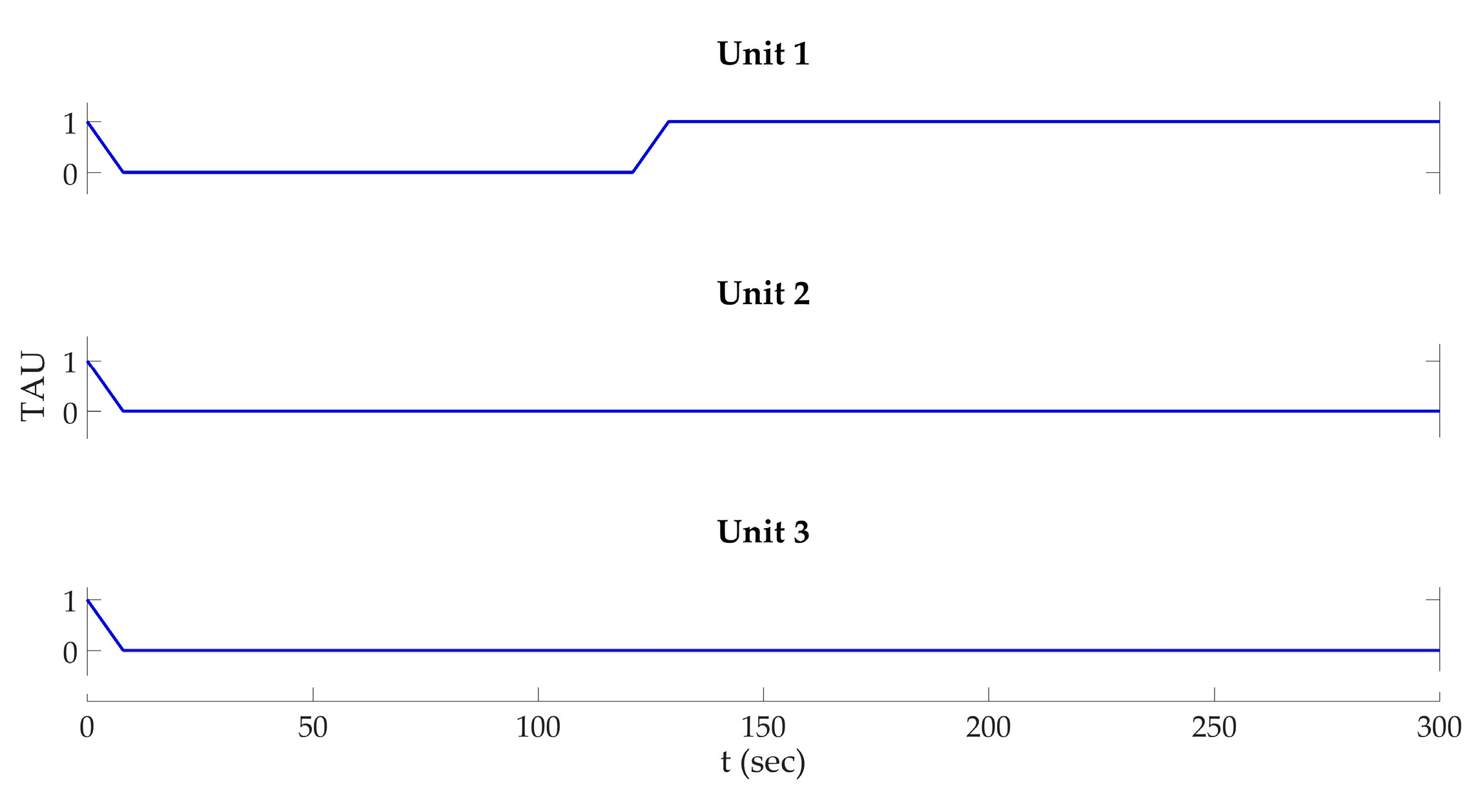
3.4. Operational Stage
4. Conclusions
- Steady state water level and safety criteria governed the location of the lower chamber and the upper chamber. The surge shaft was provided with a minimum possible area required by Thoma criteria for the economic design of the chamber surge tank. Thus, diameter of orifice (), diameter of upper chamber (), and length of lower chamber (L) were taken as the variables for optimization of the double chamber surge tank;
- Sensitivity analysis of these variables shows that did not have any effect in downsurge, and L did not have any effect in upsurge. Water level in the surge tank and damping of surge waves during downsurge and upsurge had conflicting behaviors for and L, whereas the lower value of was favorable. Further, the calculation of sensitivity indicated the was more sensitive on objectives functions. However, at the time of the worst upsurge, to maintain the maximum piezometric head in the bottom tunnel at the orifice and the maximum water level in the upper chamber of the surge tank at nearly equal levels, and had to be optimized to find the optimum ratio between the pressure amplitudes from the water hammer and the mass oscillations;
- The NSGA-II optimized the values of , , and L with a notable improvement in maximum and minimum water levels in the double chamber surge tank with viable damping of surge waves. The double chamber surge tank served as an effective limiter of maximum amplitudes of oscillation. Further, the total volume of the optimized double chamber surge tank was only 44.53% of the total volume of the simple surge tank. Hence, by providing effective throttling with an optimum volume of chambers, damping could be improved, and a huge amount of volume of surge tank could be decreased;
- In the hydropower system with multiple units, controlling the water level oscillation in surge tank is a major issue. The most effective operation mode should be adopted to limit the amplitude of surge in the surge tank. Surge can be killed by acceptance of load in multiple stages.
Author Contributions
Funding
Conflicts of Interest
References
- Boulos, P.F.; Karney, B.W.; Wood, D.J.; Lingireddy, S. Hydraulic Transient Guidelines. J. Am. Water Resour. Assoc. 2005, 97, 111–124. [Google Scholar] [CrossRef]
- Kendir, T.E.; Ozdamar, A. Numerical and experimental investigation of optimum surge tank forms in hydroelectric power plants. Renew. Energy 2013, 60, 323–331. [Google Scholar] [CrossRef]
- Pejovic, S.; Boldy, A.P.; Obradovic, D. Guidelines to Hydraulic Transient Analysis; Gower Technical: Randolph, VT, USA, 1987; ISBN 0291397239. [Google Scholar]
- Kim, S.H. Design of surge tank for water supply systems using the impulse response method with the GA algorithm. J. Mech. Sci. Technol. 2010, 24, 629–636. [Google Scholar] [CrossRef]
- Adam, N.J.; De Cesare, G.; Nicolet, C.; Billeter, P.; Angermayr, A.; Valluy, B.; Schleiss, A.J. Design of a throttled surge tank for refurbishment by increase of installed capacity at a high-head power plant. J. Hydraul. Eng. 2018, 144, 1–10. [Google Scholar] [CrossRef]
- Peter, S. Economic surge tank design by sophisticated hydraulic throttling. In Proceedings of the 28th IAHR congress, Graz, Austria, 22–27 August 1999. [Google Scholar]
- Cesare, G. De Surge tank geometry modification for power increase. In Proceedings of the Hydro Conference 2015, Bordeaux, France, 26–28 October 2015. [Google Scholar]
- Wang, S.; Liu, T.; Zou, W.; Peng, T.; Xu, K. Advantage of new differential surge chamber and its application. J. Tsinghua Univ. 1988, 28, 73–84. [Google Scholar]
- Emadi, J.; Solemani, A. Maximum water hammer sensitivity analysis. World Acad. Sci. Eng. Technol. 2011, 73, 416–419. [Google Scholar]
- Wan, W.; Li, F. Sensitivity analysis of operational time differences for a pump-valve system on a water hammer response. J. Press. Vessel Technol. 2016, 138, 1–8. [Google Scholar] [CrossRef]
- Diao, X.F.; Zhang, X.H.; Yang, Y.Y. Sensitivity analysis of restricted orifice in the hydropower station. In Proceedings of the 5th International Conference on Civil, Architectural and Hydraulic Engineering (ICCAHE 2016), Zhuhai, China, 30–31 July 2016. [Google Scholar]
- Ramos, H.; Covas, D.; Borga, A.; Loureiro, D. Surge damping analysis in pipe systems: Modelling and experiments. J. Hydraul. Res. 2004, 42, 413–425. [Google Scholar] [CrossRef]
- Yazdi, J.; Hokmabadi, A.; JaliliGhazizadeh, M.R. Optimal size and placement of water hammer protective devices in water conveyance pipelines. Water Resour. Manag. 2019, 33, 569–590. [Google Scholar] [CrossRef]
- Vereide, K.; Richter, W.; Zenz, G.; Lia, L. Surge tank research in Austria and Norway. WasserWirtschaft 2015, 105, 58–62. [Google Scholar] [CrossRef]
- Nabi, G.; Kashif, M.; Tariq, M. Hydraulic Transient Analysis of Surge Tanks: Case Study of Satpara and Golen Gol Hydropower Projects in Pakistan. Pak. J. Engg. Appl. Sci. 2011, 8, 34–48. [Google Scholar]
- Liu, D.; Liu, Q. Volume calculation for upper chamber in double-chamber Surge Tank. Water Power 1993, 11, 36–39. [Google Scholar]
- Travaš, V. Water mass oscillations in a generic surge chamber. J. Croat. Assoc. Civ. Eng. 2014, 66, 323–334. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients; Van Nostrand Reinhold: New York, NY, USA, 1979; ISBN 0442215177. [Google Scholar]
- Wylie, E.; Streeter, V.L.; Suo, L. Fluid Transients in Pipeline Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Bhattarai, K.P.; Zhou, J.; Palikhe, S.; Pandey, K.P.; Suwal, N. Numerical modeling and hydraulic optimization of a surge tank using particle swarm optimization. Water 2019, 11, 715. [Google Scholar] [CrossRef]
- Bozkus, Z.; Calamak, M. Numerical Investigation of Operation Levels in a Surge Tank of a Small Hydropower Plant. In Proceedings of the 10th International Congress on Advances in Civil Engineering; Middle East Technical University, Ankara, Turkey, 17–19 October 2012. [Google Scholar]
- Shani, T.; Gupta, T. Hydraulic transient flow analysis using Method of Characteristics. Int. J. Innov. Res. Sci. Eng. Technol. 2017, 6, 14812–14827. [Google Scholar]
- Salmanzadeh, M.; Torfi, S. Analysis of surge in pipelines systems by characteristics method. Int. J. Mech. 2011, 5, 83–90. [Google Scholar]
- Salmanzadeh, M. Numerical Method for Modeling Transient Flow in Distribution Systems. Int. J. Comput. Sci. Netw. Secur. 2013, 13, 72–78. [Google Scholar]
- Martins, N.M.C.; Brunone, B.; Meniconi, S.; Ramos, H.M.; Covas, D.I.C. CFD and 1D approaches for the unsteady friction analysis of low Reynolds number turbulent flows. J. Hydraul. Eng. 2017, 143, 1–13. [Google Scholar] [CrossRef]
- Kisan, M.; Sangathan, S.; Nehru, J.; Pitroda, S.G. IS 7396-1 (1985): Criteria for Hydraulic Design of Surge Tanks, Part 1: Simple, Restricted Orifice and Differential Surge Tanks; Bureau of Indian Standards: New Delhi, India, 1985.
- Mosonyi, E. High-Head Power Plants, 3rd ed.; Akadémiai Kiadó: Budapest, Hungary, 1991. [Google Scholar]
- Montes, J.S. Damping and stability of orifice plate surge tanks by approximate analytical technique. In Proceedings of the 7th Australasian Hydraulics and Fluid Mechanics Conference, Brisbane, Australia, 18–22 August 1980. [Google Scholar]
- Thoma, D. Zur Theorie des Wasserschlosses bei selbsttätig geregelten Turbinenanlagen; Oldenbourg: Munchen, Germany, 1910. [Google Scholar]
- Jaeger, C. Present Trends in Surge Tank Design. Proc. Inst. Mech. Eng. 1954, 168, 91–124. [Google Scholar] [CrossRef]
- National Energy Administration of China. Design Code for Surge Chamber of Hydropower stations. China Electr. Power Press 2014, NB/T 35021. Available online: www.gong123.com/dianli/2016-09-16/1182918.html#edown (accessed on 1 September 2019).
- Kisan, M.; Sangathan, S.; Nehru, J.; Pitroda, S.G. IS 7396-3 (1990): Criteria for Hydraulic Design of Surge Tanks, Part 3: Special Surge Tanks; Bureau of Indian Standards: New Delhi, India, 1990.
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, Q.; Li, H. Comparison between MOEA/D and NSGA-II on the multi-objective travelling salesman problem. Stud. Comput. Intell. 2009, 171, 309–324. [Google Scholar]
- Godnez, A.C.; Espinosa, L.E.M.; Montes, E.M. An experimental comparison of multiobjective algorithms: NSGA-II and OMOPSO. In Proceedings of the 2010 IEEE Electronics, Robotics and Automotive Mechanics Conference, Morelos, Mexico, 28 September–1 October 2010. [Google Scholar]
- Kollat, J.B.; Reed, P.M. Comparison of multi-objective evolutionary algorithms for long-term monitoring design. In Proceedings of the World Water Congress 2005: Impacts of Global Climate Change Congress, Anchorage, Alaska, 15–19 May 2005. [Google Scholar]
- Haghighipour, S.; Fathi-Moghadam, M. Optimization of hydropower conveyance systems. J. Food Agric. Environ. 2010, 8, 1093–1096. [Google Scholar]
- Afshar, H.; Kerachian, R.; Bazargan-Lari, M.R.; Niktash, A.R. Developing a closing rule curve for valves in pipelines to control the water hammer impacts: Application of the NSGA-II optimization model. In Proceedings of the Pipelines Congress 2008—Pipeline Asset Management: Maximizing Performance of Our Pipeline Infrastructure, Atlanta, GA, USA, 22–27 July 2008. [Google Scholar]
- Deb, K.; Miettinen, K. A review of nadir point estimation procedures using evolutionary approaches: A Tale of dimensionality reduction. In Proceedings of the 5th International Conference on Evolutionary Multi-Criterion Optimization, Nantes, France, 7–10 April 2009. [Google Scholar]
- Shukla, P.K.; Deb, K. On finding multiple Pareto-optimal solutions using classical and evolutionary generating methods. Eur. J. Oper. Res. 2007, 181, 1630–1652. [Google Scholar] [CrossRef]
- Hannett, L.N. Modeling and control tuning of a hydro station with units sharing a common penstock section. IEEE Trans. Power Syst. 1999, 14, 1407–1414. [Google Scholar] [CrossRef]
- Siu, T.K.; Nash, G.A.; Shawwash, Z.K. A practical hydro, dynamic unit commitment and loading model. IEEE Trans. Power Syst. 2001, 16, 301–306. [Google Scholar] [CrossRef]
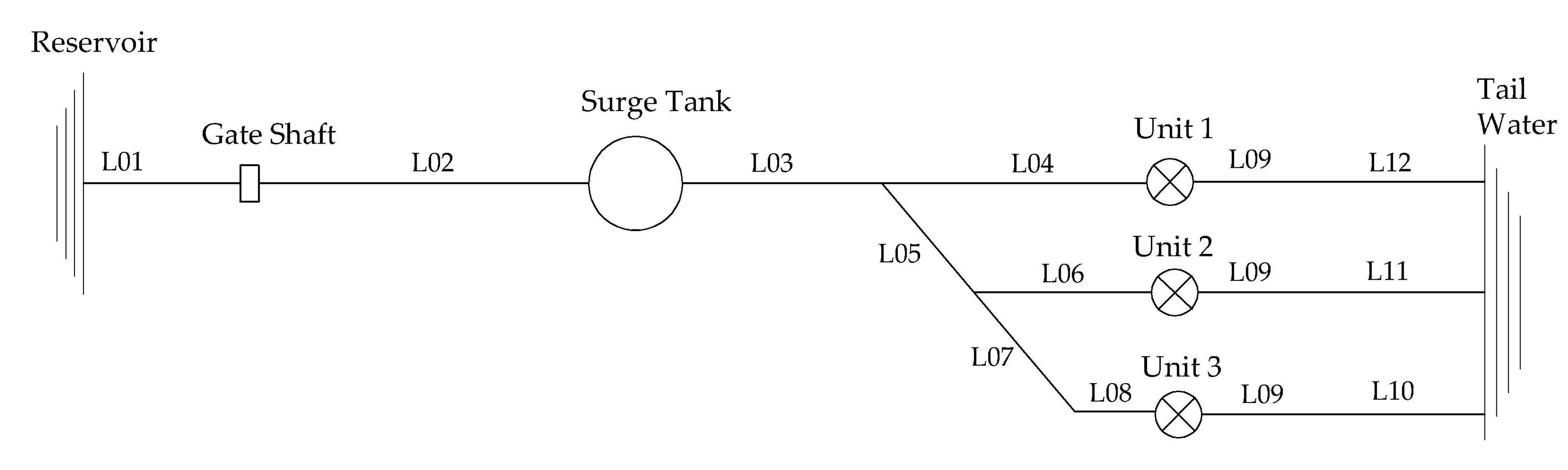
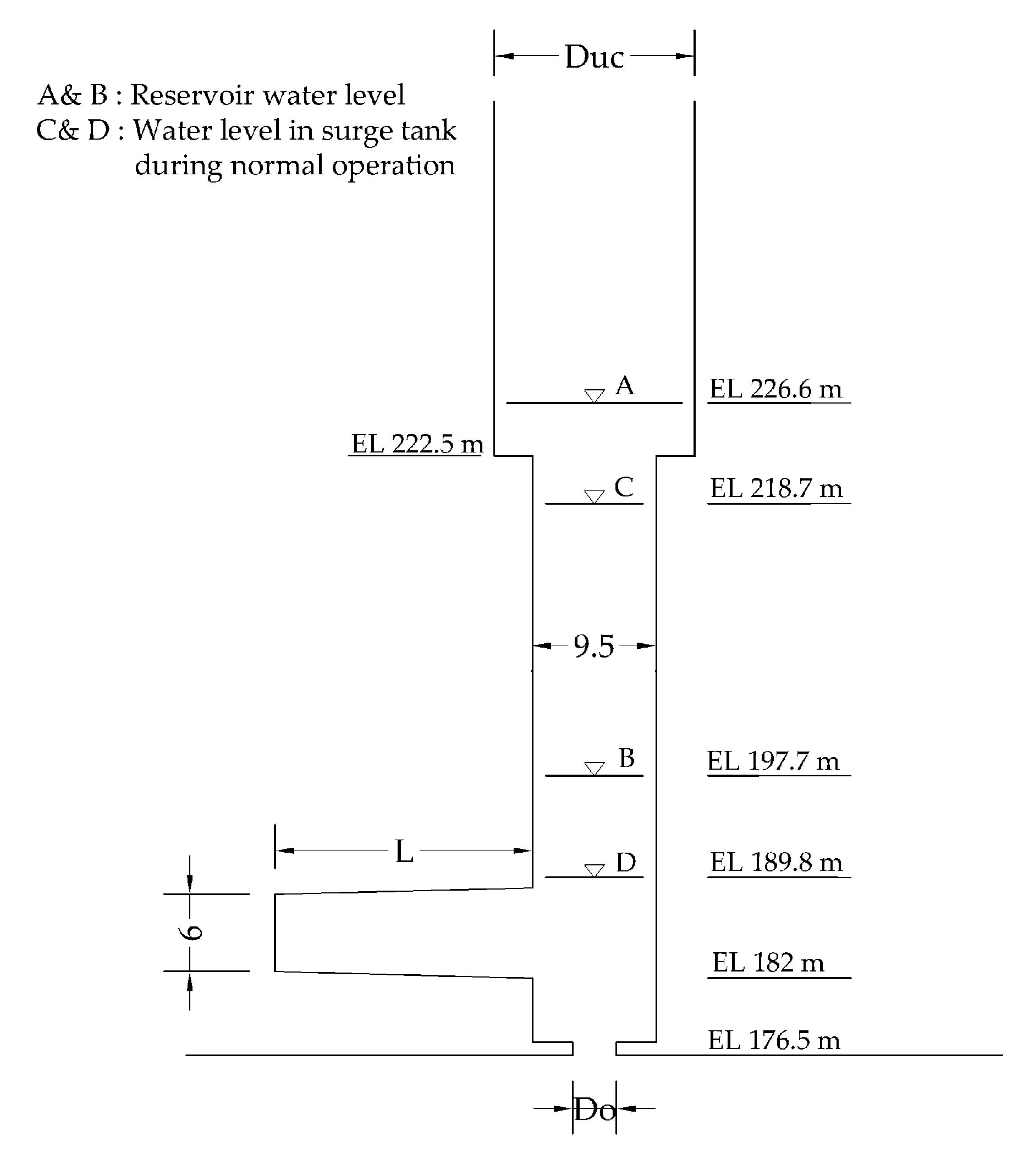

| Pipe Segment | Diameter (m) | Length (m) | No. of Segment (Nj) | Δx (m) |
|---|---|---|---|---|
| L01 | 5.5 | 236.0 | 23 | 10.26 |
| L02 | 5.5 | 3850.7 | 385 | 10.00 |
| L03 | 4.8 | 119.8 | 11 | 10.89 |
| L04 | 2.5 | 47.4 | 4 | 11.85 |
| L05 | 4.0 | 11.0 | 1 | 11.00 |
| L06 | 2.5 | 40.3 | 4 | 10.08 |
| L07 | 3.3 | 11.0 | 1 | 11.00 |
| L08 | 2.5 | 37.4 | 3 | 12.47 |
| L09 | 2.8 | 11.9 | 1 | 11.90 |
| L10 | 4.0 | 108.6 | 10 | 10.86 |
| L11 | 4.0 | 107.8 | 10 | 10.78 |
| L12 | 4.0 | 107.0 | 10 | 10.70 |
| Water Level (m) | Area of Surge Tank (m2) |
|---|---|
| 70.88 | |
| 70.88 | |
| Variable | Upsurge | Downsurge | ||
|---|---|---|---|---|
| 7.3 | 0.0006 | 4 | 0.0007 | |
| −3.6 | 0.0001 | 0 | 0 | |
| L | 0 | 0 | −0.36 | 0.0001 |
| Opt. | Pop. No. | Variable | Objective Function | Gen | |||||
|---|---|---|---|---|---|---|---|---|---|
| Upsurge | Downsurge | ||||||||
| L (m) | |||||||||
| 30 | 2.81 | 12.30 | 249.374 | 0.002648 | 135 | ||||
| I | 40 | 2.80 | 12.26 | 249.400 | 0.002656 | 105 | |||
| 50 | 2.80 | 12.23 | 249.419 | 0.002657 | 115 | ||||
| 30 | 20.04 | 183.254 | 0.002372 | 120 | |||||
| II | 40 | 20.00 | 183.245 | 0.002375 | 109 | ||||
| 50 | 20.17 | 183.275 | 0.002365 | 165 | |||||
| Objective Function | SST | DCST |
|---|---|---|
| Upsurge (m) | 248.427 | 249.400 |
| Downsurge (m) | 183.245 | 183.245 |
| Volume (m3) | 16208.9 | 7219.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhakal, R.; Zhou, J.; Palikhe, S.; Bhattarai, K.P. Hydraulic Optimization of Double Chamber Surge Tank Using NSGA-II. Water 2020, 12, 455. https://doi.org/10.3390/w12020455
Dhakal R, Zhou J, Palikhe S, Bhattarai KP. Hydraulic Optimization of Double Chamber Surge Tank Using NSGA-II. Water. 2020; 12(2):455. https://doi.org/10.3390/w12020455
Chicago/Turabian StyleDhakal, Resham, Jianxu Zhou, Sunit Palikhe, and Khem Prasad Bhattarai. 2020. "Hydraulic Optimization of Double Chamber Surge Tank Using NSGA-II" Water 12, no. 2: 455. https://doi.org/10.3390/w12020455
APA StyleDhakal, R., Zhou, J., Palikhe, S., & Bhattarai, K. P. (2020). Hydraulic Optimization of Double Chamber Surge Tank Using NSGA-II. Water, 12(2), 455. https://doi.org/10.3390/w12020455





