Modelling of Flood Inundation due to Levee Breaches: Sensitivity of Flood Inundation against Breach Process Parameters
Abstract
:1. Introduction
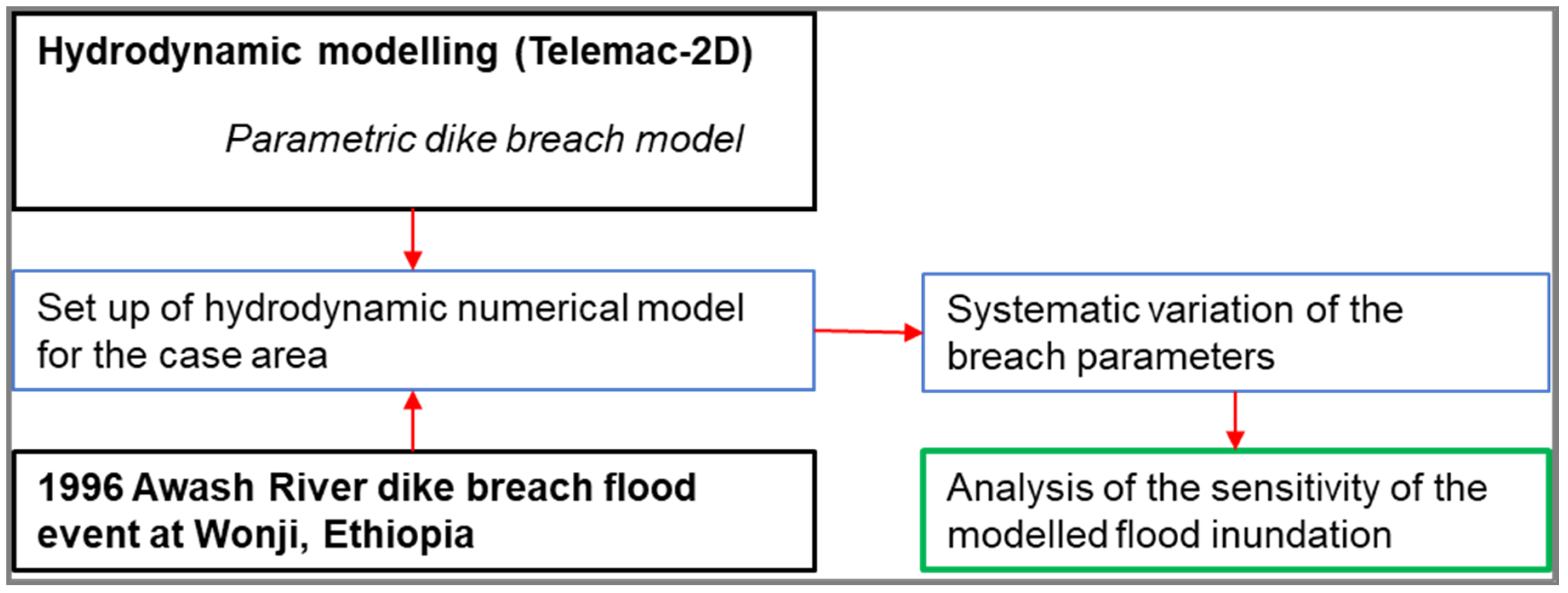
2. Methodology
2.1. Approach
2.2. Telemac-2D
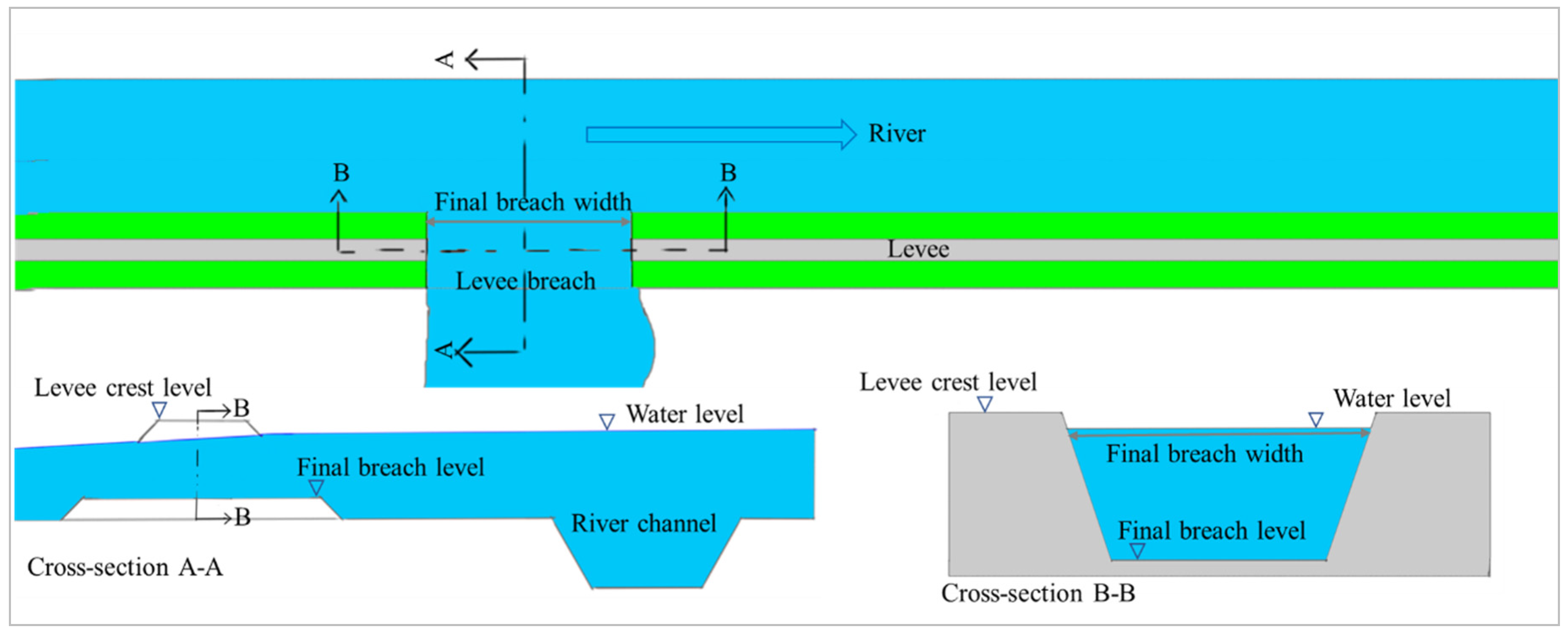
2.3. The Breach Model Used in This Investigation
2.4. The Levee Breach Case: The 1996 Awash River Levee Breach at Wonji
2.4.1. The Study Area
2.4.2. The 1996 Awash River Levee Breach at Wonji, Ethiopia
3. Model Set Up
3.1. Computational Mesh
3.2. Boundary and Initial Conditions
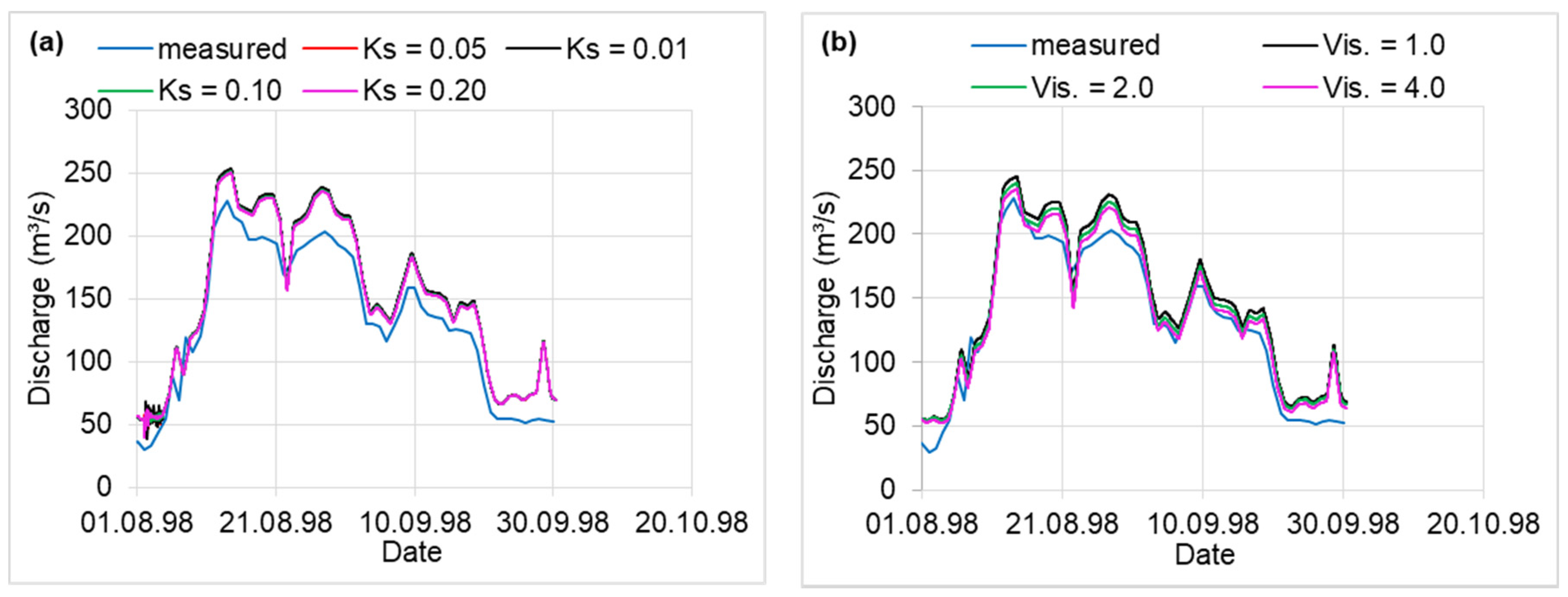
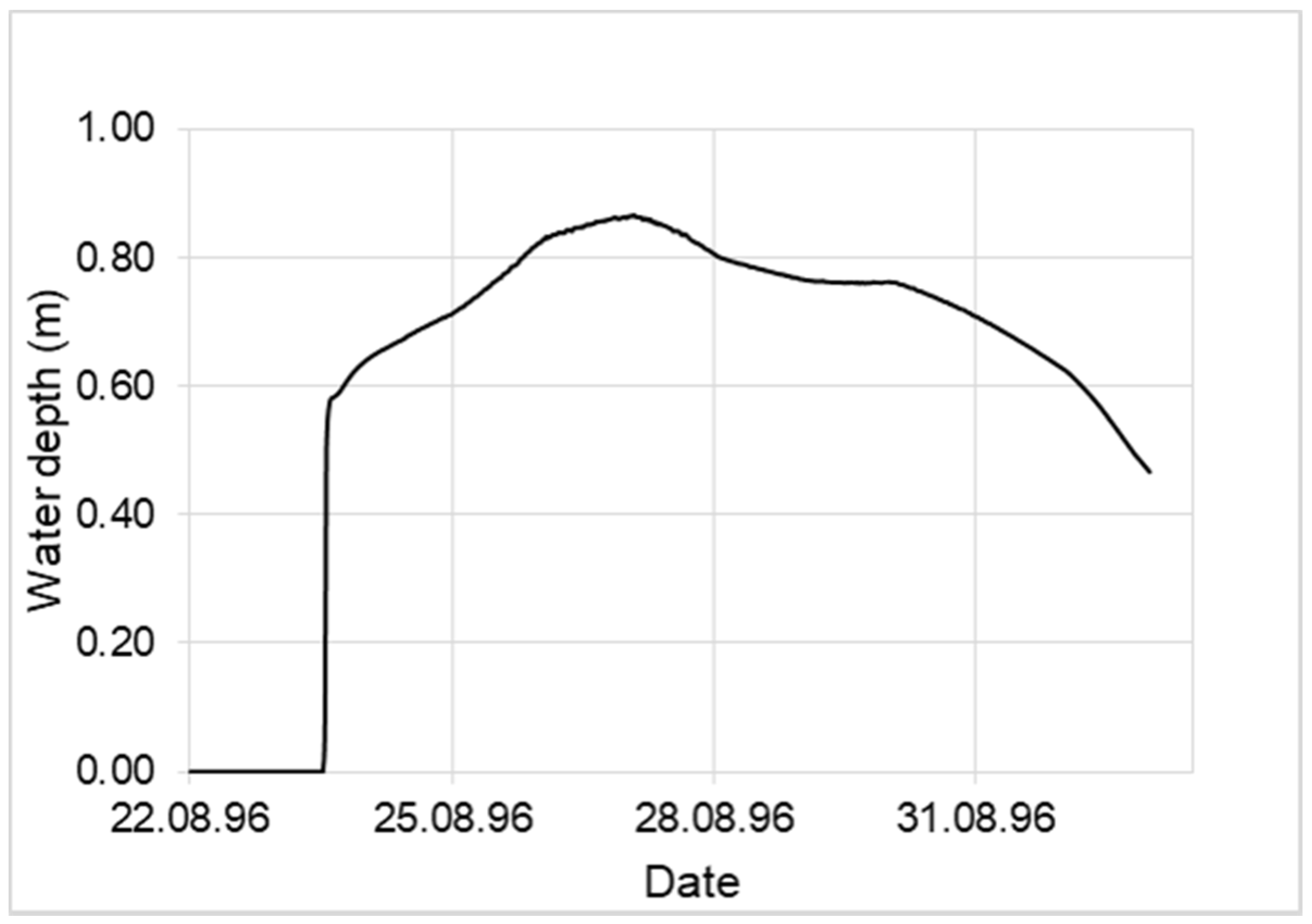
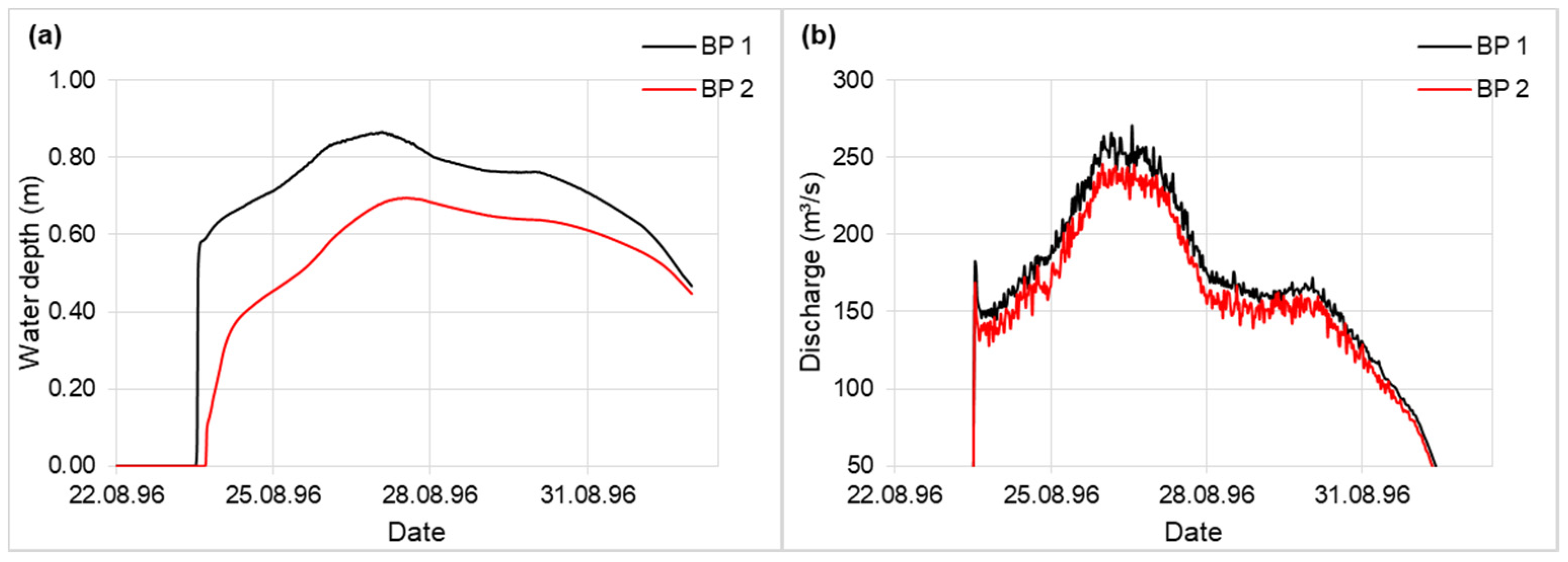
3.3. Model Calibration and Validation
4. Sensitivity Analysis of the Breach Model Parameters
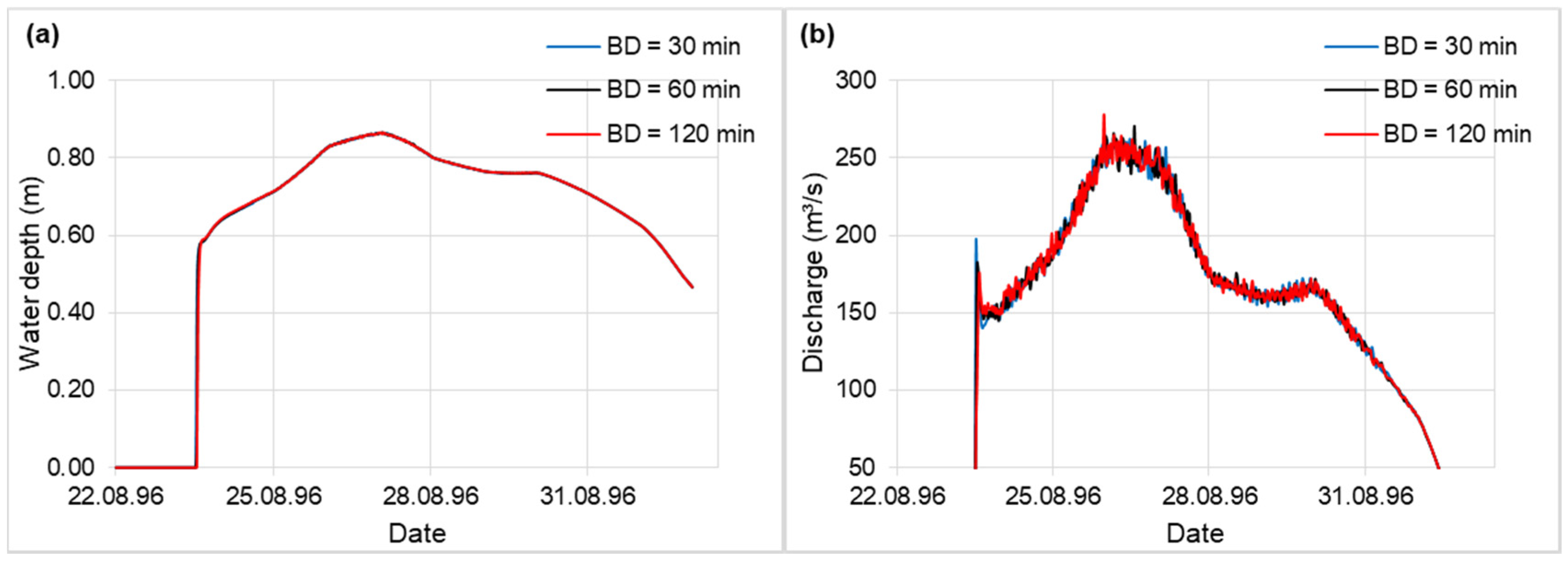
4.1. Breach Duration
4.2. Breach Start Time (Breach Initiation)
4.3. Final Breach Width
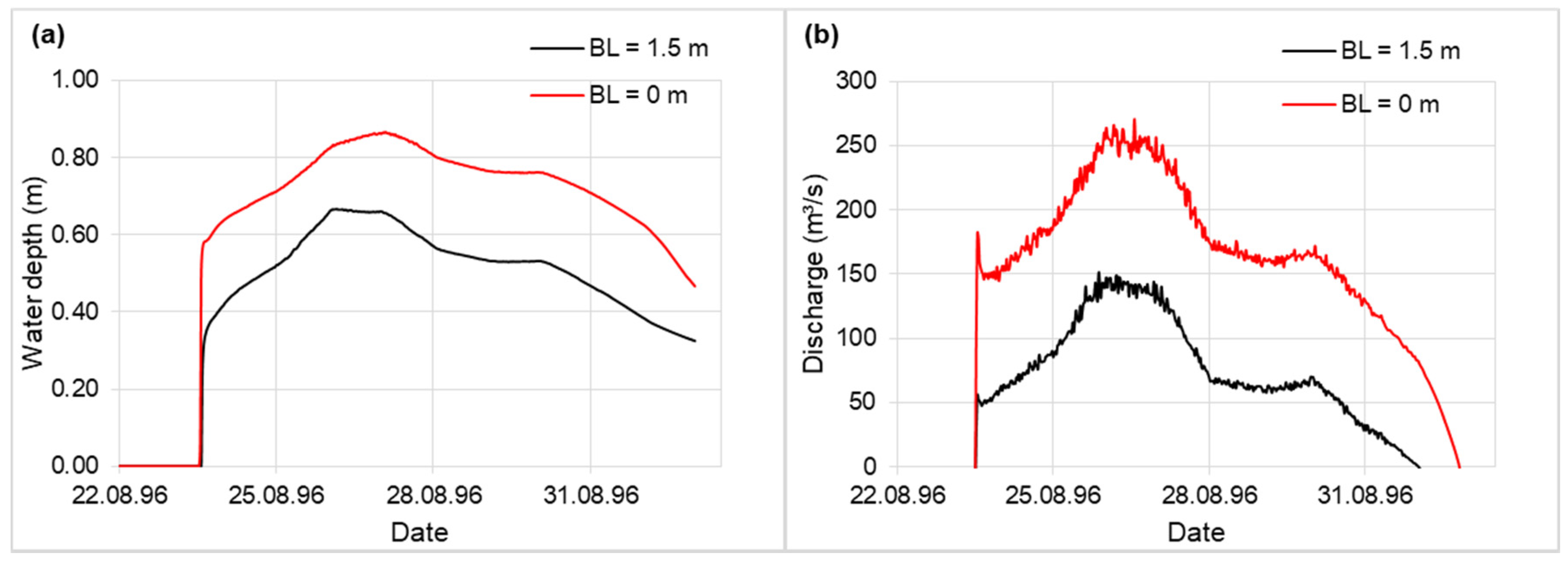
4.4. Final Breach Level
4.5. Breach Location
4.6. Erosion Type
5. Discussion
6. Conclusions
- Flood inundation due to levee breach depends on the final dimensions of the levee breach and the breach location. The final breach dimensions affect the consequence of the levee breach as the amount of water that can flow into the hinterland is the function of the breach dimensions.
- The breach location affects the consequence of the levee breach even if the discharge through the breach is not significantly influenced.
- The process of the levee breaching (breach development) has marginal to no influence on the resulting flood inundation. This is shown, however, for floods lasting over several days. Consequences of levee breaches due to flash floods lasting for short period could be sensitive to the levee breaching processes.
- Accurate and reliable methods for determining the final breach dimensions and breach location are important for a more accurate flood inundation estimation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tomscha, S.A.; Gergel, S.E.; Tomlinson, M.J. The spatial organization of ecosystem services in river-floodplains. Ecosphere 2017, 8, e01728. [Google Scholar] [CrossRef]
- Tockner, K.; Stanford, J.A. Riverine flood plains: Present state and future trends. Environ. Conserv. 2002, 29, 308–330. [Google Scholar] [CrossRef] [Green Version]
- Hohensinner, S.; Habersack, H.; Jungwirth, M.; Zauner, G. Reconstruction of the characteristics of a natural alluvial river–floodplain system and hydromorphological changes following human modifications: The Danube River (1812–1991). River Res. Appl. 2004, 20, 25–41. [Google Scholar] [CrossRef]
- Gardiner, J.; Starosolszky, Ö.; Yevjevich, V. (Eds.) Defence from Floods and Floodplain Management; Springer: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Özer, I.E.; Van Damme, M.; Jonkman, S.N. Towards an International Levee Performance Database (ILPD) and Its Use for Macro-Scale Analysis of Levee Breaches and Failures. Water 2019, 12, 119. [Google Scholar] [CrossRef] [Green Version]
- Merz, B.; Elmer, F.; Kunz, M.; Mühr, B.; Schröter, K.; Uhlemann-Elmer, S. The extreme flood in June 2013 in Germany. La Houille Blanche 2014, 57, 5–10. [Google Scholar] [CrossRef] [Green Version]
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change; Field, C.B.V., Barros, T.F., Stocker, D., Qin, D.J., Dokken, K.L., Ebi, M.D., Mastrandrea, K.J., Mach, G.-K., Plattner, S.K., Allen, M., et al., Eds.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- ASCE/EWRI Task Committee on Dam/Levee Breaching Earthen Embankment Breaching. J. Hydraul. Eng. 2011, 137, 1549–1564. [CrossRef]
- Tadesse, Y.; Fröhle, P. An Integrated Approach to Simulate Flooding Due to River Dike Breach. In Proceedings of the 11th International Conference on Hydroinformatics (HIC 2014): Informatics and the Environment: Data and Model Integration in a Heterogeneous Hydro World; Piasecki, M., Ed.; Curran: Red Hook, NY, USA, 2015; pp. 418–425. [Google Scholar]
- Ahrens, J.D. Koka Dam-River Awash Floods. Report of the Joint UN Assessment Team. Available online: http://www.africa.upenn.edu/eue_web/Awash29aug.htm (accessed on 19 August 2019).
- Sills, G.L.; Vroman, N.; Wahl, R.E.; Schwanz, N.T. Overview of New Orleans Levee Failures: Lessons Learned and Their Impact on National Levee Design and Assessment. J. Geotech. Geoenviron. Eng. 2008, 134, 556–565. [Google Scholar] [CrossRef] [Green Version]
- Van Emelen, S.; Soares-Frazão, S.; Riahi-Nezhad, C.K.; Chaudhry, M.H.; Imran, J.; Zech, Y. Simulations of the New Orleans 17th Street Canal breach flood. J. Hydraul. Res. 2012, 50, 70–81. [Google Scholar] [CrossRef]
- Nones, M.; Caviedes-Voullième, D. Computational advances and innovations in flood risk mapping. J. Flood Risk Manag. 2020, 13, 13. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Mignosa, P. Integration of a Levee Breach Erosion Model in a GPU-Accelerated 2D Shallow Water Equations Code. Water Resour. Res. 2019, 55, 682–702. [Google Scholar] [CrossRef]
- Apel, H.; Merz, B.; Thieken, A.H. Influence of dike breaches on flood frequency estimation. Comput. Geosci. 2009, 35, 907–923. [Google Scholar] [CrossRef] [Green Version]
- Viero, D.P.; D’Alpaos, A.; Carniello, L.; Defina, A. Mathematical modeling of flooding due to river bank failure. Adv. Water Resour. 2013, 59, 82–94. [Google Scholar] [CrossRef]
- Morris, M.; Hassan, M.; Kortenhaus, A.; Geisenhainer, P.; Visser, P.; Zhu, Y. Modelling breach initiation and growth. Flood Risk Manag. 2008, 581–591. [Google Scholar] [CrossRef]
- Roger, S.; Köngeter, J.; Schüttrumpf, H.; Erpicum, S.; Archambeau, P.; Pirotton, M.; Schwanenberg, D.; Dewals, B.J. Hybrid modelling of dike-break induced flows. In River Flow 2010 // River flow 2010: Proceedings of the 5th International Conference on Fluvial Hydraulics, Braunschweig, Germany, 8–10 June 2010; Dittrich, A., Ed.; Bundesanst. für Wasserbau: Karlsruhe, Germany, 2010; pp. 523–531. [Google Scholar]
- Kamrath, P.; Disse, M.; Hammer, M.; Köngeter, J. Assessment of Discharge through a Dike Breach and Simulation of Flood Wave Propagation. Nat. Hazards 2006, 38, 63–78. [Google Scholar] [CrossRef]
- Canelas, R.; Murillo, J.; Ferreira, R.M.L. Two-dimensional depth-averaged modelling of dam-break flows over mobile beds. J. Hydraul. Res. 2013, 51, 392–407. [Google Scholar] [CrossRef]
- Cantero-Chinchilla, F.N.; Castro-Orgaz, O.; Schmocker, L.; Hager, W.H.; Dey, S. Depth-averaged modelling of granular dike overtopping. J. Hydraul. Res. 2018, 56, 537–550. [Google Scholar] [CrossRef]
- Elalfy, E.; Tabrizi, A.A.; Chaudhry, M.H. Numerical and Experimental Modeling of Levee Breach Including Slumping Failure of Breach Sides. J. Hydraul. Eng. 2018, 144, 04017066. [Google Scholar] [CrossRef]
- Hoffmans, G.; Van Rijn, L. Hydraulic approach for predicting piping in dikes. J. Hydraul. Res. 2018, 56, 268–281. [Google Scholar] [CrossRef]
- Li, S.; Duffy, C.J. Fully coupled approach to modeling shallow water flow, sediment transport, and bed evolution in rivers. Water Resour. Res. 2011, 47, 61. [Google Scholar] [CrossRef]
- Mizutani, H.; Nakagawa, H.; Yoden, T.; Kawaike, K.; Zhang, H. Numerical modelling of river embankment failure due to overtopping flow considering infiltration effects. J. Hydraul. Res. 2013, 51, 681–695. [Google Scholar] [CrossRef] [Green Version]
- Murillo, J.; García-Navarro, P. An Exner-based coupled model for two-dimensional transient flow over erodible bed. J. Comput. Phys. 2010, 229, 8704–8732. [Google Scholar] [CrossRef]
- Onda, S.; Hosoda, T.; Jaćimović, N.M.; Kimura, I. Numerical modelling of simultaneous overtopping and seepage flows with application to dike breaching. J. Hydraul. Res. 2018, 57, 13–25. [Google Scholar] [CrossRef]
- Yang, Y.-S.; Yang, T.-T.; Qiu, L.-C.; Han, Y. Simulating the Overtopping Failure of Homogeneous Embankment by a Double-Point Two-Phase MPM. Water 2019, 11, 1636. [Google Scholar] [CrossRef] [Green Version]
- Singh, K.P.; Snorrason, A. Sensitivity of outflow peaks and flood stages to the selection of dam breach parameters and simulation models. J. Hydrol. 1984, 68, 295–310. [Google Scholar] [CrossRef]
- Hervouet, J.-M. Hydrodynamics of Free Surface Flows: Modelling with the Finite Element Method; John Wiley & Sons, Ltd.: Chichester, UK; Hoboken, NJ, USA, 2007. [Google Scholar]
- Open Telemac-Mascaret (Telemac). Telemac-2d-Two-Dimensional Hydrodynamic. Available online: http://www.opentelemac.org/index.php/presentation?id=17 (accessed on 22 August 2019).
- Ata, R. Telemac2D User Manual: Version v7p3. 2018. Available online: http://www.opentelemac.org/index.php/manuals/viewcategory/13-telemac-2d (accessed on 3 September 2018).
- Tadesse, Y.; Fröhle, P. Modelling of river dike breach type physical test flow with Telemac-2D. In Proceedings of the 24th Telemac-Mascaret User Conference; Dorfmann, C., Zenz, G., Eds.; Verlag der Technischen Universität Graz: Graz, Austria, 2017; pp. 107–112. [Google Scholar]
- Abebe, H.M. Sedimentation in the Koka Reservoir, Ethiopia. In Hydropower in the new Millenium, Proceedings of the 4th International Conference on Hydropower Development; Honningsvag, B., Midttomme, G.H., Repp, K., Vaskinn, K., Westeren, T., Eds.; A.A. Balkema: Lisse, The Netherlands, 2001; pp. 345–350. [Google Scholar]
- Shahin, M.M.A. An overview of reservoir sedimentation in some African river basins. In Proceedings of the Yokohama Symposium, Yokohoma, Japan, 19–21 July 1993; pp. 93–100. [Google Scholar]
- Halcrow; SOGREAH; MCE. Awash River Basin Flood Control and Watershed Management Study Project: Working Paper 5; Report obtained from The Ministry of Water Resources, Federal Democratic Republic of Ethiopia; The Ministry of Water Resources, Federal Democratic Republic of Ethiopia: Addis Ababa, Ethiopia, 2005.
- Associated Press. 20,000 Ethiopians Evacuated. Available online: https://reliefweb.int/report/ethiopia/20000-ethiopians-evacuated (accessed on 19 August 2019).
- Vorogushyn, S.; Merz, B.; Apel, H. Development of dike fragility curves for piping and micro-instability breach mechanisms. Nat. Hazards Earth Syst. Sci. 2009, 9, 1383–1401. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Castellarin, A.; Brath, A. Analysis of the effects of levee heightening on flood propagation: Example of the River Po, Italy. Hydrol. Sci. J. 2009, 54, 1007–1017. [Google Scholar] [CrossRef]
- Vorogushyn, S.; Merz, B.; Lindenschmidt, K.-E.; Apel, H. A new methodology for flood hazard assessment considering dike breaches. Water Resour. Res. 2010, 46, 125. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, C.; Förster, S.; Bronstert, A. Comparison of hydrodynamic models of different complexities to model floods with emergency storage areas. Hydrol. Process. 2008, 22, 4695–4709. [Google Scholar] [CrossRef]
- International Bank for Reconstruction and Development. The Ethiopian Electric Light and Power Authority Project; International Bank for Reconstruction and Development: Washington, DC, USA, 1964. [Google Scholar]
- Jiang, L.; Diao, M.; Sun, H.; Ren, Y. Numerical Modeling of Flow Over a Rectangular Broad-Crested Weir with a Sloped Upstream Face. Water 2018, 10, 1663. [Google Scholar] [CrossRef] [Green Version]
- Tracy, H.J. Discharge Characteristics of Broad-Crested Weirs; Geological Survey Circular No. 397; United States Department of the Interior: Washington, DC, USA, 1957.
- Dou, S.-T.; Wang, D.-W.; Yu, M.-H.; Liang, Y.-J. Numerical modeling of the lateral widening of levee breach by overtopping in a flume with 180 bend. Nat. Hazards Earth Syst. Sci. 2014, 14, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Mazzoleni, M.; Bacchi, B.; Barontini, S.; Di Baldassarre, G.; Pilotti, M.; Ranzi, R. Flooding Hazard Mapping in Floodplain Areas Affected by Piping Breaches in the Po River, Italy. J. Hydrol. Eng. 2014, 19, 717–731. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tadesse, Y.B.; Fröhle, P. Modelling of Flood Inundation due to Levee Breaches: Sensitivity of Flood Inundation against Breach Process Parameters. Water 2020, 12, 3566. https://doi.org/10.3390/w12123566
Tadesse YB, Fröhle P. Modelling of Flood Inundation due to Levee Breaches: Sensitivity of Flood Inundation against Breach Process Parameters. Water. 2020; 12(12):3566. https://doi.org/10.3390/w12123566
Chicago/Turabian StyleTadesse, Yohannis Birhanu, and Peter Fröhle. 2020. "Modelling of Flood Inundation due to Levee Breaches: Sensitivity of Flood Inundation against Breach Process Parameters" Water 12, no. 12: 3566. https://doi.org/10.3390/w12123566
APA StyleTadesse, Y. B., & Fröhle, P. (2020). Modelling of Flood Inundation due to Levee Breaches: Sensitivity of Flood Inundation against Breach Process Parameters. Water, 12(12), 3566. https://doi.org/10.3390/w12123566




