Produced Water Desalination via Pervaporative Distillation

Abstract

Herein, we report on the performance of a hybrid organic-ceramic hydrophilic pervaporation membrane applied in a vacuum membrane distillation operating mode to desalinate laboratory prepared saline waters and a hypersaline water modeled after a real oil and gas produced water. The rational for performing “pervaporative distillation” is that highly contaminated waters like produced water, reverse osmosis concentrates and industrial have high potential to foul and scale membranes, and for traditional porous membrane distillation membranes they can suffer pore-wetting and complete salt passage. In most of these processes, the hard to treat feed water is commonly softened and filtered prior to a desalination process. This study evaluates pervaporative distillation performance treating: (1) NaCl solutions from 10 to 240 g/L at crossflow Reynolds numbers from 300 to 4800 and feed-temperatures from 60 to 85 °C and (2) a real produced water composition chemically softened to reduce its high-scale forming mineral content. The pervaporative distillation process proved highly-effective at desalting all feed streams, consistently delivering <10 mg/L of dissolved solids in product water under all operating condition tested with reasonably high permeate fluxes (up to 23 LMH) at optimized operating conditions.

1. Introduction

Pervaporation (PV) is a hybrid distillation process whereby separation performance is a function of the relative solubilities (in the membrane) of the constituents in the feed as well as their relative boiling points. In practice, PV is primarily used for separation of azeotropic liquid mixtures like alcohols and water [1], polar aprotic solvents and water [2], as well as other applications such as bioethanol dehydration [3], production of non-alcoholic wine and beer [4], and catalytically active membranes for reactive-separations [5,6]. While PV has found limited practical application in water desalination to date, pervaporative desalination (PVD) has been studied for over 25 years [7,8].

Various researchers have explored the use of zeolite and carbon molecular sieve-coated ceramic membranes for PVD, where one of the key challenges is making a defect free zeolite coating that is thin enough to give a reasonable flux [9,10,11,12,13,14]. Other studies explored different types of polymeric and mixed matrix membranes applied to PVD [15,16,17,18,19,20]. Several earlier studies have explored the PVD process and even solar powered PVD [21,22,23]. Among the most comprehensive set of studies include those by Gray and co-workers [21,24,25,26,27], who have explored novel polymeric thin film composite and nanocomposite PV membrane materials as well as scaled-up process energy demand and cost; they conclude that PVD (like traditional membrane distillation, MD) will be more expensive and energy intense than RO, so it may be limited to brine concentration, where commercial RO membranes cannot operate at high enough pressures to achieve reasonable permeate recovery [26].

Despite the rather limited practical application of MD and PVD to brine concentration, water sustainability imperatives motivate efforts to achieve minimal or zero liquid discharge (MLD/ZLD) in many desalination applications. As such, the dense separating layer of PV membranes offers a potential advantage over conventional MD. In conventional MD processes, a hydrophobic membrane with pores on the scale of ~0.1 to ~0.5 μm separates the feed and permeate streams; this is depicted in Figure 1a in the form of vacuum MD (VMD). A MD membrane must be very hydrophobic and the pores of sufficient size and shape to maintain a vapor-liquid interface (or meniscus) at each pore entrance [28,29,30,31]. The feed is heated, while the permeate is either cold water, a cool sweep gas or under vacuum—the combined effects lower the trans-membrane partial pressure difference for water leading to evaporation below the boiling point. However, when a hydrophobic MD membrane experiences fouling or scaling the pores become less hydrophobic, reducing the pore liquid entry pressure (LEP) risking “pore wetting”, which leads to salt passage and complete system failure [32]. In contrast, PV employs a dense hydrophilic membrane, which first absorbs liquid water then passes it as water vapor (Figure 1b) [8,33]. The dense hydrophilic PV membrane could lose permeability due to fouling or scaling, but would not suffer process failure as happens in MD.

Herein, we report on the performance of a hybrid organic-inorganic thin film composite PVD membrane evaluated in a process mode identical to that of VMD. We evaluate the effects of feed temperature, crossflow velocity and feed water salinity (up to 240 g/L) to establish a basic understanding of the PVD membrane’s performance characteristics. We then evaluate the potential for treating a real hyper-saline produced water stream derived from upstream oil and gas production via hydraulic fracturing. The organic-inorganic thin film composite membrane was chosen because of its stability under extreme operational conditions (high salinity, temperature, acidity, etc.) [34]. This silica-based amorphous material offers a true hybrid silica pore network in which organic and inorganic fragments cooperate. The hybrid structure provides more stable bonds, lower solubility, and higher crack propagation energy resulting in more ductile material, all of which contribute to its remarkable stability.

2. Materials and Methods

2.1. Materials

The hydrophilic PV membrane used in this study, HybSi^® PVM-039, (Pervatech BV, Rijssen, The Netherlands), comprised a proprietary cross-linked organo-silane selective layer casted on an α-Al₂O₃ tubular ceramic membrane support. The thin coating of selective layer is prepared by a sol-gel process from the bis-silyl precursors, such as BTESE [(EtO)₃Si–CH₂CH₂–Si(OEt)₃] and BTESM [(EtO)₃Si–CH₂–Si(OEt)₃], that has been described in detail elsewhere [34,35]. The coating film was on the inside of the ceramic tube. The tube had exterior diameter of 10 mm, an interior diameter of 7 mm and a length of 25 cm giving an active membrane area of 0.005495 m².

All feed solutions in this study were synthetic solutions made of salts and laboratory de-ionized water (18 M-ohm). Sodium chloride (NaCl), magnesium sulfate heptahydrate (MgSO₄·7H₂O), calcium chloride dihydrate (CaCl₂·2H₂O), sodium bicarbonate (NaHCO₃), sodium bromide (NaBr), strontium chloride hexahydrate (SrCl₂·6H₂O), potassium chloride (KCl), iron(II) sulfate heptahydrate (FeSO₄·7H₂O), sodium sulfate (Na₂SO₄), sodium metasilicate (Na₂SiO₃), sodium silicate (Na₂O+SiO₂·H₂O) were purchased from Sigma-Aldrich (St. Louis, Missouri, USA) and used as received.

2.2. PVD Bench-Scale Testing Apparatus

The laboratory PVD setup is depicted in Figure 2. The membrane unit was secured in a cylinder-shaped module. The feed solution was preheated to a desired temperature by circulating it directly through a recirculating heater/chiller bath (Sahara, SCE 150-S3, Thermo Neslab) and returned to an insulated high-density polyethylene (HDPE) feed tank. A separate external thermometer (VWR) was used to directly monitor the temperature inside the feed vessel. During the experiment, the solution was drawn from the feed tank and circulated through the PV membrane module using a gear pump (75211-30 A-Mount Suction, Micropump).

The feed mixture, at elevated temperature and atmospheric pressure, was in direct contact with the interior, hydrophilic organo-silane coated side of the membrane. The permeate was removed in a vapor state from the reverse side of the membrane using a vacuum pump (GAST, Benton Harbor, MI, USA) at a vacuum of 0.85 bar. The vapor was converted into liquid state in a condenser comprising a glass coil attached to a second recirculating heater/chiller set to 5 °C. A graduated cylinder was attached to the condenser outlet to collect permeate.

2.3. Basic PVD System Performance

The PVD system performance was characterized by the observed water flux and salt rejection. The volumetric permeate flux (J) was determined from the permeate mass (M), per unit time (t), density of permeate (${\rho }_w$) and effective membrane area (A) according to,

$$J=\frac{M}{{\rho }_{w}At}$$

(1)

Experiments were performed to evaluate the impact of feed concentration, feed temperature, and feed crossflow velocity on system performance. A serious of aqueous solutions containing 10 to 240 g/L NaCl were chosen to represent the typical salt concentration of brackish water, sea water, and brine streams. Feed temperature was varied in the range of 60 to 85 °C. The feed crossflow velocity was varied to achieve different flow regimes, as reflected by Reynolds number (Re) which is calculated as

$$Re=\frac{\rho u{d}_H}{\mu }$$

(2)

where u is the channel average crossflow velocity, ρ is solution density, d_H is the hydraulic diameter (m), and μ is the solution viscosity [36,37,38,39]. Both ρ and μ were calculated at its corresponding salinity and temperature [37]. The target Reynolds number was in the range of ~300 to ~4800.

For each set of test conditions, permeate samples were collected for 30 minutes after the system stabilized. The salt concentration of the feed (c_f) and permeate (c_p) were obtained from measured electrical conductivities with a conductivity meter (Hach, Loveland, CO, USA). The salt concentration of the feed and permeate were determined from measured. The salt rejection (R) was determined by

$$R=\frac{C_f-C_p}{C_f}\times 100\%$$

(3)

The apparent diffusion coefficient of water was calculated from a simplified version of Fick’s law,

$$D_w=\frac{J\delta }{C_f-C_p}$$

(4)

where $\delta$ is the membrane coating film thickness.

The overall effect of temperature on flux, as well as the solubility and diffusivity of component within the membrane, can be reflected by an apparent activation energy, E_a, based on the Arrhenius relationship,

$$J=A·exp(-\frac{E_a}{RT})$$

(5)

where J is the permeate flux, A is the pre-exponential factor, R is the ideal gas law constant, and T is the absolute temperature.

2.4. Integrated Membrane Process for Produced Water Desalination

The performance of PVD system was evaluated by treating a simulated produced water using the composition of a real produced water sample. OLI Stream Analyzer software (OLI Systems, Morris Plains, NJ, USA) was used to evaluate solution quality with different ionic compositions. According to the simulation results from OLI, the produced water composition given by the oil & gas producer possessed an extremely high scaling potential particularly at elevated temperatures, which would substantially limit permeate water recovery in the PVD process. Therefore, integrating pre-treatment steps such as lime softening and filtration, is necessary to prevent scaling on the PVD membranes. In this study, slaked lime (CaO, Sigma Aldrich, St. Louis, MO, USA) and soda ash (Na₂CO₃, Sigma Aldrich, St. Louis, MO, USA) were used to soften synthetic produced water and the precipitated solids were filtered out using a 0.45-μm cellulose acetate membrane (EW-06645-14, Cole Parmer, Vernon Hills, IL, USA).

2.5. Energy Performance of the PVD System

The main energy requirement of the PVD system should include: the thermal energy needed to heat up the feed stream, the electrical energy required to create vacuum and the electrical energy needed to circulate the feed. The thermal energy is the largest energy component, increasing sharply with increasing temperature [40]. The evaluation of the energy consumption of the PVD system is based on the quantities of energy consumed and the quantity of treated water. The specific energy consumption SEC, which is defined as the amount of total energy supplied (heat and electrical energy in this case) to produce a unit mass of pure water [41], was calculated to evaluate the energy performance of the PVD process as [42],

$$\mathrm{SEC}=\mathrm{STEC}+\mathrm{SEEC}$$

(6)

where STEC is the specific thermal energy consumption, or the specific heat consumption, which can be calculated from the rate of heat input into the PVD system, ${\dot{Q}}_{heat}$, and the mass flow rate of pure water produced, ${\dot{m}}_{per}$ as [43],

$$\mathrm{STEC}=\frac{{\dot{Q}}_{heat}}{{\dot{m}}_{per}},$$

(7)

and SEEC is the specific electrical energy consumption defined as the amount of electrical energy consumed, $\dot{E}$, to produce a unit mass of pure water [44],

$$\mathrm{SEEC}=\frac{\dot{E}}{{\dot{m}}_{per}}.$$

(8)

The SEEC value here includes both the vacuum pump and feed recirculating pump.

The required thermal energy includes the initial thermal energy to heat up the feed from ambient temperature to desired temperature, and continuous thermal energy to keep the feed at desired temperature. Thus, the rate of thermal energy input ${\dot{Q}}_{heat}$ can be calculated as, [26]

$${\dot{Q}}_{heat}={\dot{m}}_f{C}_{p,f}\left(T_{in, f}-T_0\right)$$

(9)

where ${\dot{m}}_f$ is the mass flow rate of the feed solution; $C_{p,f}$ is the specific heat capacity of the feed; $T_0$ and $T_{in, f}$ are the temperature of the feed before heating and feed channel inlet, respectively.

The electrical energy consumption is composed of the energy needed to circulate the feed and to create vacuum on the permeate side. Therefore, the rate of electrical energy input $\dot{E}$ is calculated as [45],

$$\dot{E}={\dot{E}}_{vac}+{\dot{E}}_{cir}$$

(10)

$${\dot{E}}_{vac}=\frac{3.35\times {10}^{-3}}{{\eta }_{vac}}{T}_p{q}_0\ln (\frac{P_{atm}}{P_{vac}})$$

(11)

$${\dot{E}}_{cir}=\frac{{\dot{V}}_f\mathsf{\Delta }P}{{\eta }_{cir}}$$

(12)

where, ${\dot{E}}_{cir}$ and ${\dot{E}}_{vac}$ are the rate of electrical energy consumption of the feed flow pump and the vacuum pump, respectively; ${\eta }_{cir}\mathrm{and}$ ${\eta }_{vac}$ are the efficiency of feed and vacuum pump, respectively; ${\dot{V}}_f$ is the volumetric flow rate of the feed solution; $\mathsf{\Delta }P$ is the feed bulk pressure difference between the inlet and outlet; $T_p$ is the permeate temperature and $q_0$ is the flow rate of the air to be evacuated from the permeate line; $P_{atm}$ and $P_{vac}$ are the atmospheric and vacuum pressures, respectively.

2.6. Model Development

The transport model outputs the system average product water fluxes, which is based on a series of differential mass, momentum and heat balances and employs a forward difference numerical solution. The global average water vapor flux is determined from

$$J={{\displaystyle \int }}_0^L{J}_{x}dx$$

(13)

where the local permeate flux $J_x$ is obtained by

$$J_x=A_m(P_{mf,x}-P_v)$$

(14)

where $A_m$ is the membrane permeability, $P_{mf,x}$ is the local partial vapor pressure at feed/membrane interface, $P_v$ is the absolute pressure on the permeate side. $P_{mf,\mathrm{x}}$ is determined by the local temperature at the feed/membrane interface $T_{mf,i}$, which can be expressed in Antoine Equation [46]

$$P_{mf,x}=(\frac{1}{1+m_x})\exp (23.1964-\frac{3816.44}{T_{mf,x}-46.13})$$

(15)

where $m_i$ is the local molar fraction of salt at the feed/membrane interface.

Based on the mass balance of the feed, local cross-flow velocity is determined by [47]

$${\rho }_x{u}_x-{\rho }_0{u}_0=\frac{1}{h_c}{{\displaystyle \int }}_0^L{\rho }_x{J}_{x}dx$$

(16)

where $\rho$ represents feed density, $u$ is the feed velocity, and $h_c$ is the feed channel height. The subscript 0 denotes the value of the parameter at the membrane inlet. The density and the viscosity of the feed solution change along the membrane module length. The local feed density can be determined by [37]

$${\rho }_x=-3.033405+10.1288163k-8.750567k^2+2.663107k^3$$

(17)

where the coefficient k is calculated as

$$k=-9.9559e^{-0.004539m_x}+7.0845e^{-0.0001638\left(T_{b,x}-273\right)}+3.9093e^{0.00002551\Delta P_{h,x}}$$

(18)

where $T_{b,x}$ is the local bulk feed temperature, and $\Delta P_{h,x}$ is the local feed pressure. The local feed viscosity ${\mu }_{b,x}$ is obtained by [37]

$$\begin{gathered} {\mu }_{b,x}={\mu }_{w,x}\left(1+0.0816m_x-0.0122m_x{}^2+0.000128m_x{}^3 \\ +0.000629T_{b,x}\left(1-e^{-0.7m_x}\right)\right) \end{gathered}$$

(19)

where the local viscosity of water ${\mu }_{w,x}$ is calculated as

$${\mu }_{w,x}=2.414\times {10}^{-5}\times {10}^{\frac{247.8}{T_{b,x}-140}}$$

(20)

Local hydraulic pressure $\Delta P_{h,x}$ is determined by [47]

$$\Delta P_{h,x}=\Delta P_{h,0}-\frac{1}{2d_H}{{\displaystyle \int }}_0^L{f}_{sp,x}{\rho }_x{u}_x{}^{2}dx$$

(21)

where $\Delta P_{h,0}$ is the inlet pressure of the feed, $d_H$ is the hydraulic diameter which is the diameter of the membrane in this case, $f_{sp,x}$ is the local frictional factor determined by

$$f_{sp,x}=\{\begin{array}{c}24R{e}_x{}^{-1} (R{e}_x<2300)\\ 0.079R{e}_x{}^{-0.25} \left(R{e}_x\ge 2300\right)\end{array}$$

(22)

Local bulk feed temperature can be estimated from a heat balance [48]

$$T_{b,x}=\frac{1}{{\rho }_x{u}_x{c}_{p,x}}({\rho }_0{u}_0{c}_{p,0}{T}_{b,0}-\frac{{\rho }_w\Delta H_x}{M_w{h}_c}{{\displaystyle \int }}_0^L{J}_{x}dx)$$

(23)

where $T_{b,0}$ (K) is the inlet bulk feed temperature, ${\rho }_w$ is the density of water, $M_w$ is the molar mass of water, $\Delta H$ is the latent heat of vaporization of the feed, and $c_p$ is the feed specific heat capacity. The local value of both $\Delta H$ and $c_p$ can be calculated according to the local solute concentration, c_x, and temperature, $T_{b,x}$ [38,39]

$$\Delta H_x=1.91846\times {10}^6\times {(\frac{T_{b,x}}{T_{b,x}-33.91})}^2\times (1-\frac{c_x}{1000{\rho }_x})$$

(24)

$$\begin{array}{cc}\hfill c_{p,x}=(5.328& -9.76\times {10}^{-2}S+4.04\times {10}^{-4}{S}^2)\hfill \\ & +(-6.913\times {10}^{-3}+7.351\times {10}^{-4}S\hfill \\ & +3.15\times {10}^{-6}{S}^2)T_{b,x}\hfill \\ & +\left(9.6\times {10}^{-6}-1.927\times {10}^{-6}S+8.23\times {10}^{-9}{S}^2\right)T_{b,x}{}^2\hfill \\ & +\left(2.5\times {10}^{-9}+1.666\times {10}^{-9}S-7.125\times {10}^{-12}{S}^2\right)T_{b,x}{}^3\hfill \end{array}$$

(25)

From boundary layer heat transfer theory, temperature at the membrane surface $T_{m,x}$ can be estimated by

$$T_{m,x}=T_{b,x}-\frac{J_x\frac{{\rho }_x}{M_w}\mathsf{\Delta }H}{h_{f,x}}$$

(26)

where $h_{f,x}$ is the local heat transfer coefficient, which can be determined from Nusselt (Nu)-Reynolds (Re)–Prandtl (Pr) relationship [49,50,51],

$$N{u}_x=\frac{d_H}{k_T}{h}_{f,x}=\{\begin{array}{c}0.097R{e}_x{}^{0.73}P{r}_x{}^{0.13} (R{e}_x<1600)\\ 0.023R{e}_x{}^{0.8}P{r}_x{}^{0.3} (R{e}_x>2200)\\ 0.43R{e}_x{}^{0.59}P{r}_x{}^{0.3} \left(1600\le R{e}_x\le 2200\right)\end{array}$$

(27)

where $k_T$ is the thermal conductivity of feed water calculated as [38,39],

$$\begin{array}{cc}\hfill lo{g}_{10}\left(k_{T, x}\right)=& lo{g}_{10}\left(240+0.0002S\right)+0.434\times (2.3\hfill \\ & -\frac{343.5+0.037S}{T_{b,x}}){(1-\frac{T_{b,x}}{647+0.03S})}^{0.333}\hfill \end{array}$$

(28)

The salt concentration of the bulk feed $c_b$ is determined by [47]

$$c_{b,x}=\frac{c_{b,0}{u}_0}{u_x}$$

(29)

Accounting for concentration polarization [52], the salinity at the membrane surface $c_m$ is determined by

$$c_{m,x}=c_{b,x}\exp \left(\frac{J_x}{k_{f,x}}\right)$$

(30)

where $k_{f,x}$ (m/s) is the local mass transfer coefficient given by Sherwood (Sh) – Reynolds (Re) -Schmidt (Sc) relationship as the following,

$$\begin{array}{c}S{h}_x=\frac{k_{f,x}{d}_H}{D}\hfill \\ =\{\begin{array}{c}1.65{\left(R{e}_{x}S{c}_x\frac{d_H}{L}\right)}^{0.33} (R{e}_x<1600)\\ 0.04R{e}_x{}^{0.75}S{c}_x{}^{0.33} (R{e}_x>2200)\\ 1.65{\left(R{e}_{x}S{c}_x\frac{d_H}{L}\right)}^{0.33}+0.04R{e}_x{}^{0.75}S{c}_x{}^{0.33} \left(1600\le R{e}_x\le 2200\right)\end{array}\hfill \end{array}$$

(31)

where $S{c}_x$ is the local Schmidt number ($=\frac{{\mu }_x}{{\rho }_{x}D}$), and $D_x$ is the local diffusion coefficient of NaCl.

3. Results and Discussion

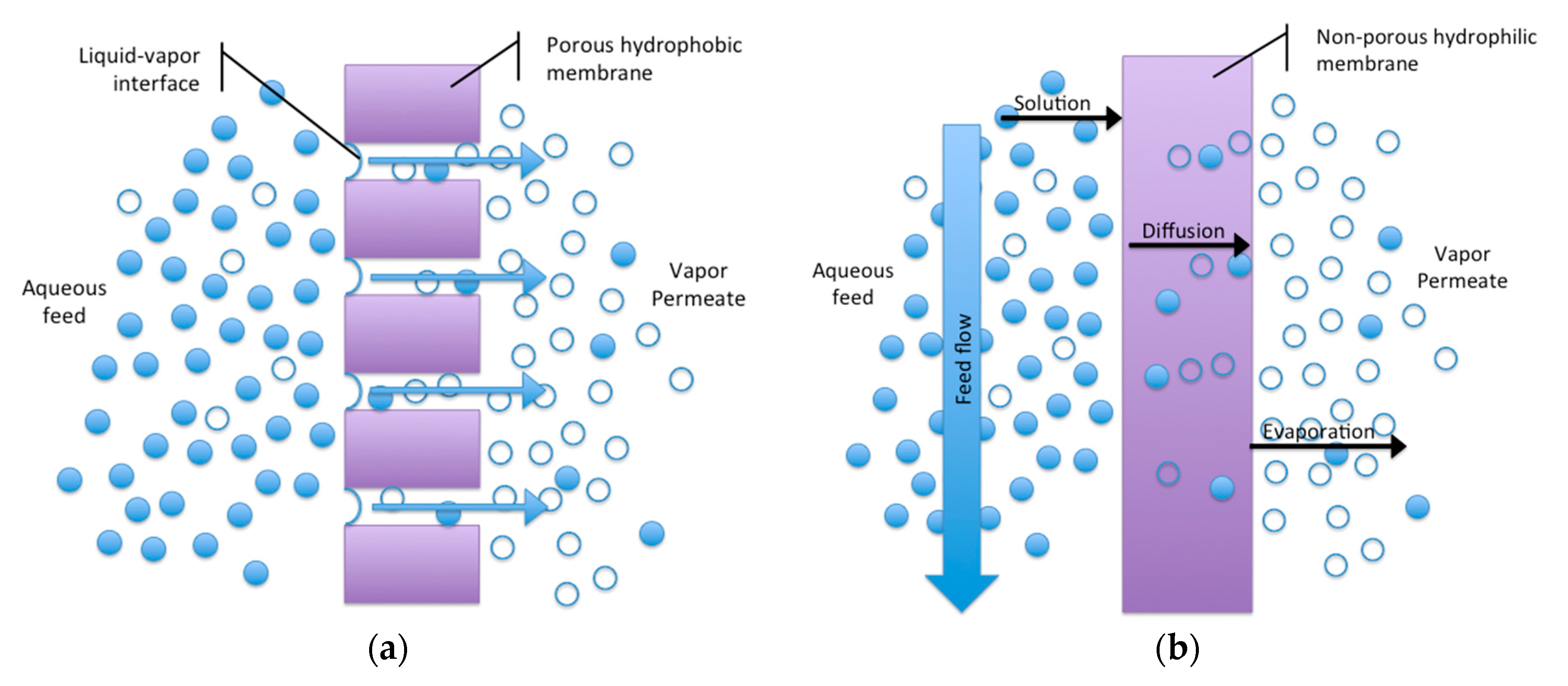
3.1. Membrane Flux

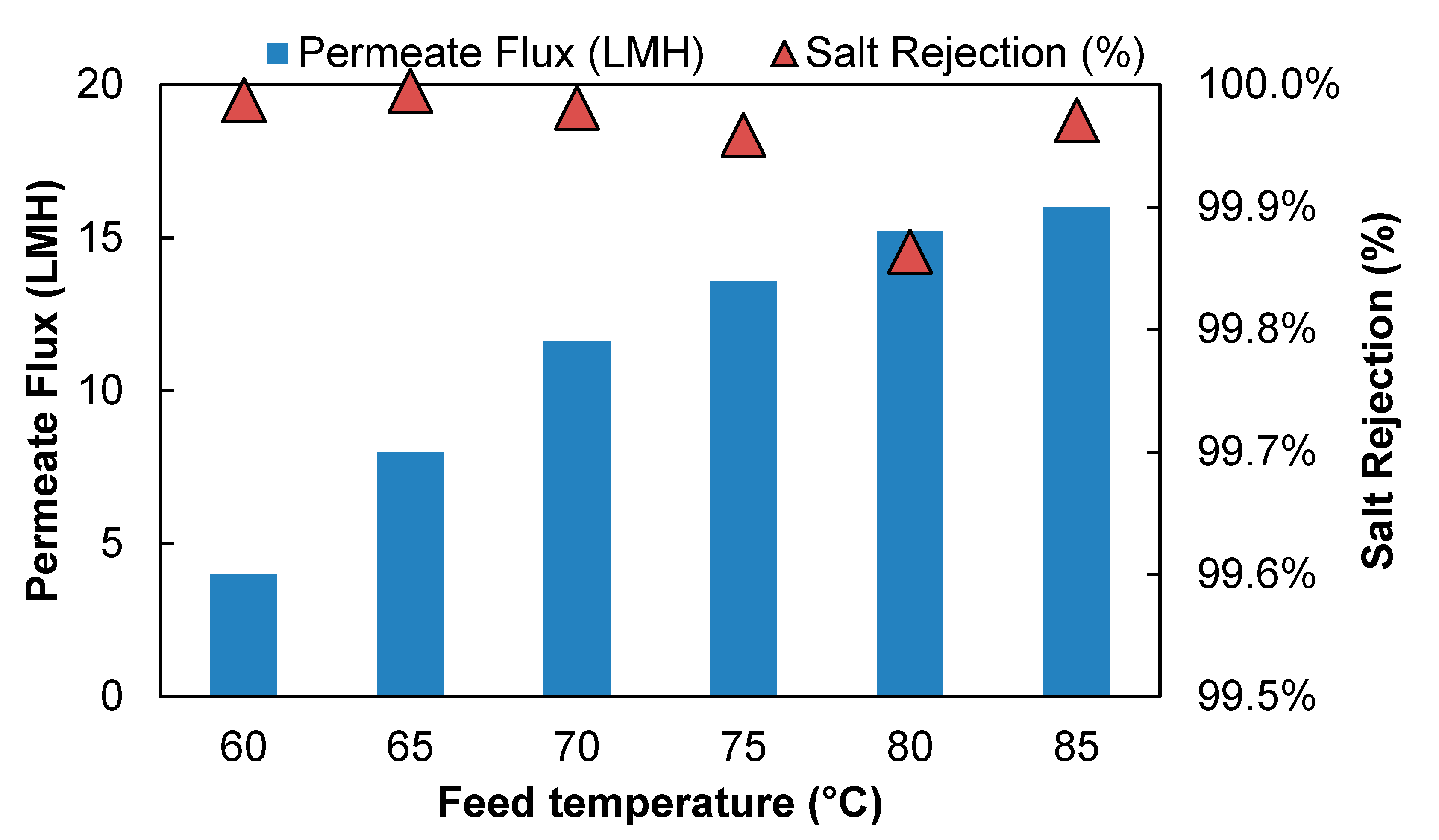
Figure 3 shows the effect of feed temperature on the PVD system performance desalinating 15 g/L NaCl solution. The feed flow rate was maintained at 0.56 L/min to keep the feed flow channel Reynolds number at 4800. As feed temperature increased from 60 °C to 85 °C, the water flux increases from 4.3 LMH to 16 LMH. A higher water flux was expected at a higher temperature, because the partial vapor pressure difference between the feed and permeate side, which is the driving force of a PVD process, is strongly affected by temperature. As the feed temperature increased, the water vapor pressure on the feed side increases, whereas the vapor pressure on the permeate side remains unchanged. As a result, the vapor pressure difference across the membrane increased which led to an increase in vapor flux.

In addition, the increase in temperature also increases water diffusion through the membrane, likely through a combination of higher bulk diffusivity and more swollen (open) membrane pore structure, resulting in higher water permeability (

Table 1. Apparent diffusion coefficient of water at different temperatures.

Temperature (°C)	Water Diffusion Coefficient (×10−10 m2/s)
	60	65	70	75	80	85
15g/L NaCl Re = 4800	0.69	1.39	2.02	2.37	2.65	2.79

). Based on free volume theory [53], momentary free volumes are created by the thermal motion of polymer chains in an amorphous region; therefore, as the temperature increased, the free volume of the membranes could increase the higher frequency and amplitude of chain motion. When the polymer-free volumes increase, water molecules diffuse through with less resistance; combined with a higher bulk diffusivity, the apparent water permeability and observed water flux increased.

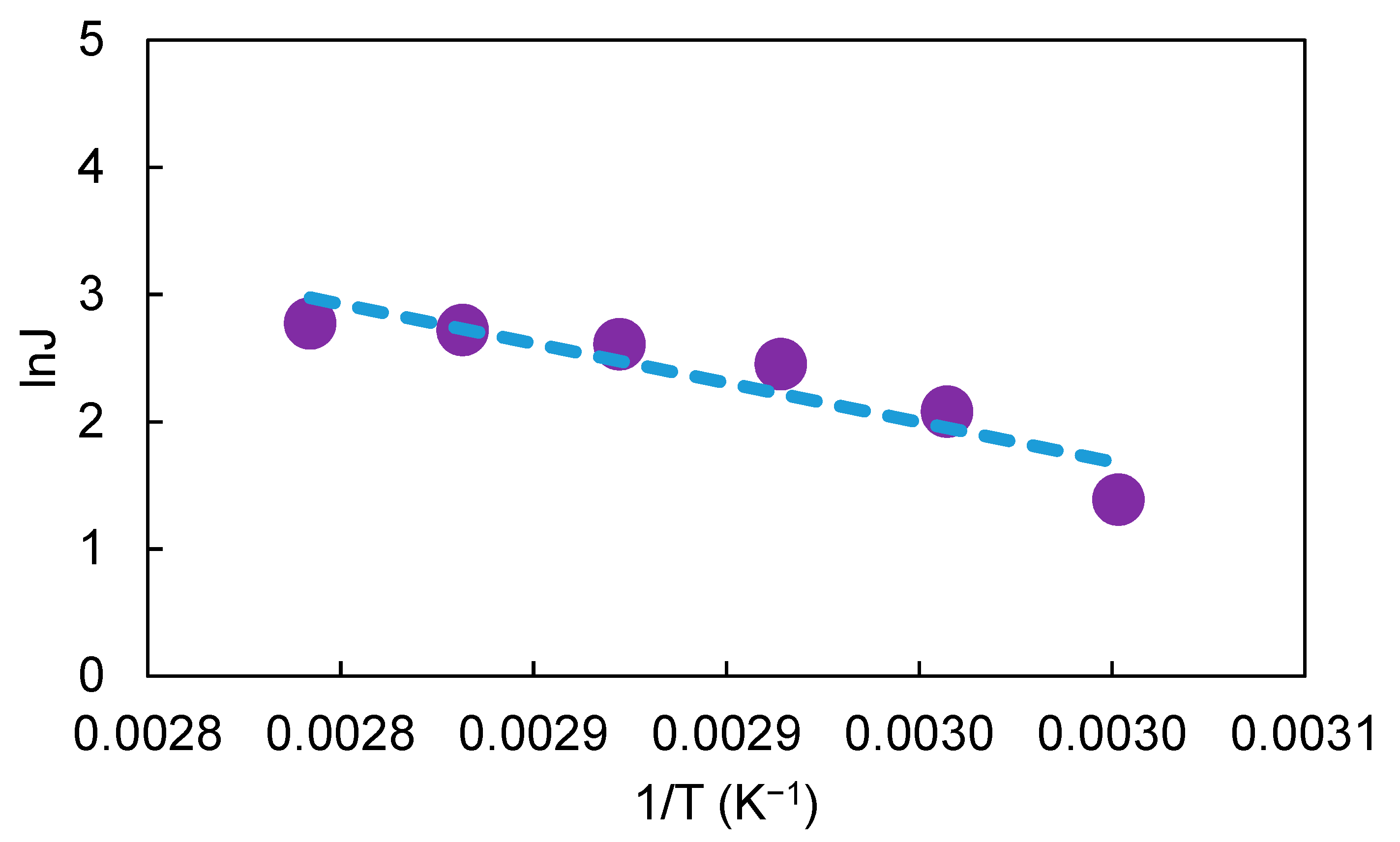
Figure 4 shows a linear Arrhenius plot of the natural logarithm of water flux versus reciprocal temperature. The apparent activation energy E_a of water in the membrane was determined to be 32.6 kJ/mol from the slope of the Arrhenius plot. Compare to other studies, the apparent activation energy of water in the Hybsi membrane is similar to other hybrid pervaporative membranes, where the activation energy in those membranes were reported to be in the range of 11.8–45 kJ/mol, depending on the different membrane materials and operating conditions [25,54,55,56,57,58]. The positive activation energy implies that permeation flux increases with increasing temperature [25], as confirmed by the results shown in Figure 3.

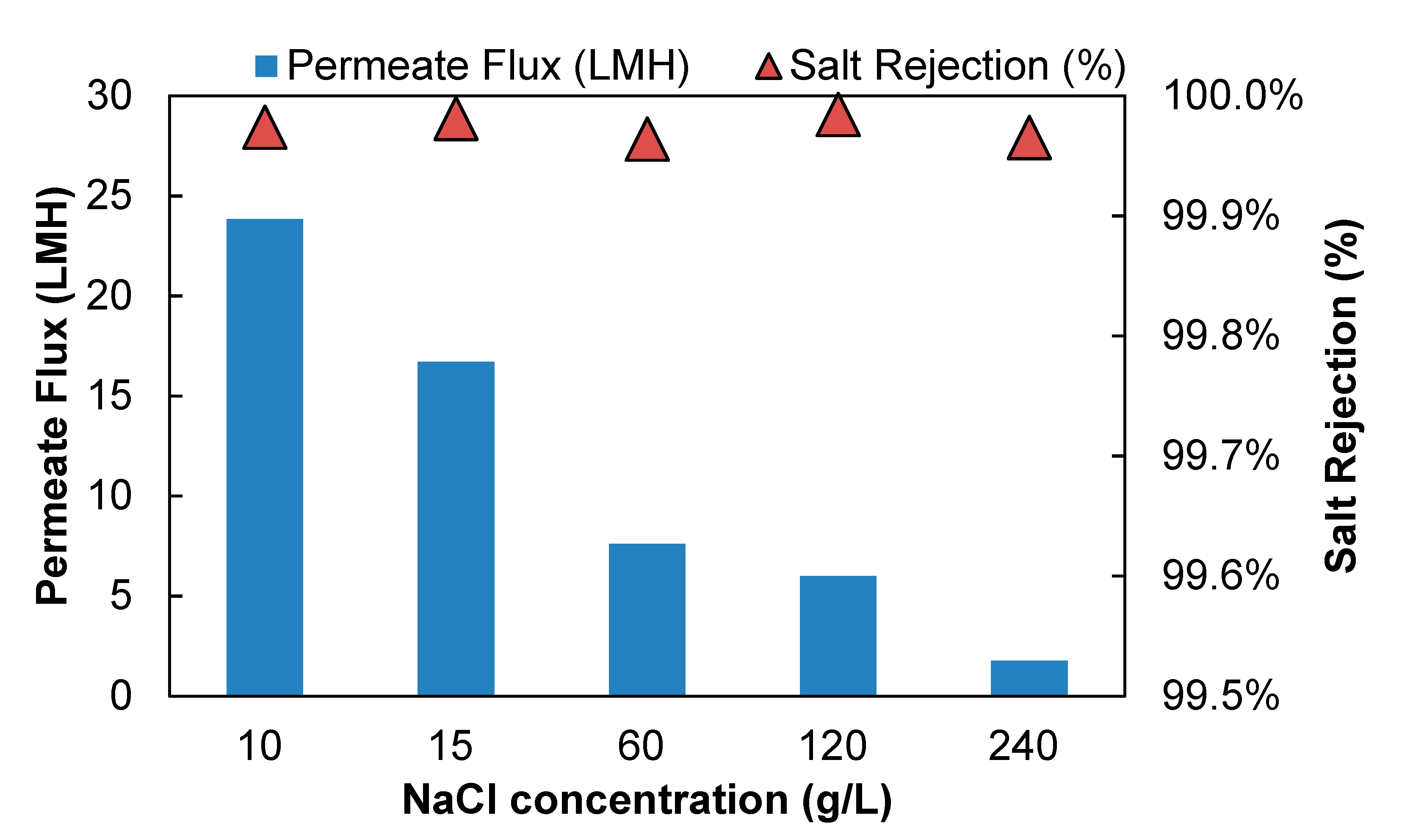
The impact of salt concentration on separation performance of aqueous salt solution is shown in Figure 5. At the temperatures of 85 °C with crossflow Reynolds number of 4800, the water flux decreased from 23.84 LMH to 1.76 LMH when NaCl concentration in the feed increased from 10 g/L to 240 g/L.

Table 2. Simulation results of parameters values with different NaCl concentration.

NaCl Concentration (g/L)	Modeling Results with 85 °C Feed and Re 4800
	10	15	60	120	240
Average surface temperature (°C)	79.7	79.7	79.6	79.4	79.3
Average surface salinity (g/L)	10.2	15.3	61.2	122.4	244.6
Partial vapor pressure difference (kPa)	29.9	29.8	29.0	28.0	26.2

demonstrates the membrane surface temperature, surface salinity, and partial vapor pressure difference (i.e., the driving force) under different feed salt concentration calculated with the model described in Section 2.6. The results show that as feed salt concentration increased, the concentration polarization got significantly worse (evidenced by more than 20 times of the membrane surface salt concentration at 240 g/L feed compared to 10 g/L feed concentration). The membrane surface temperature change with different feed concentration is minimal. The driving force for permeation (feed-side interfacial water partial pressure) decreased ~10% when NaCl concentration increased from 10 g/L to 240 g/L (Table 2). Feed salt concentration is believed to directly affect the water sorption at the liquid/membrane interface [25], because water concentration in the feed decreased as salt concentration increased, which led to the water concentration decrease in the membrane. The substantial change in membrane surface salinity could also change in membrane structure thus membrane permeability, which also plays a role decrease in flux with feed concentration (Equation (16)). These findings indicate that the mass transfer on the feed side was significantly limited by the extent of concentration polarization.

Figure 6 shows the effect of the feed crossflow Reynolds number on the pervaporation performance of the PVD system when the feed flow rate varied from 0.04 to 0.56 L/min at the feed concentration of 15 g/L and temperature of 85 °C. Permeate vapor flux substantially increased from 1.5 LMH to 16 LMH when the feed crossflow Reynolds number increased from 300 to 4800. As Re number increases, assuming the change in water diffusivity with temperature is directly proportional to T, the water diffusivity increase due to temperature increase is less than 3.6%. In

Table 3. Simulation results of parameters values with different Re.

Re	Modeling Results with Feed Contains 15 g/L NaCl @ 85 °C
	300	600	1200	2400	4800
Average surface temperature (°C)	67.6	72.1	76.3	76.6	79.7
Average surface salt concentration (g/L)	17.1	17.4	17.5	15.4	15.3
Partial vapor pressure difference (kPa)	11.5	17.4	23.9	24.4	29.8

, we present the membrane surface temperature, surface salinity, and partial vapor pressure difference under different hydraulic conditions calculated with the model described in Section 2.6. The results show that as feed flow rate increased, the flow regime in the feed channel changed from laminar flow to turbulent flow, which helped to reduce concentration polarization (evidenced by lower membrane surface salt concentration) and temperature polarization (evidenced by higher membrane surface temperature). In contrast, the driving force for permeation (feed-side interfacial water partial pressure) is almost three times higher at Re 4800 than for Re 300 (Table 3). The change in membrane surface temperature and salinity could also change in membrane structure, which could account for the additional increase in flux with temperature (Equation (14)). These findings imply that the mass transfer on the feed side was significantly limited by the extent of concentration and/or temperature polarization, which is consistent with results from other studies [25]. Therefore, both polarization phenomena need to be managed to enhance mass transfer in PVD systems.

3.2. Salt Rejection

The observed NaCl rejection of PVD system remained above 99.86% under all the tested operating conditions, which is similar to the typical rejections in conventional VMD processes [28,29,30,31]. The permeate salt concentrations were below 10 mg/L in all cases. The high salt rejection was expected because NaCl, as a non-volatile compound, is not likely to penetrate the dense PV membrane material and enter the vapor stream on the permeate side. The mass transfer in a PVD process can be described by solution-diffusion model, which indicates that sorption selectivity is more dependent on the affinity between the membrane active layer and the permeants in the solution [8,59]. As the Hybsi membrane used in the study is hydrophilic in nature [60], the much smaller water molecules should preferentially partition into the membrane, diffuse across the dense coating film and evaporate through the porous ceramic support. While some salt uptake by the coating film is likely to occur, being non-volatile there is no obvious mechanism for NaCl to make its way into the distillate [8,25].

3.3. Synthetic Produced Water Treatment with PVD Process

Produced water ranges in dramatically in quality and composition depending on the geological formation as well as the oil & gas production method employed; a comprehensive review is beyond the scope of this study, but the reader is directed to other references for more details [61,62]. The water quality (after de-oiling) of an actual produced water provided by a large California oil & gas producer (anonymity requested) is reported in the third column from the left in

Table 4. Reported and Analyzed Produced Water Quality.

	Symbol	Produced Water Quality (mg/L)	OLI Adjusted @ 25 °C (mg/L)	OLI Adjusted @ 85 °C (mg/L)	OLI after Softening at 85 °C (mg/L)
Chloride	Cl−	4258	4207.92	4378.51	4180.88
Bromide	Br−	19	18.64	18.64	18.66
Sulfate	SO42−	1717	1697.70	950.00	1694.44
Total Alkalinity	as HCO3−	296.2	304.18	115.57	9.01
Sodium	Na+	1247	1386.36	1493.64	3657.54
Potassium	K+	73	73.42	73.42	73.51
Calcium	Ca2+	1283	1281.27	912.55	0.01
Magnesium	Mg2+	341.2	394.44	394.44	0.02
Strontium	Sr2−	27.3	27.93	24.20	0.34
Silica	SiO2	32	32.00	32.00	0.07
Iron	Fe	2	2.01	2.01	0.01
pH		6.23	6.23	6.23	10.17
Solid formed	Mg in 1 L		8.64	1208.00	7579.00

. According to this water quality, synthetic PW water was made (see recipe in

Table 5. Synthetic Produced Water Recipe.

Chemical	Formula	Concentration (mg/L)
Sodium chloride	NaCl	5020.90
Magnesium sulfate heptahydrate	MgSO4·7H2O	3361.02
Calcium chloride dihydrate	CaCl2·2H2O	4641.78
Sodium bicarbonate	NaHCO3	407.80
Sodium bromide	NaBr	24.47
Strontium chloride hexahydrate	SrCl2·6H2O	81.19
Potassium chloride	KCl	139.19
Iron(II) sulfate heptahydrate	FeSO4·7H2O	10.00
Sodium sulfate	Na2SO4	539.56
Sodium silicate	Na2SiO3	139.08

) and tested in the PVD process. The results from the OLI simulations are shown in the columns to the right in Table 4. The fourth and fifth column represents the same ionic concentration at the temperature of 25 °C and 85 °C, respectively. As shown in Table 4, the solid concentration increased from 8.64 mg/L at 25 °C to 1208 mg/L at 85 °C, which indicates that the synthetic produced water possessed an extremely high scaling potential at elevated operating temperatures. Therefore, warm lime softening and membrane filtration were integrated as pre-treatment to prevent scaling on the PV membranes. The last column shows the water quality after addition of slaked lime and soda ash to reduce scaling potential. The solids were filtered with 0.45-micron membrane at high temperature before feeding the produced water into the bench scale PVD system.

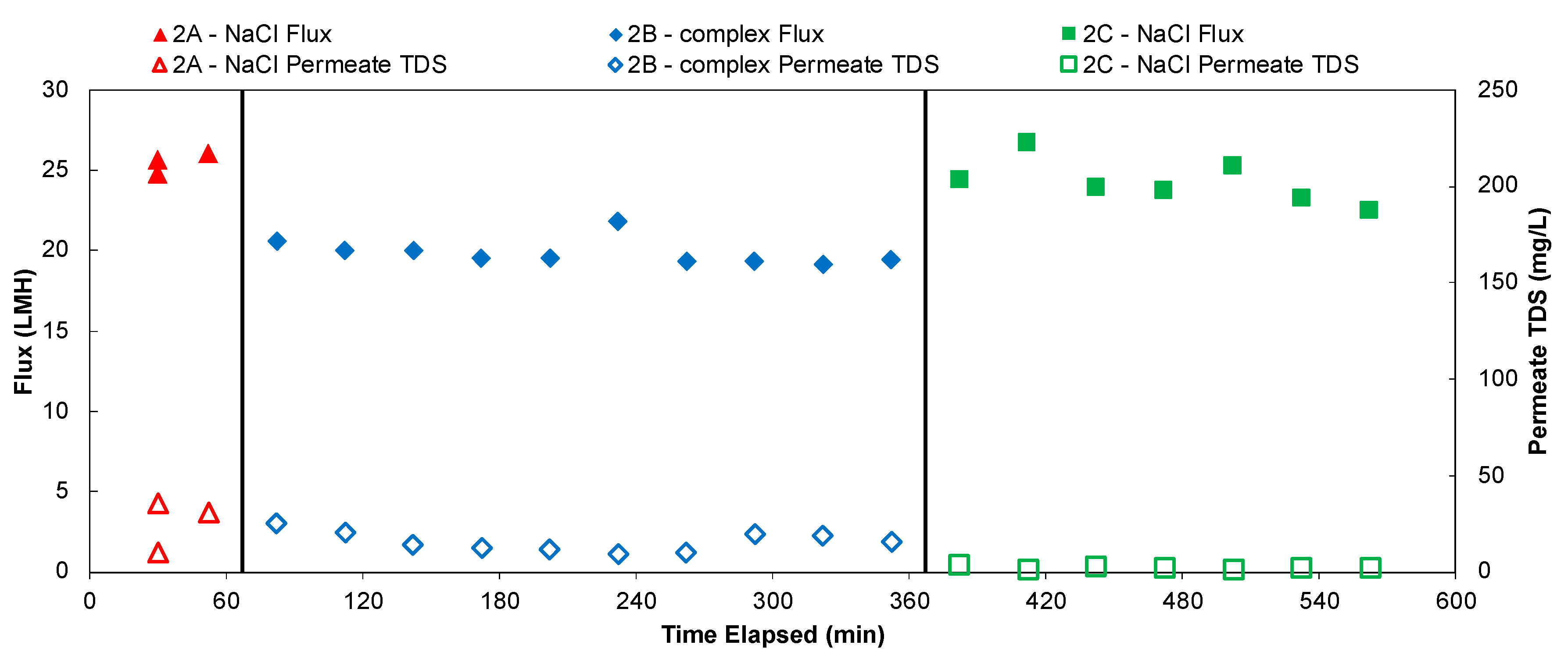
Figure 7 shows the flux and permeate water quality of a 10 h long experiment of desalinating feed solutions that contain 10 g/L TDS, with feed crossflow Reynolds number of 4800, feed water temperature of 85 °C and permeate vacuum of 0.85 bar. Permeate flux and TDS were monitored and recorded every 30 min. In the first ~1 h of the experiment, the feed solution to the system only contains 10 g/L NaCl. The feed water was changed to the softened produced water recipe (TDS = 10 g/L) in the second experiments that lasted for 5 h. Then the feed was changed back to 10 g/L NaCl for the final 4 h. The flux was relatively stable throughout, but water vapor flux declined slightly when the feed water was changed from NaCl solution to the softened produced water solution. The flux bounced back to similar level when the feed water was switched back to NaCl, therefore the effect appears reversible. This can be explained by the change in driving force on the feed side. Although the two feed solutions tested here had the same TDS, the difference in ion composition of the solution could lead to a difference in ionic strength, water activity, salt ion diffusivity and concentration polarization. Compared to NaCl solution, the synthetic produced water contains more multi-valent ions that lower the water activity of the solution, which essentially decreased water vapor pressure on the feed side [63,64,65]. The impact of feed electrolyte composition on water flux through membranes have also been investigated in other studies and a similar trend was reported that the feed solution with multiple ions tend to show lower flux [9,55,66,67]. Regarding the permeate TDS values, it stayed at a fairly constant level despite the change in feed solutions.

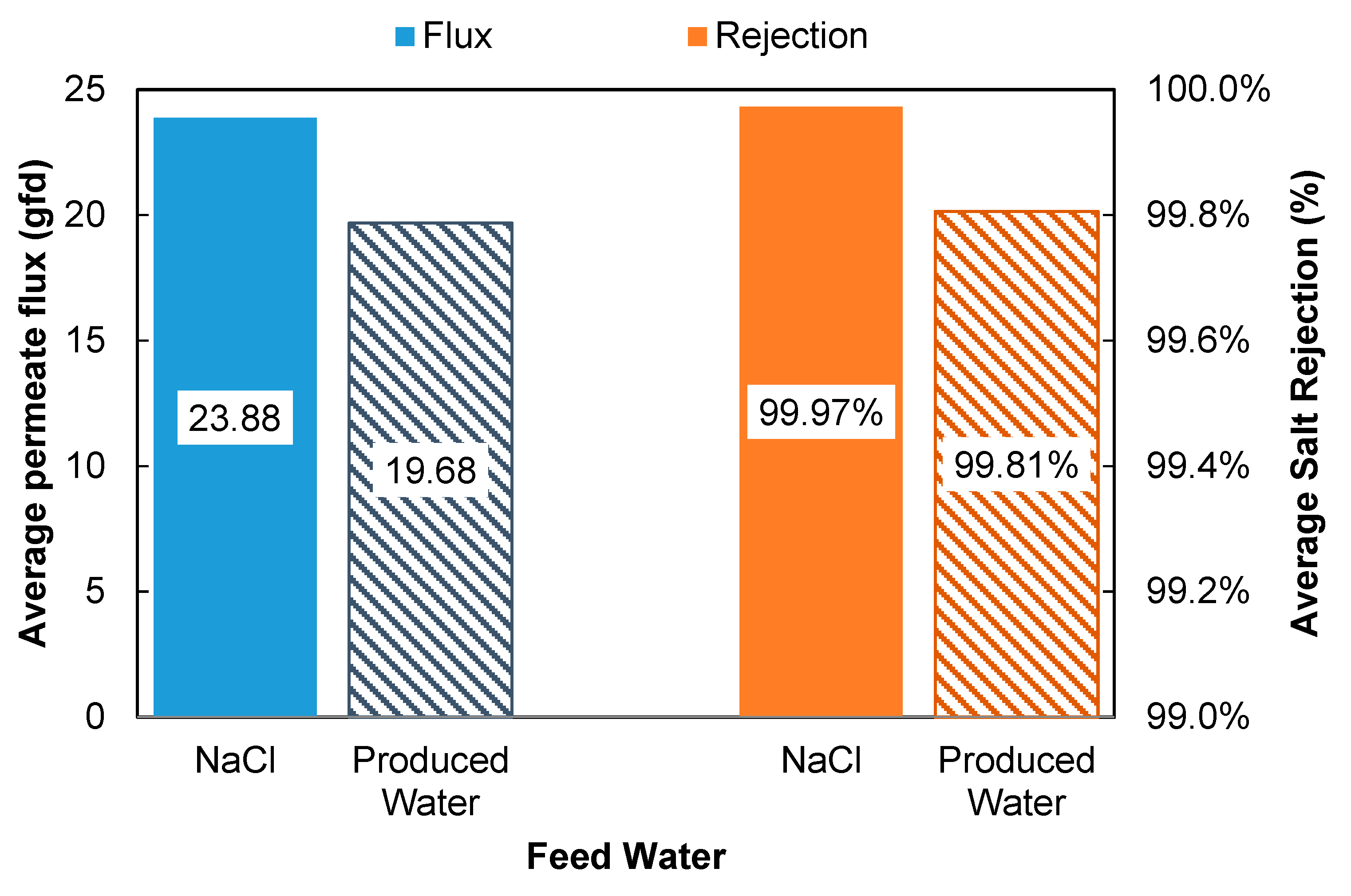
A side by side comparison of the performance data from the produced water and NaCl solution is shown in Figure 8. The results indicate that the PVD process was able to produce high quality permeate (>99.8% rejection) at 19.7 LMH and 85 °C. Compare to other PVD processes with silica-based membranes reported in literature (

Table 6. Comparison of PVD process performance with silica-based membranes.

	Feed Composition	Feed TDS (g/L)	Feed Temperature (°C)	Flux (LMH)	Salt Rejection (%)	Reference
silica	natural saline water	17.1–30.5	26–60	0.33–1.19	69.9–99.9	[68]
silica	NaCl	3–150	22	1.5–6.5	>90	[69]
La25Y75-BTESE-SiO2	NaCl	3–75	25–60	7.9–15.6	>99.9	[57]
PVA-MA-silica	NaCl	2–50	22–65	8–11.7	>99.9	[25]
PVA-MA-silica	NaCl	2	22	6.93	99.5	[21]
PVA-MA-silica	NaCl	2	65	11.7	99.9	[26]
MTES-SiO2	NaCl	35	25	2.6	90	[70]
Amorphous molecular sieve silica	NaCl	35	25	1.8	97	[70]
nickel oxide silica	NaCl	3–35	25–60	2.5–6	91.5–99.9	[71]
interlayer-free cobalt oxide silica	NaCl	3–75	22–60	7.7–20	>99.7	[72]
cobalt oxide silica	NaCl	10–75	25–75	0.2–1.8	>99	[73]
P123-silica	NaCl	0–150	25–60	9.2–19.8	>98.4	[74]
P123-silica	NaCl	3–75	22–60	2.2–7.5	>99.5	[75]
ES40-silica	NaCl	3–35	25–60	2–4.6	>99	[76]
ES40-silica	NaCl	3–35	25–60	1.8–2.32	>99	[77]
Hybsi®	NaCl	10–240	60–85	1.5–23.8	>99.9	This study
Hybsi®	Synthetic produced water	10	85	19.68	99.81	This study

), the PVD system in this study has exhibited relatively high water vapor flux and salt rejection. More importantly, the PVD system in this study demonstrated stable performance when tested in extreme operating conditions, such as high feed concentration, temperature and cross-flow velocity.

3.4. PVD Process Energy Performance

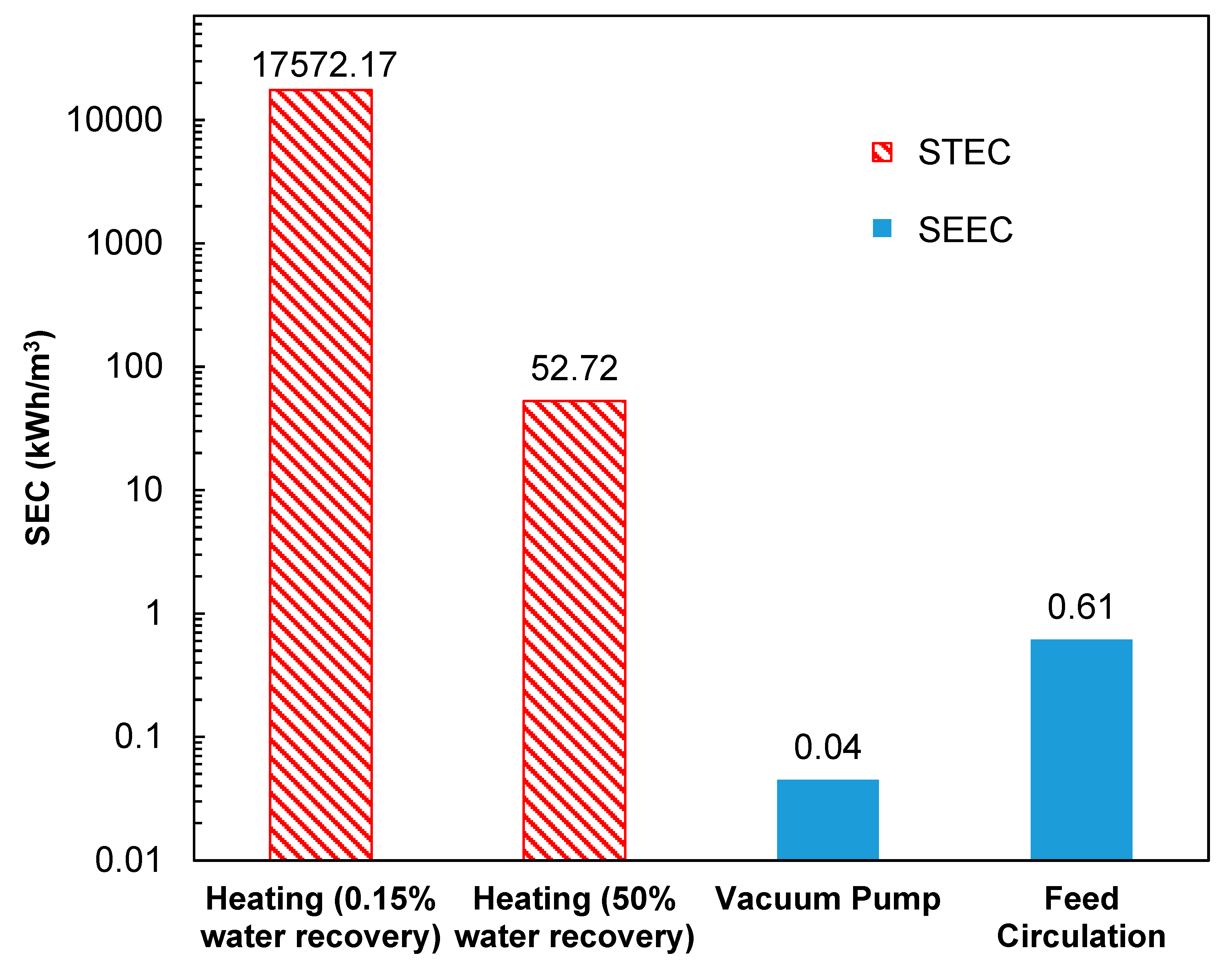
Herein, we chose a scenario to investigate the SEC of the PVD process when the system was operated to treat synthetic produced water (TDS = 10 g/L) at 85 °C with cross-flow Reynolds number of 4800 and permeate vacuum of 0.85 bar. Figure 9 shows a breakdown of the different energy components for PVD of the produced water and the NaCl feed solution. It is clear that the specific thermal energy consumption dominants the overall SEC. In a lab-scale system with low water recovery such as the one demonstrated here (~0.15% recovery), a total amount of 17.6 MWh thermal energy was needed to heat up the feed from ambient temperature to 85 °C to generate permeate flux at the rate of 23.8 LMH. In a full-scale system with a much higher water recovery (typ., 30 to 90%), the required thermal energy drops down to 52.7 kW·h/m³ at 50% water recovery. Compared to thermal energy, the electrical energy remains negligible, as indicated by the small SEEC values in Figure 8. Note that the SEC values are very sensitive to permeate flux, which could vary substantially as a function of recovery and other operating conditions.

Although the SEC values reported here only reflect the energy performance of one specific PVD system operating at a preset condition, the conclusion still holds that PVD would likely be more energy-intense at scale than other desalination processes such as reverse osmosis (RO), reverse electrodialysis (RED), multi-stage flush (MSF), multi-effect distillation (MED), and vapor compression (VC). The findings are consistent with other studies that PVD requires very little electricity, but consumes large amount of thermal energy [8,26,78]. In fact, the electrical energy needed for PVD is the lowest compare to other desalination technologies (

Table 7. Energy consumption for various desalination technologies [80,81,82].

Process	Thermal Energy (kWh/m3)	Electrical Energy (kWh/m3)
MSF	12–24	3.5–5
MED	12.2–19.1	2–2.5
VC-thermal	14.6	1.5–2
VC-mechanical	N/A	7–12
RO-seawater	N/A	3–7
RO-brackish water	N/A	0.5–2.5
ED-brackish water	N/A	2.6–5.5

MSF—multi-stage flush, MED—multi-effect distillation, VC—vapor compression, RO—reverse osmosis, ED—electrodialysis.

) [78,79,80]. If low grade or waste heat could be harvested and/or renewable energy such as solar thermal energy could be integrated to provide the thermal energy needed to drive a PVD process, the overall fossil fuel-derived energy consumption of PVD process could be dramatically lower [21,22,23,26]. Additionally, heat recovery could be considered as another strategy to lower thermal energy consumption.

The results showed that pervaporative desalination cannot compete with other desalination technologies directly from the perspective of specific energy consumption. However, PVD process still possesses some advantages that might make it attractive in some applications. First of all, PVD process is capable of desalinating hypersaline feed (up to 240 g/L from this study) such as oil and gas hydraulic fracturing produced water; thus, it can be implemented to concentrate wastewater on-site and facilitate minimal liquid discharge, directly, and if combined with a crystallizer, zero liquid discharge. Second, when waste heat or solar heat is integrated to provide “free” thermal energy, PVD requires much less electrical energy compared to other thermal process such as MSF and MED. In addition, PVD is more robust and less prone to system failure compare to traditional porous membrane-based MD processes, which suffer from pore-wetting related process failure.

4. Conclusions

Pervaporative distillation for saline water desalination has not been widely studied, despite the extensive applications of pervaporation to organic/water and organic/organic separations. In this study, a commercial ceramic-supported, cross-linked organosilane-based hydrophilic pervaporation membrane was tested using a bench-scale PVD apparatus. Results from PVD experiments suggest higher feed temperature, lower feed salt concentration, higher feed cross-flow rate, and simpler feed composition all contribute to higher permeate water flux. Observed conductivity rejection exceeded 99.9% with feed salt concentration up to 250,000 mg/L except for the more complex brackish feed electrolyte, which produced 99.81% conductivity rejection. This PVD process was proven to be an effective treatment option for hyper-saline, hard-to-treat water that can consistently deliver high product water quality (<10 mg/L of TDS) under all operating conditions tested, and high permeate flux (up to 23.8 LMH) under optimized operating conditions. The analysis of energy consumption of PVD process indicates that the high thermal energy consumption is the main energy requirement and appears to be the obstacle of scaling up. If coupled with wasted heat or solar energy, PVD still has the potential to become an efficient and promising desalination technology with optimized engineering processes.