Carbon Fixation Trends in Eleven of the World’s Largest Lakes: 2003–2018
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Herdendorf, C.E. Large lakes of the world. J. Great Lakes Res. 1982, 8, 379–412. [Google Scholar] [CrossRef]
- Downing, J.A.; Prairie, Y.; Cole, J.; Duarte, C.; Tranvik, L.; Striegl, R.G.; McDowell, W.; Kortelainen, P.; Caraco, N.; Melack, J.; et al. The global abundance and size distribution of lakes, ponds, and impoundments. Limnol. Oceanogr. 2006, 51, 2388–2397. [Google Scholar] [CrossRef] [Green Version]
- Verpoorter, C.; Kutser, T.; Seekell, D.A.; Tranvik, L.J. A global inventory of lakes based on high-resolution satellite imagery. Geophys. Res. Lett. 2014, 41, 6396–6402. [Google Scholar] [CrossRef]
- Sterner, R.W.; Keeler, B.; Polasky, S.; Poudel, R.; Rhude, K.; Rogers, M. Ecosystem services of Earth’s largest freshwater lakes. Ecosyst. Serv. 2020, 41, 101046. [Google Scholar] [CrossRef]
- Bootsma, H.A. Oceans, lakes, and inland seas: A virtual issue on the large lakes of the world. Limnol. Oceanogr. Bull. 2018, 27, 87–88. [Google Scholar] [CrossRef] [Green Version]
- Beeton, A.M. Large freshwater lakes: Present state, trends, and future. Environ. Conserv. 2002, 29, 21–38. [Google Scholar] [CrossRef]
- Cole, J.J.; Prairie, Y.T.; Caraco, N.F.; McDowell, W.H.; Tranvik, L.J.; Striegl, R.G.; Duarte, C.M.; Kortelainen, P.; Downing, J.A.; Middelburg, J.J.; et al. Plumbing the global carbon cycle: Integrating inland waters into the terrestrial carbon budget. Ecosystems 2007, 10, 172–185. [Google Scholar] [CrossRef] [Green Version]
- Williamson, C.E.; Saros, J.E.; Vincent, W.F.; Smol, J.P. Lakes and reservoirs as sentinels, integrators, and regulators of climate change. Limnol. Oceanogr. 2009, 54, 2273–2282. [Google Scholar] [CrossRef]
- Buffam, I.; Turner, M.G.; Desai, A.R.; Hanson, P.C.; Rusak, J.A.; Lottig, N.R.; Stanley, E.H.; Carpenter, S.R. Integrating aquatic and terrestrial components to construct a complete carbon budget for a north temperate lake district. Glob. Chang. Biol. 2011, 17, 1193–1211. [Google Scholar] [CrossRef]
- Tilzer, M.M.; Serruya, C. Large Lakes: Ecological Structure and Function; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Sterner, R.W.; Ostrom, P.; Ostrom, N.E.; Klump, J.V.; Steinman, A.D.; Dreelin, E.A.; Vander Zanden, M.J.; Fisk, A.T. Grand challenges for research in the Laurentian Great Lakes. Limnol. Oceanogr. 2017, 62, 2510–2523. [Google Scholar] [CrossRef]
- O’Reilly, C.M.; Alin, S.R.; Plisnier, P.-D.; Cohen, A.S.; McKee, B.A. Climate change decreases aquatic ecosystem productivity of Lake Tanganyika, Africa. Nature 2003, 424, 766–768. [Google Scholar] [CrossRef] [PubMed]
- Verburg, P.; Hecky, R.E.; Kling, H. Ecological consequences of a century of warming in Lake Tanganyika. Science 2003, 301, 505–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Austin, J.A.; Colman, S.M. Lake Superior summer water temperatures are increasing more rapidly than regional air temperatures: A positive ice-albedo feedback. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- O’Reilly, C.M.; Sharma, S.; Gray, D.K.; Hampton, S.E.; Read, J.S.; Rowley, R.J.; Schneider, P.; Lenters, J.D.; McIntyre, P.B.; Kraemer, B.M.; et al. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 2015, 42, 773–781. [Google Scholar] [CrossRef] [Green Version]
- Mason, L.A.; Riseng, C.M.; Gronewold, A.D.; Rutherford, E.S.; Wang, J.; Clites, A.; Smith, S.D.; McIntyre, P.B. Fine-scale spatial variation in ice cover and surface temperature trends across the surface of the Laurentian Great Lakes. Clim. Chang. 2016, 138, 71–83. [Google Scholar] [CrossRef]
- Prowse, T.D.; Wrona, F.J.; Reist, J.D.; Gibson, J.J.; Hobbie, J.E.; Lévesque, L.M.; Vincent, W.F. Climate change effects on hydroecology of Arctic freshwater ecosystems. AMBIO J. Hum. Environ. 2006, 35, 347–358. [Google Scholar] [CrossRef]
- Duguay, C.; Brown, L. Lake Ice. Available online: https://arctic.noaa.gov/Report-Card/Report-Card-2018/ArtMID/7878/ArticleID/785/Lake-Ice (accessed on 11 December 2020).
- Moore, M.V.; Hampton, S.E.; Izmest’Eva, L.R.; Silow, E.A.; Peshkova, E.V.; Pavlov, B.K. Climate change and the world’s “sacred sea”—Lake Baikal, Siberia. BioScience 2009, 59, 405–417. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, R.W.; Schloesser, D.W.; Leach, J.H.; Kovalak, W.P. Distribution and dispersal of the zebra mussel (Dreissena polymorpha) in the Great Lakes region. Can. J. Fish. Aquat. Sci. 1991, 48, 1381–1388. [Google Scholar] [CrossRef]
- Millard, E.; Johannsson, O.; Neilson, M.; El-Shaarawi, A. Long-term, seasonal and spatial trends in nutrients, chlorophyll a and light attenuation in Lake Ontario. In State of Lake Ontario: Past, Present and Future; Michigan State University Press: East Lansing, MI, USA, 2003; pp. 97–132. [Google Scholar]
- Barbiero, R.P.; Rockwell, D.C.; Warren, G.J.; Tuchman, M.L. Changes in spring phytoplankton communities and nutrient dynamics in the eastern basin of Lake Erie since the invasion of Dreissena spp. Can. J. Fish. Aquat. Sci. 2006, 63, 1549–1563. [Google Scholar] [CrossRef]
- Fahnenstiel, G.; Pothoven, S.; Vanderploeg, H.; Klarer, D.; Nalepa, T.; Scavia, D. Recent changes in primary production and phytoplankton in the offshore region of southeastern Lake Michigan. J. Great Lakes Res. 2010, 36, 20–29. [Google Scholar] [CrossRef]
- Yousef, F.; Shuchman, R.; Sayers, M.; Fahnenstiel, G.; Henareh, A. Water clarity of the Upper Great Lakes: Tracking changes between 1998–2012. J. Great Lakes Res. 2017, 43, 239–247. [Google Scholar] [CrossRef]
- Michalak, A.M.; Anderson, E.J.; Beletsky, D.; Boland, S.; Bosch, N.S.; Bridgeman, T.B.; Chaffin, J.D.; Cho, K.; Confesor, R.; Daloğlu, I.; et al. Record-setting algal bloom in Lake Erie caused by agricultural and meteorological trends consistent with expected future conditions. Proc. Natl. Acad. Sci. USA 2013, 110, 6448–6452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sayers, M.J.; Grimm, A.G.; Shuchman, R.A.; Bosse, K.R.; Fahnenstiel, G.L.; Ruberg, S.A.; Leshkevich, G.A. Satellite monitoring of harmful algal blooms in the Western Basin of Lake Erie: A 20-year time-series. J. Great Lakes Res. 2019, 45, 508–521. [Google Scholar] [CrossRef]
- Verschuren, D.; Johnson, T.C.; Kling, H.J.; Edgington, D.N.; Leavitt, P.R.; Brown, E.T.; Talbot, M.R.; Hecky, R.E. History and timing of human impact on Lake Victoria, East Africa. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2002, 269, 289–294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hecky, R.E.; Mugidde, R.; Ramlal, P.; Talbot, M.; Kling, G. Multiple stressors cause rapid ecosystem change in Lake Victoria. Freshw. Biol. 2010, 55, 19–42. [Google Scholar] [CrossRef] [Green Version]
- Schindler, D.W. Production of phytoplankton and zooplankton in Canadian Shield lakes. In Productivity Problems of Freshwaters; Kajak, Z., Hillbrich-Ilikowska, A., Eds.; PWN-Polish Scientific Publishers: Krakow, Poland, 1972; pp. 311–331. [Google Scholar]
- Fee, E.J.; Stainton, M.; Kling, H. Primary Production and Related Limnological Data for Some Lakes of the Yellowknife, NWT Area; Department of Fisheries and Oceans: Winnipeg, MB, Canada, 1985. [Google Scholar]
- Millard, E.; Myles, D.; Johannsson, O.; Ralph, K. Phytoplankton photosynthesis at two index stations in Lake Ontario 1987–1992: Assessment of the long-term response to phosphorus control. Can. J. Fish. Aquat. Sci. 1996, 53, 1092–1111. [Google Scholar] [CrossRef]
- Yoshida, T.; Sekino, T.; Genkai-Kato, M.; Logacheva, N.P.; Bondarenko, N.A.; Kawabata, Z.; Khodzher, T.V.; Melnik, N.; Hino, S.; Nozaki, K.; et al. Seasonal dynamics of primary production in the pelagic zone of southern Lake Baikal. Limnology 2003, 4, 53–62. [Google Scholar] [CrossRef]
- Silsbe, G. Phytoplankton Production in Lake Victoria, East Africa. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2004. [Google Scholar]
- Smith, R.E.; Hiriart-Baer, V.P.; Higgins, S.N.; Guildford, S.J.; Charlton, M.N. Planktonic primary production in the offshore waters of dreissenid-infested Lake Erie in 1997. J. Great Lakes Res. 2005, 31, 50–62. [Google Scholar] [CrossRef]
- Guildford, S.J.; Bootsma, H.A.; Taylor, W.D.; Hecky, R.E. High variability of phytoplankton photosynthesis in response to environmental forcing in oligotrophic Lake Malawi/Nyasa. J. Great Lakes Res. 2007, 33, 170–185. [Google Scholar] [CrossRef]
- Stenuite, S.; Pirlot, S.; Hardy, M.A.; Sarmento, H.; Tarbe, A.L.; Leporcq, B.; Descy, J.P. Phytoplankton production and growth rate in Lake Tanganyika: Evidence of a decline in primary productivity in recent decades. Freshw. Biol. 2007, 52, 2226–2239. [Google Scholar] [CrossRef]
- Sterner, R.W. In situ-measured primary production in Lake Superior. J. Great Lakes Res. 2010, 36, 139–149. [Google Scholar] [CrossRef]
- Fahnenstiel, G.L.; Sayers, M.J.; Shuchman, R.A.; Yousef, F.; Pothoven, S.A. Lake-wide phytoplankton production and abundance in the Upper Great Lakes: 2010–2013. J. Great Lakes Res. 2016, 42, 619–629. [Google Scholar] [CrossRef]
- Fahnenstiel, G.; Beckmann, C.; Lohrenz, S.; Millie, D.; Schofield, O.; McCormick, M. Standard Niskin and Van Dorn bottles inhibit phytoplankton photosynthesis in Lake Michigan. Int. Ver. Theor. Angew. Limnol. Verh. 2002, 28, 376–380. [Google Scholar] [CrossRef]
- Sayers, M.J.; Fahnenstiel, G.L.; Shuchman, R.A.; Bosse, K.R. A New Method to Estimate Global Freshwater Phytoplankton Carbon Fixation Using Satellite Remote Sensing: Initial Results. Int. J. Remote Sens. 2020. under review. [Google Scholar]
- Behrenfeld, M.J.; Falkowski, P.G. Photosynthetic rates derived from satellite-based chlorophyll concentration. Limnol. Oceanogr. 1997, 42, 1–20. [Google Scholar] [CrossRef]
- Ondrusek, M.E.; Bidigare, R.R.; Waters, K.; Karl, D.M. A predictive model for estimating rates of primary production in the subtropical North Pacific Ocean. Deep Sea Res. Part II Top. Stud. Oceanogr. 2001, 48, 1837–1863. [Google Scholar] [CrossRef]
- McClain, C.R.; Christian, J.R.; Signorini, S.R.; Lewis, M.R.; Asanuma, I.; Turk, D.; Dupouy-Douchement, C. Satellite ocean-color observations of the tropical Pacific Ocean. Deep Sea Res. Part II Top. Stud. Oceanogr. 2002, 49, 2533–2560. [Google Scholar] [CrossRef]
- Marra, J.; Ho, C.; Trees, C. An Alternative Algorithm for the Calculation of Primary Productivity from Remote Sensing Data; Technical Report (LDEO-2003-1); Lamont Doherty Earth Observatory: New York, NY, USA, 2003. [Google Scholar]
- Bergamino, N.; Horion, S.; Stenuite, S.; Cornet, Y.; Loiselle, S.; Plisnier, P.-D.; Descy, J.-P. Spatio-temporal dynamics of phytoplankton and primary production in Lake Tanganyika using a MODIS based bio-optical time series. Remote Sens. Environ. 2010, 114, 772–780. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef]
- Shuchman, R.A.; Leshkevich, G.; Sayers, M.J.; Johengen, T.H.; Brooks, C.N.; Pozdnyakov, D. An algorithm to retrieve chlorophyll, dissolved organic carbon, and suspended minerals from Great Lakes satellite data. J. Great Lakes Res. 2013, 39, 14–33. [Google Scholar] [CrossRef]
- Lee, Z.; Weidemann, A.; Kindle, J.; Arnone, R.; Carder, K.L.; Davis, C. Euphotic zone depth: Its derivation and implication to ocean-color remote sensing. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Iqbal, M. An Introduction to Solar Radiation; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Schwab, D.J.; Leshkevich, G.A.; Muhr, G.C. Automated mapping of surface water temperature in the Great Lakes. J. Great Lakes Res. 1999, 25, 468–481. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-Y.; Iredell, M.; et al. The NCEP climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- McCree, K.J. Photosynthetically Active Radiation. In Physiological Plant Ecology I. Encyclopedia of Plant Physiology; Lange, O.L., Nobel, P.S., Osmond, C.B., Ziegler, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 41–55. [Google Scholar]
- National Geophysical Data Center. Bathymetry of Lake Michigan. 1996. Available online: https://doi.org/10.7289/V5B85627 (accessed on 20 September 2019).
- National Geophysical Data Center. Bathymetry of Lake Erie and Lake St. Clair. 1999. Available online: https://doi.org/10.7289/V5KS6PHK (accessed on 20 September 2019).
- National Geophysical Data Center. Bathymetry of Lake Huron. 1999. Available online: https://doi.org/10.7289/V5G15XS5 (accessed on 20 September 2019).
- National Geophysical Data Center. Bathymetry of Lake Ontario. 1999. Available online: https://doi.org/10.7289/V56H4FBH (accessed on 20 September 2019).
- National Geophysical Data Center. Bathymetry of Lake Superior. 1999. Available online: https://www.ngdc.noaa.gov/mgg/greatlakes/superior.html (accessed on 20 September 2019).
- Hamilton, S. Lake Victoria Bathymetry Contours, V7. 2016. Available online: https://doi.org/10.7910/DVN/ZSWZIA (accessed on 18 September 2019).
- Lyons, R.P.; Kroll, C.N.; Scholz, C.A. An energy-balance hydrologic model for the Lake Malawi Rift Basin, East Africa. Glob. Planet. Chang. 2011, 75, 83–97. [Google Scholar] [CrossRef]
- DeBatist. Bathymetry of Lake Baikal. 2007. Available online: http://doi.org/10.1594/GFZ.SDDB.1204 (accessed on 25 September 2019).
- Schertzer, W.M.; Rouse, W.R.; Blanken, P.D. Cross-lake variation of physical limnological and climatological processes of Great Slave Lake. Phys. Geogr. 2000, 21, 385–406. [Google Scholar] [CrossRef]
- Johnson, L. Physical and chemical characteristics of Great Bear Lake, Northwest territories. J. Fish. Board Can. 1975, 32, 1971–1987. [Google Scholar] [CrossRef]
- Lang, G.; Fahnenstiel, G. Great Lakes production model: Methodology and use. In NOAA Technical Memorandum 90; NOAA Great Lakes Environmental Research Laboratory: Ann Arbor, MI, USA, 1995. [Google Scholar]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Zar, J.H. Biostatistical Analysis, 5th ed.; Pearson PLC: New York, NY, USA, 2009. [Google Scholar]
- Fee, E.; Shearer, J.; DeBruyn, E.; Schindler, E. Effects of lake size on phytoplankton photosynthesis. Can. J. Fish. Aquat. Sci. 1992, 49, 2445–2459. [Google Scholar] [CrossRef]
- Hecky, R. The eutrophication of Lake Victoria. Int. Ver. Theor. Angew. Limnol. Verh. 1993, 25, 39–48. [Google Scholar] [CrossRef]
- Malkin, S.Y.; Bocaniov, S.A.; Smith, R.E.; Guildford, S.J.; Hecky, R.E. In situ measurements confirm the seasonal dominance of benthic algae over phytoplankton in nearshore primary production of a large lake. Freshw. Biol. 2010, 55, 2468–2483. [Google Scholar] [CrossRef]
- Stewart, T.J.; Johannsson, O.E.; Holeck, K.; Sprules, W.G.; O’Gorman, R. The Lake Ontario zooplankton community before (1987–1991) and after (2001–2005) invasion-induced ecosystem change. J. Great Lakes Res. 2010, 36, 596–605. [Google Scholar] [CrossRef]
- Glooschenko, W.A.; Moore, J.E.; Munawar, M.; Vollenweider, R. Primary production in Lakes Ontario and Erie: A comparative study. J. Fish. Board Can. 1974, 31, 253–263. [Google Scholar] [CrossRef]
- Dahl, J.; Graham, D.; Johannsson, O.; Millard, E.; Myles, D. Lake Erie 1993, Western, West Central and Eastern Basins: Change in Trophic Status, and Assessment of the Abundance, Biomass and Production of the Lower Trophic Levels . Available online: https://digitalcommons.brockport.edu/cgi/viewcontent.cgi?article=1133&context=tech_rep (accessed on 11 December 2020).
- Bondarenko, N.; Guselnikova, N.E. Production of phytoplankton in southern Lake Baikal. Proc. Sib. Branch USSR Acad. Sci. 1989, 1, 77–81. [Google Scholar]
- Ogutu-Ohwayo, R.; Natugonza, V.; Musinguzi, L.; Olokotum, M.; Naigaga, S. Implications of climate variability and change for African lake ecosystems, fisheries productivity, and livelihoods. J. Great Lakes Res. 2016, 42, 498–510. [Google Scholar] [CrossRef]
- Verburg, P.; Hecky, R.E. The physics of the warming of Lake Tanganyika by climate change. Limnol. Oceanogr. 2009, 54, 2418–2430. [Google Scholar] [CrossRef]
- Vollmer, M.K.; Bootsma, H.A.; Hecky, R.E.; Patterson, G.; Halfman, J.D.; Edmond, J.M.; Eccles, D.H.; Weiss, R.F. Deep-water warming trend in Lake Malawi, East Africa. Limnol. Oceanogr. 2005, 50, 727–732. [Google Scholar] [CrossRef] [Green Version]
- Mugidde, R. The increase in phytoplankton primary productivity and biomass in Lake Victoria (Uganda). Int. Ver. Theor. Angew. Limnol. Verh. 1993, 25, 846–849. [Google Scholar] [CrossRef]
- Dobiesz, N.E.; Lester, N.P. Changes in mid-summer water temperature and clarity across the Great Lakes between 1968 and 2002. J. Great Lakes Res. 2009, 35, 371–384. [Google Scholar] [CrossRef]
- Ye, X.; Anderson, E.J.; Chu, P.Y.; Huang, C.; Xue, P. Impact of water mixing and ice formation on the warming of Lake Superior: A model-guided mechanism study. Limnol. Oceanogr. 2019, 64, 558–574. [Google Scholar] [CrossRef]
- Nalepa, T.F.; Fanslow, D.L.; Lang, G.A. Transformation of the offshore benthic community in Lake Michigan: Recent shift from the native amphipod Diporeia spp. to the invasive mussel Dreissena rostriformis bugensis. Freshw. Biol. 2009, 54, 466–479. [Google Scholar] [CrossRef] [Green Version]
- Wilson, K.A.; Howell, E.T.; Jackson, D.A. Replacement of zebra mussels by quagga mussels in the Canadian nearshore of Lake Ontario: The importance of substrate, round goby abundance, and upwelling frequency. J. Great Lakes Res. 2006, 32, 11–28. [Google Scholar] [CrossRef]
- Vanderploeg, H.A.; Nalepa, T.F.; Jude, D.J.; Mills, E.L.; Holeck, K.T.; Liebig, J.R.; Grigorovich, I.A.; Ojaveer, H. Dispersal and emerging ecological impacts of Ponto-Caspian species in the Laurentian Great Lakes. Can. J. Fish. Aquat. Sci. 2002, 59, 1209–1228. [Google Scholar] [CrossRef] [Green Version]
- Grigorovich, I.A.; Korniushin, A.V.; Gray, D.K.; Duggan, I.C.; Colautti, R.I.; MacIsaac, H.J. Lake Superior: An invasion coldspot? Hydrobiologia 2003, 499, 191–210. [Google Scholar] [CrossRef]
- Leach, J.H. Impacts of the zebra mussel (Dreissena polymorpha) on water quality and fish spawning reefs in western Lake Erie. In Zebra Mussels: Biology, Impacts, and Control; Nalepa, T.F., Schloesser, D.W., Eds.; Lewis Publishers: Boca Raton, FL, USA, 1993; pp. 381–397. [Google Scholar]
- Holland, R.E. Changes in planktonic diatoms and water transparency in Hatchery Bay, Bass Island area, western Lake Erie since the establishment of the zebra mussel. J. Great Lakes Res. 1993, 19, 617–624. [Google Scholar] [CrossRef]
- Kerfoot, W.C.; Yousef, F.; Green, S.A.; Budd, J.W.; Schwab, D.J.; Vanderploeg, H.A. Approaching storm: Disappearing winter bloom in Lake Michigan. J. Great Lakes Res. 2010, 36, 30–41. [Google Scholar] [CrossRef]
- O’Beirne, M.; Werne, J.; Hecky, R.; Johnson, T.; Katsev, S.; Reavie, E.D. Anthropogenic climate change has altered primary productivity in Lake Superior. Nat. Commun. 2017, 8, 15713. [Google Scholar] [CrossRef] [Green Version]
- Sayers, M.J.; Bosse, K.R.; Shuchman, R.A.; Ruberg, S.A.; Fahnenstiel, G.L.; Leshkevich, G.A.; Stuart, D.G.; Johengen, T.H.; Burtner, A.M.; Palladino, D. Spatial and temporal variability of inherent and apparent optical properties in western Lake Erie: Implications for water quality remote sensing. J. Great Lakes Res. 2019, 45, 490–507. [Google Scholar] [CrossRef]
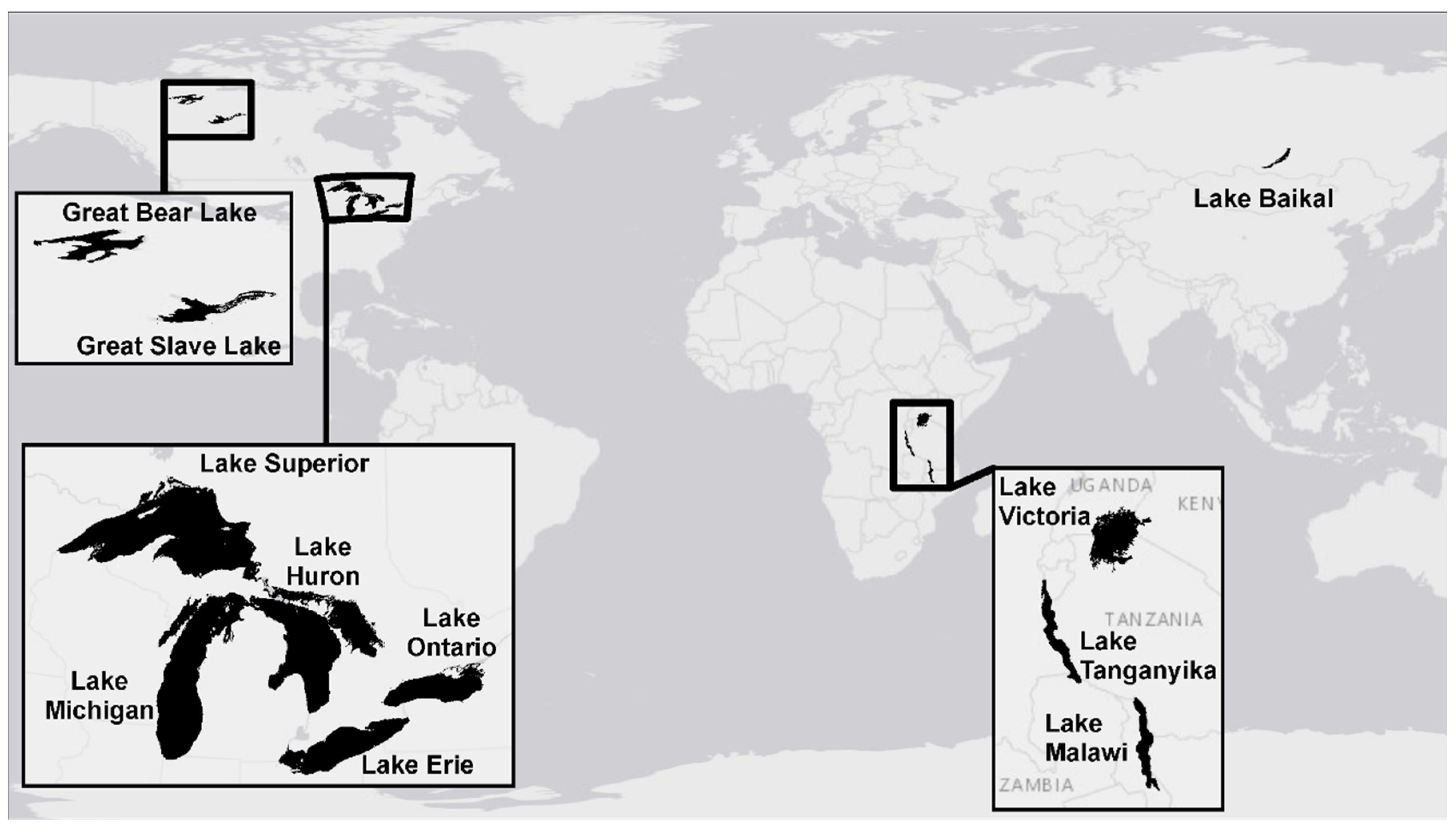
| Lake | Great Bear Lake | Great Slave Lake | Lake Baikal | Lake Erie | Lake Huron | Lake Malawi | Lake Michigan | Lake Ontario | Lake Superior | Lake Tanganyika | Lake Victoria |
|---|---|---|---|---|---|---|---|---|---|---|---|
| # Images | 25,086 | 19,782 | 15,043 | 9912 | 11,222 | 7566 | 11,343 | 9468 | 12,018 | 7753 | 7968 |
| Lake | Great Bear Lake | Great Slave Lake | Lake Baikal | Lake Erie | Lake Huron | Lake Malawi | Lake Michigan | Lake Ontario | Lake Superior | Lake Tanganyika | Lake Victoria |
|---|---|---|---|---|---|---|---|---|---|---|---|
| % Pixels Excluded | 9.4 | 9.8 | 6.0 | 0.5 | 8.7 | 7.7 | 6.4 | 3.2 | 6.9 | 7.2 | 4.1 |
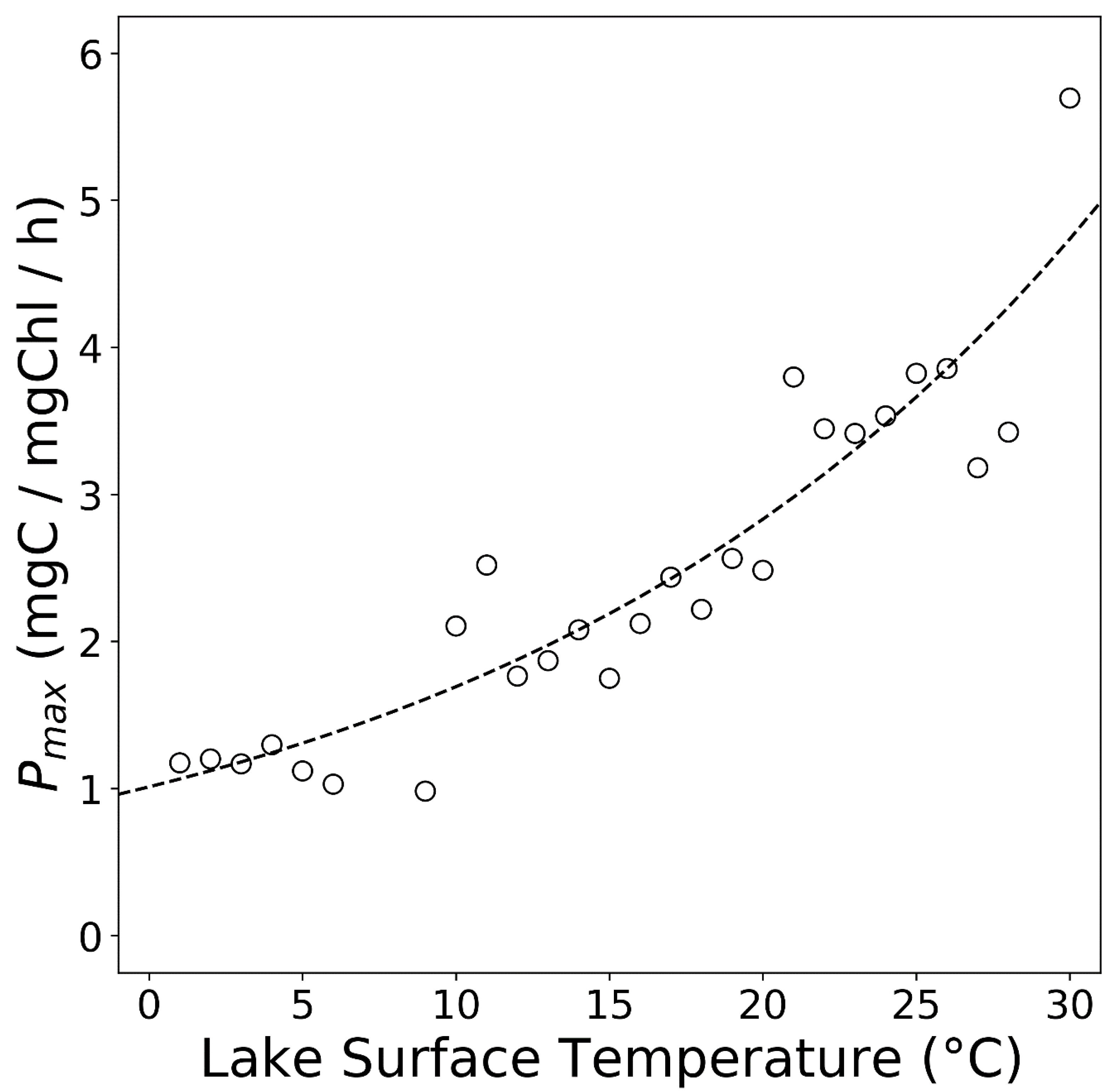
| Lake Name | Time Period | In Situ Source | Data | Mean Alpha (mgC/mg Chl/mol Photon/m2) |
|---|---|---|---|---|
| Lake Superior | 1990–1991 | [67] | Alpha, Pmax | 4 |
| Lake Huron | 2012 | [38] | Alpha, Pmax | 3 |
| Lake Michigan | 2007–2012 | [23,38] | Alpha, Pmax | 3 |
| Lake Superior | 2013 | [38] | Alpha, Pmax | 4 |
| Lake Ontario | 1987–1992 | [31] | Alpha, Pmax | 4 |
| Lake Malawi | 1997–2000 | [35] | Alpha, Pmax | 4 |
| Lake Tanganyika | 2002–2003 | [36] | Pmax |
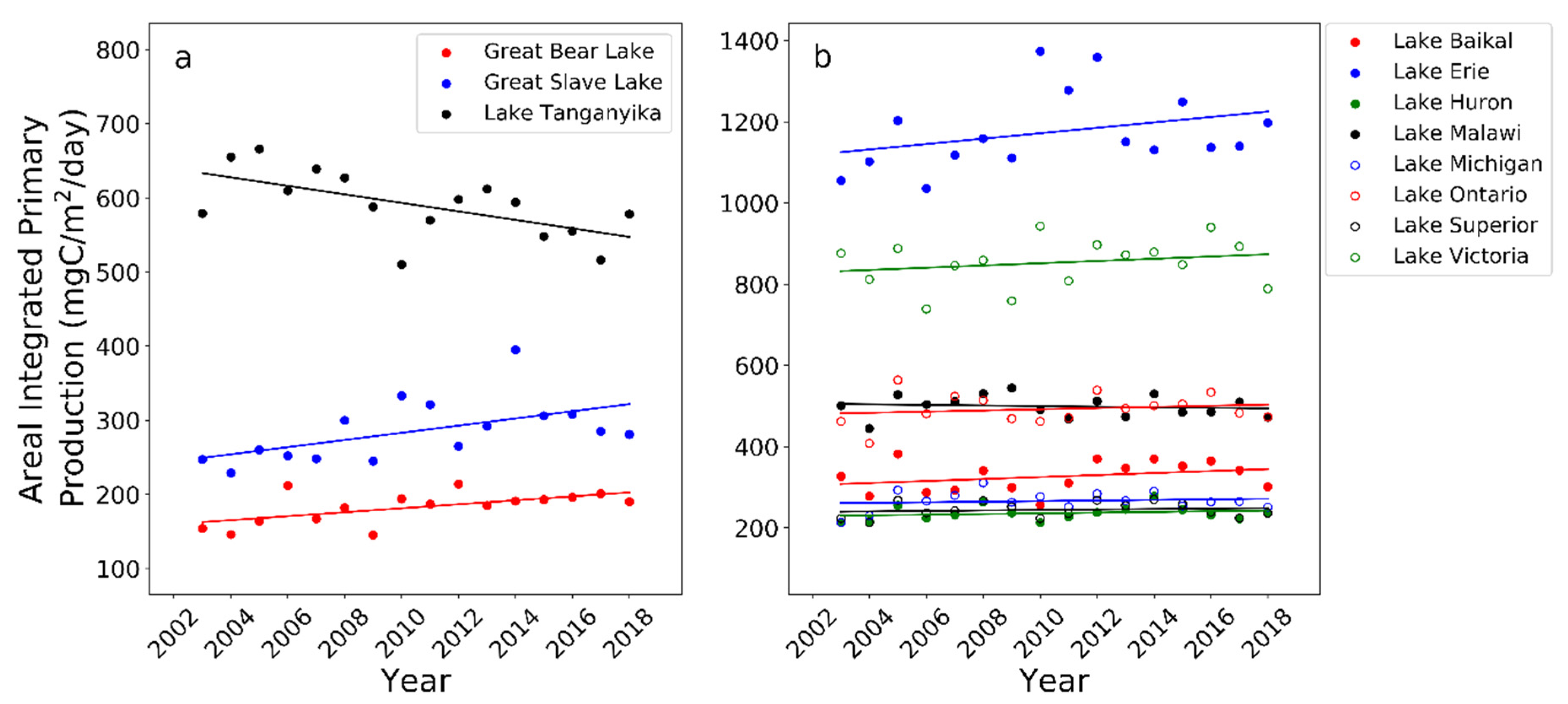
| Lake | Latitude | Mean Annual Production (mg C/m2/Day) | Minimum Annual Production (mg C/m2/Day) | Maximum Annual Production (mg C/m2/Day) | OLS Slope (p-Value) | Mean Annual Carbon Fixation (TgC/Year) |
|---|---|---|---|---|---|---|
| Great Bear Lake | 66° N | 183.0 | 145.4 (2009) | 214.1 (2012) | 2.664 (0.016) | 2.1 |
| Lake Huron | 45° N | 236.8 | 213.1 (2010) | 278.5 (2014) | 0.847 (0.407) | 5.2 |
| Lake Superior | 47° N | 244.9 | 213.6 (2004) | 270.3 (2014) | 0.605 (0.571) | 7.3 |
| Lake Michigan | 44° N | 266.7 | 213.7 (2003) | 311.8 (2008) | 0.707 (0.604) | 5.6 |
| Great Slave Lake | 62° N | 285.9 | 229.1 (2004) | 395.4 (2014) | 4.845 (0.028) | 2.8 |
| Lake Baikal | 54° N | 326.9 | 257.9 (2010) | 382.6 (2005) | 2.479 (0.238) | 3.8 |
| Lake Ontario | 44° N | 493.3 | 408.8 (2004) | 564.3 (2005) | 1.451 (0.496) | 3.4 |
| Lake Malawi | 12° S | 500.1 | 445.9 (2004) | 545.1 (2009) | −0.714 (0.641) | 5.4 |
| Lake Tanganyika | 6° S | 590.8 | 510.7 (2010) | 666.5 (2005) | −5.718 (0.013) | 7.1 |
| Lake Victoria | 1° S | 853.5 | 739.6 (2006) | 943.6 (2010) | 2.761 (0.404) | 21.4 |
| Lake Erie | 42° N | 1175.5 | 1036.1 (2006) | 1374.7 (2010) | 6.664 (0.219) | 11.0 |
| CHL | KPAR | LST | PAR | Wind Speed | |
|---|---|---|---|---|---|
| Lake Baikal | −(0.30) | −(0.24) | +(0.01) | +(0.01) | +(0.26) |
| Great Bear Lake | +(0.19) | +(0.74) | +(0.12) | +(0.11) | −(0.41) |
| Great Slave Lake | −(0.52) | −(0.11) | +(0.21) | +(0.08) | +(0.30) |
| Lake Malawi | −(0.22) | −(0.31) | +(0.59) | +(0.12) | −(0.68) |
| Lake Tanganyika | −(0.01) | −(0.03) | +(0.61) | +(0.56) | −(0.00) |
| Lake Victoria | −(0.02) | −(0.00) | −(0.97) | +(0.00) | −(0.00) |
| Lake Huron | −(0.70) | −(0.31) | +(0.47) | −(0.58) | −(0.75) |
| Lake Ontario | −(0.10) | −(0.06) | +(0.21) | +(0.06) | +(0.38) |
| Lake Michigan | −(0.21) | −(0.03) | +(0.53) | +(0.41) | −(0.34) |
| Lake Erie | −(0.25) | −(0.15) | +(0.17) | +(0.09) | +(0.70) |
| Lake Superior | +(0.26) | +(0.12) | −(0.96) | −(0.45) | −(0.18) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sayers, M.; Bosse, K.; Fahnenstiel, G.; Shuchman, R. Carbon Fixation Trends in Eleven of the World’s Largest Lakes: 2003–2018. Water 2020, 12, 3500. https://doi.org/10.3390/w12123500
Sayers M, Bosse K, Fahnenstiel G, Shuchman R. Carbon Fixation Trends in Eleven of the World’s Largest Lakes: 2003–2018. Water. 2020; 12(12):3500. https://doi.org/10.3390/w12123500
Chicago/Turabian StyleSayers, Michael, Karl Bosse, Gary Fahnenstiel, and Robert Shuchman. 2020. "Carbon Fixation Trends in Eleven of the World’s Largest Lakes: 2003–2018" Water 12, no. 12: 3500. https://doi.org/10.3390/w12123500






