Experimental and Numerical Determination of the Head Loss of a Pressure Driven Flow through an Unlined Rock-Blasted Tunnel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Survey Data and Digital Elevation Model
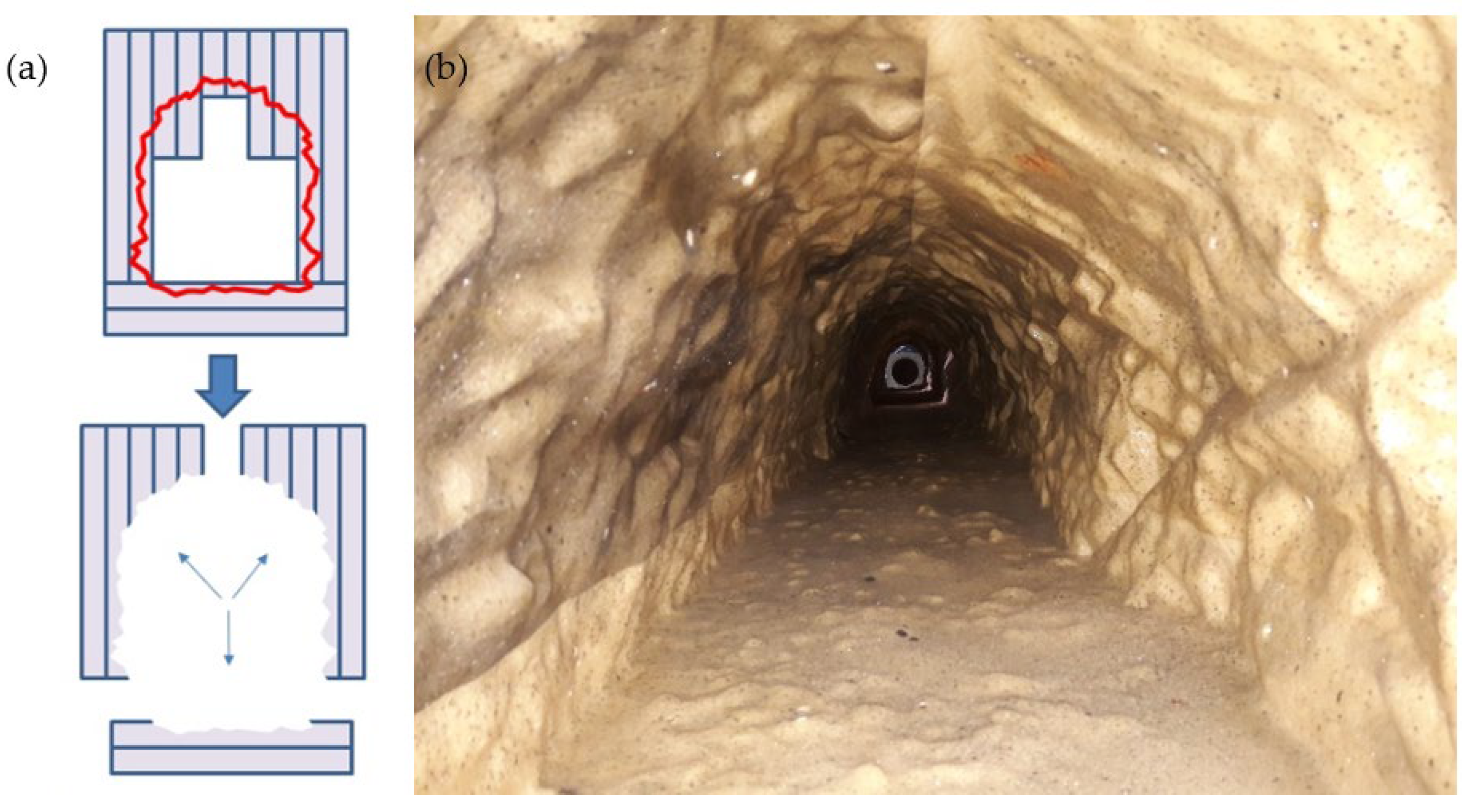
2.2. Scale Model Production
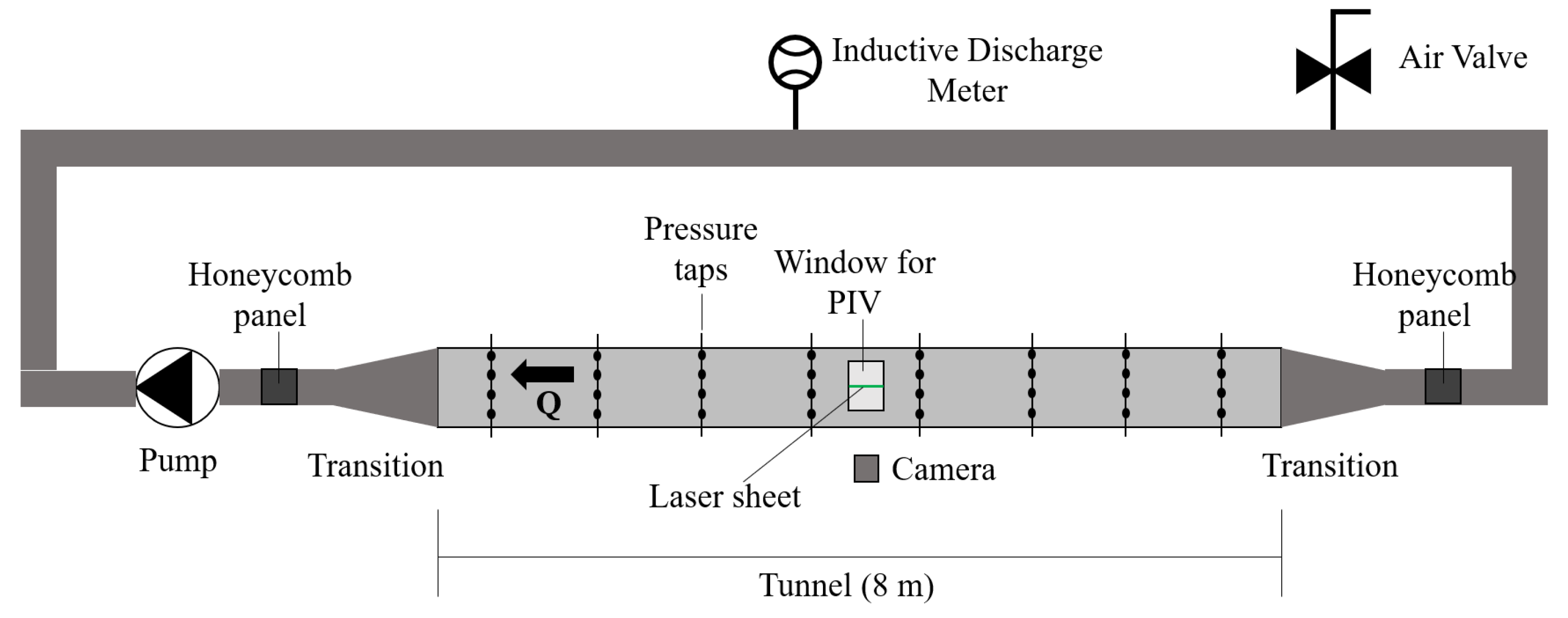
2.3. Experimental Setup and Methods
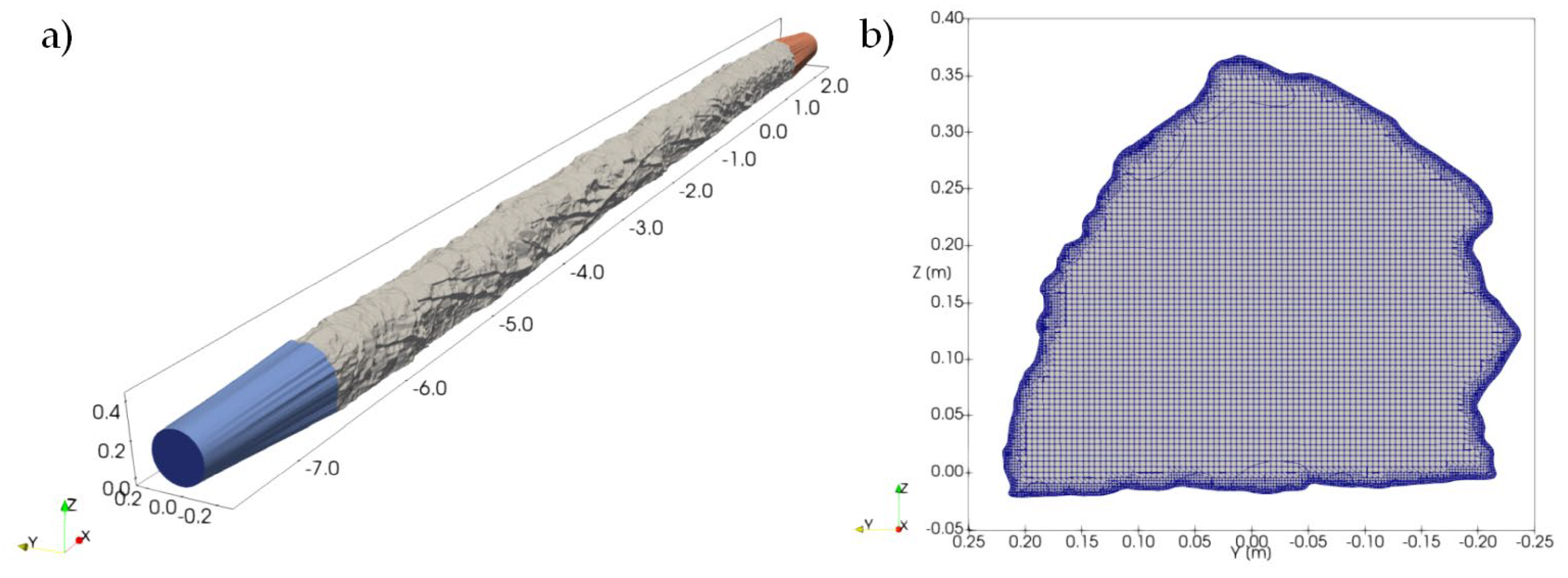
2.4. Numerical Model
3. Results
3.1. Milling Accuracy
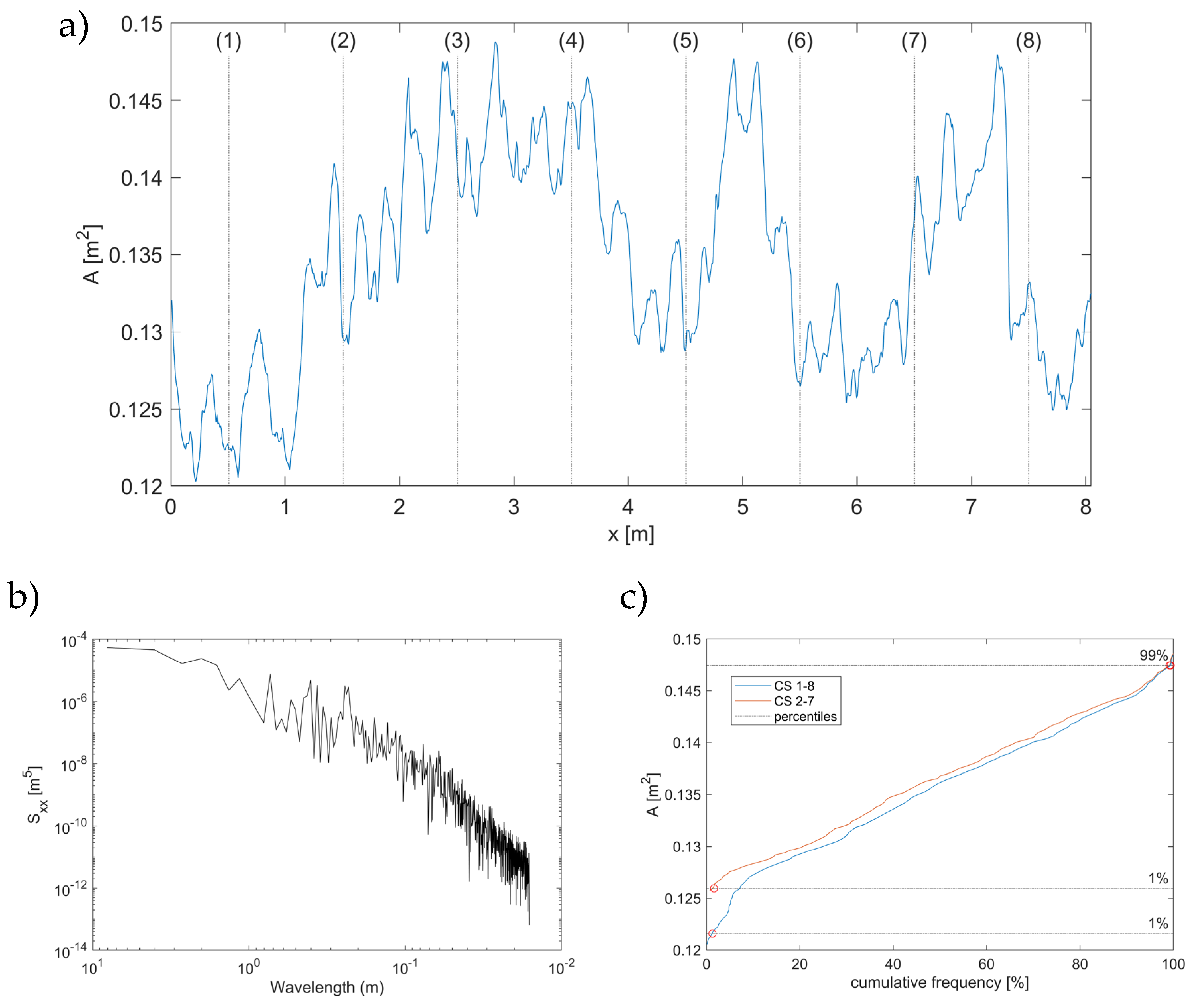
3.2. DEM Analyses
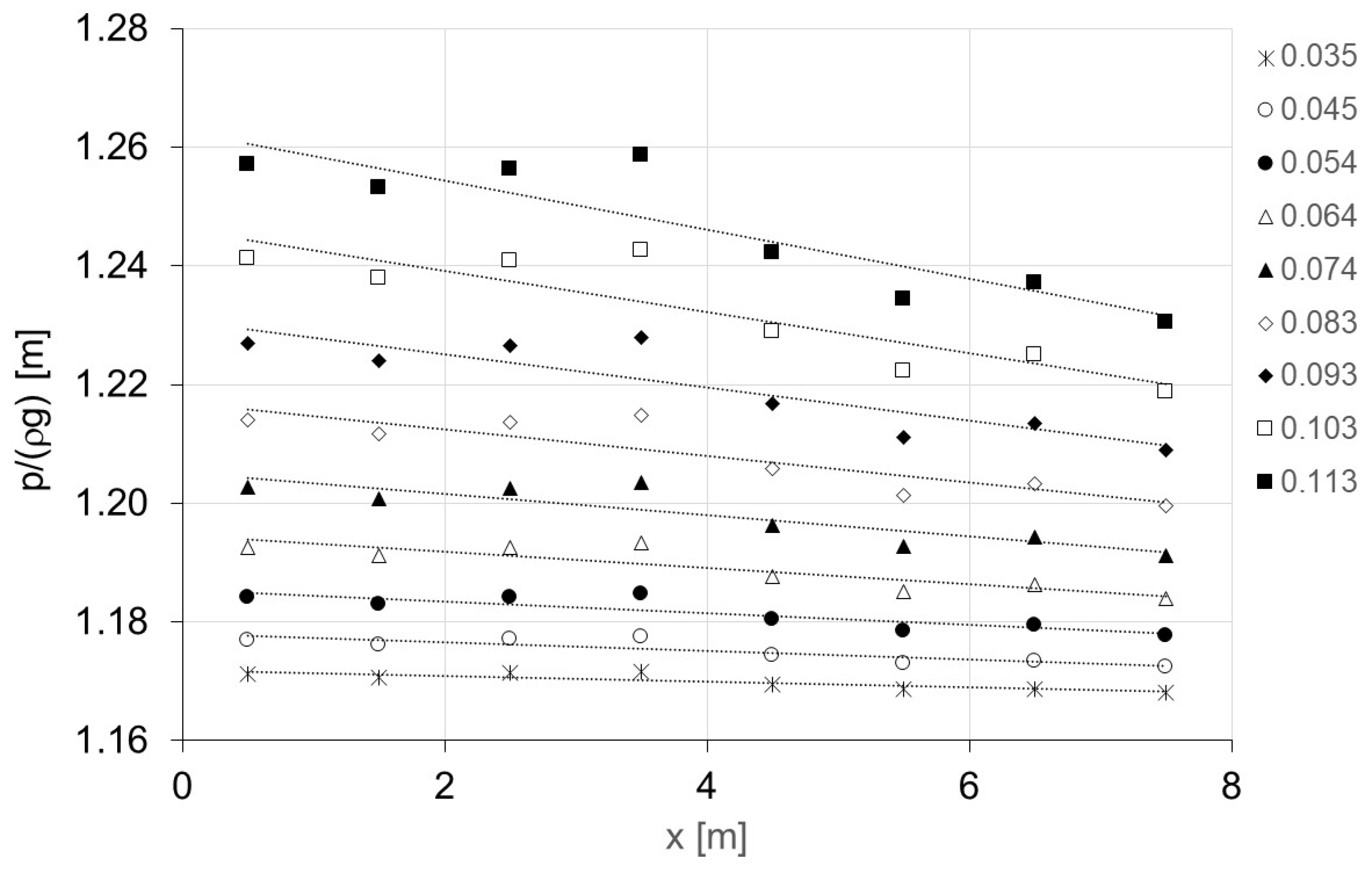
3.3. Head Loss Measurements
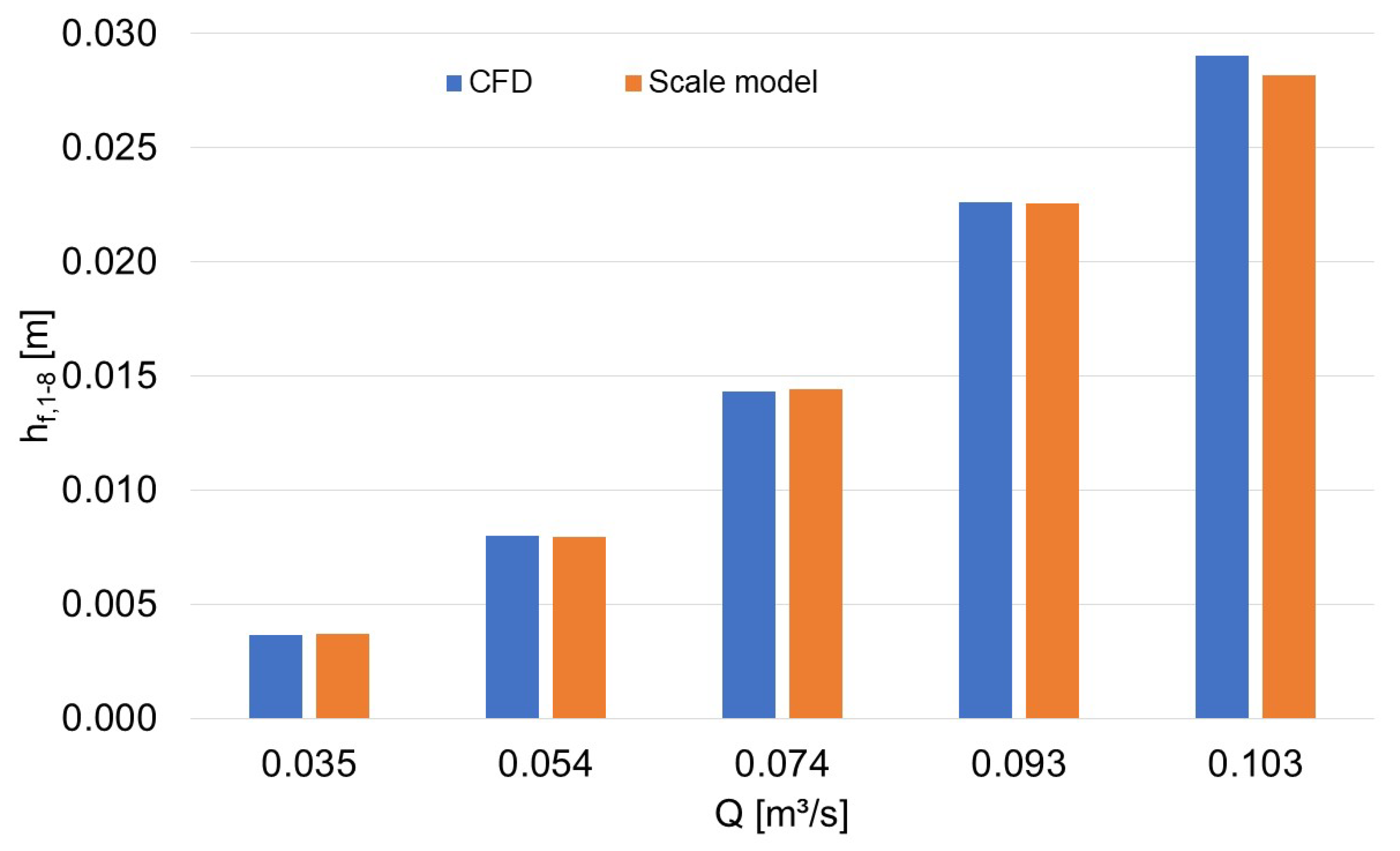
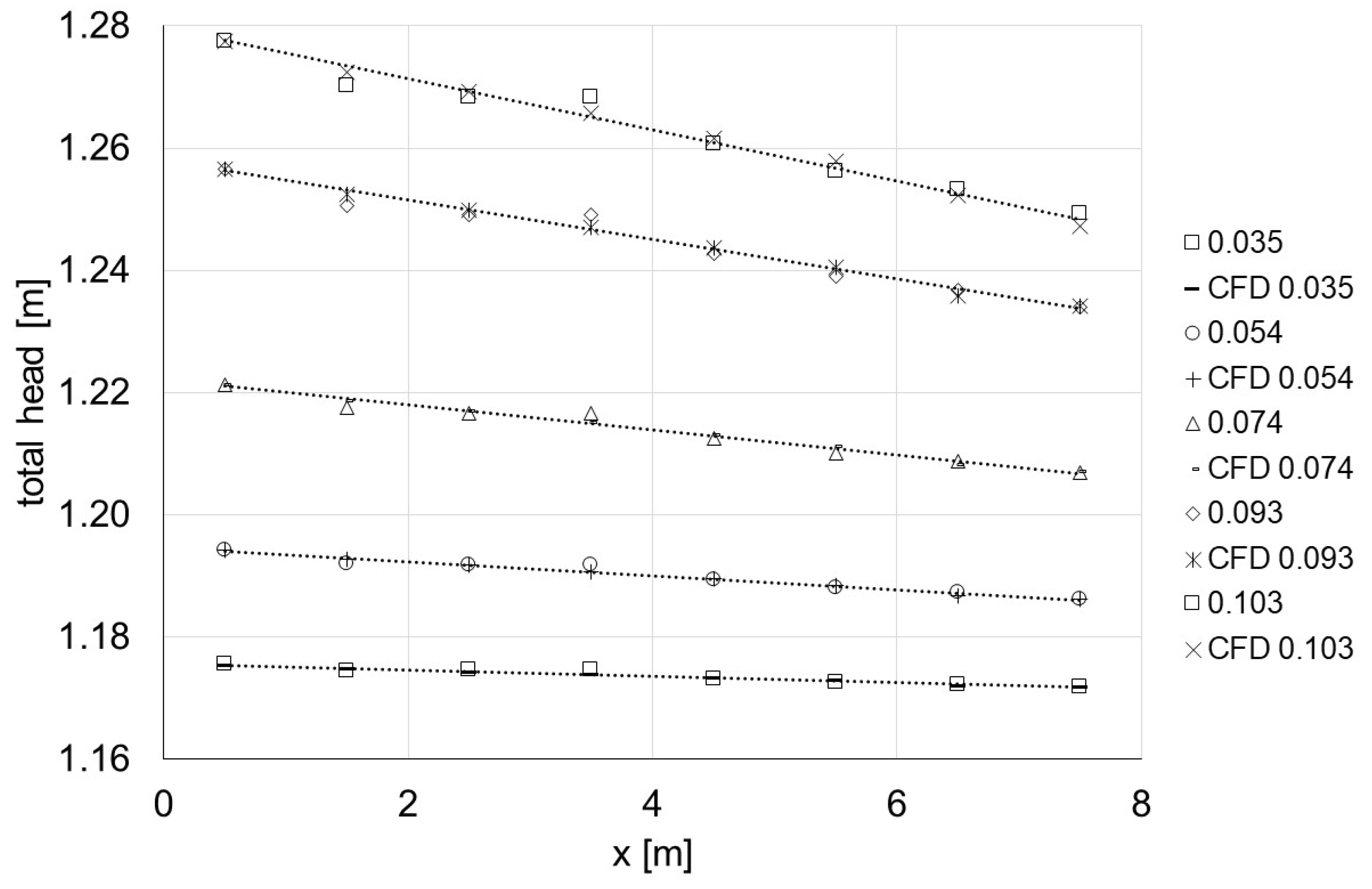
3.4. Numerical Model
4. Discussion
4.1. Accuracy of the Milled Model
4.2. Geometrical Values Derived from DEM
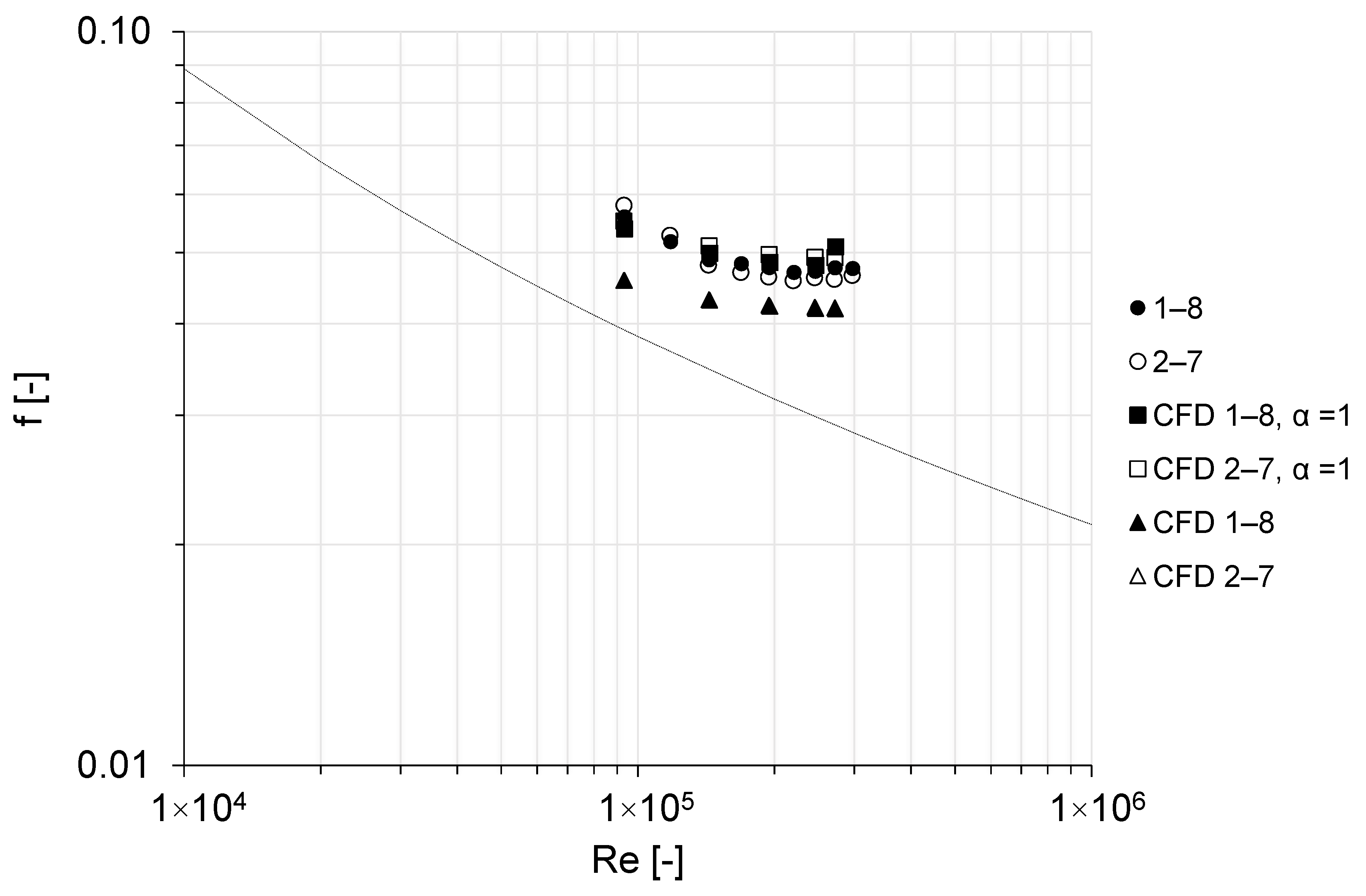
4.3. Experimental Results of Pressure, Head Loss, and Friction Factor
4.4. Numerical Simulations
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Hydropower Association (IHA). Hydropower Status Report. Available online: https://www.hydropower.org/publications/2020-hydropower-status-report (accessed on 22 July 2020).
- Energy Facts Norway. Available online: https://energifaktanorge.no/en/norsk-energiforsyning/kraftproduksjon/ (accessed on 22 July 2020).
- Lia, L.; Vereide, K. Tunneling Research. 2018. Available online: https://www.waterpowermagazine.com/features/featuretunnelling-research-6854311/ (accessed on 22 July 2020).
- Broch, E. Development of unlined pressure shafts and tunnels in Norway. Undergr. Space 1984, 8, 177–184. [Google Scholar]
- Pegram, G.G.S.; Pennington, M.S. A Method for Estimating the Hydraulic Roughness of Unlined Bored Tunnels; Water Research Commission: Pretoria, South Africa, 1996; WRC Report No: 579/1/96; ISBN 1-86845-219-0. [Google Scholar]
- Colebrook, C.F. The flow of water in unlined, lined, and partly lined rock tunnels. Proc. Inst. Civ. Eng. 1958, 11, 103–132. [Google Scholar] [CrossRef]
- Bråtveit, K.; Lia, L.; Olsen, N.R.B. An efficient method to describe the geometry and the roughness of an existing unlined hydro power tunnel. Energy Procedia 2012, 20, 200–206. [Google Scholar] [CrossRef] [Green Version]
- Moody, L.F. Friction factors for pipe flow. Trans. AMSE 1944, 66, 671–684. [Google Scholar]
- Nikuradse, J. Strömungsgesetze in Rauhen Rohren; Association of German Engineers—361. Ax. to “Research in the fields of engineering”; VDI-Verlag: Düsseldorf, Germany, 1933; Volume 4, july/august, Issue B. [Google Scholar]
- Flack, K.A.; Schultz, M.P. Roughness effects on wall-bounded turbulent flows. Phys. Fluids 2014, 26, 101305. [Google Scholar] [CrossRef] [Green Version]
- Nikora, V.I.; Stoesser, T.; Cameron, S.M.; Stewart, M.; Papadopoulos, K.; Ouro, P.; McSherry, R.; Zampiron, A.; Marusic, I.; Falconer, R.A. Friction factor decomposition for rough-wall flows: Theoretical background and application to open-channel flows. J. Fluid Mech. 2019, 872, 626–664. [Google Scholar] [CrossRef] [Green Version]
- Flack, K.A. Moving beyond Moody. J. Fluid Mech. 2018, 842, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Priha, S. Hydraulic properties of small unlined rock tunnels. J. Hydraul. Div. 1969, 95, 1181–1209. [Google Scholar]
- Rønn, P.-E.; Skog, M. New method for estimation of head loss in unlined water tunnels. In Hydropower; Balkema: Rotterdam, The Netherlands, 1997; pp. 675–682. [Google Scholar]
- Rahm, L. Friction losses in Swedish rock tunnels. Water Power 1958, 10, 457–464. [Google Scholar]
- Reinius, E. Head losses in unlined rock tunnels. Int. Water Power Dam Constr. 1970, 22, 246–252. [Google Scholar]
- Brasington, J. Terrestrial Laser Scanning: Topographic measurement and modelling. In Experimental Hydraulics, Volume II: Instrumentation and Measurement Techniques; Aberle, J., Rennie, C.D., Admiraal, D.M., Muste, M., Eds.; Taylor & Francis: New York, NY, USA, 2017; Section 4.2. [Google Scholar]
- Henning, M.; Detert, M.; Aberle, J. Photogrammetry. In Experimental Hydraulics, Volume II: Instrumentation and Measurement Techniques; Aberle, J., Rennie, C.D., Admiraal, D.M., Muste, M., Eds.; Taylor & Francis: New York, NY, USA, 2017; Section 4.4. [Google Scholar]
- Watson, C.; Marshall, J. Estimating underground mine ventilation friction factors from low density 3D data acquired by a moving LiDAR. Int. J. Min. Sci. Technol. 2018, 28, 657–662. [Google Scholar] [CrossRef]
- Hákonardóttir, K.M.; Tómasson, G.G.; Kaelin, J.; Stefánsson, B. The hydraulic roughness of unlined and shotcreted TBM-bored tunnels in volcanic rock: In situ observations and measurements at Kárahnjúkar Iceland. Tunn. Undergr. Space Tech. 2009, 24, 706–715. [Google Scholar] [CrossRef]
- Basnet, C.B.; Panthi, K.K. Roughness evaluation in shotcrete-lined water tunnels with invert concrete based on cases from Nepal. J. Rock Mech. Geotech. Eng. 2018, 10, 42–59. [Google Scholar] [CrossRef]
- Huval, C.J. Hydraulic design of unlined rock tunnels. J. Hydraul. Div. 1969, 95, 1235–1246. [Google Scholar]
- Ettema, R. Similitude. In Experimental Hydraulics, Volume I; Muste, M., Lyn, D.A., Admiraal, D.M., Ettema, R., Nikora, V., Garcia, M.H., Eds.; Taylor & Francis: New York, NY, USA, 2017; Sections 3.1–3.5. [Google Scholar]
- Hughes, S.A. Physical Models and Laboratory Techniques in Coastal Engineering; World Scientific: Singapore, 1993. [Google Scholar]
- Birkeland, R. Model Study of the Spillway of Dam Sysenvatn. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2008. (In Norwegian). [Google Scholar]
- Heller, V. Addressing similitude shortcomings. In Experimental Hydraulics, Volume I; Muste, M., Lyn, D.A., Admiraal, D.M., Ettema, R., Nikora, V., Garcia, M.H., Eds.; Taylor & Francis: New York, NY, USA, 2017; Section 3.6. [Google Scholar]
- Aberle, J.; Henry, P.Y.; Bråtveit, K. Linking physical wall roughness of unlined tunnels to hydraulic resistance. In Proceedings of the World Tunnel Congress 2017, Bergen, Norway, 5–9 June 2017. [Google Scholar]
- Henry, P.-Y.; Aberle, J.; Navaratnam, C.U.; Rüther, N. Hydraulic physical model production with Computer Numerically Controlled (CNC) manufacturing techniques. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 40, p. 05065. [Google Scholar] [CrossRef]
- Andersson, L.; Sofia Larsson, I.A.; Gunnar IHellström, J.; Burman, A.J.; Andreasson, P. Localized roughness effects in non-uniform hydraulic waterways. J. Hydraul. Res. 2020, 1–9. [Google Scholar] [CrossRef]
- Andersson, L.R.; Hellström, J.G.I.; Andreasson, P.; Lundström, T.S. Numerical Investigation of a Hydropower Tunnel: Estimating Localised Head-Loss Using the Manning Equation. Water 2019, 11, 1562. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, A.; Sparrow, E.; Gorman, J. Fluid-mechanic interactions between a pipe flow having circumferential pressure variations and a piezometer ring. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 2284–2306. [Google Scholar] [CrossRef]
- Yang, W.; Li, A.; Li, Q.; Wen, Z.; Zhao, W. Scaling law study for earthquake induced pier–water interaction experiments. Environ. Fluid Mech. 2019, 19, 55–79. [Google Scholar] [CrossRef]
- OpenFOAM. User Guide. Version 7. OpenFOAM—The OpenFOAM Foundation. 2019. Available online: https://openfoam.org (accessed on 24 July 2020).
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Lima da Silva, G.; Arima, M.; Branco, M.; Pimenta, M. Proposed Wall Function Models for Heat Transfer around a Cylinder with Rough Surface in Cross-Flow; Technical Paper 2011-38-0023; SAE: Warrendale, PA, USA, 2011. [Google Scholar] [CrossRef]
- Basnet, C.B. Applicability of Unlined/Shotcrete Lined Pressure Applicability of Unlined/Shotcrete Lines Pressure Tunnels for Hydropower Projects in the Himalaya. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2018. [Google Scholar]
- Chakraborty, A.K.; Jethwa, J.L.; Paithankar, A.G. Effects of joint orientation and rock mass quality on tunnel blasting. Eng. Geol. 1994, 37, 247–262. [Google Scholar] [CrossRef]
- Morvan, H.; Knight, D.; Wright, N.; Tang, X.; Crossley, A. The concept of roughness in fluvial hydraulics and its formulation in 1D, 2D and 3D numerical simulation models. J. Hydraul. Res. 2008, 46, 191–208. [Google Scholar] [CrossRef]


| Cross Section | x [m] | Area A [m2] | Perimeter P [m] | Hydraulic Diameter D [m] |
|---|---|---|---|---|
| 1 | 0.5 | 0.1223 | 1.412 | 0.346 |
| 2 | 1.5 | 0.1293 | 1.468 | 0.352 |
| 3 | 2.5 | 0.1401 | 1.526 | 0.367 |
| 4 | 3.5 | 0.1447 | 1.488 | 0.389 |
| 5 | 4.5 | 0.1296 | 1.461 | 0.355 |
| 6 | 5.5 | 0.1264 | 1.410 | 0.359 |
| 7 | 6.5 | 0.1381 | 1.485 | 0.372 |
| 8 | 7.5 | 0.1328 | 1.423 | 0.373 |
| 1–8 | - | 0.1357 | 1.512 | 0.359 |
| 2–7 | - | 0.1366 | 1.518 | 0.360 |
| Reach | A1 [m2] | A99 [m2] | δ [-] | s [m] | Sk [-] | Ku [-] | |
|---|---|---|---|---|---|---|---|
| 1–8 | 0.1357 | 0.1216 | 0.1474 | 21.2 | 0.014 | 0.35 | 3.27 |
| 2–7 | 0.1366 | 0.1260 | 0.1474 | 17.2 | 0.013 | 0.05 | 3.15 |
| Discharge [m3/s] | Re [-] | f1–8 [-] | f2–7 [-] | hf,1–8 [m] | hf,n [m] |
|---|---|---|---|---|---|
| 0.035 | 9.3 × 104 | 0.056 | 0.058 | 0.004 | 0.004 |
| 0.045 | 1.2 × 105 | 0.052 | 0.053 | 0.006 | - |
| 0.054 | 1.4 × 105 | 0.049 | 0.048 | 0.008 | 0.008 |
| 0.064 | 1.7 × 105 | 0.048 | 0.047 | 0.011 | - |
| 0.074 | 1.9 × 105 | 0.048 | 0.046 | 0.014 | 0.014 |
| 0.083 | 2.2 × 105 | 0.047 | 0.046 | 0.018 | - |
| 0.093 | 2.5 × 105 | 0.047 | 0.046 | 0.023 | 0.022 |
| 0.103 | 2.7 × 105 | 0.048 | 0.046 | 0.028 | 0.030 |
| 0.113 | 3.0 × 105 | 0.048 | 0.047 | 0.033 | - |
| Reach | f [-] | ||||
|---|---|---|---|---|---|
| Equation (4) | Equation (5) | Equation (6) | ΙΒΑ | Queen’s | |
| 1–8 | 0.059 | 0.054 | 0.061 | 0.069 | 0.079 |
| 2–7 | 0.047 | 0.047 | 0.049 | 0.067 | 0.080 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aberle, J.; Henry, P.-Y.; Kleischmann, F.; Navaratnam, C.U.; Vold, M.; Eikenberg, R.; Olsen, N.R.B. Experimental and Numerical Determination of the Head Loss of a Pressure Driven Flow through an Unlined Rock-Blasted Tunnel. Water 2020, 12, 3492. https://doi.org/10.3390/w12123492
Aberle J, Henry P-Y, Kleischmann F, Navaratnam CU, Vold M, Eikenberg R, Olsen NRB. Experimental and Numerical Determination of the Head Loss of a Pressure Driven Flow through an Unlined Rock-Blasted Tunnel. Water. 2020; 12(12):3492. https://doi.org/10.3390/w12123492
Chicago/Turabian StyleAberle, Jochen, Pierre-Yves Henry, Fabian Kleischmann, Christy Ushanth Navaratnam, Mari Vold, Ralph Eikenberg, and Nils Reidar Bøe Olsen. 2020. "Experimental and Numerical Determination of the Head Loss of a Pressure Driven Flow through an Unlined Rock-Blasted Tunnel" Water 12, no. 12: 3492. https://doi.org/10.3390/w12123492
APA StyleAberle, J., Henry, P.-Y., Kleischmann, F., Navaratnam, C. U., Vold, M., Eikenberg, R., & Olsen, N. R. B. (2020). Experimental and Numerical Determination of the Head Loss of a Pressure Driven Flow through an Unlined Rock-Blasted Tunnel. Water, 12(12), 3492. https://doi.org/10.3390/w12123492






