Distributions of Groundwater Age under Climate Change of Thailand’s Lower Chao Phraya Basin
Abstract
:1. Introduction
2. Materials and Data
2.1. Modelling Framework
- The semi-analytical particle-tracking method is available only for a linear velocity interpolation. MODPATH calculated velocity using interpolated velocities from inter-cell flow rates for the finite-difference approximation in the governing equation.
- The path line analysis depended on discretization of a finite-difference.
- The most important limitation is the uncertainty in boundary conditions and hydrogeologic properties. MODPATH analysis uses only information on ideal water movements, derived from MODFLOW.
2.2. Study Area
2.3. Climate
2.4. Groundwater Age Collection
3. Methods
3.1. Model Concept and Boundary Conditions
3.2. Hydraulic Parameters
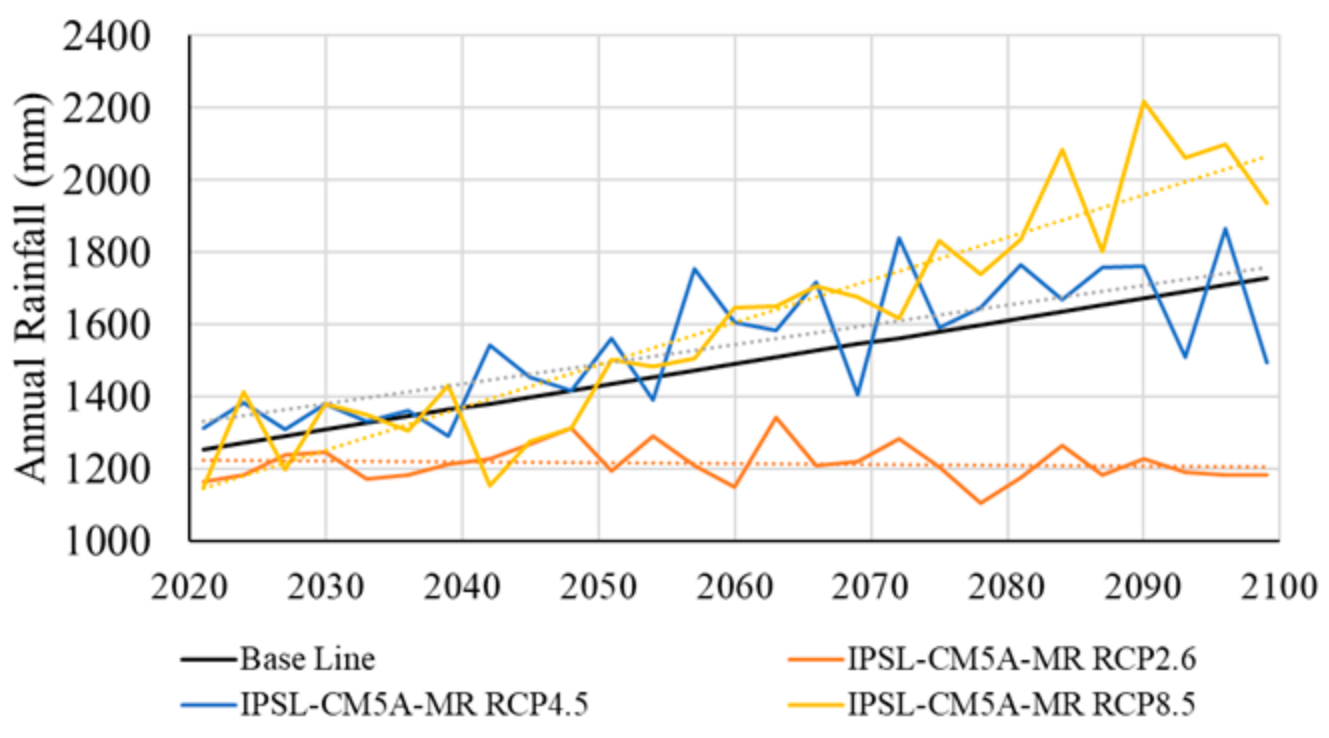
3.3. Future Climate Scenarios
3.4. Predicted Groundwater Age
4. Results and Discussion
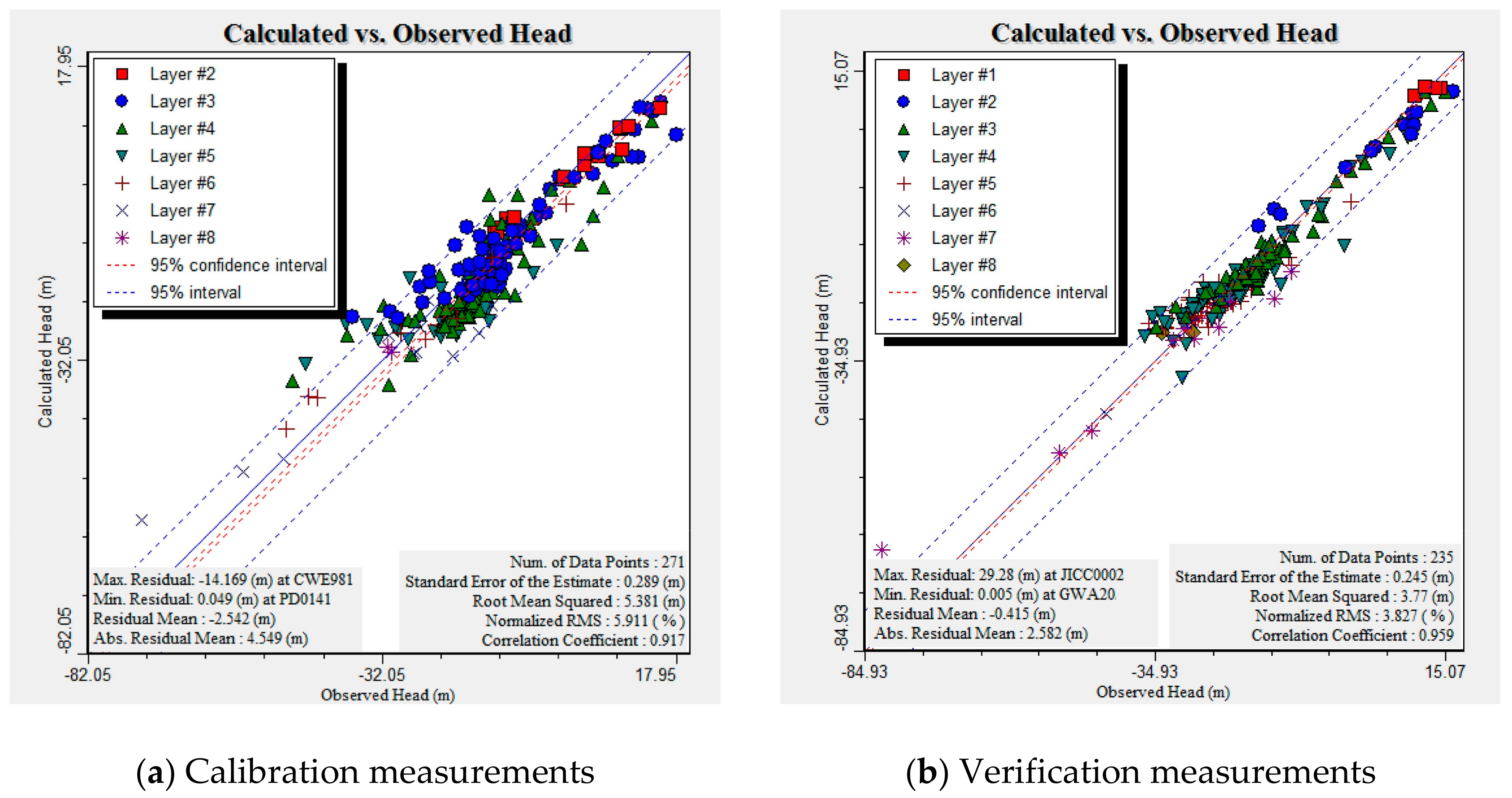
4.1. Calibration and Verification
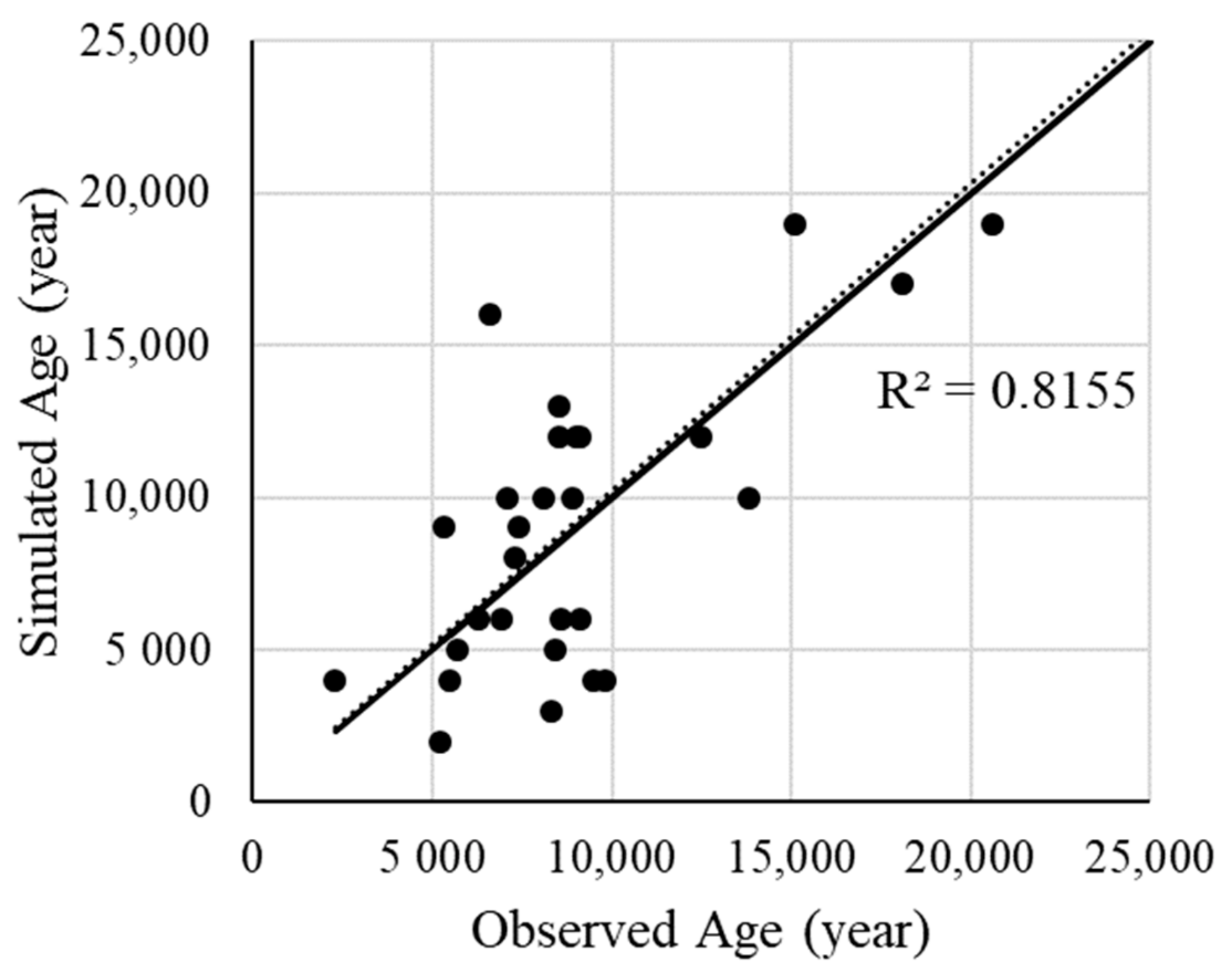
4.2. Simulated Versus Observed Groundwater Age
4.3. Predicted Groundwater Age Distribution
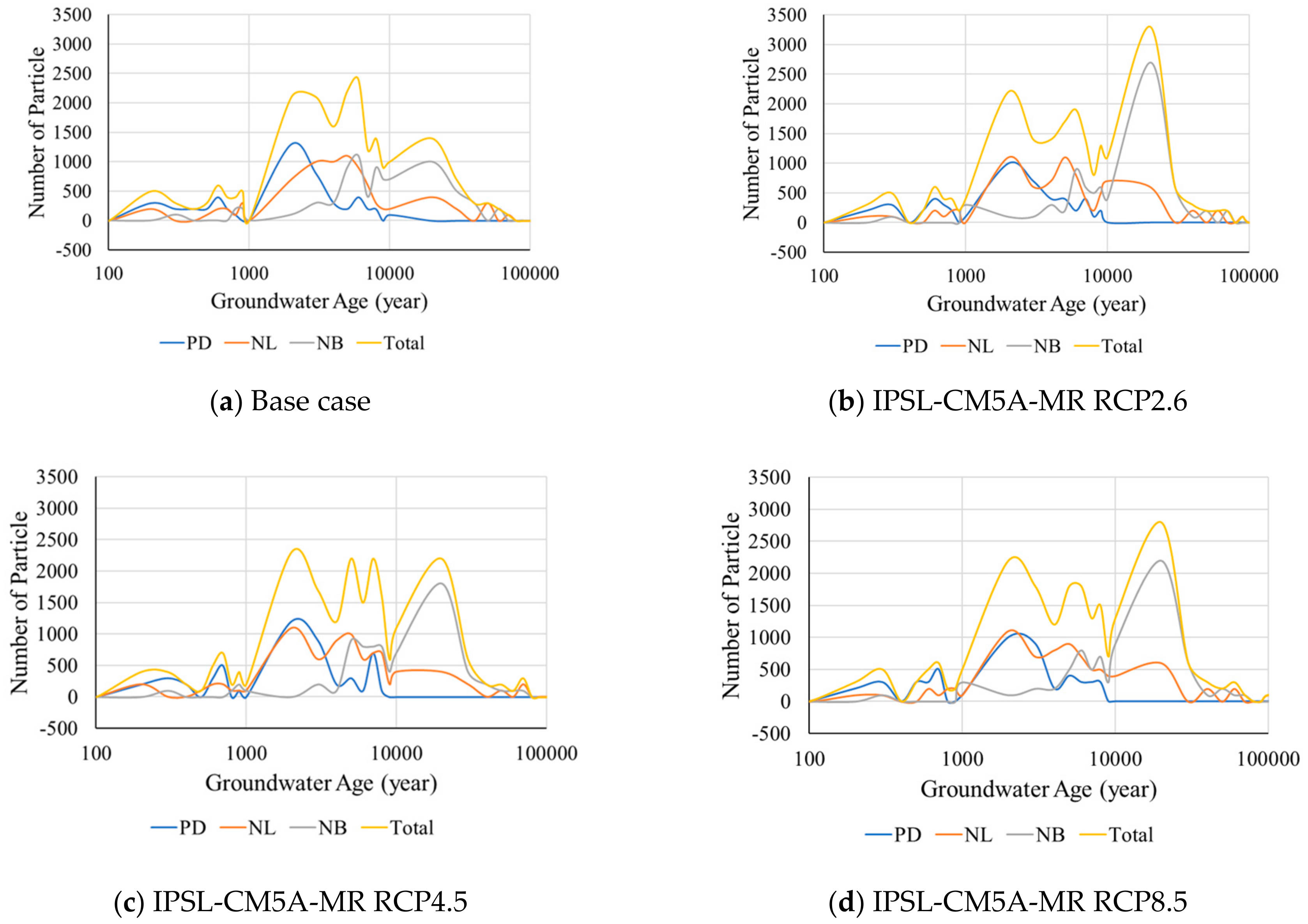
4.4. Distribution of Groundwater Age under Climate Change Impact
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tanachaichoksirikun, P.; Seeboonruang, U. Effect of Climate Change on Groundwater Age of Thailand’s Lower Chao Phraya Basin. In Proceedings of the 5th International Conference on Engineering, Applied Sciences and Technology, Luang Prabang, Laos, 2–5 July 2019; p. 639. [Google Scholar]
- Ali, R.; McFarlane, D.; Varma, S.; Dawes, W.; Emelyanova, I.; Hodgson, G.; Charles, S. Potential climate change impacts on groundwater resources of south-western Australiarn Australia. J. Hydrol. 2012, 475, 456–472. [Google Scholar] [CrossRef]
- Singh, R.D.; Kumar, C.P. Impact of Climate Change on Groundwater Resources. In Proceedings of the 2nd National Ground Water Congress, Uttarakhand, India, 22 March 2010; Volume 247667, pp. 196–221. [Google Scholar]
- Pholkern, K.; Saraphirom, P.; Srisuk, K. Potential impact of climate change on groundwater resources in the Central Huai Luang Basin, Northeast Thailand. Sci. Total Environ. 2018, 633, 1518–1535. [Google Scholar] [CrossRef] [PubMed]
- Foster, S.; Loucks, D.P. Non-Renewable Groundwater Resources-a Guide to Socially-Sustainable Management for Water-Policy Makers; IHP Series on Groundwater Unesco: Paris, France, 2006. [Google Scholar]
- Lachaal, F.; Bédir, M.; Tarhouni, J.; Leduc, C. Hydrodynamic and hydrochemical changes affecting groundwater in a semi-arid region: The deep Miocene aquifers of the Tunisian Sahel (central east Tunisia). IAHS-AISH Publ. 2010, 340, 374–381. [Google Scholar]
- Mackay, A. Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. J. Environ. Qual. 2008, 37, 2407. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014. Synthesis Report. Versión Inglés; IPCC: Geneva, Switzerland, 2014; ISBN 9789291691432. [Google Scholar]
- Sieler, K.P.; Gu, W.Z.; Stichler, W. Transient response of groundwater systems to climate changes. Geol. Soc. Spec. Publ. 2008, 288, 111–119. [Google Scholar] [CrossRef]
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M.; Hiscock, K.M.; Treidel, H.; Aureli, A. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef] [Green Version]
- Chris, M.H.; Harm, D.; Diana, M.A.; Dirk, K. Groundwater Recharge and Storage Variability in Southern Mali. In Climate Change Effects on Groundwater Resources: A Global Synthesis of Findings and Recommendations; CRC Press/Balkema, Taylor and Francis Group: London, UK, 2012; pp. 33–48. [Google Scholar]
- Taylor, R.; Callist, T. The impacts of climate change and rapid development on weathered crystalline rock aquifer systems in the humid tropics of sub-Saharan Africa: Evidence from south-western Uganda. In Climate Change Effects on Groundwater Resources: A Global Synthesis of Findings and Recommendations; Treidel, H., Martin-Bordes, J.L., Gurdak, J.J., Eds.; CRC Press/Balkema, Taylor and Francis Group: London, UK, 2012; pp. 17–32. [Google Scholar]
- White, I.; Tony, F. Reducing Groundwater Vulnerability in Carbonate Island Countries in the Pacific. In Climate Change Effects on Groundwater Resources: A Global Synthesis of Findings and Recommendations; CRC Press/Balkema, Taylor and Francis Group: London, UK, 2012; pp. 75–110. [Google Scholar]
- Tremblay, L.; Larocque, M.; Anctil, F.; Rivard, C. Teleconnections and interannual variability in Canadian groundwater levels. J. Hydrol. 2011, 410, 178–188. [Google Scholar] [CrossRef]
- Goderniaux, P.; Brouyère, S.; Wildemeersch, S.; Therrien, R.; Dassargues, A. Uncertainty of climate change impact on groundwater reserves-Application to a chalk aquifer. J. Hydrol. 2015, 528, 108–121. [Google Scholar] [CrossRef] [Green Version]
- Jackson, C.R.; Meister, R.; Prudhomme, C. Modelling the effects of climate change and its uncertainty on UK Chalk groundwater resources from an ensemble of global climate model projections. J. Hydrol. 2011, 399, 12–28. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. IPCC Special Report Enissions Scenarios: Summary for Policymakers; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Döll, P. Vulnerability to the impact of climate change on renewable groundwater resources: A global-scale assessment. Environ. Res. Lett. 2009, 4, 1–12. [Google Scholar] [CrossRef]
- Emelyanova, I.; Ali, R.; Dawes, W.; Varma, S.; Hodgson, G.; McFarlane, D. Evaluating the cumulative rainfall deviation approach for projecting groundwater levels under future climate. J. Water Clim. Chang. 2013, 4, 317–337. [Google Scholar] [CrossRef]
- Shrestha, S.; Semkuyu, D.J.; Pandey, V.P. Assessment of groundwater vulnerability and risk to pollution in Kathmandu Valley, Nepal. Sci. Total Environ. 2016, 556, 23–35. [Google Scholar] [CrossRef] [PubMed]
- Malekinezhad, H.; Banadkooki, F.B. Modeling impacts of climate change and human activities on groundwater resources using modflow. J. Water Clim. Chang. 2018, 9, 156–177. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; Van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322–329. [Google Scholar] [CrossRef] [Green Version]
- Saraphirom, P.; Wirojanagud, W.; Srisuk, K. Potential Impact of Climate Change on Area Affected by Waterlogging and Saline Groundwater and Ecohydrology Management in Northeast Thailand. Environ. Asia 2013, 6, 19–28. [Google Scholar]
- Lee, L.J.E.; Lawrence, D.S.L.; Price, M. Analysis of water-level response to rainfall and implications for recharge pathways in the Chalk aquifer, SE England. J. Hydrol. 2006, 330, 604–620. [Google Scholar] [CrossRef]
- Cook, P.G.; Herczeg, A.L. Environmental Tracers in Subsurface Hydrology; Kluwer Academic Publishers: Boston, MA, USA, 2000. [Google Scholar]
- Kazemi, G.A.; Lehr, J.H.; Pierre, P. Groundwater Age; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Sanford, W.E.; Plummer, L.N.; Mcada, D.P.; Bexfield, L.M.; Anderholm, S.K. Hydrochemical tracers in the middle Rio Grande Basin, USA: 2. Calibration of a groundwater-flow model. Hydrogeol. J. 2004, 12, 389–407. [Google Scholar] [CrossRef]
- Manning, A.H.; Solomon, D.K. An integrated environmental tracer approach to characterizing groundwater circulation in a mountain block. Water Resour. Res. 2005, 41, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Bethke, C.M.; Johnson, T.M. Groundwater age and groundwater age dating. Annu. Rev. Earth Planet. Sci. 2008, 36, 121–152. [Google Scholar] [CrossRef] [Green Version]
- Molson, J.W.; Frind, E.O. On the use of mean groundwater age, life expectancy and capture probability for defining aquifer vulnerability and time-of-travel zones for source water protection. J. Contam. Hydrol. 2012, 127, 76–87. [Google Scholar] [CrossRef]
- Zhu, Y.; Shi, L.; Wu, J.; Ye, M.; Cui, L.; Yang, J. Regional Quasi-three-dimensional unsaturated-saturated water flow model based on a vertical-horizontal splitting concept. Water 2016, 8, 195. [Google Scholar] [CrossRef] [Green Version]
- Sonnenborg, T.O.; Scharling, P.B.; Hinsby, K.; Rasmussen, E.S.; Engesgaard, P. Aquifer vulnerability assessment based on sequence stratigraphic and 39Ar transport modeling. Ground Water 2016, 54, 214–230. [Google Scholar] [CrossRef] [PubMed]
- Troldborg, L.; Jensen, K.H.; Engesgaard, P.; Refsgaard, J.C.; Hinsby, K. Using Environmental Tracers in Modeling Flow in a Complex Shallow Aquifer System. J. Hydrol. Eng. 2008, 13, 1037–1048. [Google Scholar] [CrossRef]
- Eberts, S.M.; Böhlke, J.K.; Kauffman, L.J.; Jurgens, B.C. Comparison of particle-tracking and lumped-parameter age-distribution models for evaluating vulnerability of production wells to contamination. Hydrogeol. J. 2012, 20, 263–282. [Google Scholar] [CrossRef]
- Torgersen, T.; Purtschert, R.; Phillips, F.M.; Plummer, L.N.; Sanford, W.E.; Suckow, A. Defining Groundwater Age. In Isotope Methods Dating Old Groundwater; International Atomic Energy Agency: Vienna, Austra, 2013; pp. 21–32. [Google Scholar]
- Goode, D.J. Direct simulation of groundwater age. Water Resour. Res. 1996, 32, 289–296. [Google Scholar] [CrossRef]
- Ginn, T.R. On the distribution of multicomponent mixtures over generalized exposure time in subsurface flow and reactive transport: Foundations, and formulations for groundwater age, chemical heterogeneity, and biodegradation. Water Resour. Res. 1999, 35, 1395–1407. [Google Scholar] [CrossRef]
- Varni, M.; Carrera, J. Simulation of groundwater age distributions. Water Resour. Res. 1998, 34, 3271–3281. [Google Scholar] [CrossRef]
- Woolfenden, L.R.; Ginn, T.R. Modeled ground water age distributions. Ground Water 2009, 47, 547–557. [Google Scholar] [CrossRef]
- Suckow, A. The age of groundwater-Definitions, models and why we do not need this term. Appl. Geochem. 2014, 50, 222–230. [Google Scholar] [CrossRef]
- Sanford, W. Calibration of models using groundwater age. Hydrogeol. J. 2011, 19, 13–16. [Google Scholar] [CrossRef]
- Michael, H.A.; Voss, C.I. Estimation of regional-scale groundwater flow properties in the Bengal Basin of India and Bangladesh. Hydrogeol. J. 2009, 17, 1329–1346. [Google Scholar] [CrossRef]
- Portniaguine, O.; Solomon, D.K. Parameter estimation using groundwater age and head data, Cape Cod, Massachusetts. Water Resour. Res. 1998, 34, 637–645. [Google Scholar] [CrossRef]
- Engdahl, N.B.; Ginn, T.R.; Fogg, G.E. Using groundwater age distributions to estimate the effective parameters of Fickian and non-Fickian models of solute transport. Adv. Water Resour. 2013, 54, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Sanford, W.E.; Buapeng, S. Assessment of a ground water flow model of the Bangkok Basin, Thailand, using carbon-14-based ages and paleohydrology. Hydrogeol. J. 1996, 4, 26–40. [Google Scholar] [CrossRef]
- Ginn, T.R.; Haeri, H.; Massoudieh, A.; Foglia, L. Notes on groundwater age in forward and inverse modeling. Transp. Porous Media 2009, 79, 117–134. [Google Scholar] [CrossRef] [Green Version]
- Weissmann, G.S.; Zhang, Y.; LaBolle, E.M.; Fogg, G.E. Dispersion of groundwater age in an alluvial aquifer system. Water Resour. Res. 2002, 38, 16-1–16-13. [Google Scholar] [CrossRef]
- Cornaton, F.; Perrochet, P. Groundwater age, life expectancy and transit time distributions in advective-dispersive systems: 1. Generalized reservoir theory. Adv. Water Resour. 2006, 29, 1267–1291. [Google Scholar] [CrossRef] [Green Version]
- Engdahl, N.B.; Maxwell, R.M. Quantifying changes in age distributions and the hydrologic balance of a high-mountain watershed from climate induced variations in recharge. J. Hydrol. 2015, 522, 152–162. [Google Scholar] [CrossRef]
- Bierkens, M.F.P.; Wada, Y. Non-renewable groundwater use and groundwater depletion: A review. Environ. Res. Lett. 2019, 14. [Google Scholar] [CrossRef]
- Jyrkama, M.I.; Sykes, J.F. The impact of climate change on spatially varying groundwater recharge in the grand river watershed (Ontario). J. Hydrol. 2007, 338, 237–250. [Google Scholar] [CrossRef]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. MODFLOW-2000, The, U.S. Geological Survey Modular Ground-Water Model-User Guide to Modularization Concepts and the Ground-Water Flow Process; Geological Survey: Reston, VA, USA, 2000.
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier: New York, NY, USA, 1972. [Google Scholar]
- Pollock, D. User Guide for MODPATH Version 6: A Particle Tracking Model for MODFLOW: Tech. Methods 6–A41; Geological Survey: Reston, VA, USA, 2012; Volume 58. [Google Scholar]
- Fioreze, M.; Mancuso, M.A. MODFLOW and MODPATH for hydrodynamic simulation of porous media in horizontal subsurface flow constructed wetlands: A tool for design criteria. Ecol. Eng. 2019, 130, 45–52. [Google Scholar] [CrossRef]
- Wolfgang-Albert, F.; Michl, C. Using MODFLOW/MODPATH combined with GIS analysis for groundwater modelling in the alluvial aquifer of the River Sieg, Germany. IAHS Publ. 1995, 227, 117–123. [Google Scholar]
- Mondal, N.C.; Singh, V.S. Mass transport modeling of an industrial belt using visual MODFLOW and MODPATH: A case study. J. Geog. 2009, 2, 1–19. [Google Scholar]
- Abrams, D. Correcting Transit Time Distributions in Coarse MODFLOW-MODPATH Models. Ground Water 2013, 51, 474–478. [Google Scholar] [CrossRef] [PubMed]
- Arlai, P.; Koch, M.; Kuntanakulwong, S. Statistical and stochastic approaches to assess reasonable calibrated parameters in a complex multi-aquifer system. In Proceedings of the CMWR XVI-Computational Methods in Water Resources, Copenhagen, Denmark, 19–22 June 2006; pp. 1–8. [Google Scholar]
- Tanachaichoksirikun, P.; Seeboonruang, U.; Fogg, G.E. Improving Groundwater Model in Regional Sedimentary Basin Using Hydraulic Gradients. KSCE J. Civ. Eng. 2020, 24, 1655–1669. [Google Scholar] [CrossRef]
- Piancharoen, C. Groundwater and land subsidence in Bangkok, Thailand. IAHS Publ. 1977, 355–364. [Google Scholar]
- Piancharoen, C.; Chuamthaisong, C. Groundwater of Bangkok metropolis, Thailand. IAH Mem. 1978, 11, 510–528. [Google Scholar]
- Phien-wej, N.; Giao, P.H.; Nutalaya, P. Land subsidence in Bangkok, Thailand. Eng. Geol. 2006, 82, 187–201. [Google Scholar] [CrossRef]
- Gleeson, T.; Befus, K.M.; Jasechko, S.; Luijendijk, E.; Cardenas, M.B. The global volume and distribution of modern groundwater. Nat. Geosci. 2016, 9, 161–167. [Google Scholar] [CrossRef]
- Jasechko, S.; Perrone, D.; Befus, K.M.; Bayani Cardenas, M.; Ferguson, G.; Gleeson, T.; Luijendijk, E.; McDonnell, J.J.; Taylor, R.G.; Wada, Y.; et al. Global aquifers dominated by fossil groundwaters but wells vulnerable to modern contamination. Nat. Geosci. 2017, 10, 425–429. [Google Scholar] [CrossRef] [Green Version]
- Meyer, R.; Engesgaard, P.; Hinsby, K.; Piotrowski, J.; Sonnenborg, T. Estimation of effective porosity in large-scale groundwater models by combining particle tracking, auto-calibration and 14C dating. Hydrol. Earth Syst. Sci. 2018, 22, 4843–4865. [Google Scholar] [CrossRef] [Green Version]
- Wattanasetpong, J.; Charoenvaravut, P.; Laosinwattana, W. Downscaling Climate Models in Thailand by Artificial Neural Network Method; Thesis of Civil Engineering; King Mongkut’s Institute of Technology Ladkrabang: Bangkok, Thailand, 2015. [Google Scholar]
- World Meteorological Organization. World Climate Explorer. Available online: https://climexp.knmi.nl/start.cgi (accessed on 15 September 2015).
- Ruangrassamee, P.; Khamkong, A.; Chuenchum, P. Assessment of precipitation simulations from CMIP5 climate models in Thailand. In Proceedings of the 3rd EIT International Conference on Water Resources Engineering (ICWRE3), Bangkok, Thailand, 5–7 August 2015. [Google Scholar]
- Du, X.; Lu, X.; Hou, J.; Ye, X. Improving the reliability of numerical groundwater modeling in a data-sparse region. Water 2018, 10, 289. [Google Scholar] [CrossRef] [Green Version]
- Sato, C.; Haga, M.; Nishino, J. Land subsidence and groundwater management in Tokyo. Int. Rev. Environ. Strateg. 2006, 6, 403–424. [Google Scholar]


| Well No. | Model Layer No. | Aquifers Name | Observed Groundwater Age (Years) |
|---|---|---|---|
| 1 | 3 | PD | 7100 |
| 2 | 9100 | ||
| 3 | 7300 | ||
| 4 | 18,100 | ||
| 5 | 5300 | ||
| 6 | 6900 | ||
| 7 | 9500 | ||
| 8 | 9800 | ||
| 9 | 5200 | ||
| 10 | 8300 | ||
| 11 | 18,300 | ||
| 12 | 6800 | ||
| 13 | 10,000 | ||
| 14 | 7700 | ||
| 15 | 8500 | ||
| 16 | 5700 | ||
| 17 | 2300 | ||
| 18 | 4 | NL | 8100 |
| 19 | 7400 | ||
| 20 | 8900 | ||
| 21 | 18,900 | ||
| 22 | 18,100 | ||
| 23 | 5500 | ||
| 24 | 20,900 | ||
| 25 | 19,400 | ||
| 26 | 19,900 | ||
| 27 | 12,500 | ||
| 28 | 8600 | ||
| 29 | 8400 | ||
| 30 | 5 | NB | 6300 |
| 31 | 9000 | ||
| 32 | 8500 | ||
| 33 | 18,200 | ||
| 34 | 1600 | ||
| 35 | 13,800 | ||
| 36 | 9100 | ||
| 37 | 154,000 |
| Aquifers | Porosity | Kh (m/s) | Kv (m/s) | Ss (m−1) |
|---|---|---|---|---|
| Bangkok Clay and Unconfined | 0.03 | 1 × 10−8–1 × 10−9 | 1 × 10−8–1 × 10−9 | 0.03–0.35 (Sy) |
| Bangkok | 0.2–0.3 | 5 ×10−5–6 × 10−6 | 5 × 10−9–6 × 10−10 | 1.10 × 10−5–4.80 × 10−5 |
| Phra Pradeang | 0.25–0.35 | 2 × 10−5–7 × 10−6 | 2 × 10−9–7 × 10−10 | 3.35 × 10−5–4.50 × 10−6 |
| Nakorn Luang | 0.2–0.35 | 1 × 10−4–6 × 10−6 | 1 × 10−8–6 × 10−10 | 3.85 × 10−5–9.50 × 10−6 |
| Nonthaburi | 0.3–0.35 | 2 × 10−4–7 × 10−6 | 2 × 10−8–7 × 10−10 | 3.95 × 10−5–9.50 × 10−6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanachaichoksirikun, P.; Seeboonruang, U. Distributions of Groundwater Age under Climate Change of Thailand’s Lower Chao Phraya Basin. Water 2020, 12, 3474. https://doi.org/10.3390/w12123474
Tanachaichoksirikun P, Seeboonruang U. Distributions of Groundwater Age under Climate Change of Thailand’s Lower Chao Phraya Basin. Water. 2020; 12(12):3474. https://doi.org/10.3390/w12123474
Chicago/Turabian StyleTanachaichoksirikun, Pinit, and Uma Seeboonruang. 2020. "Distributions of Groundwater Age under Climate Change of Thailand’s Lower Chao Phraya Basin" Water 12, no. 12: 3474. https://doi.org/10.3390/w12123474
APA StyleTanachaichoksirikun, P., & Seeboonruang, U. (2020). Distributions of Groundwater Age under Climate Change of Thailand’s Lower Chao Phraya Basin. Water, 12(12), 3474. https://doi.org/10.3390/w12123474





