Impact of Water Deficit on Seasonal and Diurnal Dynamics of European Beech Transpiration and Time-Lag Effect between Stand Transpiration and Environmental Drivers
Abstract
:1. Introduction
2. Materials and Methods
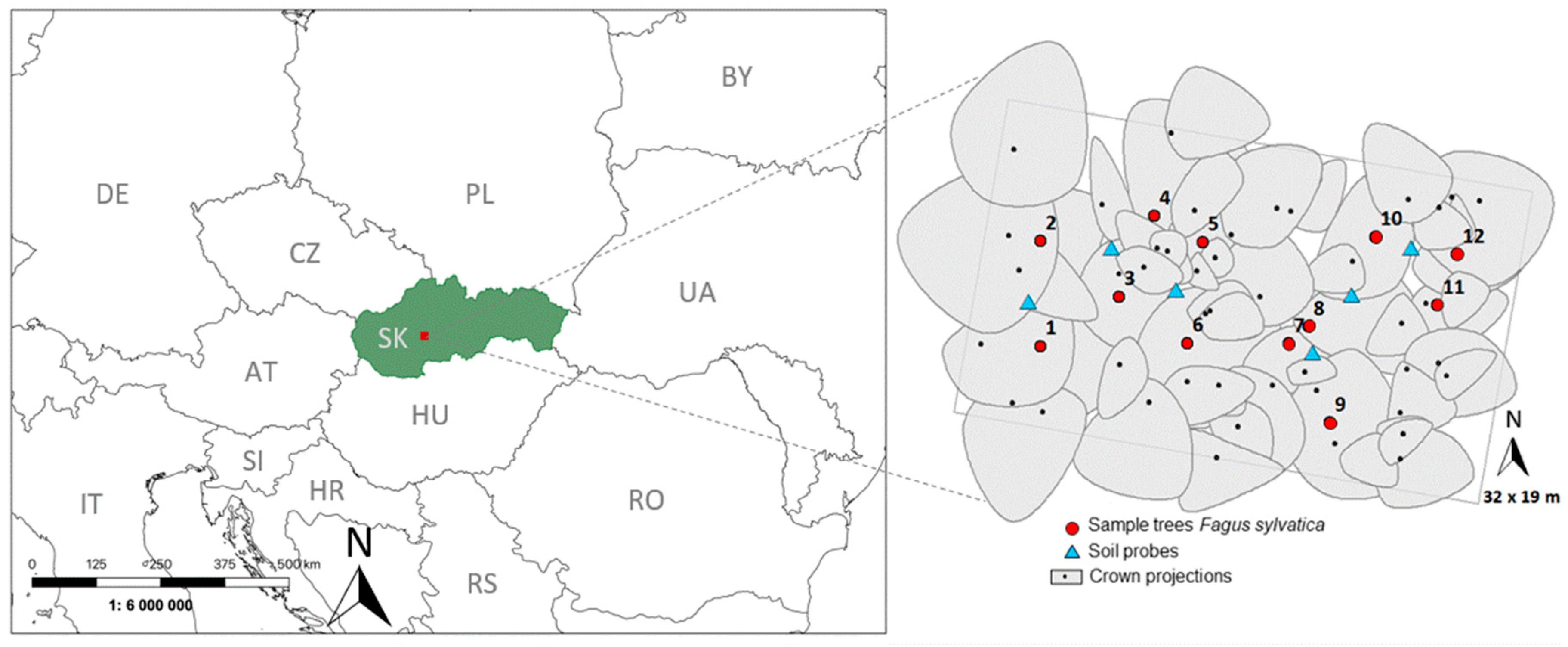
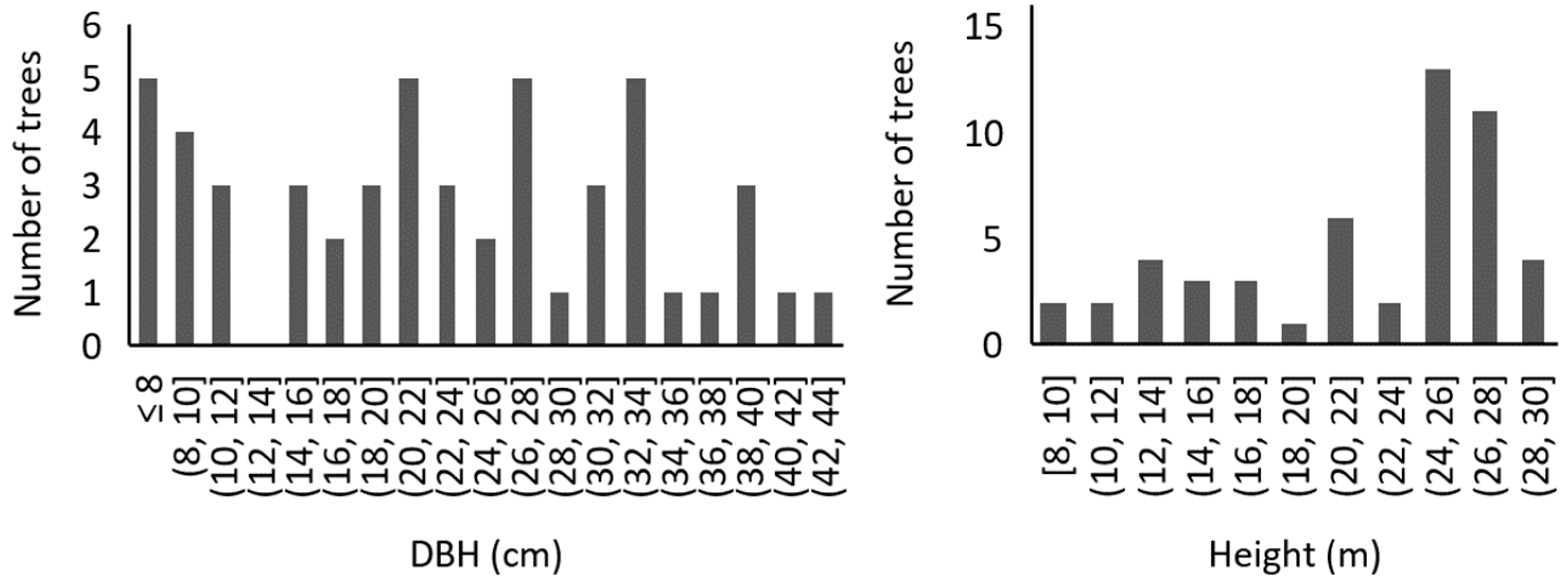
2.1. Experimental Stand
2.2. Measured and Derived Environmental Variables
2.3. Sap Flow and Scaling up to Forest Stand Level

2.4. Data Processing and Statistical Evaluation
3. Results and Discussion
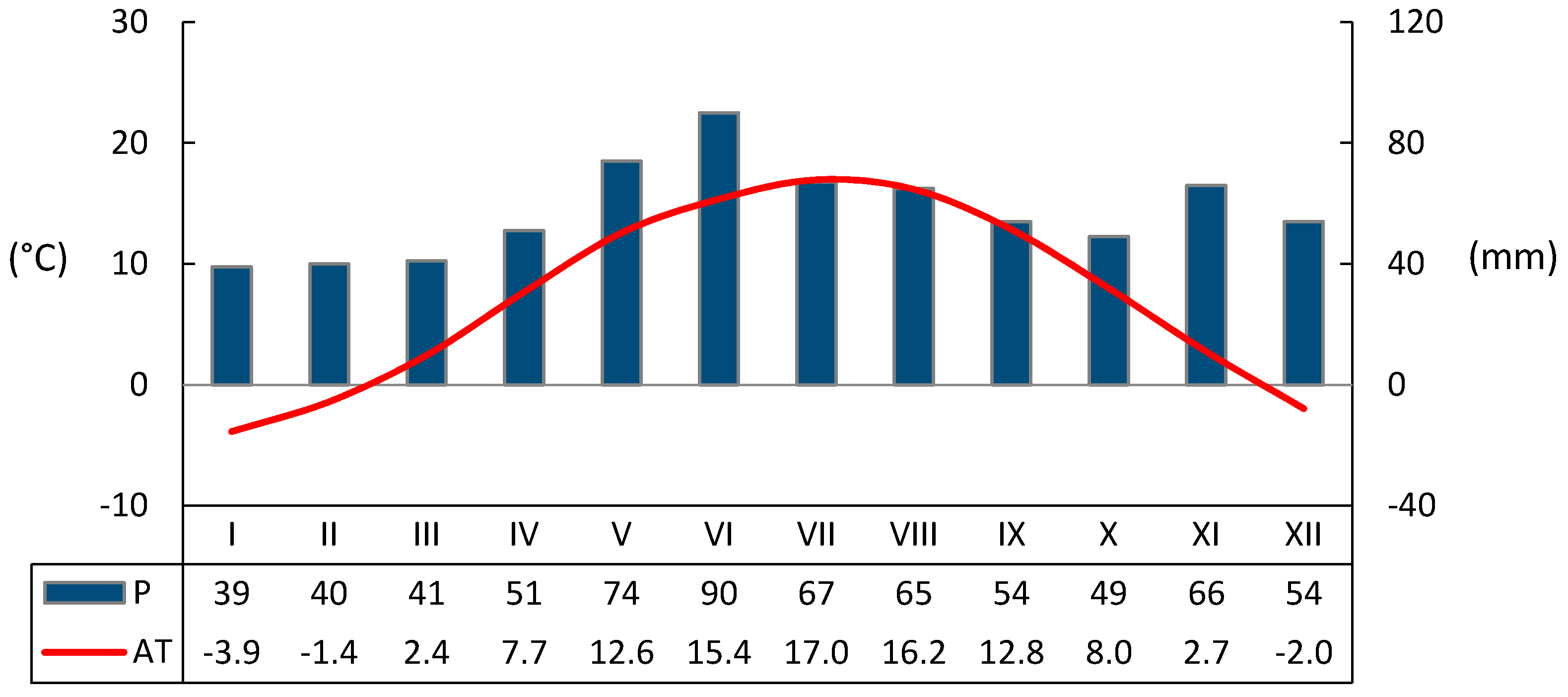
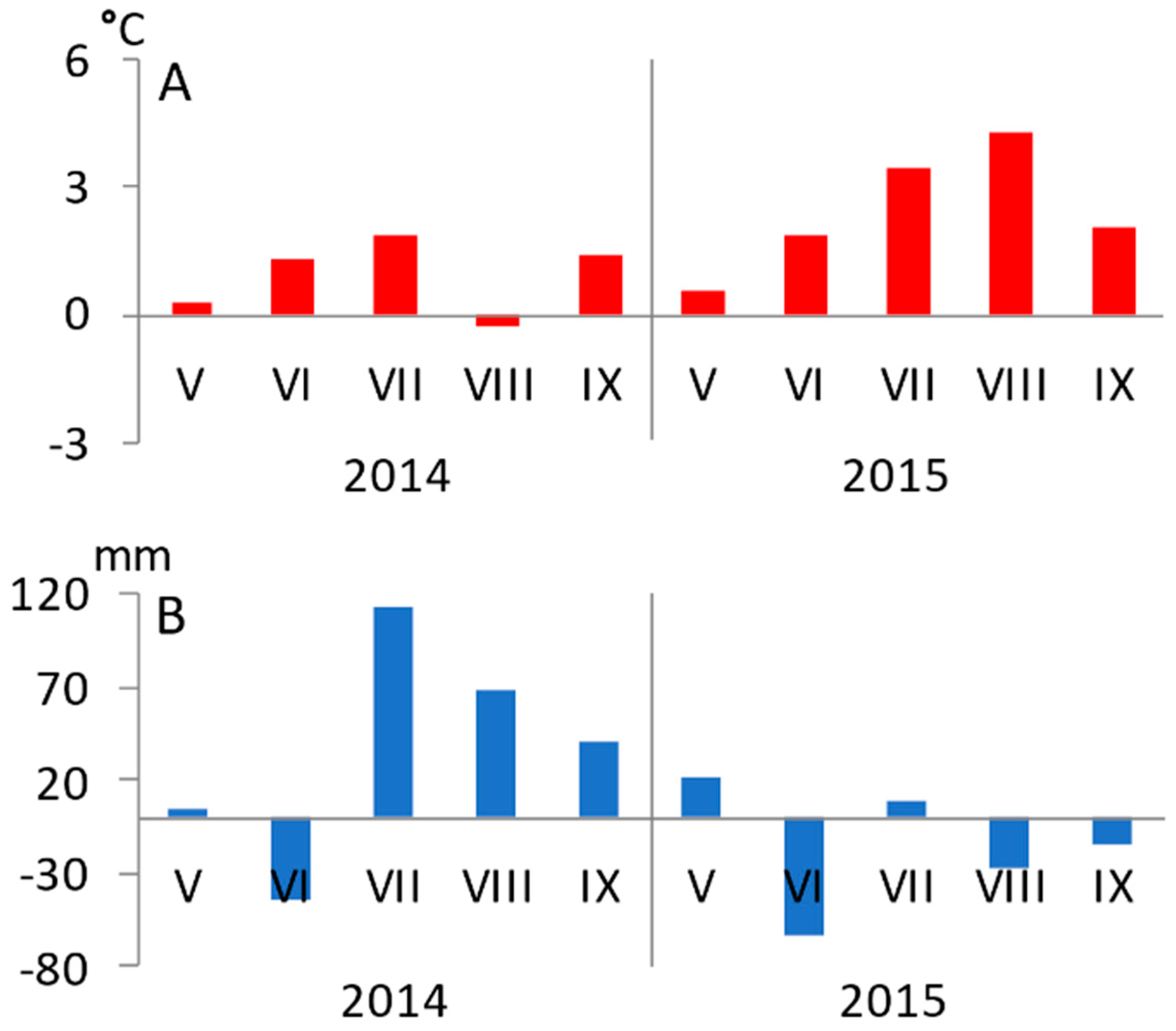
3.1. Seasonal Variation of Environmental Conditions
3.2. Seasonal Dynamics of Transpiration
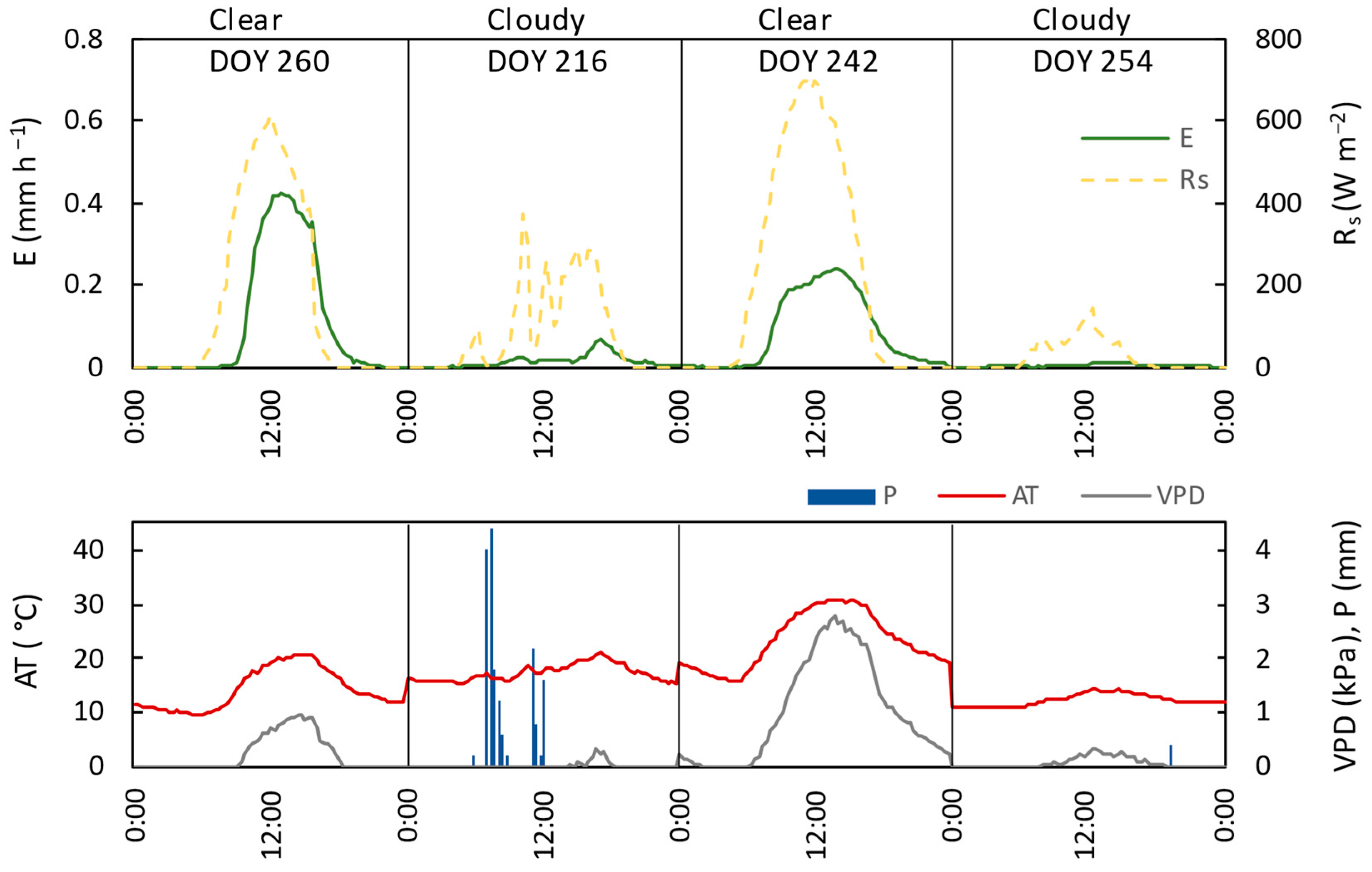
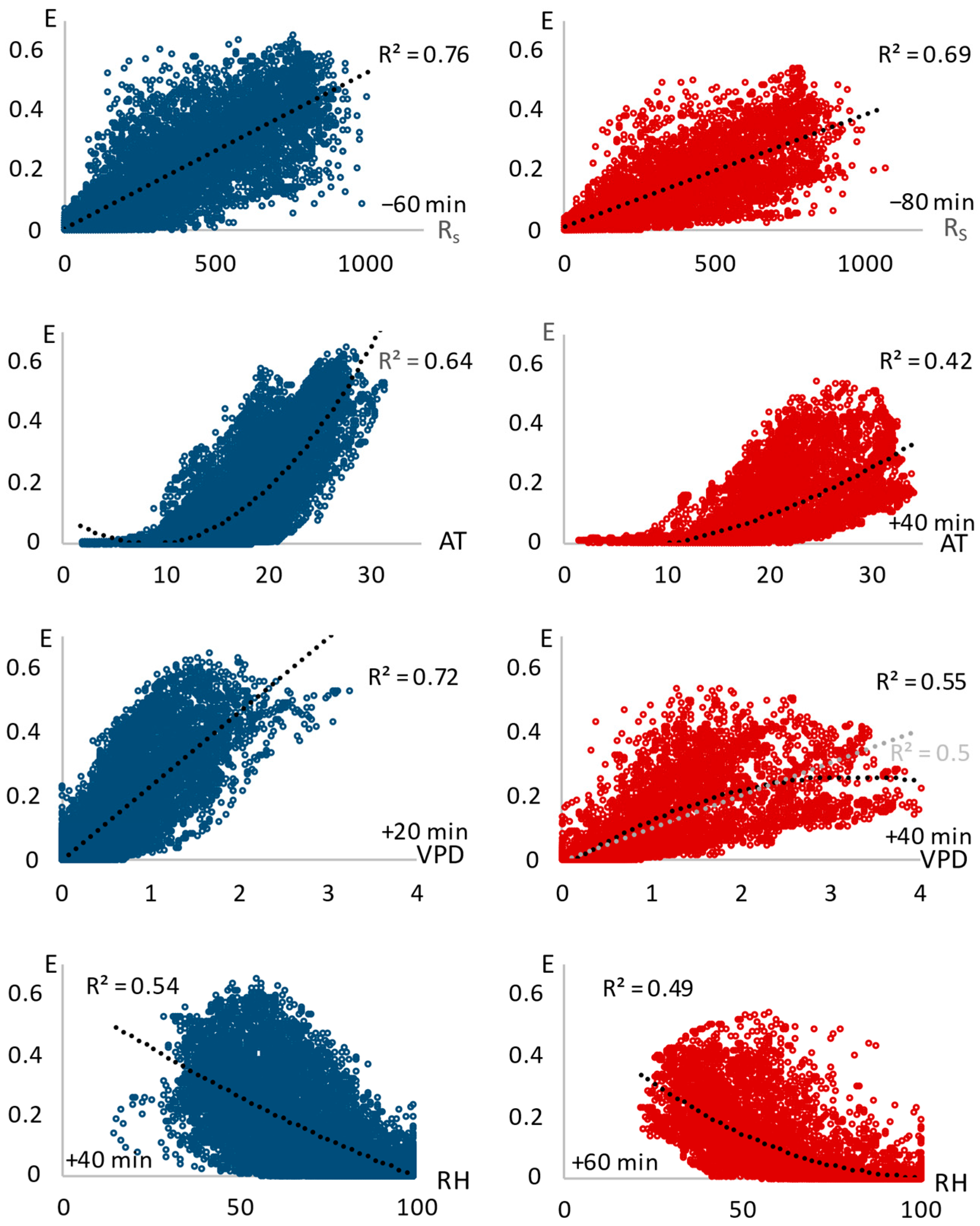
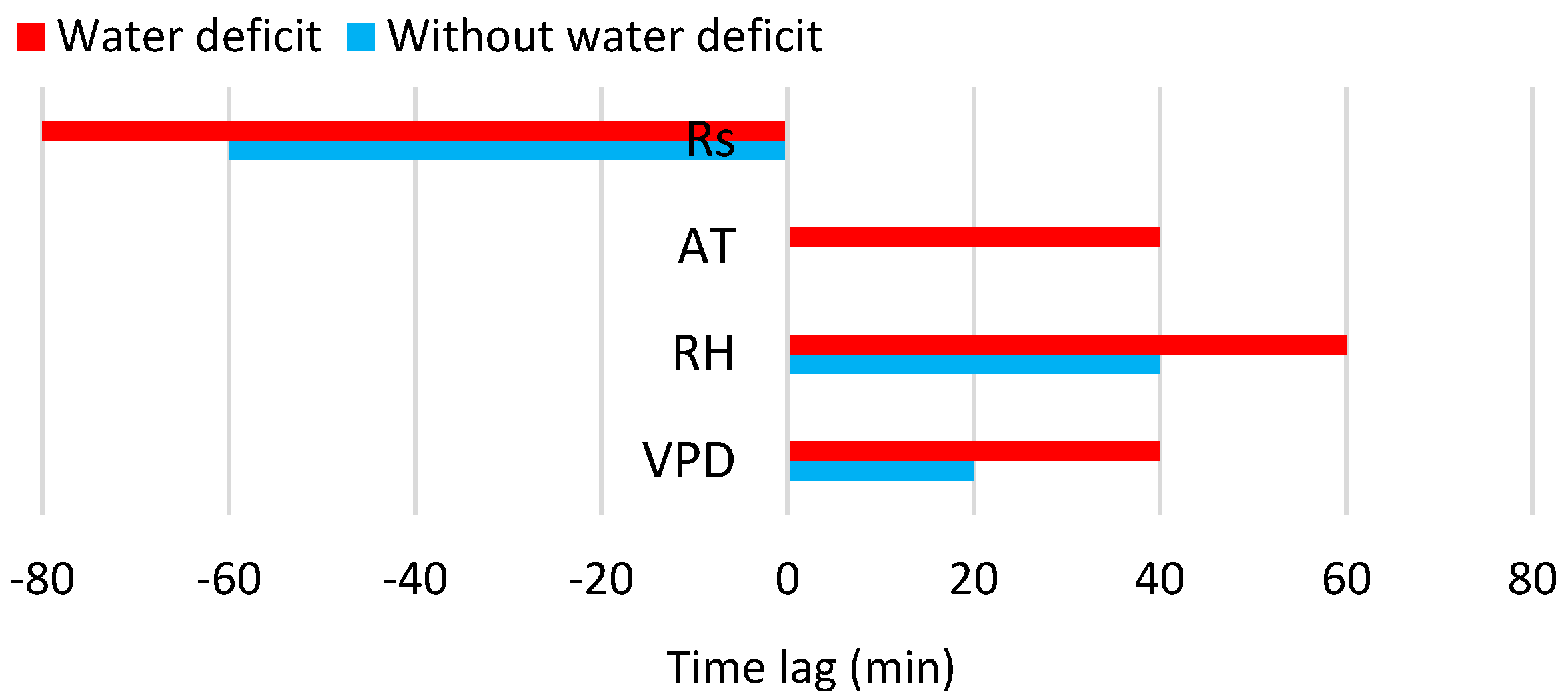
3.3. Relation of Transpiration to Environmental Conditions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial water fluxes dominated by transpiration. Nature 2013, 496, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 2014, 189–190, 115–117. [Google Scholar] [CrossRef]
- Kučera, J.; Brito, P.; Jiménez, M.S.; Urban, J. Direct Penman–Monteith parameterization for estimating stomatal conductance and modeling sap flow. Trees 2016. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. Modeling actual evapotranspiration from forested watersheds across the southeastern United States. J. Am. Water Resour. Assoc. 2003, 39, 886–896. [Google Scholar] [CrossRef]
- Zheng, H.; Yu, G.; Wang, Q.; Zhu, X.; He, H.; Wang, Y.; Zhang, J.; Li, Y.; Zhao, L.; Zhao, F.; et al. Spatial variation in annual actual evapotranspiration of terrestrial ecosystems in China: Results from eddy covariance measurements. J. Geogr. Sci. 2016, 26, 1391–1411. [Google Scholar] [CrossRef]
- Ferreira, M.I. Stress coefficients for soil water balance combined with water stress indicators for irrigation scheduling of woody crops. Horticulturae 2017, 3, 38. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, M.I.; Paço, T.A.; Silvestre, J.; Silva, R.M. Evapotranspiration estimates and water stress indicators for irrigation scheduling in woody plants. In Agricultural Water Management Research Trends; Nova Science Publishers, Inc.: New York, NY, USA, 2008; pp. 129–170. [Google Scholar]
- Čermák, J.; Kučera, J.; Nadezhdina, N. Sap flow measurements with some thermodynamic methods, flow integration within trees and scaling up from sample trees to entire forest stands. Trees 2004, 18, 529–546. [Google Scholar] [CrossRef]
- Köstner, B.; Falge, E.; Alsheimer, M. Sap Flow Measurements. Struct. Role Submerg. Macrophytes Lakes 2017, 99–112. [Google Scholar] [CrossRef]
- Tatarinov, F.A.; Kučera, J.; Cienciala, E. The analysis of physical background of tree sap flow measurement based on thermal methods. Meas. Sci. Technol. 2005, 16, 1157–1169. [Google Scholar] [CrossRef]
- Kaufmann, M.R.; Kelliher, F.M. Measuring transpiration rates. In Techniques and Approaches in Forest Tree Ecophysiology; Lassoie, J.P., Hinckley, T.M., Eds.; CRC Press: Boca Raton, FL, USA, 1991; pp. 117–140. [Google Scholar]
- Betsch, P.; Bonal, D.; Breda, N.; Montpied, P.; Peiffer, M.; Tuzet, A.; Granier, A. Drought effects on water relations in beech: The contribution of exchangeable water reservoirs. Agric. For. Meteorol. 2011, 151, 531–543. [Google Scholar] [CrossRef]
- De Swaef, T.; De Schepper, V.; Vandegehuchte, M.W.; Steppe, K. Stem diameter variations as a versatile research tool in ecophysiology. Tree Physiol. 2015, 35, 1047–1061. [Google Scholar] [CrossRef] [PubMed]
- Tenhunen, J.D.; Valentini, R.; Köstner, B.; Zimmermann, R.; Granier, A. Variation in forest gas exchange at landscape to continental scales. Ann. For. Sci. 1998, 55, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Davi, H.; Dufrêne, E.; Granier, A.; Le Dantec, V.; Barbaroux, C.; François, C.; Bréda, N. Modelling carbon and water cycles in a beech forest. Part II: Validation of the main processes from organ to stand scale. Ecol. Modell. 2005, 185, 387–405. [Google Scholar] [CrossRef] [Green Version]
- MacKay, S.L.; Arain, M.A.; Khomik, M.; Brodeur, J.J.; Schumacher, J.; Hartmann, H.; Peichl, M. The impact of induced drought on transpiration and growth in a temperate pine plantation forest. Hydrol. Process. 2012, 26, 1779–1791. [Google Scholar] [CrossRef] [Green Version]
- Breda, N.; Granier, A. Intra and interannual variations of transpiration, leaf area index and radial growth of sessile oak stand (Quercus petraea). Ann. Sci. For. 1996, 53, 521–536. [Google Scholar] [CrossRef] [Green Version]
- Eamus, D.; Boulain, N.; Cleverly, J.; Breshears, D.D. Global change-type drought-induced tree mortality: Vapor pressure deficit is more important than temperature per se in causing decline in tree health. Ecol. Evol. 2013, 3, 2711–2729. [Google Scholar] [CrossRef] [PubMed]
- Kirchen, G.; Calvaruso, C.; Granier, A.; Redon, P.O.; Van der Heijden, G.; Bréda, N.; Turpault, M.P. Local soil type variability controls the water budget and stand productivity in a beech forest. For. Ecol. Manag. 2017, 390, 89–103. [Google Scholar] [CrossRef]
- Jiao, L.; Lu, N.; Fang, W.; Li, Z.; Wang, J.; Jin, Z. Determining the independent impact of soil water on forest transpiration: A case study of a black locust plantation in the Loess Plateau, China. J. Hydrol. 2019, 572, 671–681. [Google Scholar] [CrossRef]
- Lüttschwager, D.; Jochheim, H. Drought primarily reduces canopy transpiration of exposed beech trees and decreases the share of water uptake from deeper soil layers. Forests 2020, 11, 537. [Google Scholar] [CrossRef]
- Schwinning, S. The ecohydrology of roots in rocks. Ecohydrology 2010, 3, 238–245. [Google Scholar] [CrossRef]
- Eliades, M.; Bruggeman, A.; Lubczynski, M.W.; Christou, A.; Camera, C.; Djuma, H. The water balance components of Mediterranean pine trees on a steep mountain slope during two hydrologically contrasting years. J. Hydrol. 2018, 562, 712–724. [Google Scholar] [CrossRef]
- IPCC 2018. Global warming of 1.5 °C. An IPCC Special Report on the impacts of global warming of 1.5 °C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change. In Summary for Policymakers; Masson-Delmotte, V., Zhai, P., Pörtner, H.O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; World Meteorological Organization: Geneva, Switzerland, 2019; p. 32. [Google Scholar]
- Rowell, D.P.; Jones, R.G. Causes and uncertainty of future summer drying over Europe. Clim. Dyn. 2006, 27, 281–299. [Google Scholar] [CrossRef]
- IPCC 2014. Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part. B: Regional Aspects. Europe. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Centritto, M.; Tognetti, R.; Leitgeb, E.; Střelcová, K.; Cohen, S. Chapter 3 Above Ground Processes: Anticipating Climate Change Influences. In Forest Management and the Water Cycle: An Ecosystem-Based Approach; Bredemeier, M., Cohen, S., Godbold, D.L., Lode, E., Pichler, V., Schleppi, P., Eds.; Springer: Dordrecht, The Netherlands, 2011; Volume 212, pp. 263–289. ISBN 978-90-481-9833-7. [Google Scholar]
- Williams, A.P.; Allen, C.D.; Macalady, A.K.; Griffin, D.; Woodhouse, C.A.; Meko, D.M.; Swetnam, T.W.; Rauscher, S.A.; Seager, R.; Grissino-Mayer, H.D.; et al. Temperature as a potent driver of regional forest drought stress and tree mortality. Nat. Clim. Chang. 2013, 3, 292–297. [Google Scholar] [CrossRef]
- Bertini, G.; Amoriello, T.; Fabbio, G.; Piovosi, M. Forest growth and climate change: Evidences from the ICP-Forests intensive monitoring in Italy. IForest 2011, 4, 262–267. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Dorado-Linan, I.; Akhmetzyanov, L.; Gea-Izquierdo, G.; Zlatanov, T.; Menzell, A. Influence of climate drivers and the North Atlantic Oscillation on beech growth at marginal sites across the Mediterranean. Clim. Res. 2015, 66, 229–242. [Google Scholar] [CrossRef]
- Bréda, N.; Huc, R.; Granier, A.; Dreyer, E. Temperate forest tree and stands under severe drought: A review of ecophysiological responses, adaptation processes and long-term consequences. Ann. Sci. For. 2006, 63, 625–644. [Google Scholar] [CrossRef] [Green Version]
- McDowell, N.G.; Beerling, D.J.; Breshears, D.D.; Fisher, R.A.; Raffa, K.F.; Stitt, M. The interdependence of mechanisms underlying climate-driven vegetation mortality. Trends Ecol. Evol. 2011, 26, 523–532. [Google Scholar] [CrossRef]
- Cailleret, M.; Jansen, S.; Robert, E.M.R.; Desoto, L.; Aakala, T.; Antos, J.A.; Beikircher, B.; Bigler, C.; Bugmann, H.; Caccianiga, M.; et al. A synthesis of radial growth patterns preceding tree mortality. Glob. Chang. Biol. 2017, 23, 1675–1690. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop. Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Buckley, T.N.; Mott, K.A.; Farquhar, G.D. A hydromechanical and biochemical model of stomatal conductance. Plant Cell Environ. 2003, 26, 1767–1785. [Google Scholar] [CrossRef] [Green Version]
- Buckley, T.N.; Turnbull, T.L.; Adams, M.A. Simple models for stomatal conductance derived from a process model: Cross-validation against sap flux data. Plant Cell Environ. 2012, 35, 1647–1662. [Google Scholar] [CrossRef]
- Whitley, R.; Taylor, D.; Macinnis-Ng, C.; Zeppel, M.; Yunusa, I.; O’Grady, A.; Froend, R.; Medlyn, B.; Eamus, D. Developing an empirical model of canopy water flux describing the common response of transpiration to solar radiation and VPD across five contrasting woodlands and forests. Hydrol. Process. 2013, 27, 1133–1146. [Google Scholar] [CrossRef]
- Wang, H.; Guan, H.; Simmons, C.T. Modeling the environmental controls on tree water use at different temporal scales. Agric. For. Meteorol. 2016, 225, 24–35. [Google Scholar] [CrossRef] [Green Version]
- Hong, L.; Guo, J.; Liu, Z.; Wang, Y.; Ma, J.; Wang, X.; Zhang, Z. Time-lag effect between sap flow and environmental factors of Larix principis-rupprechtii Mayr. Forests 2019, 10, 971. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Tetzlaff, D.; Soulsby, C. Hysteretic response of sap flow in Scots pine (Pinus sylvestris) to meteorological forcing in a humid low-energy headwater catchment. Ecohydrology 2019, 12. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, X.; Liu, M.; Zhang, Y.; Xu, C.; Yi, R.; Luo, W.; Soulsby, C. Hysteresis in sap flow and its controlling mechanisms for a deciduous broad-leaved tree species in a humid karst region. Sci. China Earth Sci. 2019, 62, 1744–1755. [Google Scholar] [CrossRef]
- O’Grady, A.P.; Worledge, D.; Battaglia, M. Constraints on transpiration of Eucalyptus globulus in southern Tasmania, Australia. Agric. For. Meteorol. 2008, 148, 453–465. [Google Scholar] [CrossRef]
- Xu, S.; Yu, Z. Environmental control on transpiration: A case study of a desert ecosystem in northwest china. Water 2020, 12, 1211. [Google Scholar] [CrossRef]
- Verbeeck, H.; Steppe, K.; Nadezhdina, N.; Op De Beeck, M.; Deckmyn, G.; Meiresonne, L.; Lemeur, R.; Čermák, J.; Ceulemans, R.; Janssens, I.A. Stored water use and transpiration in Scots pine: A modeling analysis with ANAFORE. Tree Physiol. 2007, 27, 1671–1685. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Zhang, Z.; Li, Z.; Tang, J.; Caldwell, P.; Zhang, W. Biophysical control of whole tree transpiration under an urban environment in Northern China. J. Hydrol. 2011, 402, 388–400. [Google Scholar] [CrossRef]
- Zeppel, M.J.B.; Murray, B.R.; Barton, C.; Eamus, D. Seasonal responses of xylem sap velocity to VPD and solar radiation during drought in a stand of native trees in temperate Australia. Funct. Plant Biol. 2004, 31, 461–470. [Google Scholar] [CrossRef]
- Geßler, A.; Keitel, C.; Kreuzwieser, J.; Matyssek, R.; Seiler, W.; Rennenberg, H. Potential risks for European beech (Fagus sylvatica L.) in a changing climate. Trees Struct. Funct. 2007, 21, 1–11. [Google Scholar] [CrossRef]
- Fritz, P. (Ed.) Ökologischer Waldumbau in Deutschland (Ecological Reconstruction of Forests in Germany); Oekom Verlag: Munich, Germany, 2006; ISBN 978-3-86581-001-4. [Google Scholar]
- Dedrick, S.; Spiecker, H.; Orazio, C.; Tomé, M.; Martinez, I. Plantation or Conversion—The Debate! Ideas Presented and Discussed at a Joint EFI Project-Centre Conference Held 21–23 May 2006 in Freiburg, Germany; European Forest Institute: Joensuu, Finland, 2007; ISBN 9789525453164. [Google Scholar]
- Green Report: Report on Forestry in the Slovak Republic per Year 2018; Ministry of Agriculture and Rural Development of the Slovak Republic and National Forest Centre: Bratislava, Slovakia, 2019.
- Jung, T. Beech decline in Central Europe driven by the interaction between Phytophthora infections and climatic extremes. For. Pathol. 2009, 39, 73–94. [Google Scholar] [CrossRef]
- Mátyás, C.; Berki, I.; Czúcz, B.; Gálos, B.; Móricz, N.; Rasztovits, E. Future of beech in Southeast Europe from the perspective of evolutionary ecology. Acta Silv. Lignaria Hung. 2010, 6, 91–110. [Google Scholar]
- Corcobado, T.; Cech, T.L.; Brandstetter, M.; Daxer, A.; Hüttler, C. Decline of European Beech in Austria: Involvement of Phytophthora spp. and Contributing Biotic and Abiotic Factors. Forests 2020, 11, 859. [Google Scholar] [CrossRef]
- Střelcová, K.; Matejka, F.; Kučera, J. Beech stand transpiration assessment—Two methodical approaches. Ekologia 2004, 22, 147–162. [Google Scholar]
- Thiel, D.; Kreyling, J.; Backhaus, S.; Beierkuhnlein, C.; Buhk, C.; Egen, K.; Huber, G.; Konnert, M.; Nagy, L.; Jentsch, A. Different reactions of central and marginal provenances of fagus sylvatica to experimental drought. Eur. J. For. Res. 2014, 133, 247–260. [Google Scholar] [CrossRef]
- Granier, A.; Reichstein, M.; Bréda, N.; Janssens, I.A.; Falge, E.; Ciais, P.; Grunwald, T.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; et al. Evidence for soil water control on carbon and water dynamics in European forests during the extremely dry year: 2003. Agric. For. Meteorol. 2007, 143, 123–145. [Google Scholar] [CrossRef]
- van der Maaten-Theunissen, M.; Bümmerstede, H.; Iwanowski, J.; Scharnweber, T.; Wilmking, M.; van der Maaten, E. Drought sensitivity of beech on a shallow chalk soil in northeastern Germany—A comparative study. For. Ecosyst. 2016, 3, 24. [Google Scholar] [CrossRef] [Green Version]
- Zimmermann, J.; Hauck, M.; Dulamsuren, C.; Leuschner, C. Climate Warming-Related Growth Decline Affects Fagus sylvatica, But Not Other Broad-Leaved Tree Species in Central European Mixed Forests. Ecosystems 2015, 18, 560–572. [Google Scholar] [CrossRef]
- Decuyper, M.; Chávez, R.O.; Čufar, K.; Estay, S.A.; Clevers, J.G.P.W.; Prislan, P.; Gričar, J.; Črepinšek, Z.; Merela, M.; de Luis, M.; et al. Spatio-temporal assessment of beech growth in relation to climate extremes in Slovenia—An integrated approach using remote sensing and tree-ring data. Agric. For. Meteorol. 2020, 287, 107925. [Google Scholar] [CrossRef]
- Scharnweber, T.; Manthey, M.; Criegee, C.; Bauwe, A.; Schröder, C.; Wilmking, M. Drought matters—Declining precipitation influences growth of Fagus sylvatica L. and Quercus robur L. in north-eastern Germany. For. Ecol. Manag. 2011, 262, 947–961. [Google Scholar] [CrossRef]
- Gennaretti, F.; Ogée, J.; Sainte-Marie, J.; Cuntz, M. Mining ecophysiological responses of European beech ecosystems to drought. Agric. For. Meteorol. 2020, 280. [Google Scholar] [CrossRef]
- Zlatník, A. Overview of groups of geobiocoene types originally wooded or shrubed. Zprávy Geogr. ČSAV Brně 1976, 13, 55–56. (In Czech) [Google Scholar]
- FAO. World Reference Base for Soil Resources 2014. International Soil Classification System for Naming Soils and Creating Legends for Soil Maps. World Soil Resources Reports No. 106. Update 2015; FAO: Rome, Italy, 2015; ISBN 9789251083697. [Google Scholar]
- Lapin, M.; Faško, P.; Melo, M.; Šťastný, P.; Tomlain, J. Klimatické oblasti [Climatic Regions]. In Atlas Krajiny Slovenskej Republiky [Landscape Atlas of the Slovak Republic]; Miklos, L., Ed.; Ministry of Environment of the Slovak Republic: Bratislava, Czechoslovakia, 2002; p. 334. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil, and grass. Proc. R. Soc. 1948, A193, 120–146. [Google Scholar]
- Granier, A.; Bréda, N.; Biron, P.; Villette, S. A lumped water balance model to evaluate duration and intensity of drought constraints in forest stands. Ecol. Modell. 1999, 116, 269–283. [Google Scholar] [CrossRef]
- Kučera, J.; Čermák, J.; Penka, M. Improved thermal method of continual recording the transpiration flow rate dynamics. Biol. Plant 1977, 19, 413–420. [Google Scholar]
- Jiří Kučera—Environmental Measuring Systems Sap Flow System EMS 81. User’s Manual. 2nd Issue. Available online: http://www.emsbrno.cz/r.axd/pdf_v_EMS81__usermanual_u_pdf.jpg?ver= (accessed on 29 November 2020).
- Lagergren, F.; Lindroth, A. Transpiration response to soil moisture in pine and spruce trees in Sweden. Agric. For. Meteorol. 2002, 112, 67–85. [Google Scholar] [CrossRef]
- Rozas, V.; Camarero, J.J.; Sangüesa-Barreda, G.; Souto, M.; García-González, I. Summer drought and ENSO-related cloudiness distinctly drive Fagus sylvatica growth near the species rear-edge in northern Spain. Agric. For. Meteorol. 2015, 201, 153–164. [Google Scholar] [CrossRef] [Green Version]
- Granier, A.; Biron, P.; Lemoine, D. Water balance, transpiration and canopy conductance in two beech stands. Agric. For. Meteorol. 2000, 100, 291–308. [Google Scholar] [CrossRef]
- Gebauer, T.; Horna, V.; Leuschner, C. Canopy transpiration of pure and mixed forest stands with variable abundance of European beech. J. Hydrol. 2012, 442–443, 2–14. [Google Scholar] [CrossRef]
- Haworth, M.; Killi, D.; Materassi, A.; Raschi, A.; Centritto, M. Impaired stomatal control is associated with reduced photosynthetic physiology in crop species grown at elevated [CO2]. Front. Plant. Sci. 2016, 7, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matejka, F.; Střelcová, K.; Hurtalová, T.; Gömöryová, E.; Ditmarová, Ľ. Seasonal changes in transpiration and soil water content in a spruce primeval forest during a dry period. In Bioclimatology and Natural Hazards; Střelcová, K., Mátyás, C., Kleidon, A., Lapin, M., Matejka, F., Blaženec, M., Škvarenina, J., Holécy, J., Eds.; Springer: Dordrecht, Germany, 2009; pp. 197–206. [Google Scholar]
- Tie, Q.; Hu, H.; Tian, F.; Guan, H.; Lin, H. Environmental and physiological controls on sap flow in a subhumid mountainous catchment in North China. Agric. For. Meteorol. 2017, 240–241, 46–57. [Google Scholar] [CrossRef]
- Bai, Y.; Zhu, G.; Su, Y.; Zhang, K.; Han, T.; Ma, J.; Wang, W.; Ma, T.; Feng, L. Hysteresis loops between canopy conductance of grapevines and meteorological variables in an oasis ecosystem. Agric. For. Meteorol. 2015, 214–215, 319–327. [Google Scholar] [CrossRef]
- Carrasco, L.O.; Bucci, S.J.; Di Francescantonio, D.; Lezcano, O.A.; Campanello, P.I.; Scholz, F.G.; Rodríguez, S.; Madanes, N.; Cristiano, P.M.; Hao, G.Y.; et al. Water storage dynamics in the main stem of subtropical tree species differing in wood density, growth rate and life history traits. Tree Physiol. 2015, 35, 354–365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tuzet, A.; Perrier, A.; Leuning, R. A coupled model of stomatal conductance and photosynthesis for winter wheat. Plant Cell Environ. 2003, 26, 1097–1116. [Google Scholar] [CrossRef]
- Poyatos, R.; Llorens, P.; Piñol, J.; Rubio, C. Response of Scots pine (Pinus sylvestris L.) and pubescent oak (Quercus pubescens Willd.) to soil and atmospheric water deficits under Mediterranean mountain climate. Ann. For. Sci. 2008, 65, 306. [Google Scholar] [CrossRef]
- Priwitzer, T.; Kurjak, D.; Kmeť, J.; Sitková, Z.; Leštianska, A. Photosynthetic response of European beech to atmospheric and soil drought. For. J. 2014, 60, 31–37. [Google Scholar] [CrossRef] [Green Version]
- Bovard, B.D.; Curtis, P.S.; Vogel, C.S.; Su, H.B.; Schmid, H.P. Environmental controls on sap flow in a northern hardwood forest. Tree Physiol. 2005, 25, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Čermák, J.; Kučera, J.; Bauerle, W.L.; Phillips, N.; Hinckley, T.M. Tree water storage and its diurnal dynamics related to sap flow and changes in stem volume in old-growth Douglas-fir trees. Tree Physiol. 2007, 27, 181–198. [Google Scholar] [CrossRef]
- Phillips, N.G.; Ryan, M.G.; Bond, B.J.; McDowell, N.G.; Hinckley, T.M.; Čermák, J. Reliance on stored water increases with tree size in three species in the Pacific Northwest. Tree Physiol. 2003, 23, 237–245. [Google Scholar] [CrossRef] [Green Version]

| 2014 | 2015 | |||||
|---|---|---|---|---|---|---|
| E (mm) | PET (mm) | E/PET | E (mm) | PET (mm) | E/PET | |
| May | 46 | 119 | 0.4 | 58 | 123 | 0.5 |
| June | 86 | 165 | 0.5 | 106 | 156 | 0.7 |
| July | 90 | 149 | 0.6 | 72 | 187 | 0.4 |
| August | 81 | 104 | 0.8 | 73 | 153 | 0.5 |
| September | 55 | 72 | 0.8 | 19 | 96 | 0.2 |
| Season | 359 | 609 | 0.59 | 328 | 716 | 0.46 |
| Component No. | Eigenvalue | Percent of Variance | Cumulative Percentage |
|---|---|---|---|
| 1 | 3.7 | 53 | 53 |
| 2 | 1.1 | 16 | 69 |
| 3 | 1.0 | 14 | 83 |
| Variables | Component 1 | Component 2 | Component 3 |
|---|---|---|---|
| RS | 0.45 | −0.23 | −0.03 |
| AT | 0.42 | 0.09 | 0.17 |
| RH | −0.46 | −0.16 | 0.00 |
| P | −0.07 | −0.19 | 0.97 |
| VPD | 0.48 | 0.18 | 0.06 |
| PET | 0.42 | −0.36 | −0.06 |
| SWP | 0.05 | 0.85 | 0.15 |
| Variable | R2 | Model | p < 0.001 | |||
| RS, AT, RH | 0.690 | E = 0.0536679 + 0.000295379 RS + 0.00499328 AT − 0.00127058 RH | ||||
| RS, AT | 0.670 | E = 0.0834326 + 0.000341555 RS + 0.00679228 AT | ||||
| RS, RH | 0.666 | E = 0.171546 + 0.000330795 RS − 0.00181746 RH | ||||
| AT, RH | 0.532 | E = 0.163561 + 0.00883183 AT − 0.00279198 RH | ||||
| Shifted variable | R2 | Model | p < 0.001 | |||
| RS-60, AT+40, RH+20 | 0.729 | E = 0.00707624 + 0.00037642 RS-60 + 0.00342536 AT+40 − 0.000541175 RH+20 | ||||
| RS-60, AT+40 | 0.726 | E = −0.0479013 + 0.000403582 RS-60 + 0.00389637 AT+40 | ||||
| RS-60, RH+20 | 0.718 | E = 0.07679 + 0.000410532 RS-60 − 0.000797576 RH-40 | ||||
| AT+40, RH+20 | 0.537 | E = 0.169809 + 0.00875072 AT+40 − 0.00285242 RH+20 | ||||
| Variable | Without Water Deficit, REW > 0.4 | Water Deficit, REW < 0.4 | ||||
|---|---|---|---|---|---|---|
| Time Lag | R2 | Equation | Time Lag | R2 | Equation | |
| Rs | −60 min | 0.76 | y = 0.0035 + 0.0005x * | −80 min | 0.69 | y = 0.0099 + 0.0004x * |
| AT | - | 0.64 | y = 0.0955 − 0.0237x + 0.0014x2 * | +40 min | 0.42 | y = −0.0408 + 0.0005x + 0.0003x2 * |
| RH | +40 min | 0.54 | y = 0.6651 − 0.0094x + 2.8194 × 10−5x2 * | +60 min | 0.49 | y = 0.5425 − 0.0105x + 5 × 10−5x2 * |
| VPD | +20 min | 0.72 | y = −0.0001 + 0.0002x * | +40 min | 0.55 | y = −0.0207 + 0.1723x − 0.0262x2 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nalevanková, P.; Sitková, Z.; Kučera, J.; Střelcová, K. Impact of Water Deficit on Seasonal and Diurnal Dynamics of European Beech Transpiration and Time-Lag Effect between Stand Transpiration and Environmental Drivers. Water 2020, 12, 3437. https://doi.org/10.3390/w12123437
Nalevanková P, Sitková Z, Kučera J, Střelcová K. Impact of Water Deficit on Seasonal and Diurnal Dynamics of European Beech Transpiration and Time-Lag Effect between Stand Transpiration and Environmental Drivers. Water. 2020; 12(12):3437. https://doi.org/10.3390/w12123437
Chicago/Turabian StyleNalevanková, Paulína, Zuzana Sitková, Jíři Kučera, and Katarína Střelcová. 2020. "Impact of Water Deficit on Seasonal and Diurnal Dynamics of European Beech Transpiration and Time-Lag Effect between Stand Transpiration and Environmental Drivers" Water 12, no. 12: 3437. https://doi.org/10.3390/w12123437
APA StyleNalevanková, P., Sitková, Z., Kučera, J., & Střelcová, K. (2020). Impact of Water Deficit on Seasonal and Diurnal Dynamics of European Beech Transpiration and Time-Lag Effect between Stand Transpiration and Environmental Drivers. Water, 12(12), 3437. https://doi.org/10.3390/w12123437






