Functional Feasibility in Optimal Evaluation of Water Distribution Network Performances
Abstract
:1. Introduction
1.1. Multi-Objective Optimization Algorithms
1.2. Account of Uncertainty in WDN Management
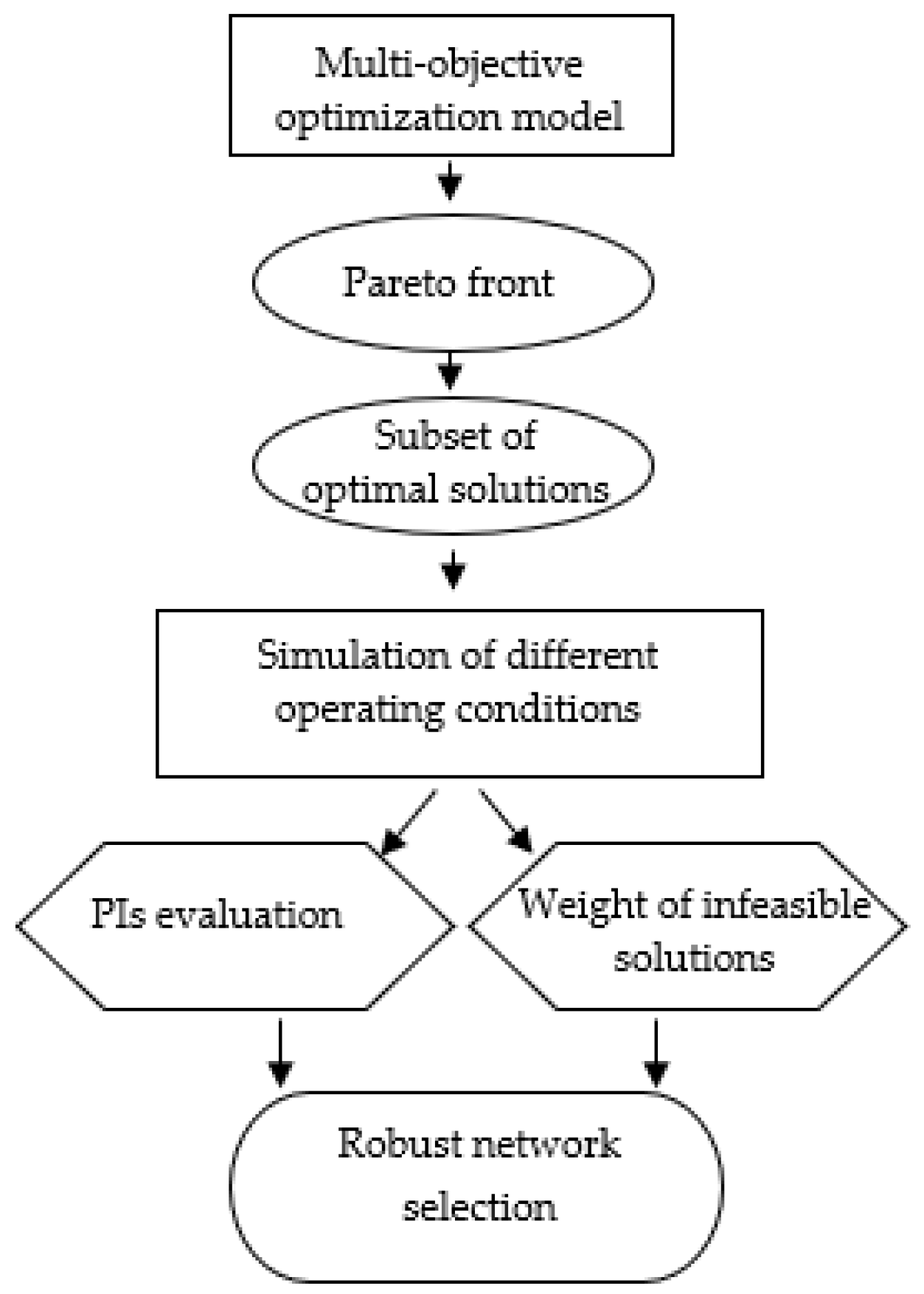
2. Materials and Methods
2.1. Optimization Model and Solution Algorithm
2.2. Performance Indices
- Demand deficit (DD) evaluated as the percentage of undelivered demand.
- Pressure range (PR) evaluated as the variation of the nodal pressure out of the optimal operating range.
2.3. Network Simulation: Pressure-Driven Analysis
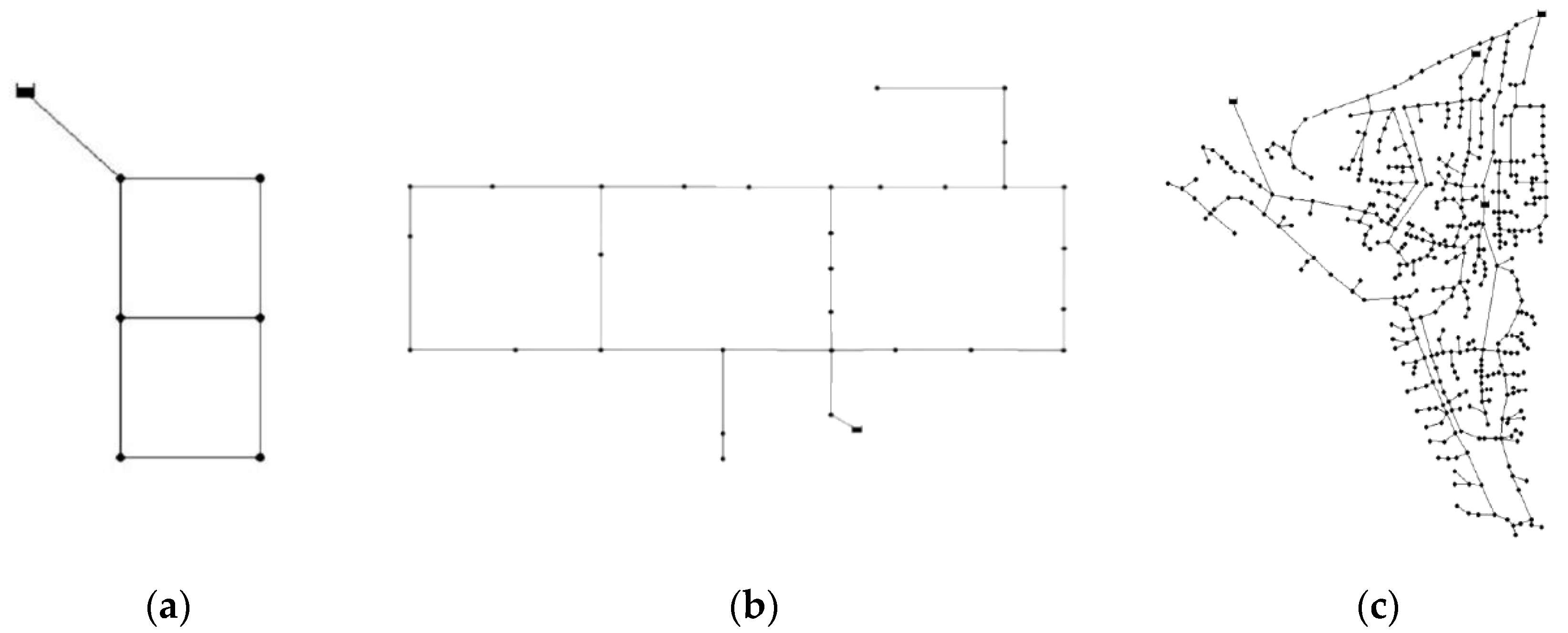
2.4. Benchmark Set-Up
2.5. Pareto Fronts and Solution Subset Selection
2.6. Operation Scenarios and Performance Assessment
- A 10% increase in the demand in all nodes;
- A 30% increase in the demand in 1/3 nodes of the network with the maximum demand;
- A 30% increase in the demand in 1/3 nodes of the network with the minimum demand.
3. Results and Discussion
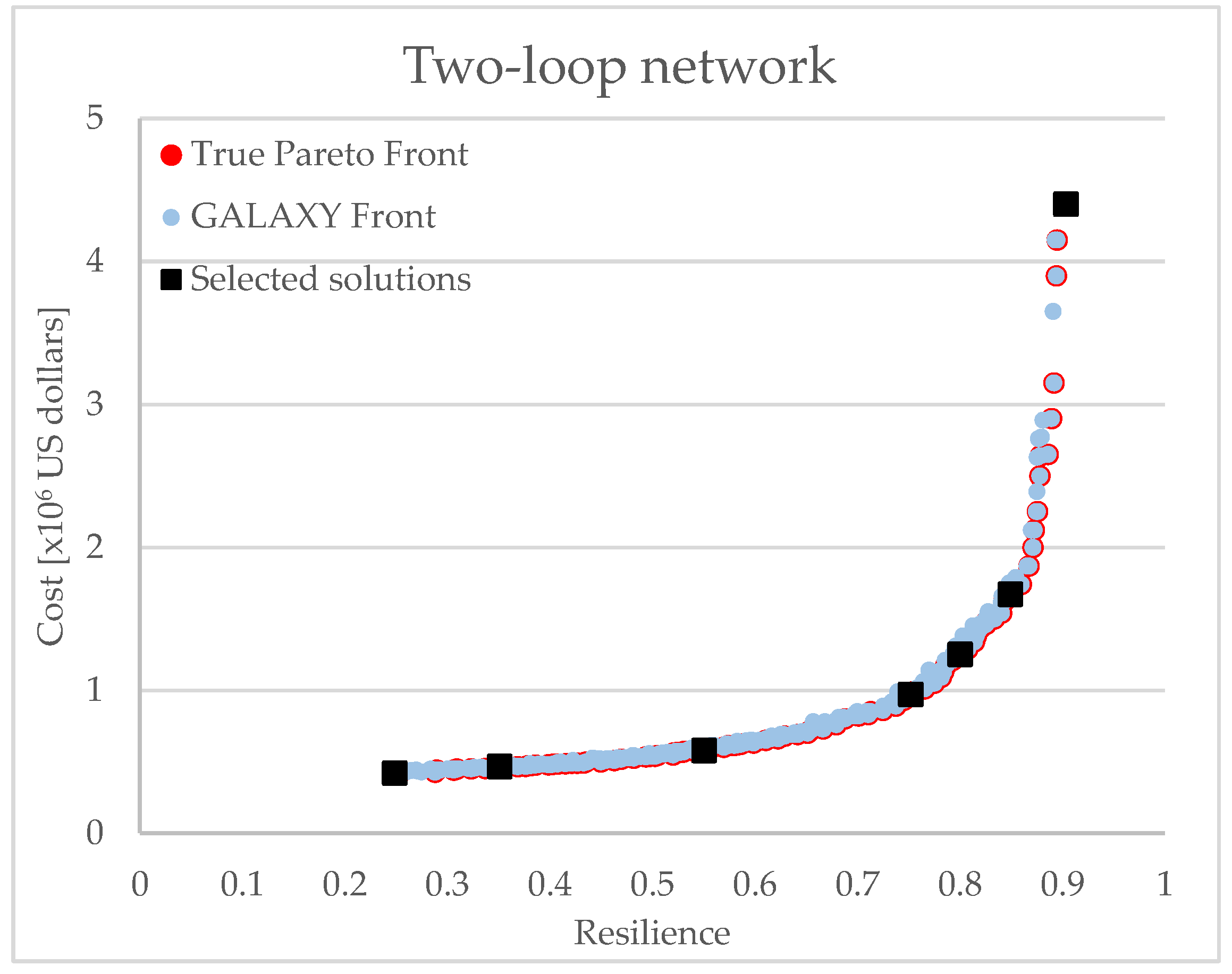
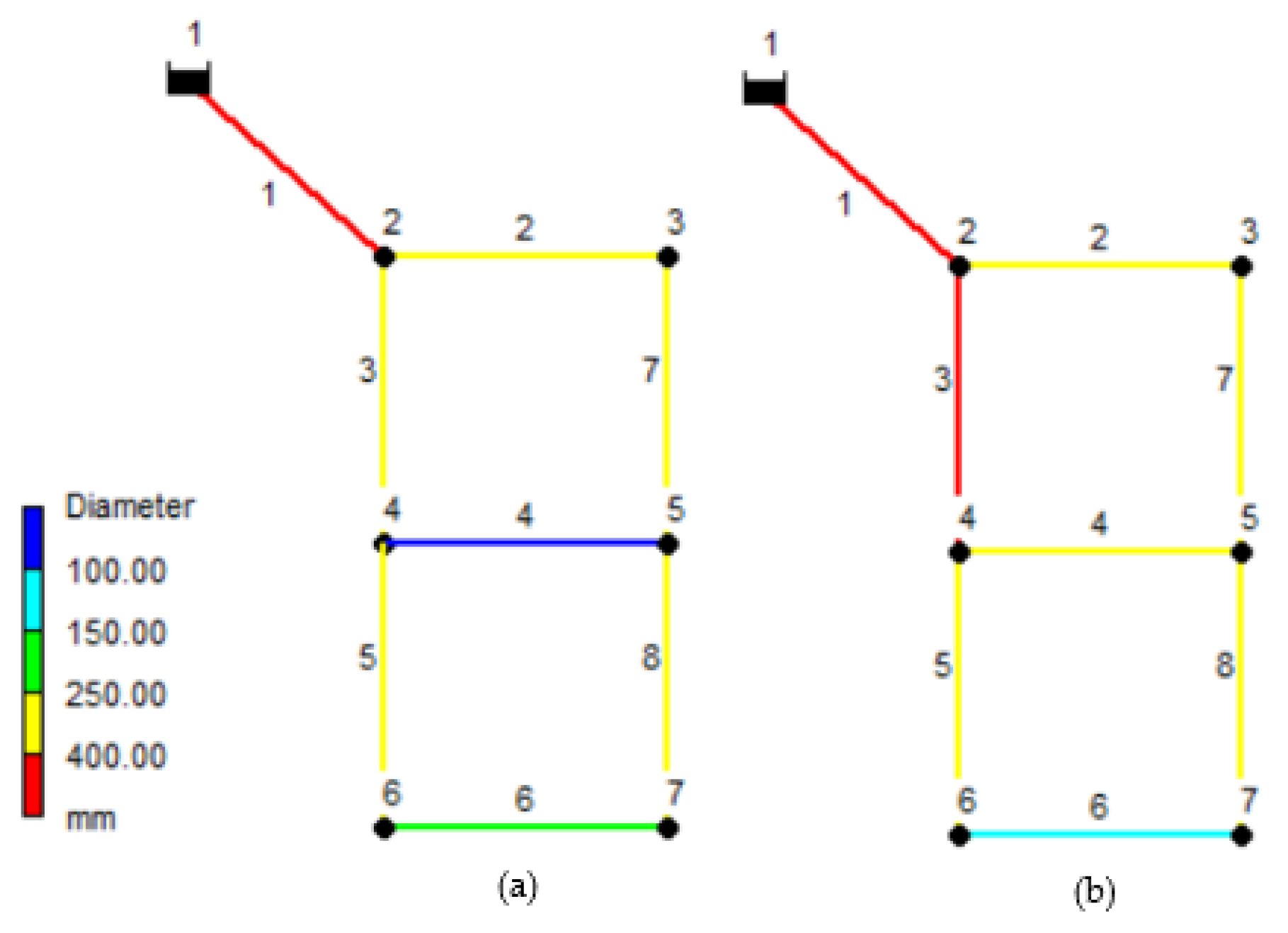
3.1. Two-Loop Network
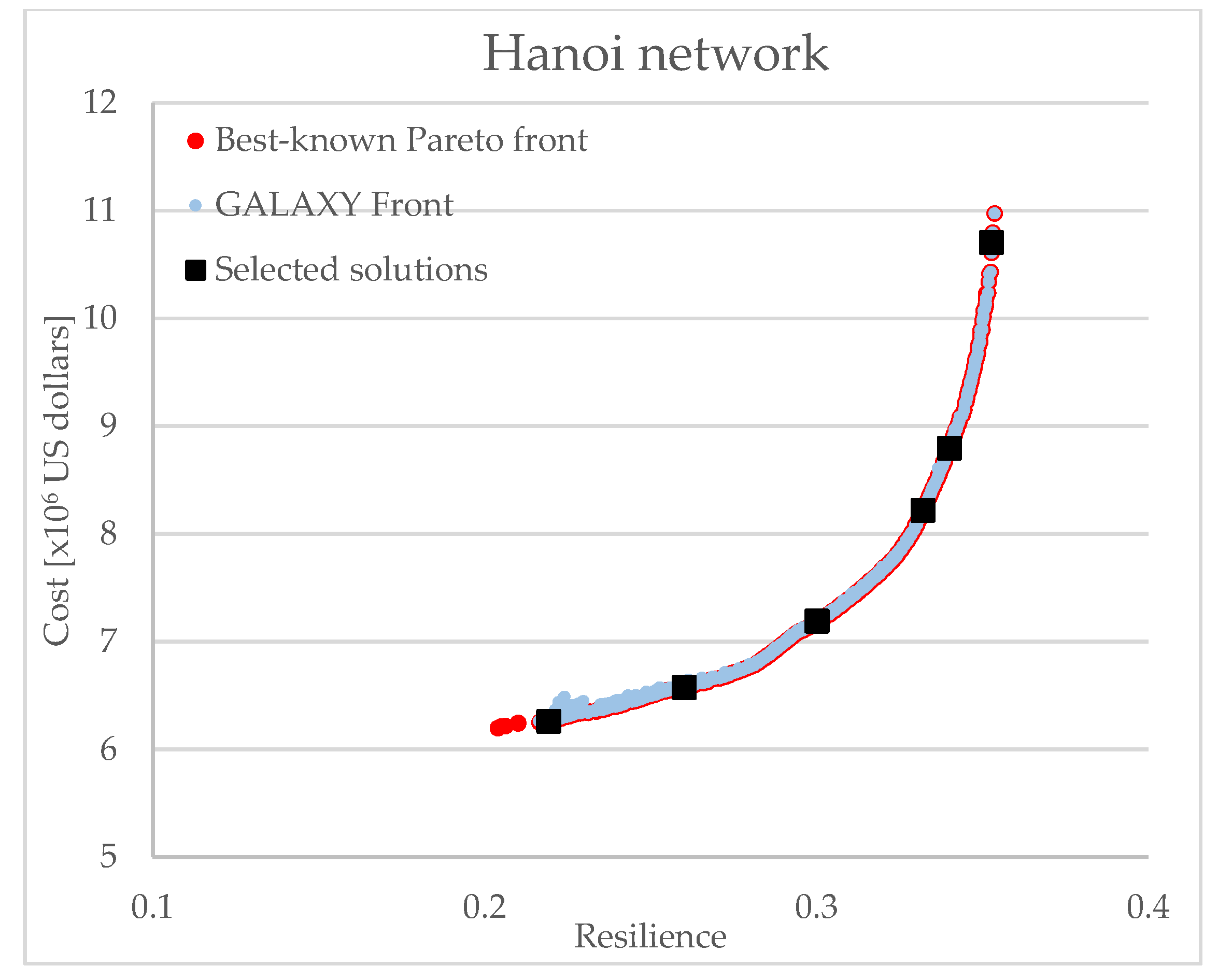
3.2. Hanoi Network
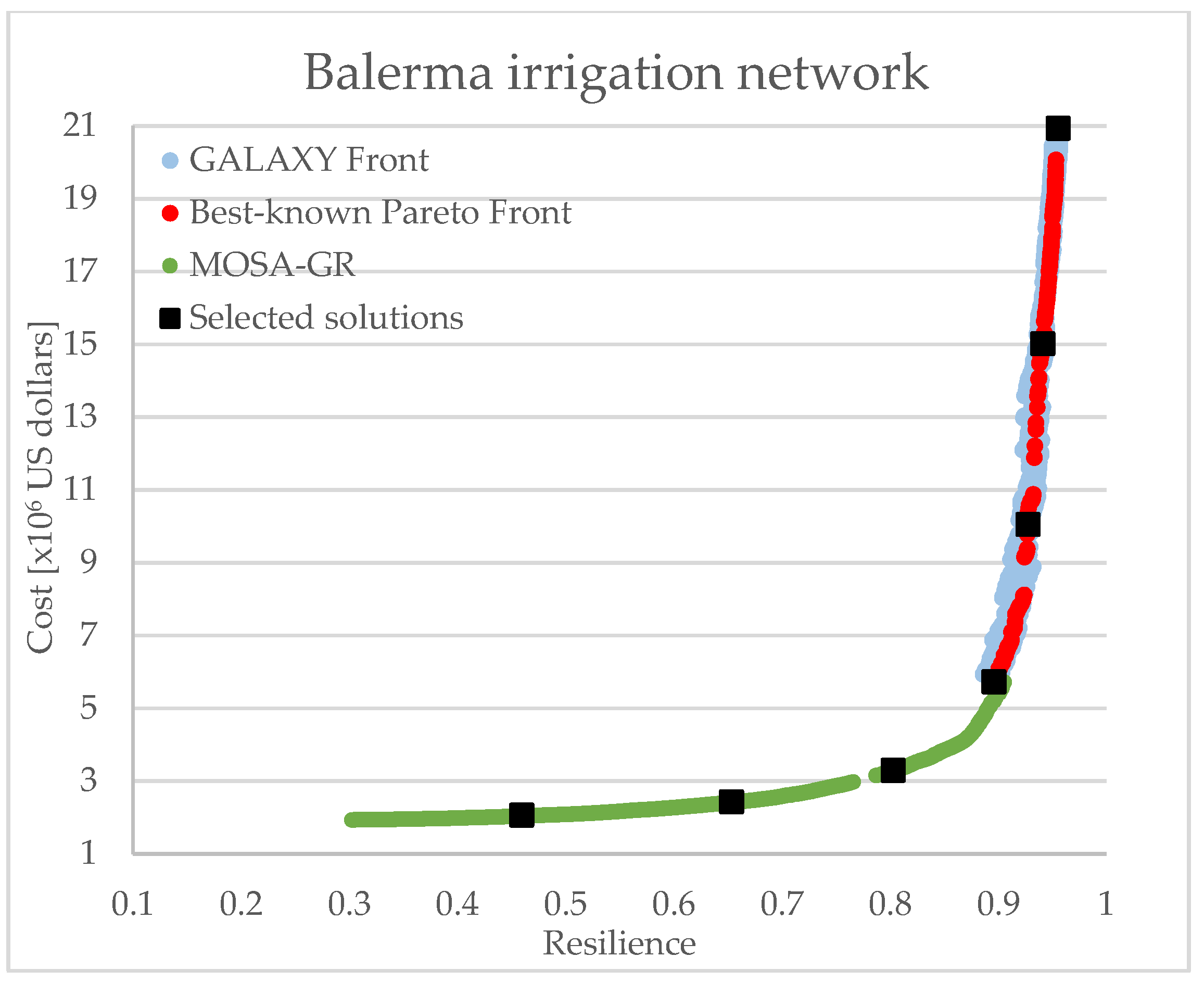
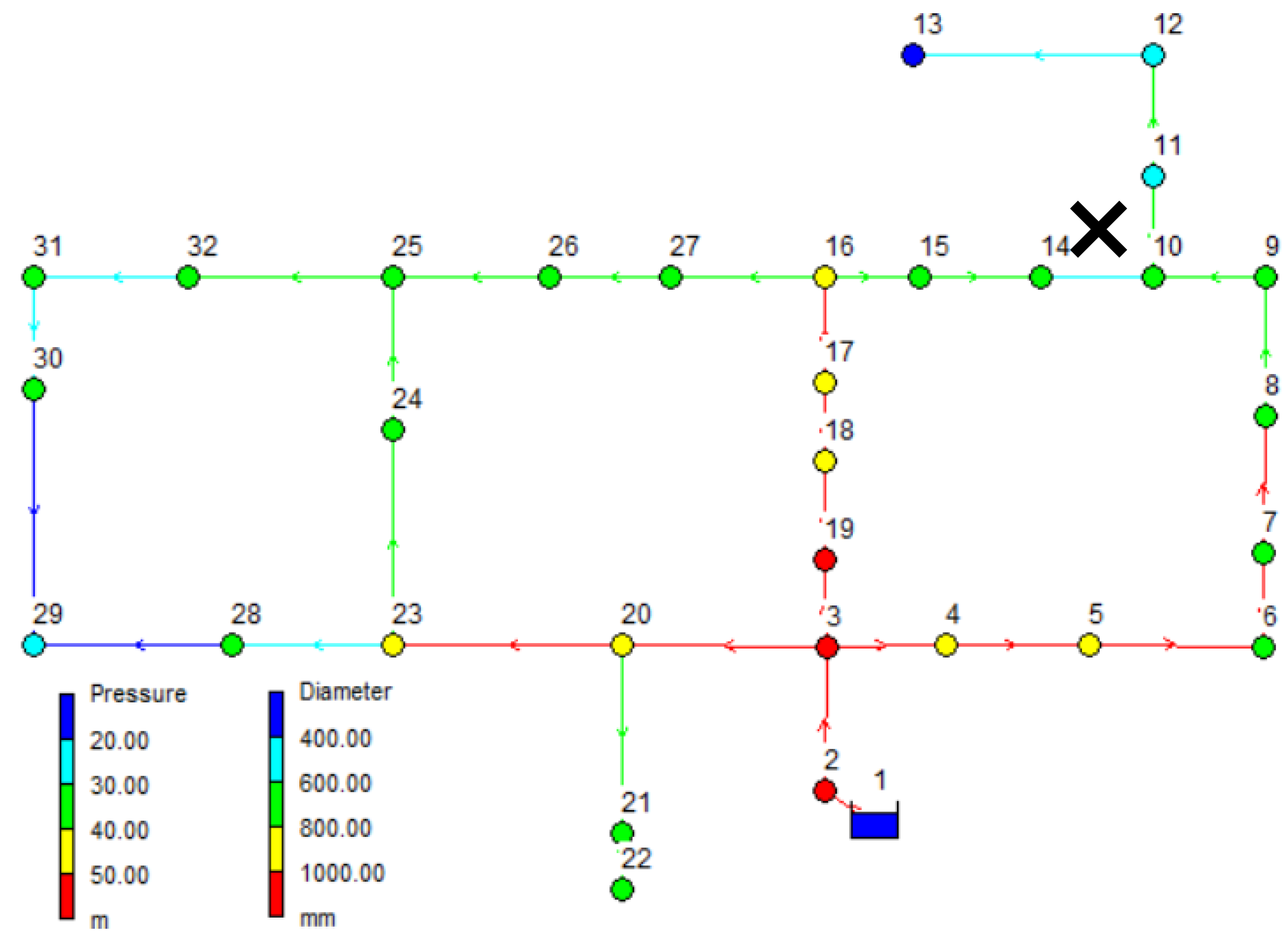
3.3. Balerma Irrigation Network
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schaake, J.; Lai, D. Linear Programming and Dynamic Programming Applications to Water Distribution Network Design; Technical Report No. 116; Department of Civil Engineering, Massachusetts Institute of Technology: Cambridge, MA, USA, 1969. [Google Scholar]
- Alperovits, E.; Shamir, U. Design of optimal water distribution systems. Water Resour. Res. 1977, 13, 885–900. [Google Scholar] [CrossRef]
- Su, Y.; Mays, L.; Duan, N.; Lansey, K. Reliability-based optimization model for water distribution systems. J. Hydraul. Eng. 1987, 113, 1539–1556. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Kuo, C.H. Genetic algorithms in pipeline optimization. J. Comput. Civil Eng. 1987, 1, 128–141. [Google Scholar] [CrossRef]
- Murphy, L.J.; Simpson, A.R. Pipe network optimization using genetic algorithms. In Proceedings of the Specialty Conference of Water Resources Planning and Management Division, American Society of Civil Engineers, Seattle, WA, USA, 1–5 May 1993. [Google Scholar]
- Simpson, A.R.; Dandy, G.C.; Murphy, J.L. Genetic algorithms compared to other techniques for pipe optimization. J. Water Resour. Plan. Manag. 1994, 120, 423–443. [Google Scholar] [CrossRef] [Green Version]
- Savic, D.A.; Walters, G.A. Genetic algorithms for least cost design of water distribution networks. J. Water Resour. Plan. Manag. 1997, 123, 67–77. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Aarts, L.E.H.; Van Laarhoven, P.J.M. Statistic cooling: A general approach to combinatorial optimization problems. Philips J. Res. 1985, 40, 193–226. [Google Scholar]
- Cunha, M.C.; Sousa, J. Water distribution design optimization: Simulated annealing approach. J. Water Resour. Plan. Manag. 1999, 125, 215–221. [Google Scholar] [CrossRef]
- Glover, F. Tabu search-part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Cunha, M.C.; Ribeiro, L. Tabu search algorithms for water network optimization. Eur. J. Oper. Res. 2004, 157, 746–758. [Google Scholar] [CrossRef] [Green Version]
- Fujiwara, O.; Khang, D.B. A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour. Res. 1987, 23, 977–982. [Google Scholar] [CrossRef]
- Cohon, J.; Marks, D. A review and evaluation of multiobjective programming techniques. Water Resour. Res. 1975, 11, 208–220. [Google Scholar] [CrossRef]
- Halhal, D.; Walters, G.A.; Ouazar, D.; Savic, D.A. Water network rehabilitation with structured messy genetic algorithm. J. Water Resour. Plan. Manag. 1997, 123, 137–146. [Google Scholar] [CrossRef] [Green Version]
- Chand, S.; Wagner, M. Evolutionary many-objective optimization: A quick-start guide. Surv. Oper. Res. Manag. Sci. 2015, 20, 35–42. [Google Scholar] [CrossRef] [Green Version]
- Srinivas, N.; Deb, K. Multi-Objective function optimization using non-dominated sorting genetic algorithms. Evol. Comput. 1995, 3, 221–248. [Google Scholar]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. Parallel Probl. Solving Nat. 2002, 6, 849–858. [Google Scholar]
- Laumanns, M.; Thiele, L.; Zitzler, E.; Deb, K. Archiving with guaranteed convergence and diversity in multi-objective optimization. In Proceedings of the Gecco-2002 Genetic and Evolutionary Computation Conference, New York, NY, USA, 9–13 July 2002; pp. 439–447. [Google Scholar]
- Kollat, J.B.; Reed, P.M. Comparing state-of-the-art evolutionary multi-objective algorithms for long-term groundwater monitoring design. Adv. Water Resour. 2006, 29, 792–807. [Google Scholar] [CrossRef]
- Hadka, D.; Reed, P. Borg: An auto-adaptive many-objective evolutionary computing framework. Evol. Comput. 2013, 21, 231–259. [Google Scholar] [CrossRef]
- Wang, Q.; Savic, D.A.; Kapelan, Z. GALAXY: A new hybrid MOEA for the optimal design of water distribution systems. Water Resour. Res. 2017, 53, 1997–2015. [Google Scholar] [CrossRef] [Green Version]
- Cunha, M.C.; Marques, J. A new multiobjective simulated annealing algorithm—MOSA-GR: Application to the optimal design of water distribution networks. Water Resour. Res. 2020, 56, e2019WR025852. [Google Scholar] [CrossRef]
- Becciu, G.; Mambretti, S.; Martins, P.S.; Moraes, R.L. Dealing with uncertainties in losses assessment in water supply networks: Preliminary results. WIT Trans. Built Environ. 2014, 139, 139–148. [Google Scholar]
- Savic, A. Coping with Risk and Uncertainty in Urban Water Infrastructure Rehabilitation Planning; Acqua e Città-I Convegno Nazionale di Idraulica Urbana, Sant’Agnello: Naples, Italy, 2005. [Google Scholar]
- Cunha, M.C.; Sousa, J.J.O. Robust design of water distribution networks for a proactive risk management. J. Water Resour. Plan. Manag. 2010, 136, 227–236. [Google Scholar] [CrossRef]
- Scarpa, F.; Lobba, A.; Becciu, G. Expeditious pump rescheduling in multisource water distribution networks. Proc. Eng. 2015, 119, 1078–1087. [Google Scholar] [CrossRef] [Green Version]
- Basupi, I.; Kapelan, Z. Flexible water distribution system design under future demand uncertainty. J. Water Resour. Plan. Manag. 2015, 141, 4014034. [Google Scholar] [CrossRef]
- Marques, J.; Cunha, M.C.; Savic, D. A multi-objective optimization of water distribution systems based on a real options approach. Environ. Model. Softw. 2015, 63, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Marques, J.; Cunha, M.C.; Savic, D.; Giustolisi, O. Water network design using a multiobjective real options framework. J. Optim. 2017, 2017, 4373952. [Google Scholar] [CrossRef]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water distribution reliability: Simulation methods. J. Water Resour. Plan. Manag. 1988, 276, 276–294. [Google Scholar] [CrossRef] [Green Version]
- Raad, D.N.; Sinske, A.N.; Van Vuuren, J.H. Comparison of four reliability surrogate measures for water distribution systems design. Water Resour. Res. 2010, 46, W05524. [Google Scholar] [CrossRef]
- Atkinson, S.; Farmani, R.; Memon, F.A.; Butler, D. Reliability indicators for water distribution system design: Comparison. J. Water Resour. Plan. Manag. 2014, 140, 160–168. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Guidolin, M.; Savic, D.M.; Kapelan, Z. Two-objective design of benchmark problems of a water distribution system via MOEAs: Towards the best-known approximation of the true pareto front. J. Water Resour. Plan. Manag. 2015, 141, 04014060. [Google Scholar] [CrossRef] [Green Version]
- Todini, E. Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Prasad, T.D.; Park, N.S. Multiobjective genetic algorithms for design of water distribution networks. J. Water Resour. Plan. Manag. 2004, 73, 73–82. [Google Scholar] [CrossRef]
- Morley, M.S.; Tricarico, C. Pressure Driven Demand Extension for EPANET; Technical Report 2008-02; Centre for Water Systems, University of Exeter: Exeter, UK, 2008. [Google Scholar]
- Rossman, L.A. EPANET 2 User’s Manual; US Environmental Protection Agency: Cincinnati, OH, USA, 2000.
- Reca, J.; Martinez, J. Genetic algorithms for the design of looped irrigation water distribution networks. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Eliadas, D.G.; Kyriakou, M.; Vrachimis, S.; Polycarpou, M.M. EPANET-MATLAB Toolkit: An open-source software for interfacing EPANET with MATLAB. In Proceedings of the 14th International Conference on Computing and Control for the Water Industry (CCWI), Hague, The Netherlands, 7–9 November 2016. [Google Scholar]
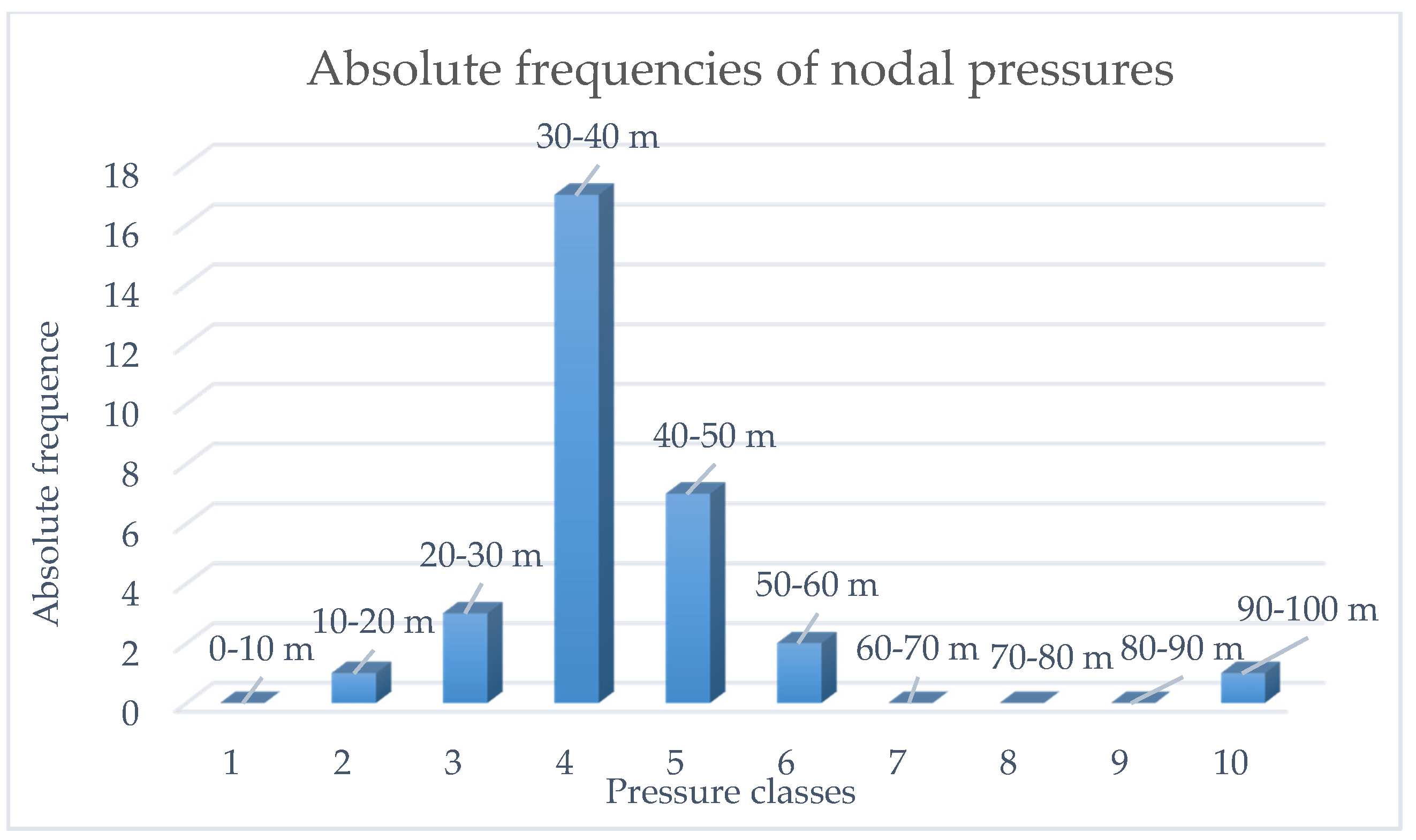
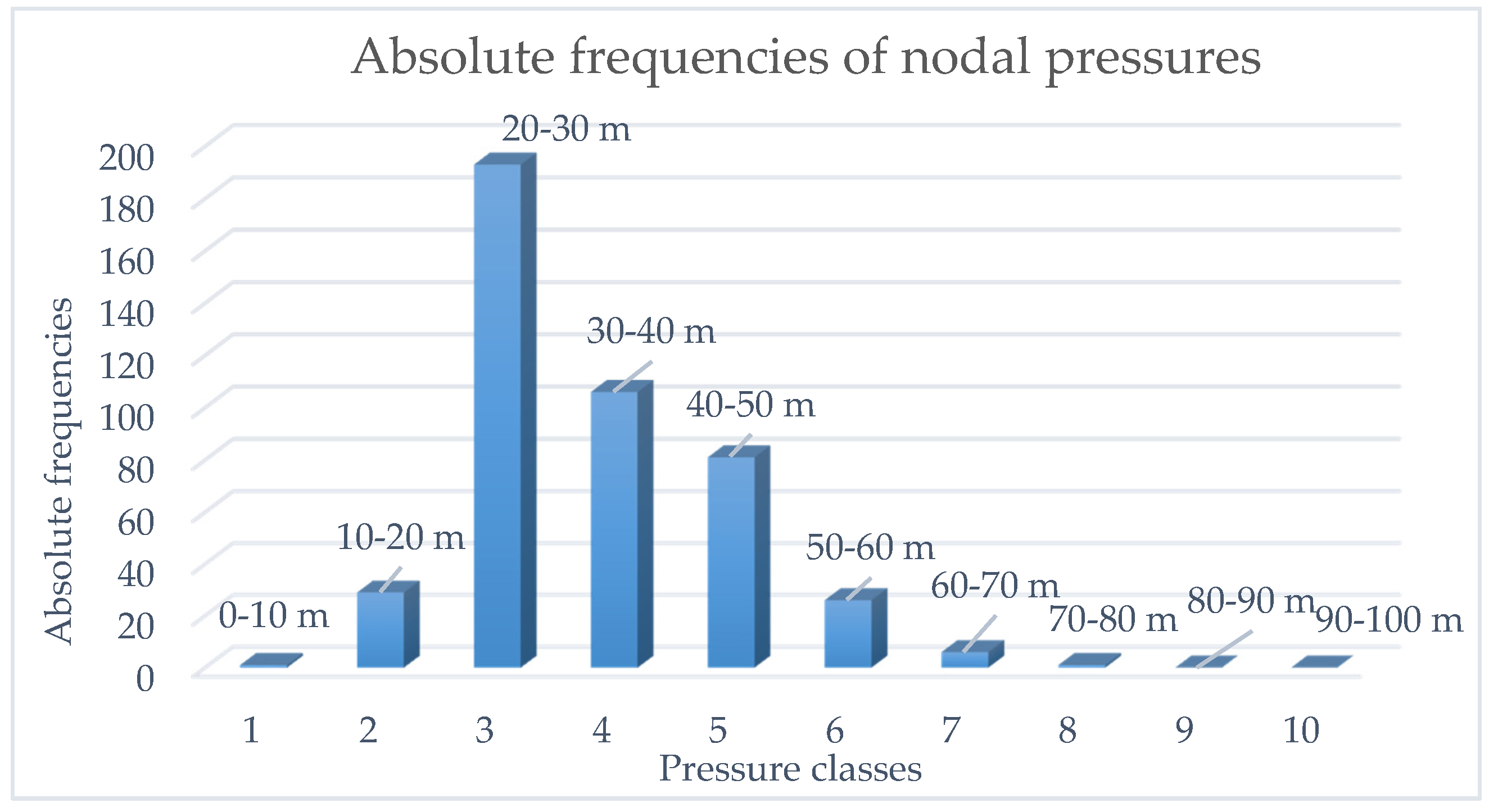
| Condition | Emitter Coefficient | Demand |
|---|---|---|
| Problem | Acronym | LC | WS | NP | NN |
|---|---|---|---|---|---|
| Two-loop network | TLN | 1 | 1 | 8 | 7 |
| Hanoi network | HAN | 1 | 1 | 34 | 32 |
| Balerma irrigation network | BIN | 1 | 4 | 454 | 443 |
| Population Size | ||||
|---|---|---|---|---|
| Problem | NFEs | Group1 | Group2 | Group3 |
| Two-loop network | 100,000 | 40 | 80 | 160 |
| Hanoi network | 600,000 | 60 | 120 | 240 |
| Balerma irrigation network | 2,000,000 | 200 | 400 | 800 |
| Network | Diameter (mm) | Cost (USD × m) | Minimum Pressure (m) |
|---|---|---|---|
| Two-loop network | 25.4; 50.8; 76.2; 101.6; 152.4; 203.2; 254; 304.8; 355.6; 406.4; 457.2; 508; 558.8; 609.6 | 2; 5; 8; 11; 16; 23; 32; 50; 60; 90; 130; 170; 300; 550 | 30 |
| Hanoi network | 304.8; 406.4; 508; 609.6; 762; 1016 | 45.72; 70.4; 98.38; 129.33; 180.74; 278.28 | 30 |
| Balerma irrigation network | 113; 126.6; 144.6; 162.8; 180.8; 226.2; 285; 361.8; 452.2; 581.8 | 7.22; 9.1; 11.92; 14.84; 18.38; 28.6; 45.39; 76.32; 124.64; 215.85 | 20 |
| Two-Loop Network | Hanoi Network | Balerma Irr Network | ||||||
|---|---|---|---|---|---|---|---|---|
| Sol | Cost | Resilience | Sol | Cost | Resilience | Sol | Cost | Resilience |
| 1 | 0.42 | 0.248 | 1 | 6.25 | 0.219 | 1 | 2.05 | 0.408 |
| 2 | 0.46 | 0.351 | 2 | 6.57 | 0.260 | 2 | 2.41 | 0.65 |
| 3 | 0.57 | 0.550 | 3 | 7.18 | 0.300 | 3 | 3.28 | 0.801 |
| 4 | 0.97 | 0.752 | 4 | 8.21 | 0.332 | 4 | 5.72 | 0.896 |
| 5 | 1.25 | 0.800 | 5 | 8.79 | 0.340 | 5 | 10.04 | 0.928 |
| 6 | 1.67 | 0.849 | 6 | 10.70 | 0.352 | 6 | 15.01 | 0.941 |
| 7 | 4.4 | 0.903 | 7 | 20.92 | 0.955 | |||
| Network | TLN | HAN | BIN | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
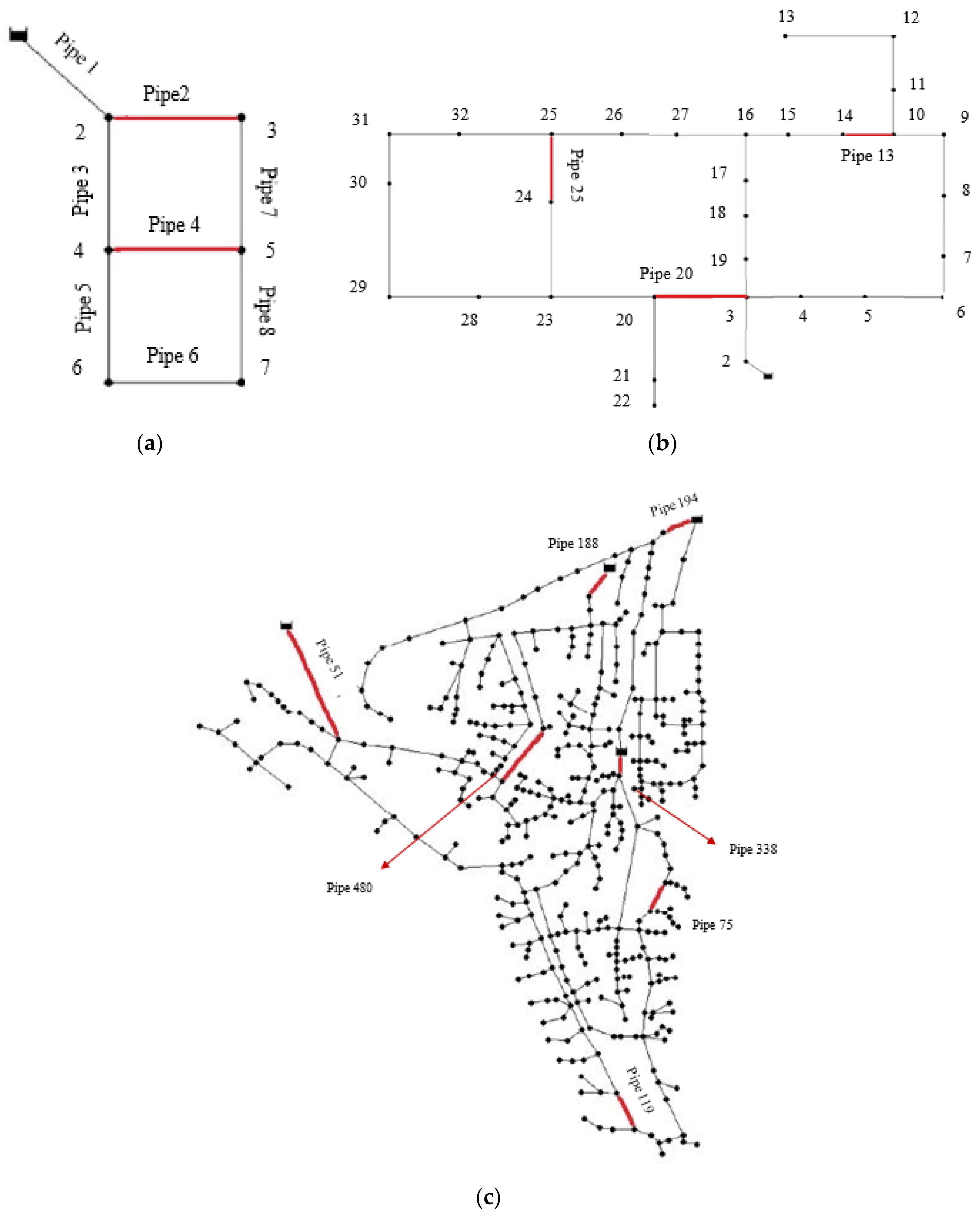
| Pipe ID | 2 | 4 | 20 | 25 | 13 | 51 | 188 | 194 | 338 | 75 | 480 | 119 |
| Length (m) | 1000 | 1000 | 2200 | 1300 | 800 | 2500 | 800 | 354 | 200 | 421 | 1450 | 314 |
| Scenario | Setup |
|---|---|
| 1 | 10% increase in the demands in all nodes; |
| 2 | 30% increase in the demands in 1/3 nodes with the maximum demand; |
| 3 | 30% increase in the demands in 1/3 nodes with the minimum demand; |
| 4 | Pipe failure; |
| 5 | 10% increase in the demands in all nodes + pipe failure; |
| 6 | 30% increase in the demands in 1/3 nodes with the maximum demand + pipe failure; |
| 7 | 30% increase in the demands in 1/3 nodes with the minimum demand + pipe failure. |
| Two-Loop Network | Hanoi Network | Balerma Irr Network | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sol | Cost (×106 USD) | In (-) | Pmin (m) | Sol | Cost (×106 USD) | In (-) | Pmin (m) | Sol | Cost (×106 USD) | In (-) | Pmin (m) |
| 1 | 0.42 | 0.248 | 30.06 | 1 | 6.25 | 0.219 | 30.05 | 1 | 2.05 | 0.408 | 20.02 |
| 2 | 0.46 | 0.351 | 31.51 | 2 | 6.57 | 0.260 | 30.12 | 2 | 2.41 | 0.65 | 20.27 |
| 3 | 0.57 | 0.550 | 35.68 | 3 | 7.18 | 0.300 | 31.65 | 3 | 3.28 | 0.801 | 22.39 |
| 4 | 0.97 | 0.752 | 39.92 | 4 | 8.21 | 0.332 | 42.63 | 4 | 5.72 | 0.896 | 22.81 |
| 5 | 1.25 | 0.800 | 40.50 | 5 | 8.79 | 0.340 | 47.06 | 5 | 10.04 | 0.928 | 22.82 |
| 6 | 1.67 | 0.849 | 41.85 | 6 | 10.70 | 0.352 | 49.66 | 6 | 15.01 | 0.941 | 22.81 |
| 7 | 4.4 | 0.903 | 42.73 | 7 | 20.92 | 0.955 | 22.82 | ||||
| Network | Sol | Average In (-) | Average PR* (-) | Average Pmin (m) | Average DD* (%) | IC (%) |
|---|---|---|---|---|---|---|
| 1 | 0.216 | 0.045 | 28.11 | 2.74 | 36.36 | |
| 2 | 0.251 | 0.075 | 24.73 | 11.49 | 27.27 | |
| 3 | 0.358 | - | 27.96 | - | - | |
| TLN | 4 | 0.658 | - | 34.73 | - | - |
| 5 | 0.716 | - | 35.31 | - | - | |
| 6 | 0.789 | - | 37.05 | - | - | |
| 7 | 0.867 | - | 38.39 | - | - |
| Network | Sol | Average In (-) | Average PR* (-) | Average Pmin (m) | Average DD* (%) | IC (%) |
|---|---|---|---|---|---|---|
| 1 | 0.184 | 0.176 | 20.93 | 18.54 | 60 | |
| 2 | 0.179 | 0.075 | 22.40 | 9.37 | 26.66 | |
| HAN | 3 | 0.199 | 0.055 | 23.68 | 9.59 | 26.66 |
| 4 | 0.214 | 0.067 | 31.26 | 4.21 | 26.66 | |
| 5 | 0.217 | 0.023 | 36.62 | 1.48 | 26.66 | |
| 6 | 0.326 | 0.022 | 36.26 | 1.99 | 6.66 |
| Sol | Scenario | Pipe ID Failure | In | Pmin (m) |
|---|---|---|---|---|
| 188 | - | Infeasible | ||
| 194 | - | Infeasible | ||
| 5 | 480 | 0.947 | 22.78 | |
| 51 | - | Infeasible | ||
| 119 | 0.938 | 22.78 | ||
| 75 | 0.935 | 22.78 | ||
| 338 | - | Infeasible | ||
| 188 | - | Infeasible | ||
| 194 | - | Infeasible | ||
| 7 | 6 | 480 | 0.946 | 22.82 |
| 51 | - | Infeasible | ||
| 119 | 0.949 | 22.82 | ||
| 75 | 0.948 | 22.82 | ||
| 338 | - | Infeasible | ||
| 188 | - | Infeasible | ||
| 194 | - | Infeasible | ||
| 7 | 480 | 0.948 | 22.72 | |
| 51 | - | Infeasible | ||
| 119 | 0.950 | 22.72 | ||
| 75 | 0.949 | 22.72 | ||
| 338 | - | Infeasible |
| Network | Sol | Average In (-) | Average PR* (-) | Average Pmin (m) | Average DD* (%) | IC (%) |
|---|---|---|---|---|---|---|
| 1 | 0.338 | 0.093 | 13.87 | 39.4 | 44.44 | |
| 2 | 0.599 | 0.073 | 17.66 | 9.52 | 44.44 | |
| 3 | 0.774 | 0.167 | 21.94 | - | 44.44 | |
| BIN | 4 | 0.888 | 0.229 | 22.79 | - | 44.44 |
| 5 | 0.918 | 0.222 | 22.78 | - | 44.44 | |
| 6 | 0.935 | 0.237 | 22.78 | - | 44.44 | |
| 7 | 0.948 | 0.237 | 22.78 | - | 44.44 |
| Sol | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Pmax [m] | 75.46 | 93.70 | 104.95 | 110.53 | 111.93 | 112.66 | 113.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuso, F.; Cunha, M.C.; Becciu, G. Functional Feasibility in Optimal Evaluation of Water Distribution Network Performances. Water 2020, 12, 3404. https://doi.org/10.3390/w12123404
Fuso F, Cunha MC, Becciu G. Functional Feasibility in Optimal Evaluation of Water Distribution Network Performances. Water. 2020; 12(12):3404. https://doi.org/10.3390/w12123404
Chicago/Turabian StyleFuso, Flavia, Maria C. Cunha, and Gianfranco Becciu. 2020. "Functional Feasibility in Optimal Evaluation of Water Distribution Network Performances" Water 12, no. 12: 3404. https://doi.org/10.3390/w12123404
APA StyleFuso, F., Cunha, M. C., & Becciu, G. (2020). Functional Feasibility in Optimal Evaluation of Water Distribution Network Performances. Water, 12(12), 3404. https://doi.org/10.3390/w12123404







