1. Introduction
Hydrological models are commonly employed to calculate the hydrological balance of a catchment using various calibration strategies (i.e., diverse objective criteria including various variables, different optimization algorithms, etc.). The applied calibration strategy affects the performance of the hydrological model. The widely used manual (expert) calibration of parameters is strongly influenced by the experience of the hydrologist; it is time-consuming and strongly affects the quality of the calibrated model [
1]. The automatic calibration, on the other hand, is fast and the performance of the model simulations are explicitly linked to the parameter values within the optimization criteria. The automatic calibration of hydrological models typically uses observed runoff time-series to optimize the parameters. This is, however, not possible in catchments with limited observations, especially if gauged stations are not available. In addition, due to equifinality, models of similar (good) performance may result from models with very different parameter sets and therefore not simulate the physical processes properly.
In ungauged catchments, the water balance can be estimated using different methods, e.g., extrapolation of hydrological model parameters [
2], the spatial proximity [
3], estimation of the spatially distributed variables from soils and other geo-spatial datasets [
4], the physical similarity [
5], scaling relationships [
6], regression-based methods [
7], the hydrological similarity [
8] and employing the runoff signatures (indices characterizing hydrologic behavior, [
9]). The methods utilising hydrological signatures can be further divided, according to the prediction methods, into hydrological modelling based methods [
10,
11], and multiple regression methods [
12,
13] including data-driven methods such as genetic programming [
14,
15] and hydrological similarity based approaches [
16].
Recently, a number of studies pointed out that relying solely on calibration of hydrological models with respect to observed runoff may result in inappropriate representation of hydrological processes and highlighted the importance of expert knowledge [
17,
18] and/or multi-objective calibration [
19].
One approach to constrain the calibration of the hydrological model is to consider hydrological signatures (typically some long-term statistics of runoff, soil moisture, snow regime). They are derived from observed or simulated time series [
20] with a purpose to supplement catchment information [
21], to evaluate model performance [
22] or to refine calibration techniques [
23]. The selection of signatures should consider their identifiability, robustness, consistency, representativeness and discriminatory power [
20].
Different processes contributing to resulting hydrograph can be also accounted for by the segmentation of the flow duration curve (FDC) within calibration of the hydrological model [
4,
24]. For instance, it has been shown that fair balance between very high and very low flows can be achieved using five segments of the FDC (Q2–Q5, Q5–Q20, Q20–Q70, Q70–Q95, Q95) and evaluating the performance for each segment and combining it into single objective function [
25].
In this paper, we explore the role of hydrological signatures within calibration of the hydrological model. Specifically, we like to answer following questions: To what extent do hydrological signatures improve calibration of conceptual hydrological model? Is calibration of conceptual hydrological model possible considering hydrological signatures only? A hydrological model Bilan is used to determine the hydrological balance for 20 gauged catchments in the Czech Republic utilizing four different calibration strategies: (1) expert calibration, (2) standard automatic calibration, (3) the standard automatic calibration considering hydrological signatures together with runoff and soil moisture time series, and (4) hydrological signatures only. The objectives of this study are to (i) evaluate the performance of different calibration strategies, (ii) assess the added value of hydrological signatures and soil moisture estimates, and (iii) determine to what extent are the time series data necessary when modelling hydrological balance.
This paper is structured as follows:
Section 2 introduces the area of interest and input data. The hydrological model Bilan, four calibration strategies and model evaluation are described in
Section 3. Results and discussion are presented in
Section 4 and
Section 5 together with a detailed assessment of the calibration strategies with respect to goodness-of-fit (GOF), uncertainty of Bilan model parameters (BP), and runoff signatures (RS). The paper is concluded in
Section 5.
2. Study Area and Data
The 20 considered catchments are located in the Czech Republic, where long-term mean precipitation for the 1981–2010 (climatological reference period for Czech Republic) period is 709.5 mm, mean annual temperature is 7.9 °C and mean runoff is 205.5 mm [
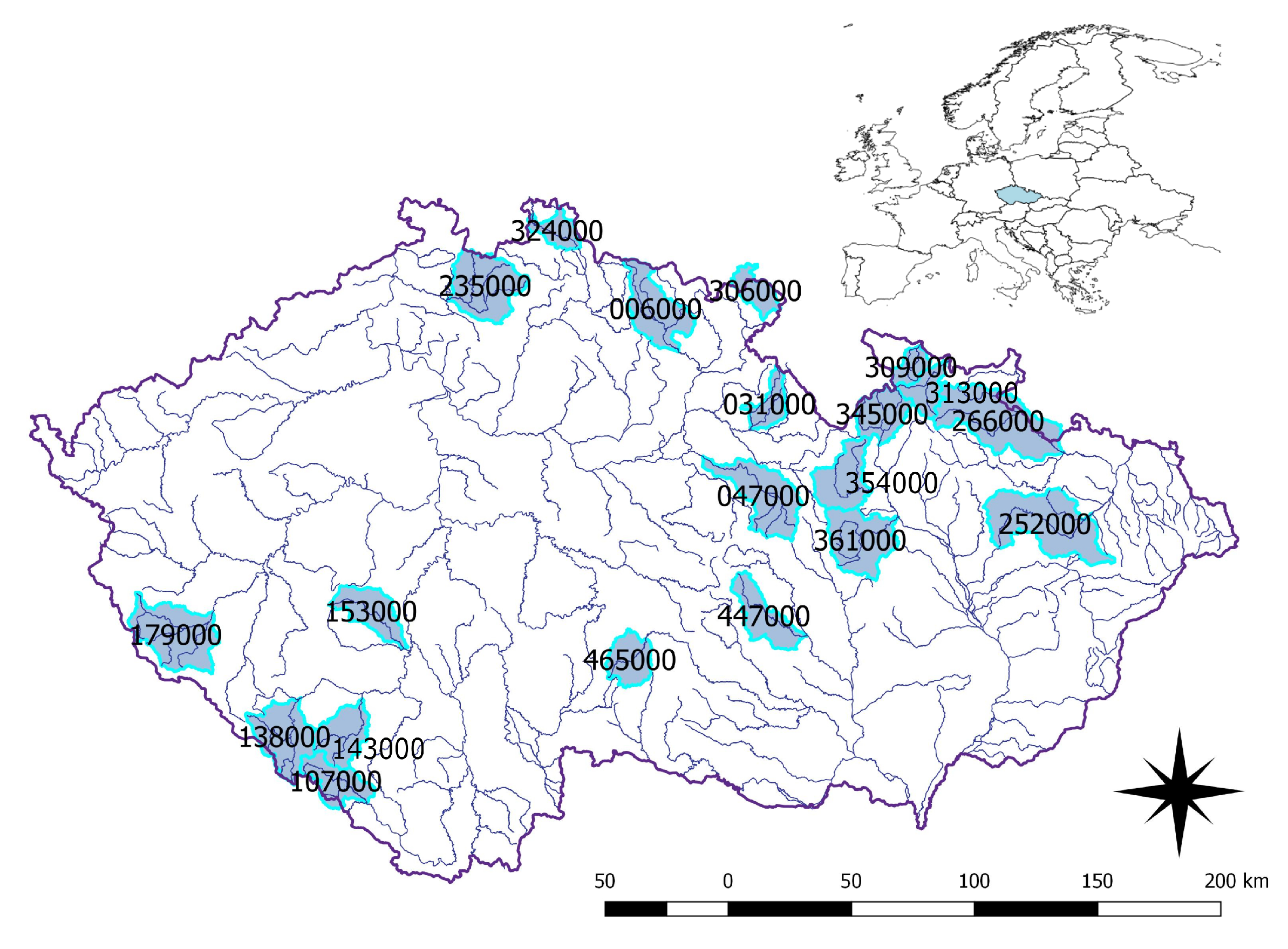
26]. The selected catchments are shown in
Figure 1, with the numbers referring to catchment IDs. The majority of the catchments is located in the northern part of the territory (235000-Ploučnice, 324000-Smědá, 006000-Labe, 306000-Stěnava, 031000-Bělá-Častolovice, 309000-Vidnávka, 313000-Bělá-Mikulovice, 266000-Opava, 354000-Moravská Sázava, the others extend into the central part (047000-Loučná, 361000-Trebůvka, 252000-Odra, 447000-Loučka) and southern part of the territory (179000-Radbuza, 153000-Skalice, 143000-Volyňka, 138000-Otava, 107000-Teplá Vltava). Only catchments with freely available data (in the time of preparation of this study) without significant anthropogenic influence were selected. For selected catchments, mean annual precipitation is 792.5 mm, mean temperature is 7.3 °C, average annual soil water storage is 997.1 mm and mean annual runoff is 318.8 mm. The catchment areas range from 348 to 932
, with a mean size of 454
.
Monthly time series of temperature (°C), precipitation (mm) and observed runoff (mm) were provided for each catchment by the Czech Hydrometeorological Institute and the soil moisture estimates (mm) by the Global Change Research Institute of the Czech Academy of Sciences. The soil moisture estimates are based on the simulation of the SoilClim model—a model for water balance and the hydric and thermic soil regime assessment [
27].
3. Methods
The hydrological model Bilan was used for the assessment of water balance in 20 catchments (
Figure 1) considering four calibration strategies: expert calibration, standard automatic calibration, calibration considering runoff and soil moisture time series in combination with hydrological signatures, and calibration with hydrological signatures only. The resulting parameter sets were then evaluated with respect to: (i) goodness-of-fit between observed and simulated runoff (GOF, hydroGOF [
28]), (ii) uncertainty of the Bilan model parameters and (BP) (iii) selected runoff and soil moisture signatures (RS). This section introduces the model, the calibrations strategies and the evaluation metrics.
3.1. Bilan Hydrological Model
The hydrological model Bilan [
29,
30] is a conceptual rainfall-runoff model that is used for water balance assessment in the Czech Republic. For partly or fully conceptual models, some parameters cannot be considered as physically measured (or measurable) quantities and thus have to be estimated on the basis of the available data and information [
31]. The structure of the model is formed by a number of storage components and a set of their relationships based on basic principles of water balance as well as simple mathematical concepts such as linear reservoir. This structure is similar to a well-known hydrology model HBV (Hydrologiska Byråns Vattenbalansavdelning model) [
32]. The water balance in model Bilan is described in three zones: on the ground, in the aeration zone, including vegetation cover, and in the groundwater [
33].
The input variables are described in
Table 1, in our case we used the input variable precipitation (
P (mm)), air temperature (
T (°C)) and optional time-series-soil water (mm)). In the model are individual components divided as input data, water balance component, and resulting parameters. The monthly type used algorithms depend on the condition of the particular month. Used mean monthly temperature as well as in the daily type the model distinguish the winter and summer conditional. In the monthly regime the total runoff (
(mm)) is calculated as a sum of direct runoff (
), interflow (
I), and baseflow (
) [
30].
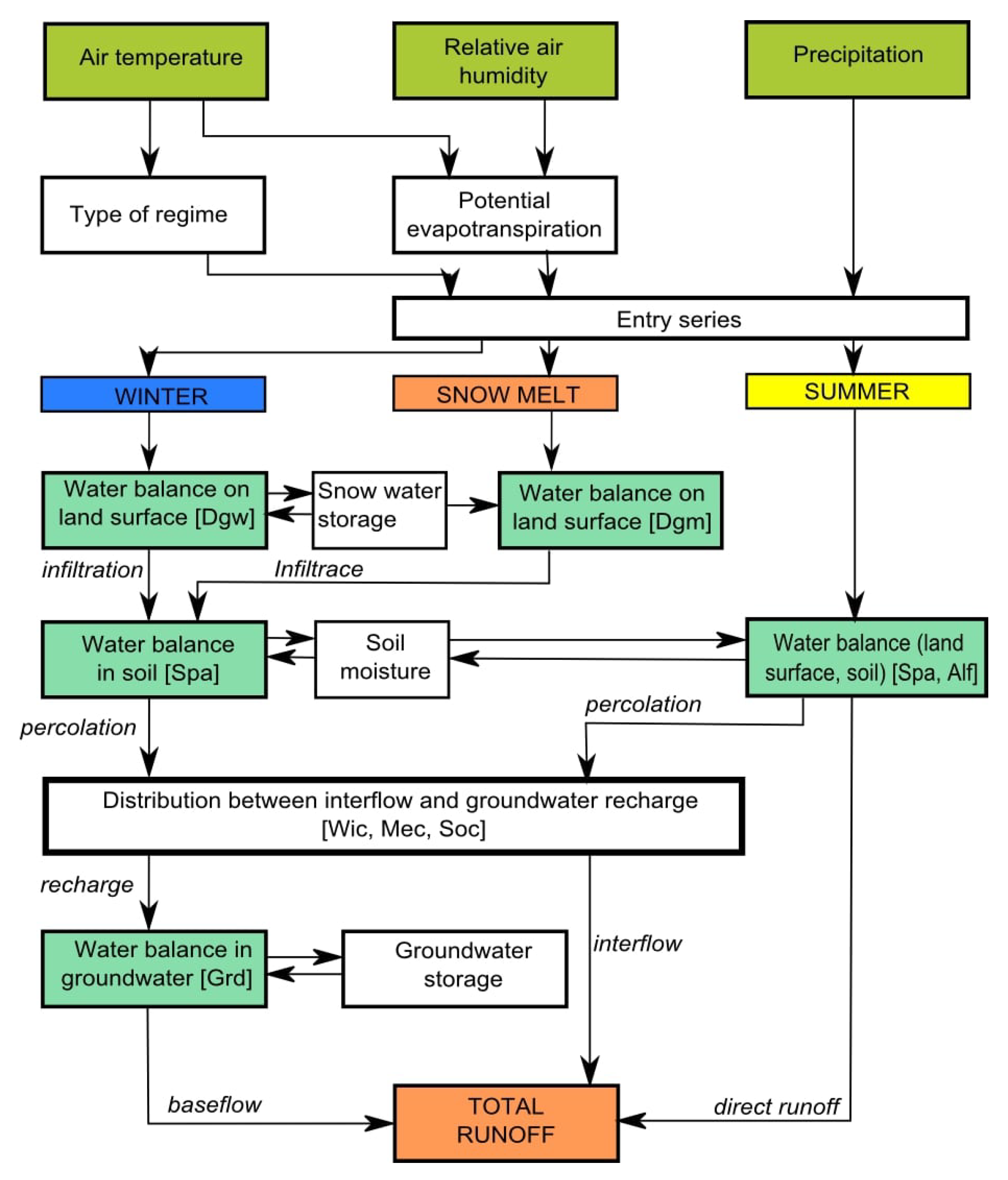
The model is shown in
Figure 2 displaying input data, simulated storages and fluxes. See [
34,
35,
36,
37] for further details. The parameters of the model are identified (calibrated) using shuffled complex evolution (SCE-UA), Ref. [
38] in combination with the differential evolution (DE) method [
39]. The algorithm is stochastic and therefore allows for assessment of the uncertainty in the model parameters by repeated calibration. The standard calibration involves minimization of the error in simulated runoff in comparison to observed runoff represented by the value of the selected objective function (OF). However, the model also allows for widening the OF to consider also time series of other variables (typically soil moisture or baseflow estimates) or even individual hydrological signatures such as mean or variance of runoff, indicators of extremes etc.
3.2. Calibration Strategies
The purpose of testing the four calibration strategies was to find such calibration setup that would minimize the bias in simulated water balance and the uncertainty in the estimated model parameters. In addition, while the first three calibration strategies (expert, standard automatic, time series with hydrological signatures) require time series of observed runoff, the fourth (calibration with hydrological signatures) can also be applied at ungauged catchments since the hydrological signatures can often be successfully interpolated from available data or estimated from general formulas.
The available time period (1981–2016) was split into calibration (1981–1998) and validation (1999–2016) period, the former being used for the identification of model parameters and the latter for the evaluation of model performance. Since the stochastic optimization algorithm implemented in the Bilan model allows for the assessment of parameter uncertainty, we fitted the model 15 times for all calibration strategies except for the expert calibration for which only the “best” parameter set was provided.
3.2.1. Expert Calibration
This strategy builds upon knowledge of the catchments and experience with hydrological modelling and is frequently applied in the case of studies for individual catchments over the Czech Republic. Typically, the expert constrains the optimization ranges of model parameters and then runs the optimization procedure. In this perspective, this calibration strategy does not always result in the best possible match between observed and simulated runoff, but at the same time, it ensures that all water balance components have reasonable values and respect physical conditions of the catchments. Therefore throughout the paper, we take these results as a reference. The parameter sets considered here were provided by experts from T. G. Masaryk Water Research Institute (developer of the Bilan model).
3.2.2. Standard Automatic Calibration
The standard automatic calibration, uses differential evolution to minimize the error between time series of observed and simulated runoff. The advantage of the automatic calibration is that it is faster than manual calibration and can be applied over large sets of catchments. It often also results in a better match between observed and simulated runoff than the manual calibration. The downside of the automatic calibration is that for some catchments the simulated water balance (and/or model parameters) may not be realistic resulting in, e.g., excessive ground water or soil water accumulation, unrealistic snow cover, etc.
3.2.3. Calibration with Hydrological Signatures
The last two calibration strategies involve hydrological signatures either in combination with runoff and/or soil moisture time series or as the only component of the objective function (OF). Model calibration was performed in 15 iterations. As the hydrological signatures, we used mean, standard deviation and interquartile range of runoff and soil moisture. The difference between the time series in the OFs was represented by mean percent bias, the match between the hydrological signatures by relative percent difference. The individual components of the OFs were summed to result in a single value. In this paper we considered 52 OFs as given in
Table A1. More than a half of the OFs uses only signatures.
The OFs can be split into six groups:
Single-component OFs with runoff (R);
Single-component OFs with soil moisture (SW);
Two-component OFs with runoff (R2);
Two-component OFs with soil moisture (SW2);
Two-component OFs with runoff and soil moisture (RSW);
Three-component OFs (RSW2).
The specific combinations of variables, time series and signatures is clear from
Table A1.
The aim of the introduction of hydrological signatures and/or soil moisture time series is to constrain the uncertainty in model parameters experienced with the automatic calibration and to test whether reasonable runoff simulation can be obtained without observed runoff time series.
3.3. Model Evaluation
The performance of each calibrated parameter set was evaluated with respect to the results of the expert calibration. This means that we like to evaluate to what extent we are able to obtain results close to the expert calibration but with limited information (and without expert knowledge). The parameter sets were evaluated considering:
- (a)
Goodness-of-fit expressed (GOF) as the root mean square error (RMSE; [
40]) and Kling–Gupta efficiency (KGE; [
41]) of the simulated runoff with respect to runoff simulated by the parameter set resulting from the expert calibration (further denoted as the expert simulation).
The RMSE is given by
where
is expert simulation for
i-th case,
the average of the expert simulation and
N is the total number of simulated values. It was used as standard statistical metric, that gives a relatively high weight to large errors.
The KGE is calculated according to
where
s is numeric weight vector of length 3 (here with all elements equal to 1), which combines the Pearson product-moment correlation coefficient (
r), the ratio between the standard deviations (
) and the ratio between the mean of the expert simulation and simulation calibrated with particular OF (
).
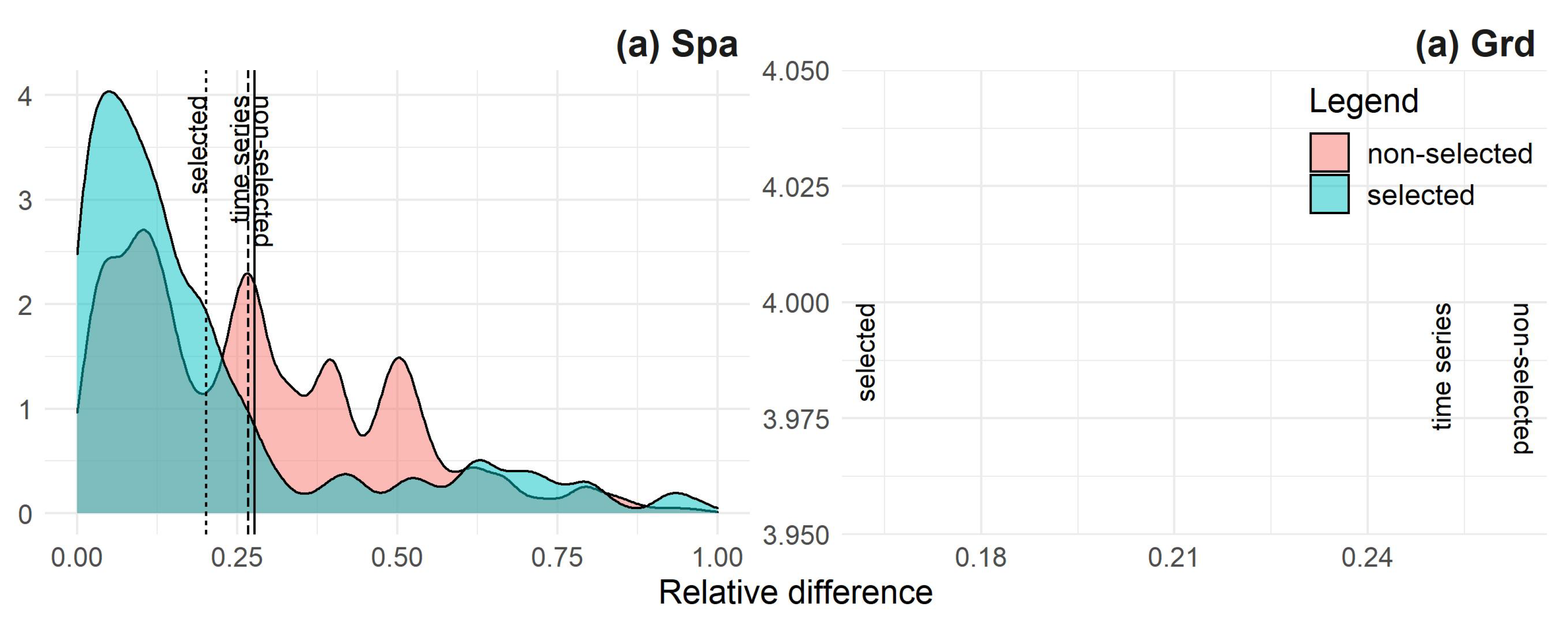
- (b)
difference in the distribution of Bilan model parameters (BP) Spa (controlling soil depth) and Grd (controlling baseflow) between expert-calibrated parameters (see
Section 3.2) and calibration with particular OF.
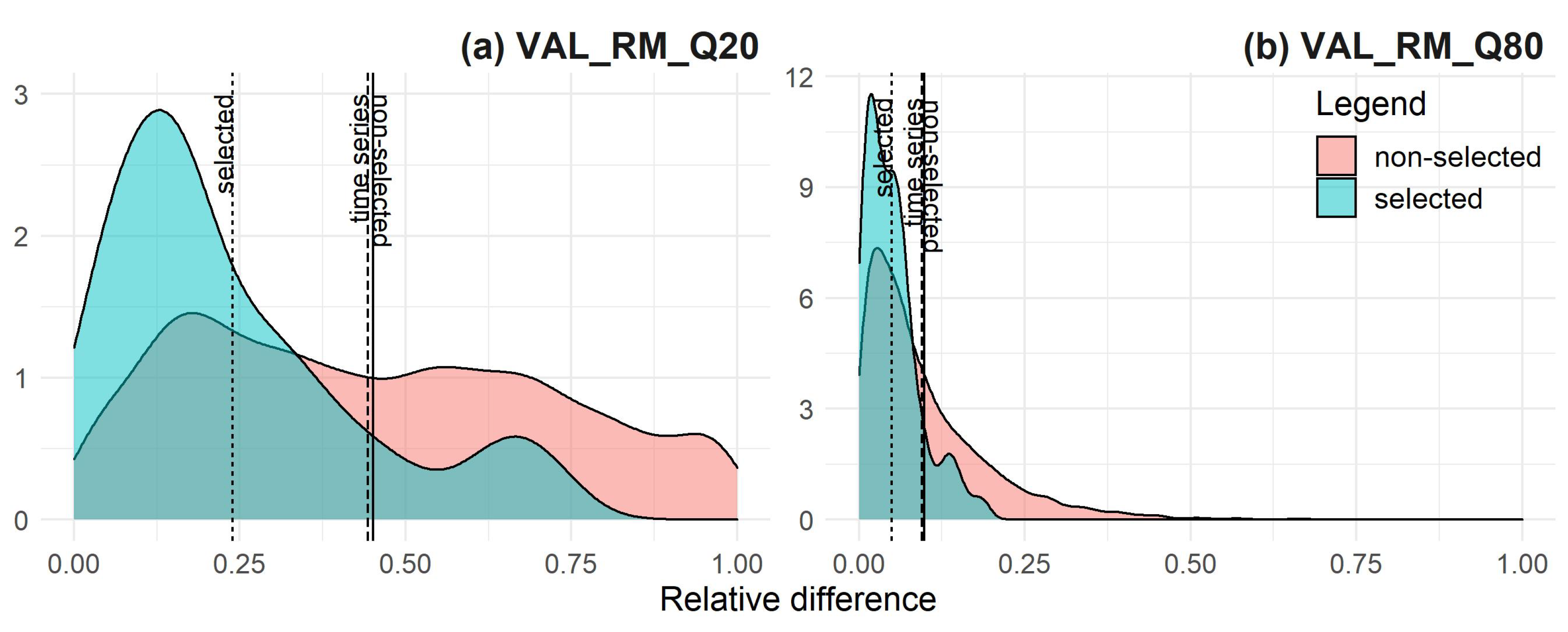
- (c)
relative difference in mean and the 20th (Q20) and 80th (Q80) percentile of runoff and soil moisture from the expert simulation with respect to the same signatures from the simulation calibrated with particular OF.
The relative differences are preferred here over the absolute in order to allow for comparison between catchments. To assess the performance of different calibration strategies, we subsequently ranked the results of individual strategies, according to the criteria above, for each catchment. The calibration strategies with the overall best performance were further evaluated separately as well-denoted selected characteristics.