CliGAN: A Structurally Sensitive Convolutional Neural Network Model for Statistical Downscaling of Precipitation from Multi-Model Ensembles
Abstract
:1. Introduction
- Develop a methodology to downscale large-scale precipitation, given by several AOGCMs, to regional-scale precipitation by statistical downscaling using convolution neural network and generative adversarial training.
- Propose a novel loss function which is a combination of content loss, structural loss, and adversarial loss, which improves the prediction of global and regional qualities of the downscaled precipitation.
2. Methods
2.1. Study Area and Datasets
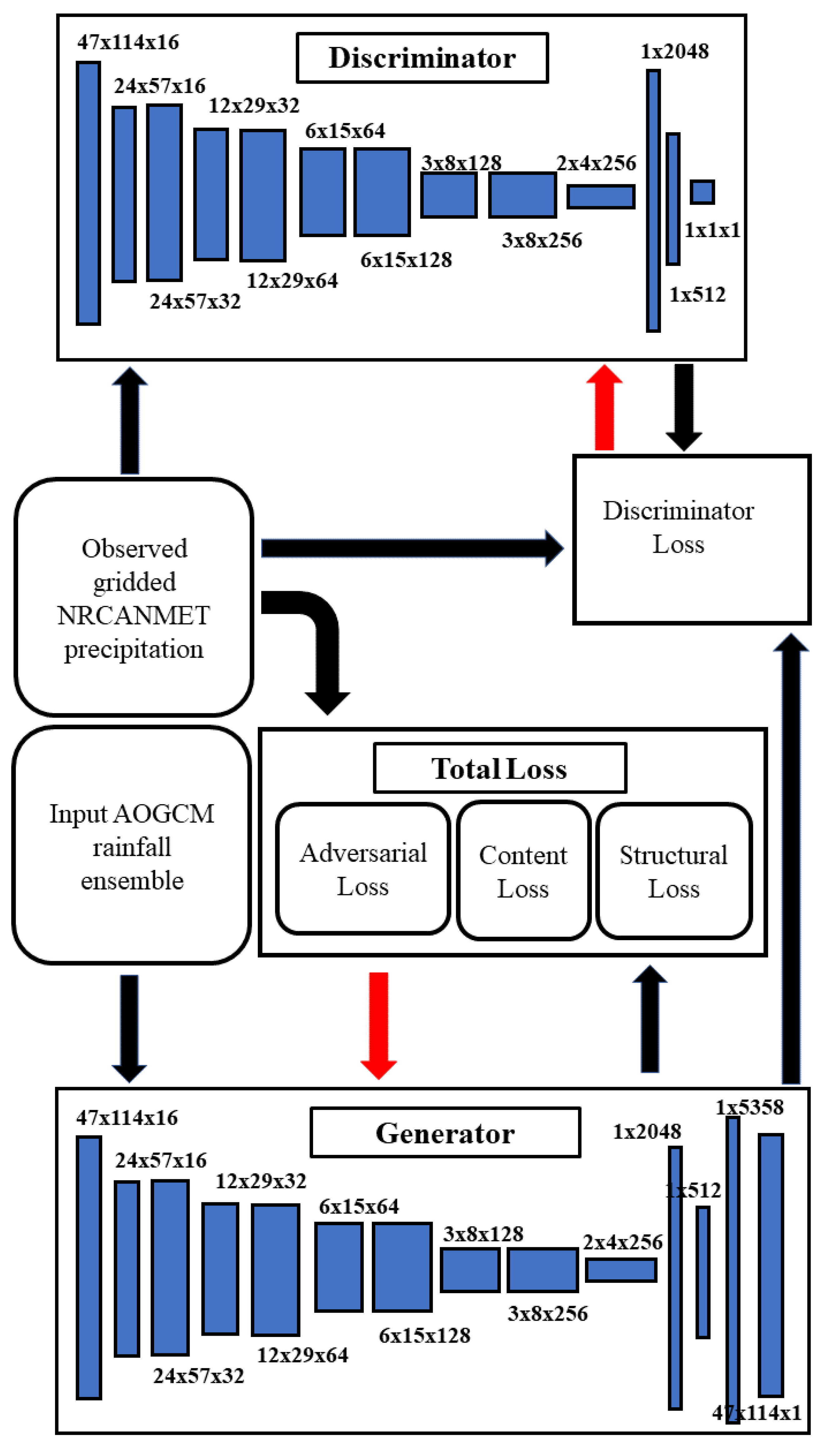
2.2. Downscaling Method
2.2.1. Adversarial Training
2.2.2. Downscaling Total Loss
2.2.3. Networks
2.2.4. Training Details
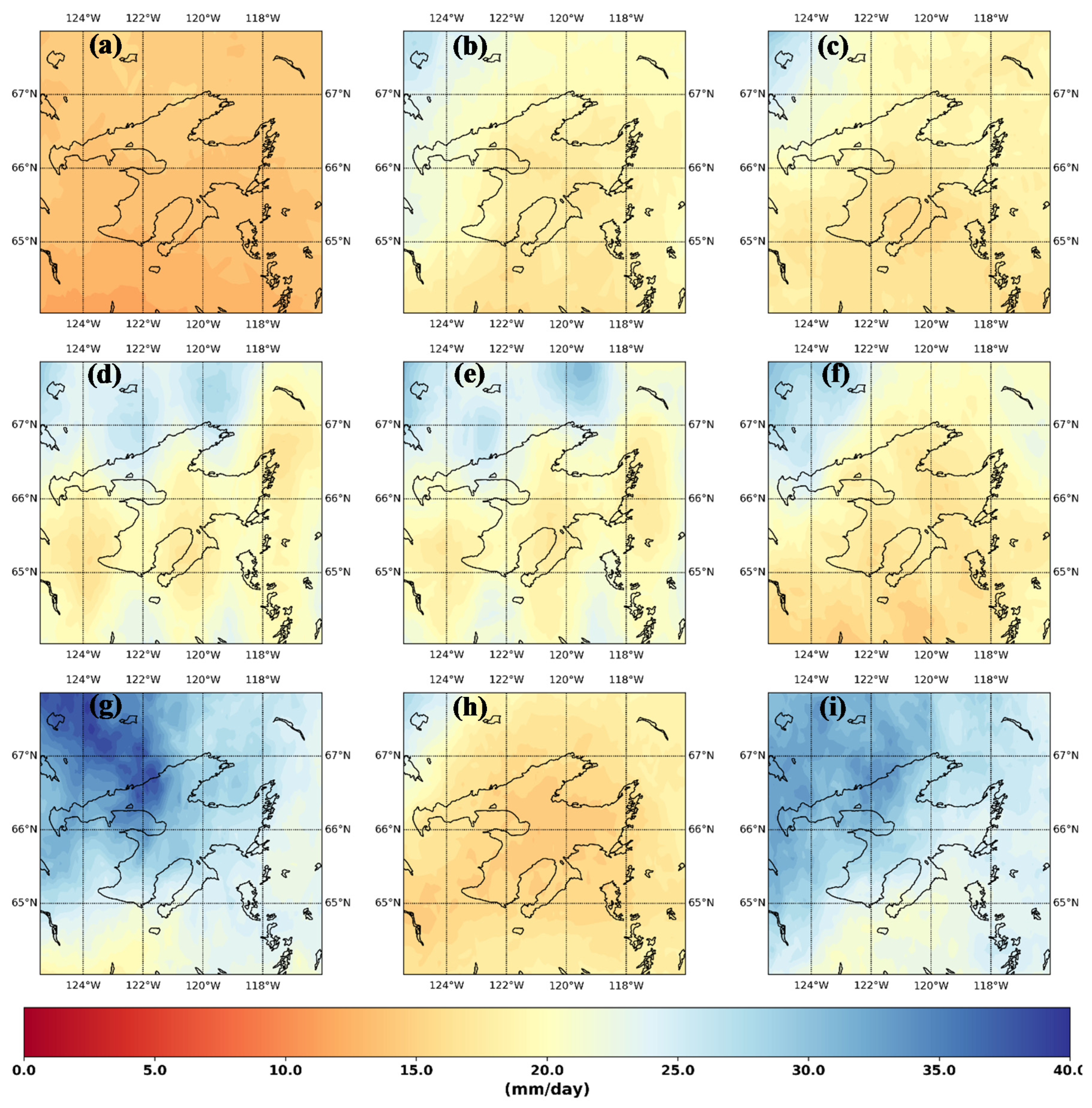
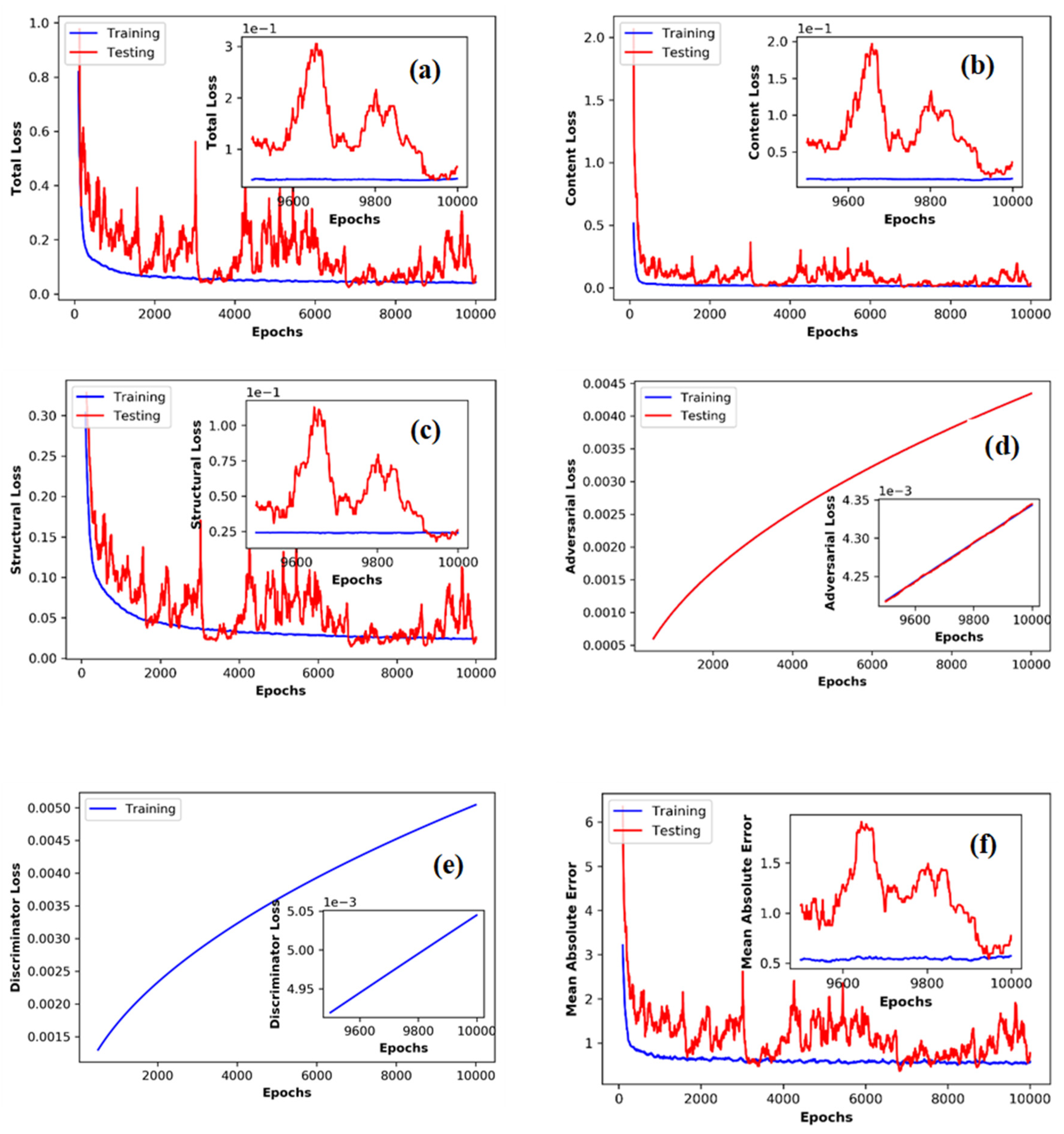
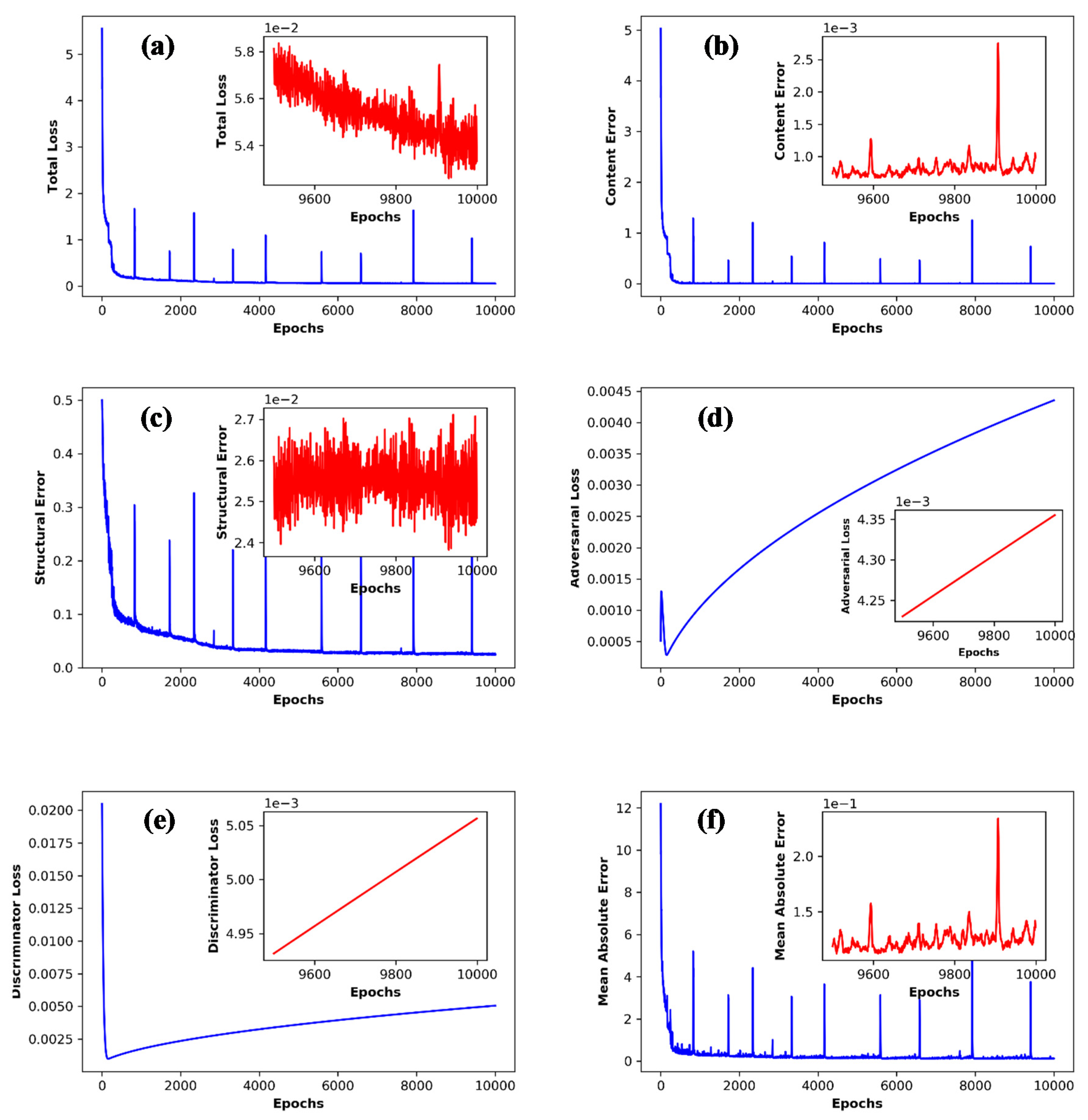
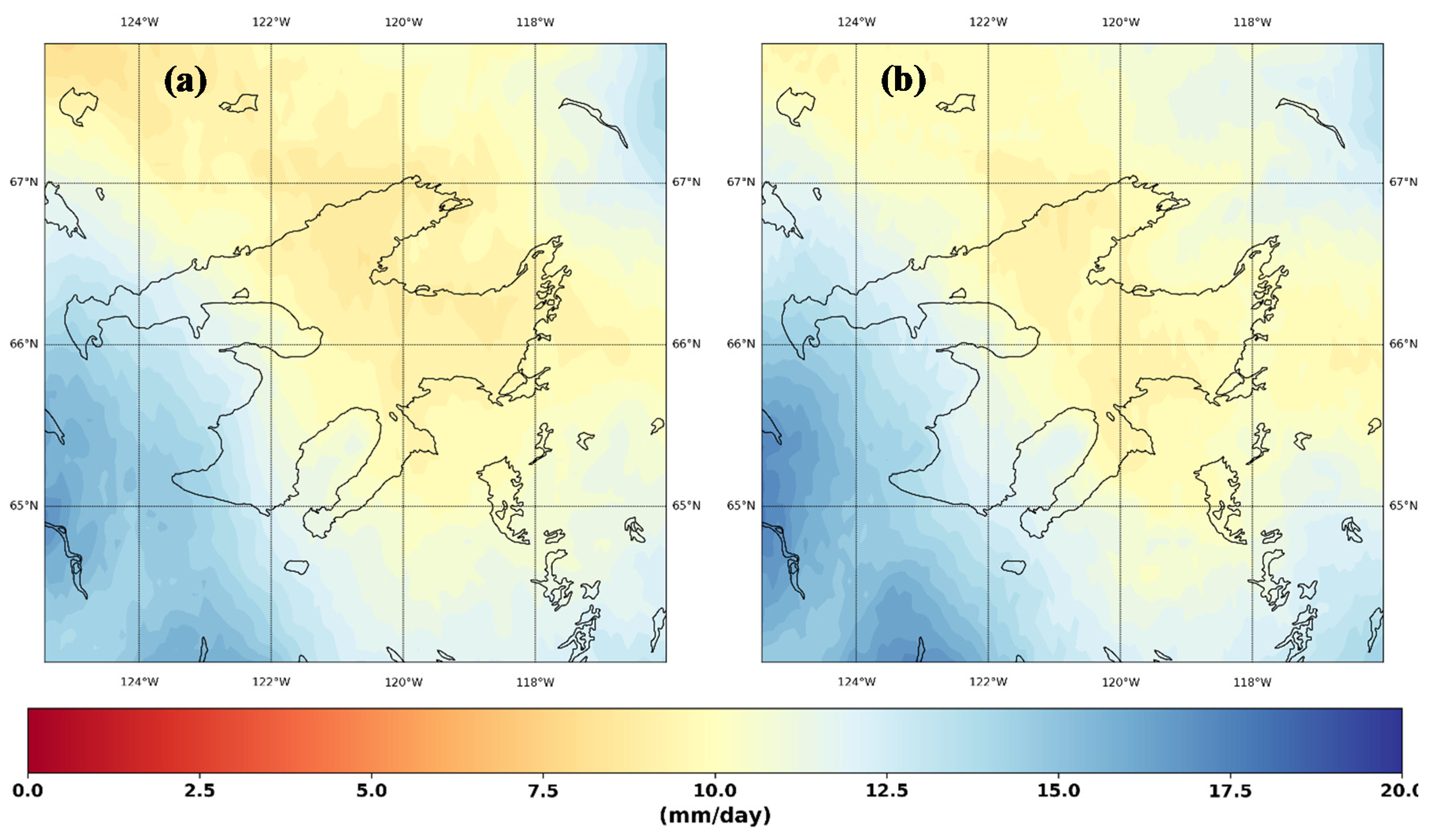
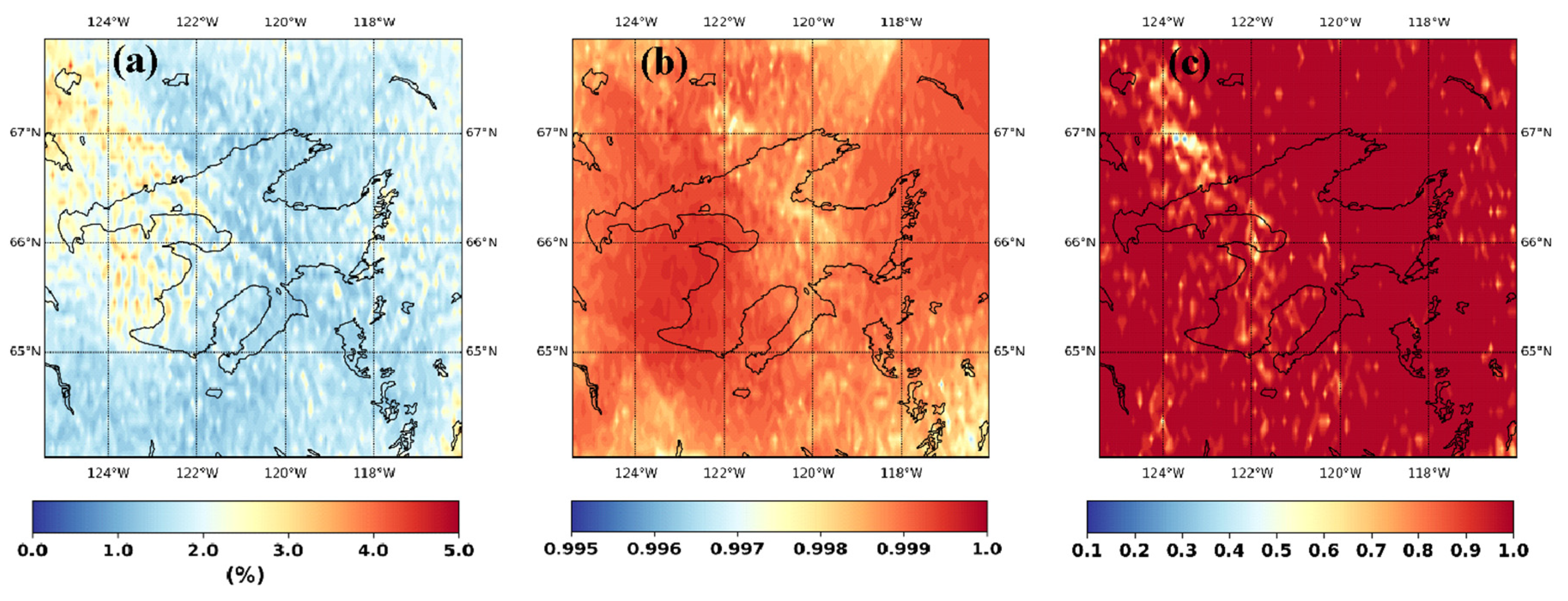
3. Results and Discussion
4. Conclusions
- Our framework can utilize diverse information present in different AOGCM simulations to create a spatially coherent field similar to observational data. The approach is similar in spirit to reliability ensemble averaging (REA) proposed by [75], within a CNN and adversarial training context.
- The MSSIM index allowed us to get an insight into the model’s regional characteristics and suggest relying solely on point-based error functions that are widely used in statistical downscaling and may not be enough to simulate regional characteristics of precipitation variables reliably.
- Further use of total loss function, which is a combination of adversarial, content, and structural loss within a CNN-based downscaling method, may lead to higher quality downscaled products.
- The adversarial loss can provide a meaningful gradient to weight optimization when traditional loss functions fail in near convergence variabilities.
Author Contributions
Funding
Conflicts of Interest
Availability of Data and Material
Code Availability
References
- Tryhorn, L.; DeGaetano, A. A comparison of techniques for downscaling extreme precipitation over the Northeastern United States. Int. J. Clim. 2011, 31, 1975–1989. [Google Scholar] [CrossRef]
- Chaudhuri, C.; Srivastava, R.; Srivastava, R. A novel approach for statistical downscaling of future precipitation over the Indo-Gangetic Basin. J. Hydrol. 2017, 547, 21–38. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.; Woo, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Plouffe, C.C.; Robertson, C.; Chandrapala, L. Comparing interpolation techniques for monthly rainfall mapping using multiple evaluation criteria and auxiliary data sources: A case study of Sri Lanka. Environ. Model. Softw. 2015, 67, 57–71. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK, 2007; 976p. [Google Scholar]
- Prudhomme, C.; Jakob, D.; Svensson, C. Uncertainty and climate change impact on the flood regime of small uk catchments. J. Hydrol. 2003, 277, 1–23. [Google Scholar] [CrossRef]
- Smith, R.L.; Tebaldi, C.; Nychka, D.; Mearns, L.O. Bayesian modeling of uncertainty in ensembles of climate models. J. Am. Stat. Assoc. 2009, 104, 97–116. [Google Scholar] [CrossRef]
- Randall, D.; Wood, R.; Bony, S.; Colman, R.; Fichefet, T.; Fyfe, J.; Kattsov, V.; Pitman, A.; Shukla, J.; Srinivasan, J.; et al. Cilmate models and their evaluation. In Climate Change 2007: The Physical Science Basis, in Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K., Tignor, M., Miller, H., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Hughes, J.P.; Guttorp, P. A class of stochastic models for relating synoptic atmospheric patterns to regional hydrologic phenomena. Water Resour. Res. 1994, 30, 1535–1546. [Google Scholar] [CrossRef]
- Widmann, M.; Bretherton, C.S.; Salathé, E.P., Jr. Statistical precipitation downscaling over the north-western united states using numerically simulated precipitation as a predictor. J. Clim. 2003, 16, 799–816. [Google Scholar] [CrossRef]
- Knutti, R.; Furrer, R.; Tebaldi, C.; Cermak, J.; Meehl, G.A. Challenges in Combining Projections from Multiple Climate Models. J. Clim. 2010, 23, 2739–2758. [Google Scholar] [CrossRef] [Green Version]
- Trigo, R.M.; Palutikof, J.P. Precipitation scenarios over iberia: A comparison between direct gcm output and different downscaling techniques. J. Clim. 2001, 14, 4422–4446. [Google Scholar] [CrossRef]
- Brissette, F.; Khalili, M.; Leconte, R. Efficient stochastic generation of multisite synthetic precipitation data. J. Hydrol. 2007, 345, 121–133. [Google Scholar] [CrossRef]
- Maurer, E.P. Uncertainty in hydrologic impacts of climate change in the Sierra Nevada, California under two emissions scenarios. Clim. Chang. 2007, 82, 309–325. [Google Scholar] [CrossRef] [Green Version]
- Trzaska, S.; Schnarr, E. A Review of Downscaling Methods for Climate Change Projections; CIESIN, the Center for International Earth Science Information Network, Columbia University, Based at Columbia’s Lamont campus in Palisades: New York, NY, USA, 2014. [Google Scholar]
- Maraun, D.; Wetterhall, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48, RG3003. [Google Scholar] [CrossRef]
- Hewitson, B.; Crane, R.G. Crane Regional-scale climate prediction from the GISS GCM. Palaeogeogr. Palaeoclim. Palaeoecol. 1992, 97, 249–267. [Google Scholar] [CrossRef]
- Dibike, Y.B.; Coulibaly, P. Hydrologic impact of climate change in the Saguenay watershed: Comparison of downscaling methods and hydrologic models. J. Hydrol. 2005, 307, 145–163. [Google Scholar] [CrossRef]
- Murphy, J.M.; Sexton, D.; Barnett, D.N.; Jones, G.S.; Webb, M.J.; Collins, M.; Stainforth, D.A. Quantifying uncertainties in climate change from a large ensemble of general circulation model predictions. Nature 2004, 430, 768–772. [Google Scholar] [CrossRef]
- Wilby, R.L.; Harris, I. A framework for assessing uncertainties in climate change impacts: Low-flow scenarios for the river thames, UK. Water Resour. Res. 2006, 42, W02419. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B. Mixtures of stochastic processes: Applications to statistical downscaling. Clim. Res. 1996, 7, 185–193. [Google Scholar] [CrossRef] [Green Version]
- Richardson, C.W. Stochastic simulation of daily precipitation, temperature, and solar radiation. Water Resour. Res. 1981, 17, 182–190. [Google Scholar] [CrossRef]
- Kuchar, L. Using wgenk to generate synthetic daily weather data for modelling of agricultural processes. Math. Comput. Simul. 2004, 17, 69–75. [Google Scholar] [CrossRef]
- Schoof, J.T.; Arguez, A.; Brolley, J.; O’Brien, J. A new weather generator based on spectral properties of surface air temperatures. Agric. For. Meteorol. 2005, 135, 241–251. [Google Scholar] [CrossRef]
- Hanson, C.L.; Johnson, G.L. Gem (generation of weather elements for multiple applications): Its application in areas of complex terrain. Hydrol. Water Resour. Ecol. Headwaters 1998, 248, 27–32. [Google Scholar]
- Soltani, A.; Hoogenboom, G. A statistical comparison of the stochastic weather generators wgen and simmeteo. Clim. Res. 2003, 24, 215–230. [Google Scholar] [CrossRef] [Green Version]
- Semenov, M.A.; Barrow, E.M. Use of a stochastic weather generator in the development of climate change scenarios. Clim. Chang. 1997, 35, 397–414. [Google Scholar] [CrossRef]
- Wilks, D.S.; Wilby, R.L. The weather generation game: A review of stochastic weather models. Prog. Phys. Geogr. 1999, 23, 329–357. [Google Scholar] [CrossRef]
- Sharif, M.; Burn, D.H. Simulating climate change scenarios using an improved k-nearest neighbor model. J. Hydrol. 2006, 325, 179–196. [Google Scholar] [CrossRef]
- Brandsma, T.; Buishand, T.A. Buishand Simulation of extreme precipitation in the rhine basin by nearest-neighbour resampling. Hydrol. Earth Syst. Sci. 1998, 325, 195–209. [Google Scholar] [CrossRef]
- Yates, D.; Gangopadhyay, S.; Rajagopalan, B.; Strzepek, K. A technique for generating regional climate scenarios using a nearest-neighbour algorithm. Water Resour. Res. 2003, 39, 1199–1213. [Google Scholar] [CrossRef] [Green Version]
- Brown, B.G.; Katz, R.W. Regional analysis of temperature extremes: Spatial analog for climate change? J. Clim. 1995, 8, 108–119. [Google Scholar] [CrossRef] [Green Version]
- Crane, R.G.; Hewitson, B.C. Doubled co2 precipitation changes for the susquehanna basin: Down-scaling from the genesis general circulation model. Int. J. Climatol. 1998, 18, 65–76. [Google Scholar] [CrossRef]
- Cannon, A.J.; Whitfield, P.H. Downscaling recent streamflow conditions in British Columbia. Canada using ensemble neural network models. J. Hydrol. 2020, 259, 136–151. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dawson, C.; Barrow, E. Sdsm—A decision support tool for the assessment of regional climate change impacts. Environ. Model. Softw. 2002, 17, 147–159. [Google Scholar] [CrossRef]
- Tripathi, S.; Srinivas, V.V.; Nanjundiah, R.S. Downscaling of precipitation for climate change scenarios: A support vector machine approach. J. Hydrol. 2006, 330, 621–640. [Google Scholar] [CrossRef]
- Zorita, E.; von Storch, H. The analog method—A simple statistical downscaling technique: Comparison with more complicated methods. J. Clim. 1999, 12, 2474–2489. [Google Scholar] [CrossRef]
- Wilby, R.L.; Hassan, H.; Hanaki, K. Statistical downscaling of hydrometeorological variables using general circulation model output. J. Hydrol. 1998, 205, 1–19. [Google Scholar] [CrossRef]
- Gutierrez, J.M.; Cofiño, A.S.; Cano, R.; Rodríguez, M.A. Clustering methods for statistical downscaling in short-range weather forecasts. Mon. Weather Rev. 2004, 132, 2169–2183. [Google Scholar] [CrossRef]
- Haylock, M.R.; Cawley, G.C.; Harpham, C.; Wilby, R.L.; Goodess, C.M. Downscaling heavy precipitation over the United Kingdom: A comparison of dynamical and statistical methods and their future scenarios. Int. J. Climatol. 2006, 26, 1397–1415. [Google Scholar] [CrossRef]
- Anh, D.T.; Van, S.P.; Dang, T.D.; Hoang, L.P. Downscaling rainfall using deep learning long short-term memory and feedforward neural network. Int. J. Clim. 2019, 39, 4170–4188. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. In The Handbook of Brain Theory and Neural Networks; Arbib, M.A., Ed.; MIT Press: Cambridge, MA, USA, 1998; pp. 255–258. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems, Proceedings of the 25th International Conference on Neural Information Processing Systems—Volume 1; ACM: New York, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Wang, Q.; Yuan, Z.; Du, Q.; Li, X. GETNET: A General End-to-End 2-D CNN Framework for Hyperspectral Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8692. [Google Scholar]
- Hashmi, M.Z.; Shamseldin, A.Y.; Melville, B.W. Statistical downscaling of precipitation: State-of-the-art and application of bayesian multi-model approach for uncertainty assessment. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 6535–6579. [Google Scholar] [CrossRef]
- Benestad, R.E. Downscaling precipitation extremes. Theor. Appl. Clim. 2010, 100, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: San Diego, CA, USA, 1995; 467p. [Google Scholar]
- Sungkawa, I.; Rahayu, A. Extreme Rainfall Prediction using Bayesian Quantile Regression in Statistical Downscaling Modeling. Procedia Comput. Sci. 2019, 157, 406–413. [Google Scholar] [CrossRef]
- Zorzetto, E.; Marani, M. Extreme value metastatistical analysis of remotely sensed rainfall in ungauged areas: Spatial downscaling and error modelling. Adv. Water Resour. 2020, 135, 103483. [Google Scholar] [CrossRef]
- Vandal, T.; Kodra, E.; Ganguly, S.; Michaelis, A.; Nemani, R.; Ganguly, A.R. Deepsd: Generating high resolution climate change projections through single image super-resolution. In Proceedings of the 23rd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1663–1672. [Google Scholar]
- Cheng, J.; Kuang, Q.; Shen, C.; Liu, J.; Tan, X.; Liu, W. ResLap: Generating High-Resolution Climate Prediction through Image Super-Resolution. IEEE Access 2020, 8, 39623–39634. [Google Scholar] [CrossRef]
- Onishi, R.; Sugiyama, D.; Matsuda, K. Super-Resolution Simulation for Real-Time Prediction of Urban Micrometeorology. SOLA 2019, 15, 178–182. [Google Scholar] [CrossRef] [Green Version]
- Ji, Y.; Zhi, X.; Tian, Y.; Peng, T.; Huo, Z.; Ji, L. Downscaling of Precipitation Forecasts Based on Single Image Super-Resolution. In EGU General Assembly EGU General Assembly Conference Abstracts; EGU2020-8533; European Geophysical Union General Assembly: Vienna, Austria, 2020. [Google Scholar] [CrossRef]
- Niu, B.; Wen, W.; Ren, W.; Zhang, X.; Yang, L.; Wang, S.; Zhang, K.; Cao, X.; Shen, H. Single Image Super-Resolution via a Holistic Attention Network. arXiv 2020, arXiv:2008.08767. [Google Scholar]
- Ai, W.; Tu, X.; Cheng, S.; Xie, M. Single Image Super-Resolution via Residual Neuron Attention Networks. arXiv 2020, arXiv:2005.10455. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Advances in Neural Information Processing Systems (NIPS), Proceedings of the 27th International Conference on Neural Information Processing Systems—Volume 2; ACM: New York, NY, USA, 2014; pp. 2672–2680. [Google Scholar]
- Stengel, K.; Glaws, A.; Hettinger, D.; King, R.N. Adversarial super-resolution of climatological wind and solar data. Proc. Natl. Acad. Sci. USA 2020, 117, 16805–16815. [Google Scholar] [CrossRef]
- Lantz, T.C.; Kokelj, S.V. Increasing rates of retrogressive thaw slump activity in the Mackenzie Delta region, N.W.T., Canada. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Wilcox, E.J.; Keim, D.; De Jong, T.; Walker, B.; Sonnentag, O.; Sniderhan, A.E.; Mann, P.; Marsh, P. Tundra shrub expansion may amplify permafrost thaw by advancing snowmelt timing. Arct. Sci. 2019, 5, 202–217. [Google Scholar] [CrossRef] [Green Version]
- Quinton, W.; Hayashi, M.; Chasmer, L. Permafrost-thaw-induced land-cover change in the Canadian subarctic: Implications for water resources. Hydrol. Process. 2011, 25, 152–158. [Google Scholar] [CrossRef]
- Vors, L.S.; Boyce, M.S. Global declines of caribou and reindeer. Glob. Chang. Biol. 2009, 15, 2626–2633. [Google Scholar] [CrossRef]
- Ford, J.D.; McDowell, G.; Pearce, T. The adaptation challenge in the Arctic. Nat. Clim. Chang. 2015, 5, 1046–1053. [Google Scholar] [CrossRef]
- Hutchinson, M.F.; McKenney, D.W.; Lawrence, K.; Pedlar, J.H.; Hopkinson, R.F.; Milewska, E.; Papadopol, P. Development and Testing of Canada-Wide Interpolated Spatial Models of Daily Minimum–Maximum Temperature and Precipitation for 1961–2003. J. Appl. Meteorol. Clim. 2009, 48, 725–741. [Google Scholar] [CrossRef]
- Wetterhall, F.; Halldin, S.; Xu, C.-Y. Statistical precipitation downscaling in central sweden with the analogue method. J. Hydrol. 2005, 306, 174–190. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein gan. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Villani, C. Optimal Transport: Old and New; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 338. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Zeiler, M.D. Adadelta: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Chen, H.; Sun, J.; Chen, X. Projection and uncertainty analysis of global precipitation-related extremes using CMIP5 models. Int. J. Clim. 2014, 34, 2730–2748. [Google Scholar] [CrossRef]
- Manzanas, R.; Lucero, A.; Weisheimer, A.; Gutiérrez, J.M. Can bias correction and statistical downscaling methods improve the skill of seasonal precipitation forecasts? Clim. Dyn. 2018, 50, 1161–1176. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F.; O Mearns, L. Probability of regional climate change calculated using the reliability ensemble averaging (REA) method. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Frei, C.; Schöll, R.; Fukutome, S.; Schmidli, J.; Vidale, P.L. Future change of precipitation extremes in Europe: Intercomparison of scenarios from regional climate models. J. Geophys. Res. 2006, 111, D06105. [Google Scholar] [CrossRef] [Green Version]
- Hundecha, Y.; Bárdossy, A. Statistical downscaling of extremes of daily precipitation and temperature and construction of their future scenarios. Int. J. Climatol. 2008, 28, 589–610. [Google Scholar] [CrossRef]

| AOGCM | Institution | Grid Type | Horizontal Dimension (Lon/Lat) | Vertical Levels |
|---|---|---|---|---|
| BCC ESM | Beijing Climate Center | T42 | 128 × 64 | 26 |
| CAN ESM5 | Canadian Centre for Climate Modelling and Analysis, Environment and Climate Change Canada | T63 | 128 × 64 | 49 |
| CESM2 | National Center for Atmospheric Research | 0.9 × 1.25 finite volume grid | 288 × 192 | 70 |
| CNRM CM6.1 | Centre National de Recherches Meteorologiques | T127 | 256 × 128 | 91 |
| CNRM ESM2 | Centre National de Recherches Meteorologiques | T127 | 256 × 128 | 91 |
| GFDL CM4 | Geophysical Fluid Dynamics Laboratory | C96 | 360 × 180 | 33 |
| HAD GEM3 | Met Office Hadley Centre | N96 | 192 × 144 | 85 |
| MRI | Meteorological Research Institute, Tsukuba, Ibaraki 305-0052, Japan | TL159 | 320 × 160 | 80 |
| UK ESM1 | Met Office Hadley Centre | N96 | 192 × 144 | 85 |
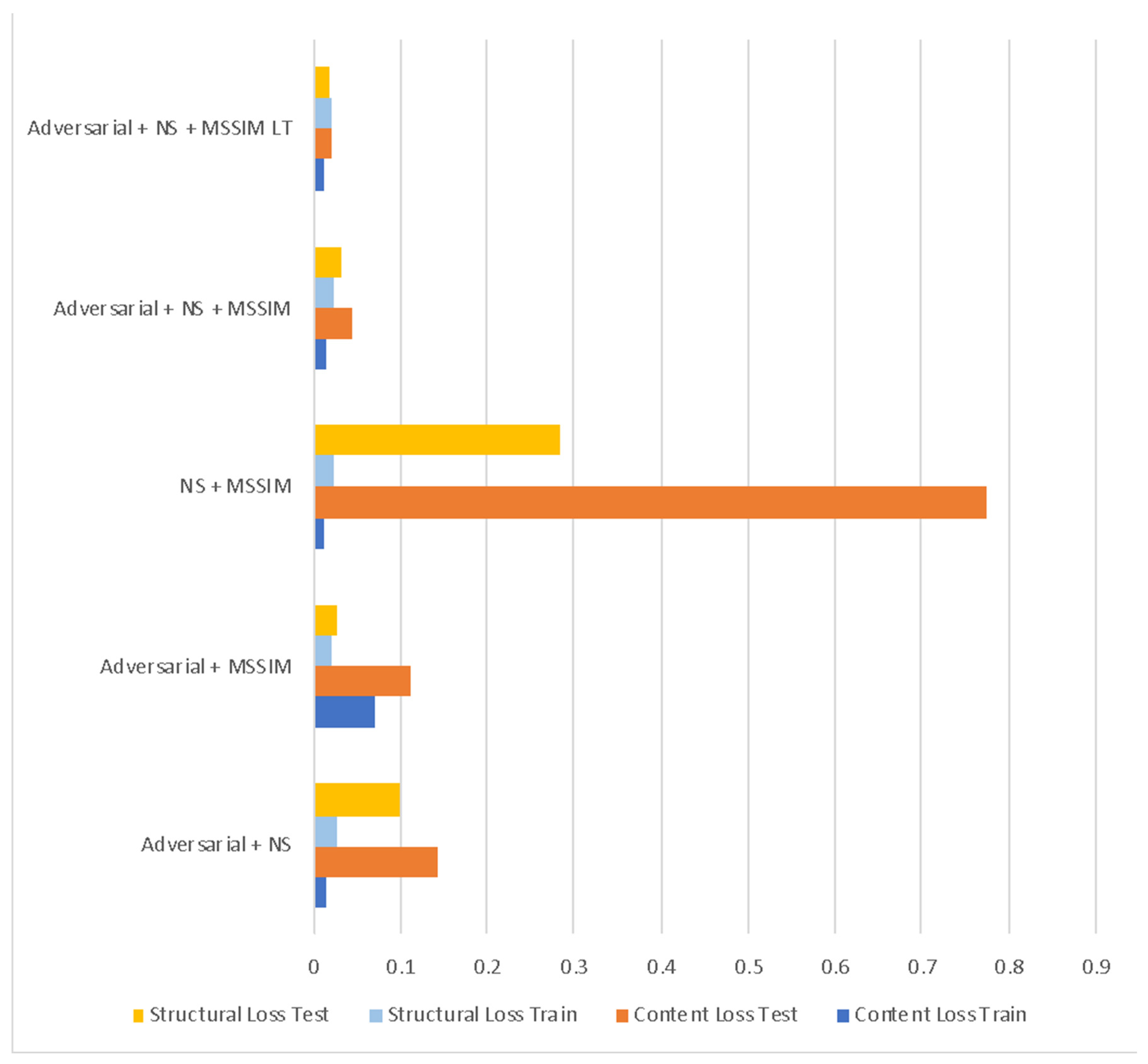
| Loss Combination | Content Loss | Structural Loss | ||
|---|---|---|---|---|
| Train | Test | Train | Test | |
| Adversarial + NS | 0.015 | 0.142 | 0.025 | 0.100 |
| Adversarial + MSSIM | 0.070 | 0.110 | 0.019 | 0.025 |
| NS + MSSIM | 0.011 | 0.774 | 0.024 | 0.283 |
| Adversarial + NS + MSSIM | 0.015 | 0.043 | 0.024 | 0.033 |
| Adversarial + NS + MSSIM LT | 0.011 | 0.020 | 0.021 | 0.017 |
| Performance/Model | GAN | MAE | PCA |
|---|---|---|---|
| MAE | 1.71 | 1.85 | 2.7 |
| NS | 0.996 | 0.995 | 0.991 |
| Correlation | 0.9987 | 0.9986 | 0.995 |
| KS p-value | ~1−48 | ~1−25 | ~1−8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaudhuri, C.; Robertson, C. CliGAN: A Structurally Sensitive Convolutional Neural Network Model for Statistical Downscaling of Precipitation from Multi-Model Ensembles. Water 2020, 12, 3353. https://doi.org/10.3390/w12123353
Chaudhuri C, Robertson C. CliGAN: A Structurally Sensitive Convolutional Neural Network Model for Statistical Downscaling of Precipitation from Multi-Model Ensembles. Water. 2020; 12(12):3353. https://doi.org/10.3390/w12123353
Chicago/Turabian StyleChaudhuri, Chiranjib, and Colin Robertson. 2020. "CliGAN: A Structurally Sensitive Convolutional Neural Network Model for Statistical Downscaling of Precipitation from Multi-Model Ensembles" Water 12, no. 12: 3353. https://doi.org/10.3390/w12123353
APA StyleChaudhuri, C., & Robertson, C. (2020). CliGAN: A Structurally Sensitive Convolutional Neural Network Model for Statistical Downscaling of Precipitation from Multi-Model Ensembles. Water, 12(12), 3353. https://doi.org/10.3390/w12123353





