Application of the SCS–CN Method to the Hancheon Basin on the Volcanic Jeju Island, Korea
Abstract
1. Introduction
2. Theoretical Backgrounds
2.1. The SCS–CN Method
2.2. Estimation of CN by Analyzing the Rainfall–Runoff Data
3. Study Basin and Rainfall Events
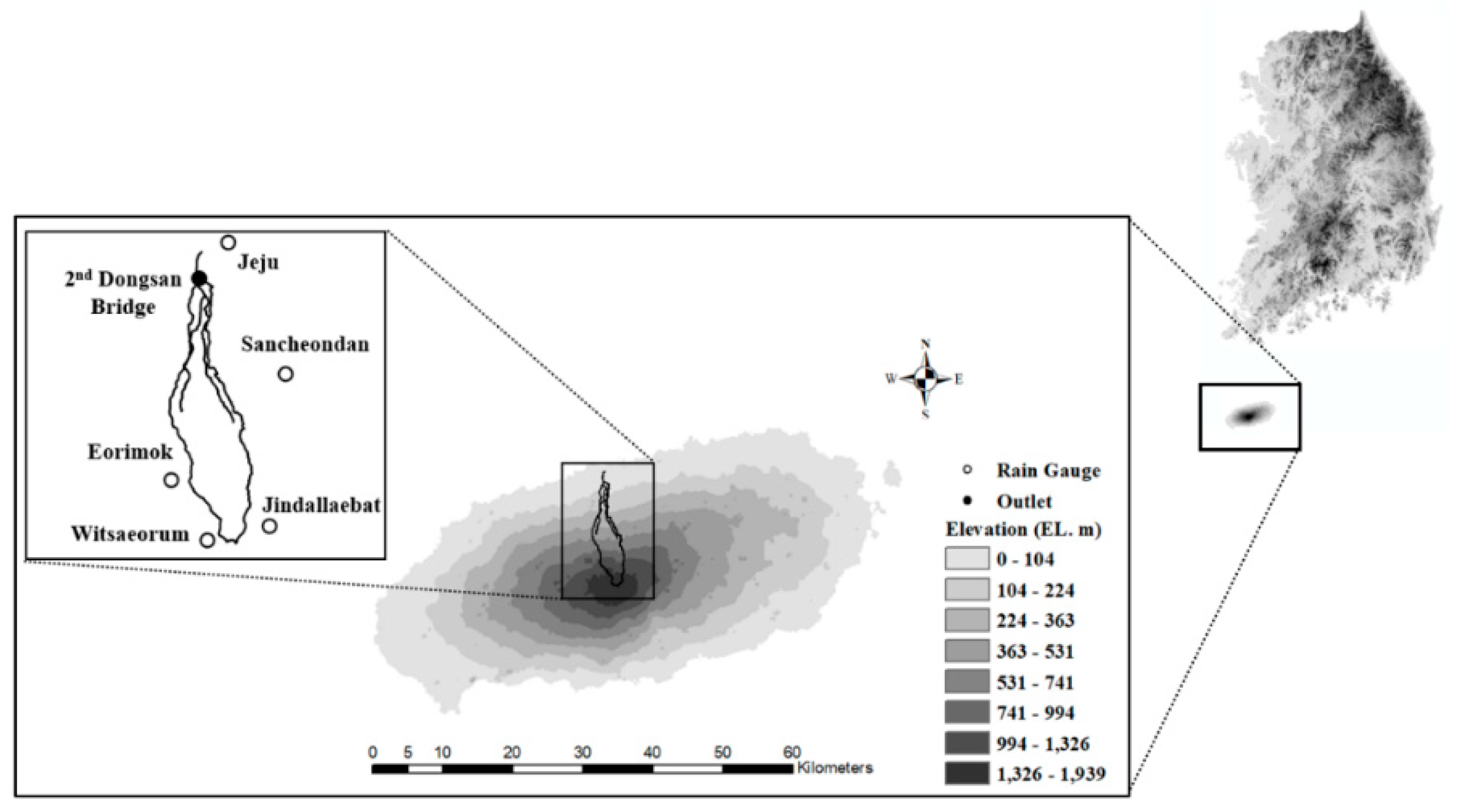
3.1. Study Basin
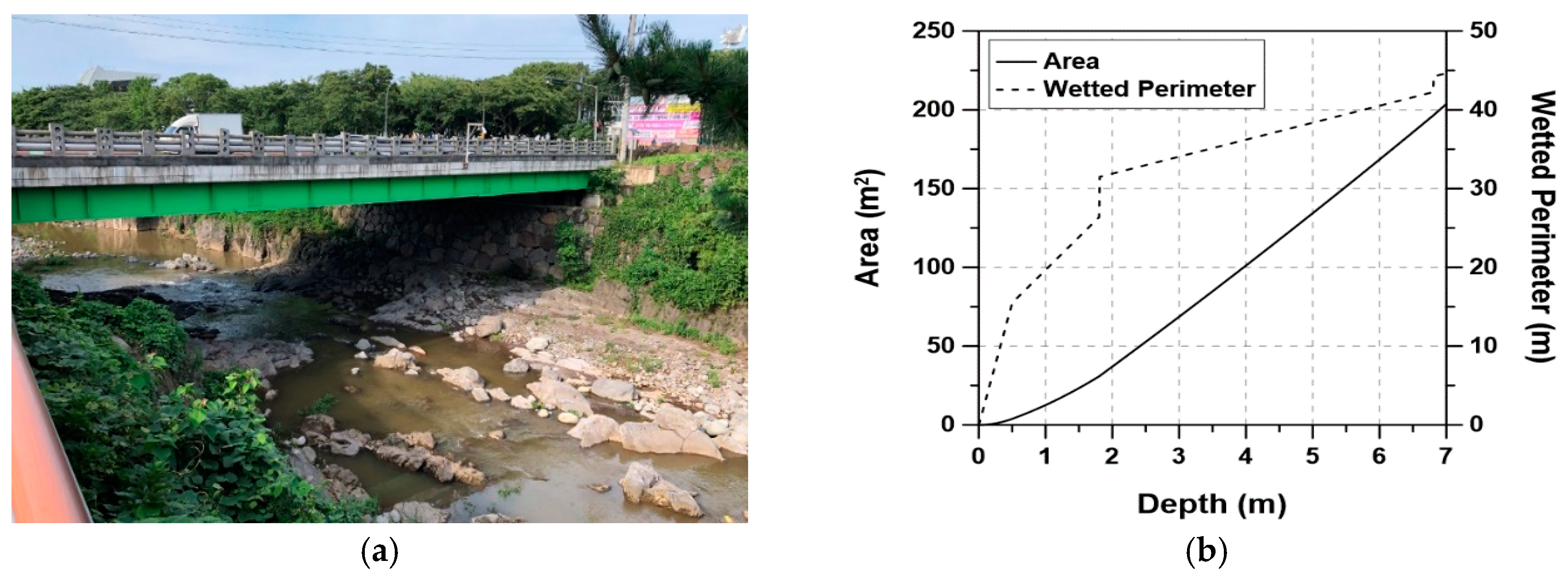
3.2. Data
4. Results and Discussions
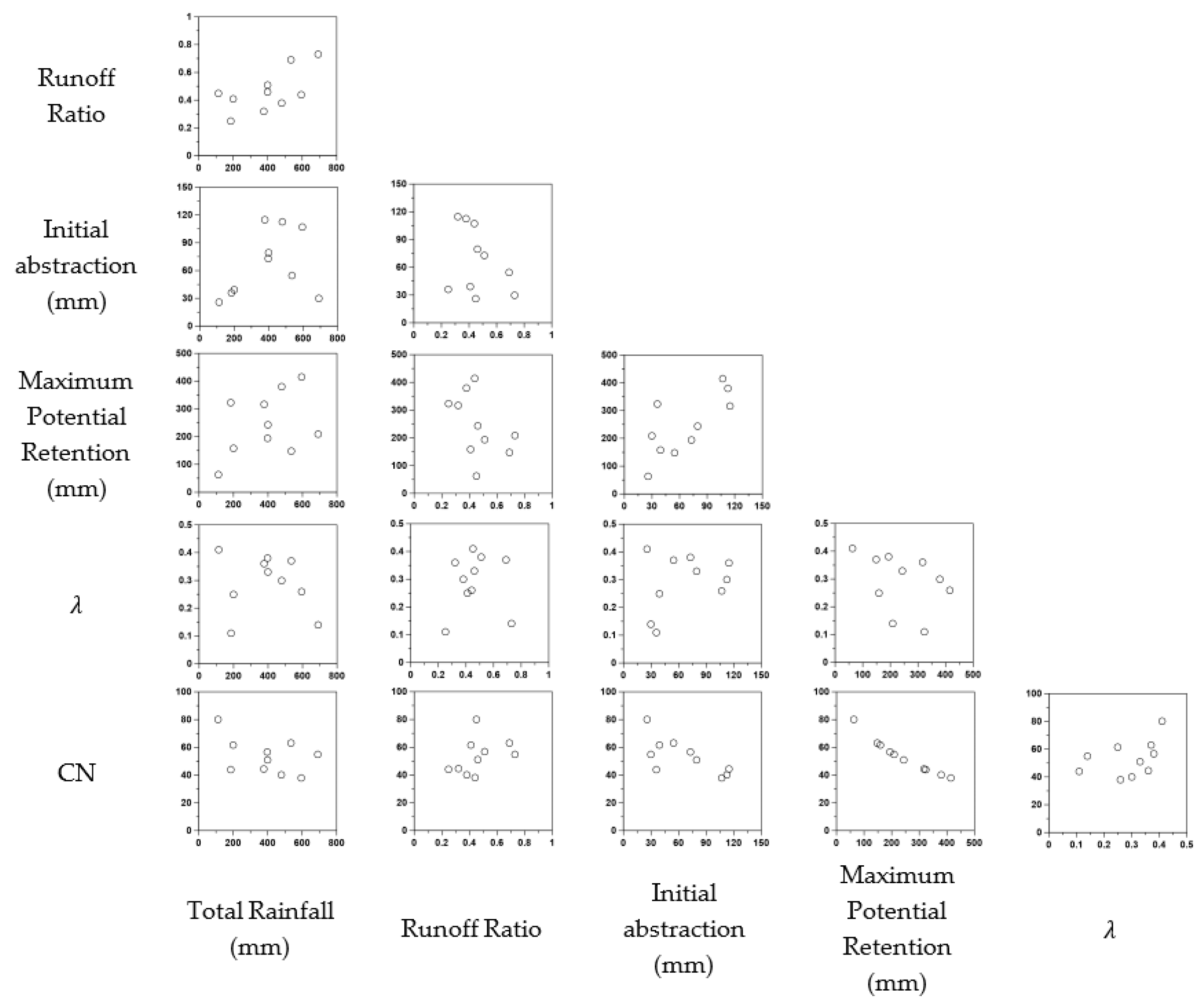
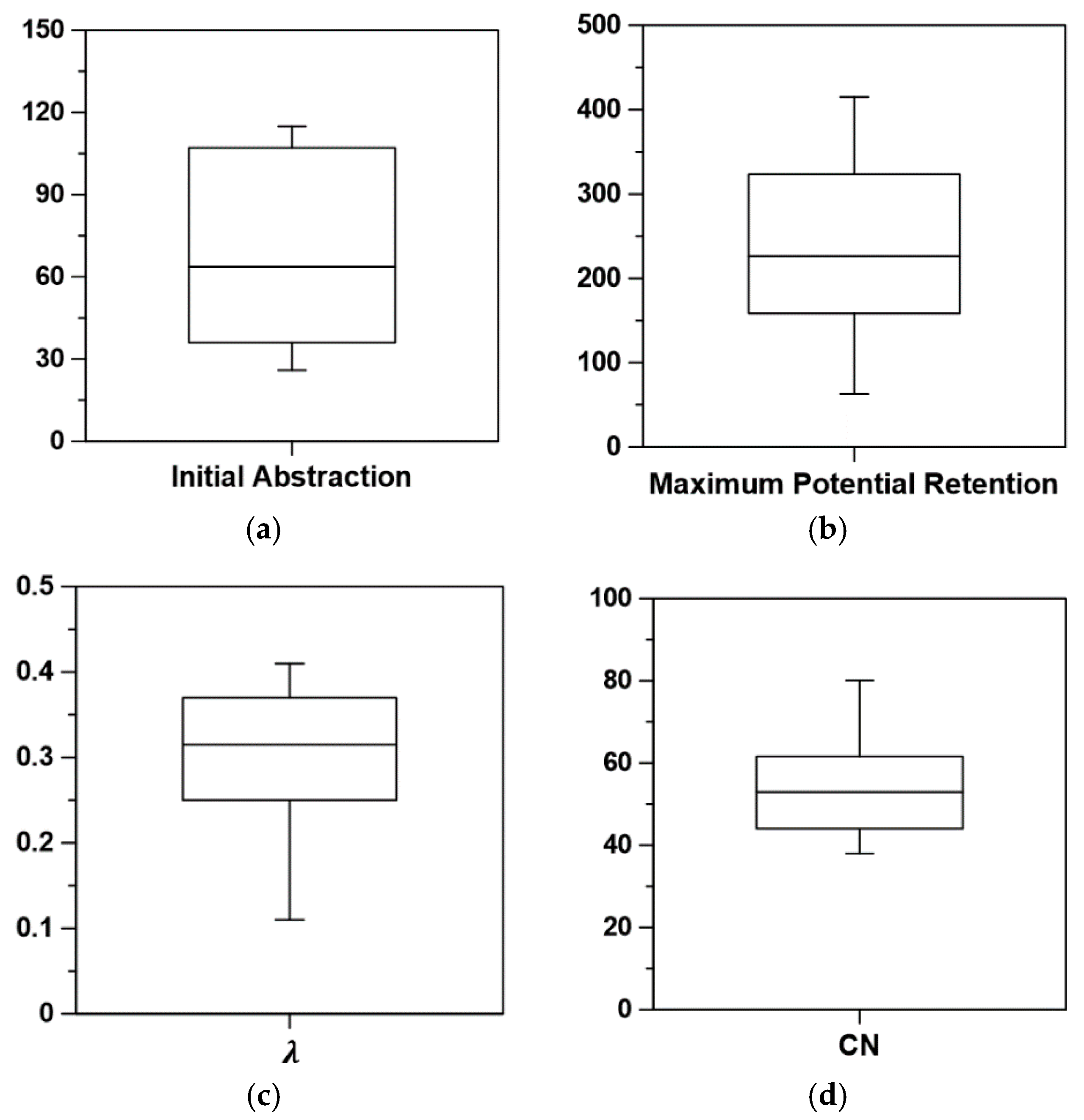
4.1. Initial Abstraction and CN
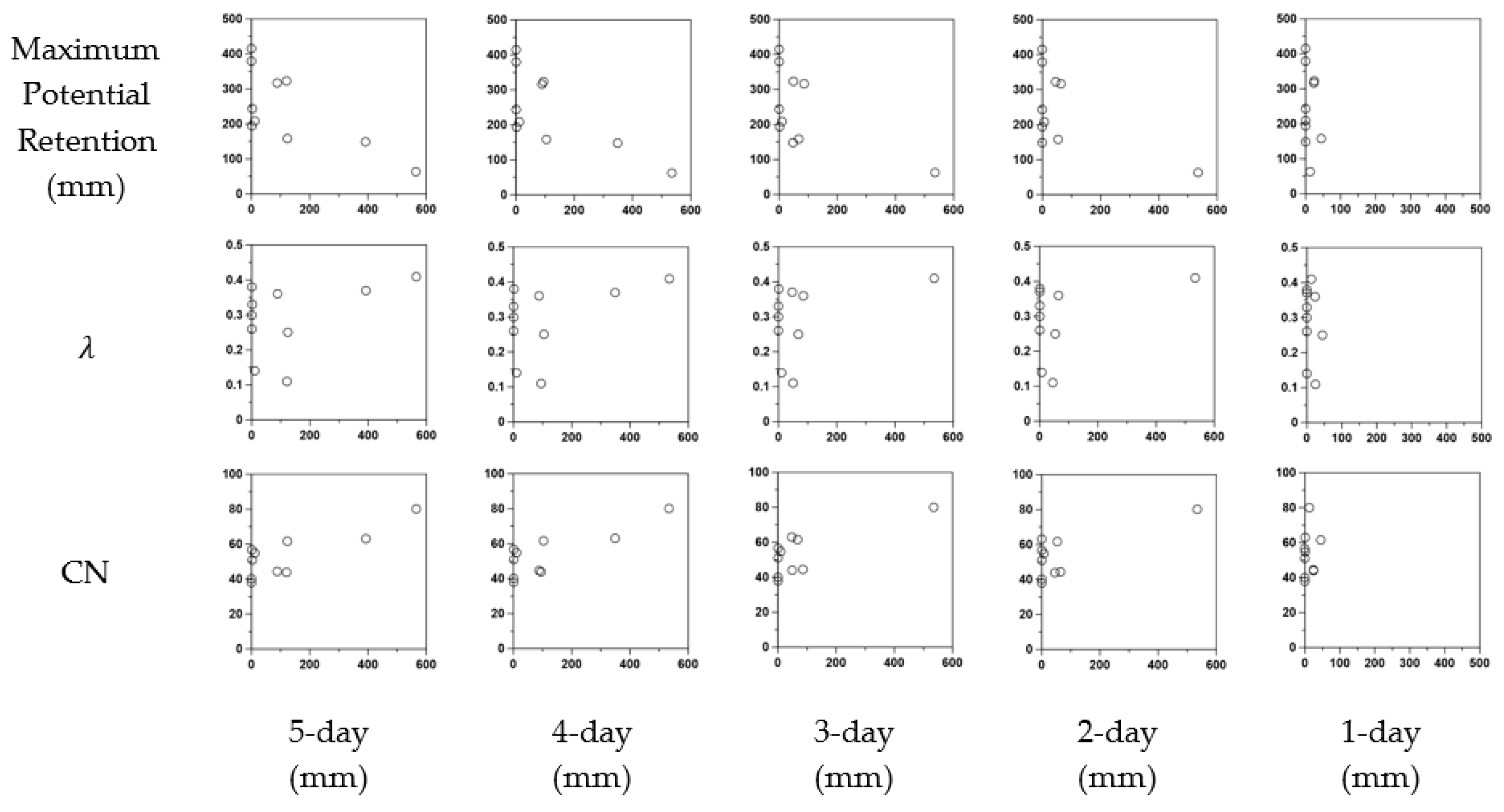
4.2. Effect of AMC
4.3. Classification Rules for Hydrological Soil Group
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kar, K.K.; Yang, S.K.; Lee, J.H. Assessing unit hydrograph parameters and peak runoff responses from storm rainfall events: A case study in Hancheon Basin of Jeju Island. JESI 2014, 24, 437–447. [Google Scholar] [CrossRef][Green Version]
- Lau, L.S.; Mink, J.F. Hydrology of the Hawaiian Islands; University of Hawaii Press: Honolulu, HI, USA, 2006. [Google Scholar]
- Kim, C.G.; Kim, N.W. Evaluation and complementation of observed flow in the Hancheon watershed in Jeju Island using a physically-based watershed model. J. Korea Water Resour. Assoc. 2016, 49, 951–959. [Google Scholar]
- Jeju Special Self-Governing Province. Comprehensive Investigation of Hydrogeology and Groundwater Resources in Jeju Island (III); Jeju Special Self-Governing Province: Jeju, Korea, 2003.
- Jung, W.; Yang, S. Simulation on runoff of rivers in Jeju Island using SWAT model. JESI 2009, 18, 1045–1055. [Google Scholar]
- Soil Conservation Service (SCS). National Engineering Handbook—Section 4: Hydrology; SCS: Washington, DC, USA, 1972.
- Ministry of Environment (ME). Design Flood Estimation Tips; ME: Sejong, Korea, 2019.
- Jeju Special Self-Governing Province. Establishment of Jeju-Type River Master Plan and Development of River Facility Management Manual; Jeju Special Self-Governing Province: Jeju, Korea, 2013.
- Ha, K.; Park, W.; Moon, D. Estimation of direct runoff variation according to land use changes in Jeju Island. Econ. Environ. Geol. 2009, 42, 343–356. [Google Scholar]
- Rural Development Administration (RDA). Agro-Environment Research 2006; RDA: Jeonju, Korea, 2007; pp. 141–176.
- Jung, W. The Estimation of Parametric Runoff Characteristics and Flood Discharge Based on Riverine in-situ Measurements in Jeju Island. Ph.D. Thesis, Jeju National University, Jeju, Korea, 2013. [Google Scholar]
- Sharpley, A.N.; Williams, J.R. EPIC-Erosion/Productivity Impact Calculator: 1. Model Documentation; USDA: Washington, DC, USA, 1990.
- Jung, W.; Yang, S.; Kim, D. Flood discharge to decision of parameters in Han Stream watershed. JESI 2014, 23, 533–541. [Google Scholar] [CrossRef]
- Yang, S.; Kim, M.; Kang, B.; Kim, Y.; Kang, M. Estimation of flood discharge based on observation data considering the hydrological characteristics of the Han Stream basin in Jeju Island. JESI 2017, 26, 1321–1331. [Google Scholar] [CrossRef]
- Leta, O.T.; El-Kadi, A.I.; Dulai, H.; Ghazal, K.A. Assessment of climate change impacts on water balance components of Heeia watershed in Hawaii. J. Hydrol. Reg. Stud. 2016, 8, 182–197. [Google Scholar] [CrossRef]
- Alahmadi, F.; Rahman, N.A.; Yusop, Z. Hydrological modeling of ungauged arid volcanic environments at upper Bathan catchment, Madinah, Saudi Arabia. J. Teknol. 2016, 789, 9–14. [Google Scholar]
- Shehata, M.; Mizunaga, H. Flash flood risk assessment for Kyushu Island, Japan. Environ. Earth Sci. 2018, 77, 76. [Google Scholar] [CrossRef]
- Odongo, V.O.; Mulatu, D.W.; Muthoni, F.K.; van Oel, P.R.; Meins, F.M.; van der Tol, C.; Skidmore, A.K.; Groen, T.A.; Becht, R.; Onyando, J.O.; et al. Coupling socio-economic factors and eco-hydrological processes using a cascade-modeling approach. J. Hydrol. 2014, 518, 49–59. [Google Scholar] [CrossRef]
- Capra, L.; Coviello, V.; Borselli, L.; Márquez-Ramírez, V.H.; Arámbula-Mendoza, R. Hydrological control of large hurricane-induced lahars: Evidence from rainfall-runoff modeling, seismic and video monitoring. Nat. Hazards Earth Syst. Sci. 2018, 18, 781–794. [Google Scholar] [CrossRef]
- Woodward, D.E.; Hawkins, R.H.; Jiang, R.; Hjelmfelt, A.T., Jr.; Van Mullem, J.A.; Quan, Q.D. Runoff curve number method: Examination of the initial abstraction ratio. In Proceedings of the World Water & Environmental Resources Congress 2003, Philadelphia, PA, USA, 23–26 June 2003; pp. 1–10. [Google Scholar]
- Baltas, E.A.; Dervos, N.A.; Mimikow, M.A. Technical note: Determination of the SCS initial abstraction ratio in an experimental watershed in Greece. Hydrol. Earth Syst. Sci. 2007, 11, 1825–1829. [Google Scholar] [CrossRef]
- Beck, H.E.; de Jue, R.A.M.; Schellekens, J.; van Dijk, A.I.J.M.; Bruijnzeel, L.A. Improving curve number based strom runoff estimates using soil moisture proxies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 250–259. [Google Scholar] [CrossRef]
- Shi, Z.H.; Chen, L.D.; Fang, N.F.; Qin, D.F.; Cai, C.F. Research on the SCS-CN initial abstraction ratio using rainfall-runoff event analysis in the Three Gorges Area, China. Catena 2009, 77, 1–7. [Google Scholar] [CrossRef]
- Yuan, Y.; Nie, W.; McCutcheon, S.C.; Taguas, E.V. Initial abstraction and curve numbers for semiarid watersheds in Southeastern Arizona. Hydrol. Process. 2014, 28, 774–783. [Google Scholar] [CrossRef]
- Ponce, V.M.; Hawkins, R.H. Runoff curve number: Has it reached maturity? J. Hydrol. Eng. 1996, 1, 11–19. [Google Scholar] [CrossRef]
- Babu, P.S.; Mishra, S.K. Improved SCS-CN–inspired model. J. Hydrol. Eng. 2012, 17, 1164–1172. [Google Scholar] [CrossRef]
- Hjelmfelt, A.T.; Kramer, K.A.; Burwell, R.E. Curve numbers as random variables. In Proceedings of the International Symposium on Rainfall-Runoff Modeling; Water Resources Publishing: Littleton, CO, USA, 1982; pp. 365–373. [Google Scholar]
- Sorooshian, S.; Duan, Q.; Gupta, V.K. Calibration of rainfall-runoff models: Application of global optimization to the Sacramento Soil Moisture Accounting Model. Water Resour. Res. 1993, 29, 1185–1194. [Google Scholar] [CrossRef]
- Yuan, Y.; Mitchell, J.K.; Hirschi, M.C.; Cooke, R.A. Modified SCS curve number method for predicting subsurface drainage flow. Trans. ASABE 2001, 44, 1673–1682. [Google Scholar] [CrossRef]
- Hawkins, R.H.; Ward, T.J.; Woodward, D.E.; Van Mullem, J.A. Curve Number Hydrology: State of the Practice; ASCE: Reston, VA, USA, 2008. [Google Scholar]
- Mishra, S.K.; Singh, V.P. Soil Conservation Service Curve Number (SCS-CN) Methodology; Springer: Berlin, Germany, 2003. [Google Scholar]
- Williams, J.R.; LaSeur, W.V. Water yield model using SCS curve numbers. J. Hydr. Eng. Div. 1976, 102, 1241–1253. [Google Scholar]
- Hawkins, R.H. Runoff curve numbers with varying site moisture. J. Irrig. Drain. Div. 1978, 104, 389–398. [Google Scholar]
- Soni, B.; Mishra, G.C. Soil Water Accounting Using SCS Hydrological Soil Classification; National Institute of Hydrology: Roorkee, India, 1985.
- Mishra, S.K.; Goel, N.K.; Seth, S.M.; Srivastava, D.K. An SCS-CN-based long-term daily flow simulation model for a hilly catchment. In Proceedings of the International Symposium Hydrology of Ungauged Streams in Hilly Regions for Small Hydro Power Development, New Delhi, India, 9–10 March 1998; pp. 9–10. [Google Scholar]
- Chen, C.L. An evaluation of the mathematics and physical significance of the soil conservation service curve number procedure for estimating runoff volume. In Proceedings of the International Symposium on Rainfall-Runoff Modeling, Mississippi State, MS, USA, 18–21 May 1982; pp. 387–418. [Google Scholar]
- Rallison, R.E.; Miller, N. Past, present, and future SCS runoff procedure. In Rainfall-Runoff Relationship; International Symposium on Rainfall-Runoff Modeling: Littleton, CO, USA, 1982; pp. 353–364. [Google Scholar]
- Park, C.H.; Yoo, C.; Kim, J.H. Sensitivity analysis of runoff curve number to the rainfall conditions. J. Korea Soc. Civ. Eng. B. 2005, 25, 501–508. [Google Scholar]
- Yoo, C.; Park, C.H.; Kim, J.H. Revised AMC for the application of SCS method: 2. Revised AMC. J. Korea Water Resour. Assoc. 2005, 38, 963–972. [Google Scholar] [CrossRef]
- Hawkins, R.H. Asymptotic determination of runoff curve numbers from data. J. Irrig. Drain. Eng. 1993, 119, 334–345. [Google Scholar] [CrossRef]
- Rezaei-Sadr, H. Influence of coarse soils with high hydraulic conductivity on the applicability of the SCS-CN method. Hydrol. Sci. J. 2017, 62, 843–848. [Google Scholar] [CrossRef]
- Santikari, V.P.; Murdoch, L.C. Including effects of watershed heterogeneity in the curve number method using variable initial abstraction. Hydrol. Earth Syst. Sci. 2018, 22, 4725–4743. [Google Scholar] [CrossRef]
- Soulis, K.X. Estimation of SCS curve number variation following forest fires. Hydrol. Sci. J. 2018, 63, 1332–1346. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. SCS-CN parameter determination using rainfall-runoff data in heterogeneous watersheds-the two-CN system approach. Hydrol. Earth Syst. Sci. 2012, 16, 1001–1015. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. Identification of the SCS-CN parameter spatial distribution using rainfall-runoff data in heterogeneous watersheds. Water Resour. Manag. 2013, 27, 1737–1749. [Google Scholar] [CrossRef]
- Bonta, J.V. Determination of watershed curve number using derived distribution. J. Irrig. Drain. Eng. 1997, 123, 28–36. [Google Scholar] [CrossRef]
- Ajmal, M.; Waseem, M.; Ahn, J.H.; Kim, T.W. Runoff estimation using the NRCS slope-adjusted curve number in mountainous watersheds. J. Irrig. Drain. Eng. 2016, 142, 04016002. [Google Scholar] [CrossRef]
- Yang, S.; Kim, D.; Jung, W. Rainfall-Runoff characteristics in a Jeju stream considering antecedent precipitation. JESI 2014, 23, 553–560. [Google Scholar]
- Jeju Special Self-Governing Province. Master Plan for Local Rivers Management in Jeju-si and Preparation of River Facility Management; Jeju Special Self-Governing Province: Jeju, Korea, 2018.
- Korea Meteorological Administration (KMA). 2012 Typhoon Analysis Report; KMA: Seoul, Korea, 2013. [Google Scholar]
- Costa, J.E.; Spicer, K.R.; Cheng, R.T.; Haeni, F.P.; Melcher, N.B.; Thurman, E.M.; Plant, W.J.; Keller, W.C. Measuring stream discharge by non-contact methods: A proof-of-concept experiment. Geophys. Res. Lett. 2000, 27, 553–556. [Google Scholar] [CrossRef]
- Hauet, A.; Kruger, A.; Krajewski, W.F.; Bradley, A.; Muste, M.; Creutin, J.D.; Wilson, M. Experimental system for real-time discharge estimation using an image-based method. J. Hydrol. Eng. 2008, 13, 105–110. [Google Scholar] [CrossRef]
- Le Coz, J.; Hauet, A.; Pierrefeu, G.; Dramais, G.; Camenen, B. Performance of image-based velocimetry (LSPIV) applied to flash-flood discharge measurements in Mediterranean rivers. J. Hydrol. 2010, 394, 42–52. [Google Scholar] [CrossRef]
- Kim, D.; Yang, S.; Jung, W. Error analysis for electromagnetic surface velocity and discharge measurement in rapid mountain stream flow. JESI 2014, 23, 543–552. [Google Scholar]
- Hu, K.S.; Jung, J.H. Hydrologic classification and its application of the Korean soil. J. Korean Soc. Agric. Eng. 1987, 4, 48–61. [Google Scholar]
- Jung, J.H.; Jang, S.P.; Kim, J.I.; Jung, Y.T.; Hu, K.S.; Park, H. Classification of hydrologic soil group to estimate runoff ratio. J. Korean Soc. Agric. Eng. 1995, 27, 12–23. [Google Scholar]
- Lee, Y.; Kang, M.; Park, C.; Yoo, C. Suggestion of classification rule of hydrological soil groups considering the results of the revision of soil series: A case study on Jeju Island. J. Korea Water Resour. Assoc. 2019, 52, 35–49. [Google Scholar]


| Rainfall Event # | Time (Duration) | Total Rainfall (mm) | Maximum Intensity (mm/h) | Mean Intensity (mm/h) | Comments |
|---|---|---|---|---|---|
| 1 | 18 July 2012. 06:00–19 July 2012. 16:00 (34 h) | 200.0 | 38.4 | 5.9 | Typhoon Khanun |
| 2 | 23 August 2012. 02:00–25 August 2012. 03:00 (49 h) | 377.7 | 63.0 | 7.7 | Convective |
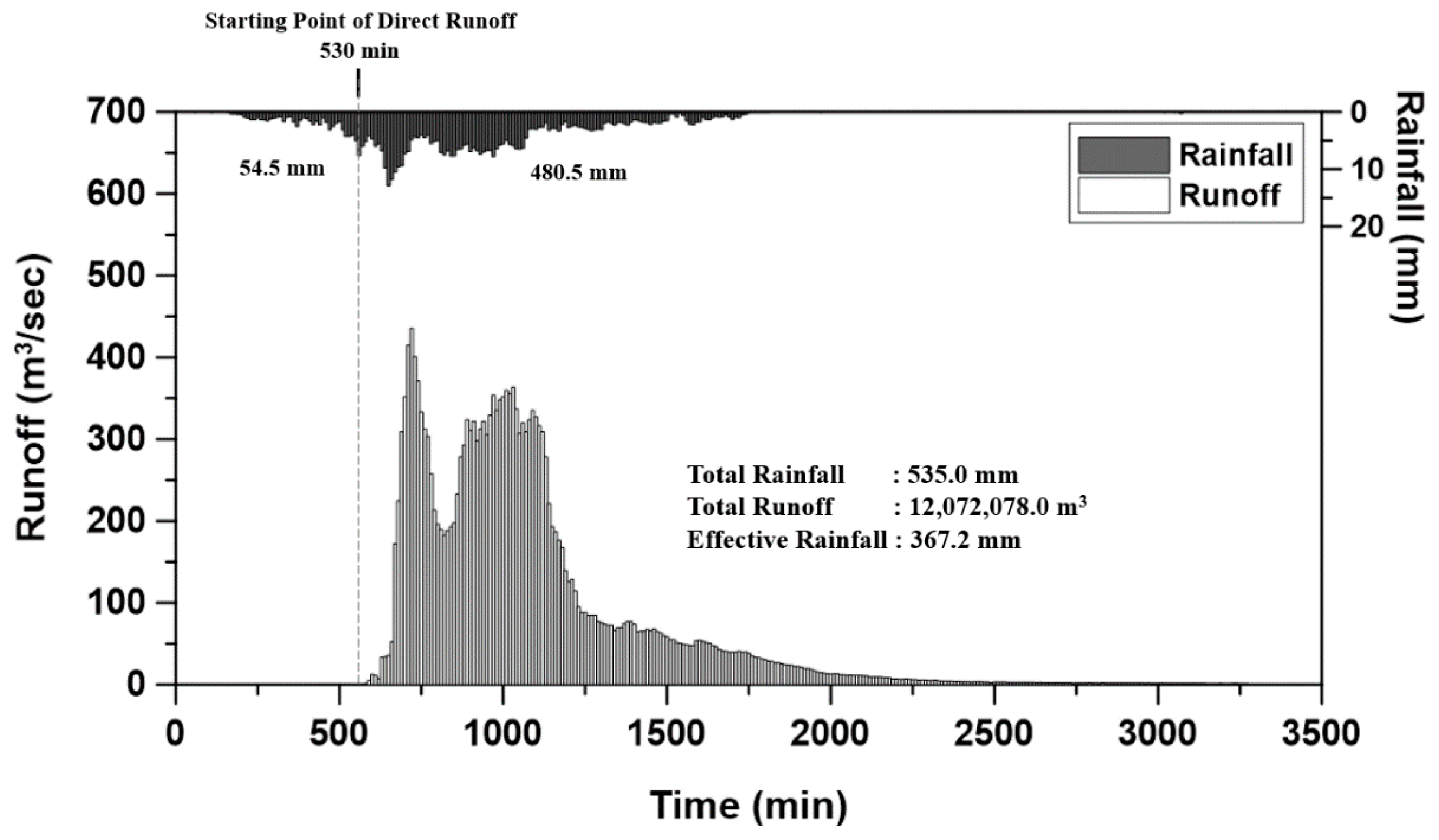
| 3 | 27 August 2012. 12:00–28 August 2012. 17:00 (29 h) | 535.0 | 76.8 | 18.4 | Typhoon Bolaven |
| 4 | 29 August 2012. 14:00–30 August 2012. 16:00 (26 h) | 113.0 | 49.2 | 4.0 | Typhoon Tembin |
| 5 | 15 September 2012. 19:00–17 September 2012. 23:00 (52 h) | 691.5 | 71.4 | 13.3 | Typhoon Sanba |
| 6 | 31 July 2014. 16:00–04 August 2014. 12:00 (92 h) | 400.0 | 70.8 | 4.4 | Typhoon Nakri |
| 7 | 22 August 2018. 13:00–24 August 2018. 05:00 (40 h) | 398.2 | 45.0 | 10.0 | Typhoon Soulik |
| 8 | 4 October 2018. 16:00–6 October 2018. 14:00 (46 h) | 480.0 | 50.4 | 10.5 | Typhoon Kong-rey |
| 9 | 6 September 2019. 00:00–7 September 2019. 16:00 (40 h) | 185.2 | 30.6 | 4.6 | Typhoon Lingling |
| 10 | 21 September 2019. 08:00–22 September 2019. 20:00 (36 h) | 594.5 | 39.0 | 16.4 | Typhoon Tapah |
| Rainfall Event# | Mean | Maximum | ||||
|---|---|---|---|---|---|---|
| Flow Velocity (m/s) | Depth (m) | Discharge (m3/s) | Flow Velocity (m/s) | Depth (m) | Discharge (m3/s) | |
| 1 | 2.39 | 0.82 | 98.70 | 4.90 | 2.73 | 187.43 |
| 2 | 2.85 | 0.92 | 55.42 | 7.24 | 2.72 | 203.33 |
| 3 | 2.89 | 1.34 | 133.79 | 7.07 | 4.18 | 422.71 |
| 4 | 2.23 | 0.56 | 53.53 | 5.87 | 2.66 | 134.48 |
| 5 | n/a | 1.43 | n/a | n/a | 4.52 | n/a |
| 6 | 2.29 | 0.92 | 50.11 | 4.65 | 2.48 | 230.28 |
| 7 | 3.22 | 0.94 | 89.88 | 7.23 | 2.74 | 289.52 |
| 8 | 4.19 | 0.88 | 99.57 | 7.34 | 2.53 | 304.20 |
| 9 | 2.07 | 0.79 | 39.51 | 7.25 | 1.80 | 106.88 |
| 10 | 3.28 | 1.10 | 87.13 | 7.31 | 2.46 | 188.75 |
| Rainfall Event# | Antecedent Five-Day Rainfall (mm) | Total Rainfall (mm) | Direct Runoff (mm) | Runoff Ratio | Initial Abstraction (mm) | Maximum Potential Retention (mm) | CN | |
|---|---|---|---|---|---|---|---|---|
| 1 | 123.8 | 200.0 | 81.0 | 0.41 | 39.2 | 158.4 | 0.25 | 61.6 |
| 2 | 88.4 | 377.7 | 119.1 | 0.32 | 114.9 | 317.1 | 0.36 | 44.5 |
| 3 | 392.2 | 535.0 | 367.2 | 0.69 | 54.5 | 148.3 | 0.37 | 63.1 |
| 4 | 564.8 | 113.0 | 50.5 | 0.45 | 25.9 | 63.0 | 0.41 | 80.1 |
| 5 | 10.7 | 691.5 | 502.6 | 0.73 | 29.8 | 208.8 | 0.14 | 54.9 |
| 6 | 2.2 | 400.0 | 182.1 | 0.46 | 79.5 | 243.6 | 0.33 | 51.0 |
| 7 | 1.0 | 398.2 | 203.7 | 0.51 | 72.9 | 194.2 | 0.38 | 56.7 |
| 8 | 0.0 | 480.0 | 180.7 | 0.38 | 112.6 | 379.6 | 0.30 | 40.1 |
| 9 | 120.5 | 185.0 | 47.1 | 0.25 | 36.0 | 323.4 | 0.11 | 44.0 |
| 10 | 0.0 | 594.5 | 263.2 | 0.44 | 107.1 | 415.2 | 0.26 | 38.0 |
| Initial Abstraction (mm) | Maximum Potential Retention (mm) | CN | ||
|---|---|---|---|---|
| Minimum | 25.9 | 63.0 | 0.11 | 38.0 |
| Frist Quartile | 36.0 | 158.4 | 0.25 | 44.0 |
| Median | 63.7 | 226.2 | 0.32 | 53.0 |
| Third Quartile | 107.1 | 323.4 | 0.37 | 61.6 |
| Maximum | 114.9 | 415.2 | 0.41 | 80.1 |
| Rainfall Event# | 5-day (mm) | 4-day (mm) | 3-day (mm) | 2-day (mm) | 1-day (mm) |
|---|---|---|---|---|---|
| 1 | 123.8 | 103.5 | 68.0 | 54.3 | 44.6 |
| 2 | 88.4 | 88.0 | 85.7 | 64.5 | 23.7 |
| 3 | 392.2 | 348.8 | 47.4 | 0.2 | 0.1 |
| 4 | 564.8 | 534.9 | 534.8 | 534.2 | 12.3 |
| 5 | 10.7 | 10.7 | 10.7 | 7.0 | 0.2 |
| 6 | 2.2 | 0.5 | 0.0 | 0.0 | 0.0 |
| 7 | 1.0 | 1.0 | 1.0 | 0.0 | 0.0 |
| 8 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 9 | 120.5 | 94.6 | 49.7 | 45.6 | 24.1 |
| 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, M.; Yoo, C. Application of the SCS–CN Method to the Hancheon Basin on the Volcanic Jeju Island, Korea. Water 2020, 12, 3350. https://doi.org/10.3390/w12123350
Kang M, Yoo C. Application of the SCS–CN Method to the Hancheon Basin on the Volcanic Jeju Island, Korea. Water. 2020; 12(12):3350. https://doi.org/10.3390/w12123350
Chicago/Turabian StyleKang, Minseok, and Chulsang Yoo. 2020. "Application of the SCS–CN Method to the Hancheon Basin on the Volcanic Jeju Island, Korea" Water 12, no. 12: 3350. https://doi.org/10.3390/w12123350
APA StyleKang, M., & Yoo, C. (2020). Application of the SCS–CN Method to the Hancheon Basin on the Volcanic Jeju Island, Korea. Water, 12(12), 3350. https://doi.org/10.3390/w12123350





