Sewer Network Layout Selection and Hydraulic Design Using a Mathematical Optimization Framework
Abstract
1. Introduction
- we propose an MIP to model the LS problem over a network with general topography,
- we extend the methodology in Duque et al. [9] to generate a hydraulic design, and
- we propose a novel iterative scheme in which the objective function in the LS model approximates the true hydraulic-based cost, and this approximation is refined as the method progresses.
2. Problem Statement and Definitions
- The network must transport water from a discrete number of sources (manholes, sinks, etc.) to an outfall at a specific location [8].
- The flow moves by gravity over a tree-like structured network.
- There is a manhole between adjacent pipes due to changes in slope, diameter and/or flow direction [40].
- A uniform flow is assumed for the hydraulic design of each pipe [40].
- The HD methodology can use the Manning or Darcy–Weisbach and Colebrook–White resistance equations.
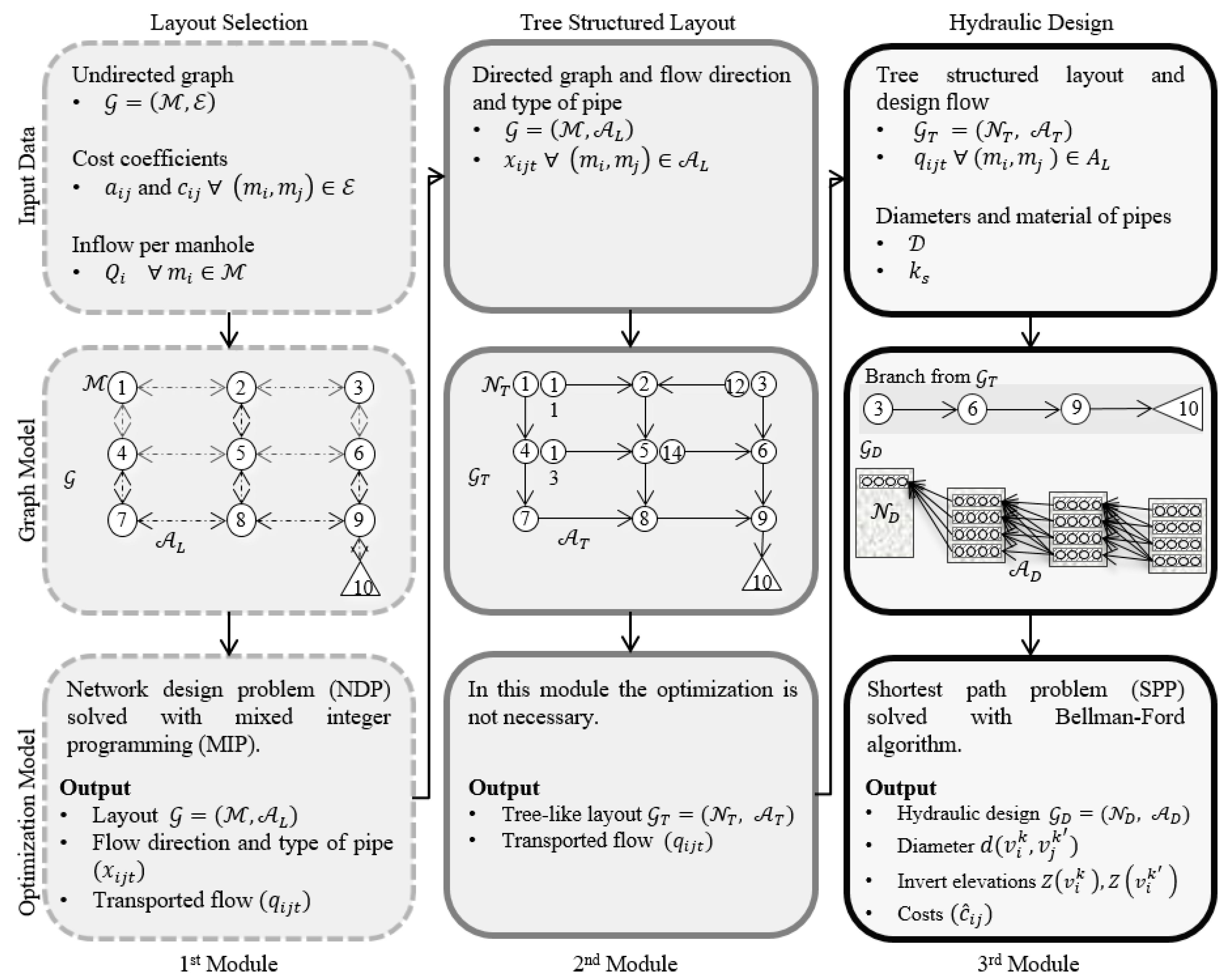
2.1. Layout Selection
2.2. Hydraulic Design
3. Methodology
3.1. Layout Selection Model
- is a binary variable that takes the value of one if the flow direction between manholes and is from to and the connection is of type .
- is a nonnegative real-valued variable that represents the amount of flow from to if the connection type is , in the same units as the inflow in each manhole .
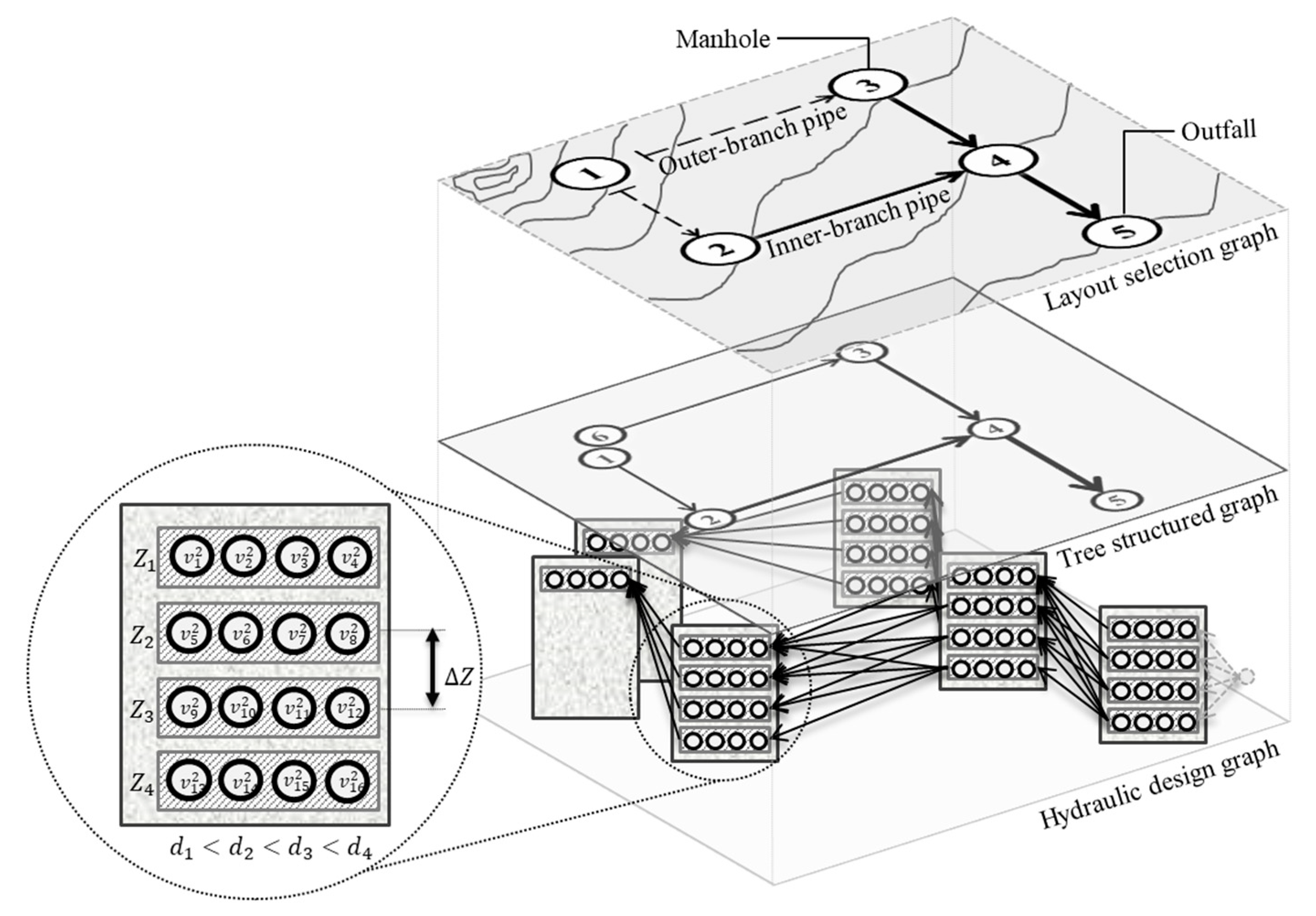
3.2. Layout Representation as a Tree-Like Directed Graph
- ,
- , and
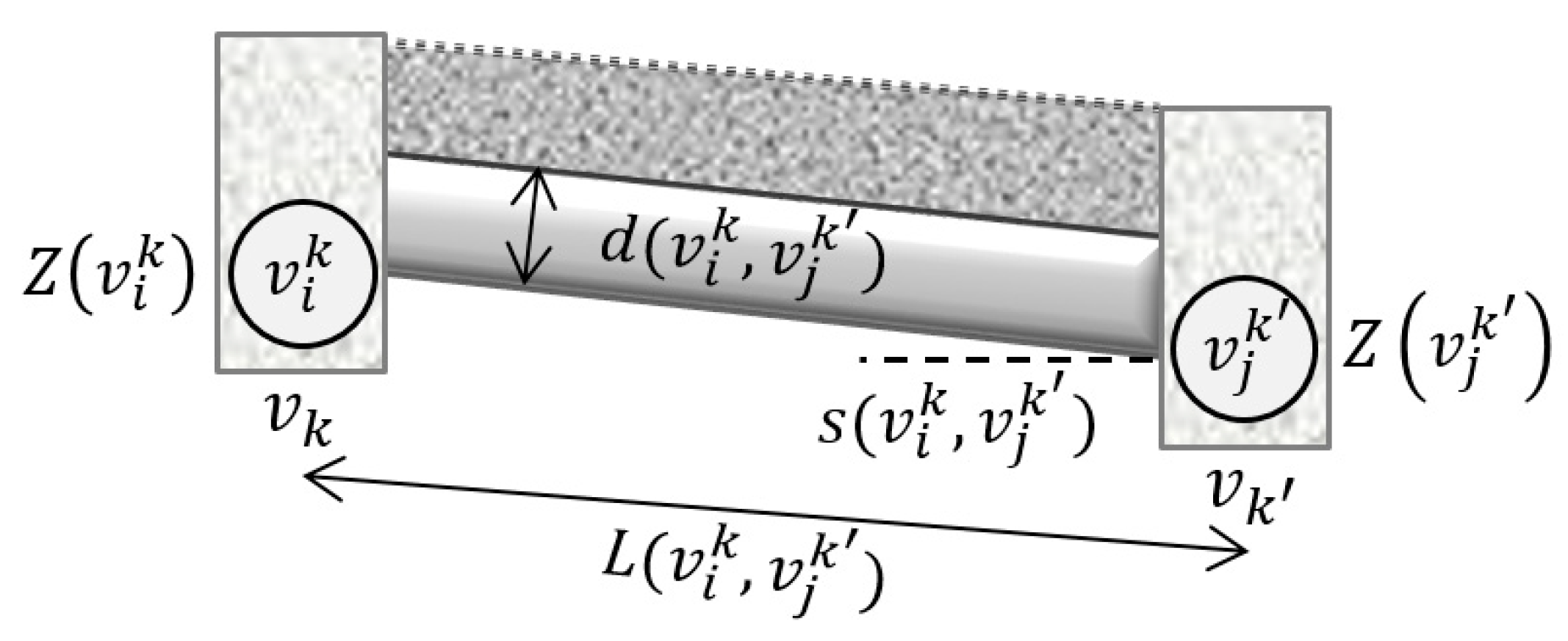
3.3. Hydraulic Design Model and Solution Approach
- is the set of nodes in the HD graph , where is the th design node associated to the tree node and is the last design node in the outfall node . Therefore, is the union of disjoint subsets for every tree node , i.e., .
- is the set of arcs of the HD graph .
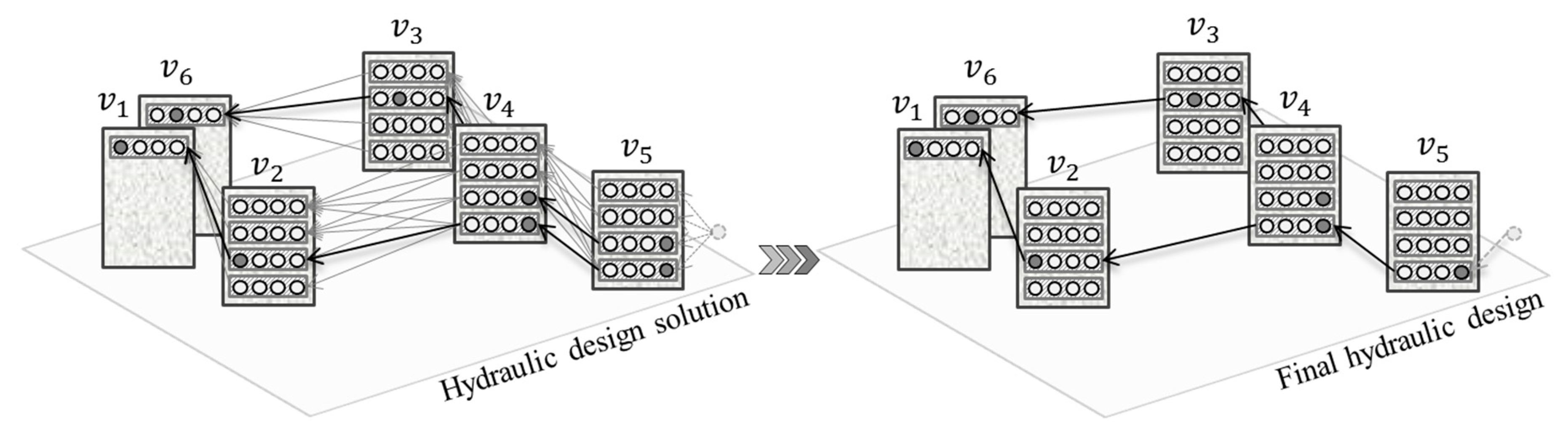
- Add a dummy design node connecting every design node in the outfall (see Figure 1);
- Assign a cost value for every arc in
- Reverse all arcs in and execute the Bellman–Ford algorithm [45] to obtain the one-to-all shortest paths from the outfall node to every other node in ;
- Retrieve the best paths from to any design node in ;
- Select the deepest and largest diameter pipe when multiple design arcs that are part of different shortest paths belong to the same tree arc , since only one pipe should exist in each section.
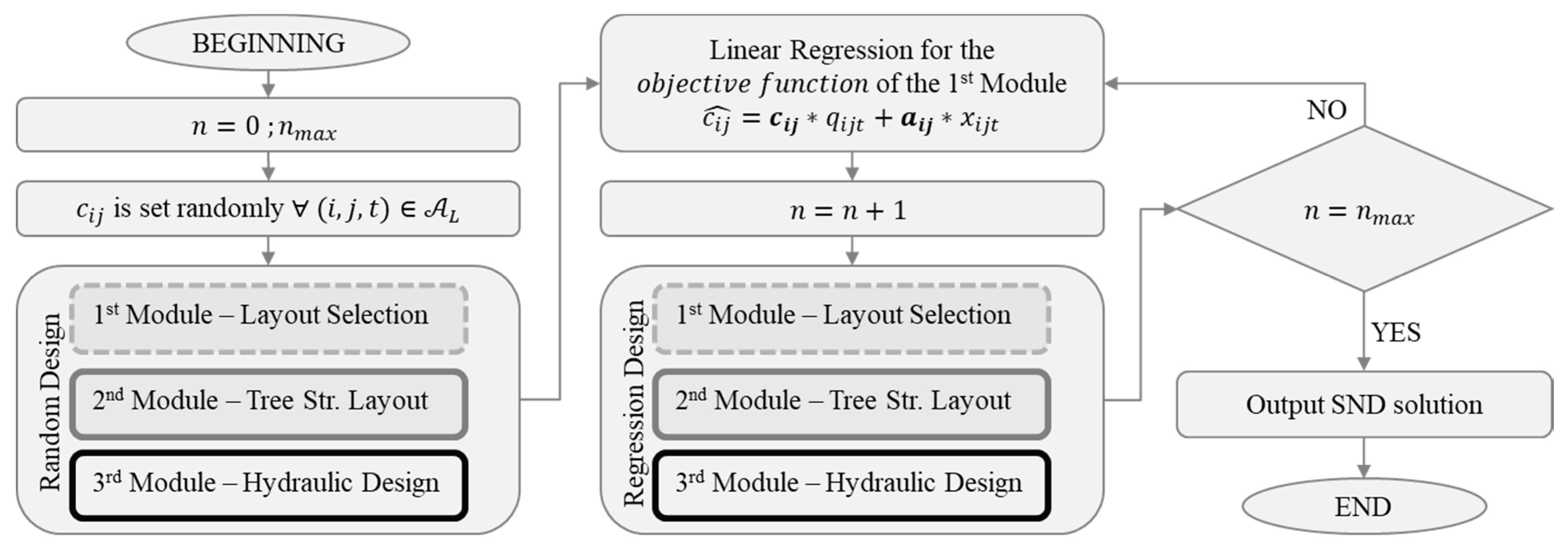
3.4. Iterative Scheme
3.5. Software and Data
3.6. Case Studies
4. Results
4.1. Benchmark Li and Matthew
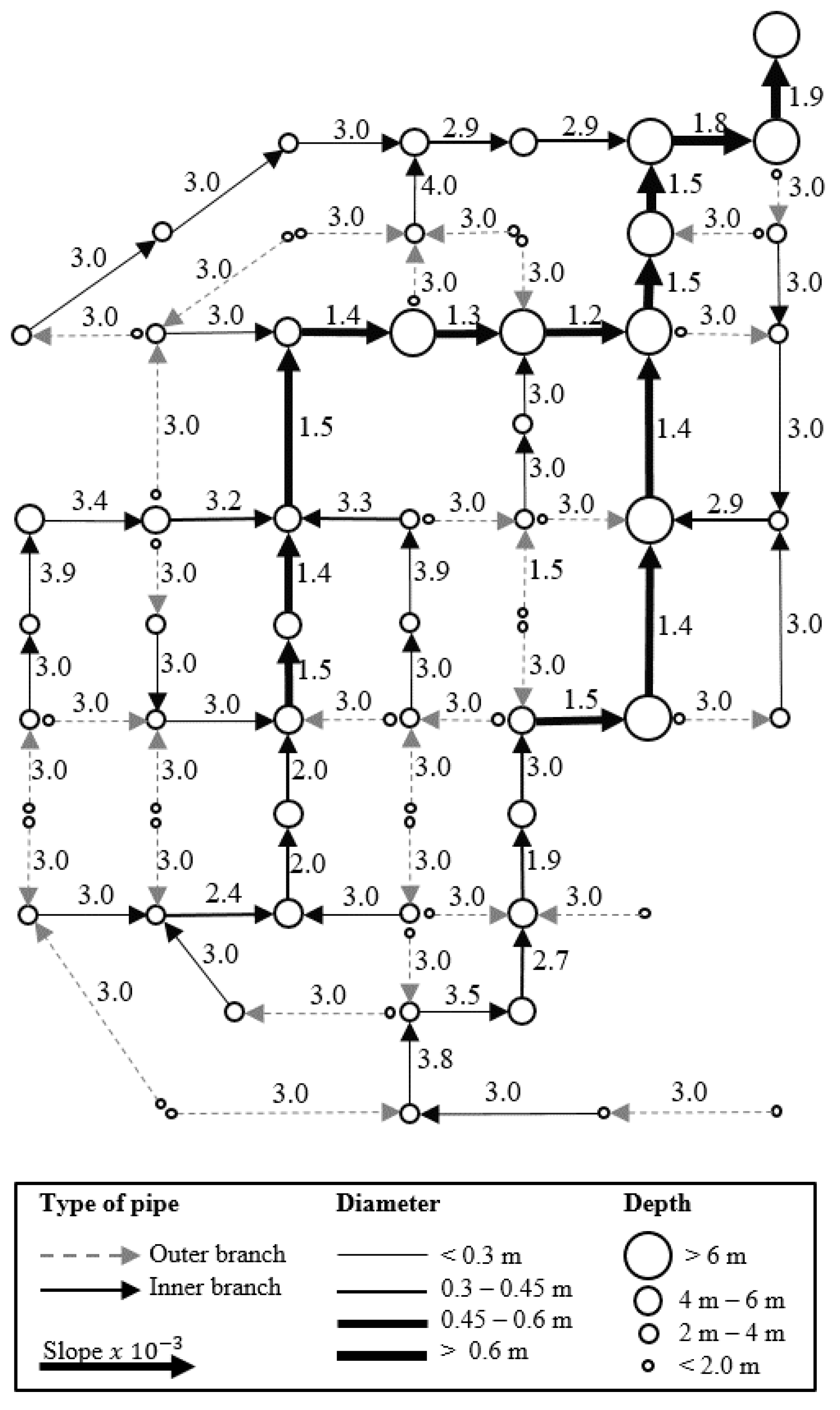
4.2. Benchmark Moeini and Afshar
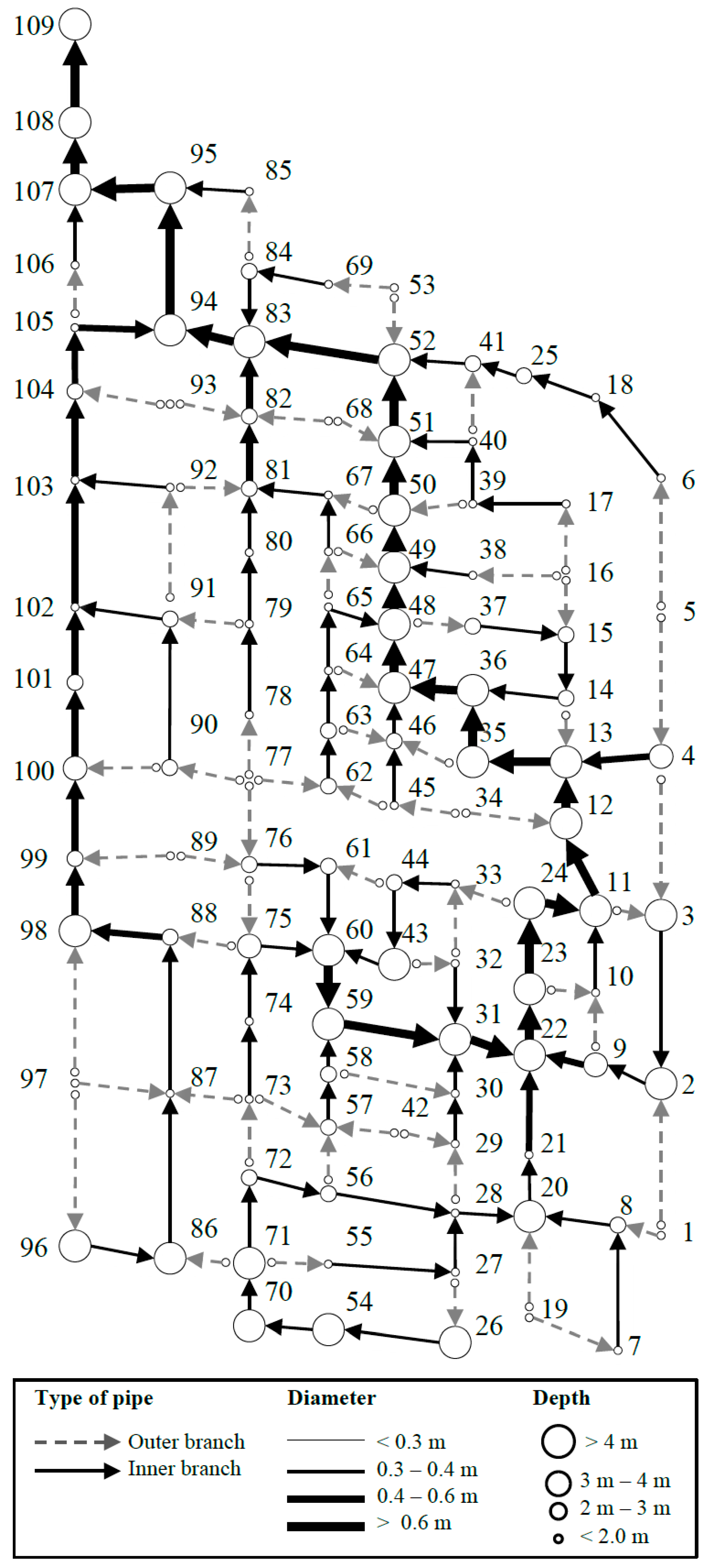
4.3. Real Network: Chicó
4.4. Convergence Curves
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Layout Selection | |
| is the graph that represents the layout selection problem. | |
| is the set of nodes representing manholes. | |
| is the set of undirected edges representing links between two nodes and . | |
| is the inflow at manhole . | |
| is the total flow in the system reaching the outfall manhole . | |
| is the ground elevation at manhole . | |
| is the set of possible types of pipes, containing outer-branch pipes () and inner-branch pipes (). | |
| is the set of directed links between two manholes, and , so that . is the binary decision variable that represents the flow direction and connection type in the network layout, for all and . | |
| is the continuous decision variable that represents the flow through arc of type , for all and . | |
| is a large positive number. | |
| Tree-structured Layout | |
| is the graph that represents the selected layout as a tree-structured network. | |
| is the set of nodes in the tree-structured graph | |
| is a label that represents the index of the manhole associated to tree node | |
| is a subset of that contains tree nodes associated with manhole . | |
| is the set of arcs in the tree-structured graph. | |
| Hydraulic Design | |
| is the auxiliary graph used to represent the hydraulic design problem. | |
| is the set of nodes in the hydraulic design graph , which is divided in subsets of nodes related with the tree node . | |
| is the set of arcs of the hydraulic design graph . | |
| is the discrete set of commercially available pipe diameters. | |
| is the discrete decision variable that represents a possible diameter for an upstream pipe of tree node and manhole . | |
| is the continuous decision variable that represents the elevation above a reference level of a node of the graph . | |
| is the slope for each pipe, fully determined by the invert elevations and at the extremes of the arc which represents a pipe. | |
| is the absolute roughness of the pipes. |
References
- Elimam, A.A.; Charalambous, C.; Ghobrial, F.H. Optimum design of large sewer networks. J. Environ. Eng. 1989, 115, 1171–1190. [Google Scholar] [CrossRef]
- Swamee, P.K.; Sharma, A.K. Optimal design of a sewer line using linear programming. Appl. Math. Model. 2013, 37, 4430–4439. [Google Scholar] [CrossRef]
- Gupta, M.; Rao, P.; Jayakumar, K. Optimization of integrated sewerage system by using simplex method. VFSTR J. STEM 2017, 3, 2455-2062. [Google Scholar]
- Safavi, H.; Geranmehr, M.A. Optimization of sewer networks using the mixed-integer linear programming. Urban Water J. 2017, 14, 452–459. [Google Scholar] [CrossRef]
- Holland, M.E. Computer Models of Waste-Water Collection Systems. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, May 1966. [Google Scholar]
- Mansouri, M.; Khanjani, M. Optimization of sewer networks using nonlinear programming. J. Water Wastewater. 1999, 10, 20–30. [Google Scholar]
- Mays, L.W.; Yen, B.C. Optimal cost design of branched sewer systems. Water Resour. Res. 1975, 11, 37–47. [Google Scholar] [CrossRef]
- Walters, G.A. The design of the optimal layout for a sewer network. Eng. Optim. 1985, 9, 37–50. [Google Scholar] [CrossRef]
- Duque, N.; Duque, D.; Saldarriaga, J. A new methodology for the optimal design of series of pipes in sewer systems. J. Hydroinf. 2016, 18, 757–772. [Google Scholar] [CrossRef]
- Kulkarni, V.S.; Khanna, P. Pumped wastewater collection systems optimization. J. Environ. Eng. 1985, 111, 589–601. [Google Scholar] [CrossRef]
- Afshar, M.H. Rebirthing genetic algorithm for storm sewer network design. Sci. Iran. 2012, 19, 11–19. [Google Scholar] [CrossRef]
- Haghighi, A.; Bakhshipour, A.E. Optimization of sewer networks using an adaptive genetic algorithm. Water Resour. Manag. 2012, 26, 3441–3456. [Google Scholar] [CrossRef]
- Palumbo, A.; Cimorelli, L.; Covelli, C.; Cozzolino, L.; Mucherino, C.; Pianese, D. Optimal design of urban drainage networks. Civ. Eng. Environ. Syst. 2014, 31, 79–96. [Google Scholar] [CrossRef]
- Cozzolino, L.; Cimorelli, L.; Covelli, C.; Mucherino, C.; Pianese, D. An innovative approach for drainage network sizing. Water 2015, 7, 546–567. [Google Scholar] [CrossRef]
- Cisty, M. Hybrid genetic algorithm and linear programming method for least-cost design of water distribution systems. Water Resour. Manag. 2010, 24, 1–24. [Google Scholar] [CrossRef]
- Hassan, W.H.; Jassem, M.H.; Mohammed, S.S. A GA-HP model for the optimal design of sewer networks. Water Resour. Manag. 2018, 32, 865–879. [Google Scholar] [CrossRef]
- Afshar, M.H. A parameter free continuous ant colony optimization algorithm for the optimal design of storm sewer networks: Constrained and unconstrained approach. Adv. Eng. Softw. 2010, 41, 188–195. [Google Scholar] [CrossRef]
- Moeini, R.; Afshar, M.H. Arc based ant colony optimization algorithm for optimal design of gravitational sewer networks. Ain Shams Eng. J. 2017, 8, 207–223. [Google Scholar] [CrossRef]
- Yeh, S.F.; Chang, Y.J.; Lin, M.D. Optimal design of sewer network by tabu search and simulated annealing. In Proceedings of the 2013 IEEE International Conference on Industrial Engineering and Engineering Management, Bangkok, Thailand, 10–13 December 2013; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2013; pp. 1636–1640. [Google Scholar]
- Haghighi, A.; Bakhshipour, A.E. Deterministic integrated optimization model for sewage collection networks using tabu search. J. Water Resour. Plan. Manag. 2015, 141. [Google Scholar] [CrossRef]
- Ahmadi, A.; Zolfagharipoor, M.A.; Nafisi, M. Development of a hybrid algorithm for the optimal design of sewer networks. J. Water Resour. Plan. Manag. 2018, 144. [Google Scholar] [CrossRef]
- Afshar, M.; Zaheri, M.; Kim, J. Improving the efficiency of cellular automata for sewer network design optimization problems using adaptive refinement. Procedia Eng. 2016, 154, 1439–1447. [Google Scholar] [CrossRef]
- Rohani, M.; Afshar, M.H. Optimal design of Sewer network using Cellular Automata. SCIREA J. Hydraul. Eng. 2016, 1, 1–17. [Google Scholar]
- Zaheri, M.M.; Ghanbari, R.; Afshar, M.H. A two-phase simulation–optimization cellular automata method for sewer network design optimization. Eng. Optim. 2019, 52, 620–636. [Google Scholar] [CrossRef]
- Navin, P.K.; Mathur, Y.P.; Kumar, D. Layout optimization of sewer network using minimum cumulative flow in the sewer network. In Advances in Waste Management; Springer Science and Business Media LLC.: Berlin, Germany, 2018; pp. 333–343. [Google Scholar]
- Hsie, M.; Wu, M.Y.; Huang, C.Y. Optimal urban sewer layout design using Steiner tree problems. Eng. Optim. 2019, 51, 1980–1996. [Google Scholar] [CrossRef]
- Walters, G.A.; Smith, D.K. Evolutionary design algorithm for optimal layout of tree networks. Eng. Optim. 1995, 24, 261–281. [Google Scholar] [CrossRef]
- Haghighi, A. Loop-by-loop cutting algorithm to generate layouts for urban drainage systems. J. Water Resour. Plan. Manag. 2013, 139, 693–703. [Google Scholar] [CrossRef]
- Afshar, M.H.; Mariño, M.A. Application of an ant algorithm for layout optimization of tree networks. Eng. Optim. 2006, 38, 353–369. [Google Scholar] [CrossRef]
- Moeini, R.; Afshar, M.H. Layout and size optimization of sanitary sewer network using intelligent ants. Adv. Eng. Softw. 2012, 51, 49–62. [Google Scholar] [CrossRef]
- Moeini, R.; Afshar, M.H. Extension of the hybrid ant colony optimization algorithm for layout and size optimization of sewer networks. J. Environ. Informatics 2019, 33, 68–81. [Google Scholar] [CrossRef]
- Navin, P.K.; Mathur, Y.P. Layout and component size optimization of sewer network using spanning tree and modified PSO algorithm. Water Resour. Manag. 2016, 30, 3627–3643. [Google Scholar] [CrossRef]
- Mays, L.W.; Wenzel, H.G. Optimal design of multilevel branching sewer systems. Water Resour. Res. 1976, 12, 913–917. [Google Scholar] [CrossRef]
- Li, G.; Matthew, R.G.S. New approach for optimization of urban drainage systems. J. Environ. Eng. 1990, 116, 927–944. [Google Scholar] [CrossRef]
- Diogo, A.F.; Graveto, V.M. Optimal layout of sewer systems: A deterministic versus a stochastic model. J. Hydraul. Eng. 2006, 132, 927–943. [Google Scholar] [CrossRef]
- Rohani, M.; Afshar, M.; Moeini, R. Layout and size optimization of sewer networks by hybridizing the GHCA model with heuristic algorithms. Scientia Iranica. Trans. A Sch. J. 2015, 22, 1742–1754. [Google Scholar]
- Bakhshipour, A.E.; Makaremi, Y.; Dittmer, U. Multiobjective design of sewer networks. J. Hydraul. Struct. 2017, 3, 49–56. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2006. [Google Scholar]
- Smith, D.K.; Ahuja, R.K.; Magnanti, T.L.; Orlin, J.B. Network Flows: Theory, Algorithms, and Applications. J. Oper. Res. Soc. 1994, 45, 1340. [Google Scholar] [CrossRef]
- Butler, D.; Davies, J.W. Urban Drainage, 3rd ed.; Spon Press: Milton Park, UK; Abingdon, UK, 2011. [Google Scholar]
- Bertsimas, D.; Tsitsiklis, J.N. Introduction to Linear Optimization; Athena Scientific: Belmont, MA, USA, 1997; Volume 6, pp. 479–530. [Google Scholar]
- Johnson, D.S.; Lenstra, J.K.; Kan, A.R. The complexity of the network design problem. Networks 1978, 8, 279–285. [Google Scholar] [CrossRef]
- FICO. Fair Isaac Corporation FICO. In Xpress-MP optimizer: Reference Manual; Leamington Spa, Release 20.0; FICO: Warwickshire, UK, 2009; pp. 19–23. Available online: https://www.msi-jp.com/xpress/learning/square/optimizer.pdf (accessed on 8 June 2020).
- Gurobi Optimizer, 5.0. Available online: http://www.gurobi.com (accessed on 8 June 2020).
- Bellman, R. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Pan, T.C.; Kao, J.J. GA-QP Model to optimize sewer system design. J. Environ. Eng. 2009, 135, 17–24. [Google Scholar] [CrossRef]
- Liu, C.; Han, H.G.; Wang, C.; Qiao, J. An adaptive differential evolution algorithm for sewer networks design. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2014; pp. 3577–3583. [Google Scholar]
- Haghighi, A.; Bakhshipour, A.E. Reliability-based layout design of sewage collection systems in flat areas. Urban Water J. 2016, 13, 790–802. [Google Scholar] [CrossRef]

| Constraint | Value | Condition | |
|---|---|---|---|
| 1 | Minimum diameter | 0.2 m | Always |
| 2 | Maximum filling ratio | 0.6 | |
| 0.7 | |||
| 0.75 | |||
| 0.8 | |||
| 3 | Minimum velocity | 0.7 | |
| 0.8 | |||
| 4 | Maximum velocity | 5.0 | |
| 5 | Minimum gradient | 0.003 | Flow rate < 0.015 |
| Method | Researchers | Optimized Layout | Construction Cost (Yuan) × 106 |
|---|---|---|---|
| MGA | Pan and Kao [46] | No | 1.91 |
| Adaptive GA | Haghighi and Bakhshipour [12] | No | 1.84 |
| MILP | Safavi and Geranmehr [4] | No | 1.57 |
| SDE-GOBL | Liu et al. [47] | No | 1.53 |
| Loop-by-loop cutting algorithm and GA-DDDP | Haghighi and Bakhshipour [28] | Yes | 1.59 |
| Loop-by-loop cutting algorithm and TS | Haghighi and Bakhshipour [20] | Yes | 1.43 |
| Reliability - DDDP | Haghighi and Bakhshipour [48] | Yes | 2.41 |
| ACOA-TGA-NLP | Moeini and Afshar [31] | Yes | 1.39 |
| MIP and DP | (Present work) | Yes | 1.29 |
| ACOA-TGA-NLP [31] | DP (Present work) with Fixed Layout [31] | MIP and DP (Present Work) | |
|---|---|---|---|
| Costs | |||
| Construction Cost | ¥ 640,845 * | ¥ 400,940 | ¥ 369,498 |
| Maintenance Cost | ¥ 269,155 * | ¥ 168,395 | ¥ 155,189 |
| Total Cost | ¥ 910,000 * | ¥ 569,335 | ¥ 524,687 |
| Computational effort | |||
| Iterations [–] | 10 | 1 | 30 |
| Time [min] | 198 | 4 | 115 |
| Physical characteristics | |||
| Average diameter [m] | 0.331 ** | 0.262 | 0.267 |
| Average depth [m] | Not reported | 2.07 | 1.95 |
| Outfall diameter [m] | 1.05 ** | 0.7 | 0.8 |
| Outfall depth [m] | Not reported | 6.6 | 5.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duque, N.; Duque, D.; Aguilar, A.; Saldarriaga, J. Sewer Network Layout Selection and Hydraulic Design Using a Mathematical Optimization Framework. Water 2020, 12, 3337. https://doi.org/10.3390/w12123337
Duque N, Duque D, Aguilar A, Saldarriaga J. Sewer Network Layout Selection and Hydraulic Design Using a Mathematical Optimization Framework. Water. 2020; 12(12):3337. https://doi.org/10.3390/w12123337
Chicago/Turabian StyleDuque, Natalia, Daniel Duque, Andrés Aguilar, and Juan Saldarriaga. 2020. "Sewer Network Layout Selection and Hydraulic Design Using a Mathematical Optimization Framework" Water 12, no. 12: 3337. https://doi.org/10.3390/w12123337
APA StyleDuque, N., Duque, D., Aguilar, A., & Saldarriaga, J. (2020). Sewer Network Layout Selection and Hydraulic Design Using a Mathematical Optimization Framework. Water, 12(12), 3337. https://doi.org/10.3390/w12123337







