Uncertainty Relations in Hydrodynamics
Abstract
1. Introduction
2. Classical Variation and Optimal Control
3. General Setup for Stochastic Variation
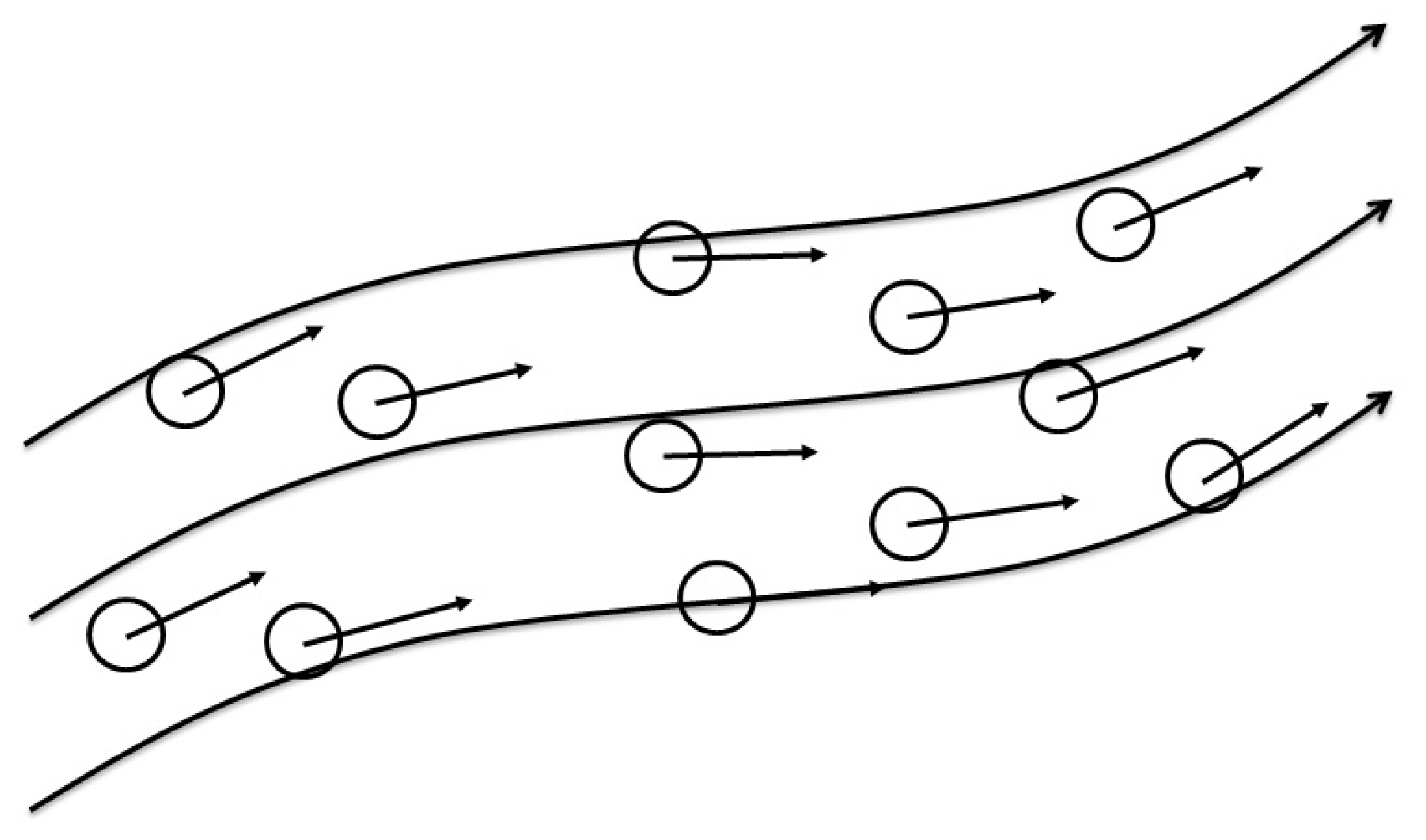
3.1. Zigzag Trajectory and Two Brownian Motions
3.2. Mean Forward and Backward Derivatives
3.3. Fokker-Planck Equation and Consistency Condition
4. Stochastic Variational Method for Particle
4.1. Stochastic Action and Its Variation
4.2. Schrödinger Equation
4.3. Stochastic Noether Theorem
5. Uncertainty Relations for Particles in SVM
5.1. Stochastic Hamiltonian Formalism
5.2. Inequalities in SVM and Quantum-Mechanical Uncertainty Relations
5.3. Generalized Bracket
6. Uncertainty Relations for Continuum Media
6.1. Brief Summary of Variational Approach to Ideal Fluid
6.2. Derivation of Compressible NSF Equation in SVM
6.3. Uncertainty Relations in Fluid
6.4. Uncertainty Relations in Quantum Field Theory and SVM
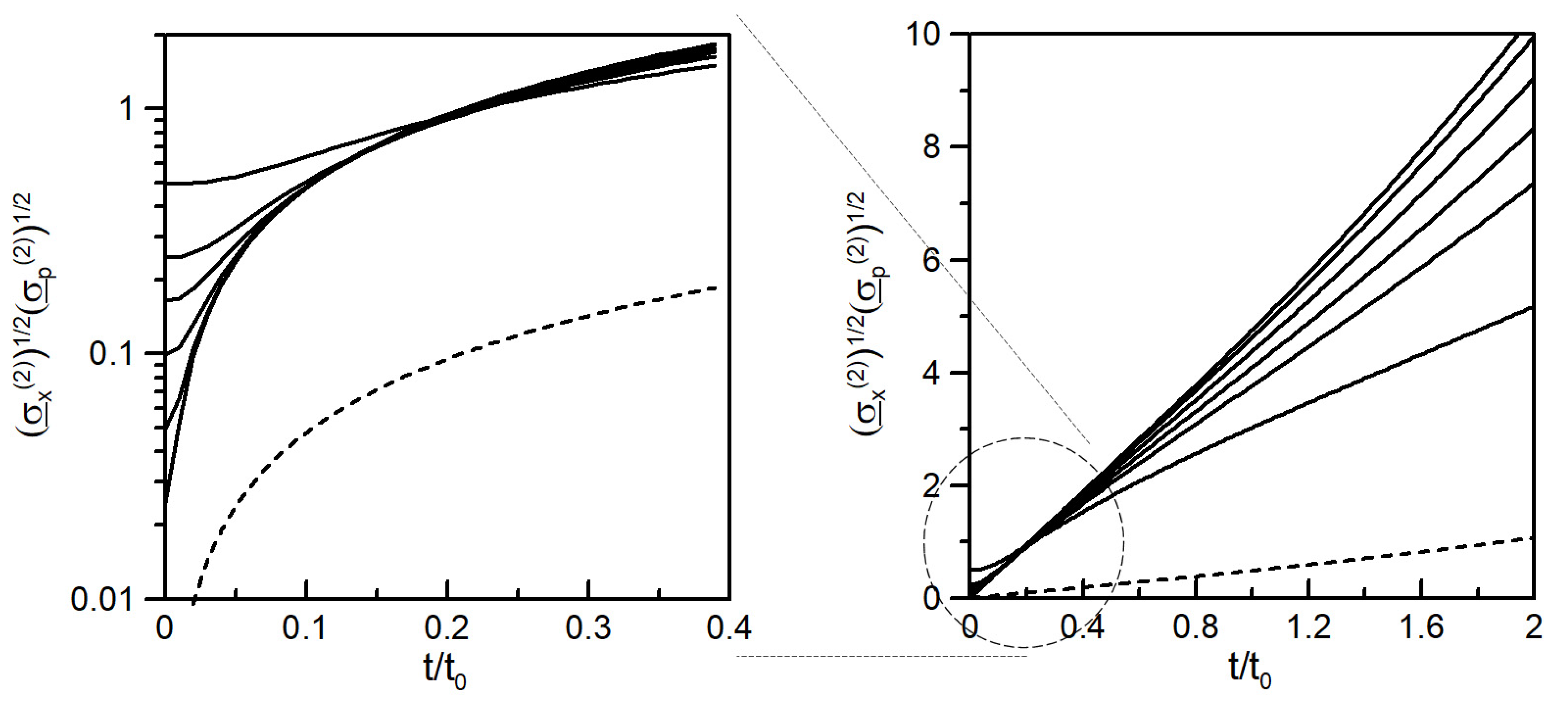
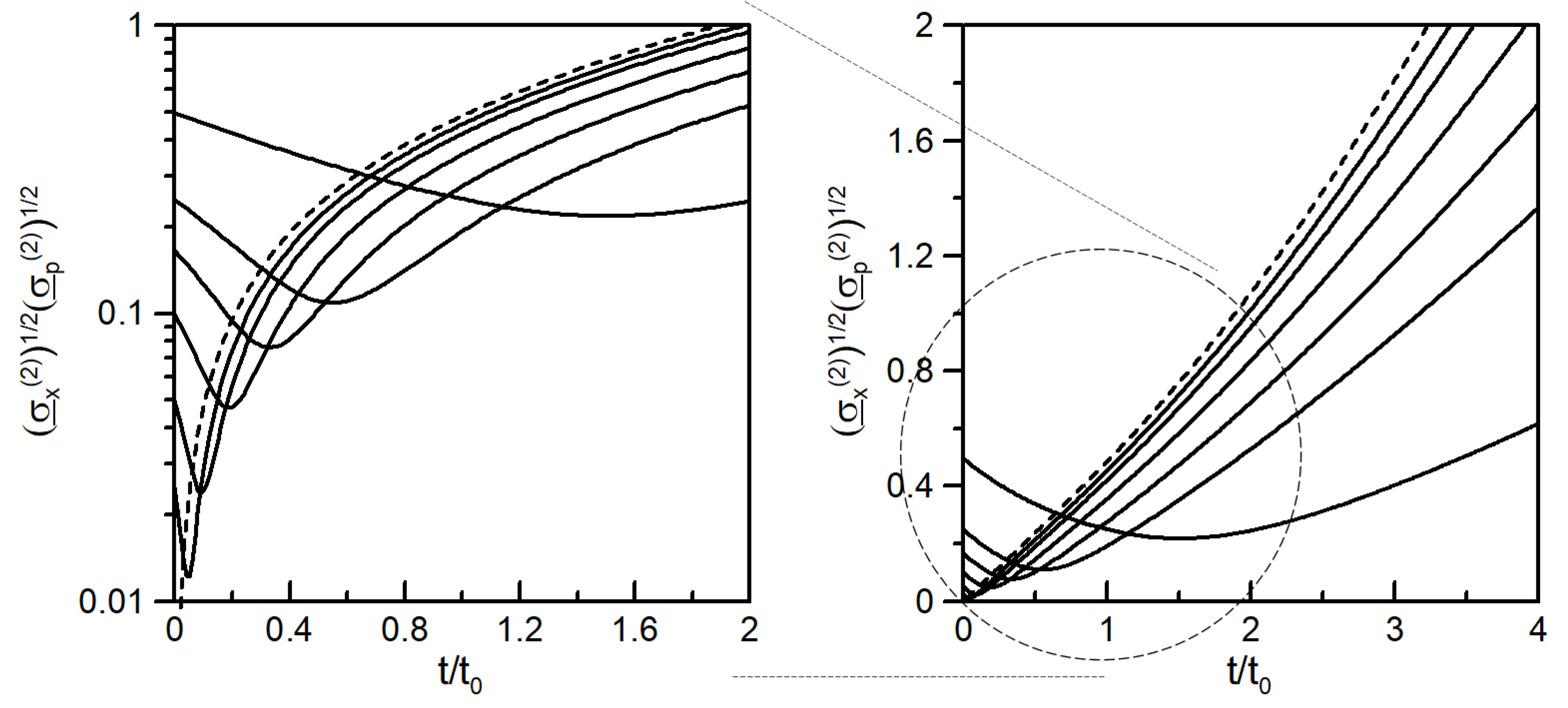
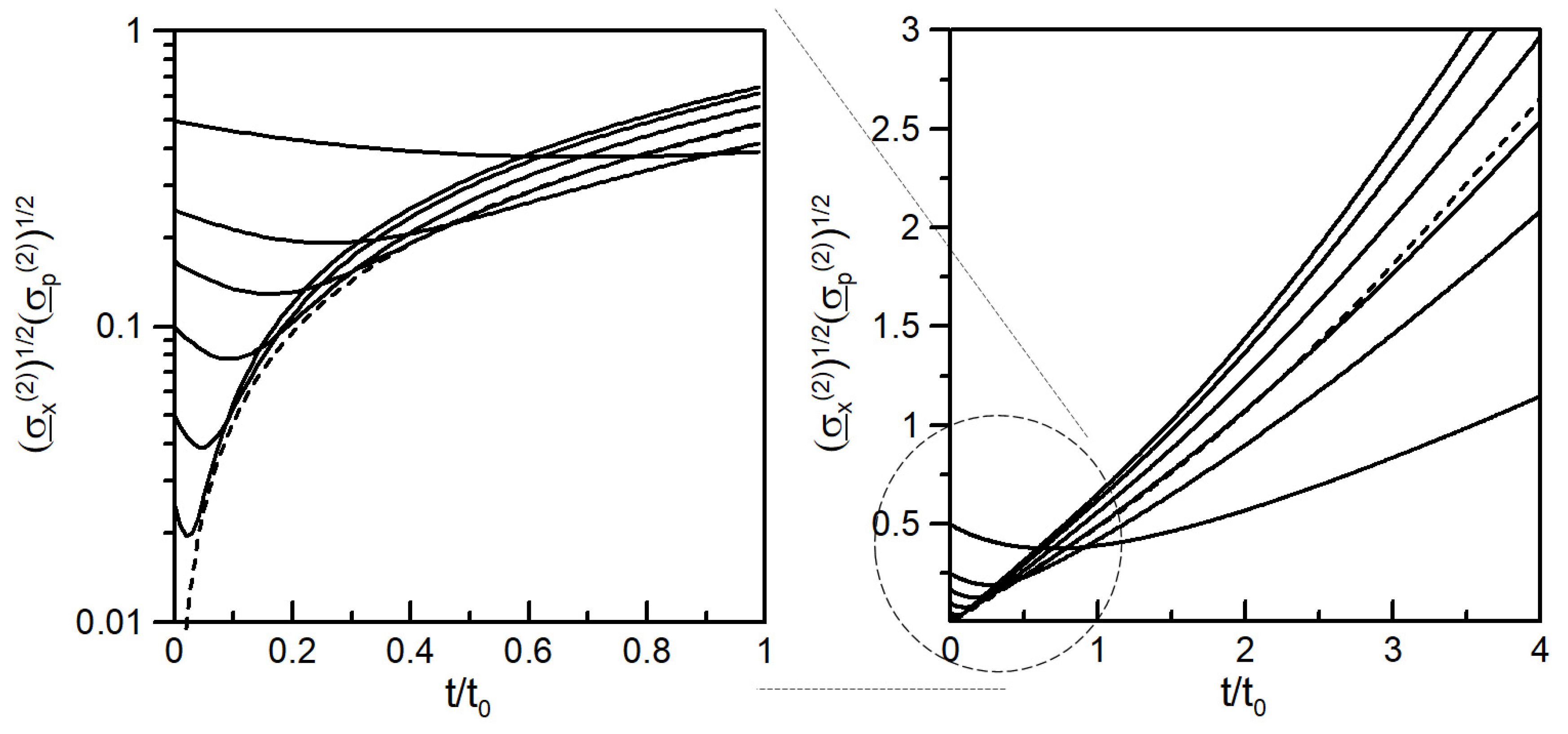
7. Numerical Examples and Uncertainty Relations for Liquid and Gas
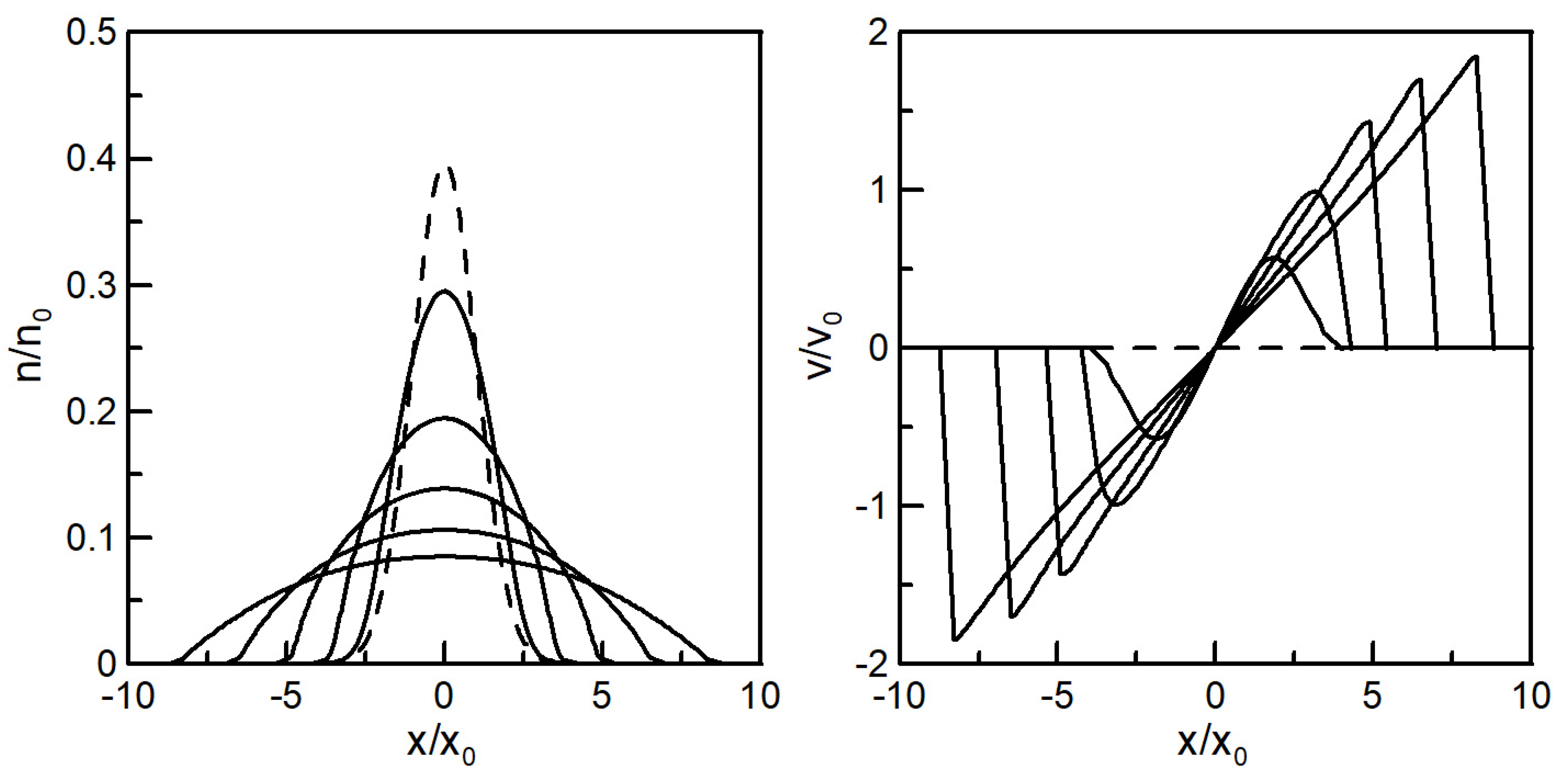
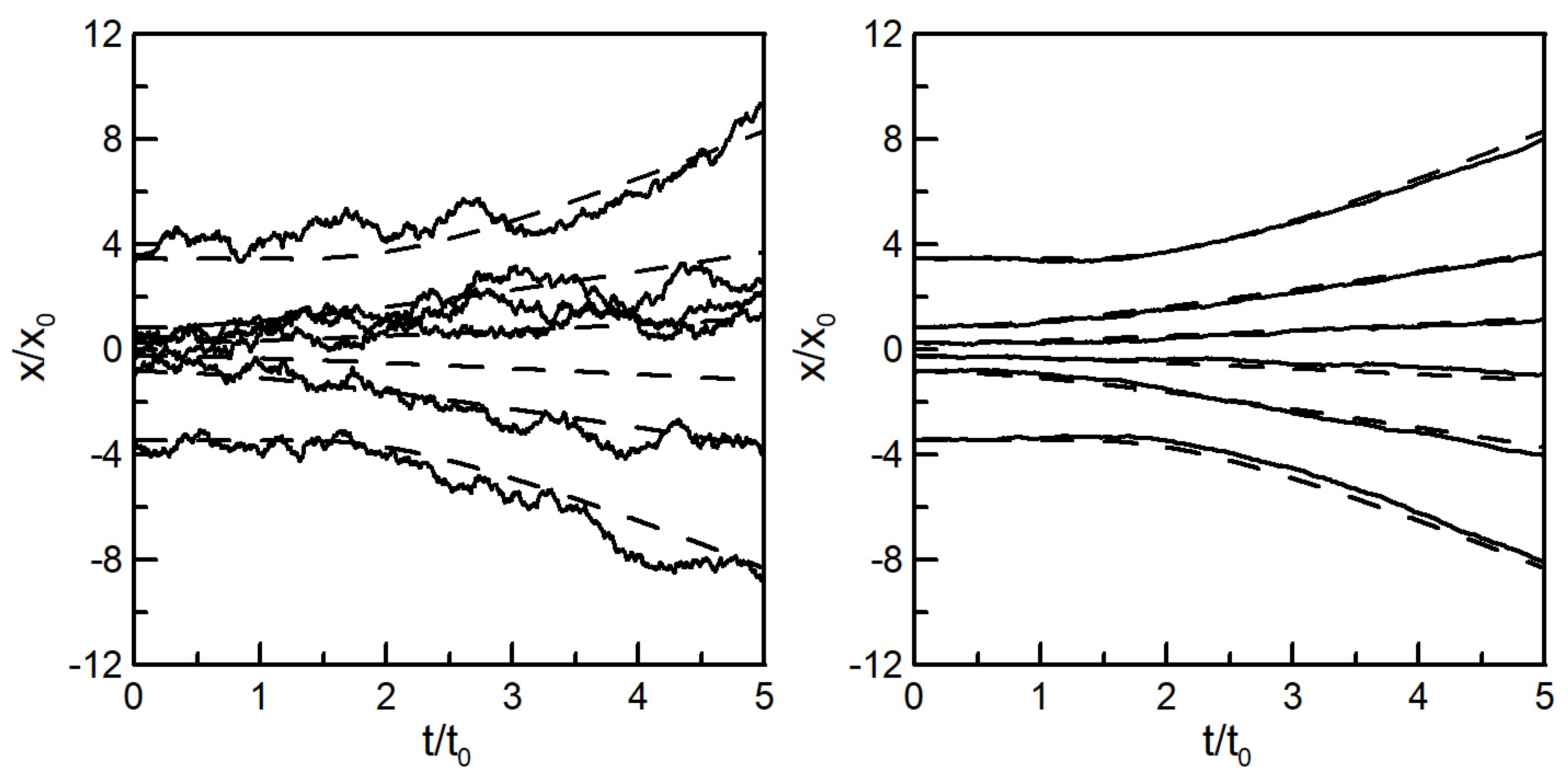
7.1. Time Evolution of the NSF Equation in 1 + 1 Dimension
7.2. Uncertainty Relations for Gaussian Initial Condition
8. Discussions and Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A. Ito’s Lemma
Appendix B. Bernoulli Equation in Quantum Hydrodynamics
Appendix C. Relation to Quantum Mechanical Standard Deviation
Appendix D. The Positivity of the Kinetic Term of the Lagrangian
Appendix E. Gross-Pitaevskii Equation
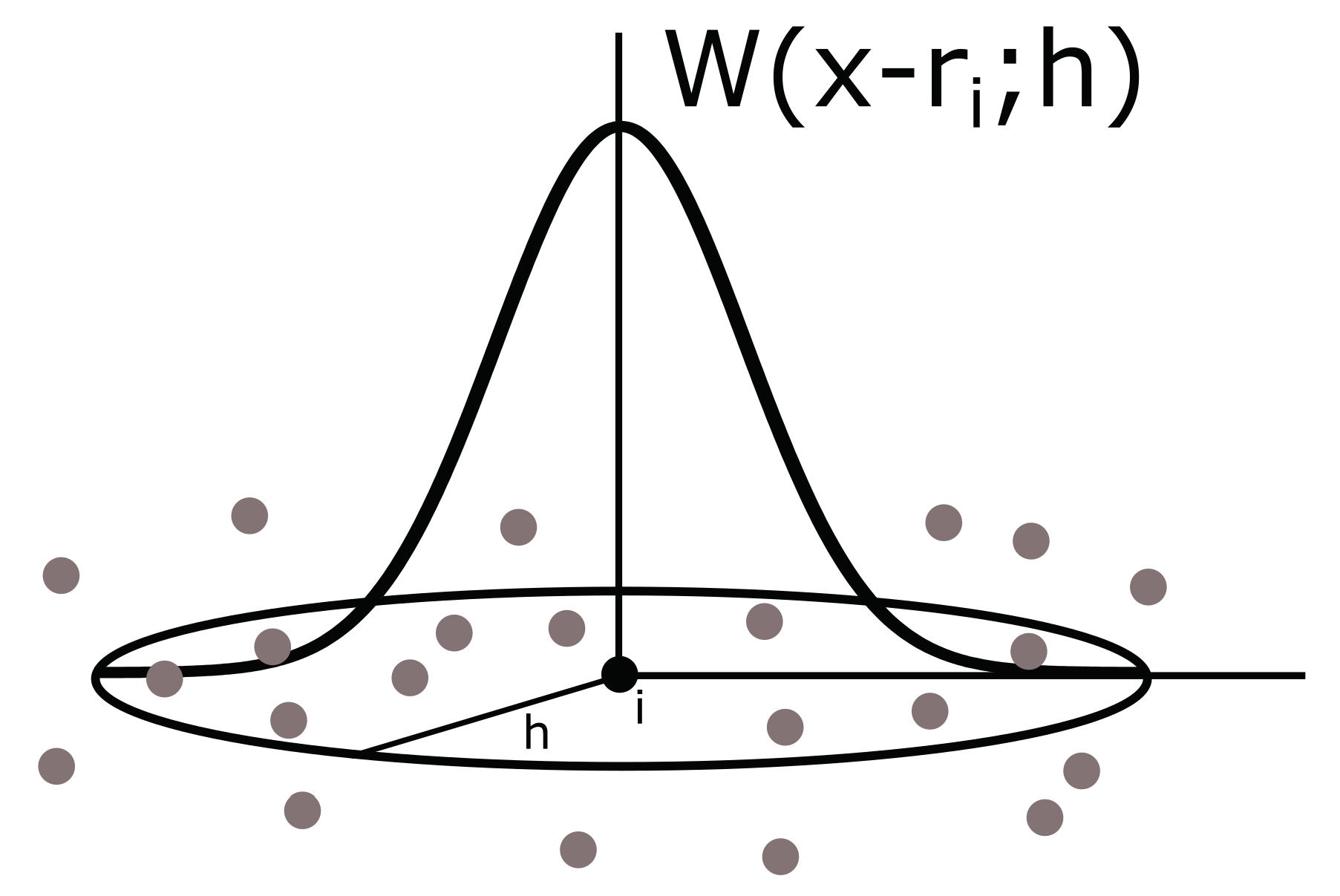
Appendix F. Smoothed Particle Hydrodynamics
References
- Lanczos, C. The Variational Principles of Mechanics, 4th ed.; University of Toronto Press: Tronto, ON, USA, 1970. [Google Scholar]
- Strutt, A.; Lord Rayleigh, H.J.W. Some general theorems relating to vibrations. Proc. Math. Soc. Lond. 1971, s1–s4, 357. [Google Scholar]
- Inoue, A.; Funaki, T. On a new derivation of the Navier-Stokes equation. Comm. Math. Phys. 1979, 65, 83. [Google Scholar] [CrossRef]
- Nakagomi, T.; Yasue, K.; Zambrini, J.C. Stochastic variational derivations of the Navier-Stokes equation. Lett. Math. Phys. 1981, 160, 337. [Google Scholar] [CrossRef]
- Yasue, K. Variational principle for Navier-Stokes equation. J. Funct. Anal. 1983, 51, 133. [Google Scholar] [CrossRef][Green Version]
- Gomes, D. A variational formulation for the Navier-Stokes equation. Comm. Math. Phys. 2005, 257, 227. [Google Scholar] [CrossRef]
- Eyink, G.L. Stochastic least-action principle for the incompressible Navier-Stokes equation. Phys. D 2010, 239, 1236. [Google Scholar] [CrossRef]
- Arnaudon, M.; Cruzeiro, A.B. Lagrangian Navier-Stokes diffusions on manifolds: Variational principle and stability. Bull. Sci. Math. 2012, 136, 857. [Google Scholar] [CrossRef]
- Koide, T.; Kodama, T. Navier-Stokes, Gross-Pitaevskii and generalized diffusion equations using the stochastic variational method. J. Phys. A 2012, 45, 255204. [Google Scholar] [CrossRef][Green Version]
- Delbaen, F.; Qiu, J.; Tang, S. Forward-backward stochastic differential systems associated to Navier-Stokes equations in the whole space. Sto. Proc. Appl. 2015, 125, 2516. [Google Scholar] [CrossRef]
- Novikov, A.; Khalil, K.S. A stochastic Lagrangian particle system for the Navier-Stokes equations. arXiv 2017, arXiv:1709.01536. [Google Scholar]
- Marner, F.; Scholle, M.; Herrmannand, D.; Gaskell, P.H. Competing Lagrangians for incompressible and compressible viscous flow. R. Soc. Open Sci. 2018, 6, 181595. [Google Scholar] [CrossRef] [PubMed]
- Cruzeiro, A.B. Navier-Stokes and stochastic Navier-Stokes equations via Lagrange multipliers. J. Geom. Mech. 2019, 11, 553. [Google Scholar] [CrossRef]
- Yasue, K. Stochastic calculus of variation. J. Funct. Anal. 1981, 41, 327. [Google Scholar] [CrossRef]
- Ozawa, M. Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurement. Phys. Rev. A 2003, 67, 042105. [Google Scholar] [CrossRef]
- Erhart, J.; Sponar, S.; Sulyok, G.; Badurek, G.; Ozawa, M.; Hasegawa, Y. Experimental demonstration of a universally valid error-disturbance uncertainty relation in spin measurements. Nat. Phys. 2012, 8, 185. [Google Scholar] [CrossRef]
- Kaneda, F.; Baek, S.; Ozawa, M.; Edamatsu, K. Experimental Test of Error-Disturbance Uncertainty Relations by Weak Measurement. Phys. Rev. Lett. 2014, 112, 020402. [Google Scholar] [CrossRef]
- Ringbauer, M.; Biggerstaff, D.N.; Broom, M.A.; Fedrizzi, A.; Branciard, C.; White, A.G. Experimental Joint Quantum Measurements with Minimum Uncertainty. Phys. Rev. Lett. 2014, 112, 020401. [Google Scholar] [CrossRef]
- Demirel, B.; Sponar, S.; Sulyok, G.; Ozawa, M.; Hasegawa, Y. Experimental Test of Residual Error-Disturbance Uncertainty Relations for Mixed Spin-1/2 States. Phys. Rev. Lett. 2016, 117, 140402. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172. [Google Scholar] [CrossRef]
- Koide, T.; Kodama, T. Generalization of uncertainty relation for quantum and stochastic systems. Phys. Lett. A 2018, 382, 1472. [Google Scholar] [CrossRef]
- Gazeau, J.-P.; Koide, T. Uncertainty relation for angle from a quantum-hydrodynamical perspective. Ann. Phys. 2020, 416, 168159. [Google Scholar] [CrossRef]
- Lindgren, J.; Liukkonen, J. The Heisenberg Uncertainty Principle as an Endogenous Equilibrium Property of Stochastic Optimal Control Systems in Quantum Mechanics. Symmetry 2020, 12, 1533. [Google Scholar] [CrossRef]
- Holland, C.J. A new energy characterization of the smallest eigenvalue of the schrödinger equation. Commun. Pur. Appl. Math. 1977, 30, 755. [Google Scholar] [CrossRef]
- Ioannis, K. On a stochastic representation for the principal eigenvalue of a second-order differential equation. Stochastics 1980, 3, 305. [Google Scholar] [CrossRef][Green Version]
- Papiez, L. Stochastic optimal control and quantum mechanics. J. Math. Phys. 1982, 23, 1017. [Google Scholar] [CrossRef]
- Fleming, W.H. Stochastic Calculus of Variations and Mechanics. J. Optim. Theory App. 1983, 41, 55. [Google Scholar] [CrossRef]
- Guerra, F.; Morato, L.M. Quantization of dynamical systems and stochastic control theory. Phys. Rev. D 1983, 27, 1774. [Google Scholar] [CrossRef]
- Rosenbrock, H.H. A Variational Principle for Quantum Mechanics. Phys. Lett. 1985, 110, 343. [Google Scholar] [CrossRef]
- Marra, R. Variational principles for conservative and dissipative diffusions. Phys. Rev. D 1987, 36, 1724. [Google Scholar] [CrossRef]
- Serva, M. Relativistic stochastic processes associated to Klein-Gordon equation. Ann. Inst. Henri Poincaré 1988, 49, 415. [Google Scholar]
- Kime, K.; Blaquiere, A. From two stochastic optimal control problems to the Schrodinger equation. In Modeling and Control of Systems. Lecture Notes in Control and Information Sciences; Blaquiere, A., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; Volume 121. [Google Scholar]
- Jaekel, M.T. Lagrangians of Stochastic Mechanics. J. Phys. A 1990, 23, 3497. [Google Scholar] [CrossRef]
- Pavon, M. Hamilton’s principle in stochastic mechanics. J. Math. Phys. 1995, 36, 6774. [Google Scholar] [CrossRef]
- Nagasawa, M. Stochastic Processes in Quantum Physics; Birkhäuser: Heidelberg, Germany, 2000. [Google Scholar]
- Kappen, H.J. Linear Theory for Control of Nonlinear Stochastic Systems. Phys. Rev. Lett. 2005, 95, 200201. [Google Scholar] [CrossRef] [PubMed]
- Cresson, J.; Darses, S. Stochastic embedding of dynamical systems. J. Math. Phys. 2007, 48, 072703. [Google Scholar] [CrossRef]
- Holm, D.D. Variational principles for stochastic fluid dynamics. Proc. R. Soc. Lond. A 2015, 471, 2014.0963. [Google Scholar] [CrossRef]
- Kurihara, Y. Stochastic metric space and quantum mechanics. J. Phys. Commun. 2018, 2, 035025. [Google Scholar] [CrossRef]
- Ohsumi, A. An interpretation of the Schödinger equation in quantum mechanics from the control-theoretic point of view. Automatica 2019, 99, 181. [Google Scholar] [CrossRef]
- Lindgren, J.; Liukkonen, J. Quantum Mechanics can be understood through stochastic optimization on spacetimes. Sci. Rep. 2019, 9, 19984. [Google Scholar] [CrossRef]
- Koide, T.; Kodama, T. Novel effect induced by spacetime curvature in quantum hydrodynamics. Phys. Lett. A 2019, 383, 2713. [Google Scholar] [CrossRef]
- Koide, T.; Kodama, T. Variational formulation of compressible hydrodynamics in curved spacetime and symmetry of stress tensor. J. Phys. A 2020, 53, 215701. [Google Scholar] [CrossRef]
- Nelson, E. Derivation of the Schrödinger Equation from Newtonian Mechanics. Phys. Rev. 1966, 150, 1079. [Google Scholar] [CrossRef]
- Zambrini, J.C. Stochastic Dynamics: A Review of Stochastic Calculus of Variations. Int. J. Theor. Phys. 1985, 24, 277. [Google Scholar] [CrossRef]
- Koide, T.; Kodama, T.; Tsushima, K. Unified description of classical and quantum behaviours in a variational principle. J. Phys. Conf. Ser. 2015, 626, 012055. [Google Scholar] [CrossRef]
- Cruzeiro, A.B. Stochastic Approaches to Deterministic Fluid Dynamics: A Selective Review. Water 2020, 12, 864. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Methods: For Physics, Chemistry and the Natural Sciences; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Biane, P. Itô’s stochastic calculus and Heisenberg commutation relations. Stoch. Proc. Their Appl. 2010, 120, 698. [Google Scholar] [CrossRef]
- Koide, T. How is an optimized path of classical mechanics affected by random noise? J. Phys. Conf. Ser. 2013, 410, 012025. [Google Scholar] [CrossRef]
- Madelung, E. Quantentheorie in hydrodynamischer Form. Z. Phys. 1927, 40, 322. [Google Scholar] [CrossRef]
- Bohm, D. A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Variables. I. Phys. Rev. 1952, 85, 166. [Google Scholar] [CrossRef]
- Holland, P.R. The Quantum Theory of Motion: An Account of the de Broglie-Bohm Causal Interpretation of Quantum Mechanics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Benseny, A.; Albareda, G.; Sanz, A.S.; Mompart, J.; Oriols, X. Applied Bohmian mechanics. Eur. Phys. J. D 2014, 68, 286. [Google Scholar] [CrossRef]
- Nelson, E. Field theory and the future of stochastic mechanics. Lect. Notes Phys. 1986, 262, 438. [Google Scholar]
- Koide, T. Microscopic derivation of causal diffusion equation using the projection operator method. Phys. Rev. E 2005, 72, 026135. [Google Scholar] [CrossRef] [PubMed]
- Takabayasi, T. On the Formulation of Quantum Mechanics associated with Classical Pictures. Prog. Theor. Phys. 1952, 8, 143. [Google Scholar] [CrossRef]
- Wallstrom, T.C. On the derivation of the Schrödinger equation from stochastic mechanics. Phys. Lett. 1989, 2, 113. [Google Scholar]
- Misawa, T. Noether’s theorem in symmetric stochastic calculus of variations. J. Math. Phys. 1988, 29, 2178. [Google Scholar] [CrossRef]
- Misawa, T.; Yasue, K. Canonical stochastic dynamical systems. J. Math. Phys. 1987, 28, 2569. [Google Scholar] [CrossRef]
- Nambu, Y. Generalized Hamiltonian Dynamics. Phys. Rev. D 1973, 7, 2405. [Google Scholar] [CrossRef]
- Elsas, J.H.G.; Koide, T.; Kodama, T. Noether’s Theorem of Relativistic-Electromagnetic Ideal Hydrodynamics. Braz. J. Phys. 2015, 45, 334. [Google Scholar] [CrossRef][Green Version]
- Brenner, H. Is the tracer velocity of a fluid continuum equal to its mass velocity? Phys. Rev. E 2004, 70, 061201. [Google Scholar] [CrossRef]
- Brenner, H. Fluid mechanics in fluids at rest. Phys. Rev. E 2012, 86, 016307. [Google Scholar] [CrossRef]
- Klimontovich, Y.L. On the need for and the possibility of a unified description of kinetic and hydrodynamic processes. Theor. Math. Phys. 1992, 92, 909. [Google Scholar] [CrossRef]
- Ottinger, H.C. Beyond Equilibrium Thermodynamics; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Graur, I.A.; Meolens, J.G.; Zeitoun, D.E. Analytical and numerical description for isothermal gas flows in microchannels. Microfluids Nanofluids 2006, 2, 64. [Google Scholar] [CrossRef]
- Greenshields, C.J.; Reese, J.M. The structure of shock waves as a test of Brenner’s modifications to the Navier-Stokes equations. J. Fluid Mech. 2007, 580, 407. [Google Scholar] [CrossRef]
- Eu, B.C. Molecular representation of molar domain (volume), evolution equations, and linear constitutive relations for volume transport. J. Chem. Phys. 2008, 129, 094502. [Google Scholar] [CrossRef] [PubMed]
- Dongari, N.; Durst, F.; Chakraborty, S. Predicting microscale gas flows and rarefaction effects through extended Navier-Stokes-Fourier equations from phoretic transport considerations. Microfluids Nanofluids 2010, 9, 831. [Google Scholar] [CrossRef]
- Dadzie, S.K.; Reese, J.M.; Mclnnes, C.R. A continuum model of gas flows with localized density variations. Physica A 2008, 387, 6079. [Google Scholar] [CrossRef]
- Koide, T.; Ramos, R.O.; Vicente, G.S. Bivelocity Picture in the Nonrelativistic Limit of Relativistic Hydrodynamics. Braz. J. Phys. 2015, 45, 102. [Google Scholar] [CrossRef]
- Reddy, M.H.L.; Dadzie, S.K.; Ocone, R.; Borg, M.K.; Reese, J.M. Recasting Navier-Stokes equations. J. Phys. Commun. 2019, 3, 105009. [Google Scholar] [CrossRef]
- de Souza, R.D.; Koide, T.; Kodama, T. Hydrodynamic approaches in relativistic heavy ion reactions. Prog. Part. Nucl. Phys. 2016, 86, 35. [Google Scholar] [CrossRef]
- Korteweg, D.J. Sur la forme que prennent les equations des mouvements des fluides si l’on tient compte des forces capillaires causees par des variations de densite considerables mais connues et la theorie de la capillarit edens l‘hypothese d’une variation continue de la densite. Arch. Neerl. Sci. Exactes Nat. II 1901, 6, 1. [Google Scholar]
- Bresch, D.; Gisclon, M.; Lacroix-Violet, I. On Navier-Stokes-Korteweg and Euler-Korteweg Systems: Application to Quantum Fluids Models. Arch. Ration. Mech. Anal. 2019, 233, 975. [Google Scholar] [CrossRef]
- Koide, T.; Kodama, T. Stochastic variational method as quantization scheme: Field quantization of complex Klein-Gordon equation. Prog. Theor. Exp. Phys. 2015, 093A03. [Google Scholar] [CrossRef]
- Morawetz, K. Fluctuations due to the nonlocal character of collisions. New J. Phys. 2007, 9, 313. [Google Scholar] [CrossRef]
- Morawetz, K. Nonequilibrium thermodynamics with binary quantum correlations. Phys. Rev. E 2017, 96, 032106. [Google Scholar] [CrossRef] [PubMed]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Gazeau, J.-P. Coherent States in Quantum Physics; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Carruthers, P.; Nieto, M.M. Phase and Angle Variables in Quantum Mechanics. Rev. Mod. Phys. 1968, 40, 411. [Google Scholar] [CrossRef]
- Ohnuki, Y.; Kitakado, S. Fundamental algebra for quantum mechanics on SD and gauge potentials. J. Math. Phys. 1993, 34, 2827. [Google Scholar] [CrossRef]
- Tanimura, S. Gauge field, parity and uncertainty relation of quantum mechanics on S S1. Prog. Theor. Phys. 1993, 90, 271. [Google Scholar] [CrossRef][Green Version]
- Kastrup, H.A. Quantization of the canonically conjugate pair angle and orbital angular momentum. Phys. Rev. A 2006, 73, 052104. [Google Scholar] [CrossRef]
- Gazeau, J.-P.; Szafraniec, F.H. Three paths toward the quantum angle operator. Ann. Phys. 2016, 375, 16. [Google Scholar] [CrossRef]
- Fresneda, R.; Gazeau, J.-P.; Noguera, D. Quantum localisation on the circle. J. Math. Phys. 2018, 59, 052105. [Google Scholar] [CrossRef]
- Hanauske, M.; Steinheimer, J.; Motornenko, A.; Vovchenko, V.; Bovard, L. Neutron Star Mergers: Probing the EoS of Hot, Dense Matter by Gravitational Waves. Particles 2019, 2, 44–56. [Google Scholar] [CrossRef]
- Hanauske, M.; Bovard, L.; Most, E.; jan Steinheimer, J.P.; Motornenko, A.; Vovchenko, V.; Dexheimer, V.; Schramm, S.; Stocker, H. Detecting the Hadron-Quark Phase Transition with Gravitational Waves. Universe 2019, 5, 156. [Google Scholar] [CrossRef]
- de Falco, D.; de Martino, S.; de Siena, S. Position-Momentum Uncertainty Relations in Stochastic Mechanics. Phys. Rev. Lett. 1982, 49, 181. [Google Scholar] [CrossRef]
- Loffredo, M.I.; Morato, L.M. Stochastic quantization for a system of N identical interacting Bose particles. J. Phys. A Math. Theor. 2007, 40, 8709. [Google Scholar] [CrossRef][Green Version]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Monthly notices of the royal astronomical society. Mon. Not. R. Astron. Soc. 1977, 181, 375. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1997, 82, 1013. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonçalves de Matos, G.; Kodama, T.; Koide, T. Uncertainty Relations in Hydrodynamics. Water 2020, 12, 3263. https://doi.org/10.3390/w12113263
Gonçalves de Matos G, Kodama T, Koide T. Uncertainty Relations in Hydrodynamics. Water. 2020; 12(11):3263. https://doi.org/10.3390/w12113263
Chicago/Turabian StyleGonçalves de Matos, Gyell, Takeshi Kodama, and Tomoi Koide. 2020. "Uncertainty Relations in Hydrodynamics" Water 12, no. 11: 3263. https://doi.org/10.3390/w12113263
APA StyleGonçalves de Matos, G., Kodama, T., & Koide, T. (2020). Uncertainty Relations in Hydrodynamics. Water, 12(11), 3263. https://doi.org/10.3390/w12113263




