Effect of Shearing on Non-Darcian Fluid Flow Characteristics through Rough-Walled Fracture
Abstract
:1. Introduction
2. Numerical Study
2.1. Fracture Model
2.2. Numerical Method
3. Results and Discussion
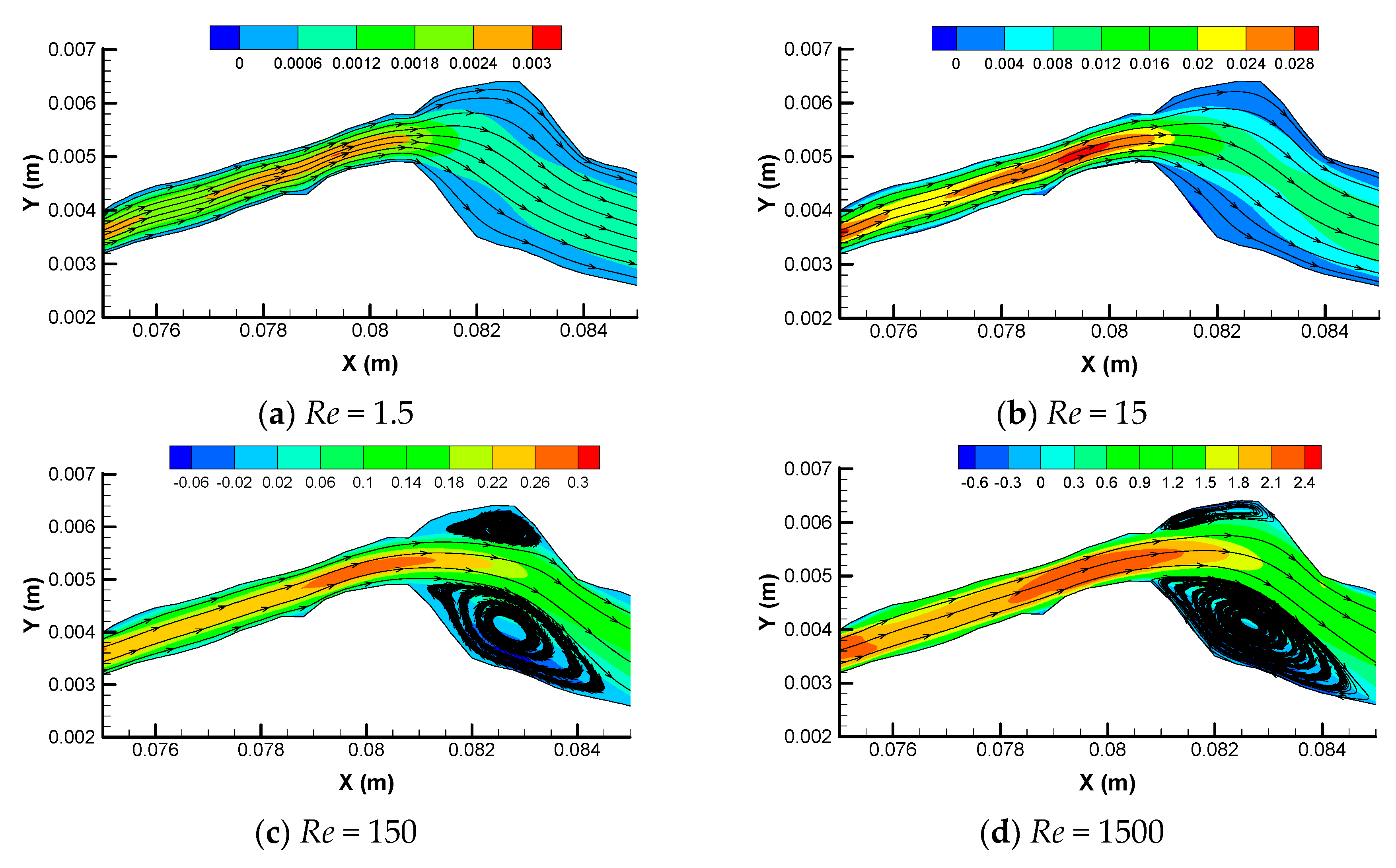
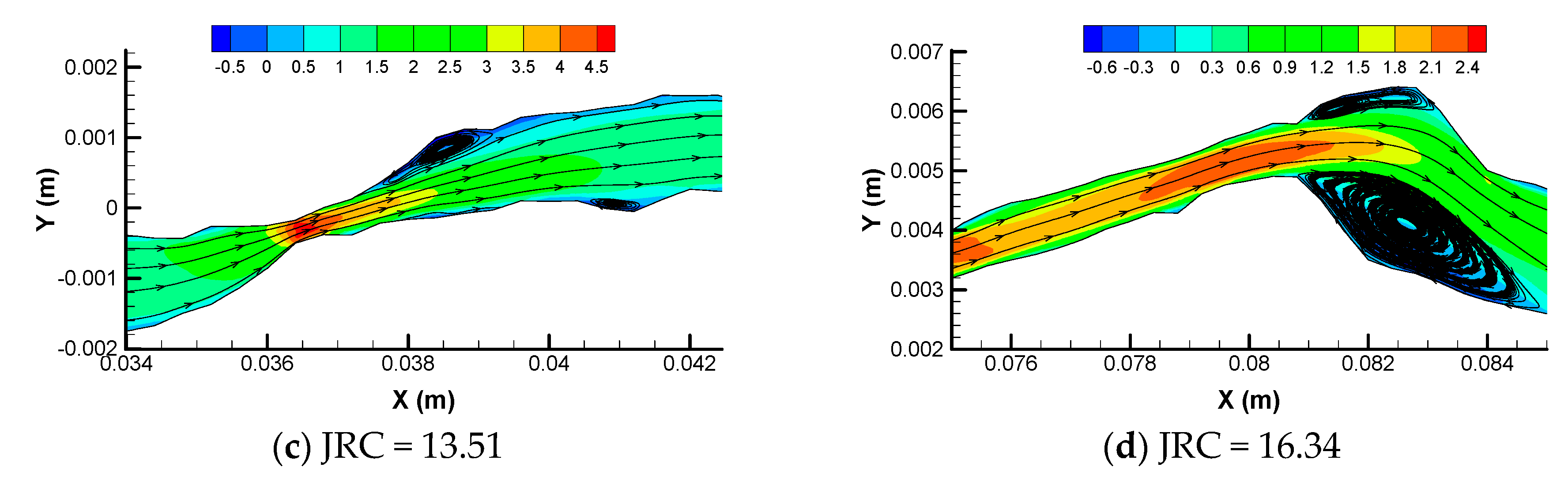
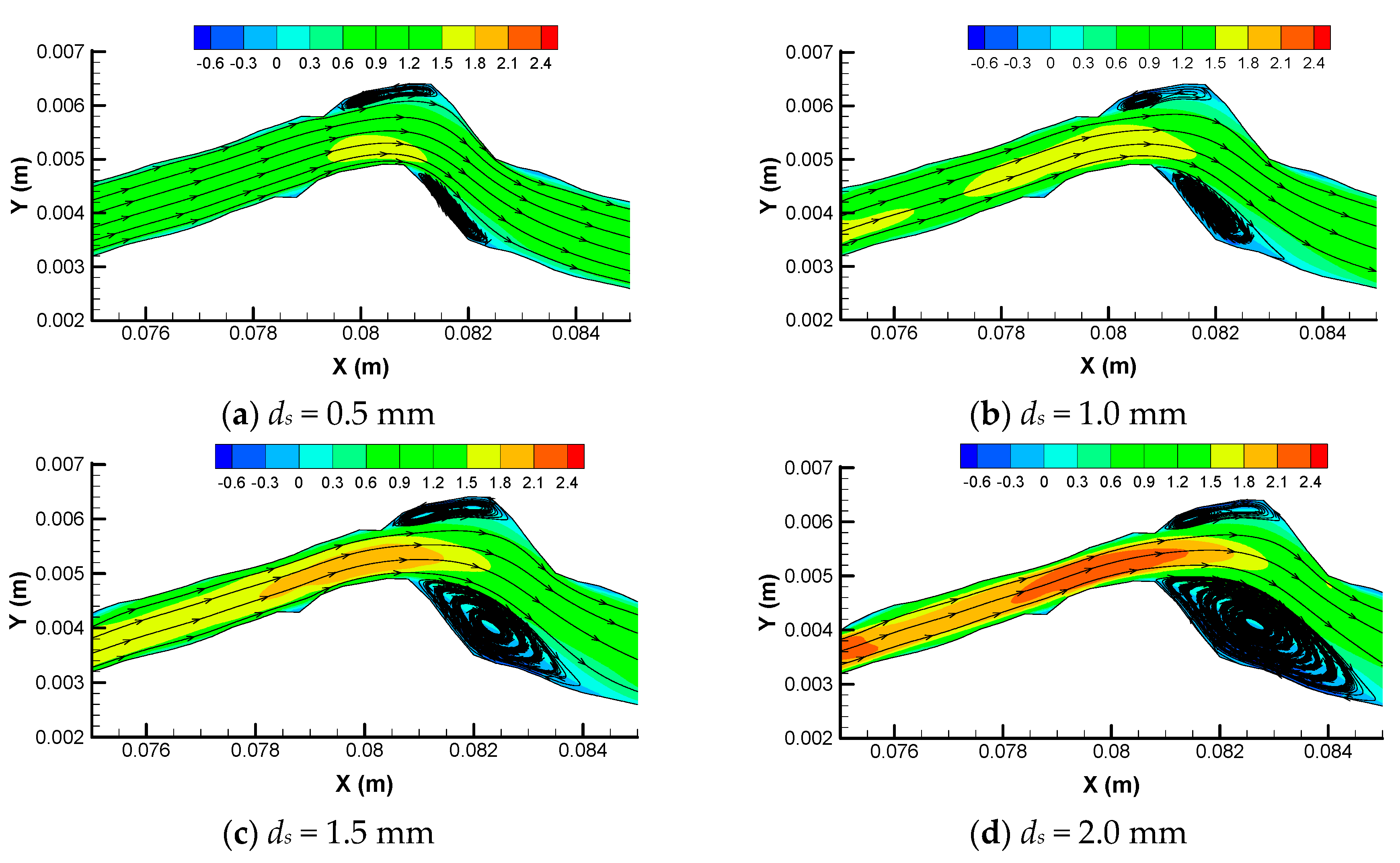
3.1. Emergence of Eddies
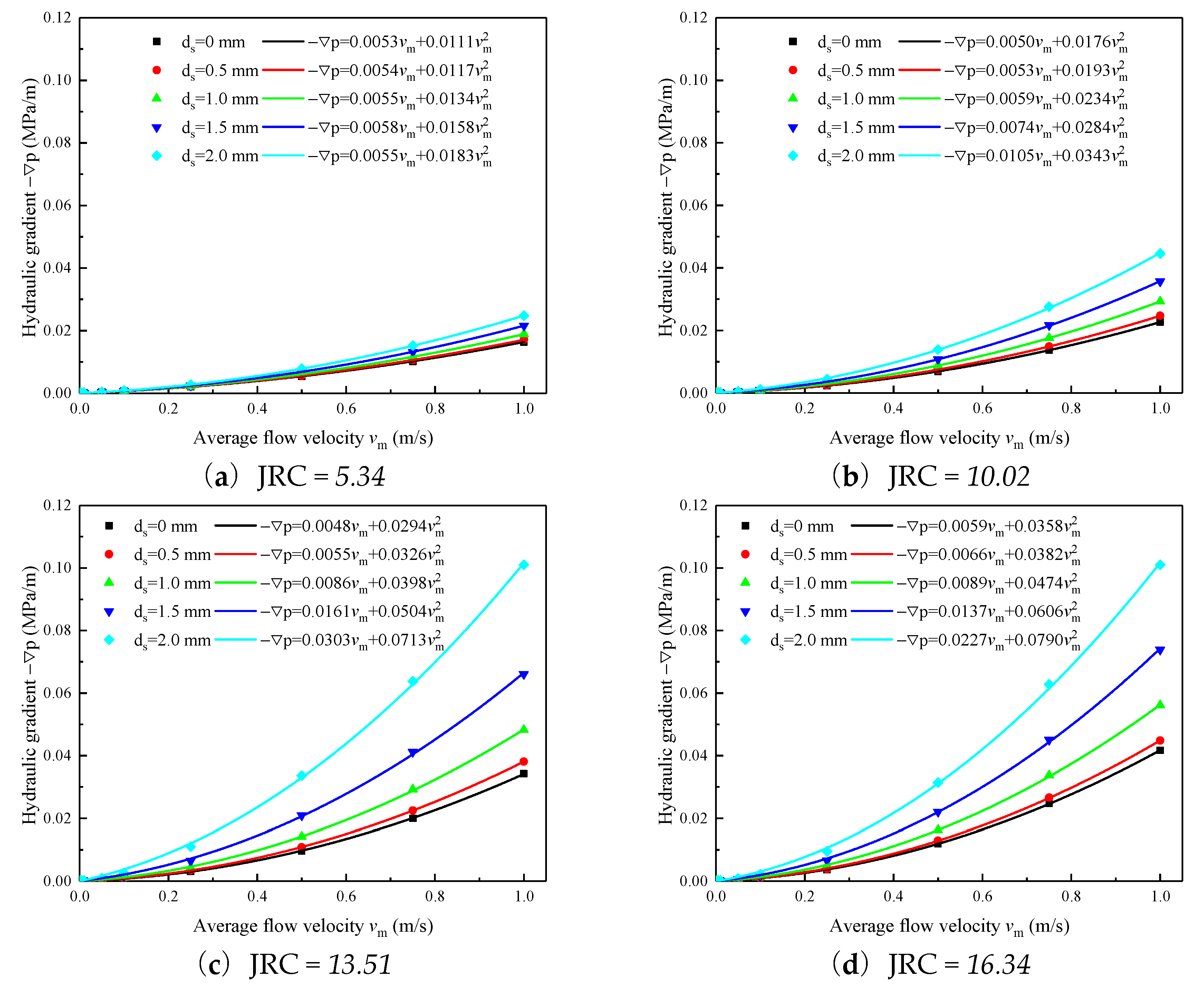
3.2. Correlation between Inlet Flow Velocity and Hydraulic Gradient
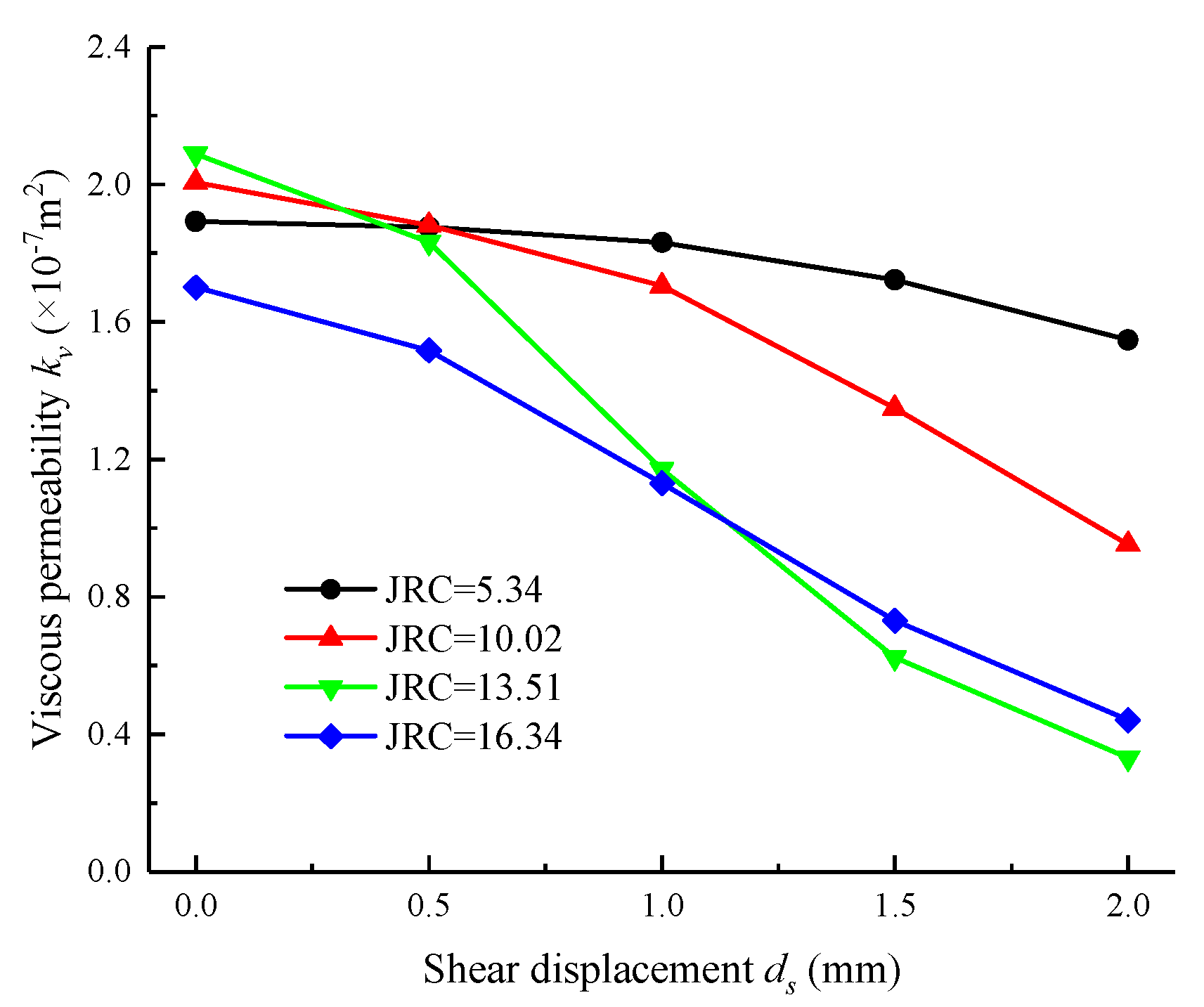
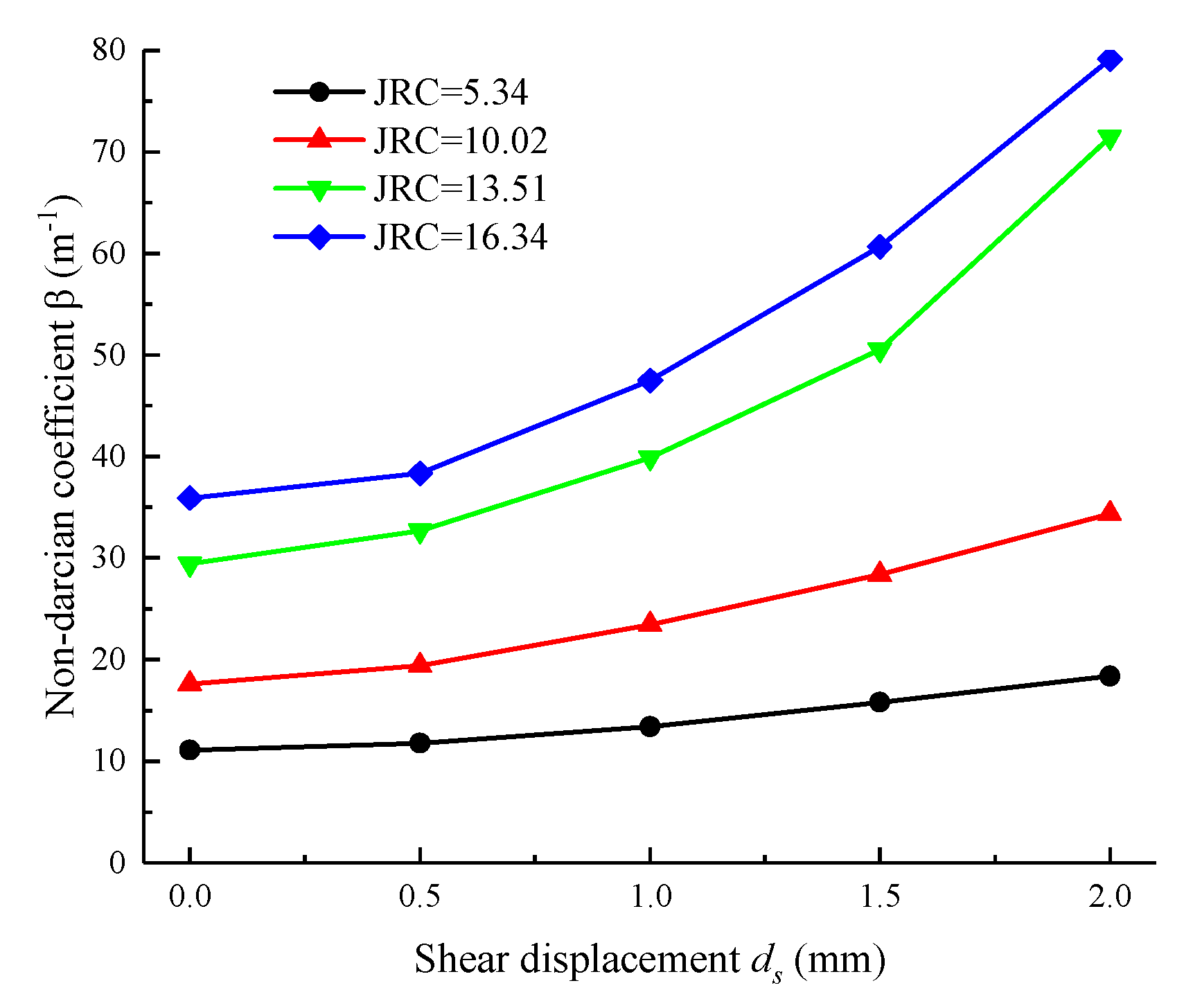
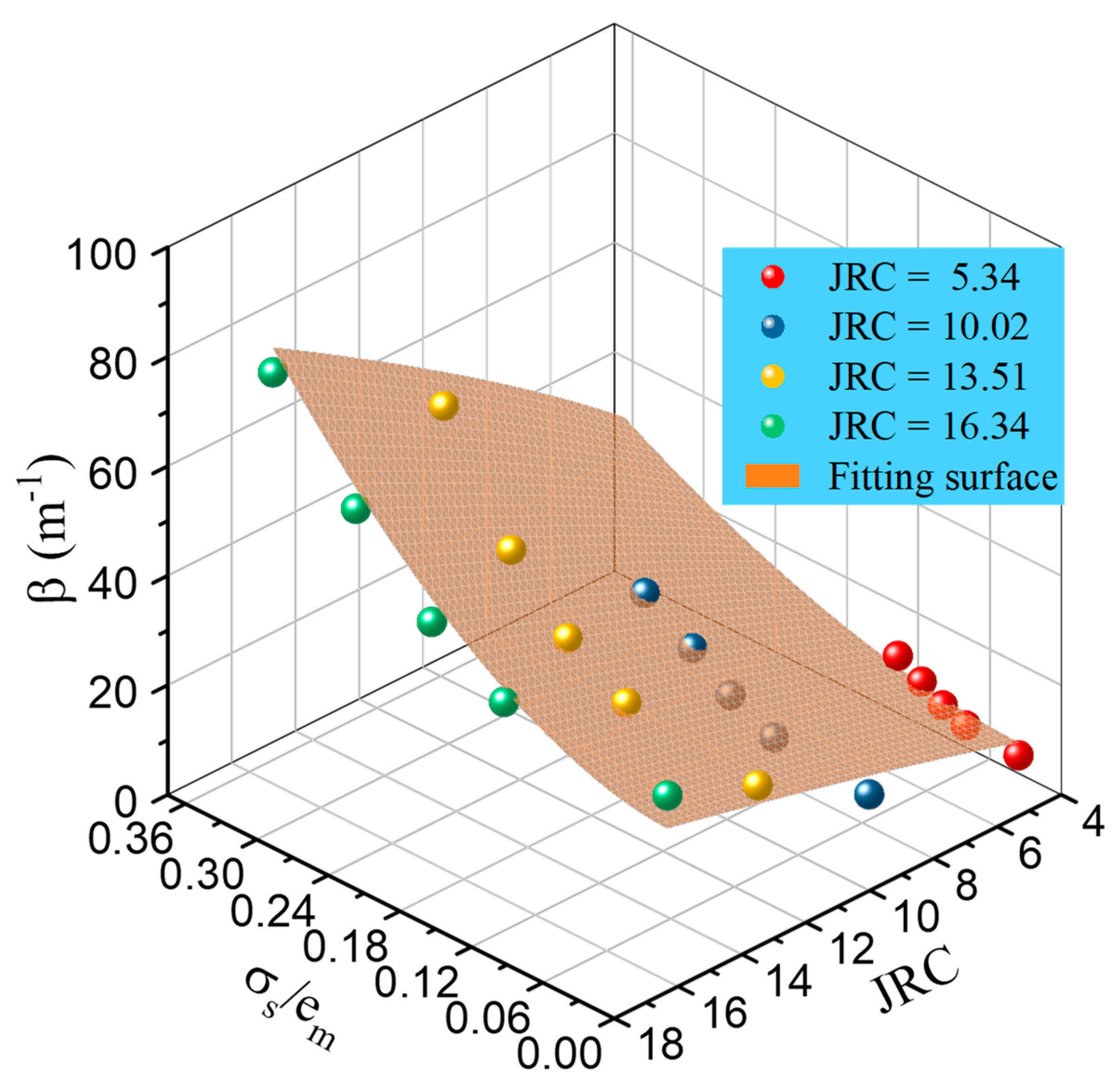
3.3. Forchheimer Coefficients
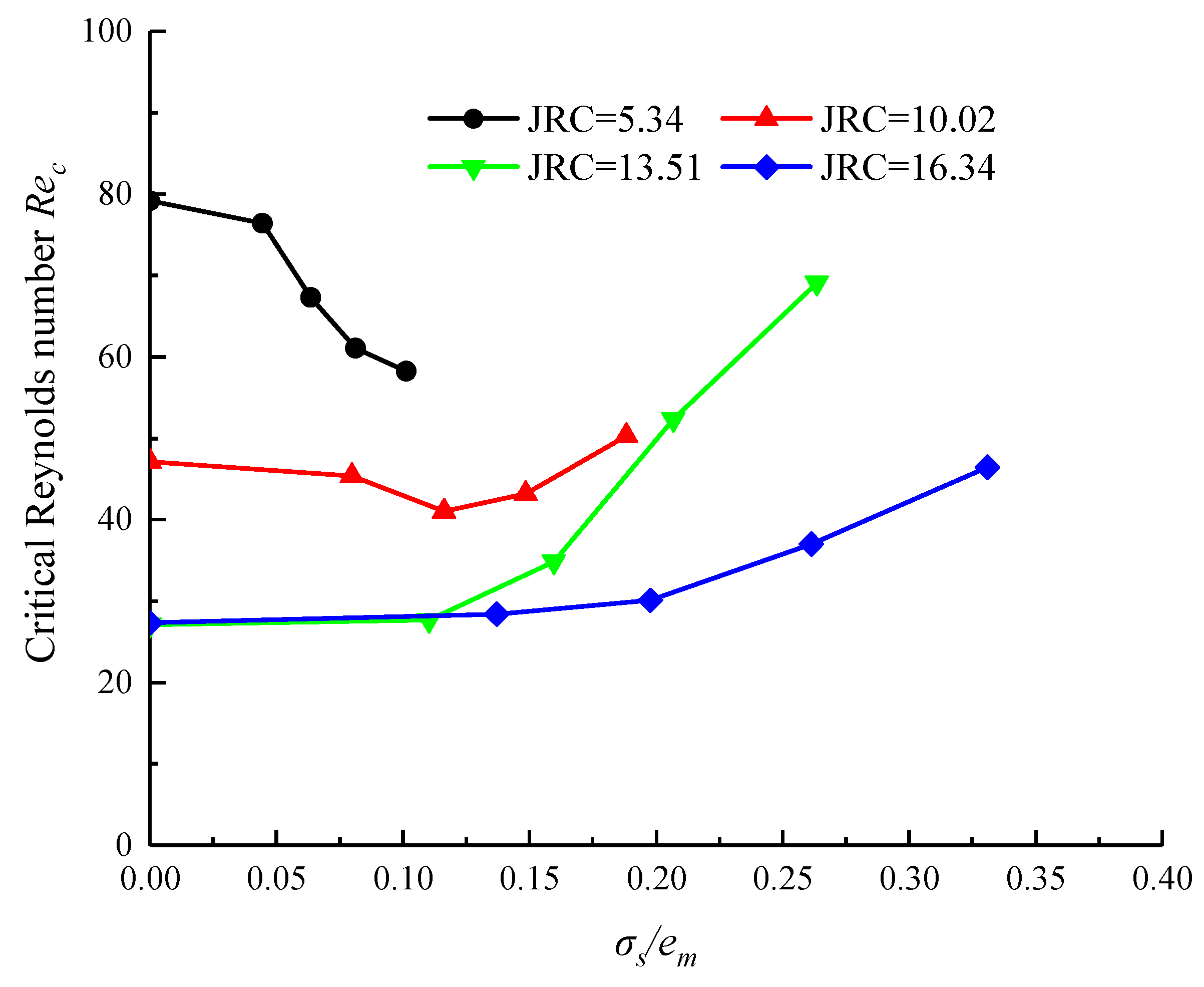
3.4. Critical Reynolds Number
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Long, J.C.S.; Remer, J.S.; Wilson, C.R.; Witherspoon, P.A. Porous media equivalents for networks of discontinuous fractures. Water Resour. Res. 1982, 18, 645–658. [Google Scholar] [CrossRef] [Green Version]
- Brush, D.J.; Thomson, N.R. Fluid flow in synthetic rough-walled fractures: Navier-Stokes, Stokes, and local cubic law simulations. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Min, K.-B.; Rutqvist, J.; Tsang, C.-F.; Jing, L. Stress-dependent permeability of fractured rock masses: A numerical study. Int. J. Rock Mech. Min. Sci. 2004, 41, 1191–1210. [Google Scholar] [CrossRef] [Green Version]
- Qian, J.; Zhan, H.; Luo, S.; Zhao, W. Experimental evidence of scale-dependent hydraulic conductivity for fully developed turbulent flow in a single fracture. J. Hydrol. 2007, 339, 206–215. [Google Scholar] [CrossRef]
- Zou, L.; Jing, L.; Cvetkovic, V. Roughness decomposition and nonlinear fluid flow in a single rock fracture. Int. J. Rock Mech. Min. Sci. 2015, 75, 102–118. [Google Scholar] [CrossRef]
- Chen, Y.F.; Zhou, J.Q.; Hu, S.-H.; Hu, R.; Zhou, C.B. Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures. J. Hydrol. 2015, 529, 993–1006. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Al-Yaarubi, A.; Pain, C.C.; Grattoni, C.A. Non-linear regimes of fluid flow in rock fractures. Int. J. Rock Mech. Min. Sci. 2004, 41, 1–7. [Google Scholar] [CrossRef]
- Zhang, Z.; Nemcik, J. Fluid flow regimes and nonlinear flow characteristics in deformable rock fractures. J. Hydrol. 2013, 477, 139–151. [Google Scholar] [CrossRef]
- Koyama, T.; Neretnieks, I.; Jing, L. A numerical study on differences in using Navier–Stokes and Reynolds equations for modeling the fluid flow and particle transport in single rock fractures with shear. Int. J. Rock Mech. Min. Sci. 2008, 45, 1082–1101. [Google Scholar] [CrossRef] [Green Version]
- Xie, L.Z.; Gao, C.; Ren, L.; Li, C.B. Numerical investigation of geometrical and hydraulic properties in a single rock fracture during shear displacement with the Navier–Stokes equations. Environ. Earth Sci. 2015, 73, 7061–7074. [Google Scholar] [CrossRef]
- Zou, L.; Jing, L.; Cvetkovic, V. Shear-enhanced nonlinear flow in rough-walled rock fractures. Int. J. Rock Mech. Min. Sci. 2017, 97, 33–45. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.-Q.; Wang, M.; Wang, L.; Chen, Y.-F.; Zhou, C.-B. Emergence of Nonlinear Laminar Flow in Fractures During Shear. Rock Mech. Rock Eng. 2018, 51, 3635–3643. [Google Scholar] [CrossRef]
- Rong, G.; Yang, J.; Cheng, L.; Zhou, C. Laboratory investigation of nonlinear flow characteristics in rough fractures during shear process. J. Hydrol. 2016, 541, 1385–1394. [Google Scholar] [CrossRef]
- Xiong, X.; Li, B.; Jiang, Y.; Koyama, T.; Zhang, C. Experimental and numerical study of the geometrical and hydraulic characteristics of a single rock fracture during shear. Int. J. Rock Mech. Min. Sci. 2011, 48, 1292–1302. [Google Scholar] [CrossRef]
- Javadi, M.; Sharifzadeh, M.; Shahriar, K.; Mitani, Y. Critical Reynolds number for nonlinear flow through rough-walled fractures: The role of shear processes. Water Resour. Res. 2014, 50, 1789–1804. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Jiang, Y.; Luan, H.; Sugimoto, S. Effect of shearing on hydraulic properties of rough-walled fractures under different boundary conditions. Energy Sci. Eng. 2020, 8, 865–879. [Google Scholar] [CrossRef]
- Rong, G.; Yang, J.; Cheng, L.; Tan, J.; Peng, J.; Zhou, C. A Forchheimer Equation-Based Flow Model for Fluid Flow Through Rock Fracture During Shear. Rock Mech. Rock Eng. 2018, 51, 2777–2790. [Google Scholar] [CrossRef]
- Xie, H.; Wang, J.-A.; Xie, W.-H. Fractal effects of surface roughness on the mechanical behavior of rock joints. Chaos Solitons Fractals 1997, 8, 221–252. [Google Scholar] [CrossRef]
- Jelly, T.O.; Busse, A. Reynolds and dispersive shear stress contributions above highly skewed roughness. J. Fluid Mech. 2018, 852, 710–724. [Google Scholar] [CrossRef] [Green Version]
- De Marchis, M. Large eddy simulations of roughened channel flows: Estimation of the energy losses using the slope of the roughness. Comput. Fluids 2016, 140, 148–157. [Google Scholar] [CrossRef]
- De Marchis, M.; Saccone, D.; Milici, B.; Napoli, E. Large Eddy Simulations of Rough Turbulent Channel Flows Bounded by Irregular Roughness: Advances Toward a Universal Roughness Correlation. Flow Turbul. Combust. 2020, 105, 627–648. [Google Scholar] [CrossRef]
- Zoorabadi, M.; Saydam, S.; Timms, W.; Hebblewhite, B. Non-linear flow behaviour of rough fractures having standard JRC profiles. Int. J. Rock Mech. Min. Sci. 2015, 76, 192–199. [Google Scholar] [CrossRef]
- Dou, Z.; Chen, Z.; Zhou, Z.; Wang, J.; Huang, Y. Influence of eddies on conservative solute transport through a 2D single self-affine fracture. Int. J. Heat Mass Transf. 2018, 121, 597–606. [Google Scholar] [CrossRef]
- Chen, Y.; Lian, H.; Liang, W.; Yang, J.; Nguyen, V.P.; Bordas, S.P.A. The influence of fracture geometry variation on non-Darcy flow in fractures under confining stresses. Int. J. Rock Mech. Min. Sci. 2019, 113, 59–71. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Tse, R.; Cruden, D.M. Estimating joint roughness coefficients. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 303–307. [Google Scholar] [CrossRef]
- Yeo, I.W.; de Freitas, M.H.; Zimmerman, R.W. Effect of shear displacement on the aperture and permeability of a rock fracture. Int. J. Rock Mech. Min. Sci. 1998, 35, 1051–1070. [Google Scholar] [CrossRef]
- Huang, N.; Liu, R.; Jiang, Y.; Li, B.; Yu, L. Effects of fracture surface roughness and shear displacement on geometrical and hydraulic properties of three-dimensional crossed rock fracture models. Adv. Water Resour. 2018, 113, 30–41. [Google Scholar] [CrossRef]
- Zhang, Q.; Luo, S.; Ma, H.; Wang, X.; Qian, J. Simulation on the water flow affected by the shape and density of roughness elements in a single rough fracture. J. Hydrol. 2019, 573, 456–468. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Zeng, Z.; Grigg, R. A Criterion for Non-Darcy Flow in Porous Media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar] [CrossRef]
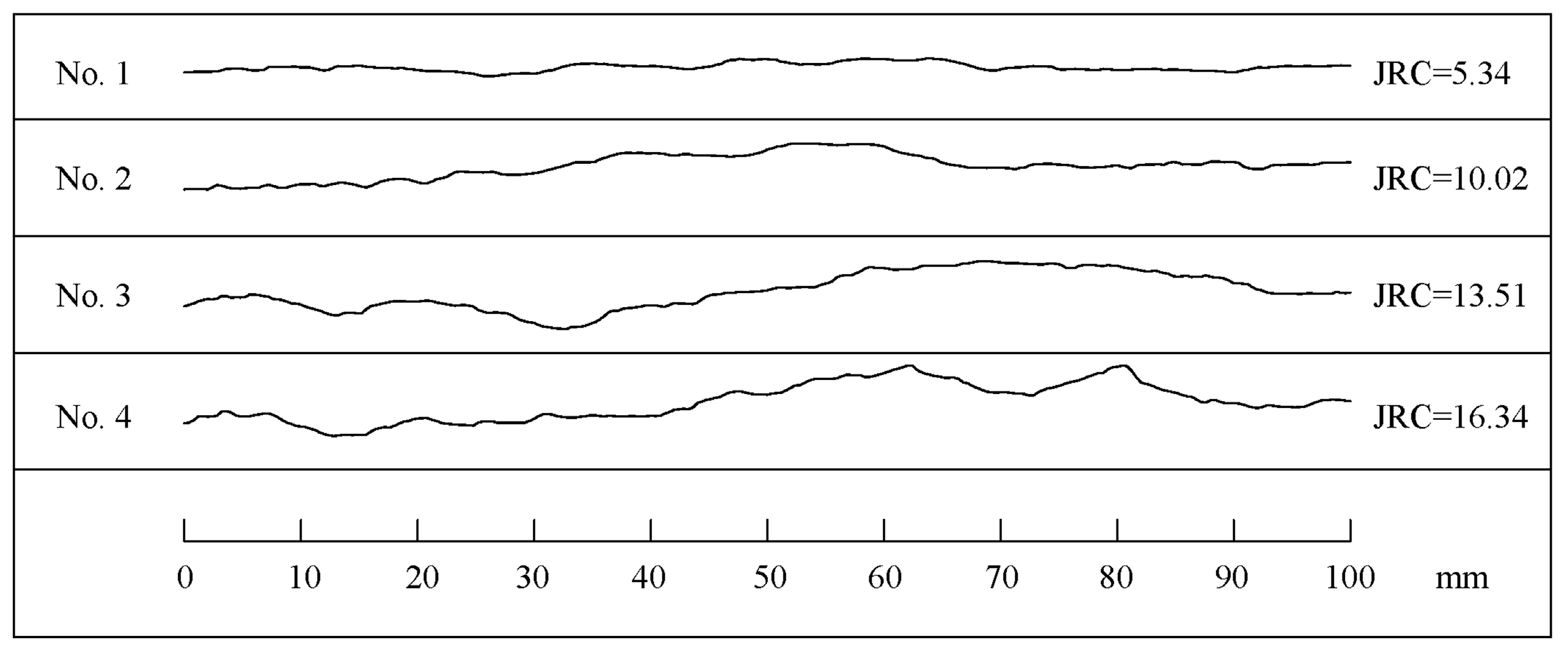

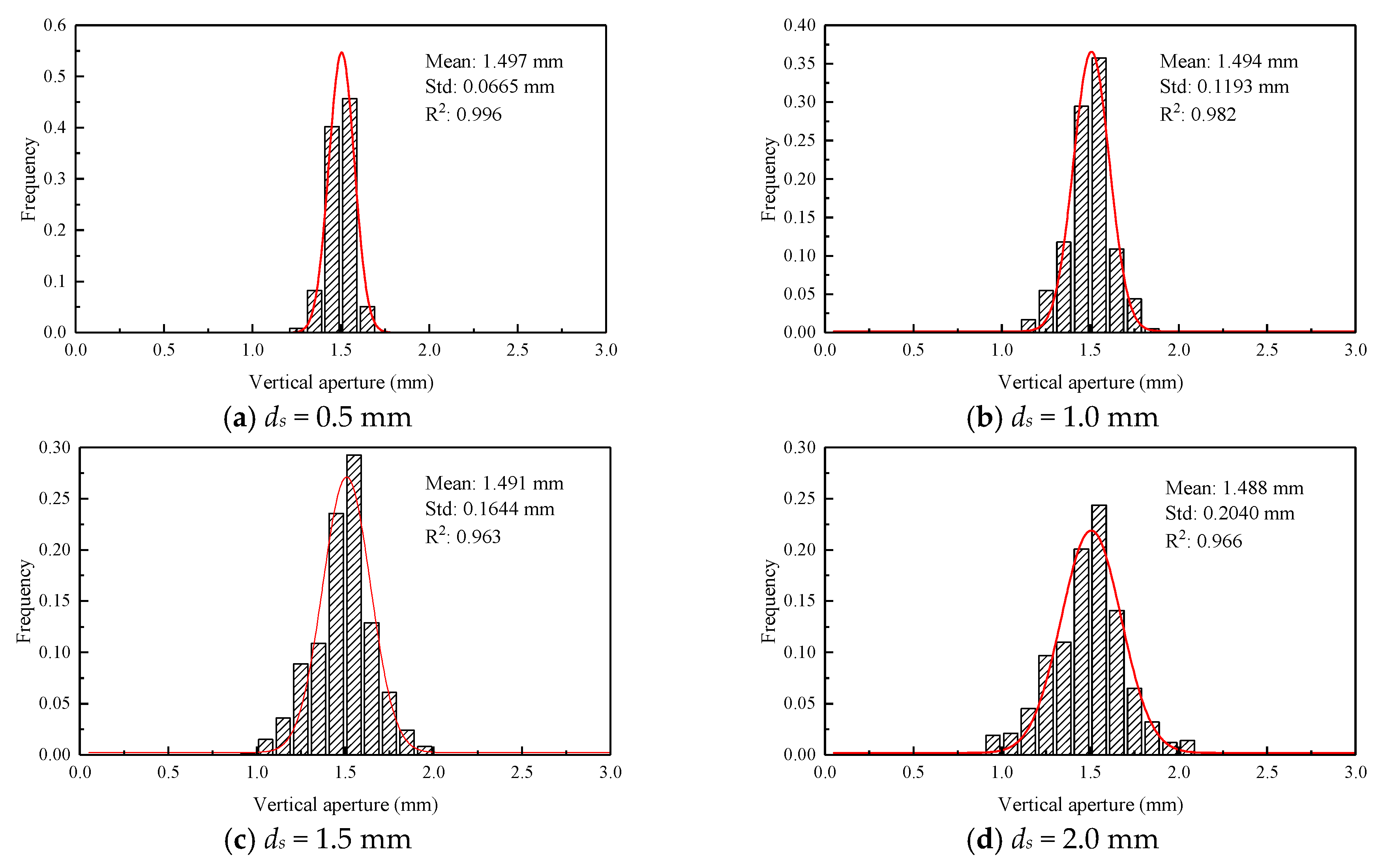
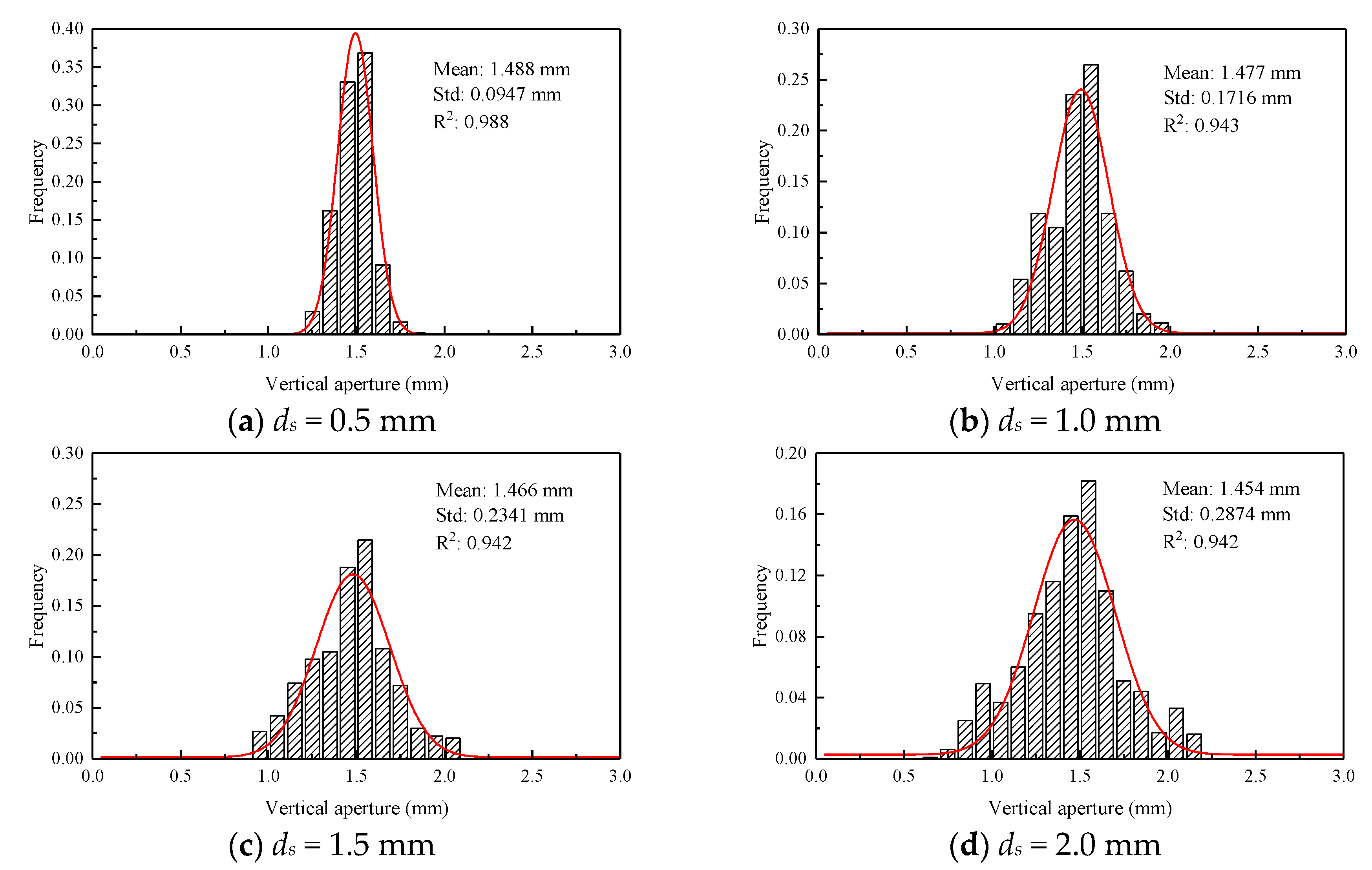
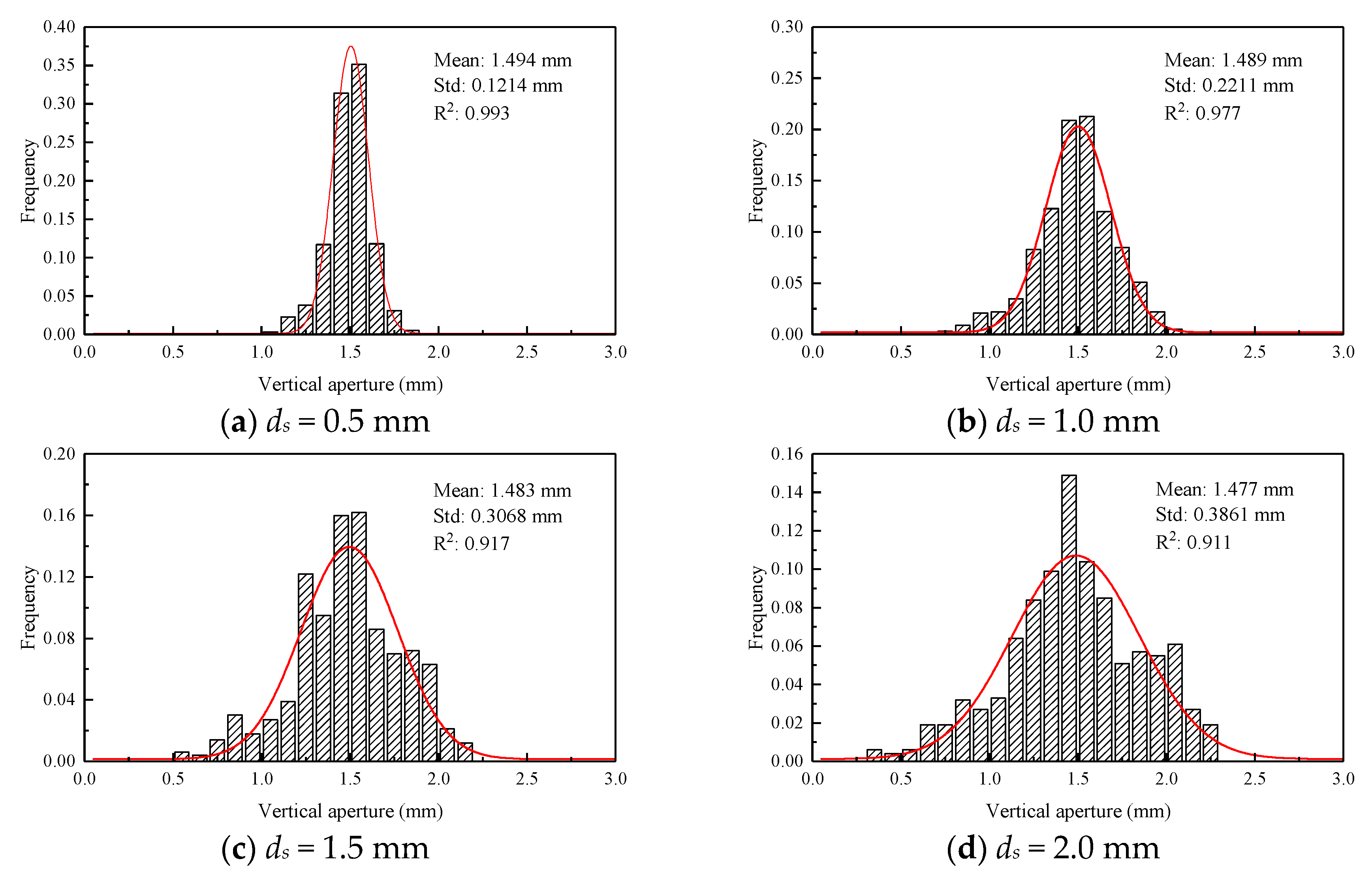

| JRC | Shear Displacement ds (mm) | |||
|---|---|---|---|---|
| 5.34 | 0.5 | 1.497 | 0.0665 | 0.0444 |
| 1.0 | 1.494 | 0.1193 | 0.0799 | |
| 1.5 | 1.491 | 0.1644 | 0.1103 | |
| 2.0 | 1.488 | 0.2040 | 0.1371 | |
| 10.02 | 0.5 | 1.488 | 0.0947 | 0.0636 |
| 1.0 | 1.477 | 0.1716 | 0.1162 | |
| 1.5 | 1.466 | 0.2341 | 0.1597 | |
| 2.0 | 1.454 | 0.2874 | 0.1977 | |
| 13.51 | 0.5 | 1.494 | 0.1214 | 0.0813 |
| 1.0 | 1.489 | 0.2211 | 0.1485 | |
| 1.5 | 1.483 | 0.3068 | 0.2069 | |
| 2.0 | 1.477 | 0.3861 | 0.2614 | |
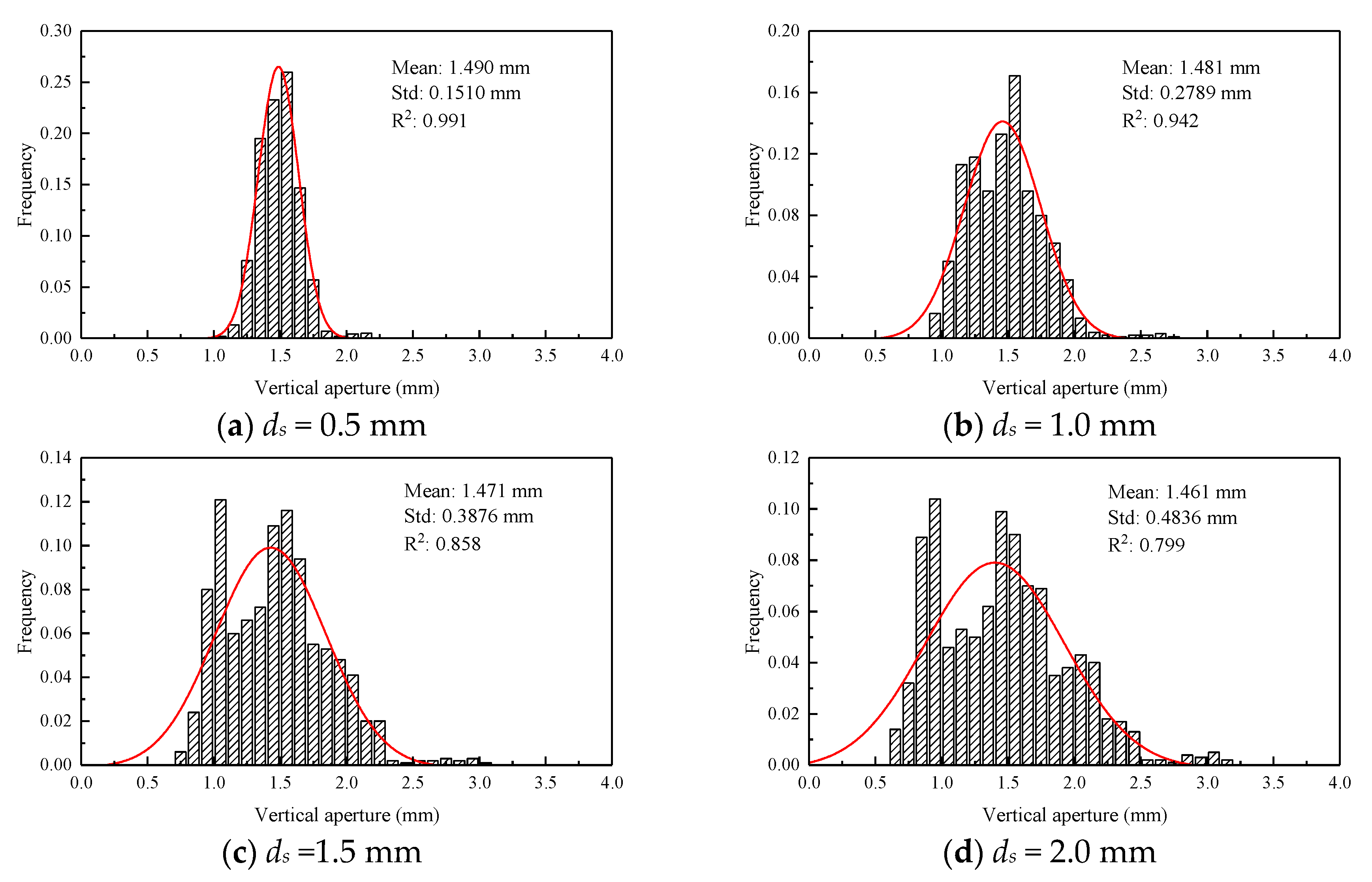
| 16.34 | 0.5 | 1.490 | 0.1510 | 0.1013 |
| 1.0 | 1.481 | 0.2789 | 0.1883 | |
| 1.5 | 1.471 | 0.3876 | 0.2635 | |
| 2.0 | 1.461 | 0.4836 | 0.3310 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Xu, W.; Yan, L.; Xu, J.; He, M.; Xie, W.-C. Effect of Shearing on Non-Darcian Fluid Flow Characteristics through Rough-Walled Fracture. Water 2020, 12, 3260. https://doi.org/10.3390/w12113260
Li B, Xu W, Yan L, Xu J, He M, Xie W-C. Effect of Shearing on Non-Darcian Fluid Flow Characteristics through Rough-Walled Fracture. Water. 2020; 12(11):3260. https://doi.org/10.3390/w12113260
Chicago/Turabian StyleLi, Biao, Weiya Xu, Long Yan, Jianrong Xu, Mingjie He, and Wei-Chau Xie. 2020. "Effect of Shearing on Non-Darcian Fluid Flow Characteristics through Rough-Walled Fracture" Water 12, no. 11: 3260. https://doi.org/10.3390/w12113260





