Influence of Calibration Parameter Selection on Flash Flood Simulation for Small to Medium Catchments with MISDc-2L Model
Abstract
1. Introduction
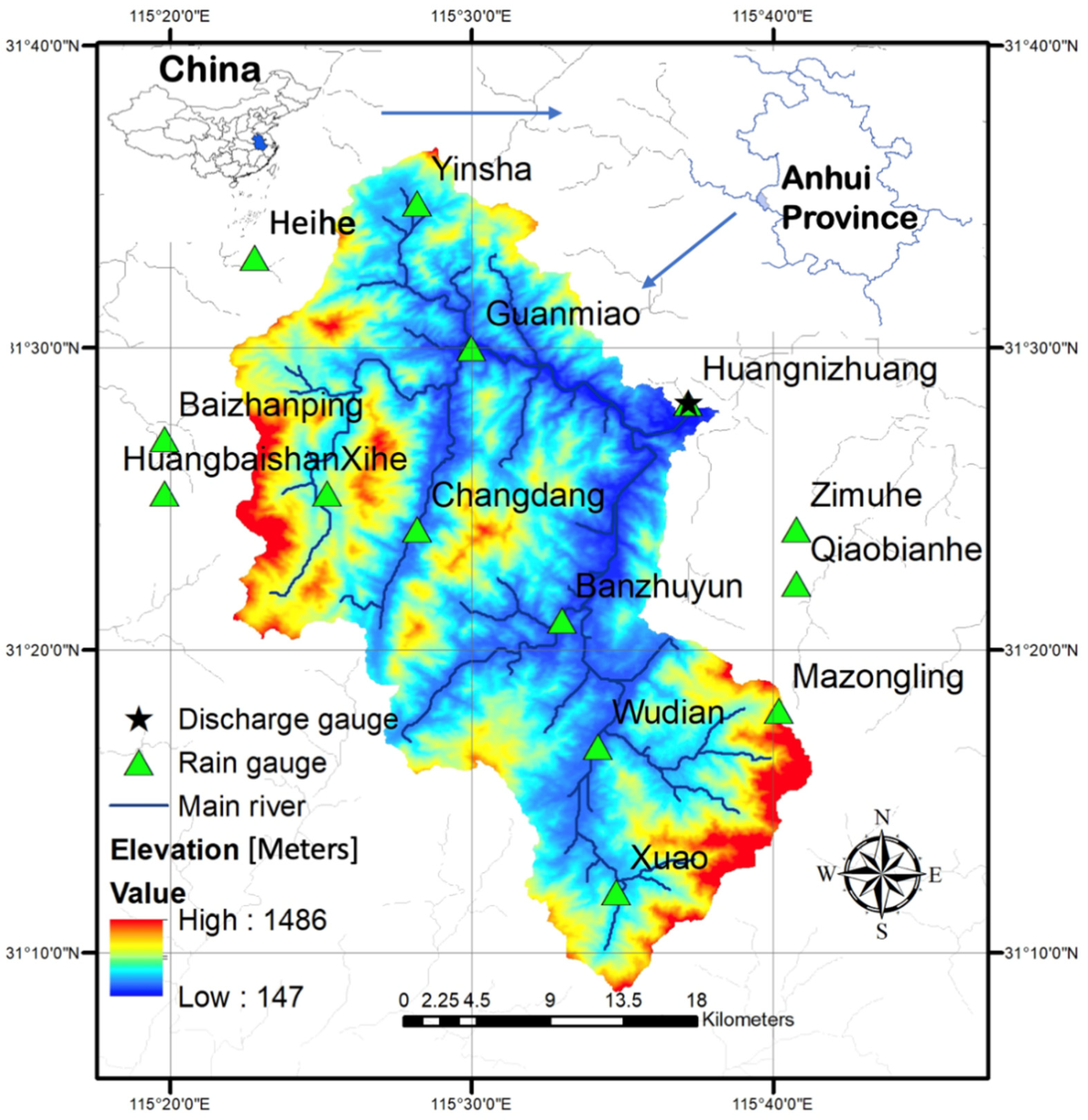
2. Study Area
3. Data and Methods
3.1. Data Collection
3.1.1. Discharge Data
3.1.2. Meteorological Data
3.2. MISDc-2L Model
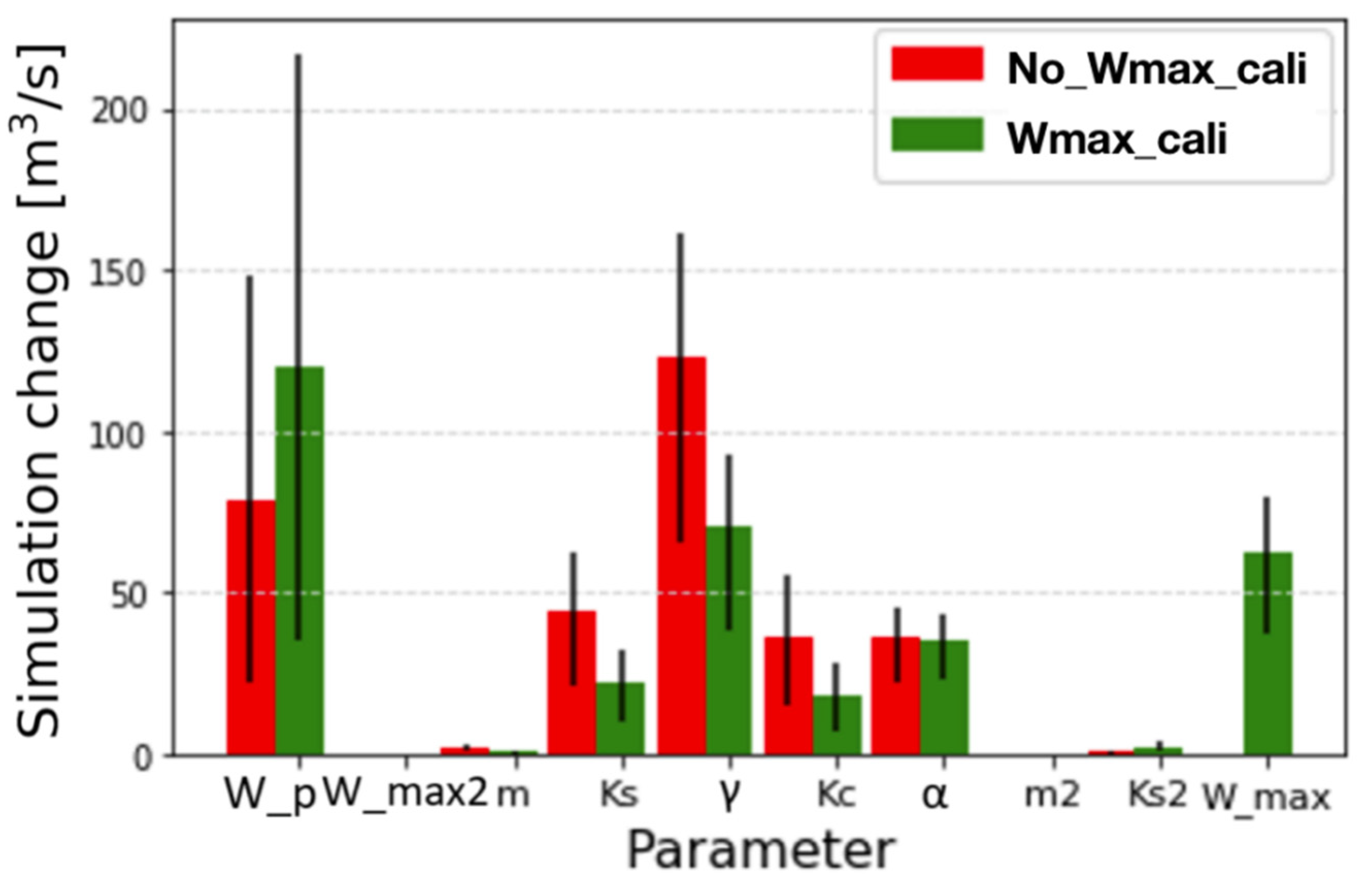
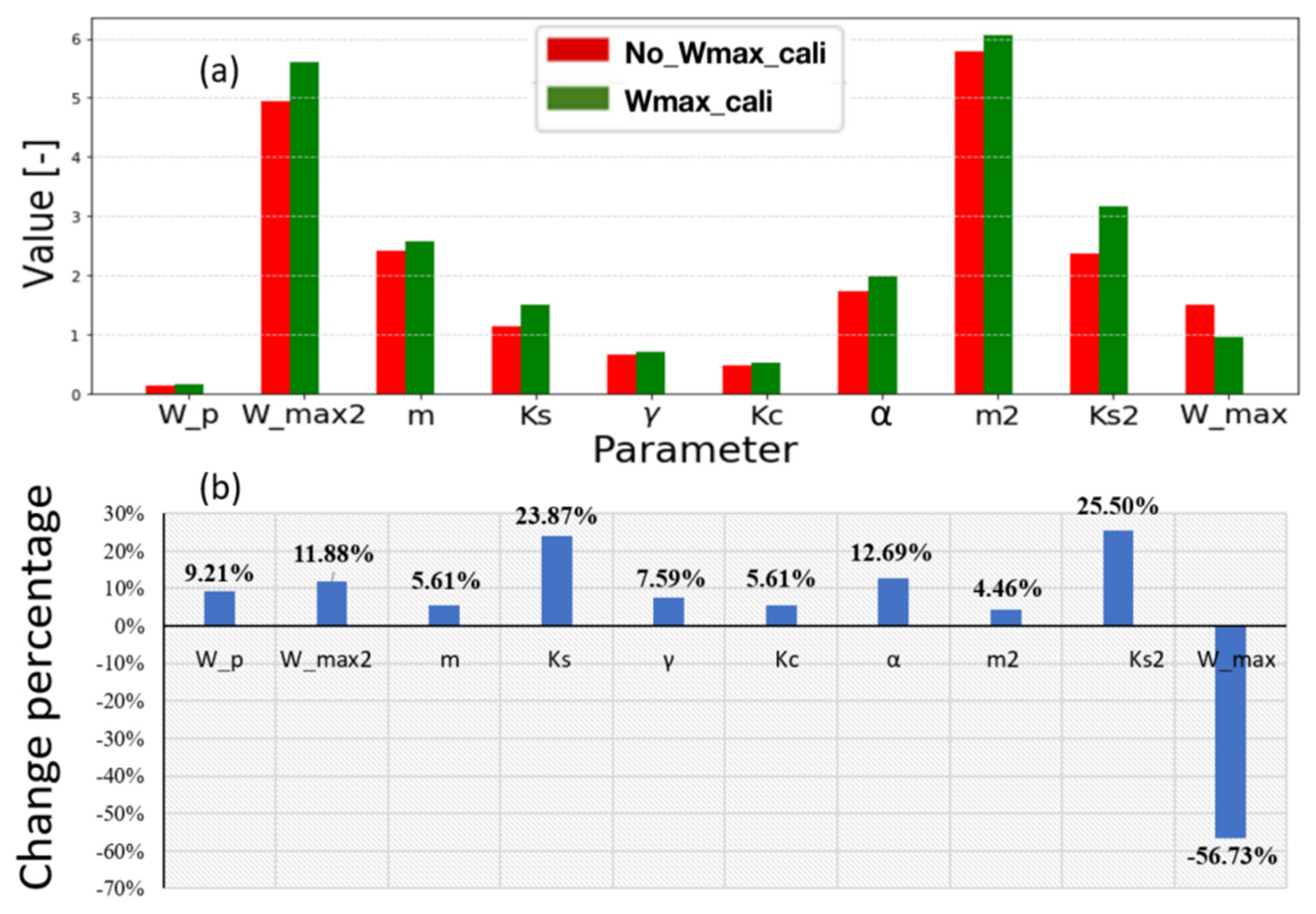
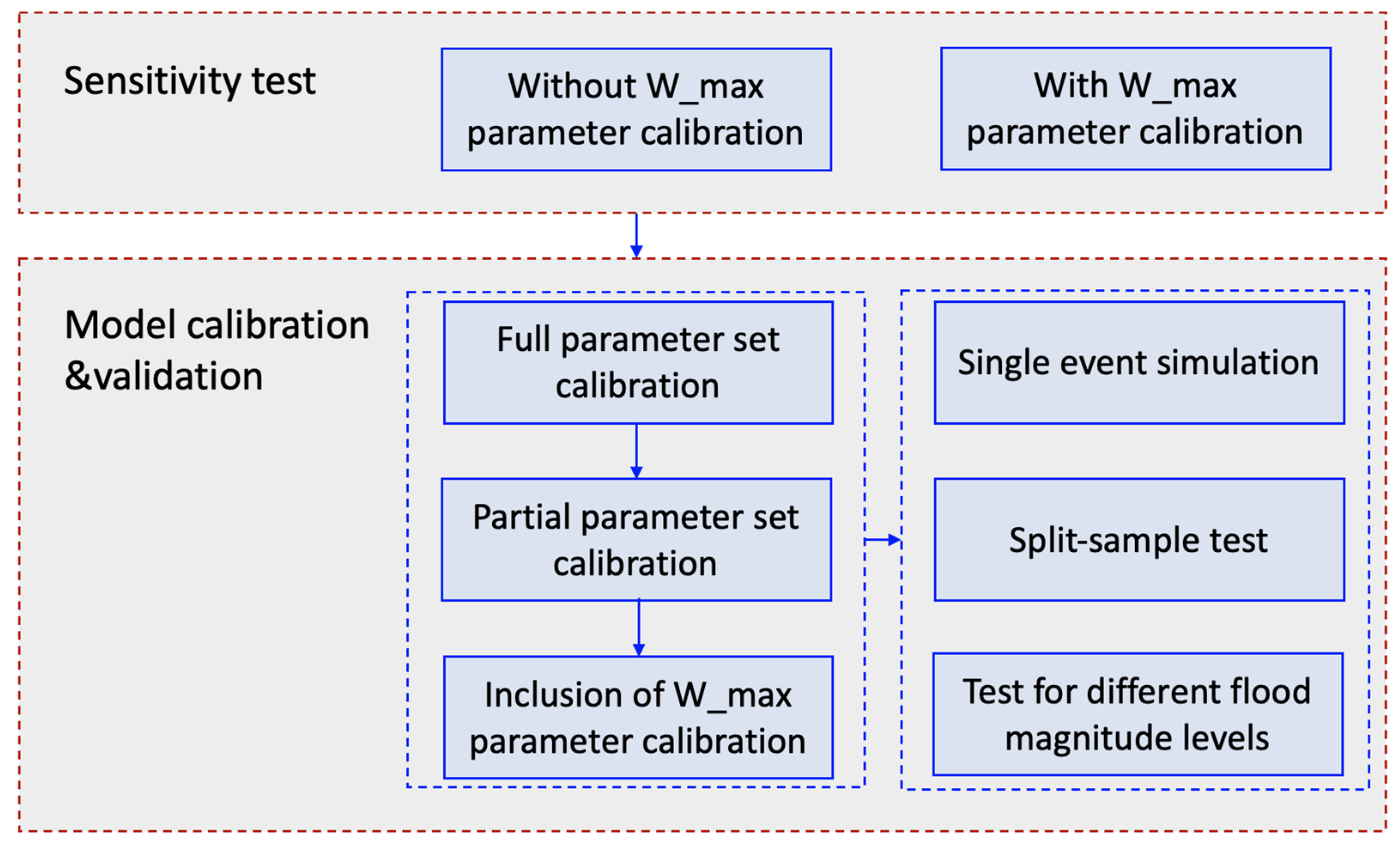
3.3. Sensitivity Test
3.4. Model Calibration and Validation
4. Results
4.1. Full versus Partial Parameter Set Calibration Strategies for Flood Simulations
4.2. Impact of W_max Calibration on Flood Simulations
4.3. Comparison of Different Calibration Schemes for Flood Simulations with “Split-Sample” Test
4.4. Model Performance of Flood Simulations for Different Magnitude Levels
5. Discussion
5.1. The Impact of Parameter Reduction of the Calibration Process on Flood Simulation
5.2. The Importance of W_Max Parameter Estimation in Flood Simulation
5.3. The Influence of Objective Function on Flood Simulations
5.4. Other Issues Related to Flood Simulations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gaume, E.; Borga, M.; Llassat, M.C.; Maouche, S.; Lang, M.; Diakakis, M. Mediterranean Extreme Floods and Flash Floods; IRD Editions: Marseille, France, 2016. [Google Scholar]
- Ragettli, S.; Zhou, J.; Wang, H.; Liu, C.; Guo, L. Modeling flash floods in ungauged mountain catchments of China: A decision tree learning approach for parameter regionalization. J. Hydrol. 2017, 555, 330–346. [Google Scholar] [CrossRef]
- Tramblay, Y.; Bouvier, C.; Ayral, P.-A.; Marchandise, A. Impact of rainfall spatial distribution on rainfall-runoff modelling efficiency and initial soil moisture conditions estimation. Nat. Hazards Earth Syst. Sci. 2011, 11, 157–170. [Google Scholar] [CrossRef]
- Brocca, L.; Liersch, S.; Melone, F.; Moramarco, T.; Volk, M. Application of a model-based rainfall-runoff database as efficient tool for flood risk management. Hydrol. Earth Syst. Sci. 2013, 17, 3159–3169. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, R.; Guo, L.; Tian, J.; Zhang, X.; Ding, L.; Wang, C.; Shang, Y. Forecasting and Providing Warnings of Flash Floods for Ungauged Mountainous Areas Based on a Distributed Hydrological Model. Water 2017, 9, 776. [Google Scholar] [CrossRef]
- Yin, J.; Gentine, P.; Zhou, S.; Sullivan, S.C.; Wang, R.; Zhang, Y.; Guo, S. Large increase in global storm runoff extremes driven by climate and anthropogenic changes. Nat. Commun. 2018, 9, 4389. [Google Scholar] [CrossRef] [PubMed]
- Karymbalis, E.; Katsafados, P.; Chalkias, C.; Gaki-Papanastassiou, K. An integrated study for the evaluation of natural and anthropogenic causes of flooding in small catchments based on geomorphological and meteorological data and modeling techniques: The case of the Xerias torrent (Corinth, Greece). Z. Geomorphol. Suppl. Issues 2012, 56, 45–67. [Google Scholar] [CrossRef]
- Kobold, M.; Brilly, M. The use of HBV model for flash flood forecasting. Nat. Hazards Earth Syst. Sci. 2006, 6, 407–417. [Google Scholar] [CrossRef]
- Tegegne, G.; Park, D.K.; Kim, Y.-O. Comparison of hydrological models for the assessment of water resources in a data-scarce region, the Upper Blue Nile River Basin. J. Hydrol. Reg. Stud. 2017, 14, 49–66. [Google Scholar] [CrossRef]
- Das, T.; Bárdossy, A.; Zehe, E.; He, Y. Comparison of conceptual model performance using different representations of spatial variability. J. Hydrol. 2008, 356, 106–118. [Google Scholar] [CrossRef]
- Lobligeois, F.; Andréassian, V.; Perrin, C.; Tabary, P.; Loumagne, C. When does higher spatial resolution rainfall information improve streamflow simulation? An evaluation using 3620 flood events. Hydrol. Earth Syst. Sci. 2014, 18, 575–594. [Google Scholar] [CrossRef]
- Boithias, L.; Sauvage, S.; Lenica, A.; Roux, H.; Abbaspour, K.C.; Larnier, K.; Dartus, D.; Sánchez-Pérez, J.M. Simulating Flash Floods at Hourly Time-Step Using the SWAT Model. Water 2017, 9, 929. [Google Scholar] [CrossRef]
- Li, D.; Qu, S.; Shi, P.; Chen, X.; Xue, F.; Gou, J.; Zhang, W. Development and Integration of Sub-Daily Flood Modelling Capability within the SWAT Model and a Comparison with XAJ Model. Water 2018, 10, 1263. [Google Scholar] [CrossRef]
- Huang, Y.; Bárdossy, A.; Zhang, K. Sensitivity of hydrological models to temporal and spatial resolutions of rainfall data. Hydrol. Earth Syst. Sci. 2019, 23, 2647–2663. [Google Scholar] [CrossRef]
- Kapangaziwiri, E.; Hughes, D.; Wagener, T. Incorporating uncertainty in hydrological predictions for gauged and ungauged basins in southern Africa. Hydrol. Sci. J. 2012, 57, 1000–1019. [Google Scholar] [CrossRef]
- He, B.; Huang, X.; Ma, M.; Chang, Q.; Tu, Y.; Li, Q.; Zhang, K.; Hong, Y. Analysis of flash flood disaster characteristics in China from 2011 to 2015. Nat. Hazards 2018, 90, 407–420. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Yen, H.; Collick, A.S.; Tilahun, S.A.; Langan, S.; Steenhuis, T.S. Evaluation of CFSR, TMPA 3B42 and ground-based rainfall data as input for hydrological models, in data-scarce regions: The upper Blue Nile Basin, Ethiopia. Catena 2017, 152, 242–251. [Google Scholar] [CrossRef]
- Xin, Z.; Shi, K.; Wu, C.; Wang, L.; Ye, L. Applicability of Hydrological Models for Flash Flood Simulation in Small Catchments of Hilly Area in China. Open Geosci. 2019, 11, 1168–1181. [Google Scholar] [CrossRef]
- Yu, D.; Xie, P.; Dong, X.; Hu, X.; Liu, J.; Li, Y.; Peng, T.; Ma, H.; Wang, K.; Xu, S. Improvement of the SWAT model for event-based flood simulation on a sub-daily timescale. Hydrol. Earth Syst. Sci. 2018, 22, 5001–5019. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W.; Hasenauer, S.; Hahn, S. Assimilation of Surface- and Root-Zone ASCAT Soil Moisture Products Into Rainfall-Runoff Modeling. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2542–2555. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T. Distributed rainfall-runoff modelling for flood frequency estimation and flood forecasting. Hydrol. Process. 2011, 25, 2801–2813. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Barbetta, S.; Papathanasiou, C.; Mimikou, M.; Moramarco, T. Using globally available soil moisture indicators for flood modelling in Mediterranean catchments. Hydrol. Earth Syst. Sci. 2014, 18, 839–853. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Ciabatta, L.; Moramarco, T.; Gabellani, S.; Albergel, C.; De Rosnay, P.; Puca, S.; Wagner, W. The Use of H-SAF Soil Moisture Products for Operational Hydrology: Flood Modelling over Italy. Hydrology 2015, 2, 2–22. [Google Scholar] [CrossRef]
- Massari, C.; Camici, S.; Ciabatta, L.; Brocca, L. Exploiting Satellite-Based Surface Soil Moisture for Flood Forecasting in the Mediterranean Area: State Update Versus Rainfall Correction. Remote Sens. 2018, 10, 292. [Google Scholar] [CrossRef]
- Masseroni, D.; Cislaghi, A.; Camici, S.; Massari, C.; Brocca, L. A reliable rainfall–runoff model for flood forecasting: Review and application to a semi-urbanized watershed at high flood risk in Italy. Hydrol. Res. 2016, 48, 726–740. [Google Scholar] [CrossRef]
- Liu, D.; Xu, Y.; Guo, S.; Liu, P.; Rheinheimer, D.E. A modified Green–Ampt model for water infiltration and preferential flow. Hydrol. Res. 2016, 47, 1172–1181. [Google Scholar] [CrossRef][Green Version]
- Beven, K. Down to Basics: Runoff Processes and the Modelling Process. In Rainfall-Runoff Modelling; Wiley: Hoboken, NJ, USA, 2012; pp. 1–23. [Google Scholar] [CrossRef]
- Sun, R.; Hernández, F.; Liang, X.; Yuan, H. A Calibration Framework for High-Resolution Hydrological Models Using a Multiresolution and Heterogeneous Strategy. Water Resour. Res. 2020, 56, e2019WR026541. [Google Scholar] [CrossRef]
- Foglia, L.; Hill, M.C.; Mehl, S.W.; Burlando, P. Sensitivity analysis, calibration, and testing of a distributed hydrological model using error-based weighting and one objective function. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Fernández-Pato, J.; Caviedes-Voullième, D.; García-Navarro, P. Rainfall/runoff simulation with 2D full shallow water equations: Sensitivity analysis and calibration of infiltration parameters. J. Hydrol. 2016, 536, 496–513. [Google Scholar] [CrossRef]
- Gan, Y.; Liang, X.-Z.; Duan, Q.; Ye, A.; Di, Z.; Hong, Y.; Li, J. A systematic assessment and reduction of parametric uncertainties for a distributed hydrological model. J. Hydrol. 2018, 564, 697–711. [Google Scholar] [CrossRef]
- Beck, M.B. Water quality modeling: A review of the analysis of uncertainty. Water Resour. Res. 1987, 23, 1393–1442. [Google Scholar] [CrossRef]
- Cheng, C.-T.; Zhao, M.-Y.; Chau, K.W.; Wu, X.-Y. Using genetic algorithm and TOPSIS for Xinanjiang model calibration with a single procedure. J. Hydrol. 2006, 316, 129–140. [Google Scholar] [CrossRef]
- Haan, C.T.; Barfield, B.J.; Hayes, J.C. 13-Hydrologic Modeling. In Design Hydrology and Sedimentology for Small Catchments; Haan, C.T., Barfield, B.J., Hayes, J.C., Eds.; Academic Press: San Diego, CA, USA, 1994; pp. 455–474. [Google Scholar]
- Chen, F.; Dudhia, J. Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Doorenbos, J.; Pruitt, W. Appendix II—Background and development of methods to predict reference crop evapotranspiration (ETo). In Guidelines for Predicting Crop Water Requirements; FAO: Rome, Italy, 1977; pp. 108–119. [Google Scholar]
- Famiglietti, J.S.; Wood, E.F. Multiscale modeling of spatially variable water and energy balance processes. Water Resour. Res. 1994, 30, 3061–3078. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T. On the estimation of antecedent wetness conditions in rainfall–runoff modelling. Hydrol. Process. Int. J. 2008, 22, 629–642. [Google Scholar] [CrossRef]
- Corradini, C.; Melone, F.; Ubertini, L. A Semi-Distributed Model for Direct Runoff Estimate; IASTED ACTA Press: Anahheim, CA, USA, 1995; pp. 541–545. [Google Scholar]
- Andreadis, K.M.; Clark, E.A.; Wood, A.W.; Hamlet, A.F.; Lettenmaier, D.P. Twentieth-Century Drought in the Conterminous United States. J. Hydrometeorol. 2005, 6, 985–1001. [Google Scholar] [CrossRef]
- Corradini, C.; Morbidelli, R.; Saltalippi, C.; Melone, F. An adaptive model for flood forecasting on medium size basins. Appl. Simul. Model. 2002, 555–559. [Google Scholar]
- Haan, C.T.; Barfield, B.J.; Hayes, J.C. 3-Rainfall-Runoff Estimation in Storm Water Computations. In Design Hydrology and Sedimentology for Small Catchments; Haan, C.T., Barfield, B.J., Hayes, J.C., Eds.; Academic Press: San Diego, CA, USA, 1994; pp. 37–103. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Larry, W. Mays. Applied Hydrology, International ed.; MacGraw-Hill, Inc.: New York, NY, USA, 1988; p. 149. [Google Scholar]
- Gan, T.Y.; Dlamini, E.M.; Biftu, G.F. Effects of model complexity and structure, data quality, and objective functions on hydrologic modeling. J. Hydrol. 1997, 192, 81–103. [Google Scholar] [CrossRef]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424, 264–277. [Google Scholar] [CrossRef]
- Gupta, M. Model Calibration and Uncertainty Estimation. In Encyclopedia of Hydrological Sciences; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Matonse, A.H.; Kroll, C.N. Applying hillslope-storage models to improve low flow estimates with limited streamflow data at a watershed scale. J. Hydrol. 2013, 494, 20–31. [Google Scholar] [CrossRef]
- Son, K.; Sivapalan, M. Improving model structure and reducing parameter uncertainty in conceptual water balance models through the use of auxiliary data. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Muleta, M.K.; Nicklow, J.W. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar] [CrossRef]
- Van Werkhoven, K.; Wagener, T.; Reed, P.; Tang, Y. Sensitivity-guided reduction of parametric dimensionality for multi-objective calibration of watershed models. Adv. Water Resour. 2009, 32, 1154–1169. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ sensitivity analysis of a complex environmental model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Mahapatra, S.; Jha, M.K.; Biswal, S.; Senapati, D. Assessing Variability of Infiltration Characteristics and Reliability of Infiltration Models in a Tropical Sub-humid Region of India. Sci. Rep. 2020, 10, 1515. [Google Scholar] [CrossRef] [PubMed]
- Tügel, F.; Özgen-Xian, I.; Marafini, E.; Hadidi, A.; Hinkelmann, R. Flash flood simulations for an Egyptian city-mitigation measures and impact of infiltration. Urban Water J. 2020, 17, 396–406. [Google Scholar] [CrossRef]
- Tian, J.; Liu, J.; Wang, Y.; Wang, W.; Li, C.; Hu, C. A coupled atmospheric–hydrologic modeling system with variable grid sizes for rainfall–runoff simulation in semi-humid and semi-arid watersheds: How does the coupling scale affects the results? Hydrol. Earth Syst. Sci. 2020, 24, 3933–3949. [Google Scholar] [CrossRef]
- Mizukami, N.; Rakovec, O.; Newman, A.J.; Clark, M.P.; Wood, A.W.; Gupta, H.V.; Kumar, R. On the choice of calibration metrics for “high-flow” estimation using hydrologic models. Hydrol. Earth Syst. Sci. 2019, 23, 2601–2614. [Google Scholar] [CrossRef]
- Santos, L.; Thirel, G.; Perrin, C. Technical note: Pitfalls in using log-transformed flows within the KGE criterion. Hydrol. Earth Syst. Sci. 2018, 22, 4583–4591. [Google Scholar] [CrossRef]
- Pool, S.; Vis, M.; Seibert, J. Evaluating model performance: Towards a non-parametric variant of the Kling-Gupta efficiency. Hydrol. Sci. J. 2018, 63, 1941–1953. [Google Scholar] [CrossRef]
- López, P.L.; Sutanudjaja, E.H.; Schellekens, J.; Sterk, G.; Bierkens, M.F.P. Calibration of a large-scale hydrological model using satellite-based soil moisture and evapotranspiration products. Hydrol. Earth Syst. Sci. 2017, 21, 3125–3144. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Mathevet, T.; Gupta, H.; Perrin, C.; Andréassian, V.; Le Moine, N. Assessing the performance and robustness of two conceptual rainfall-runoff models on a worldwide sample of watersheds. J. Hydrol. 2020, 585, 124698. [Google Scholar] [CrossRef]
- Camici, S.; Massari, C.; Ciabatta, L.; Marchesini, I.; Brocca, L. Which rainfall score is more informative about the performance in river discharge simulation? A comprehensive assessment on 1318 basins over Europe. Hydrol. Earth Syst. Sci. 2020, 24, 4869–4885. [Google Scholar] [CrossRef]
- Brocca, L.; Filippucci, P.; Hahn, S.; Ciabatta, L.; Massari, C.; Camici, S.; Schüller, L.; Bojkov, B.; Wagner, W. SM2RAIN–ASCAT (2007–2018): Global daily satellite rainfall data from ASCAT soil moisture observations. Earth Syst. Sci. Data 2019, 11, 1583–1601. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degre, A. Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: A review. Biotechnol. Agron. Soc. Environ. 2013, 17, 392–406. [Google Scholar]
- Mel, R.; Lionello, P. Storm Surge Ensemble Prediction for the City of Venice. Weather Forecast. 2014, 29, 1044–1057. [Google Scholar] [CrossRef]
- Mel, R.; Lionello, P. Probabilistic Dressing of a Storm Surge Prediction in the Adriatic Sea. Adv. Meteorol. 2016, 2016, 3764519. [Google Scholar] [CrossRef]
- House, P.; Lannoy, G.I.; Walker, J. Hydrologic Data Assimilation. In Approaches to Managing Disaster—Assessing Hazards, Emergencies and Disaster Impacts; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef]
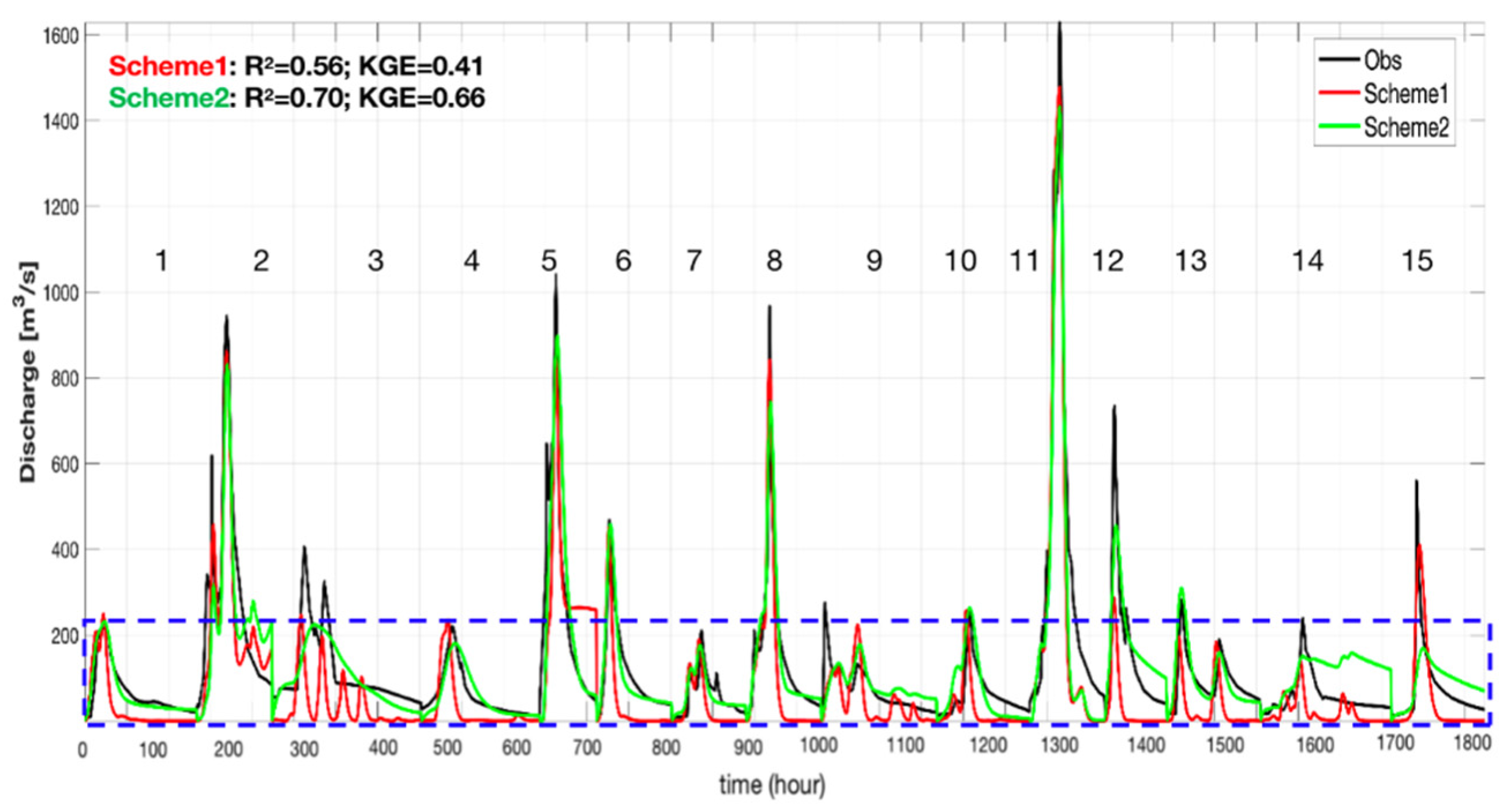
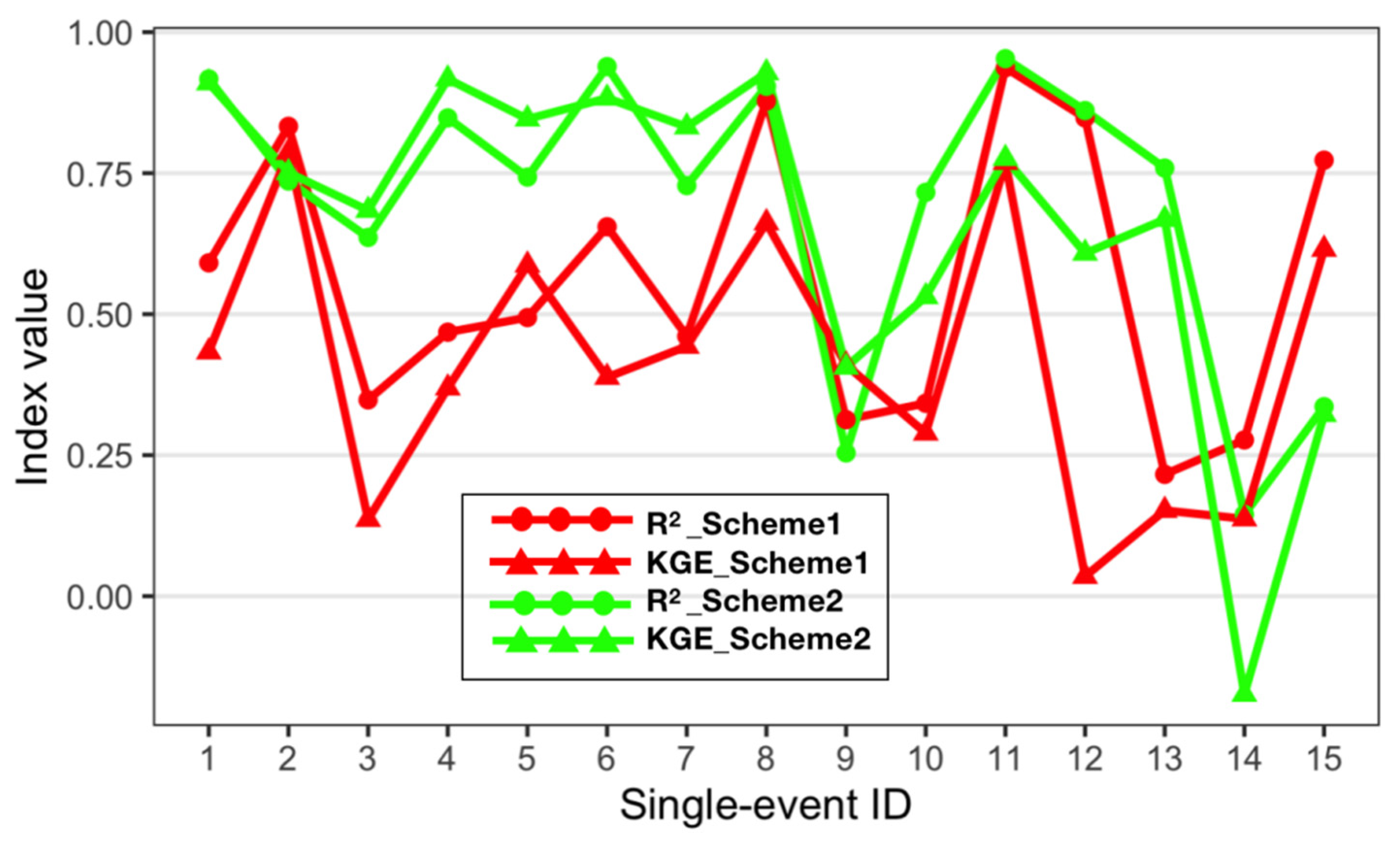
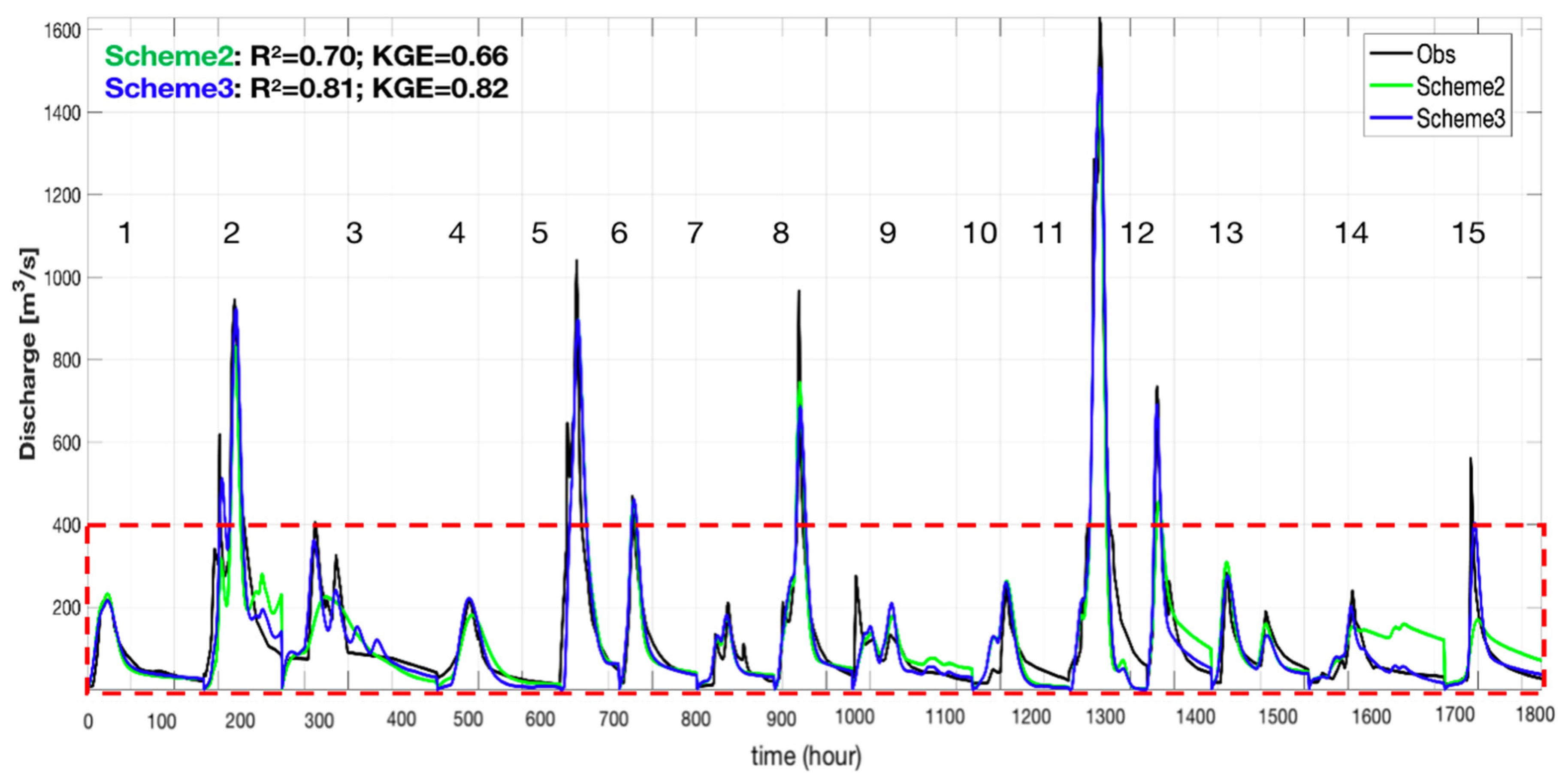
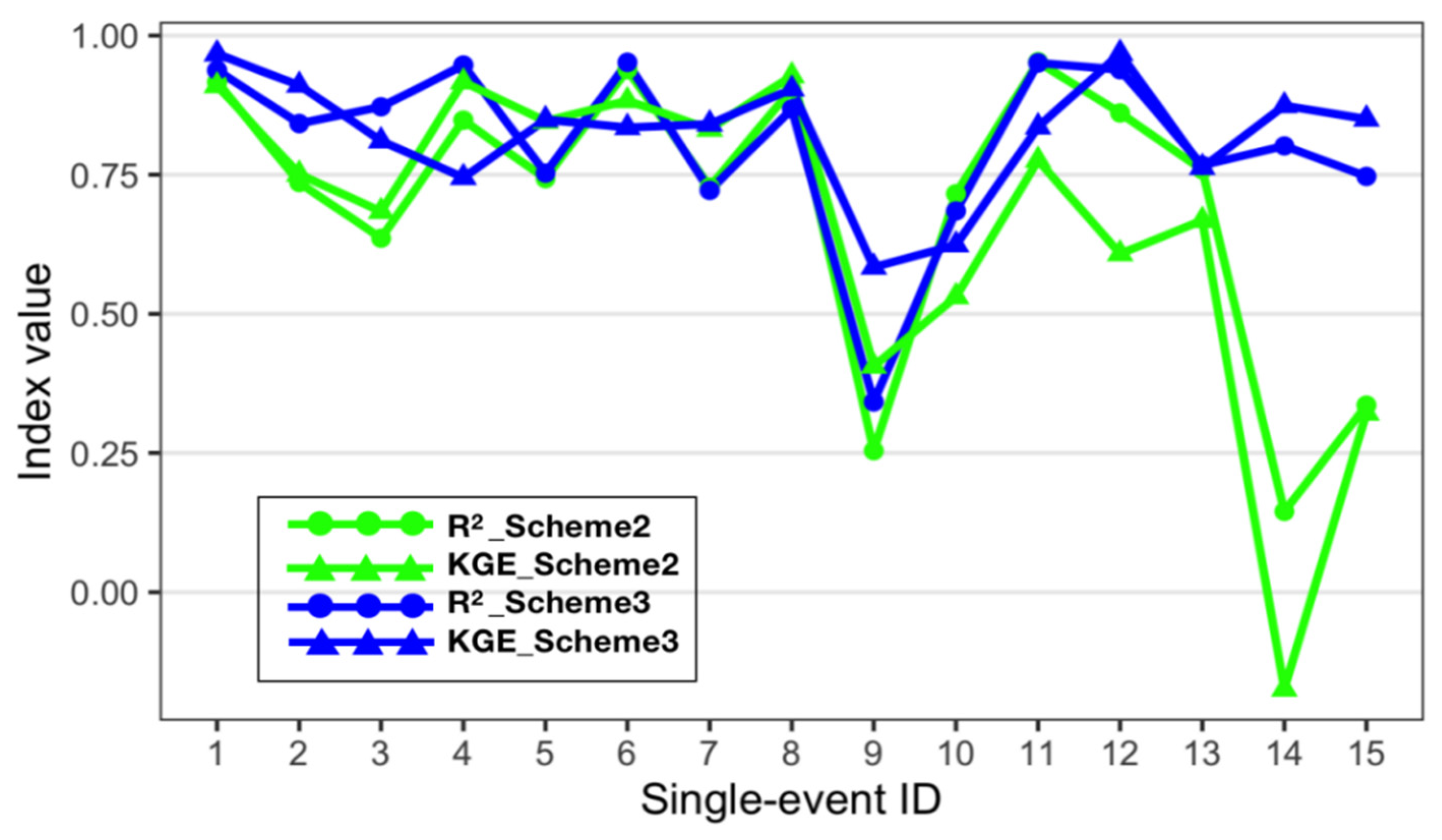
| Event No. | Single-Event ID | Date of Flood Start | Dates of Flood End | Peak Discharge (m3/s) | Maximum Rainfall (mm) | Magnitude Level of Flood Events |
|---|---|---|---|---|---|---|
| 1 | 20100608 | 08/06/2010 | 14/06/2010 | 216 | 22.4 | Low |
| 2 | 20100611 | 11/07/2010 | 15/07/2010 | 944.06 | 37.1 | High |
| 3 | 20100719 | 19/07/2010 | 27/07/2010 | 405 | 36.3 | Medium |
| 4 | 20100902 | 02/09/2010 | 09/09/2010 | 220 | 69 | Low |
| 5 | 20110618 | 18/06/2011 | 21/06/2011 | 1040 | 29 | High |
| 6 | 20110624 | 24/06/2011 | 28/06/2011 | 467.8 | 49.5 | Medium |
| 7 | 20110810 | 10/08/2011 | 13/08/2011 | 210 | 34 | Low |
| 8 | 20120613 | 13/07/2012 | 17/07/2012 | 966.44 | 44.5 | High |
| 9 | 20120809 | 09/08/2012 | 15/08/2012 | 275.02 | 18 | Medium |
| 10 | 20130624 | 24/06/2013 | 28/06/2013 | 261.53 | 33.5 | Medium |
| 11 | 20130706 | 06/07/2013 | 10/07/2013 | 1628.5 | 47.5 | High |
| 12 | 20140704 | 04/07/2014 | 07/07/2014 | 734 | 34 | High |
| 13 | 20140831 | 31/08/2014 | 05/09/2014 | 281.7 | 26 | Medium |
| 14 | 20150626 | 26/06/2015 | 03/07/2015 | 239.1 | 20 | Low |
| 15 | 20150809 | 09/08/2015 | 14/08/2015 | 560 | 53 | High |
| Station ID | Station Name | Longitude (Degree) | Latitude (Degree) |
|---|---|---|---|
| 1 | Chandang | 115.47 | 31.4 |
| 2 | Xihe | 115.42 | 31.42 |
| 3 | Guanmiao | 115.5 | 31.5 |
| 4 | Yinsha | 115.47 | 31.58 |
| 5 | Xuao | 115.58 | 31.2 |
| 6 | Wudian | 115.57 | 31.28 |
| 7 | Banzhuyun | 115.55 | 31.35 |
| 8 | Huangnizhuang | 115.62 | 31.47 |
| 9 | Mazongling | 115.67 | 31.3 |
| 10 | Qiaobianhe | 115.68 | 31.37 |
| 11 | Zimuhe | 115.68 | 31.4 |
| 12 | Huangbaishan | 115.33 | 31.42 |
| 13 | Baizhanping | 115.33 | 31.45 |
| 14 | Heihe | 115.38 | 31.55 |
| Parameter | Description | Unit | Range of Variability |
|---|---|---|---|
| W_max | Maximum water capacity of the 1st layer | mm | 50–700 |
| W_max2 | Maximum water capacity of the 2nd layer | mm | 300–4000 |
| W_p | Initial condition | / | 0–1 |
| m | Exponent of drainage for the 1st layer | / | 2–10 |
| m2 | Exponent of drainage for the 2nd layer | / | 5–20 |
| Ks | Hydraulic conductivity of the 1st layer | mm/day | 0.1–20.0 |
| Ks2 | Hydraulic conductivity of the 2nd layer | mm/day | 0.01–45 |
| γ | Coefficient lag–time relationship | / | 0.5–3.5 |
| Kc | Parameter of potential evapotranspiration | / | 0.4–2 |
| α | Exponent of the infiltration relationship | / | 1–15 |
| Scheme | Description | Parameters for Calibration |
|---|---|---|
| S1 | Calibration with 9 parameters | W_max2, W_p, m, m2, Ks, Ks2, γ, Kc, α |
| S2 | Calibration with 5 parameters | γ, W_p, Ks, α, Kc |
| S3 | Calibration with 6 parameters | γ, W_p, Ks, α, Kc, W_max |
| Scheme | Calibration | Validation | ||
|---|---|---|---|---|
| R2 | KGE | R2 | KGE | |
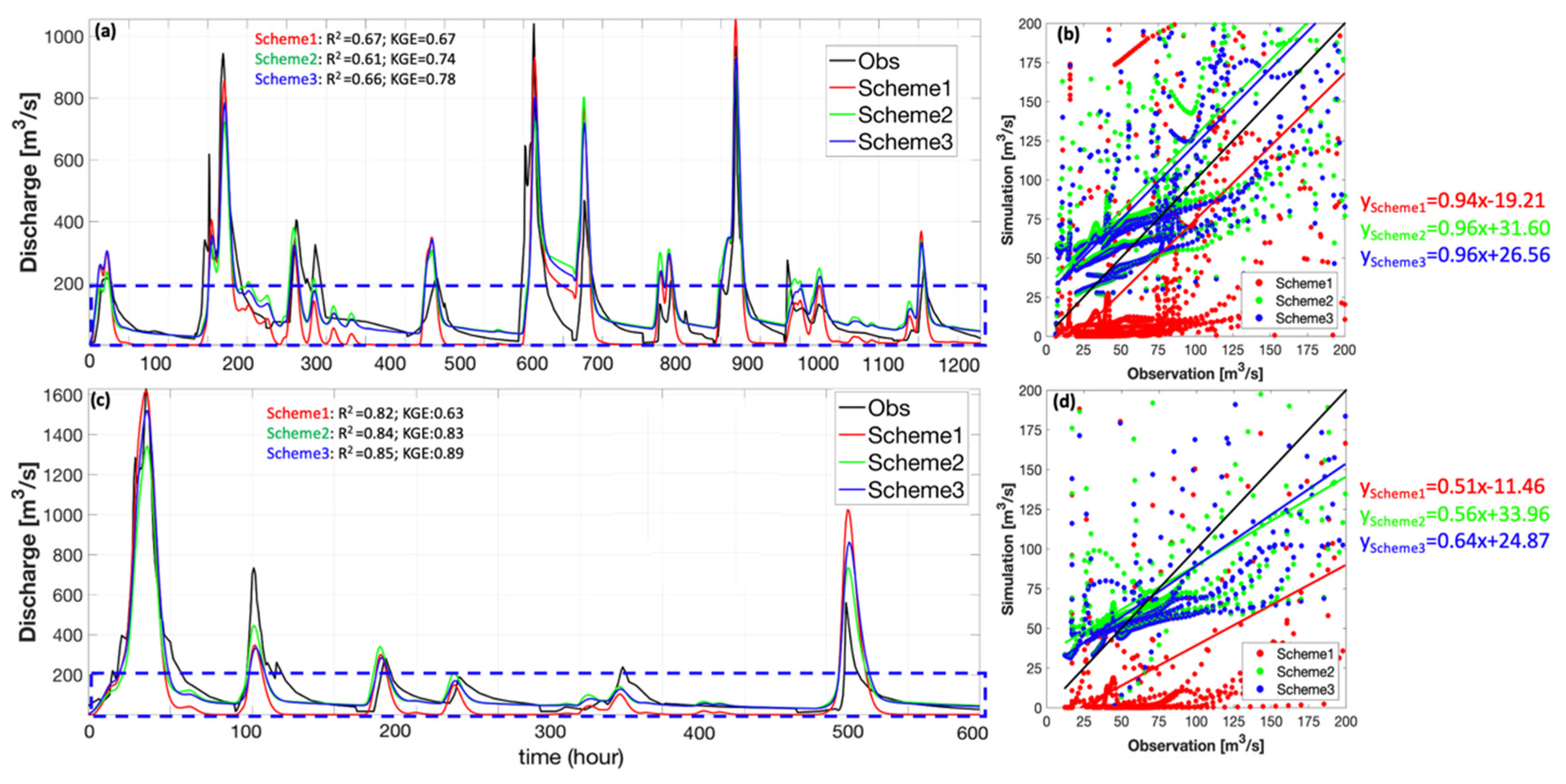
| S1 | 0.67 | 0.67 | 0.82 | 0.63 |
| S2 | 0.61 | 0.74 | 0.84 | 0.83 |
| S3 | 0.66 | 0.78 | 0.85 | 0.89 |
| Magnitude | Scheme | Calibration | Validation | ||
|---|---|---|---|---|---|
| R2 | KGE | R2 | KGE | ||
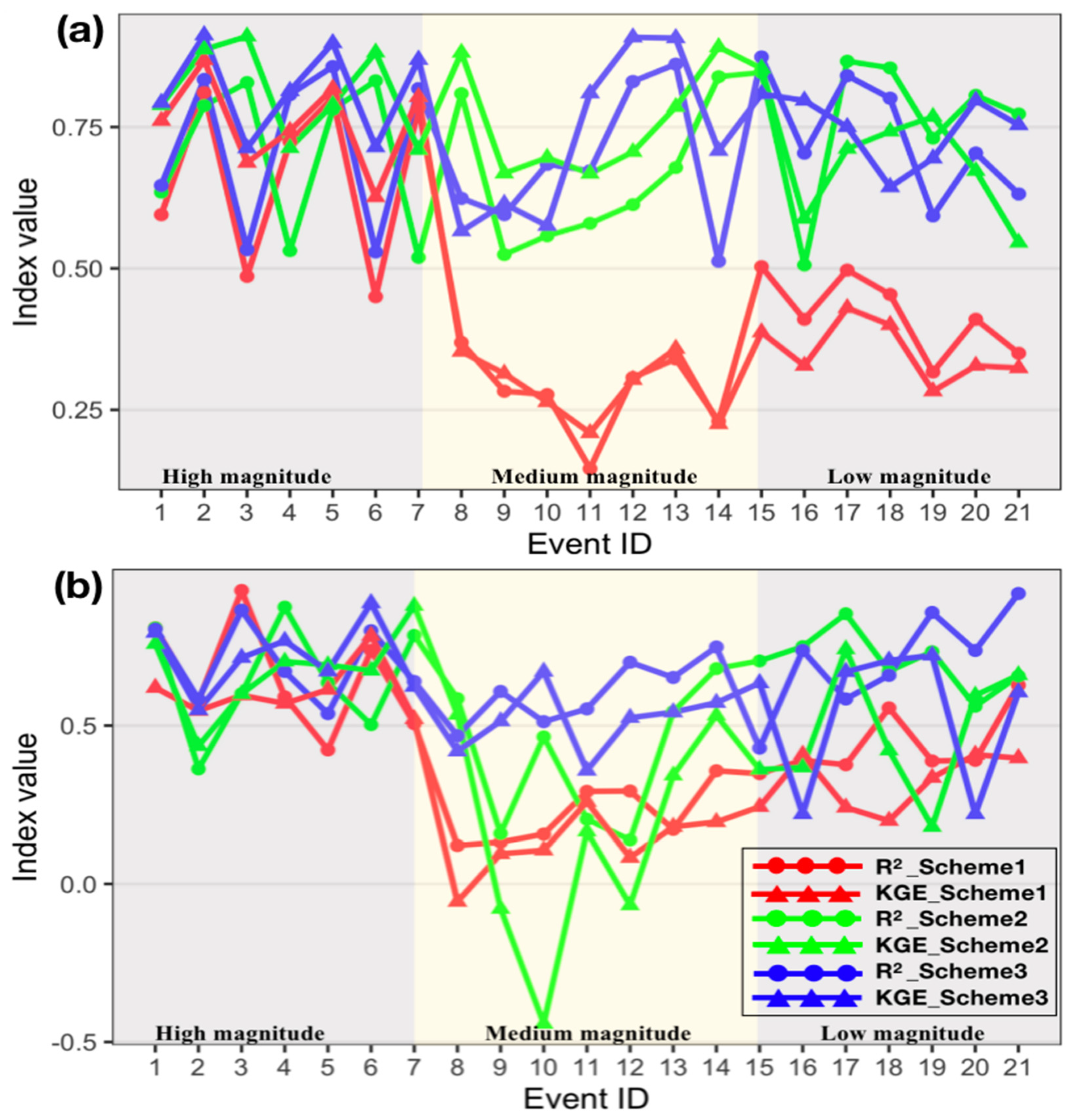
| High-magnitude (Events 1–7) | S1 | 0.66 | 0.76 | 0.65 | 0.61 |
| S2 | 0.70 | 0.81 | 0.65 | 0.68 | |
| S3 | 0.72 | 0.82 | 0.70 | 0.72 | |
| Medium-magnitude (Events 8–14) | S1 | 0.28 | 0.29 | 0.22 | 0.12 |
| S2 | 0.65 | 0.76 | 0.40 | 0.14 | |
| S3 | 0.68 | 0.73 | 0.61 | 0.51 | |
| Low-magnitude (Events 15–21) | S1 | 0.42 | 0.35 | 0.44 | 0.32 |
| S2 | 0.77 | 0.70 | 0.70 | 0.47 | |
| S3 | 0.73 | 0.75 | 0.70 | 0.54 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, N.T.; He, W.; Zhu, Y.; Lü, H. Influence of Calibration Parameter Selection on Flash Flood Simulation for Small to Medium Catchments with MISDc-2L Model. Water 2020, 12, 3255. https://doi.org/10.3390/w12113255
Nguyen NT, He W, Zhu Y, Lü H. Influence of Calibration Parameter Selection on Flash Flood Simulation for Small to Medium Catchments with MISDc-2L Model. Water. 2020; 12(11):3255. https://doi.org/10.3390/w12113255
Chicago/Turabian StyleNguyen, Ngoc Tu, Wei He, Yonghua Zhu, and Haishen Lü. 2020. "Influence of Calibration Parameter Selection on Flash Flood Simulation for Small to Medium Catchments with MISDc-2L Model" Water 12, no. 11: 3255. https://doi.org/10.3390/w12113255
APA StyleNguyen, N. T., He, W., Zhu, Y., & Lü, H. (2020). Influence of Calibration Parameter Selection on Flash Flood Simulation for Small to Medium Catchments with MISDc-2L Model. Water, 12(11), 3255. https://doi.org/10.3390/w12113255





