Assessment of Population Exposure to Urban Flood at the Building Scale
Abstract
1. Introduction
2. Study Area and Data
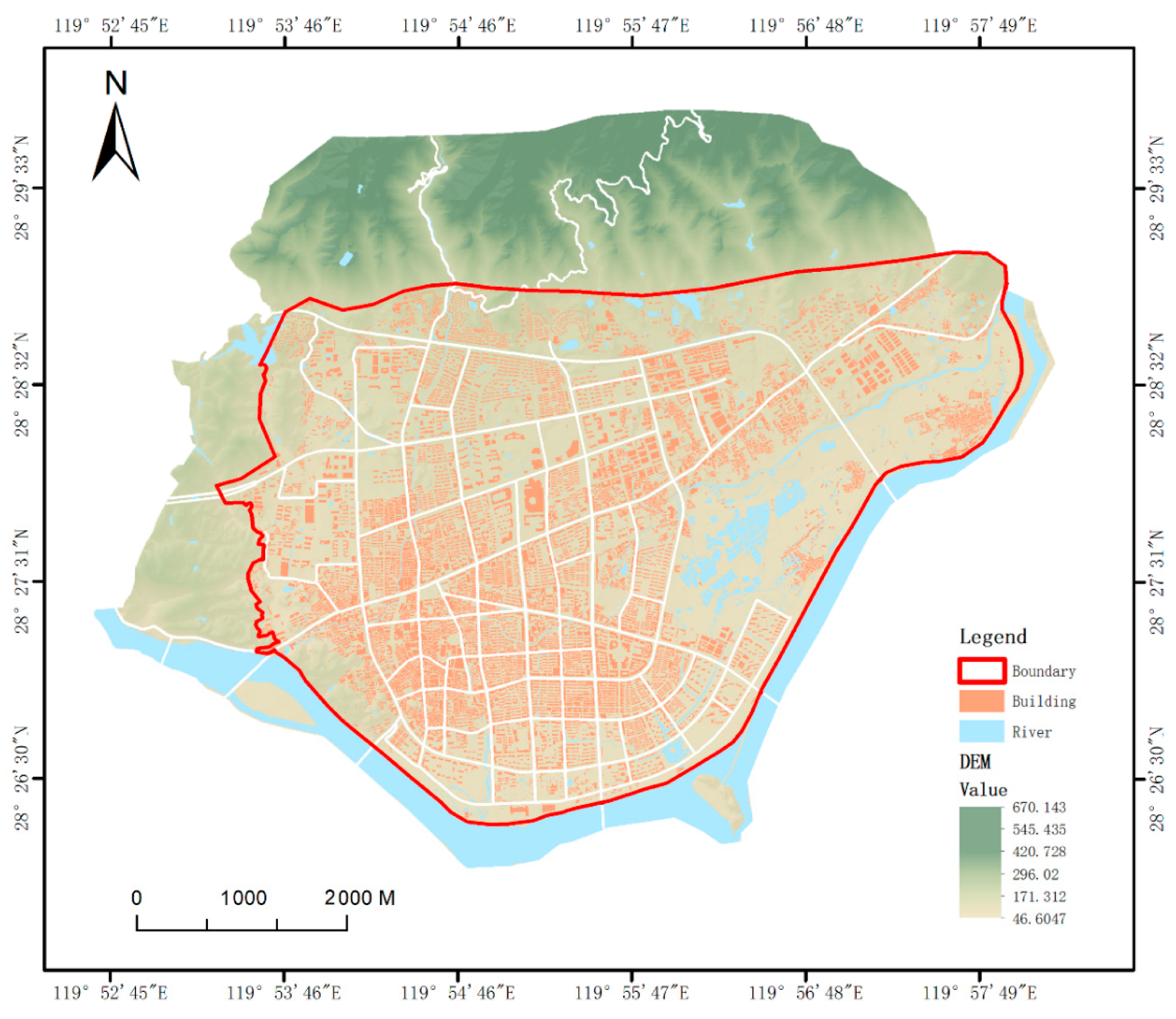
2.1. Study Area
2.2. Data Source
- (1)
- Basic geographic data were provided by the Lishui City Surveying and Mapping Center, including digital elevation model (DEM), water system, transportation, building, administrative division, and underground drainage pipe network datasets. DEM data with 5 m resolution were used for terrain analysis. Administrative area and building pattern data assisted in the spatialization of demographic data. Water system and underground pipeline data were used for flood simulations.
- (2)
- POIs were obtained through the API of Baidu Maps, which is one of the most popular electronic maps in China. The total number of POIs in the study area was 11,092. To facilitate data processing, POIs were divided into 10 types including medical facilities, market shopping, restaurants, government agencies, companies, life services, education and training, residential quarters, transportation facilities, and tourist attractions.
- (3)
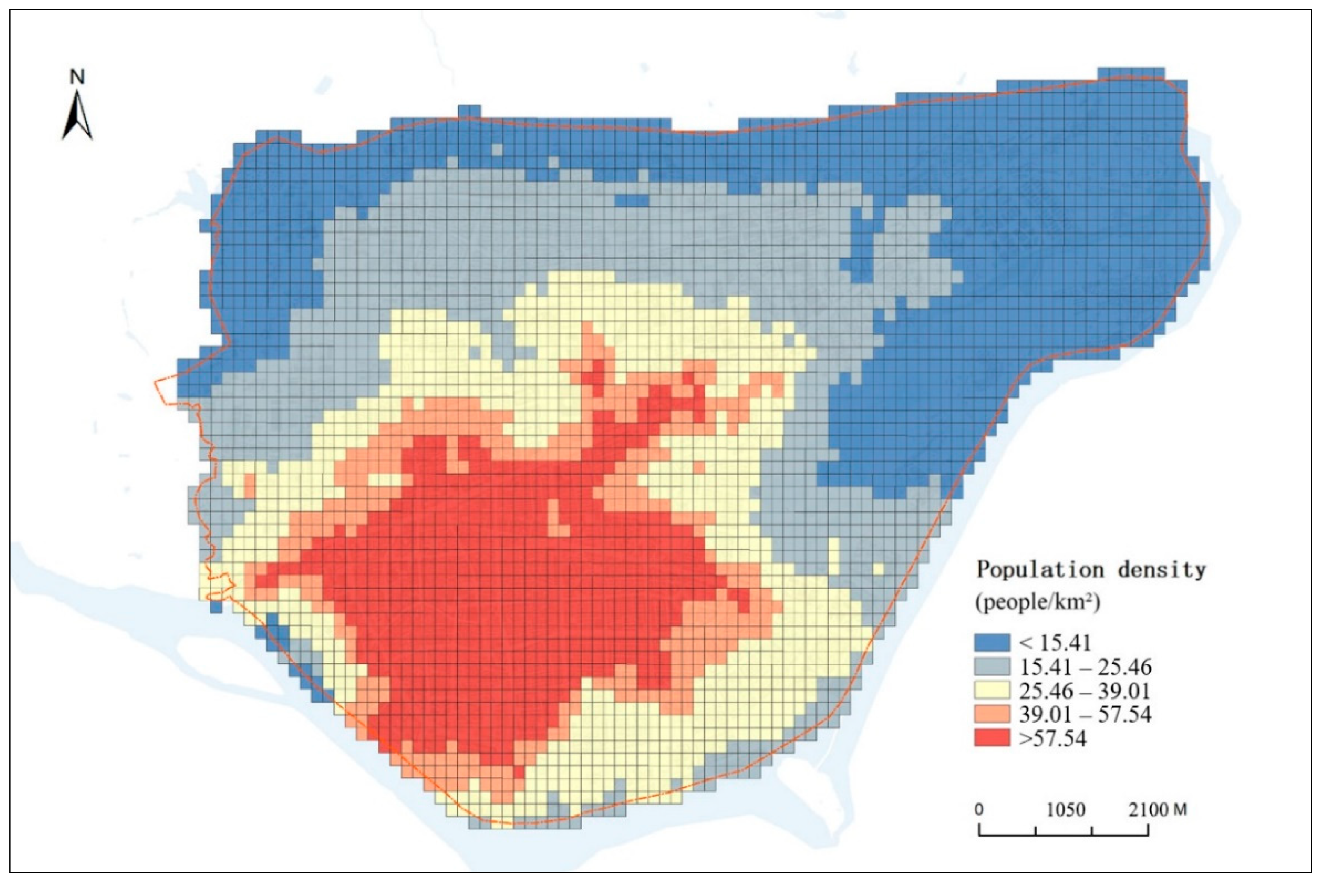
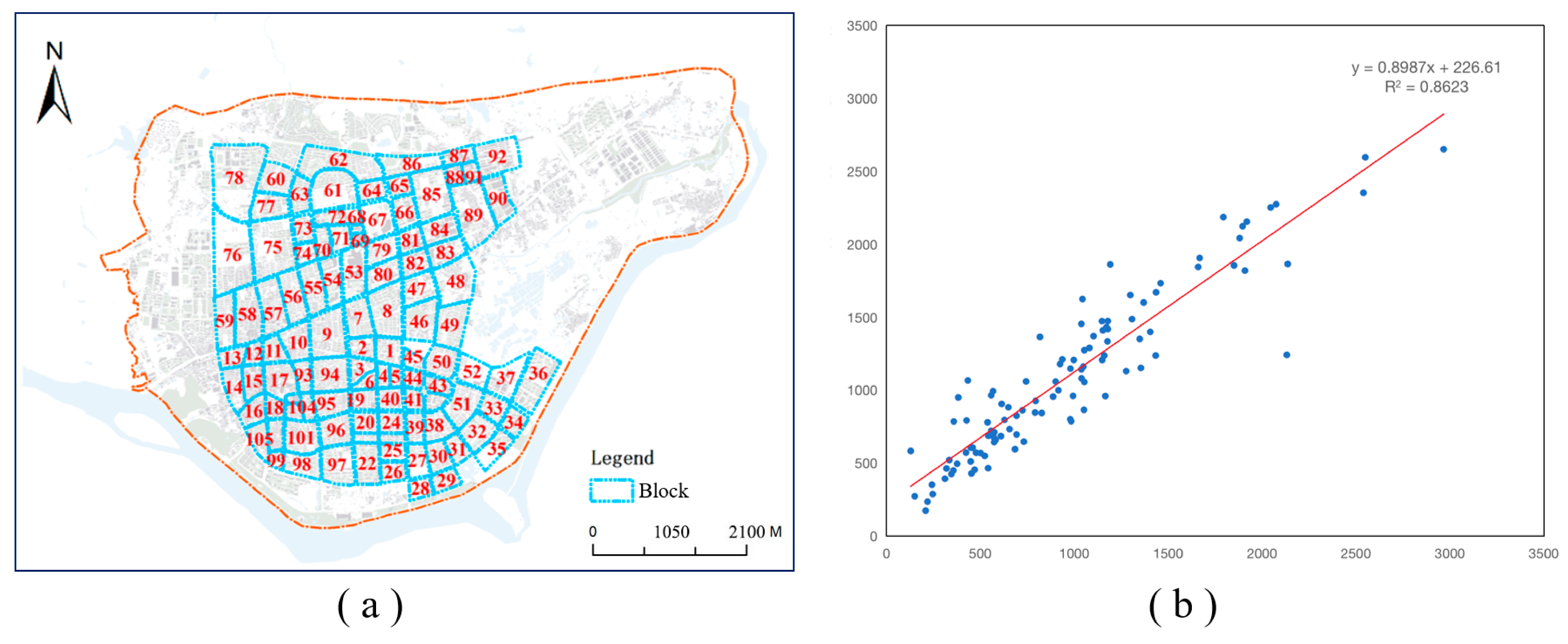
- The WorldPop dataset (the spatial distribution of population in 2015, China) was selected as the population grid dataset, which is available online (https://www.worldpop.org/geodata/summary?id=5279). Compared with other population grid datasets (GPW, GRUMP, and WorldPop), WorldPop has high accuracy and resolution in China [29] and is the result of a global population distribution mapping project led by the Geographic Data Institute of the University of Southampton in the United Kingdom. It is generated using a random forest algorithm by integrating multi-source data from population censuses, satellites, mobile devices, etc., with a grid resolution of 3 arc (approximately 100 m at the equator). This high spatial resolution means it is widely used in disaster assessment, socio-economics, and other fields. The WorldPop dataset for the study area is shown in Figure 2. From the official website of the Lishui government (http://sq.inlishui.com), we collected census data of 18 communities (25 communities in total). The WorldPop dataset has certain accuracy relative to the census, with an R2 value of 0.7673. However, the RMSE value is 3396.3060, which may be caused by the fact that the floating population is not included in the WorldPop data.
3. Methodology
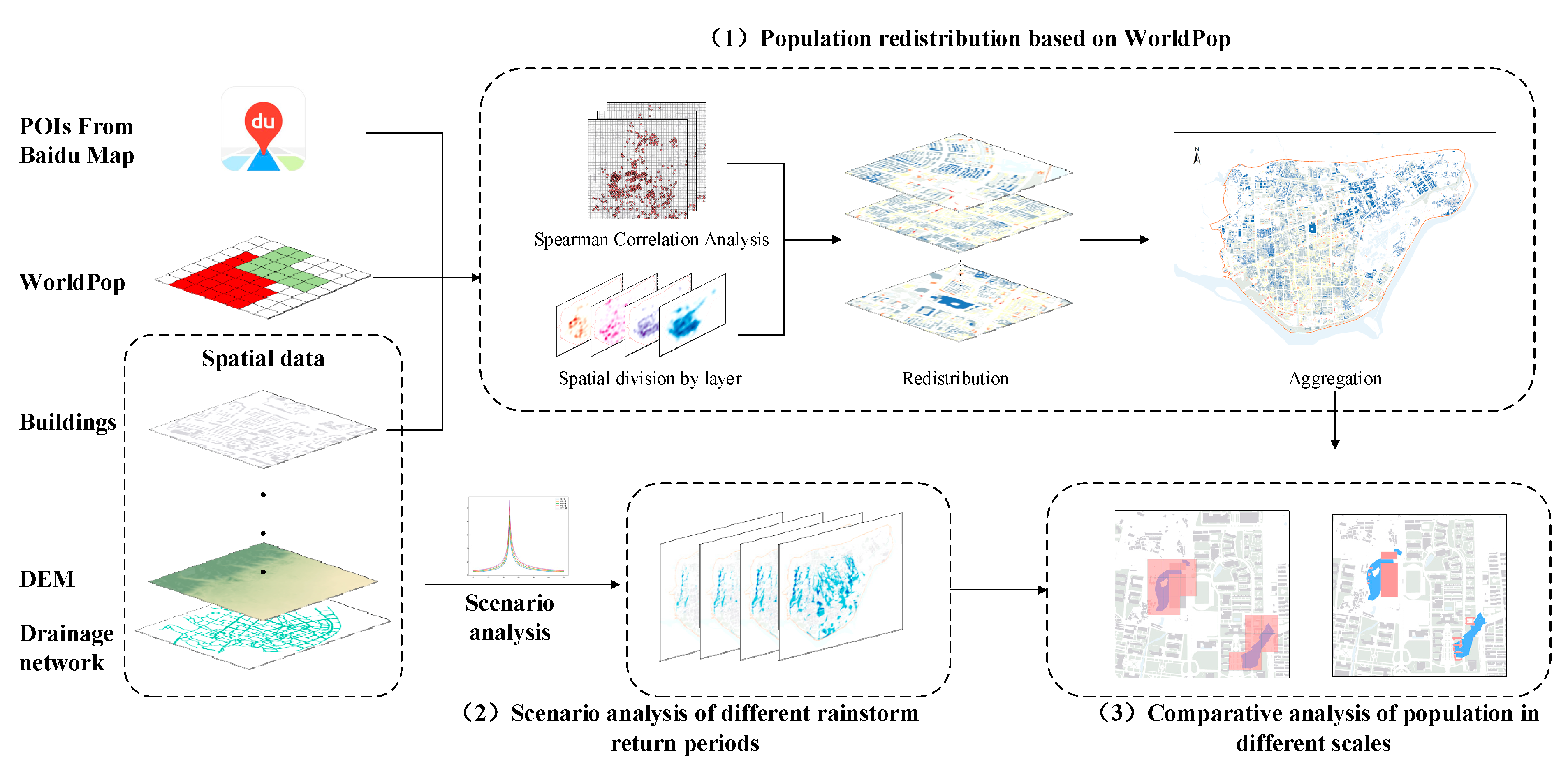
3.1. Mapping the Population at the Building Scale
3.1.1. Correlation Analysis between POIs and Population Grid
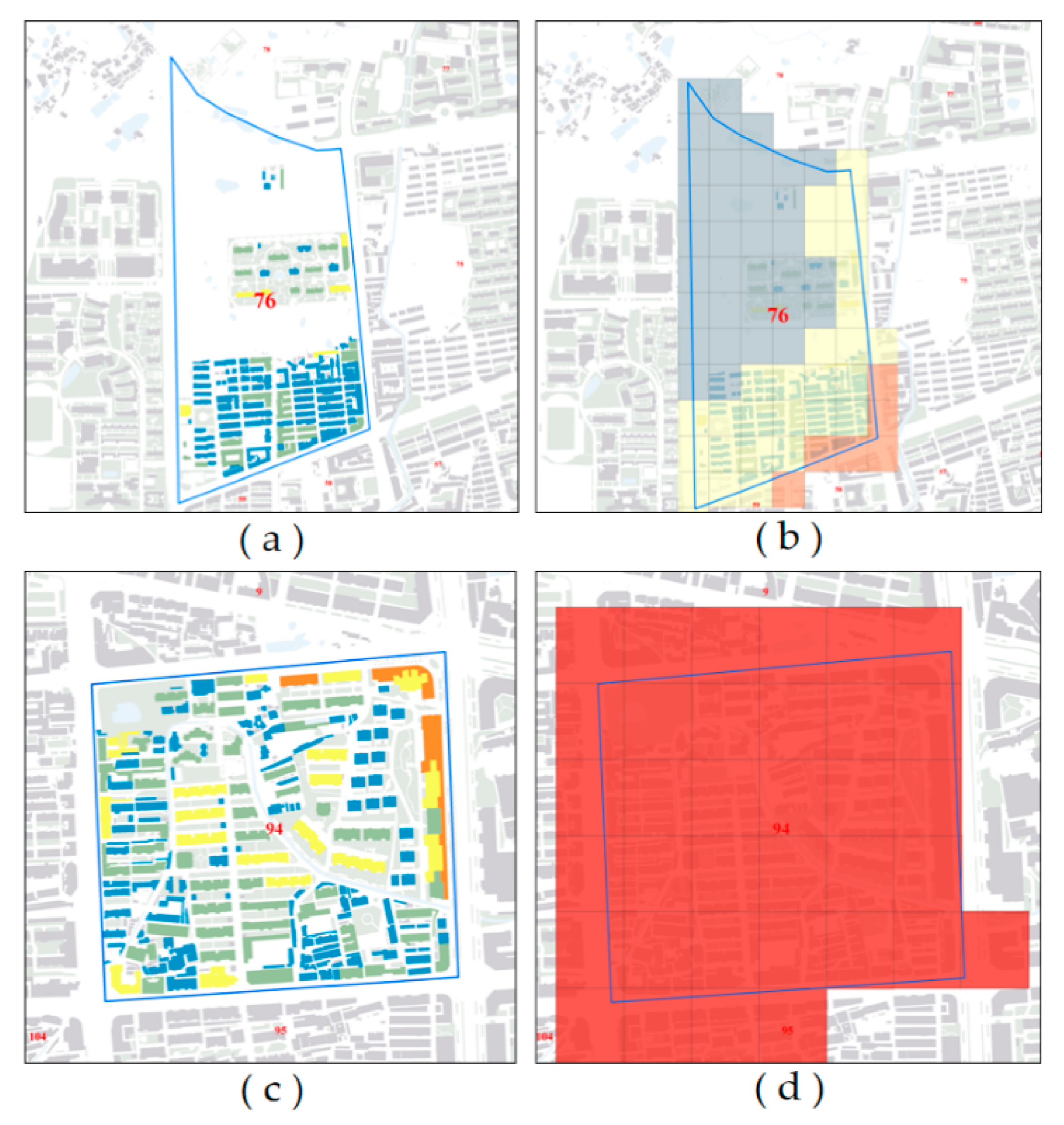
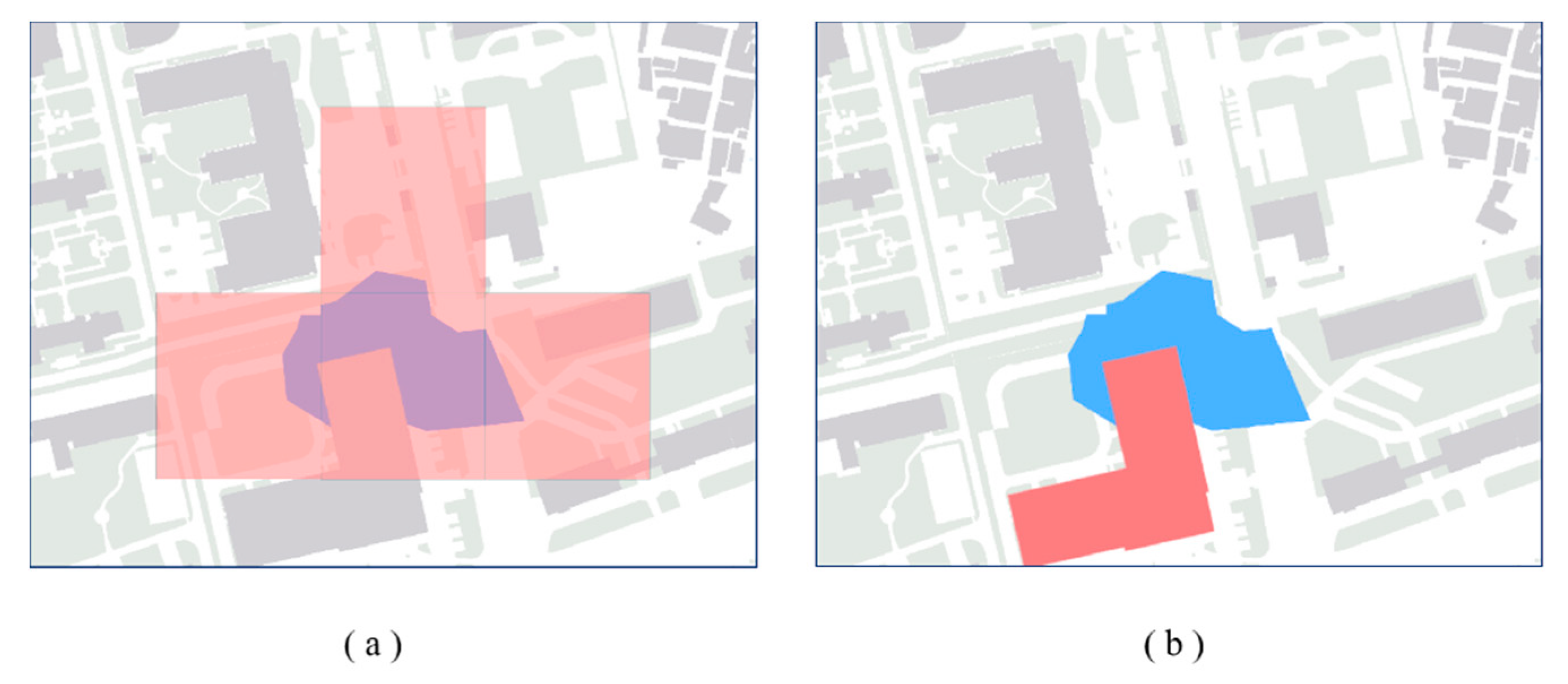
3.1.2. Population Redistribution
| Algorithm 1. Population Redistribution | |
| Input: POIs, Buildings B | |
| Output: | |
| 1: | For each type i |
| 2: | Create Thiessen Polygon TPi |
| 3: | Overlay TPi and Buildings B |
| 4: | For each polygon tp in TPi |
| 5: | If tp contains Building b |
| 6: | Then |
| 7: | Else |
| 8: | For each Building b |
| 9: | |
| 10: | return ; |
3.1.3. Accuracy Assessment
3.2. Flood Model
3.3. Scenario Design
4. Results and Discussion
4.1. Correlation Analysis between POIs and Population Grid
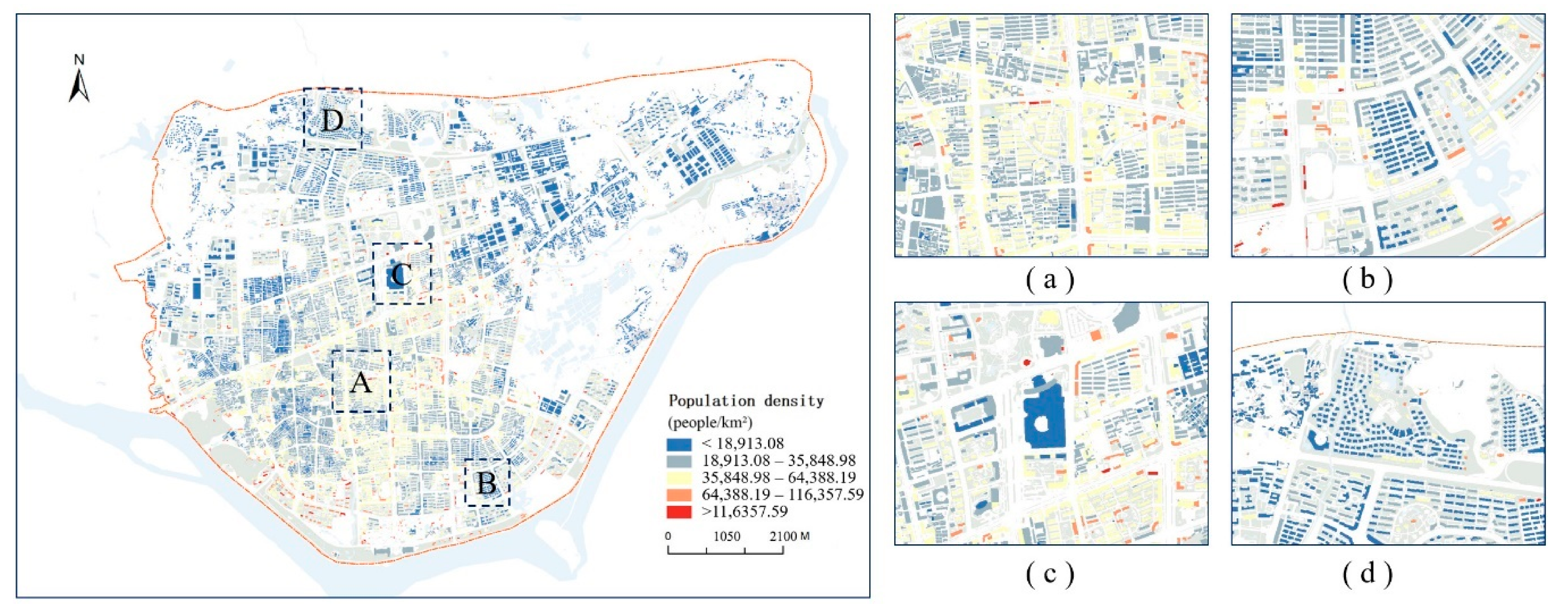
4.2. Results of Downscaling Gridded Population Mapping
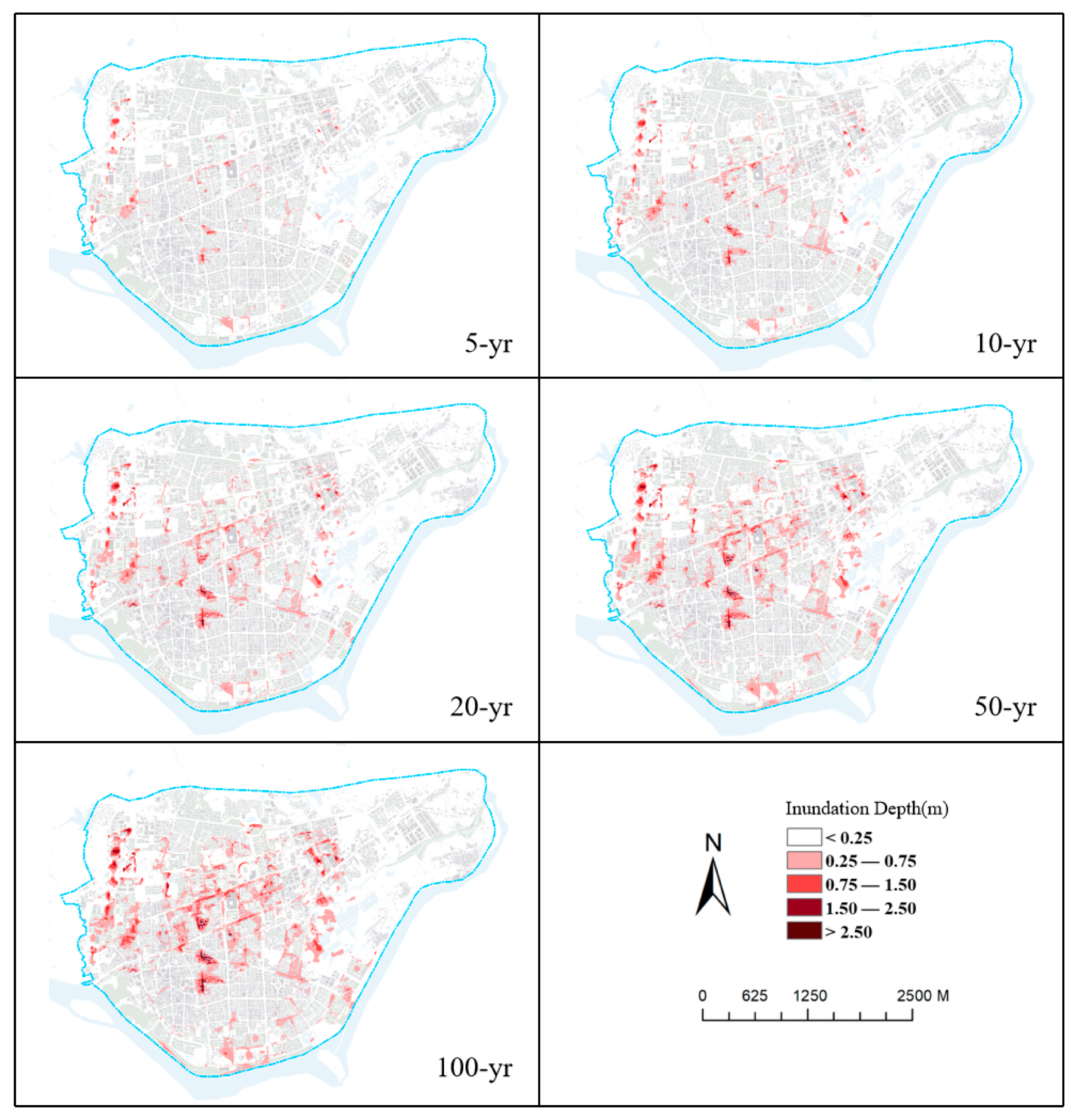
4.3. Results of Flooding Simulation
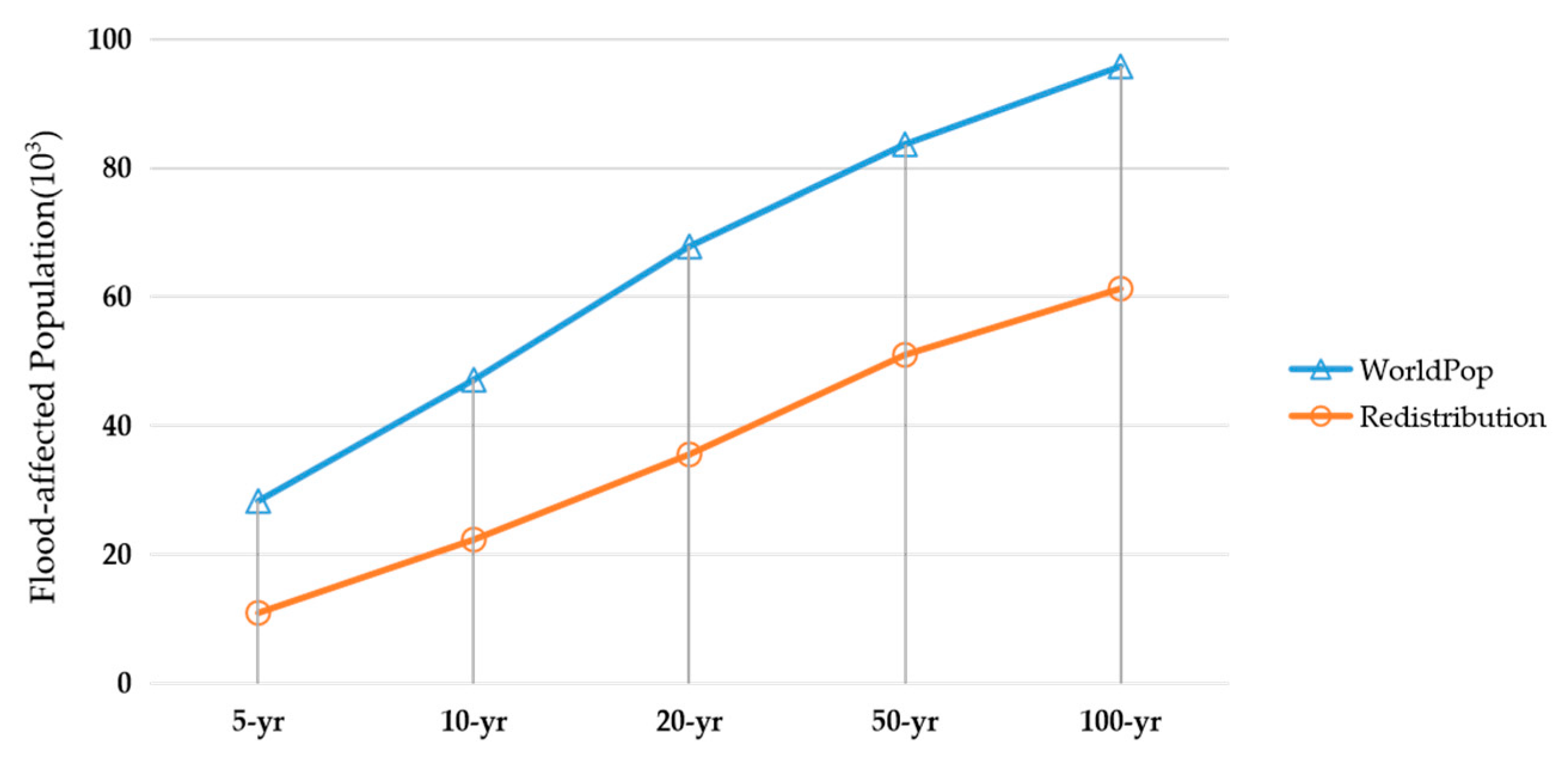
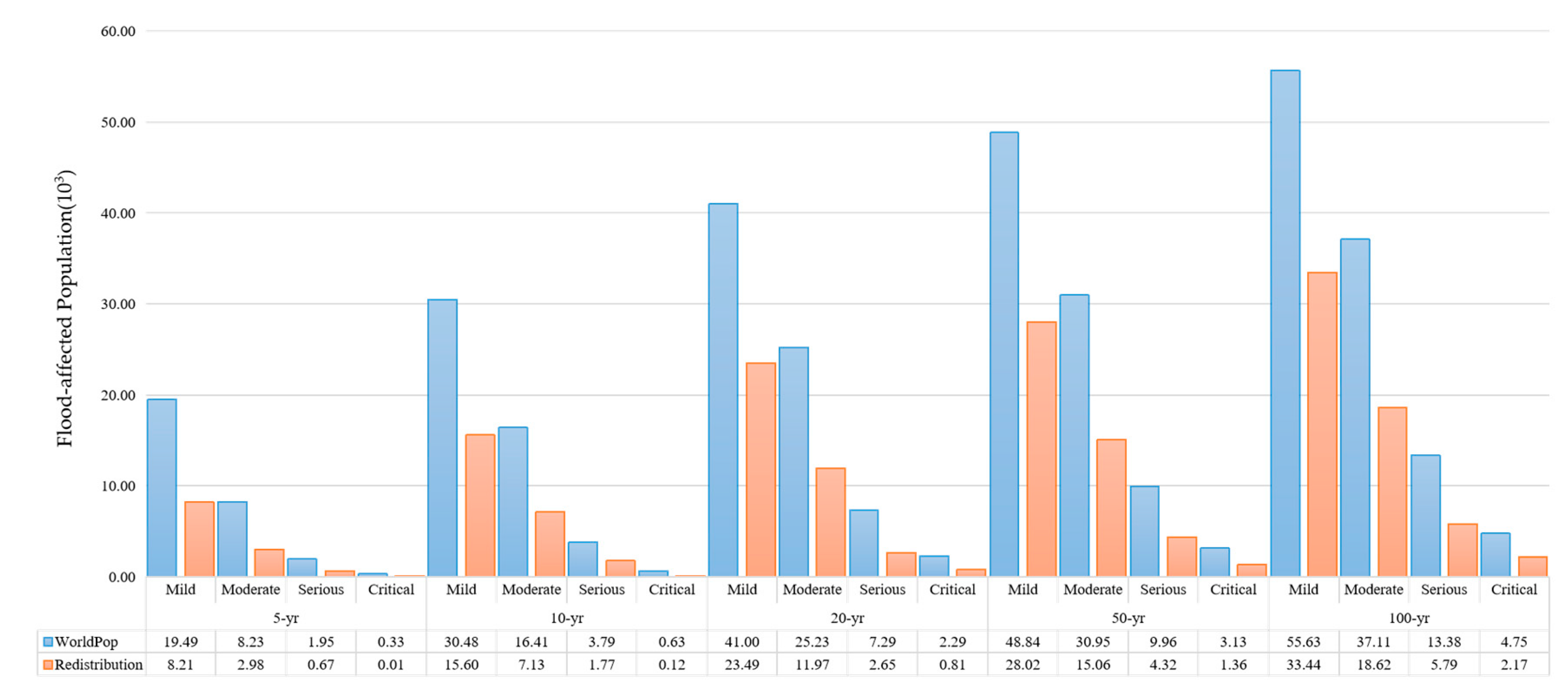
4.4. Assessment of the Affected Population
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Edenhofer, O. Climate Change 2014: Mitigation of Climate Change; Cambridge University Press: Cambridge, UK, 2015; Volume 3, ISBN 1-107-05821-X. [Google Scholar]
- UNISDR. The Human Cost of Natural Disasters: A Global Perspective; Centre for Research on the Epidemiology of Disaster (CRED): Brussels, Belgium, 2015. [Google Scholar]
- CRED Crunch 58—Disaster Year in Review (2019); CRED: Brussels, Belgium, 2019.
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Gain, A.K.; Mojtahed, V.; Biscaro, C.; Balbi, S.; Giupponi, C. An integrated approach of flood risk assessment in the eastern part of Dhaka City. Nat. Hazards 2015, 79, 1499–1530. [Google Scholar] [CrossRef]
- Dai, Q.; Zhu, X.; Zhuo, L.; Han, D.; Liu, Z.; Zhang, S. A hazard-human coupled model (HazardCM) to assess city dynamic exposure to rainfall-triggered natural hazards. Environ. Model. Softw. 2020, 127, 104684. [Google Scholar] [CrossRef]
- Freire, S.; Aubrecht, C. Integrating population dynamics into mapping human exposure to seismic hazard. Nat. Hazards Earth Syst. Sci. 2012, 12, 3533–3543. [Google Scholar] [CrossRef]
- Dell’Acqua, F.; Gamba, P.; Jaiswal, K. Spatial aspects of building and population exposure data and their implications for global earthquake exposure modeling. Nat. Hazards 2013, 68, 1291–1309. [Google Scholar] [CrossRef]
- Smith, A.; Bates, P.D.; Wing, O.; Sampson, C.; Quinn, N.; Neal, J. New estimates of flood exposure in developing countries using high-resolution population data. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef]
- Langford, M.; Higgs, G.; Radcliffe, J.; White, S. Urban population distribution models and service accessibility estimation. Comput. Environ. Urban Syst. 2008, 32, 66–80. [Google Scholar] [CrossRef]
- Wu, C.; Murray, A.T. A cokriging method for estimating population density in urban areas. Comput. Environ. Urban Syst. 2005, 29, 558–579. [Google Scholar] [CrossRef]
- Batty, M. Fifty Years of Urban Modeling: Macro-Statics to Micro-Dynamics. In The Dynamics of Complex Urban Systems; Physica-Verlag HD: Heidelberg, Germany, 2007; pp. 1–20. [Google Scholar]
- Mennis, J. Generating Surface Models of Population Using Dasymetric Mapping. Prof. Geogr. 2003, 55, 31–42. [Google Scholar] [CrossRef]
- Deichmann, U.; Street, H.; Balk, D.; Yetman, G. Transforming Population Data for Interdisciplinary Usages: From Census to Grid; Center for International Earth Science Information Network: Washington, DC, USA, 2001. [Google Scholar]
- Balk, D.L.; Deichmann, U.; Yetman, G.; Pozzi, F.; Hay, S.I.; Nelson, A. Determining Global Population Distribution: Methods, Applications and Data. In Advances in Parasitology; Elsevier: Amsterdam, The Netherlands, 2006; Volume 62, pp. 119–156. ISBN 978-0-12-031762-2. [Google Scholar]
- LandScan: A global population database for estimating populations at risk. In Remotely-Sensed Cities; Mesev, V., Ed.; CRC Press: Boca Raton, FL, USA, 2003; pp. 301–314. ISBN 978-0-429-18116-0. [Google Scholar]
- Gaughan, A.E.; Stevens, F.R.; Linard, C.; Jia, P.; Tatem, A.J. High Resolution Population Distribution Maps for Southeast Asia in 2010 and 2015. PLoS ONE 2013, 8, e55882. [Google Scholar] [CrossRef]
- Zhu, X.; Dai, Q.; Han, D.; Zhuo, L.; Zhu, S.; Zhang, S. Modeling the high-resolution dynamic exposure to flooding in a city region. Hydrol. Earth Syst. Sci. 2019, 23, 3353–3372. [Google Scholar] [CrossRef]
- Hossain, M.K.; Meng, Q. A fine-scale spatial analytics of the assessment and mapping of buildings and population at different risk levels of urban flood. Land Use Policy 2020, 99, 104829. [Google Scholar] [CrossRef]
- Kounadi, O.; Ristea, A.; Leitner, M.; Langford, C. Population at risk: Using areal interpolation and Twitter messages to create population models for burglaries and robberies. Cartogr. Geogr. Inf. Sci. 2018, 45, 205–220. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Liu, X.; Li, X.; Zhang, J.; Liang, Z.; Mai, K.; Zhang, Y. Mapping fine-scale population distributions at the building level by integrating multisource geospatial big data. Int. J. Geogr. Inf. Sci. 2017, 1–25. [Google Scholar] [CrossRef]
- Yu, B.; Lian, T.; Huang, Y.; Yao, S.; Ye, X.; Chen, Z.; Yang, C.; Wu, J. Integration of nighttime light remote sensing images and taxi GPS tracking data for population surface enhancement. Int. J. Geogr. Inf. Sci. 2019, 33, 687–706. [Google Scholar] [CrossRef]
- Song, Y.; Huang, B.; Cai, J.; Chen, B. Dynamic assessments of population exposure to urban greenspace using multi-source big data. Sci. Total Environ. 2018, 634, 1315–1325. [Google Scholar] [CrossRef]
- Zhao; Li; Zhang; Du Improving the Accuracy of Fine-Grained Population Mapping Using Population-Sensitive POIs. Remote Sens. 2019, 11, 2502. [CrossRef]
- Dong, P.; Ramesh, S.; Nepali, A. Evaluation of small-area population estimation using LiDAR, Landsat TM and parcel data. Int. J. Remote Sens. 2010, 31, 5571–5586. [Google Scholar] [CrossRef]
- Silván-Cárdenas, J.L.; Wang, L.; Rogerson, P.; Wu, C.; Feng, T.; Kamphaus, B.D. Assessing fine-spatial-resolution remote sensing for small-area population estimation. Int. J. Remote Sens. 2010, 31, 5605–5634. [Google Scholar] [CrossRef]
- Bakillah, M.; Liang, S.; Mobasheri, A.; Jokar Arsanjani, J.; Zipf, A. Fine-resolution population mapping using OpenStreetMap points-of-interest. Int. J. Geogr. Inf. Sci. 2014, 28, 1940–1963. [Google Scholar] [CrossRef]
- de Ruig, L.T.; Haer, T.; de Moel, H.; Botzen, W.J.W.; Aerts, J.C.J.H. A micro-scale cost-benefit analysis of building-level flood risk adaptation measures in Los Angeles. Water Resour. Econ. 2019, 100147. [Google Scholar] [CrossRef]
- Bai, Z.; Wang, J.; Wang, M.; Gao, M.; Sun, J. Accuracy Assessment of Multi-Source Gridded Population Distribution Datasets in China. Sustainability 2018, 10, 1363. [Google Scholar] [CrossRef]
- Hu, S.; He, Z.; Wu, L.; Yin, L.; Xu, Y.; Cui, H. A framework for extracting urban functional regions based on multiprototype word embeddings using points-of-interest data. Comput. Environ. Urban Syst. 2020, 80, 101442. [Google Scholar] [CrossRef]
- Gao, S.; Janowicz, K.; Couclelis, H. Extracting urban functional regions from points of interest and human activities on location-based social networks. Trans. GIS 2017, 21, 446–467. [Google Scholar] [CrossRef]
- Niu, N.; Liu, X.; Jin, H.; Ye, X.; Liu, Y.; Li, X.; Chen, Y.; Li, S. Integrating multi-source big data to infer building functions. Int. J. Geogr. Inf. Sci. 2017, 31, 1871–1890. [Google Scholar] [CrossRef]
- Yang, X.; Ye, T.; Zhao, N.; Chen, Q.; Yue, W.; Qi, J.; Zeng, B.; Jia, P. Population Mapping with Multisensor Remote Sensing Images and Point-Of-Interest Data. Remote Sens. 2019, 11, 574. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, R.; Ge, Y.; Jin, Y.; Xia, Z. Downscaling Census Data for Gridded Population Mapping With Geographically Weighted Area-to-Point Regression Kriging. IEEE Access 2019, 7, 149132–149141. [Google Scholar] [CrossRef]
- Bates, P.D.; De Roo, A.P.J. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Wood, M.; Hostache, R.; Neal, J.; Wagener, T.; Giustarini, L.; Chini, M.; Corato, G.; Matgen, P.; Bates, P. Calibration of channel depth and friction parameters in the LISFLOOD-FP hydraulic model using medium-resolution SAR data and identifiability techniques. Hydrol. Earth Syst. Sci. 2016, 20, 4983–4997. [Google Scholar] [CrossRef]
- Yang, Q.; Dai, Q.; Han, D.; Zhu, X.; Zhang, S. Impact of the storm sewer network complexity on flood simulations according to the stroke scaling method. Water 2018, 10, 645. [Google Scholar] [CrossRef]
| ID | Type | Quantity | Correlation | Weight |
|---|---|---|---|---|
| 1 | Market shopping | 2220 | 0.7494 | 0.1245 |
| 2 | Restaurant | 2801 | 0.7010 | 0.1165 |
| 3 | Government institution | 584 | 0.6662 | 0.1107 |
| 4 | Domestic service | 2562 | 0.6056 | 0.1006 |
| 5 | Medical facility | 214 | 0.5892 | 0.0979 |
| 6 | Residential area | 1163 | 0.5762 | 0.0957 |
| 7 | Company | 462 | 0.5717 | 0.0950 |
| 8 | Tourist attraction | 422 | 0.5416 | 0.0900 |
| 9 | Education and training | 358 | 0.5354 | 0.0890 |
| 10 | Transportation facility | 306 | 0.4827 | 0.0802 |
| Mild | Moderate | Serious | Critical | Total | |
|---|---|---|---|---|---|
| 5-yr | 0.2998 | 0.1154 | 0.0296 | 0.0008 | 0.4456 |
| 10-yr | 0.5844 | 0.2632 | 0.0745 | 0.0043 | 0.9264 |
| 20-yr | 0.8450 | 0.4258 | 0.1065 | 0.0278 | 1.4051 |
| 50-yr | 0.9854 | 0.5595 | 0.1642 | 0.0560 | 1.7654 |
| 100-yr | 1.1457 | 0.6909 | 0.2342 | 0.0868 | 2.1575 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Dai, Q.; Zhao, B.; Shao, J. Assessment of Population Exposure to Urban Flood at the Building Scale. Water 2020, 12, 3253. https://doi.org/10.3390/w12113253
Zhu S, Dai Q, Zhao B, Shao J. Assessment of Population Exposure to Urban Flood at the Building Scale. Water. 2020; 12(11):3253. https://doi.org/10.3390/w12113253
Chicago/Turabian StyleZhu, Shaonan, Qiang Dai, Binru Zhao, and Jiaqi Shao. 2020. "Assessment of Population Exposure to Urban Flood at the Building Scale" Water 12, no. 11: 3253. https://doi.org/10.3390/w12113253
APA StyleZhu, S., Dai, Q., Zhao, B., & Shao, J. (2020). Assessment of Population Exposure to Urban Flood at the Building Scale. Water, 12(11), 3253. https://doi.org/10.3390/w12113253







