A New Approach to Calculate the Water Exploitation Index (WEI+)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Water Exploitation Index (WEI+)
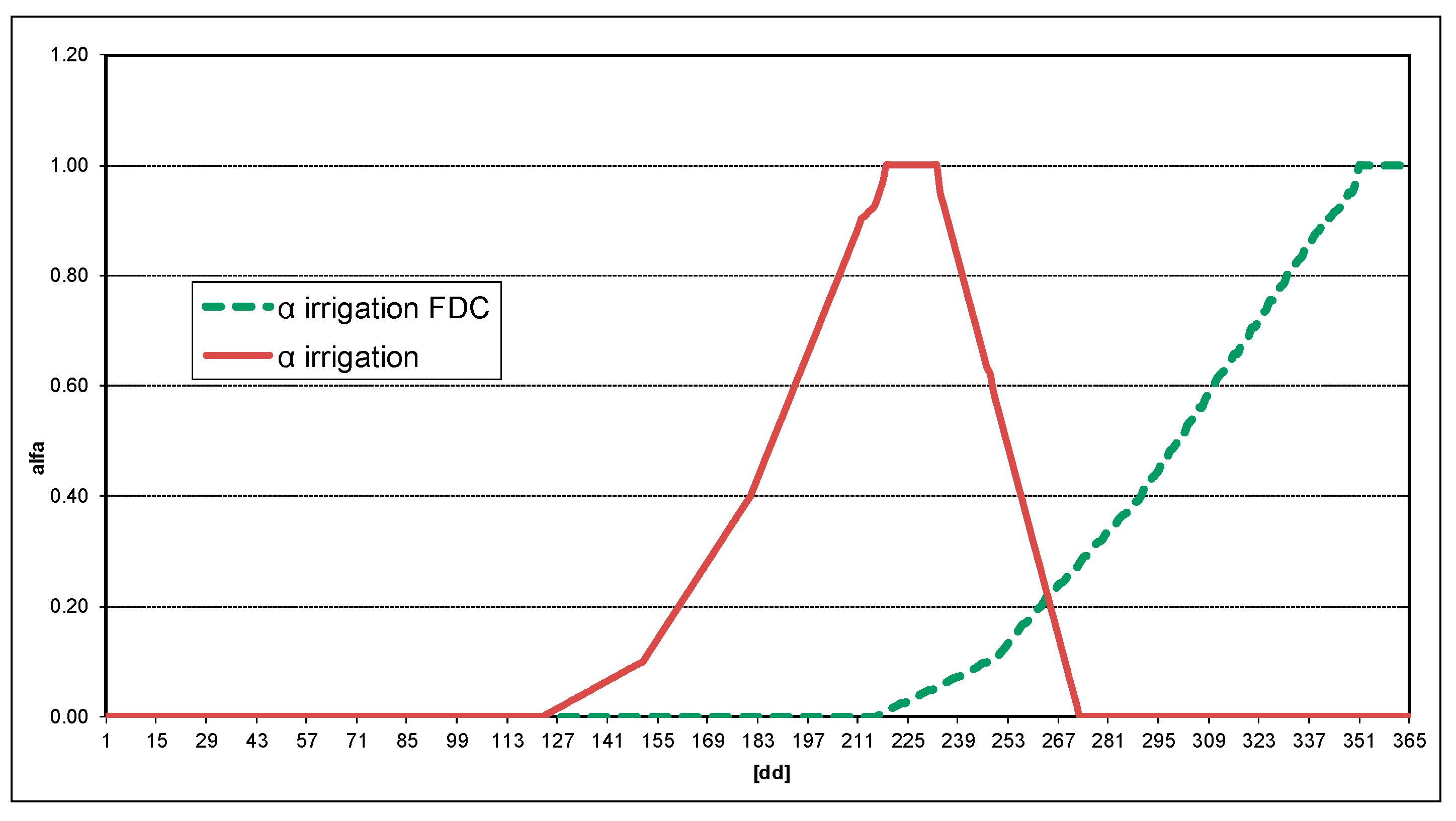
2.2. Water Abstractions Evaluation
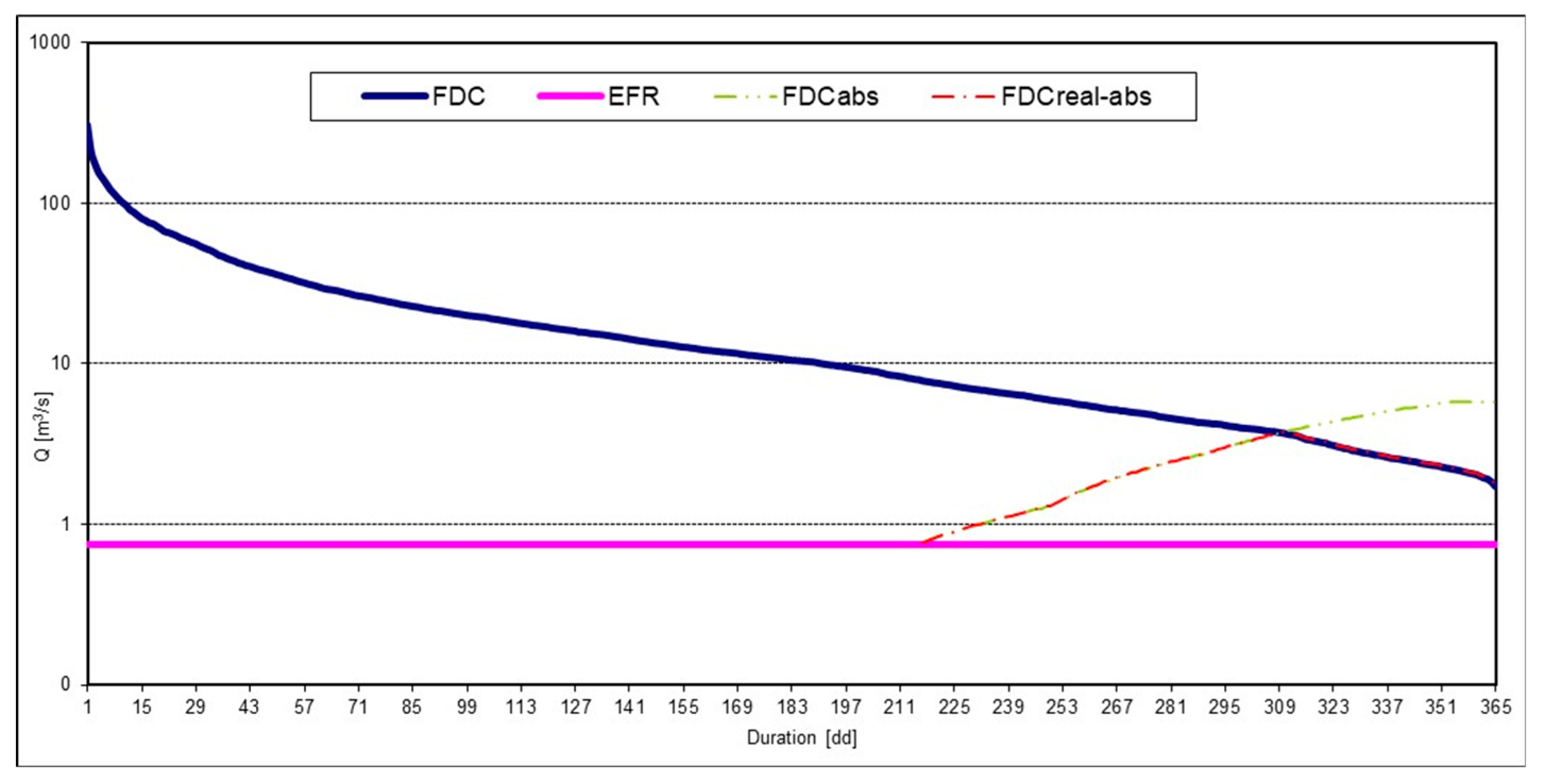
2.3. Flow Duration Curves and Renewable Water Resources Evaluation
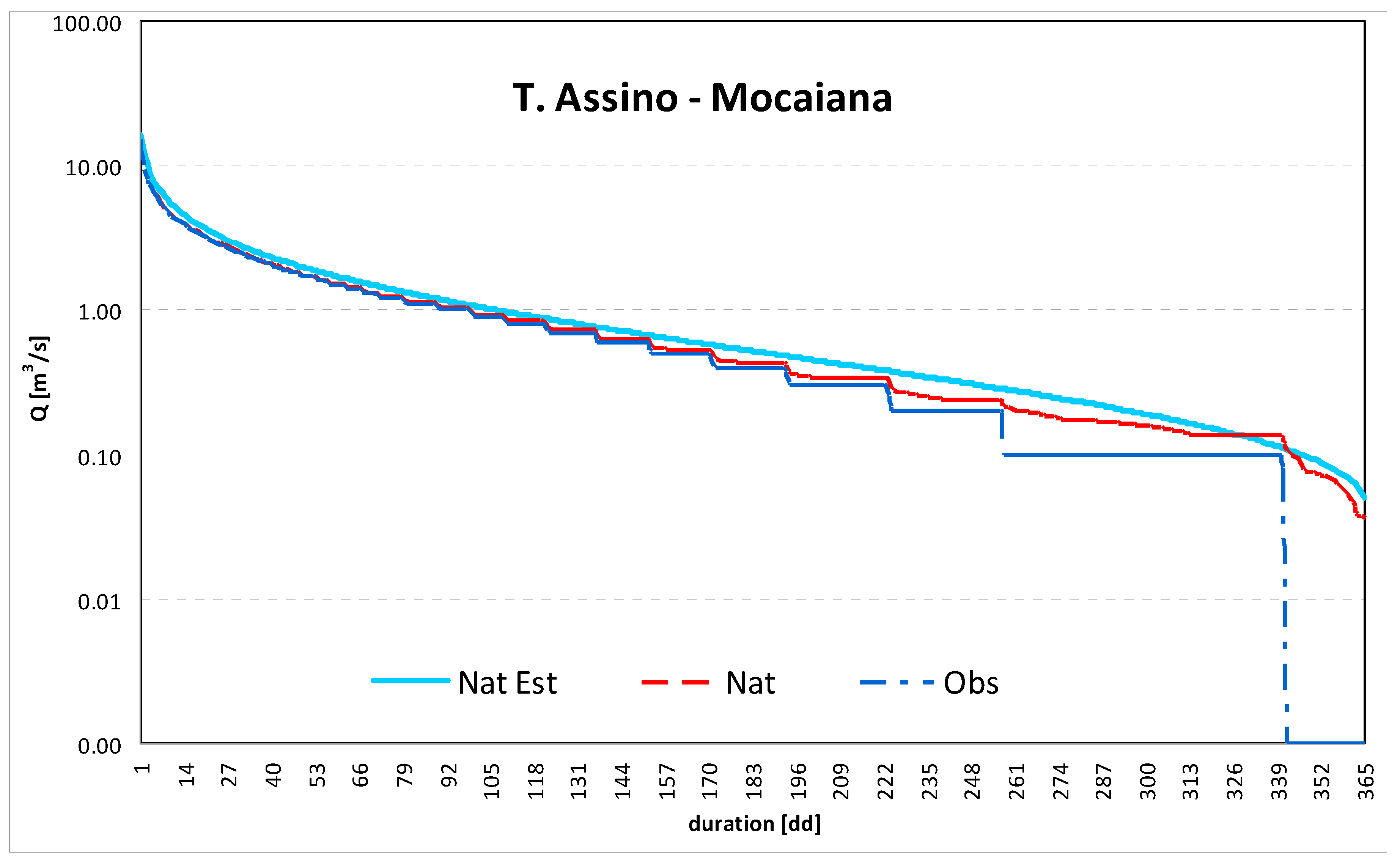
3. Case Study and Results
4. Discussion
- The utility of the WEI+ in drought management is linked to its detailed evaluation in basins and sub-basins;
- The WEI+ values are more significant if evaluated in a specific period, such as the peak month.
5. Conclusions
- The use of the natural FDC to calculate renewable water resources, assuming this volume to be equal to the area underlying the curve;
- The adoption of a WEB-GIS system for water abstractions, in order to calculate the value of “abstraction-returns” in all the basins and sub-basins;
- The use of regionalization techniques for the natural FDC to calculate the renewable water resources in ungauged basins and sub-basins.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Faergemann, H. Update on Water Scarcity and Droughts indicator development. In EC Expert Group on Water Scarcity & Droughts; European Environment Agency: Brussels, Belgium, 2012; pp. 1–23. [Google Scholar]
- Wable, P.S.; Jha, M.K.; Shekhar, A. Comparison of Drought Indices in a Semi-Arid River Basin of India. Water Resour. Manag. 2019, 33, 75–102. [Google Scholar] [CrossRef]
- Tsakiris, G. Drought Risk Assessment and Management. Water Resour. Manag. 2017, 31, 3083–3095. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology; American Meteorological Society: Anaheim, CA, USA; Boston, MA, USA, 1993; pp. 179–184. [Google Scholar]
- Saada, N.; Romman, A.A. Multi-site Modeling and Simulation of the Standardized Precipitation Index (SPI) in Jordan. J. Hydrol. Reg. Stud. 2017, 14, 83–91. [Google Scholar] [CrossRef]
- Dabanlı, I.; Mishra, A.K.; Sen, Z. Long-term spatio-temporal drought variability in Turkey. J. Hydrol. 2017, 552, 779–792. [Google Scholar] [CrossRef]
- Lu, J.; Jia, L.; Menenti, M.; Yan, Y.; Zheng, C.; Zhou, J. Performance of the Standardized Precipitation Index Based on the TMPA and CMORPH Precipitation Products for Drought Monitoring in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1387–1396. [Google Scholar] [CrossRef]
- Meschiatti, M.C.; Blain, G.C. Increasing the regional availability of the Standardized Precipitation Index: An operational approach. Bragantiacampinas 2016, 75, 507–521. [Google Scholar] [CrossRef] [Green Version]
- Juliani, B.H.T.; Okawa, C.M.P. Application of a Standardized Precipitation Index for meteorological drought analysis of a semi-arid climate influence in Minas Gerais, Brasil. Hydrology 2017, 4, 26. [Google Scholar] [CrossRef] [Green Version]
- Elkollaly, M.; Khadr, M.; Zeidan, B. Drought analysis in the Eastern Nile basin using the standardized precipitation index. Environ. Sci. Pollut. Res. 2018, 25, 30772–30786. [Google Scholar] [CrossRef]
- Merabti, A.; Martins, D.S.; Meddi, N.; Pereira, L.S. Spatial and Time Variability of Drought Based on SPI and RDI with Various Time Scales. Water Resour. Manag. 2018, 32, 1087–1100. [Google Scholar] [CrossRef]
- Massachusetts Drought Management Task Force, Standardized Precipitation Index (SPI). Available online: https://www.mass.gov/service-details/standardized-precipitation-index-spi (accessed on 13 May 2020).
- India Meteorological Department, Standardized Precipitation Index. Available online: http://www.imdpune.gov.in/hydrology/hydr_products.html (accessed on 13 May 2020).
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Ward, A.S.; Bejarano, M.D.; Iglesias, A.; Asenjo, V.; Garrote, L. Analysis of Current and Future SPEI Droughts in the La Plata Basin Based on Results from the Regional Eta Climate Model. Water 2017, 9, 857. [Google Scholar] [CrossRef] [Green Version]
- Liu, A.; Pan, Y.; Zhu, X.; Yang, T.; Bai, J.; Sun, Z. Drought evolution and its impact on the crop yield in the North China Plain. J. Hydrol. 2018, 564, 984–996. [Google Scholar] [CrossRef]
- Mohsenipour, M.; Shahid, S.; Chung, E.; Wang, X. Changing Pattern of Droughts during Cropping Seasons of Bangladesh. Water Resour. Manag. 2018, 32, 1555–1568. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef] [Green Version]
- Pfister, S.; Koehler, A.; Hellweg, S. Assessing the Environmental Impacts of Freshwater Consumption in LCA. Environ. Sci. Technol. 2009, 43, 4098–4104. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Miao, C.; Tang, X.; Duan, Q.; Heb, X. A nonparametric standardized runoff index for characterizing hydrological drought on the Loess Plateau, China. Glob. Planet. Chang. 2018, 161, 53–65. [Google Scholar] [CrossRef]
- Bayissa, Y.; Maskey, S.; Tadesse, T.; van Andel, S.J.; Moges, S.; van Griensven, A.; Solomatine, D. Comparison of the Performance of Six Drought Indices in Characterizing Historical Drought for the Upper Blue Nile Basin, Ethiopia. Geosciences 2018, 8, 81. [Google Scholar] [CrossRef] [Green Version]
- Zou, L.; Xia, J.; She, D. Analysis of Impacts of Climate Change and Human Activities on hydrological Drought: A Case Study in the Wei River Basin, China. Water Resour. Manag. 2018, 32, 1421–1438. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, M.; Wang, L.; Zhou, T. Understanding and seasonal forecasting of hydrological drought in the Anthropocene. Hydrol. Earth Syst. Sci. 2018, 21, 5477–5492. [Google Scholar] [CrossRef] [Green Version]
- Nilsalab, P.; Gheewala, S.H.; Silalertruksa, T. Methodology development for including environmental water requirement in the water stress index considering the case of Thailand. J Clean. Prod. 2017, 167, 1002–1008. [Google Scholar] [CrossRef]
- Ngo, T.T.; Le, N.T.; Hoang, T.M.; Luong, D.H. Water Scarcity in Vietnam: A Point of View on Virtual Water Perspective. Water Resour. Manag. 2018, 32, 3579–3593. [Google Scholar] [CrossRef]
- Nilsalab, P.; Gheewala, S.H.; Pfister, S. Method Development for Including Environmental Water Requirement in the Water Stress Index. Water Resour. Manag. 2018, 32, 1585–1598. [Google Scholar] [CrossRef]
- Liu, J.; Yang, H.; Gosling, S.N.; Kummu, M.; Flörke, M.; Pfister, S.; Hanasaki, N.; Wada, Y.; Zhang, X.; Zheng, C.; et al. Water scarcity assessments in the past, present, and future. Earth’s Future 2017, 5, 545–559. [Google Scholar] [CrossRef] [PubMed]
- SOER 2015—The European Environment-State and Outlook 2015-Countries and Regions-Mediterranean Sea Region. Available online: https://www.eea.europa.eu/soer/2015/countries/mediterranean (accessed on 31 May 2020).
- Contreras, S.; Hunink, J.E. Water accounting at the basin scale: Water use and supply (2000-2010) in the Segura River Basin using the SEEA framework. In Future Water Technical Report n. 133; DG-ENV- European Commission: Cartagena, Spain, 2015. [Google Scholar]
- De Roo, A.; Bisselink, B.; Beck, H.; Bernhard, J.; Burek, P.; Reynaud, A.; Pastori, M.; Lavalle, C.; Jacobs, C.; Baranzelli, C.; et al. Modelling Water Demand and Availability Scenarios for Current and Future Land Use and Climate in the Sava River Basin; Publications Office of the European Union: Luxembourg, 2016; EUR 27701 EN. [Google Scholar] [CrossRef]
- Karabulut, A.; Egoh, B.N.; Lanzanova, D.; Grizzetti, B.; Bidoglio, G.; Pagliero, L.; Bouraoui, F.; Aloe, A.; Reynaud, A.; Maes, J.; et al. Mapping water provisionig services to support the ecosystem–water–food–energy nexus in the Danube river basin. Ecosyst. Serv. 2016, 17, 278–292. [Google Scholar] [CrossRef]
- European Environment Agency. Results and lessons from implementing the Water Assets Accounts in the EEA area. In Technical Report n.7/2013; European Environment Agency: Luxembourg, 2013. [Google Scholar] [CrossRef]
- Pedro-Monzonís, M.; Solera, A.; Ferrer, J.; Estrela, T.; Paredes-Arquiola, J. A review of water scarcity and drought indexes in water resources planning and management. J. Hydrol. 2015, 527, 482–493. [Google Scholar] [CrossRef] [Green Version]
- Blum, A.G.; Archfield, S.A.; Vogel, R.M. On the probability distribution of daily streamflow in the United States. Hydrol. Earth Syst. Sci. 2017, 21, 3093–3103. [Google Scholar] [CrossRef] [Green Version]
- Waseem, M.; Shin, J.Y.; Kim, T.W. Comparing Spatial Interpolation Schemes for Constructing a Flow Duration Curve in an Ungauged Basin. Water Resour. Manag. 2015, 29, 2249–2265. [Google Scholar] [CrossRef]
- Atieh, M.; Gharabaghi, B.; Rudra, R. Entropy-based neural networks model for flow duration curves at ungauged sites. J. Hydrol. 2015, 529, 1007–1020. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P. A statistical, parsimonious, empirical framework for regional flow duration curve shape prediction in high permeability Mediterranean region. J. Hydrol. 2013, 507, 174–185. [Google Scholar] [CrossRef]
- Ziolkowska, J.R.; Ziolkowski, B. Effectiveness of Water Management in Europe in the 21st Century. Water Resour. Manag. 2016, 30, 2261–2274. [Google Scholar] [CrossRef]
- Santato, S.; Mysiak, J.; Pérez-Blanco, C.D. The Water Abstraction License Regime in Italy: A Case for Reform? Water 2016, 8, 103. [Google Scholar] [CrossRef] [Green Version]
- European Environment Agency. The European Environment State and Outlook 2015: Synthesis Report; European Environment Agency: Copenhagen, Denmark; Publications Office of the European Union: Luxembourg, 2015. [CrossRef]
- Delipetrev, B.; Jonoski, A.; Solomatine, D.P. Development of a web application for water resources based on open source software. Comput. Geosci. 2014, 62, 35–42. [Google Scholar] [CrossRef]
- Casadei, S.; Pierleoni, A.; Bellezza, M. Sustainability of Water Withdrawals in the Tiber River Basin (Central Italy). Sustainability 2018, 10, 485. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Linoli, A. Physical, agricultural and economic Italy today. In Land Reclamation, Irrigation and Flood Protection in Italy over the Centuries; ITAL-ICID; Italian Committee for Irrigation and Drainage: Rome, Italy, 2006. [Google Scholar]
- L’vovich, M.I. Hydrologic budget of continents and estimate of the balance of global fresh water resources. Sov. Hydrol. 1972, 4, 349–360. [Google Scholar]
- Casadei, S. Base flow index analysis of some hydrographic basins in Central Italy. Idrotecnica 1995, 3, 177–191. (In Italian) [Google Scholar]
- Boni, C.; Bono, P.; Cappelli, G. Hydrogeological Map. In Hydrogeological Scheme of Central Italy; Italian National Research Council, Sapienza University of Rome: Rome, Italy, 1987. [Google Scholar]
- Manciola, P.; Casadei, S. Low flow index and hydrogeological characteristics. In Proceedings of the National Conference in Hydraulic Engineering—ASCE, Nashville, TN, USA, 29 July–2 August 1991. [Google Scholar]
- Vogel, R.M.; Fennessey, N.M. Flow duration curves. I: New interpretation and confidence intervals. J. Water Resour. Plan. Manag. 1994, ASCE 120, 485–504. [Google Scholar] [CrossRef]
- León, D.G.; Standardi, G.; Staccione, A. An integrated approach for the estimation of agricultural drought costs. Land Use Policy 2021, 100, 1–10. [Google Scholar] [CrossRef]
- European Environment Agency. Water Exploitation Index Plus (WEI+) for River Basin Districts (2002–2014) GIS Map Application before October 2018. Available online: https://www.eea.europa.eu/data-and-maps/explore-interactive-maps/water-exploitation-index-for-river-1 (accessed on 22 August 2018).
- European Environment Agency. Water Exploitation Index Plus (WEI+) for River Basin Districts (1990–2015) GIS Map Application Published 10 Oct 2018 Last Modified 28 Nov 2019. Available online: https://www.eea.europa.eu/data-and-maps/explore-interactive-maps/water-exploitation-index-for-river-2 (accessed on 29 January 2020).
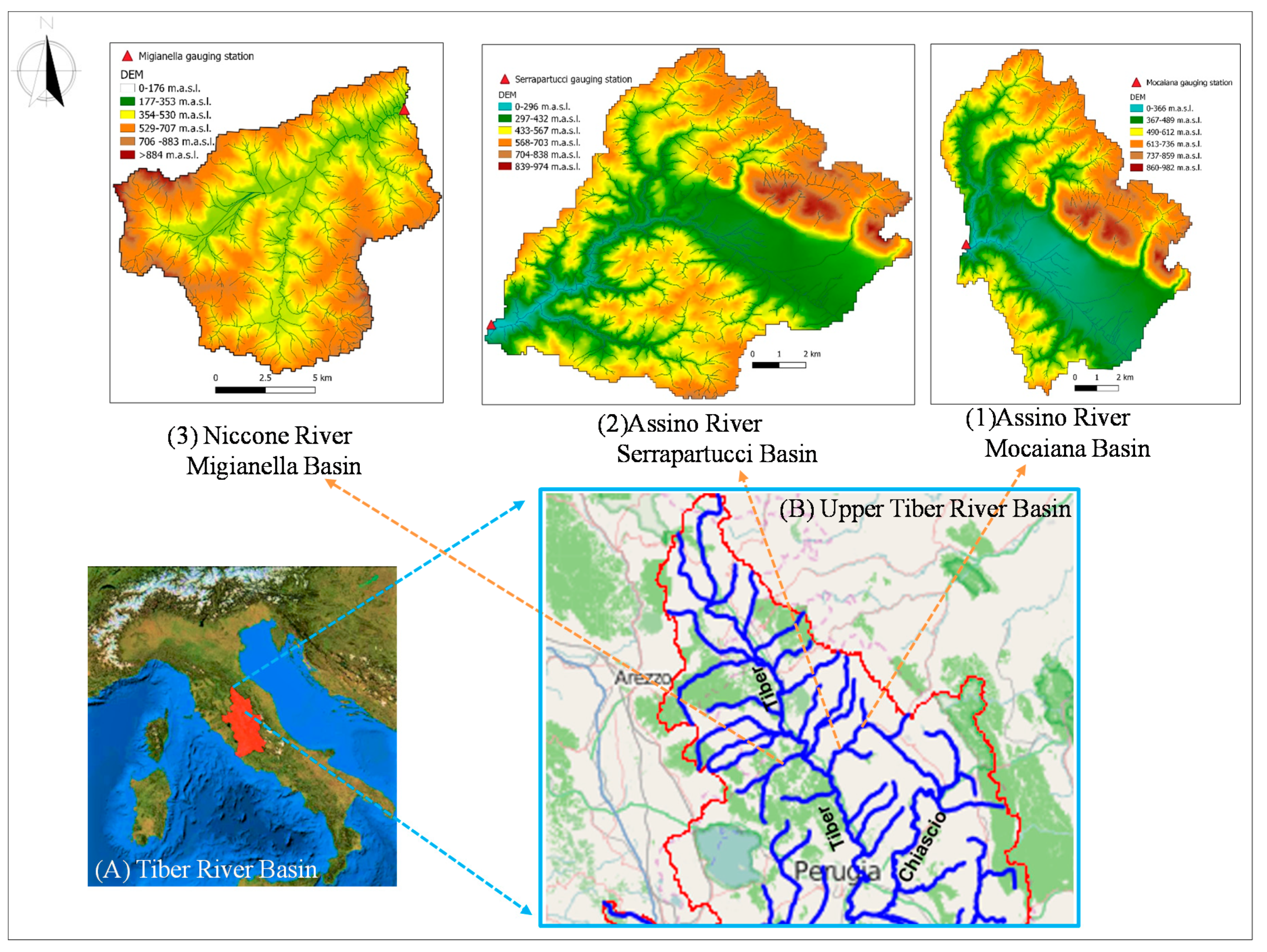
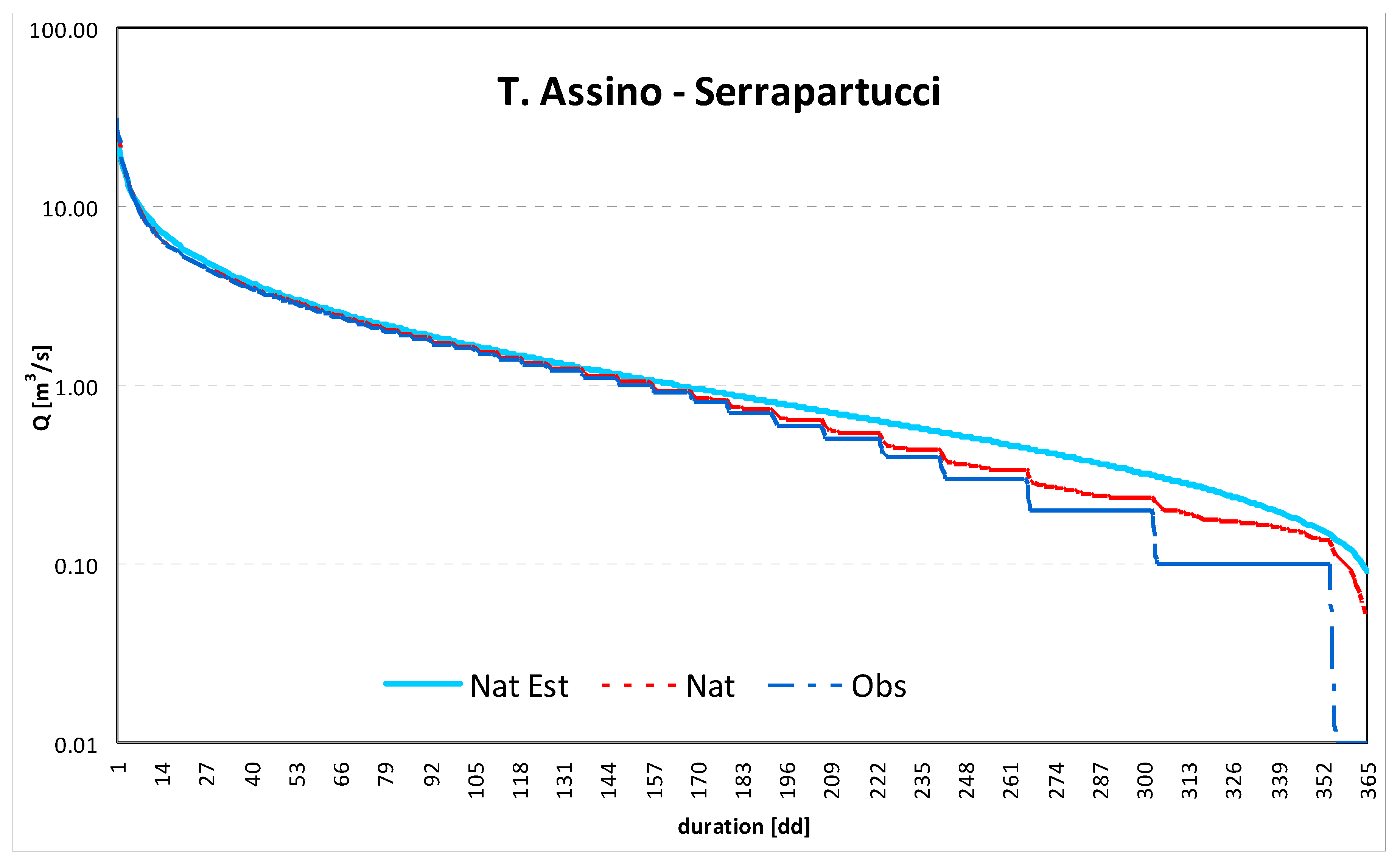
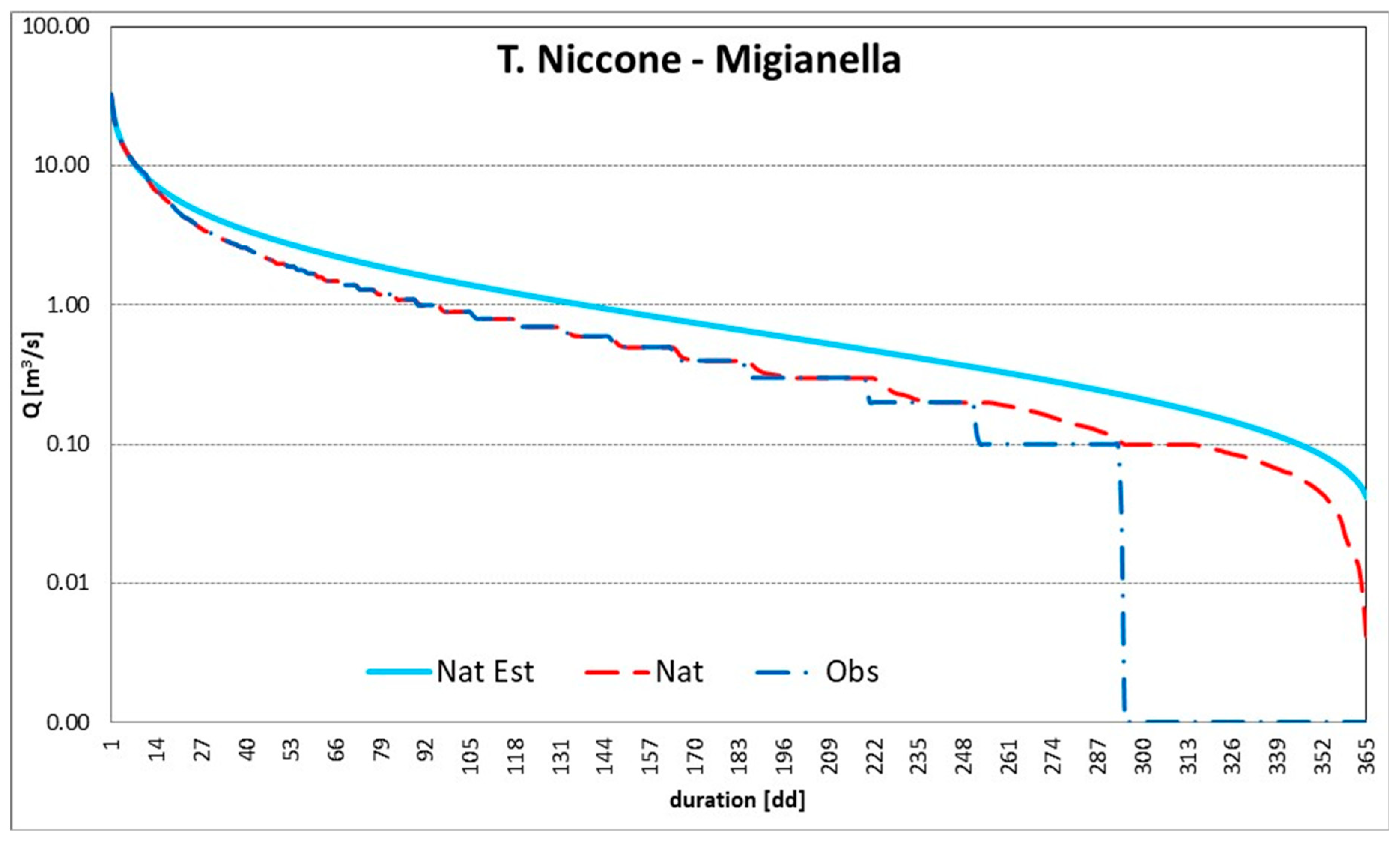
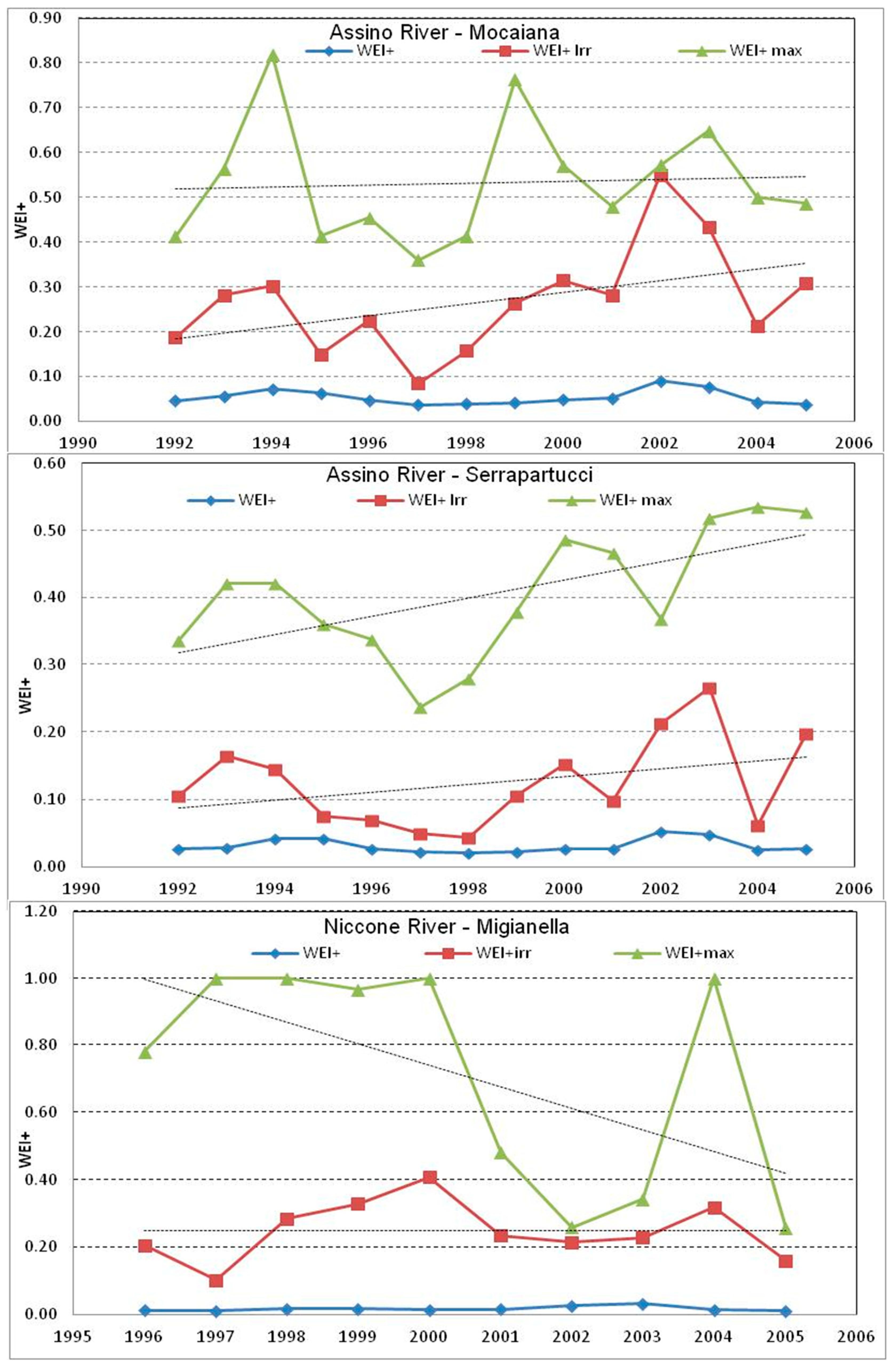
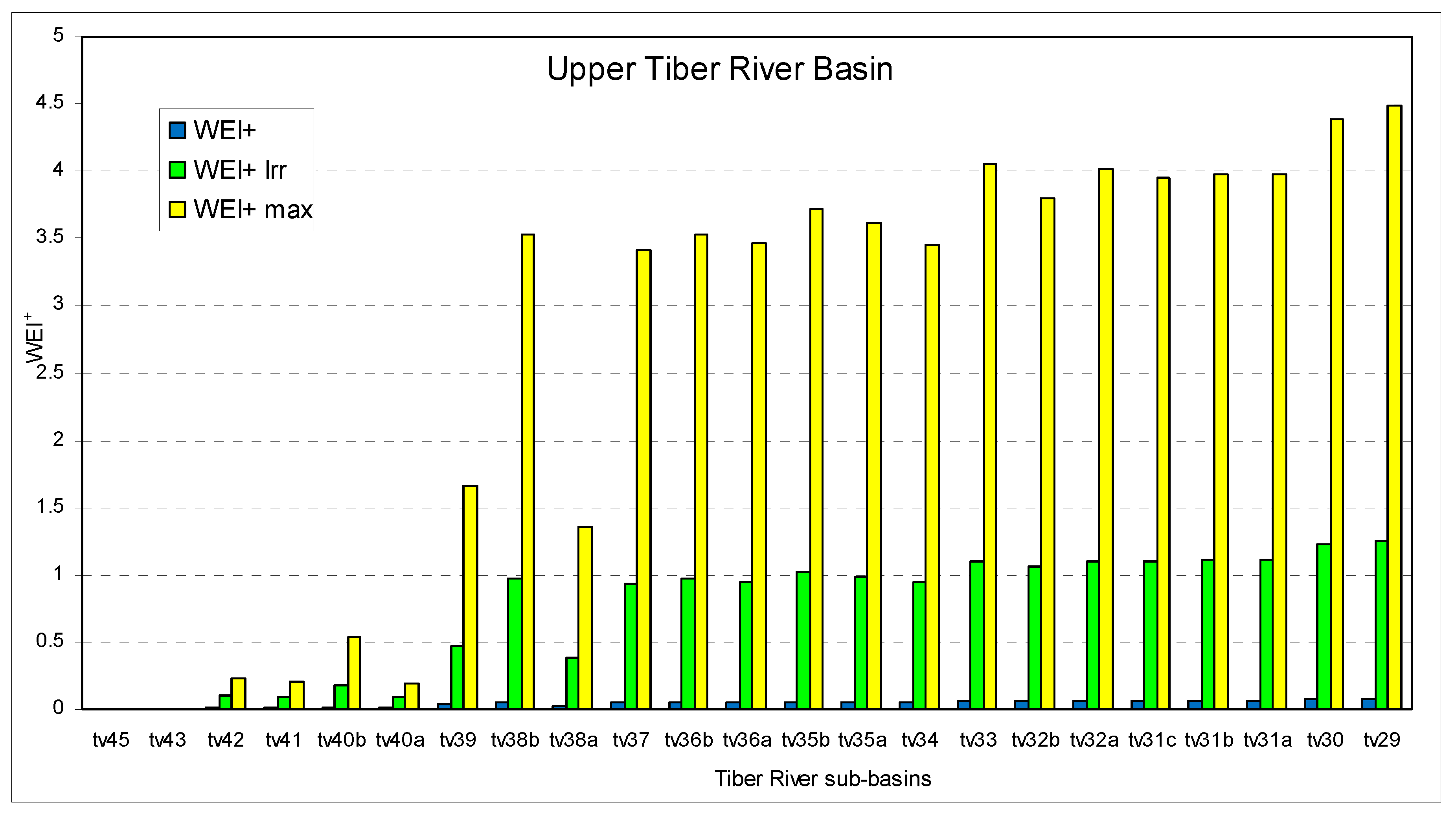
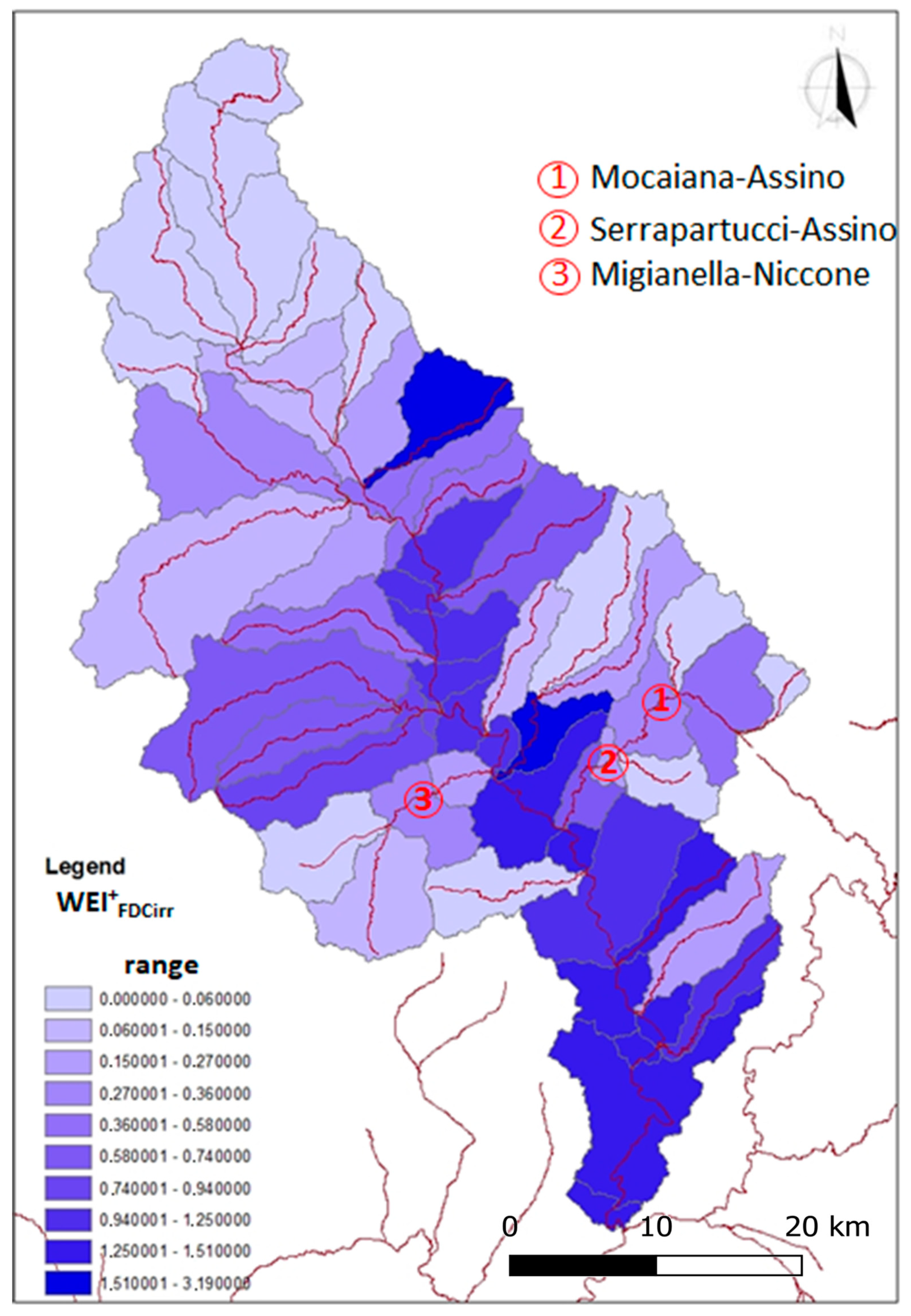
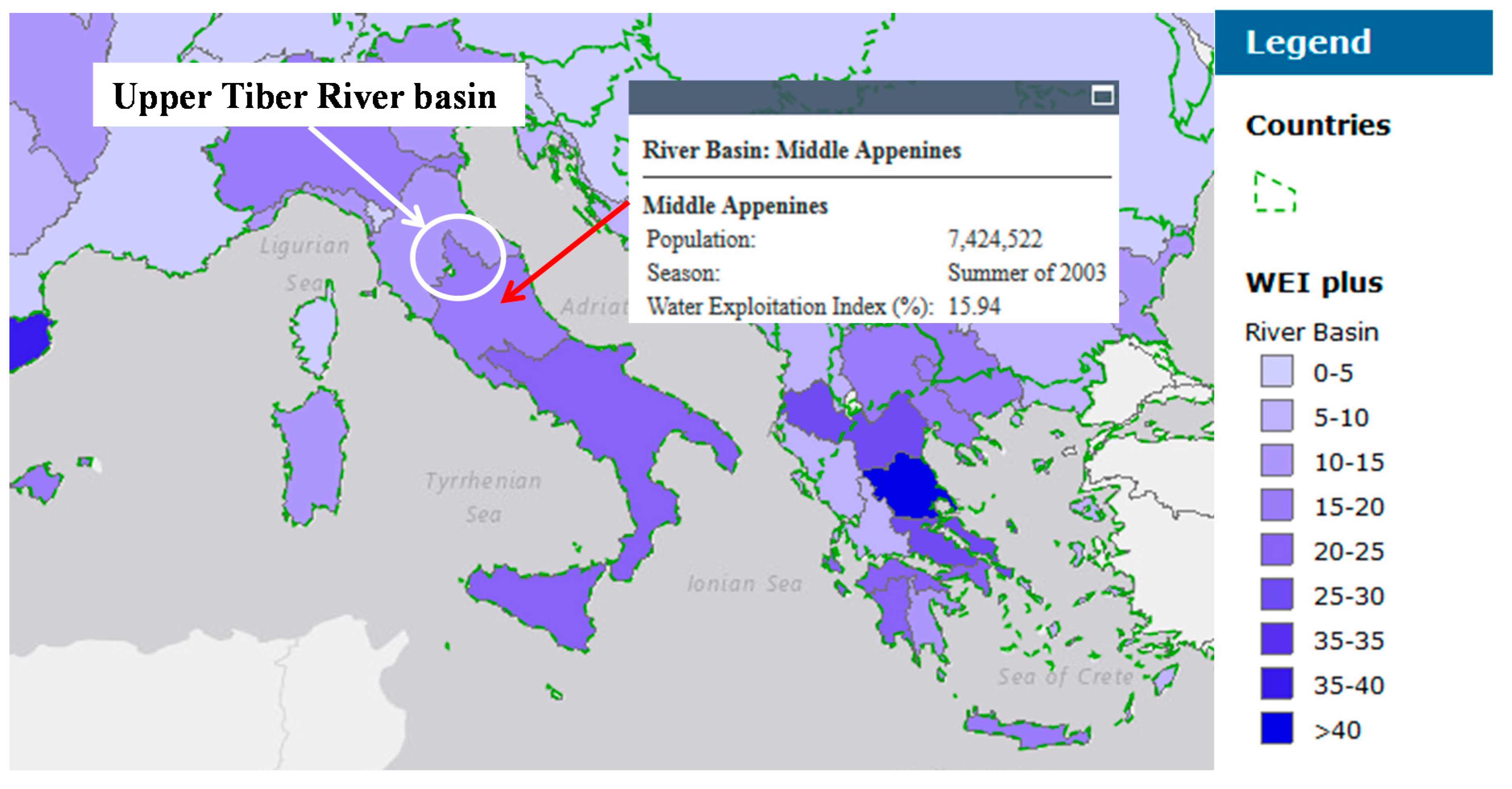
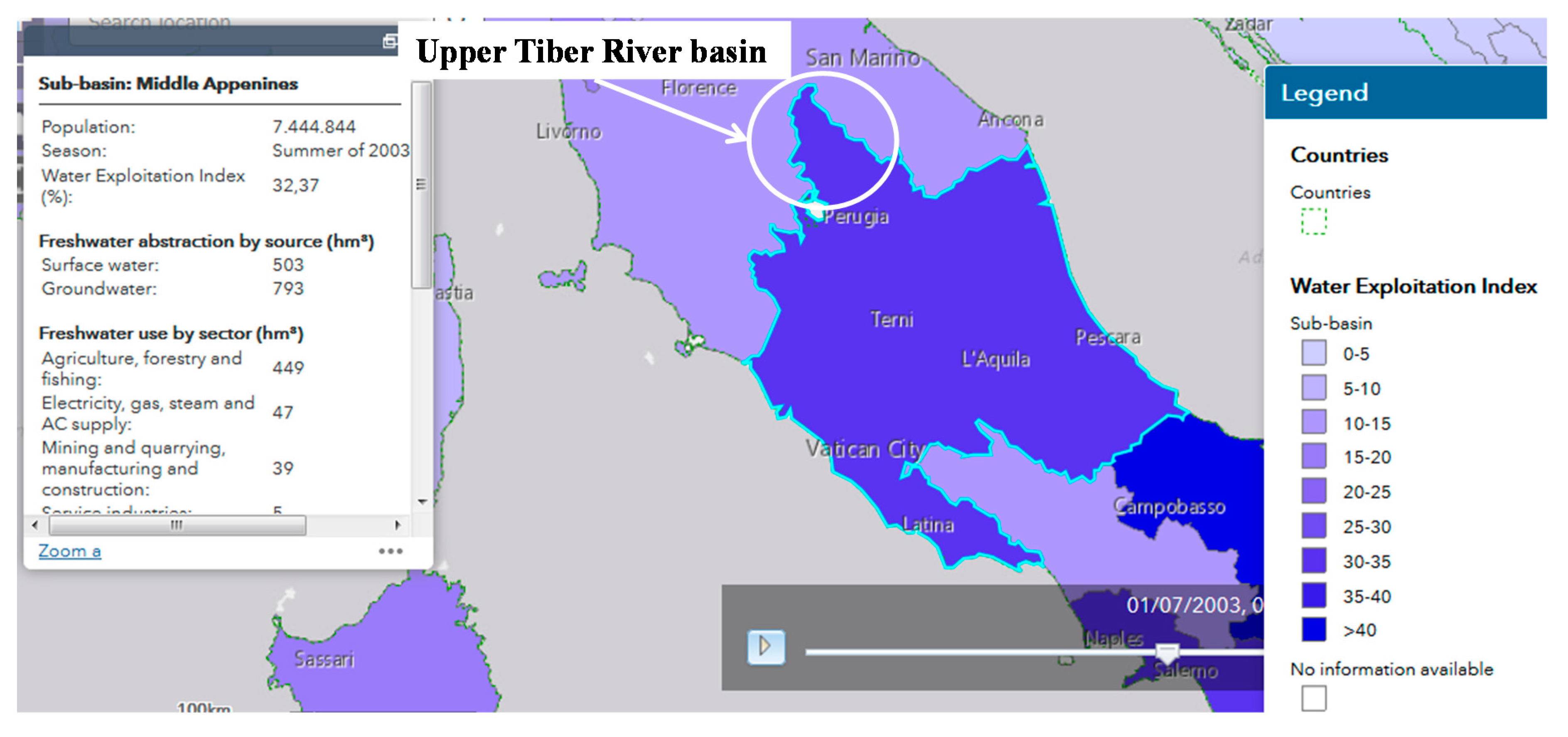
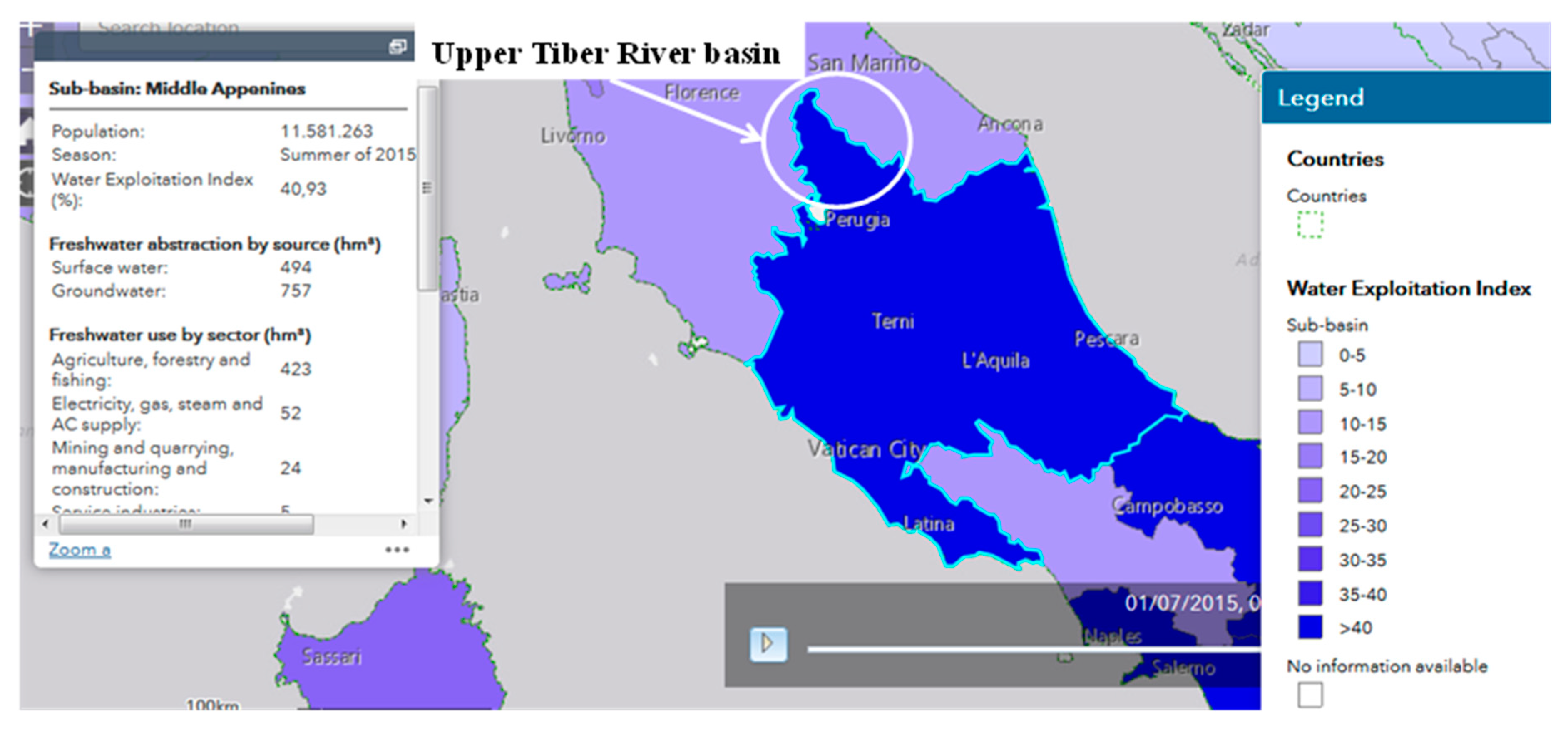
| Basin | Hydrometric Station | Observed Period | Area | BFI | Max Abstractions | |||
|---|---|---|---|---|---|---|---|---|
| Station Name | River | From–To | Size (Years) | (km2) | (%) | Irri. (L/S) | Domestic (L/S) | |
| Tiber | Mocaiana | Assino | 1992–2005 | 14 | 102.0 | 48 | 79 | 82.18 |
| Tiber | Serrapartucci | Assino | 1992–2005 | 14 | 165.7 | 49 | 102 | 85.09 |
| Tiber | Migianella | Niccone | 1996–2005 | 10 | 135.7 | 42 | 130 | 0.10 |
| Hydrometric Station | WEI+FDCirr | WEI+irr | WEI+FDCmax | WEI+max | ||
|---|---|---|---|---|---|---|
| Id. | Station Same | River | ||||
| 1 | Mocaiana | Assino | 0.39 | 0.27 | 1.02 | 0.53 |
| 2 | Serrapartucci | Assino | 0.20 | 0.13 | 0.71 | 0.41 |
| 3 | Migianella | Niccone | 0.29 | 0.25 | 1.07 | 0.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casadei, S.; Peppoloni, F.; Pierleoni, A. A New Approach to Calculate the Water Exploitation Index (WEI+). Water 2020, 12, 3227. https://doi.org/10.3390/w12113227
Casadei S, Peppoloni F, Pierleoni A. A New Approach to Calculate the Water Exploitation Index (WEI+). Water. 2020; 12(11):3227. https://doi.org/10.3390/w12113227
Chicago/Turabian StyleCasadei, Stefano, Francesco Peppoloni, and Arnaldo Pierleoni. 2020. "A New Approach to Calculate the Water Exploitation Index (WEI+)" Water 12, no. 11: 3227. https://doi.org/10.3390/w12113227





