A WCSPH Particle Shifting Strategy for Simulating Violent Free Surface Flows
Abstract
1. Introduction
2. Governing Equations
3. Numerical Method
3.1. The Discrete System of Equations
3.2. Enhanced Particle Shifting Technique
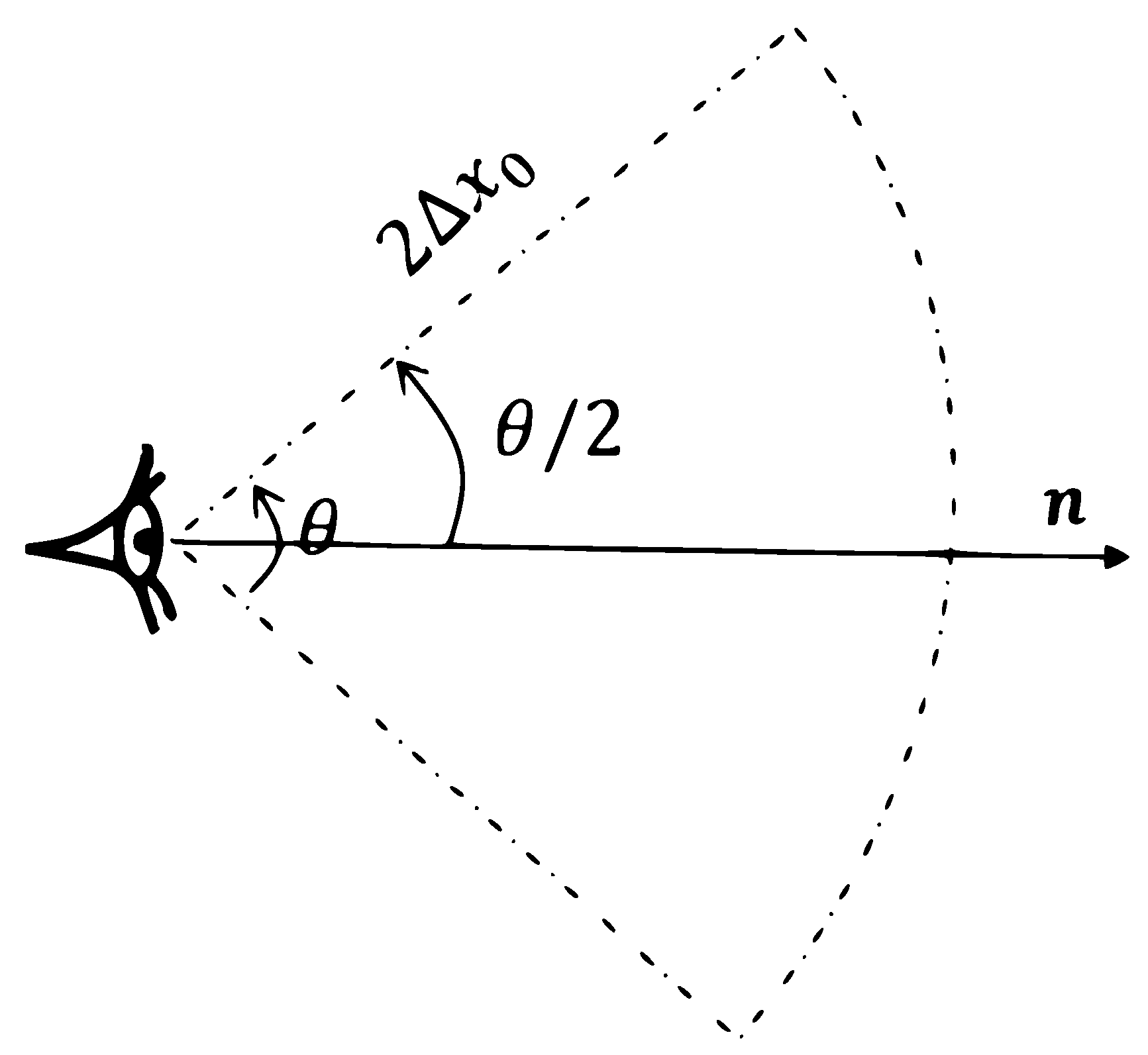
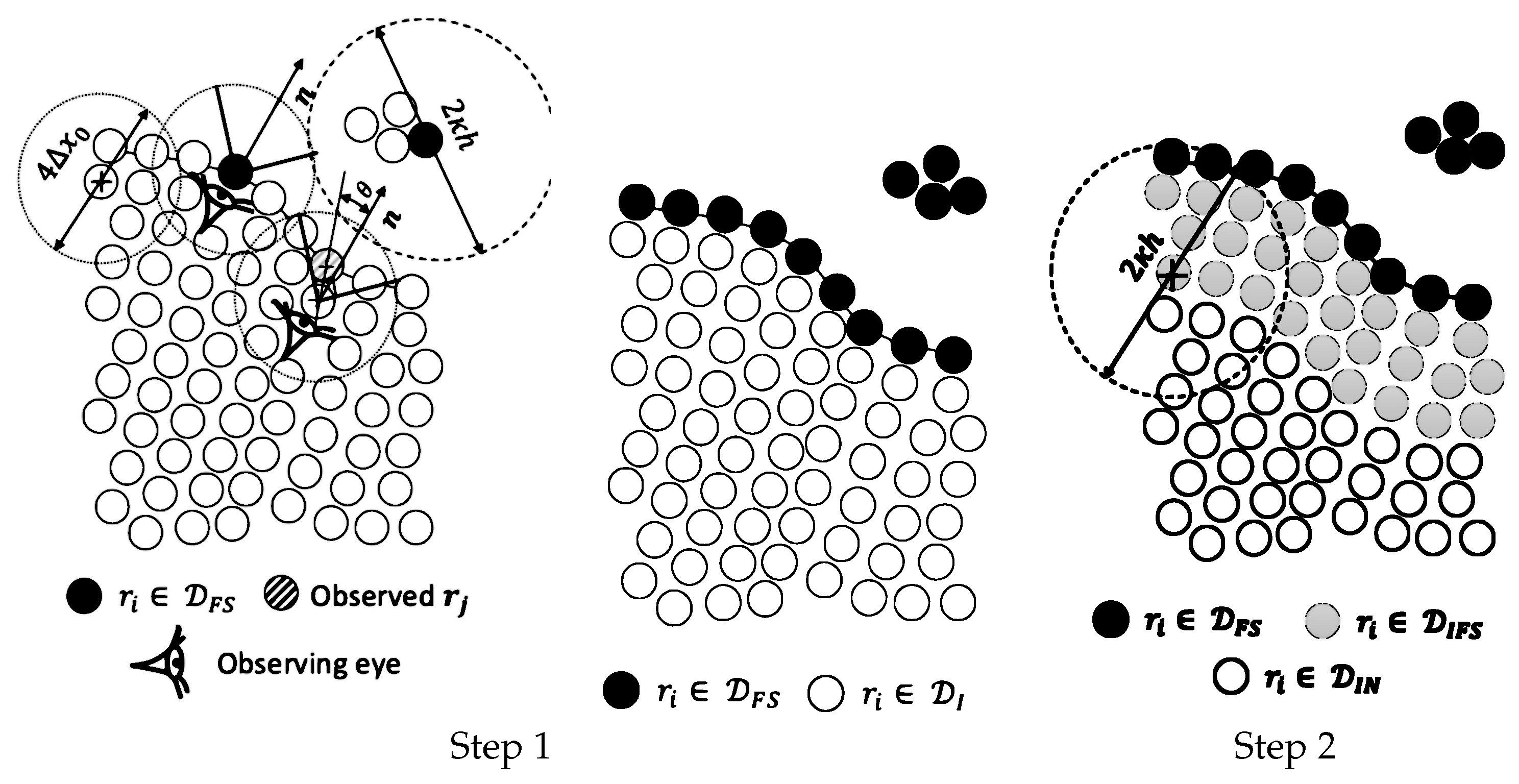
3.2.1. Free Surface Detection Algorithm
3.2.2. Modified Particle Shifting Equation
4. Validation
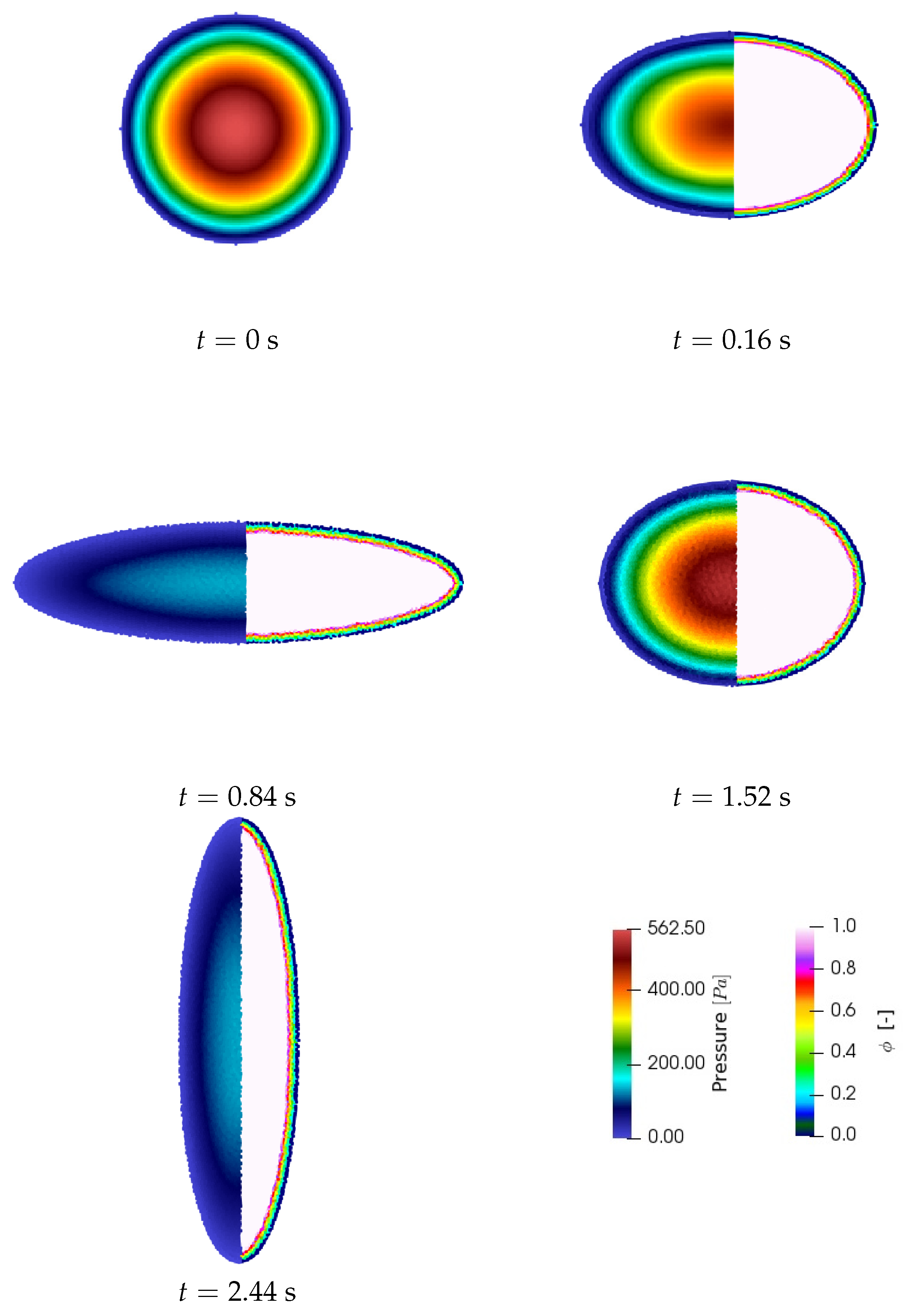
4.1. Oscillating Droplet Uunder a Central Conservative Force Field
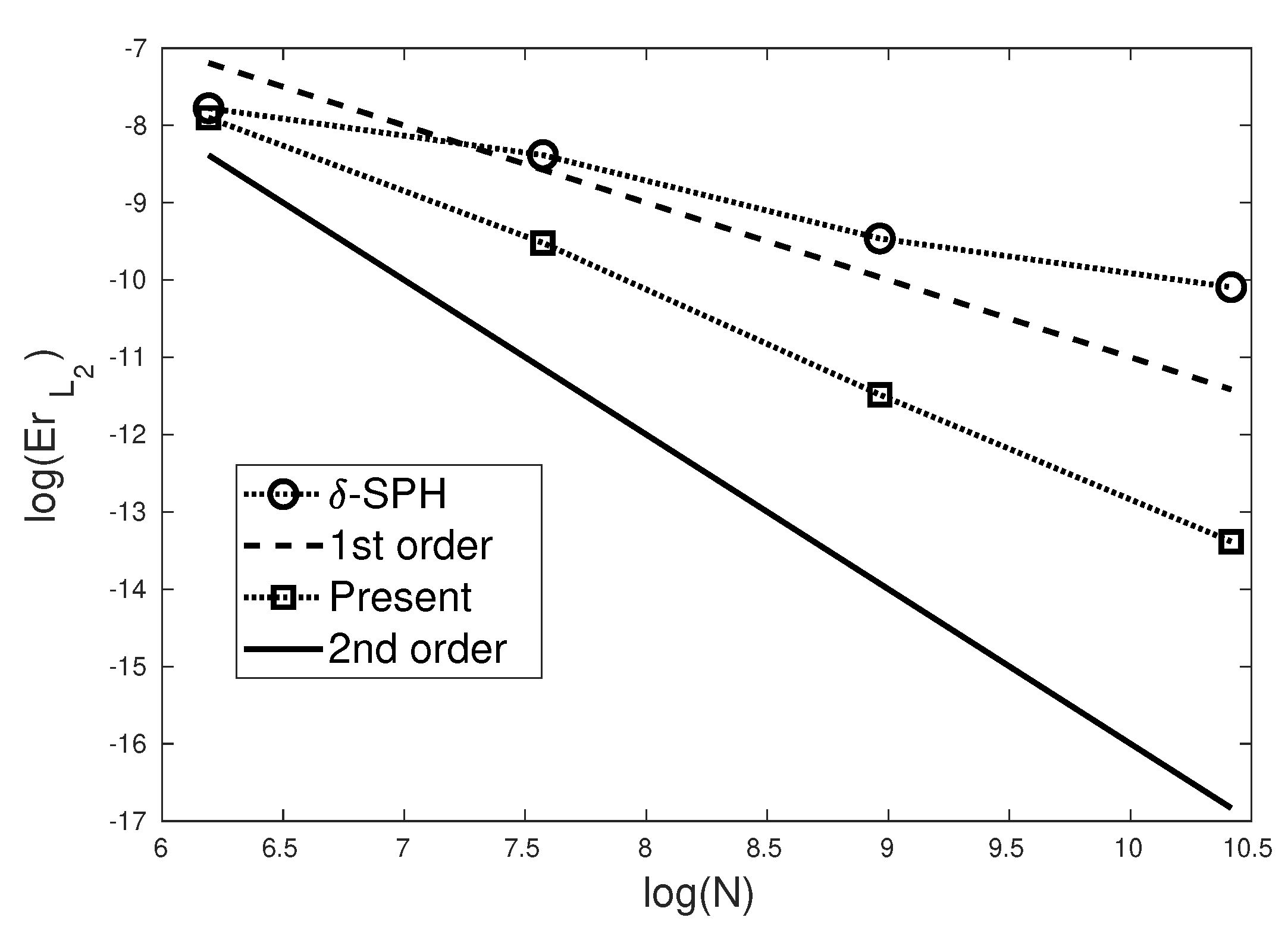
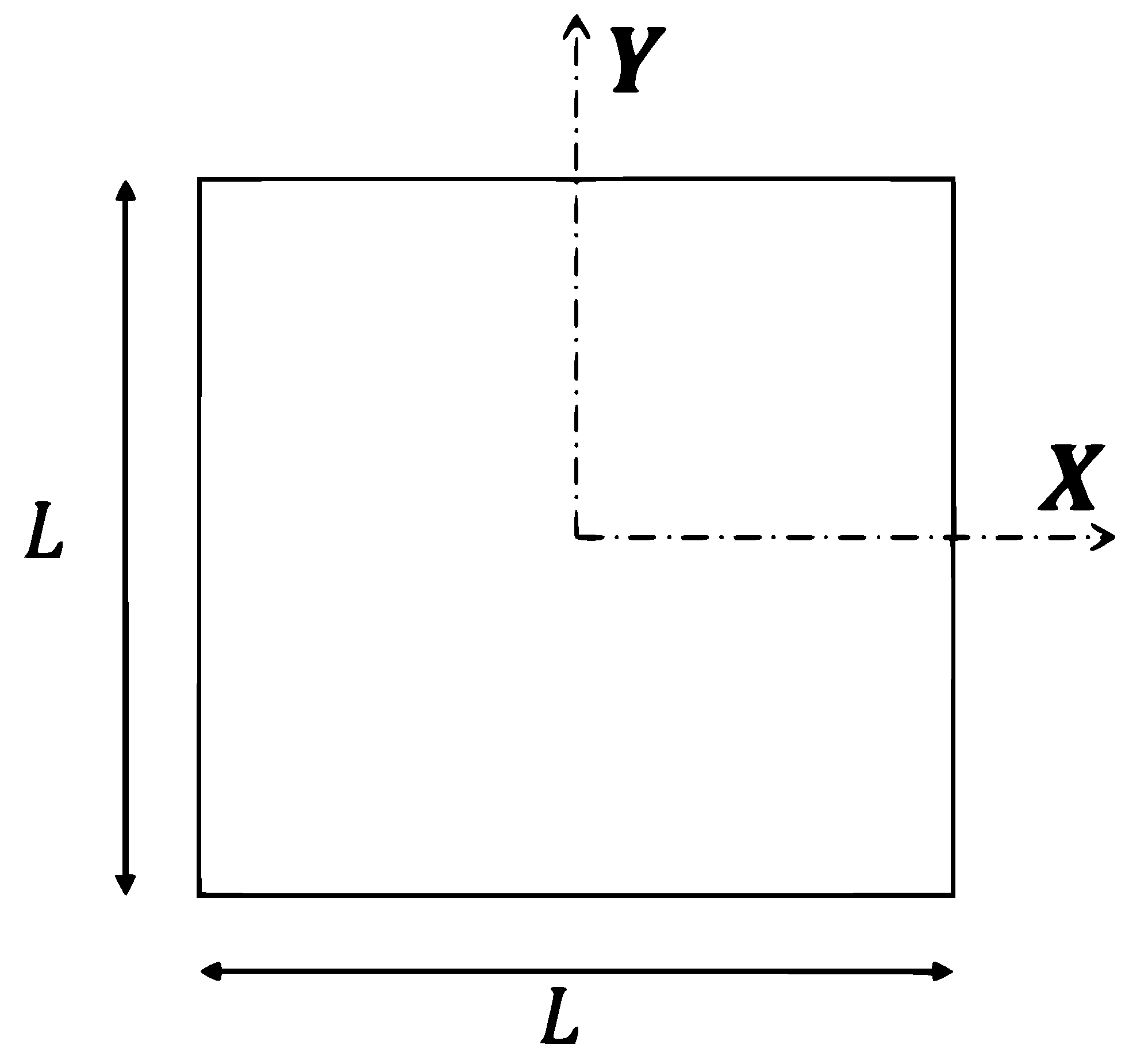
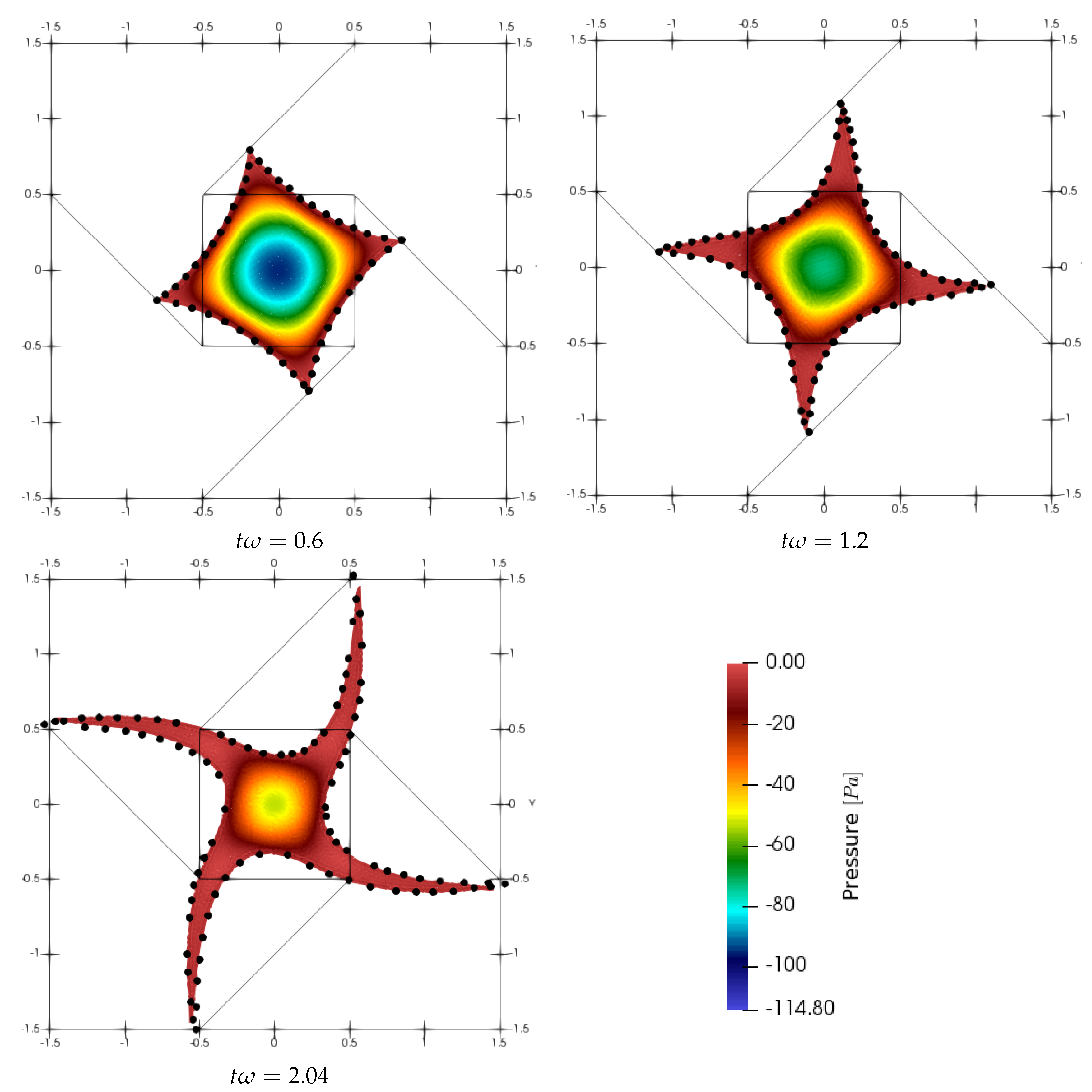
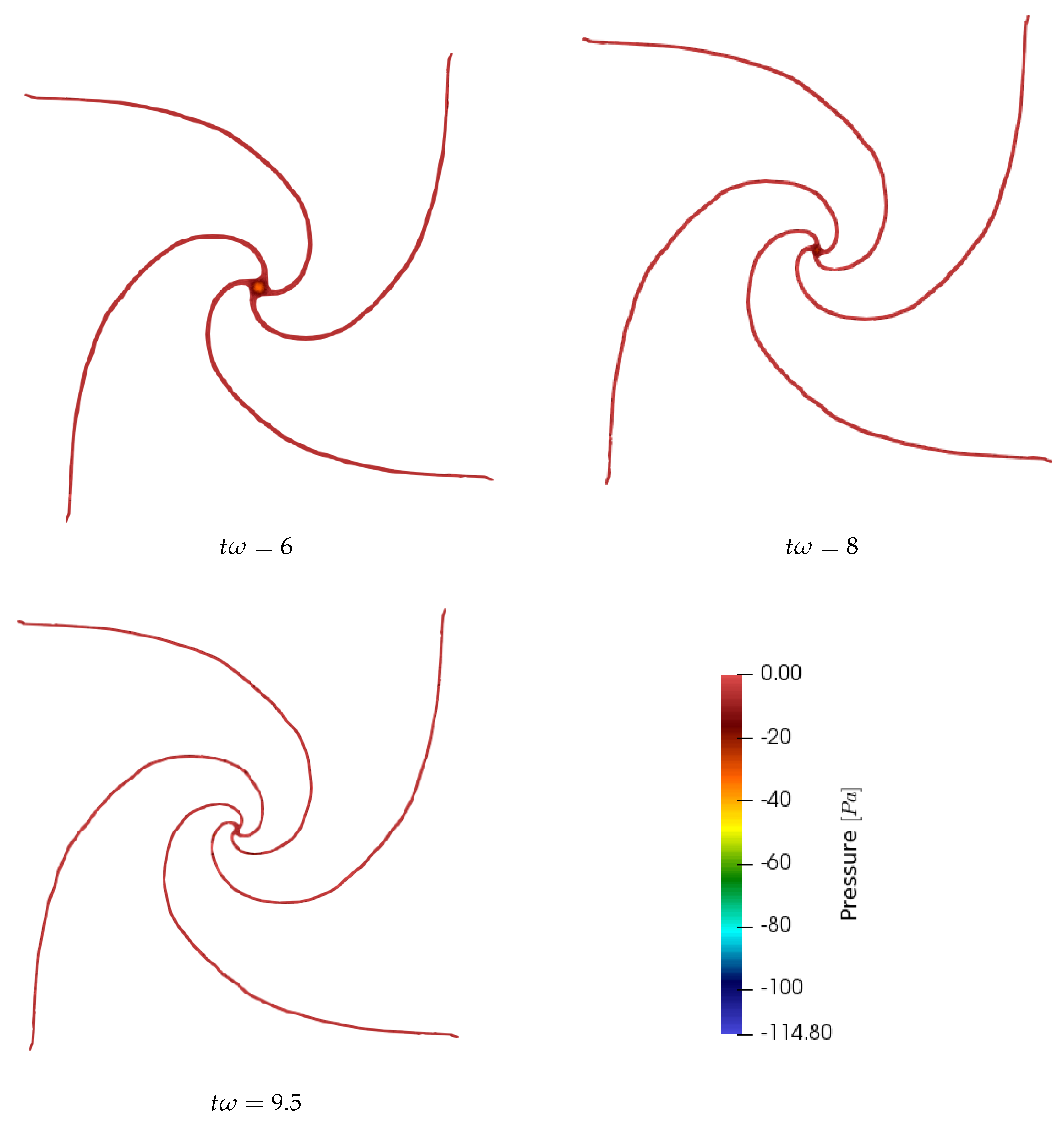
4.2. Evolution of an Initially-Square Fluid Patch
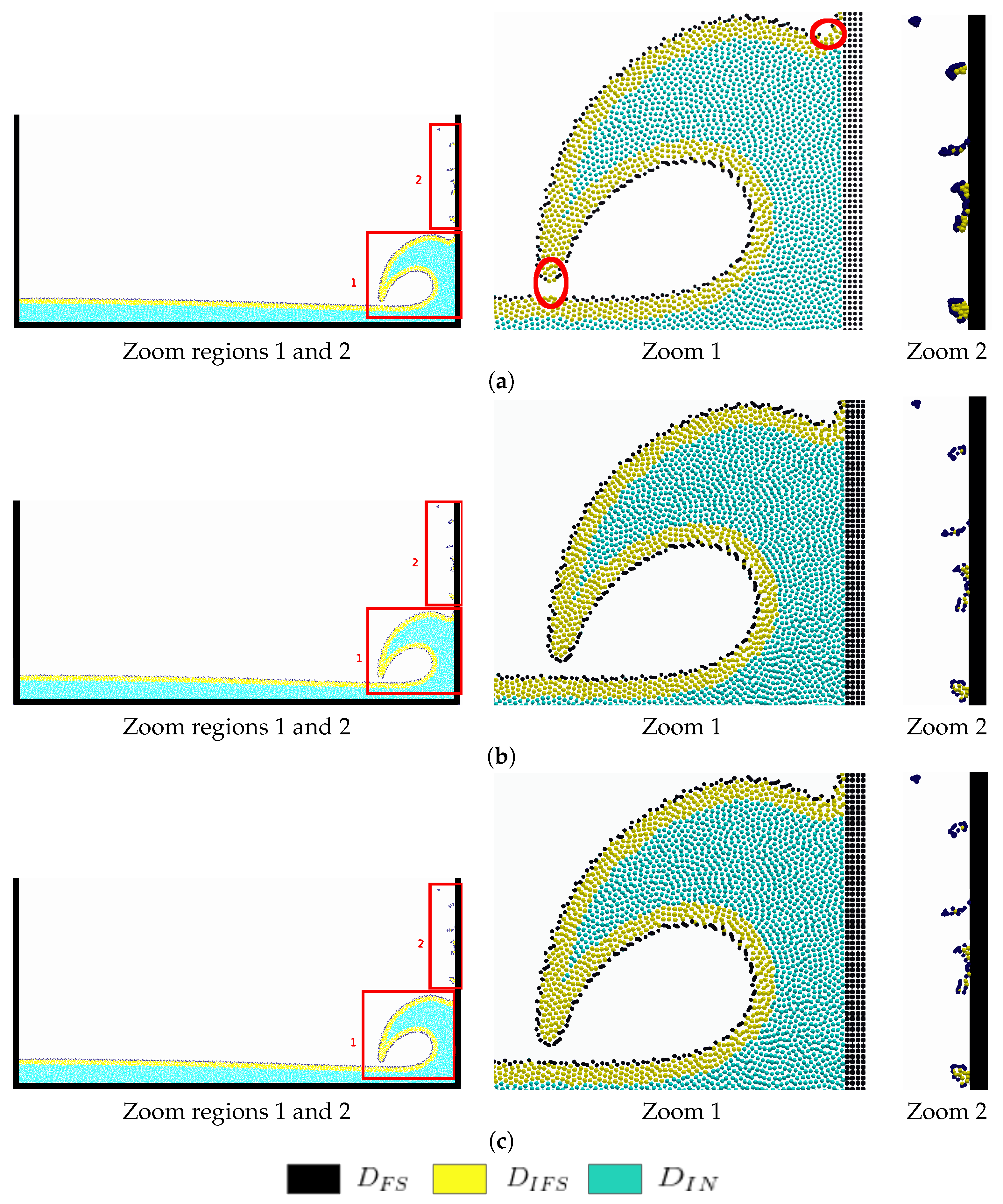
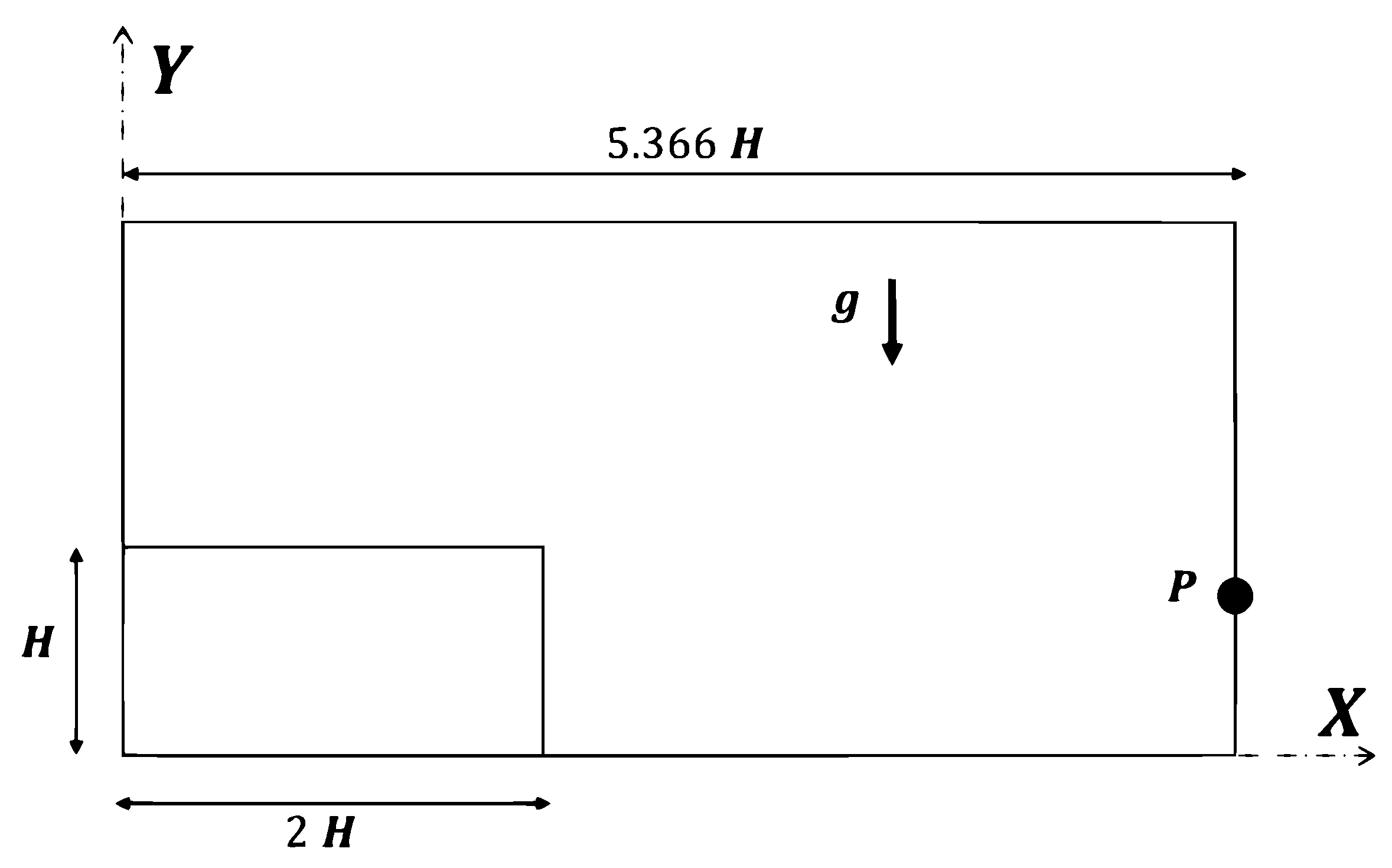
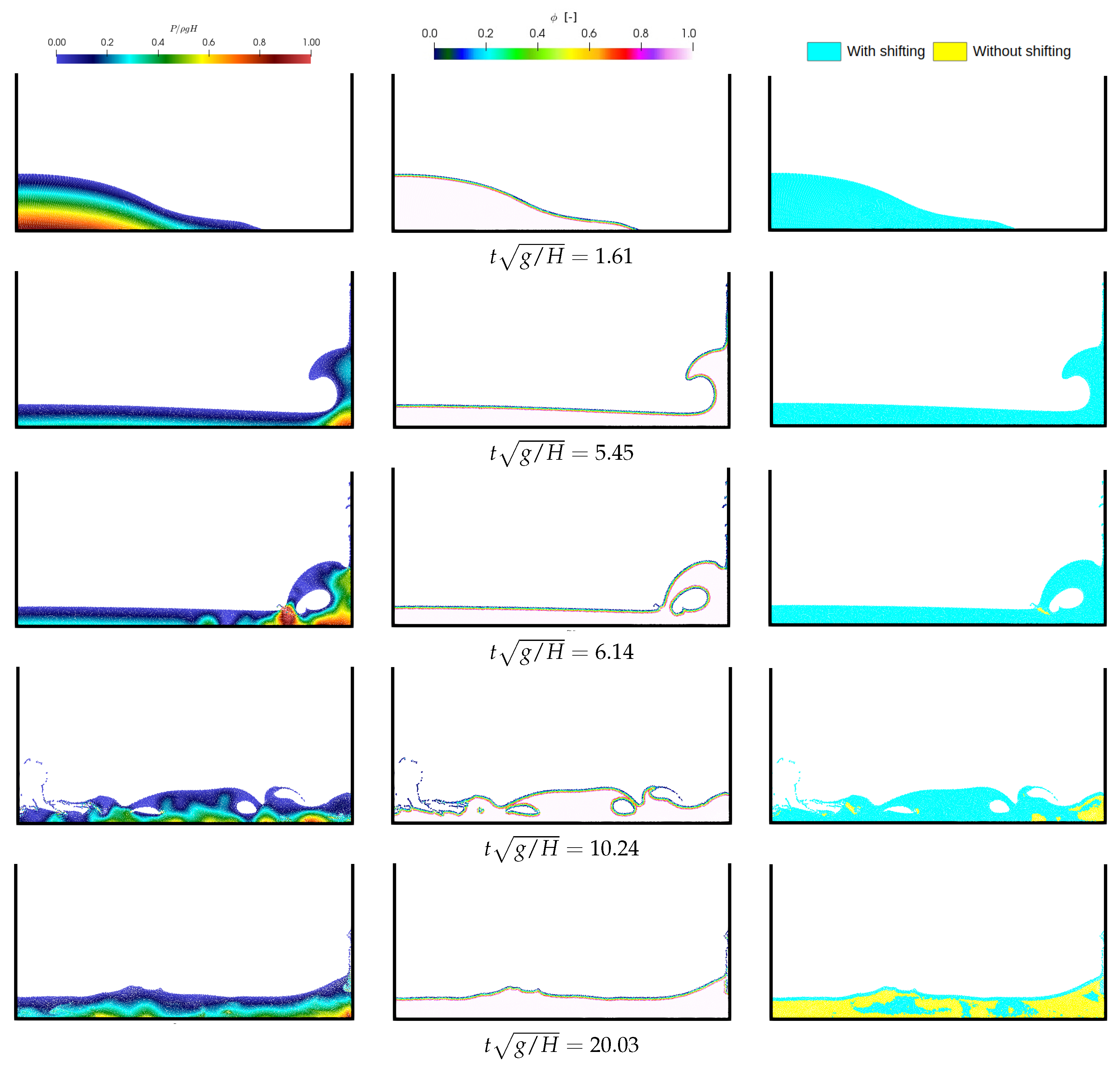
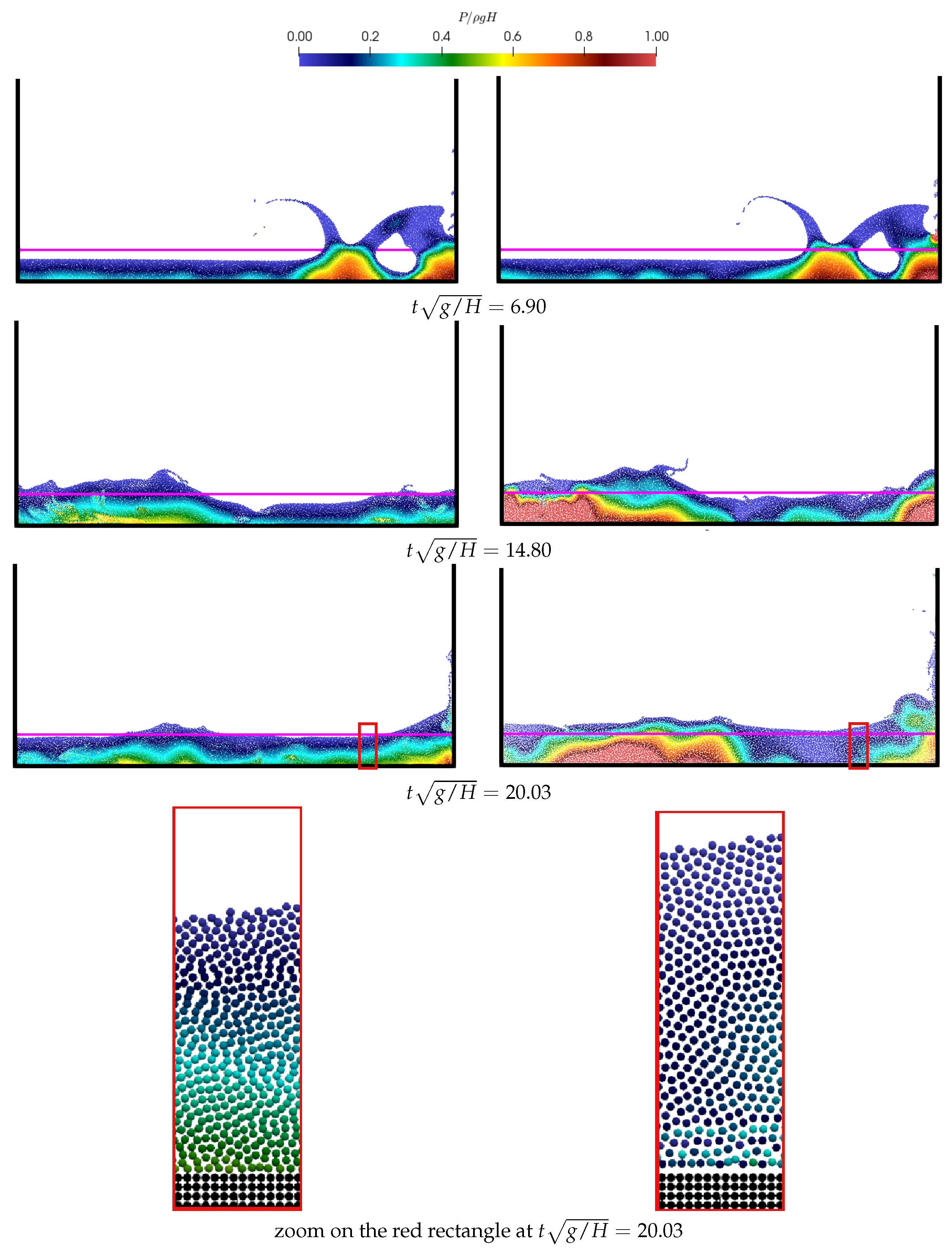
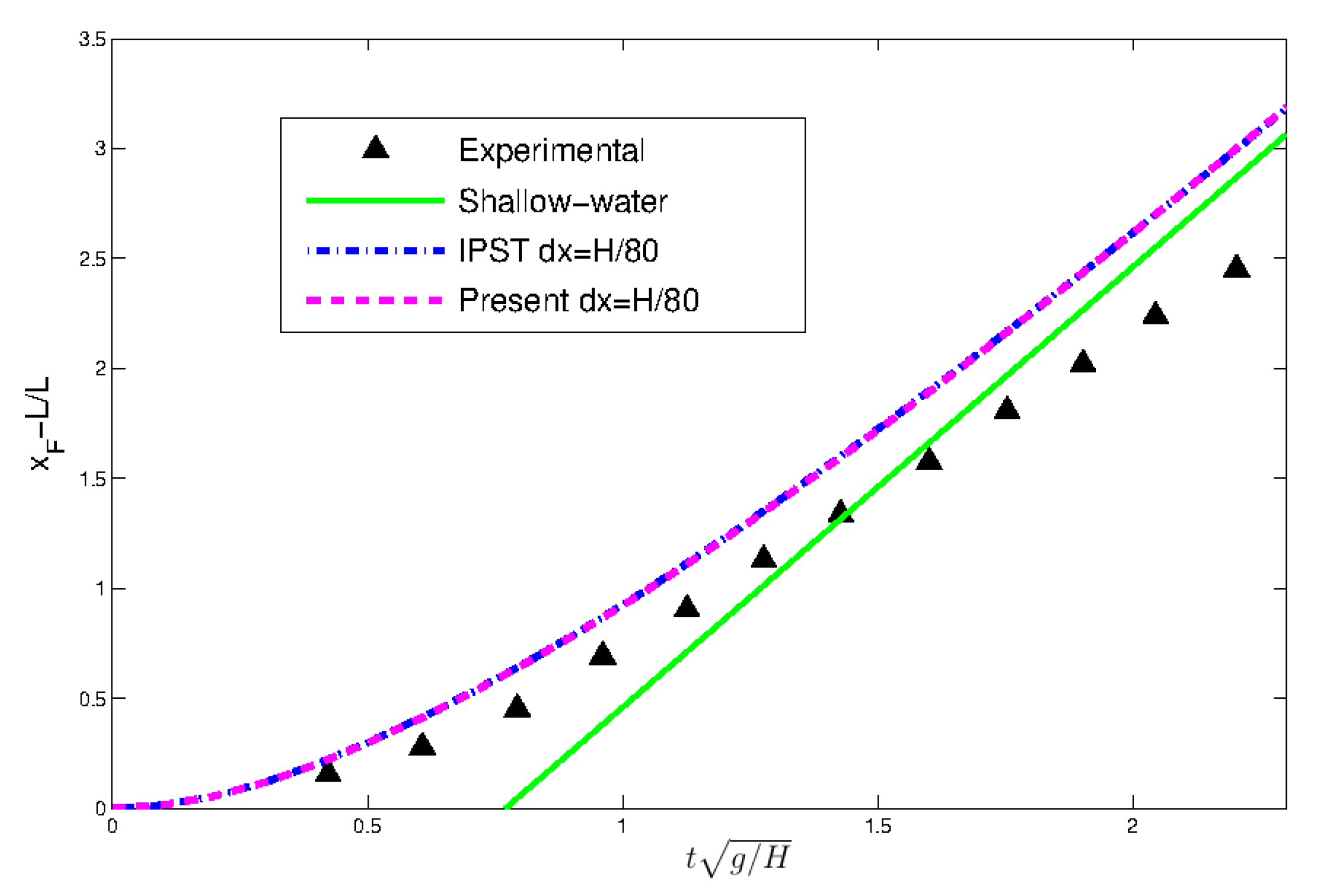
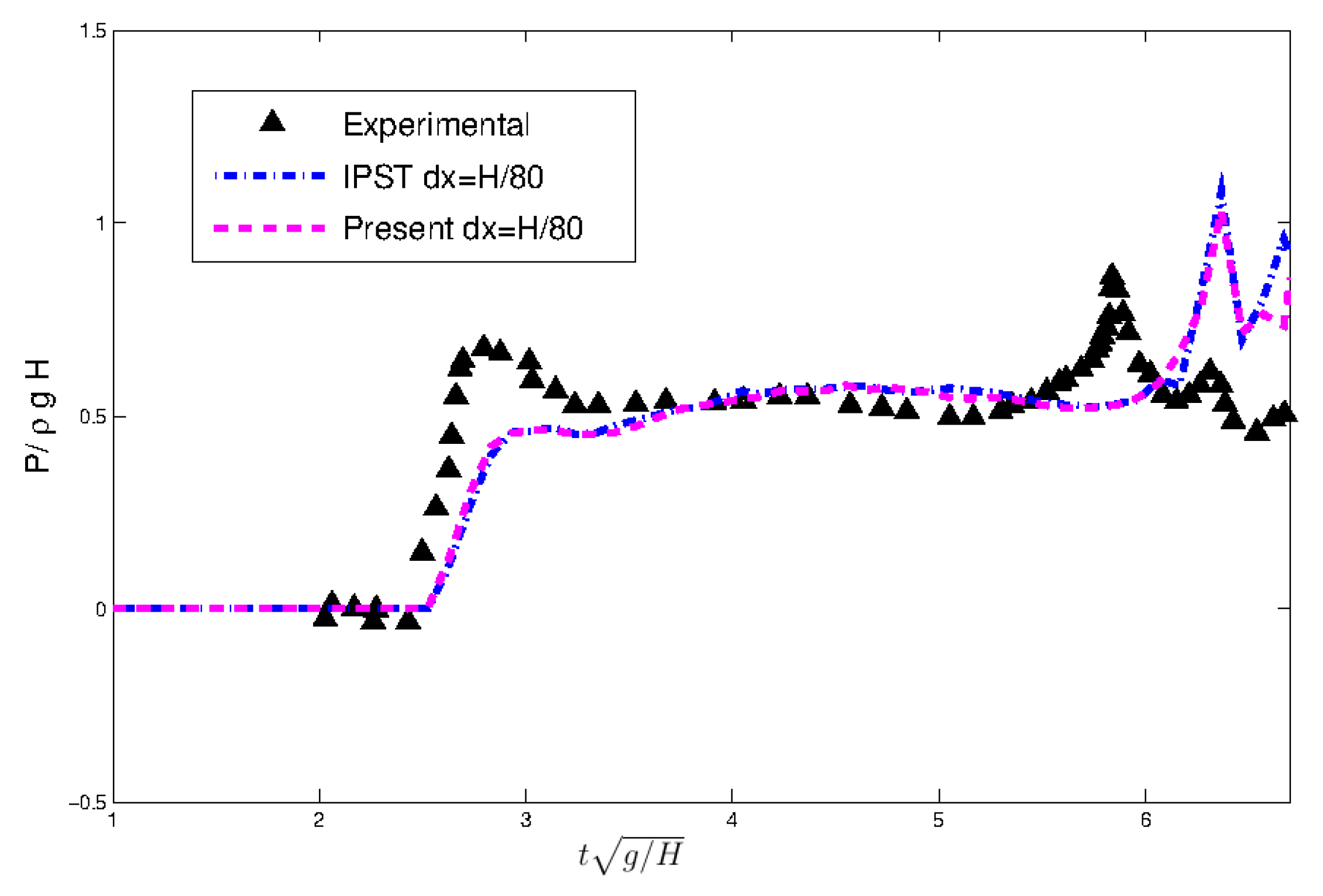
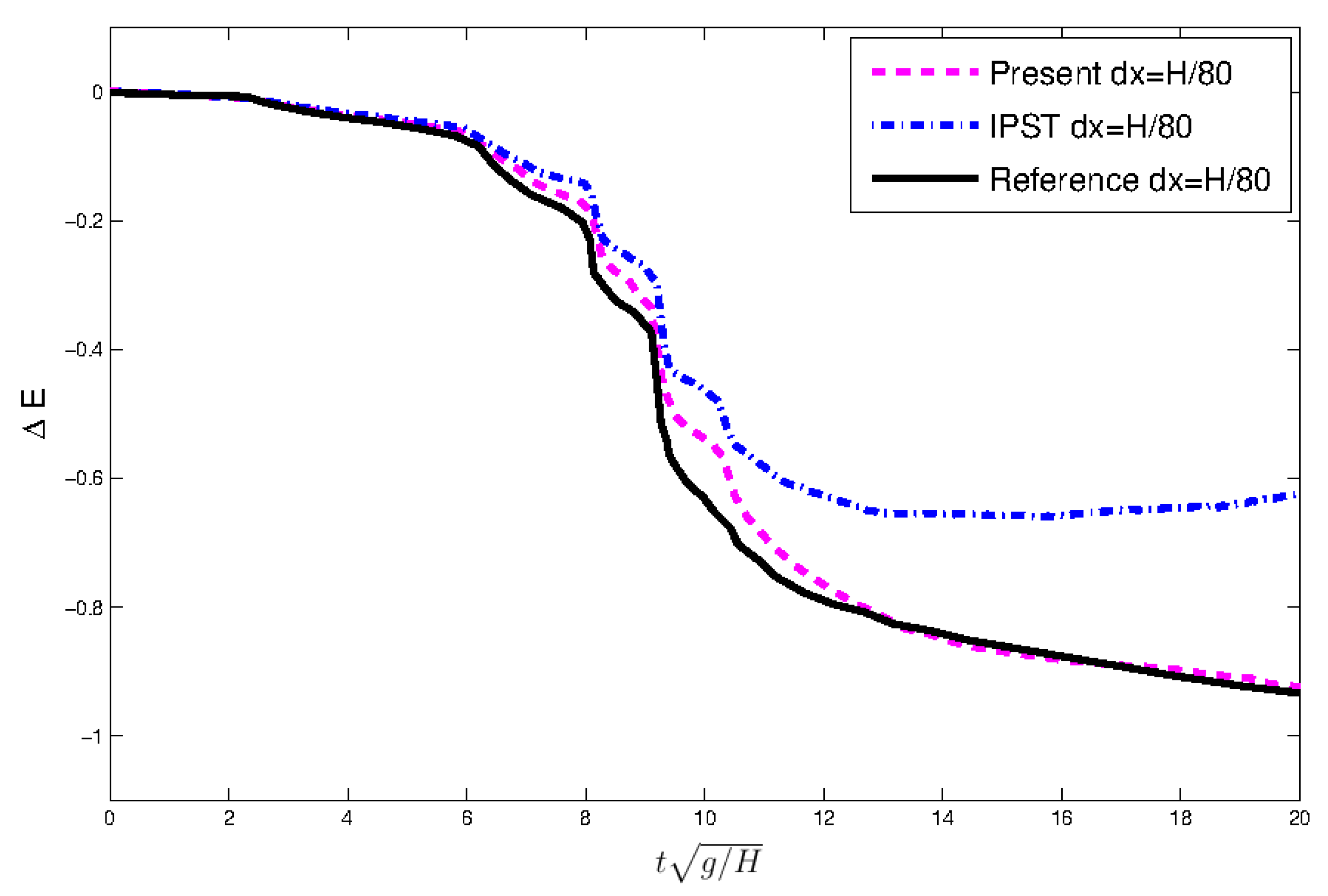
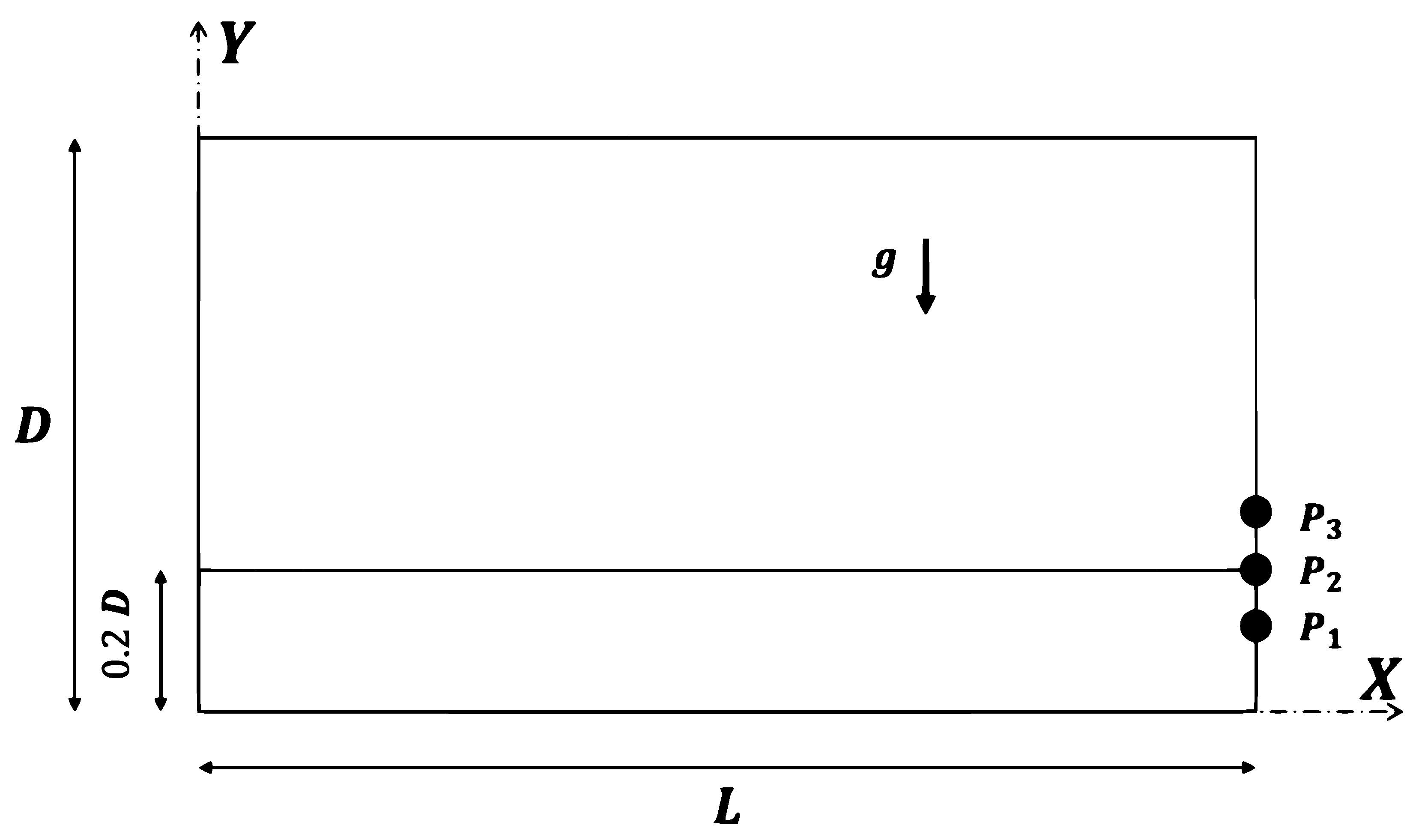
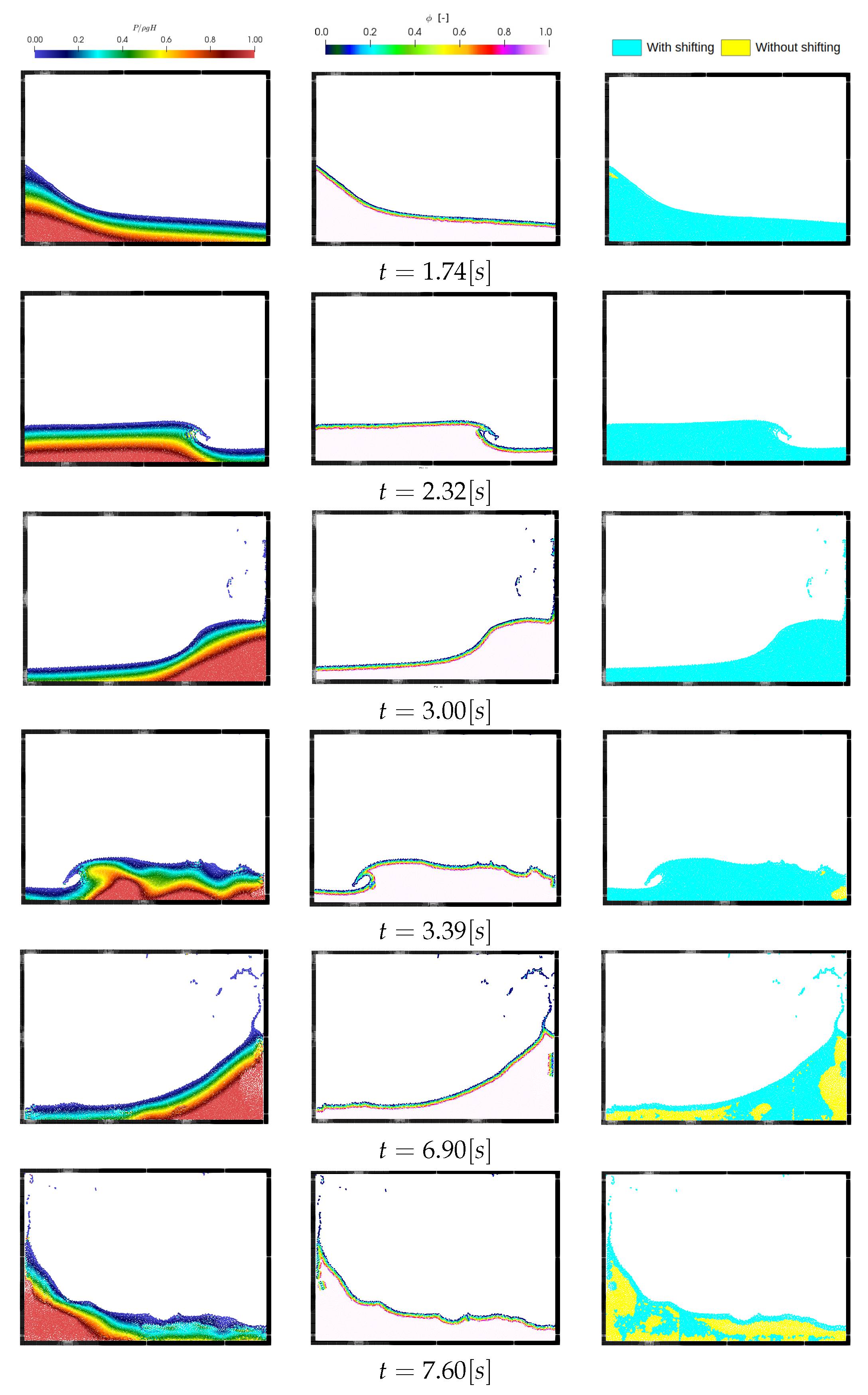
4.3. Dam Break Problem
4.4. Sloshing in a Rectangular Tank
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics and its diverse applications. Ann. Rev. Fluid Mech. 2012, 44, 323–346. [Google Scholar] [CrossRef]
- Ramírez, L.; Nogueira, X.; Khelladi, S.; Krimi, A.; Colominas, I. A very accurate Arbitrary Lagrangian– Eulerian meshless method for Computational Aeroacoustics. Comput. Methods Appl. Mech. Eng. 2018, 342, 116–141. [Google Scholar] [CrossRef]
- Tafuni, A.; Sahin, I. Hydrodynamic loads on vibrating cantilevers under a free surface in viscous fluids with SPH. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2013; Volume 56321, p. V07BT08A013. [Google Scholar]
- González-Cao, J.; Altomare, C.; Crespo, A.; Domínguez, J.; Gómez-Gesteira, M.; Kisacik, D. On the accuracy of DualSPHysics to assess violent collisions with coastal structures. Comput. Fluids 2019, 179, 604–612. [Google Scholar] [CrossRef]
- Mogan, S.C.; Chen, D.; Hartwig, J.; Sahin, I.; Tafuni, A. Hydrodynamic analysis and optimization of the Titan submarine via the SPH and Finite–Volume methods. Comput. Fluids 2018, 174, 271–282. [Google Scholar] [CrossRef]
- Verbrugghe, T.; Domínguez, J.M.; Altomare, C.; Tafuni, A.; Vacondio, R.; Troch, P.; Kortenhaus, A. Non-linear wave generation and absorption using open boundaries within DualSPHysics. Comput. Phys. Commun. 2019, 240, 46–59. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.; Hall, M.; Altomare, C.; Wu, M.; Stratigaki, V.; Troch, P.; Cappietti, L.; Gómez-Gesteira, M. SPH simulation of floating structures with moorings. Coast. Eng. 2019, 153, 103560. [Google Scholar] [CrossRef]
- Kazemi, E.; Koll, K.; Tait, S.; Shao, S. SPH modelling of turbulent open channel flow over and within natural gravel beds with rough interfacial boundaries. Adv. Water Res. 2020, 140, 103557. [Google Scholar] [CrossRef]
- Krimi, A.; Rezoug, M.; Khelladi, S.; Nogueira, X.; Deligant, M.; Ramírez, L. Smoothed particle hydrodynamics: A consistent model for interfacial multiphase fluid flow simulations. J. Comput. Phys. 2018, 358, 53–87. [Google Scholar] [CrossRef]
- Krimi, A.; Khelladi, S.; Nogueira, X.; Deligant, M.; Ata, R.; Rezoug, M. Multiphase smoothed particle hydrodynamics approach for modeling soil–water interactions. Adv. Water Res. 2018, 121, 189–205. [Google Scholar] [CrossRef]
- Omidvar, P.; Kheirkhahan, M.; Hosseini, K. Simulation of two-phase Newtonian and non-Newtonian systems using smoothed particle hydrodynamics and herschel-bulkley model. J. Hydraul. 2019, 14, 19–33. [Google Scholar]
- Omidvar, P.; Nikeghbali, P. Simulation of violent water flows over a movable bed using smoothed particle hydrodynamics. J. Marine Sci. Technol. 2017, 22, 270–287. [Google Scholar] [CrossRef]
- Lo, E.Y.; Shao, S. Simulation of near-shore solitary wave mechanics by an incompressible SPH method. Appl. Ocean Res. 2002, 24, 275–286. [Google Scholar]
- Ataie-Ashtiani, B.; Shobeyri, G. Numerical simulation of landslide impulsive waves by incompressible smoothed particle hydrodynamics. Int. J. Numer. Methods Fluids 2008, 56, 209–232. [Google Scholar] [CrossRef]
- Fatehi, R.; Rahmat, A.; Tofighi, N.; Yildiz, M.; Shadloo, M.S. Density-based smoothed particle hydrodynamics methods for incompressible flows. Comput. Fluids 2019, 185, 22–33. [Google Scholar] [CrossRef]
- Nogueira, X.; Ramírez, L.; Clain, S.; Loubère, R.; Cueto-Felgueroso, L.; Colominas, I. High-accurate SPH method with multidimensional optimal order detection limiting. Comput. Methods Appl. Mech. Eng. 2016, 310, 134–155. [Google Scholar] [CrossRef]
- Vila, J. On particle weighted methods and smooth particle hydrodynamics. Math. Models Methods Appl. Sci. 1999, 9, 161–209. [Google Scholar] [CrossRef]
- Inutsuka, S.I. Reformulation of smoothed particle hydrodynamics with Riemann solver. J. Comput. Phys. 2002, 179, 238–267. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, X.; Adams, N.A. A weakly compressible SPH method based on a low-dissipation Riemann solver. J. Comput. Phys. 2017, 335, 605–620. [Google Scholar] [CrossRef]
- Fourtakas, G.; Stansby, P.; Rogers, B.; Lind, S. An Eulerian–Lagrangian incompressible SPH formulation (ELI-SPH) connected with a sharp interface. Comput. Methods Appl. Mech. Eng. 2018, 329, 532–552. [Google Scholar] [CrossRef]
- Lind, S.J.; Stansby, P. High-order Eulerian incompressible smoothed particle hydrodynamics with transition to Lagrangian free-surface motion. J. Comput. Phys. 2016, 326, 290–311. [Google Scholar] [CrossRef]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touzé, D.; Graziani, G. δ-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Meringolo, D.D.; Marrone, S.; Colagrossi, A.; Liu, Y. A dynamic δ-SPH model: How to get rid of diffusive parameter tuning. Comput. Fluids 2019, 179, 334–355. [Google Scholar] [CrossRef]
- Krimi, A.; Ramírez, L.; Khelladi, S.; Navarrina, F.; Deligant, M.; Nogueira, X. Improved δ-SPH Scheme with Automatic and Adaptive Numerical Dissipation. Water 2020, 12, 2858. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Ann. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical diffusive terms in weakly-compressible SPH schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Swegle, J.; Hicks, D.; Attaway, S. Smoothed particle hydrodynamics stability analysis. J. Comput. Phys. 1995, 116, 123–134. [Google Scholar] [CrossRef]
- Monaghan, J.J. SPH without a tensile instability. J. Comput. Phys. 2000, 159, 290–311. [Google Scholar] [CrossRef]
- Oger, G.; Marrone, S.; Le Touzé, D.; De Leffe, M. SPH accuracy improvement through the combination of a quasi-Lagrangian shifting transport velocity and consistent ALE formalisms. J. Comput. Phys. 2016, 313, 76–98. [Google Scholar] [CrossRef]
- Antuono, M.; Bouscasse, B.; Colagrossi, A.; Marrone, S. A measure of spatial disorder in particle methods. Comput. Phys. Commun. 2014, 185, 2609–2621. [Google Scholar] [CrossRef]
- Matsunaga, T.; Koshizuka, S.; Hosaka, T.; Ishii, E. Moving surface mesh-incorporated particle method for numerical simulation of a liquid droplet. J. Comput. Phys. 2020, 409, 109349. [Google Scholar] [CrossRef]
- Sun, P.; Colagrossi, A.; Marrone, S.; Zhang, A. The δ-plus-SPH model: Simple procedures for a further improvement of the SPH scheme. Comput. Methods Appl. Mech. Eng. 2017, 315, 25–49. [Google Scholar] [CrossRef]
- Lind, S.J.; Xu, R.; Stansby, P.K.; Rogers, B.D. Incompressible smoothed particle hydrodynamics for free-surface flows: A generalised diffusion-based algorithm for stability and validations for impulsive flows and propagating waves. J. Comput. Phys. 2012, 231, 1499–1523. [Google Scholar] [CrossRef]
- Sun, P.; Colagrossi, A.; Marrone, S.; Antuono, M.; Zhang, A.M. A consistent approach to particle shifting in the δ-Plus-SPH model. Comput. Methods Appl. Mech. Eng. 2019, 348, 912–934. [Google Scholar] [CrossRef]
- Wang, P.P.; Meng, Z.F.; Zhang, A.M.; Ming, F.R.; Sun, P.N. Improved particle shifting technology and optimized free-surface detection method for free-surface flows in smoothed particle hydrodynamics. Comput. Methods Appl. Mech. Eng. 2019, 357, 112580. [Google Scholar] [CrossRef]
- Shao, S.; Lo, E.Y. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv. Water Res. 2003, 26, 787–800. [Google Scholar] [CrossRef]
- Shao, S. Incompressible SPH simulation of wave breaking and overtopping with turbulence modelling. Int. J. Numer. Methods Fluids 2006, 50, 597–621. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Shao, S. Corrected incompressible SPH method for accurate water-surface tracking in breaking waves. Coast. Eng. 2008, 55, 236–250. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Shao, S. Enhanced predictions of wave impact pressure by improved incompressible SPH methods. Appl. Ocean Res. 2009, 31, 111–131. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. Modified moving particle semi-implicit methods for the prediction of 2D wave impact pressure. Coast. Eng. 2009, 56, 419–440. [Google Scholar] [CrossRef]
- Schwaiger, H.F. An implicit corrected SPH formulation for thermal diffusion with linear free surface boundary conditions. Int. J. Numer. Methods Eng. 2008, 75, 647–671. [Google Scholar] [CrossRef]
- Lee, E.S.; Moulinec, C.; Xu, R.; Violeau, D.; Laurence, D.; Stansby, P. Comparisons of weakly compressible and truly incompressible algorithms for the SPH mesh free particle method. J. Comput. Phys. 2008, 227, 8417–8436. [Google Scholar] [CrossRef]
- Marrone, S.; Colagrossi, A.; Le Touzé, D.; Graziani, G. Fast free-surface detection and level-set function definition in SPH solvers. J. Comput. Phys. 2010, 229, 3652–3663. [Google Scholar] [CrossRef]
- Barecasco, A.; Terissa, H.; Naa, C.F. Simple free-surface detection in two and three-dimensional SPH solver. arXiv 2013, arXiv:1309.4290. [Google Scholar]
- Jandaghian, M.; Shakibaeinia, A. An enhanced weakly-compressible MPS method for free-surface flows. Comput. Methods Appl. Mech. Eng. 2020, 360, 112771. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Morris, J.P. Simulating surface tension with smoothed particle hydrodynamics. Int. J. Numer. Methods Fluids 2000, 33, 333–353. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G.; Lam, K. Constructing smoothing functions in smoothed particle hydrodynamics with applications. J. Comput. Appl. Math. 2003, 155, 263–284. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Dehnen, W.; Aly, H. Improving convergence in smoothed particle hydrodynamics simulations without pairing instability. Mon. Not. R. Astron. Soc. 2012, 425, 1068–1082. [Google Scholar] [CrossRef]
- Sun, P.; Colagrossi, A.; Marrone, S.; Antuono, M.; Zhang, A. Multi-resolution Delta-plus-SPH with tensile instability control: Towards high Reynolds number flows. Comput. Phys. Commun. 2018, 224, 63–80. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S.; Molteni, D. Free-surface flows solved by means of SPH schemes with numerical diffusive terms. Comput. Phys. Commun. 2010, 181, 532–549. [Google Scholar] [CrossRef]
- Williamson, J. Low-storage runge-kutta schemes. J. Comput. Phys. 1980, 35, 48–56. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.Y.; Adams, N.A. A generalized wall boundary condition for smoothed particle hydrodynamics. J. Comput. Phys. 2012, 231, 7057–7075. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Shimizu, Y. Comparative study on accuracy and conservation properties of two particle regularization schemes and proposal of an optimized particle shifting scheme in ISPH context. J. Comput. Phys. 2017, 332, 236–256. [Google Scholar] [CrossRef]
- Meringolo, D.; Colagrossi, A.; Marrone, S.; Aristodemo, F. On the filtering of acoustic components in weakly-compressible SPH simulations. J. Fluids Struct. 2017, 70, 1–23. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Rafiee, A. A simple SPH algorithm for multi-fluid flow with high density ratios. Int. J. Numer. Methods Fluids 2013, 71, 537–561. [Google Scholar] [CrossRef]
- Le Touzé, D.; Colagrossi, A.; Colicchio, G.; Greco, M. A critical investigation of smoothed particle hydrodynamics applied to problems with free-surfaces. Int. J. Numer. Methods Fluids 2013, 73, 660–691. [Google Scholar] [CrossRef]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef]
- Zheng, X.; Shao, S.; Khayyer, A.; Duan, W.; Ma, Q.; Liao, K. Corrected first-order derivative ISPH in water wave simulations. Coast. Eng. J. 2017, 59, 1750010. [Google Scholar] [CrossRef]
- Colagrossi, A. A Meshless Lagrangian Method for Free-Surface and Interface Flows with Fragmentation. Ph.D. Thesis, University Roma, Roma, Italy, 2005; pp. 1–234. [Google Scholar]
- Khayyer, A.; Gotoh, H. Enhancement of stability and accuracy of the moving particle semi-implicit method. J. Comput. Phys. 2011, 230, 3093–3118. [Google Scholar] [CrossRef]
- Oger, G.; Doring, M.; Alessandrini, B.; Ferrant, P. An improved SPH method: Towards higher order convergence. J. Comput. Phys. 2007, 225, 1472–1492. [Google Scholar] [CrossRef]
- Martin, J.C.; Moyce, W.J.; Martin, J.; Moyce, W.; Penney, W.G.; Price, A.; Thornhill, C. Part IV. An experimental study of the collapse of liquid columns on a rigid horizontal plane. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1952, 244, 312–324. [Google Scholar]
- Zhou, Z.; De Kat, J.; Buchner, B. A nonlinear 3D approach to simulate green water dynamics on deck. In Proceedings of the Seventh International Conference on Numerical Ship Hydrodynamics, Nantes, France, 19–22 July 1999; pp. 1–15. [Google Scholar]
- Buchner, B. Green Water on Ship-Type Offshore Structures. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Mokos, A.; Rogers, B.D.; Stansby, P.K.; Domínguez, J.M. Multi-phase SPH modelling of violent hydrodynamics on GPUs. Comput. Phys. Commun. 2015, 196, 304–316. [Google Scholar] [CrossRef]
- Chen, Z.; Zong, Z.; Liu, M.; Zou, L.; Li, H.; Shu, C. An SPH model for multiphase flows with complex interfaces and large density differences. J. Comput. Phys. 2015, 283, 169–188. [Google Scholar] [CrossRef]
- Zhang, T.; Koshizuka, S.; Xuan, P.; Li, J.; Gong, C. Enhancement of stabilization of MPS to arbitrary geometries with a generic wall boundary condition. Comput. Fluids 2019, 178, 88–112. [Google Scholar] [CrossRef]
- Greco, M. A Two-Dimensional Study of Green-Water Loading. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2001. [Google Scholar]
- Cherfils, J.M. Développements et Applications de la Méthode SPH Aux écoulements Visqueux à Surface Libre. Ph.D. Thesis, CNRS-Université du Havre, Le Havre, France, 2011. [Google Scholar]
- Ritter, A. Die fortpflanzung der wasserwellen. Z. Ver. Dtsch. Ing. 1892, 36, 947–954. [Google Scholar]
- Rezavand, M.; Zhang, C.; Hu, X. A weakly compressible SPH method for violent multi-phase flows with high density ratio. J. Comput. Phys. 2020, 402, 109092. [Google Scholar] [CrossRef]
- Bellezi, C.A.; Cheng, L.Y.; Okada, T.; Arai, M. Optimized perforated bulkhead for sloshing mitigation and control. Ocean Eng. 2019, 187, 106171. [Google Scholar] [CrossRef]
- ARAI, M.; Hata, R.; Cheng, L.Y. Sloshing in vertical and horizontal axisymmetric tanks. J. Jpn. Soc. Naval Arch. Ocean Eng. 2018, 27, 117–123. [Google Scholar] [CrossRef]
- Rafiee, A.; Pistani, F.; Thiagarajan, K. Study of liquid sloshing: Numerical and experimental approach. Comput. Mech. 2011, 47, 65–75. [Google Scholar] [CrossRef]
- Cao, X.; Ming, F.; Zhang, A. Sloshing in a rectangular tank based on SPH simulation. Appl. Ocean Res. 2014, 47, 241–254. [Google Scholar] [CrossRef]
- Winkler, D.; Meister, M.; Rezavand, M.; Rauch, W. gpuSPHASE—A shared memory caching implementation for 2D SPH using CUDA. Comput. Phys. Commun. 2017, 213, 165–180. [Google Scholar] [CrossRef]


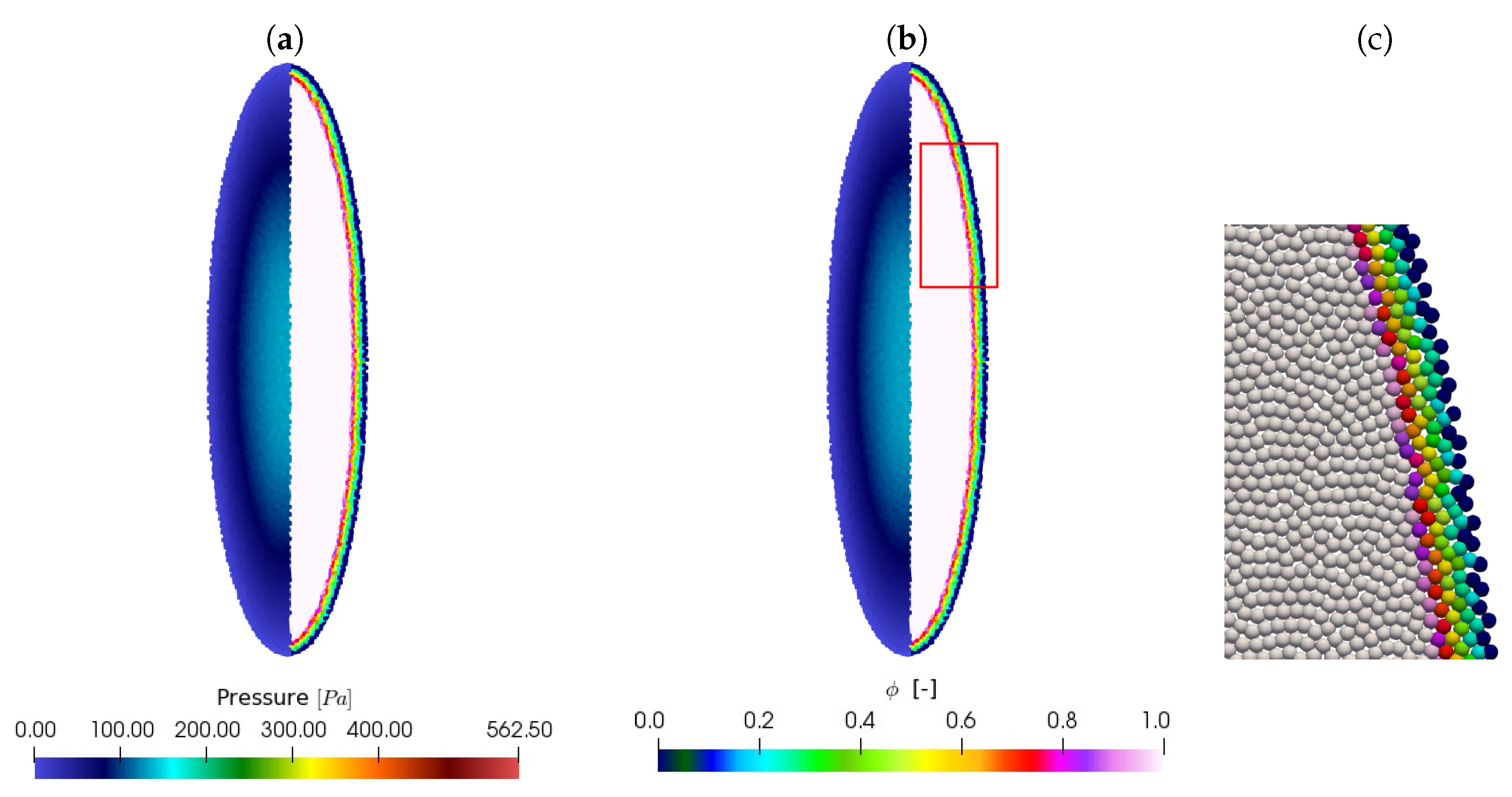

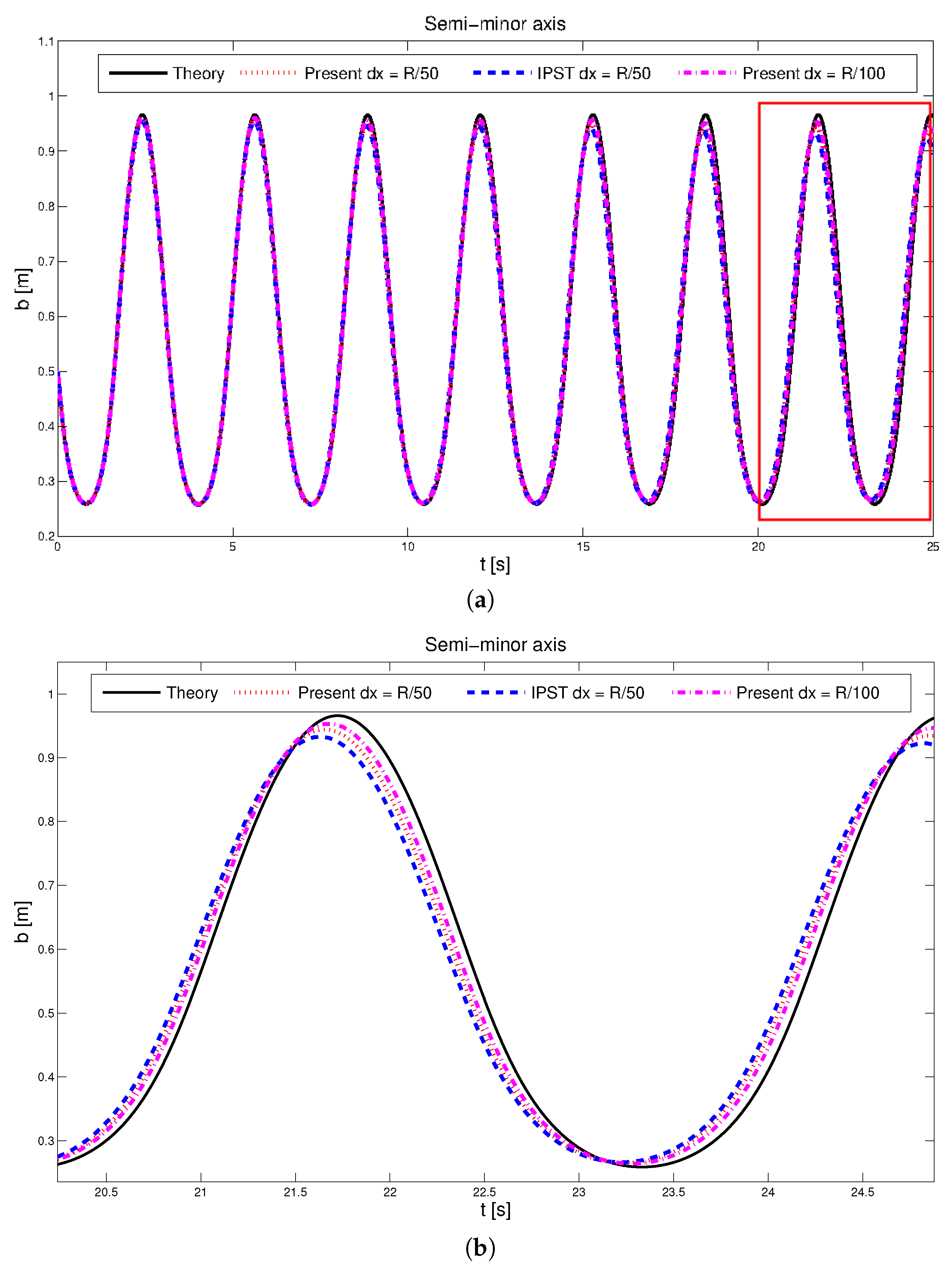
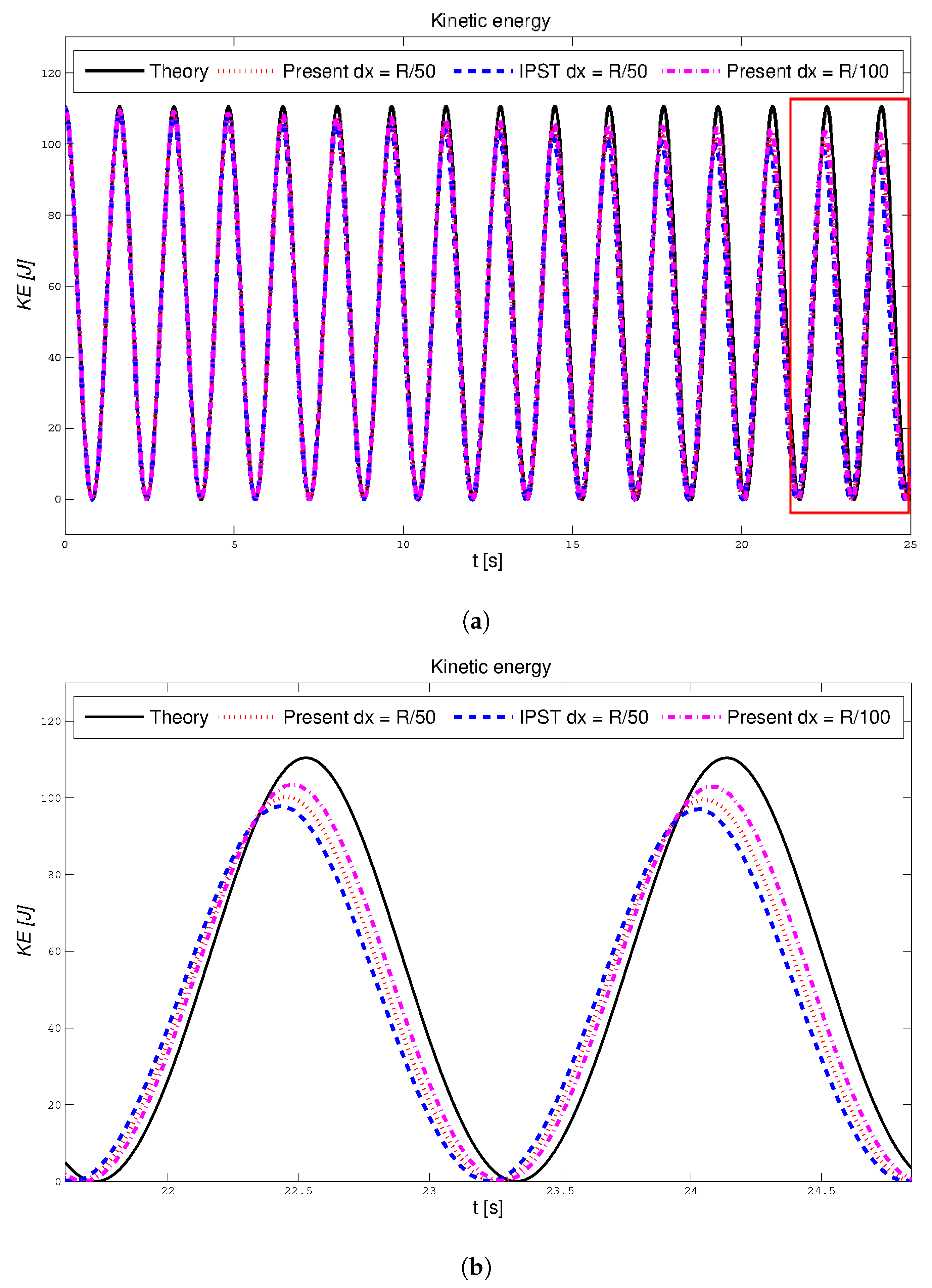
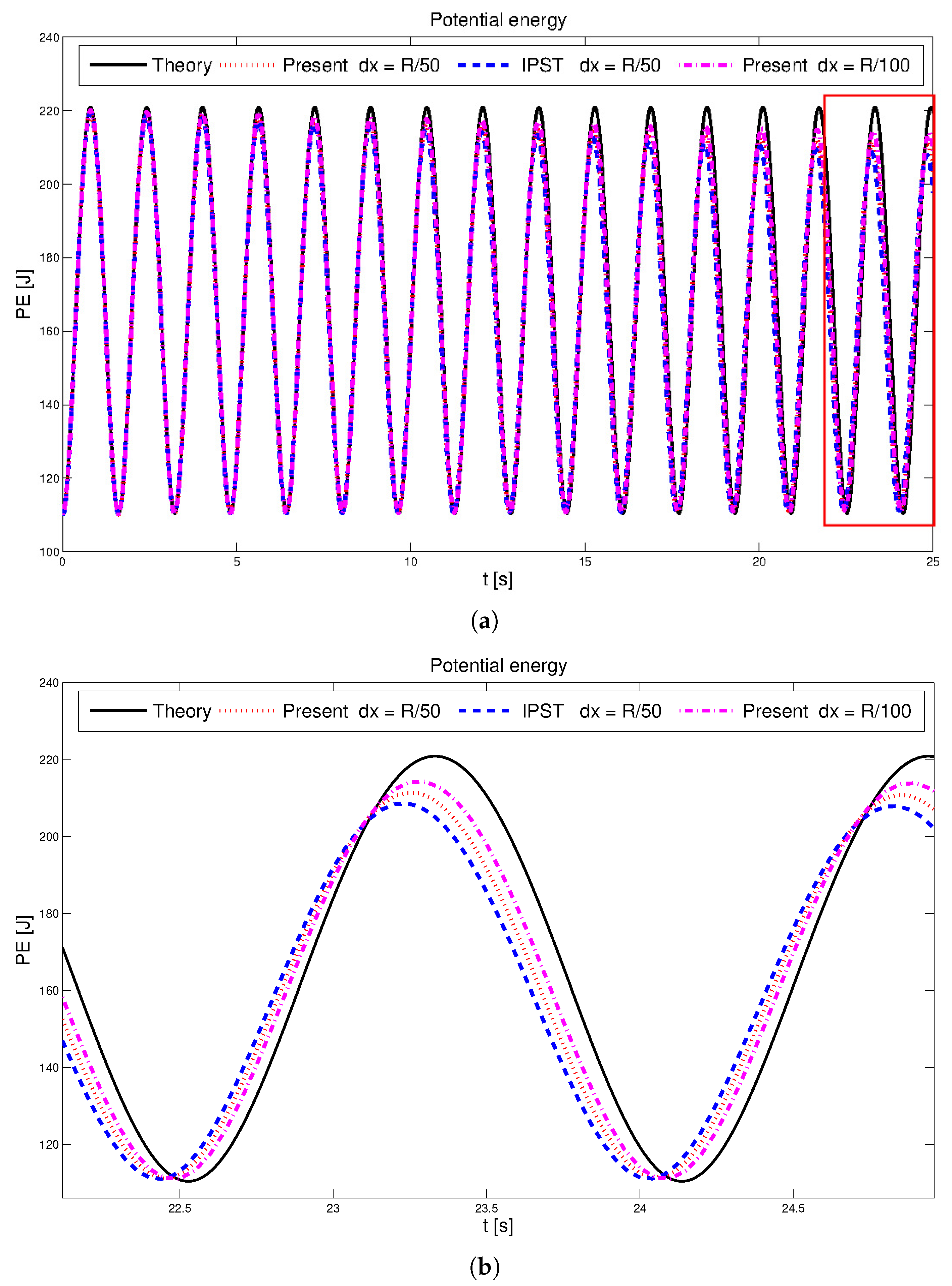

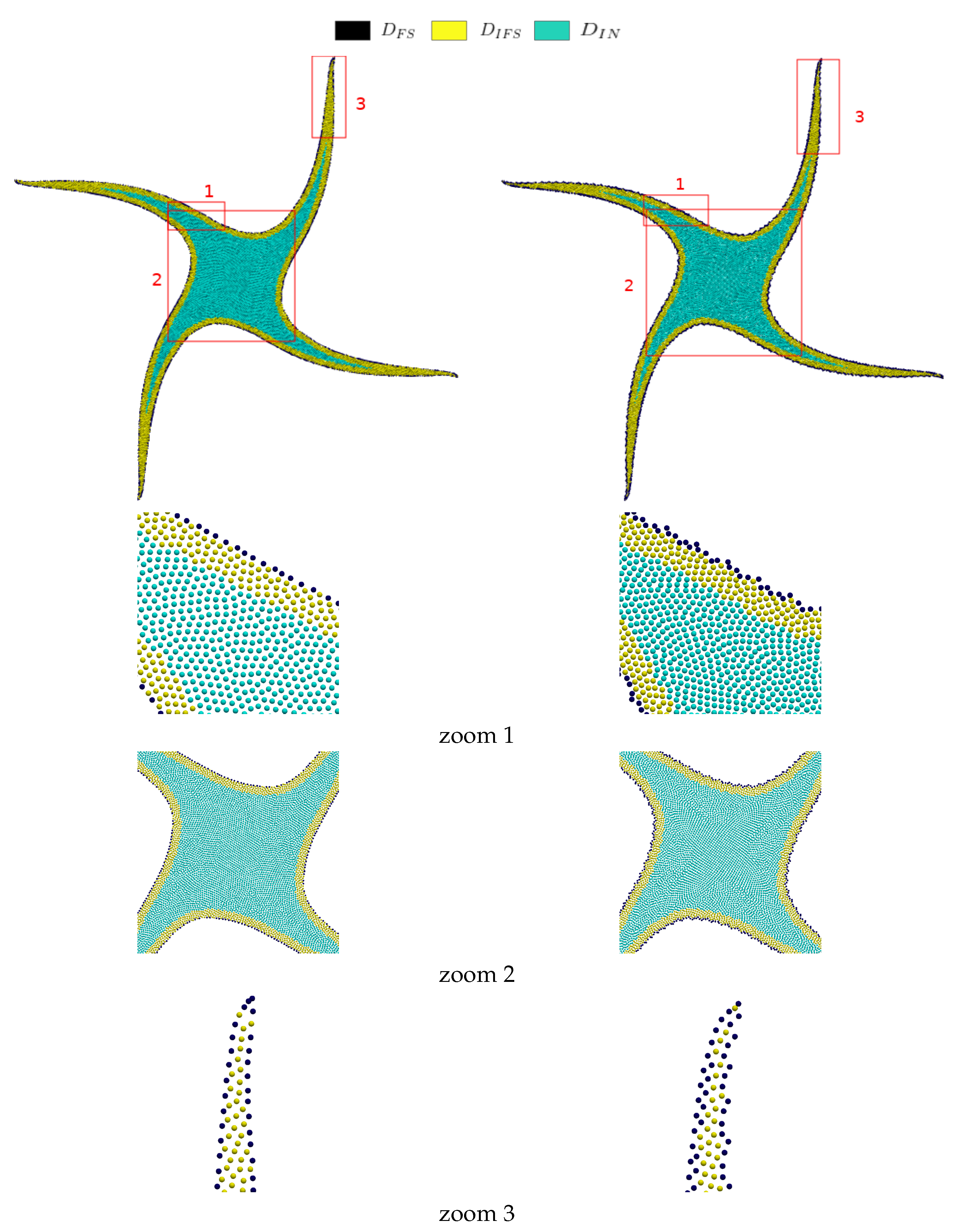
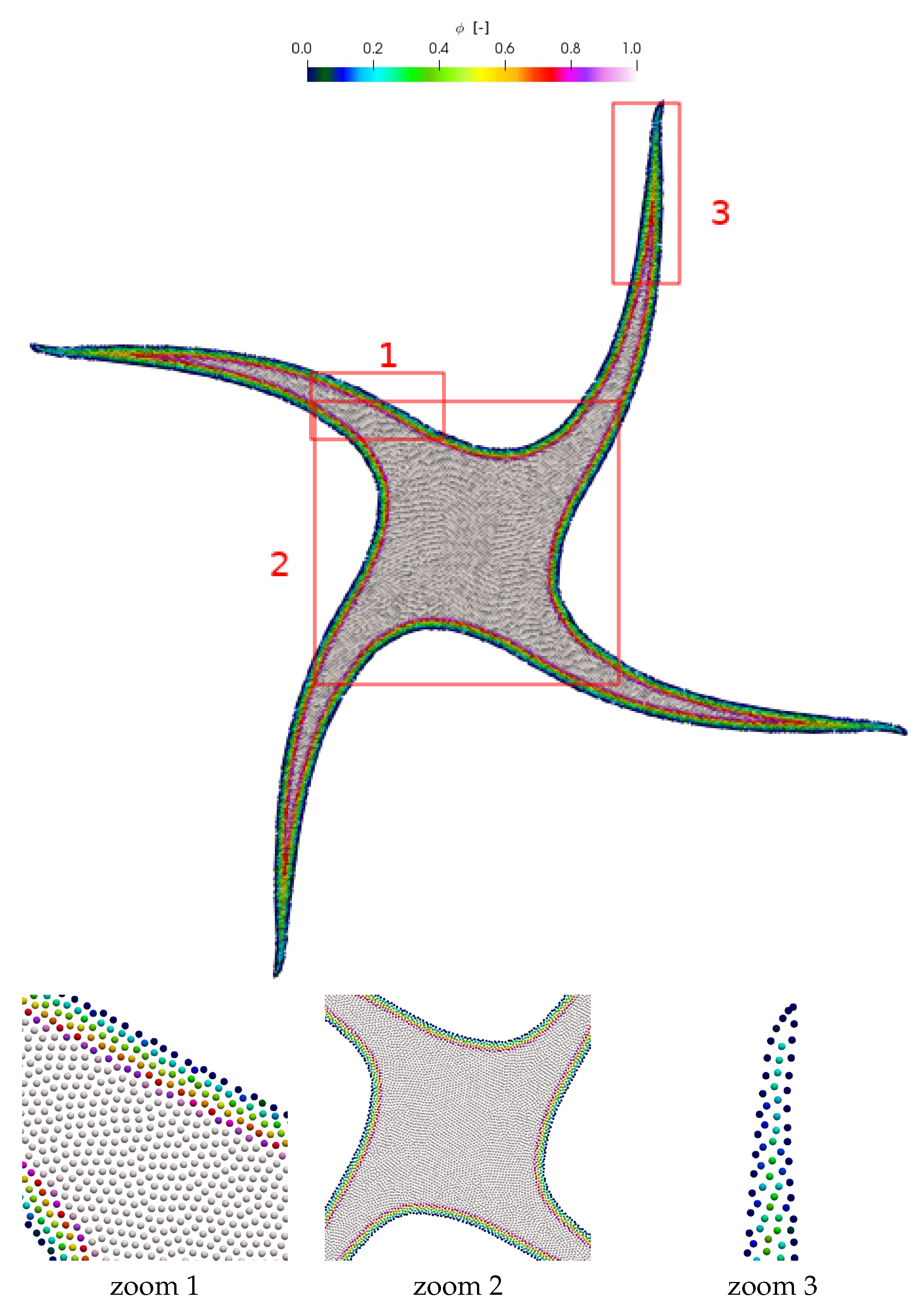
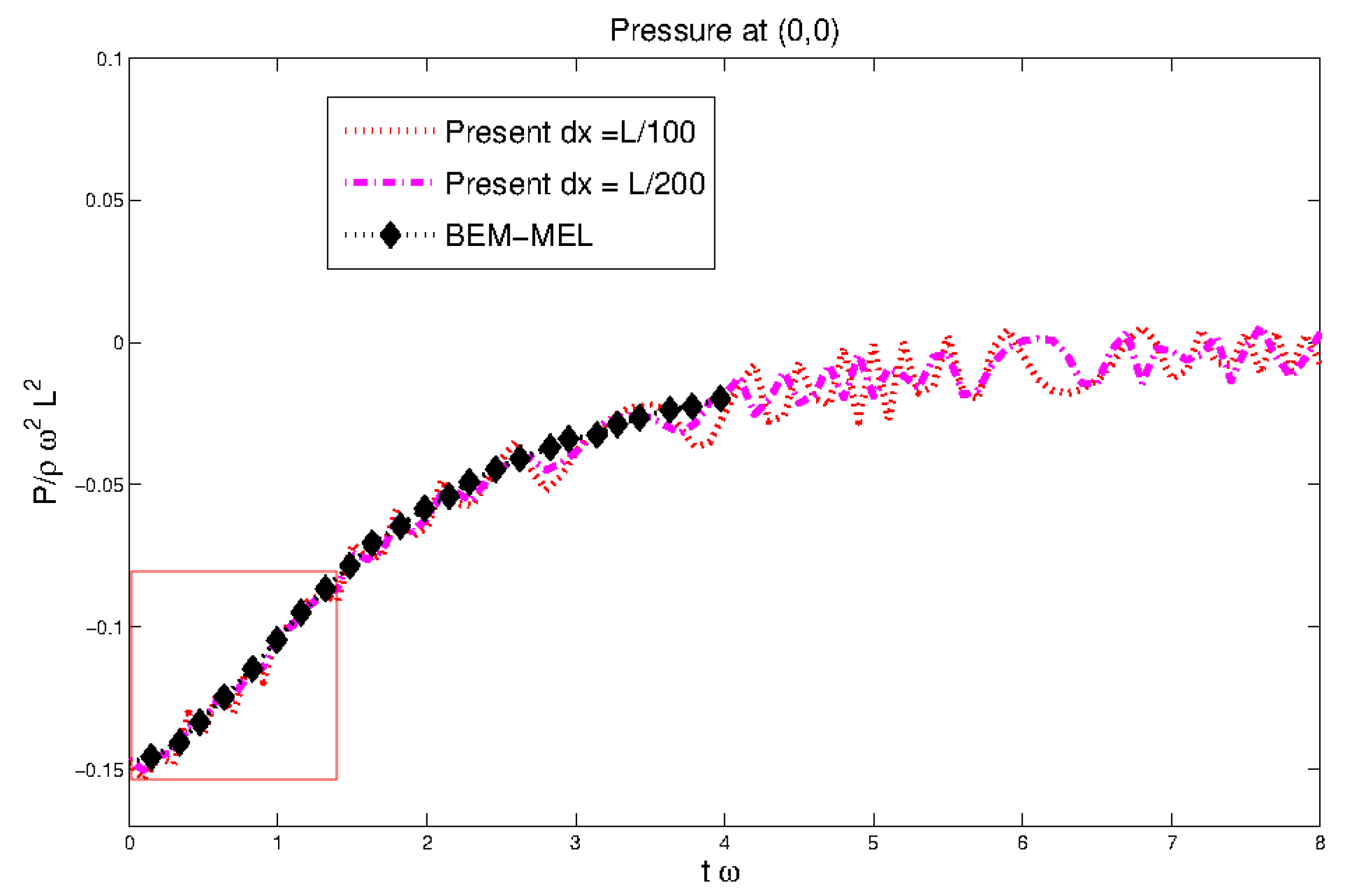

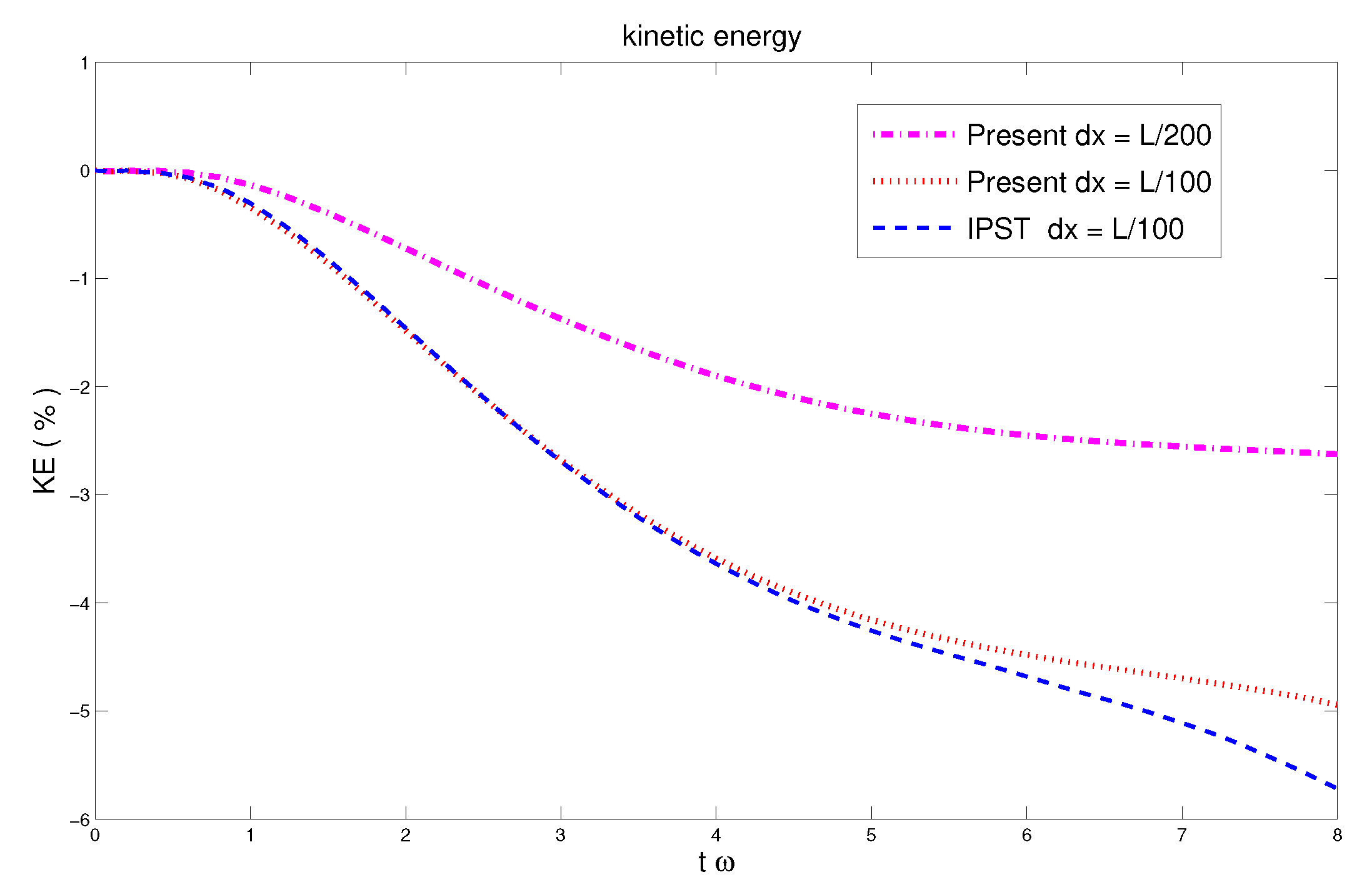
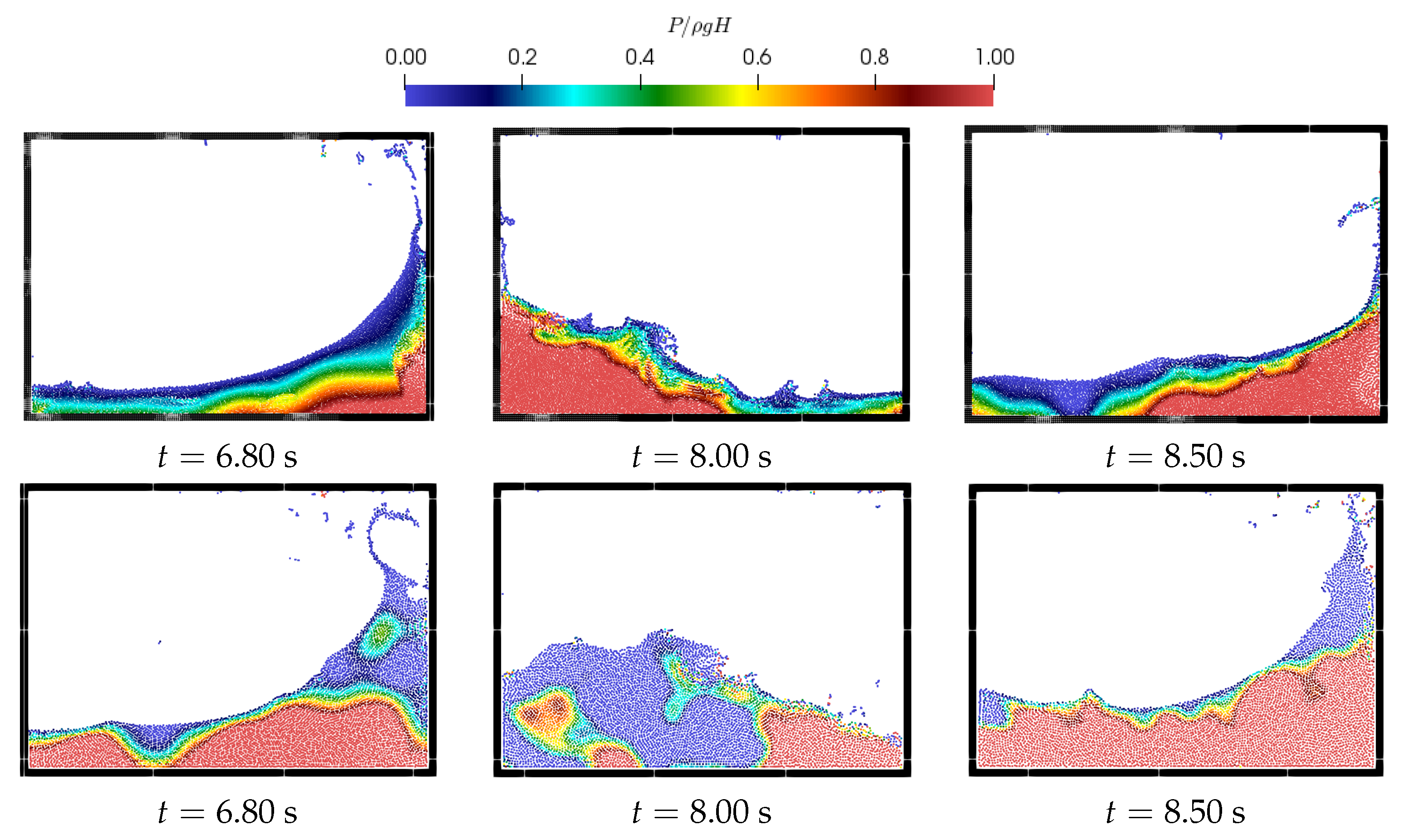
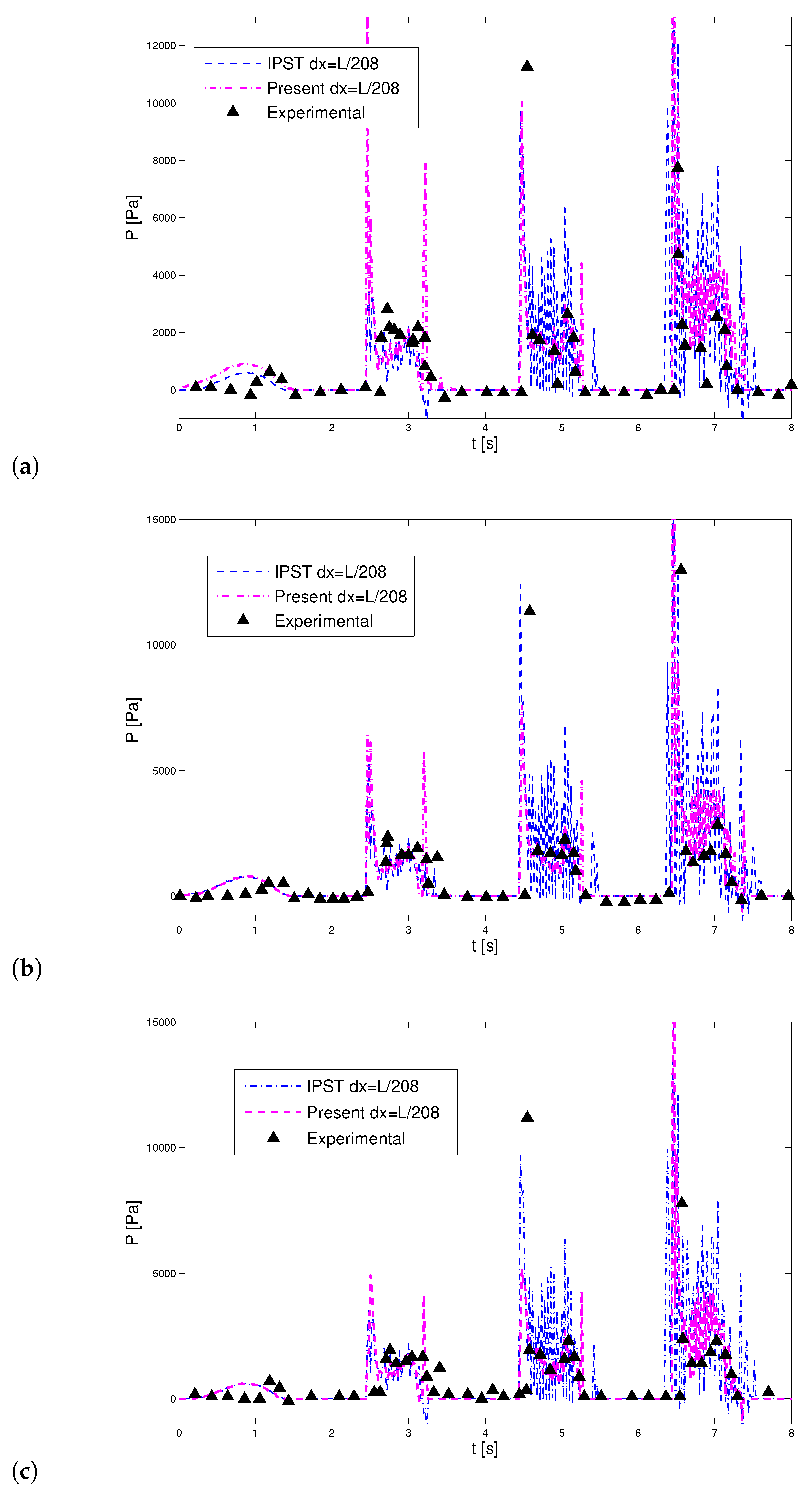
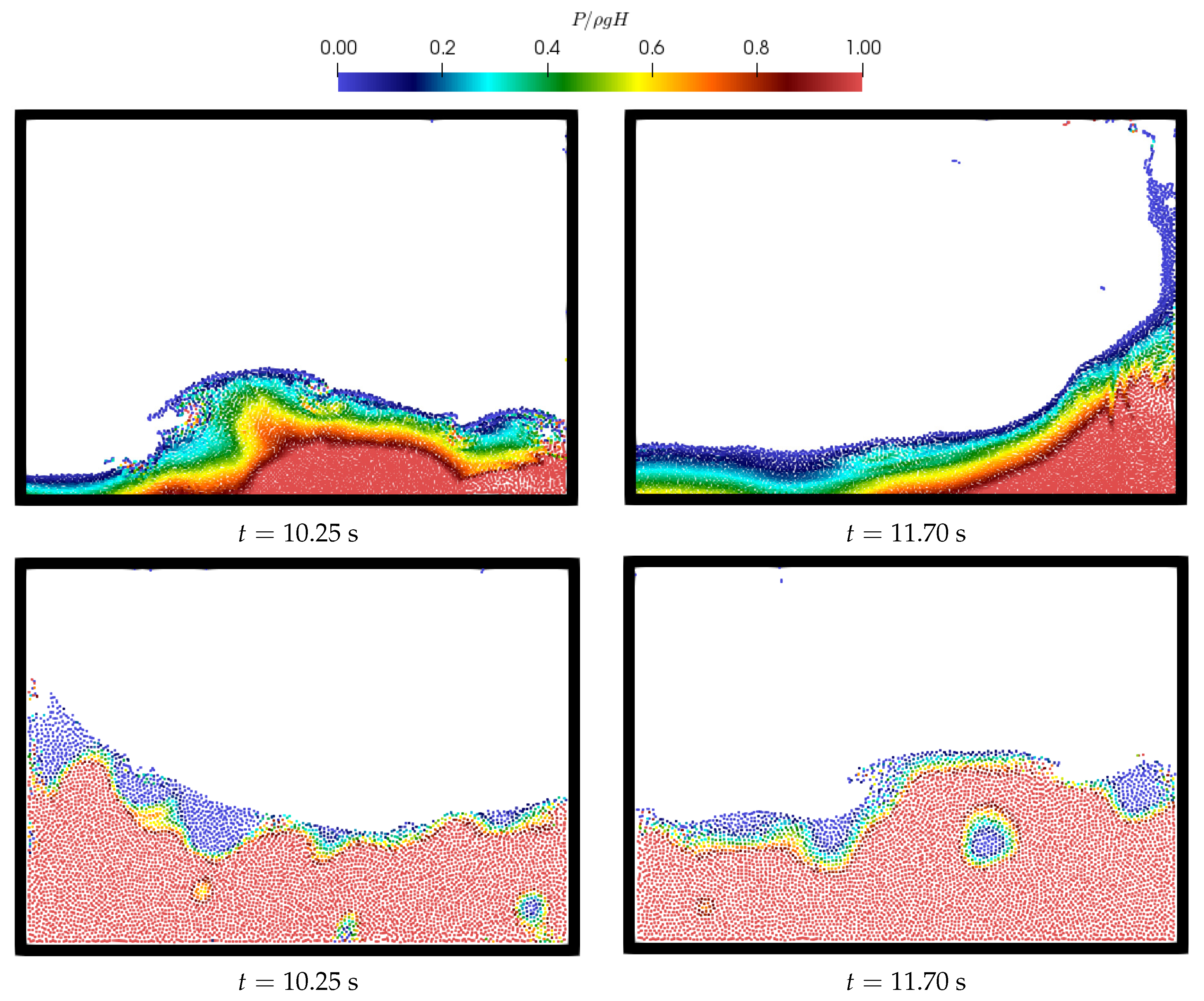
| Particle Shifting Model | Computational Time in s |
|---|---|
| Present particle shifting formulation | 6813 |
| IPST [37] | 6608 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krimi, A.; Jandaghian, M.; Shakibaeinia, A. A WCSPH Particle Shifting Strategy for Simulating Violent Free Surface Flows. Water 2020, 12, 3189. https://doi.org/10.3390/w12113189
Krimi A, Jandaghian M, Shakibaeinia A. A WCSPH Particle Shifting Strategy for Simulating Violent Free Surface Flows. Water. 2020; 12(11):3189. https://doi.org/10.3390/w12113189
Chicago/Turabian StyleKrimi, Abdelkader, Mojtaba Jandaghian, and Ahmad Shakibaeinia. 2020. "A WCSPH Particle Shifting Strategy for Simulating Violent Free Surface Flows" Water 12, no. 11: 3189. https://doi.org/10.3390/w12113189
APA StyleKrimi, A., Jandaghian, M., & Shakibaeinia, A. (2020). A WCSPH Particle Shifting Strategy for Simulating Violent Free Surface Flows. Water, 12(11), 3189. https://doi.org/10.3390/w12113189






