Impact of the Mean Daily Air Temperature Calculation on the Rainfall-Runoff Modelling
Abstract
1. Introduction
2. Data and Methods
2.1. Data and Study Area
2.2. Hydrological Modelling
2.3. Measurement Error of the Model Input Data
3. Results and Discussion
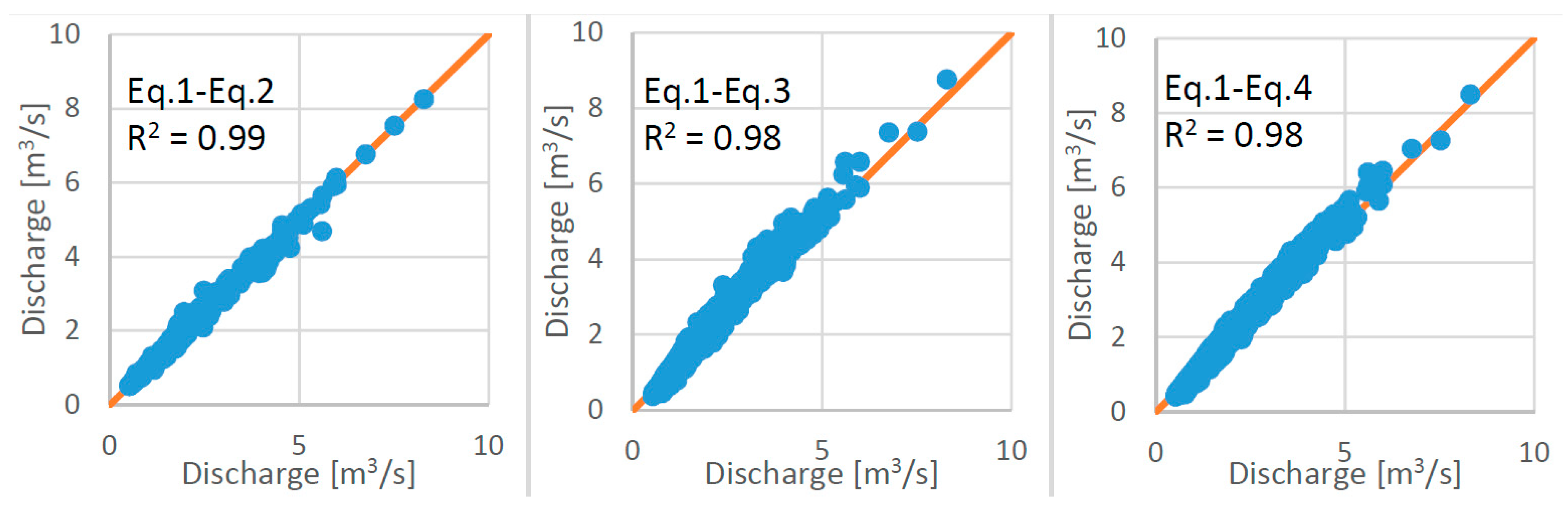
3.1. Mean Daily Air Temperature Calculation Using Multiple Equations
3.2. Impact of the Mean Daily Air Temperature on the Rainfall-Runoff Modelling Results
3.3. Impact of the Measurements Error on the Rainfall-Runoff Modelling Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Addor, N.; Melsen, L.A. Legacy, Rather Than Adequacy, Drives the Selection of Hydrological Models. Water Resour. Res. 2019, 55, 378–390. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Fowler, K.J.A.; Peel, M.C.; Woods, R.A. Modular Assessment of Rainfall-Runoff Models Toolbox (MARRMoT) v1.2: An open-source, extendable framework providing implementations of 46 conceptual hydrologic models as continuous state-space formulations. Geosci. Model Dev. 2019, 12, 2463–2480. [Google Scholar] [CrossRef]
- Bezak, N.; Šraj, M.; Rusjan, S.; Mikoš, M. Impact of the rainfall duration and temporal rainfall distribution defined using the Huff curves on the hydraulic flood modelling results. Geosciences 2018, 8, 69. [Google Scholar] [CrossRef]
- Valéry, A.; Andréassian, V.; Perrin, C. “As simple as possible but not simpler”: What is useful in a temperature-based snow-accounting routine? Part 2—Sensitivity analysis of the Cemaneige snow accounting routine on 380 catchments. J. Hydrol. 2014, 517, 1176–1187. [Google Scholar] [CrossRef]
- Sezen, C.; Bezak, N.; Šraj, M. Hydrological modelling of the karst Ljubljanica River catchment using lumped conceptual model. Acta Hydrotech. 2018, 31, 87–100. [Google Scholar] [CrossRef]
- Sezen, C.; Bezak, N.; Bai, Y.; Šraj, M. Hydrological modelling of karst catchment using lumped conceptual and data mining models. J. Hydrol. 2019, 576, 98–110. [Google Scholar] [CrossRef]
- Lavtar, K.; Bezak, N.; Šraj, M. Rainfall-runoff modeling of the nested non-homogeneous Sava River sub-catchments in Slovenia. Water 2020, 12, 128. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall-runoff model? Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall-runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Valéry, A.; Andréassian, V.; Perrin, C. “As simple as possible but not simpler”: What is useful in a temperature-based snow-accounting routine? Part 1—Comparison of six snow accounting routines on 380 catchments. J. Hydrol. 2014, 517, 1166–1175. [Google Scholar] [CrossRef]
- Ruelland, D. Should altitudinal gradients of temperature and precipitation inputs be inferred from key parameters in snow-hydrological models? Hydrol. Earth Syst. Sci. 2020, 24, 2609–2632. [Google Scholar] [CrossRef]
- Du, X.; Shrestha, N.K.; Ficklin, D.L.; Wang, J. Incorporation of the equilibrium temperature approach in a Soil and Water Assessment Tool hydroclimatological stream temperature model. Hydrol. Earth Syst. Sci. 2018, 22, 2343–2357. [Google Scholar] [CrossRef]
- Weiss, A.; Hays, C.J. Calculating daily mean air temperatures by different methods: Implications from a non-linear algorithm. Agric. For. Meteorol. 2005, 128, 57–65. [Google Scholar] [CrossRef]
- Bonacci, O.; Željković, I.; Trogrlić, R.Š.; Milković, J. Differences between true mean daily, monthly and annual air temperatures and air temperatures calculated with three equations: A case study from three Croatian stations. Theor. Appl. Climatol. 2013, 114, 271–279. [Google Scholar] [CrossRef]
- Ma, Y.; Guttorp, P. Estimating daily mean temperature from synoptic climate observations. Int. J. Climatol. 2013, 33, 1264–1269. [Google Scholar] [CrossRef]
- Sakellariou, N.K.; Kambezidis, H.D. Improving the estimation of the true mean monthly and true mean annual air temperatures in Greece. Atmos. Sci. Lett. 2016, 17, 13–18. [Google Scholar] [CrossRef][Green Version]
- Villarini, G.; Khouakhi, A.; Cunningham, E. On the impacts of computing daily temperatures as the average of the daily minimum and maximum temperatures. Atmos. Res. 2017, 198, 145–150. [Google Scholar] [CrossRef]
- Bonacci, O.; Roje-Bonacci, T. Analyses of the Zagreb Grič observatory air temperatures indices for the period 1881 to 2017. Acta Hydrotech. 2018, 31, 67–85. [Google Scholar] [CrossRef]
- Bonacci, O.; Željković, I. Differences between true mean temperatures and means calculated with four different approaches: A case study from three Croatian stations. Theor. Appl. Climatol. 2018, 131, 733–743. [Google Scholar] [CrossRef]
- Oudin, L.; Michel, C.; Anctil, F. Which potential evapotranspiration input for a lumped rainfall-runoff model? Part 1 - Can rainfall-runoff models effectively handle detailed potential evapotranspiration inputs? J. Hydrol. 2005, 303, 275–289. [Google Scholar] [CrossRef]
- Oudin, L.; Moulin, L.; Bendjoudi, H.; Ribstein, P. Estimating potential evapotranspiration without continuous daily data: Possible errors and impact on water balance simulations | Estimation de l’évapotranspiration potentielle sans données journalières régulières: Erreurs possibles et impact sur les simul. Hydrol. Sci. J. 2010, 55, 209–222. [Google Scholar] [CrossRef]
- Vaisala QMT103. Available online: http://www.inemet.com/pdf/sensores/qmt103.pdf (accessed on 10 July 2020).
- Dolšak, D.; Bezak, N.; Šraj, M. Temporal characteristics of rainfall events under three climate types in Slovenia. J. Hydrol. 2016, 541, 1395–1405. [Google Scholar] [CrossRef]
- Conner, G.; Foster, S. Searching for the daily mean temperature. In Proceedings of the 17th Conference on Applied Climatology, 88th Annual Meeting American Meteorological Society, Whistler, BC, Canada, 11 August 2008. [Google Scholar]
- National Oceanic and Atmospheric Administration U.S. Available online: https://www.ncdc.noaa.gov/wdcmet/data-access-search-viewer-tools/world-weather-records-wwr-clearinghouse (accessed on 10 July 2020).
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Coron, L.; Thirel, G.; Delaigue, O.; Perrin, C.; Andréassian, V. The suite of lumped GR hydrological models in an R package. Environ. Model. Softw. 2017, 94, 166–171. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Mathevet, T.; Andréassian, V. A downward structural sensitivity analysis of hydrological models to improve low-flow simulation. J. Hydrol. 2011, 411, 66–76. [Google Scholar] [CrossRef]
- Coron, L.; Perrin, C.; Delaigue, O.; Thirel, G.; Michel, C. airGR: Suite of GR Hydrological Models for Precipitation-Runoff Modelling 2018. Available online: https://cran.r-project.org/web/packages/airGR/index.html (accessed on 10 July 2020).
- Michel, C. Hydrologie Appliquée aux Petits Bassins Ruraux; Cemagref: Grenoble, France, 1991. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- WMO OTT Pluvio—Weighing Gauge. 2020. Available online: https://www.wmo.int/pages/prog/www/IMOP/publications/IOM-84_Lab_RI/IOM-84_DataSheets/WeighingGauge_Germany_OTTpluvio.pdf (accessed on 10 July 2020).
- Wauben, W. KNMI Contribution to the WMO Laboratory Intercomparison of Rainfall Intensity Gauges; KNMI: De Bilt, The Netherlands, 2006; Available online: http://bibliotheek.knmi.nl/knmipubTR/TR287.pdf (accessed on 10 July 2020).
- VEGA VEGAPULS 67. Available online: https://www.vega.com/en/products/product-catalog/level/radar/vegapuls-67 (accessed on 10 July 2020).
- OTT OTT PLS - Pressure Level Sensor. Available online: https://www.ott.com/products/water-level-1/ott-pls-pressure-level-sensor-959/ (accessed on 10 July 2020).
- Herschy, R. Hydrometry: Principles and Practice; Wiley: Hoboken, NJ, USA, 1999; ISBN 978-0-471-97350-8. [Google Scholar]
- Renard, B.; Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Gupta, A.; Govindaraju, R.S. Propagation of structural uncertainty in watershed hydrologic models. J. Hydrol. 2019, 575, 66–81. [Google Scholar] [CrossRef]
- Bai, Y.; Bezak, N.; Sapač, K.; Klun, M.; Zhang, J. Short-Term Streamflow Forecasting Using the Feature-Enhanced Regression Model. Water Resour. Manag. 2019, 33, 4783–4797. [Google Scholar] [CrossRef]
- Perrin, C.; Oudin, L.; Andreassian, V.; Rojas-Serna, C.; Michel, C.; Mathevet, T. Impact of limited streamflow data on the efficiency and the parameters of rainfall-runoff models. Hydrol. Sci. J. 2007, 52, 131–151. [Google Scholar] [CrossRef]
- Juston, J.; Seibert, J.; Johansson, P.-O. Temporal sampling strategies and uncertainty in calibrating a conceptual hydrological model for a small boreal catchment. Hydrol. Process. 2009, 23, 3093–3109. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Vidmar, A.; Brilly, M.; Sapač, K.; Kryžanowski, A. Efficient calibration of a conceptual hydrological model based on the enhanced Gauss-Levenberg-Marquardt procedure. Appl. Sci. 2020, 10, 3841. [Google Scholar] [CrossRef]
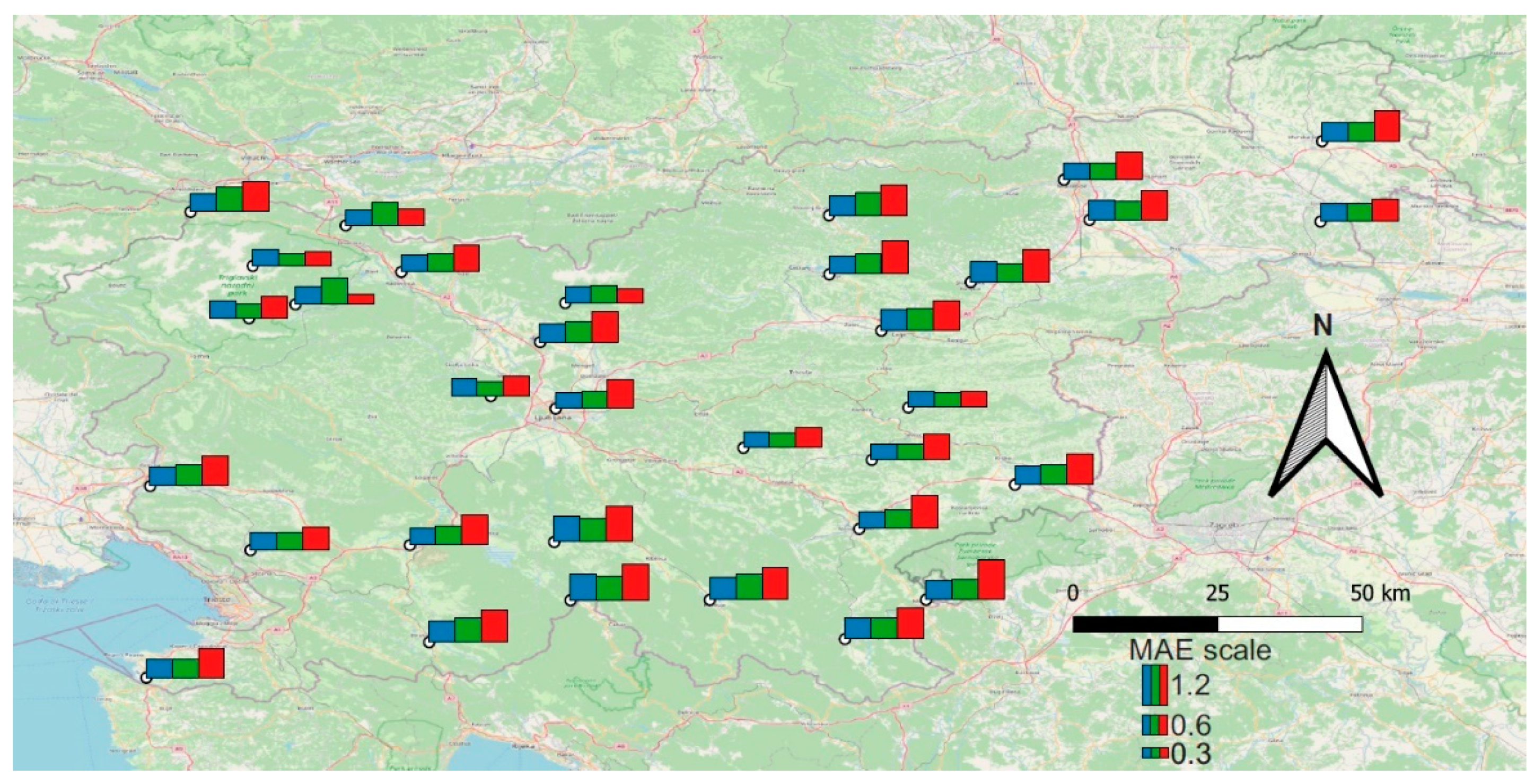
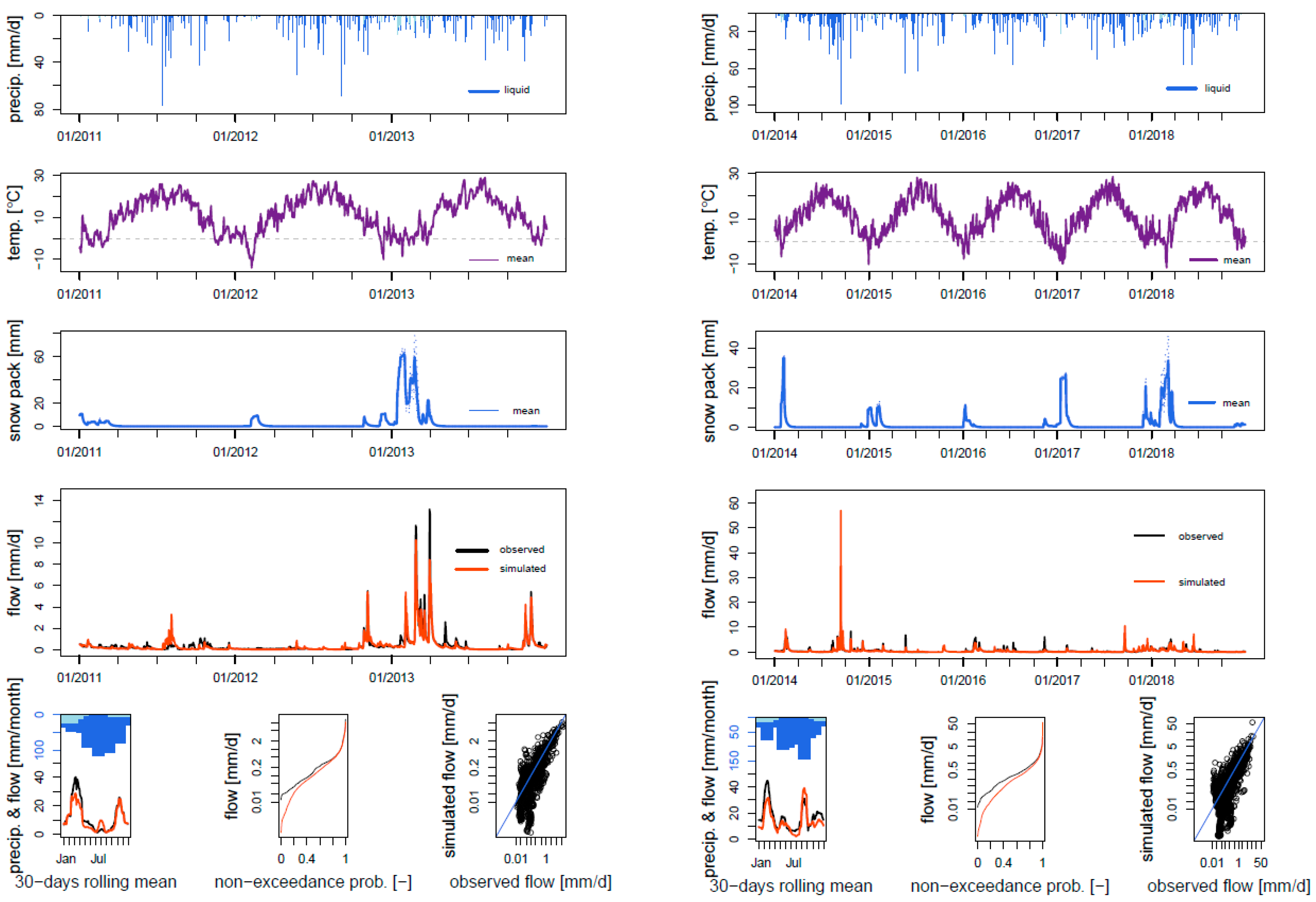

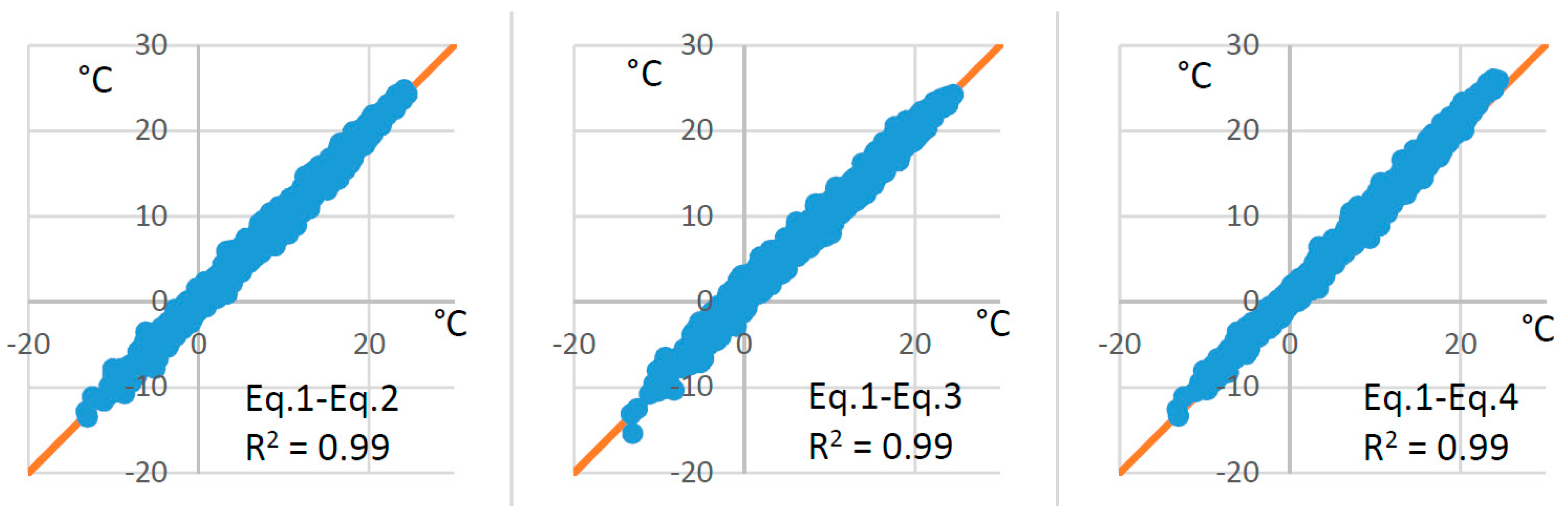
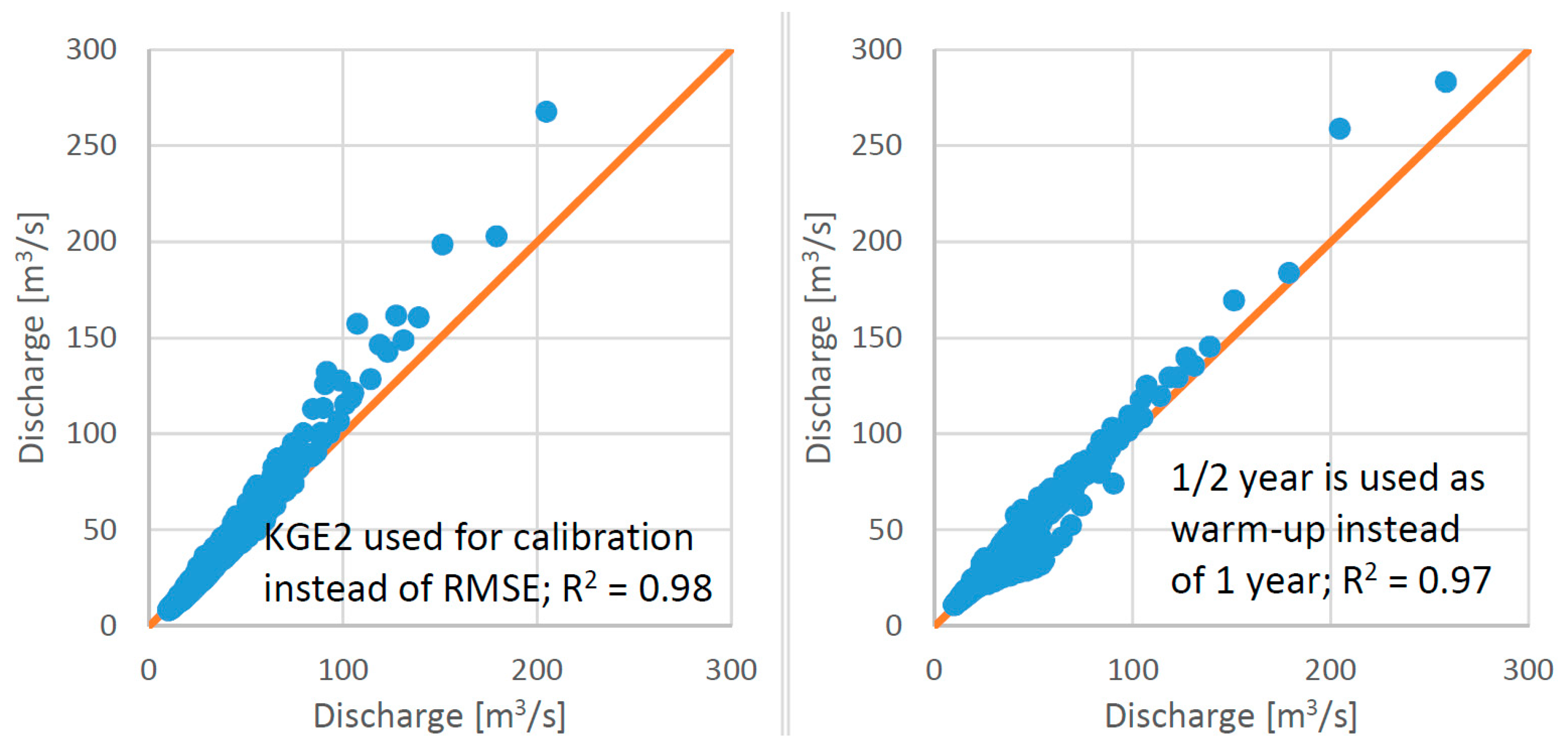
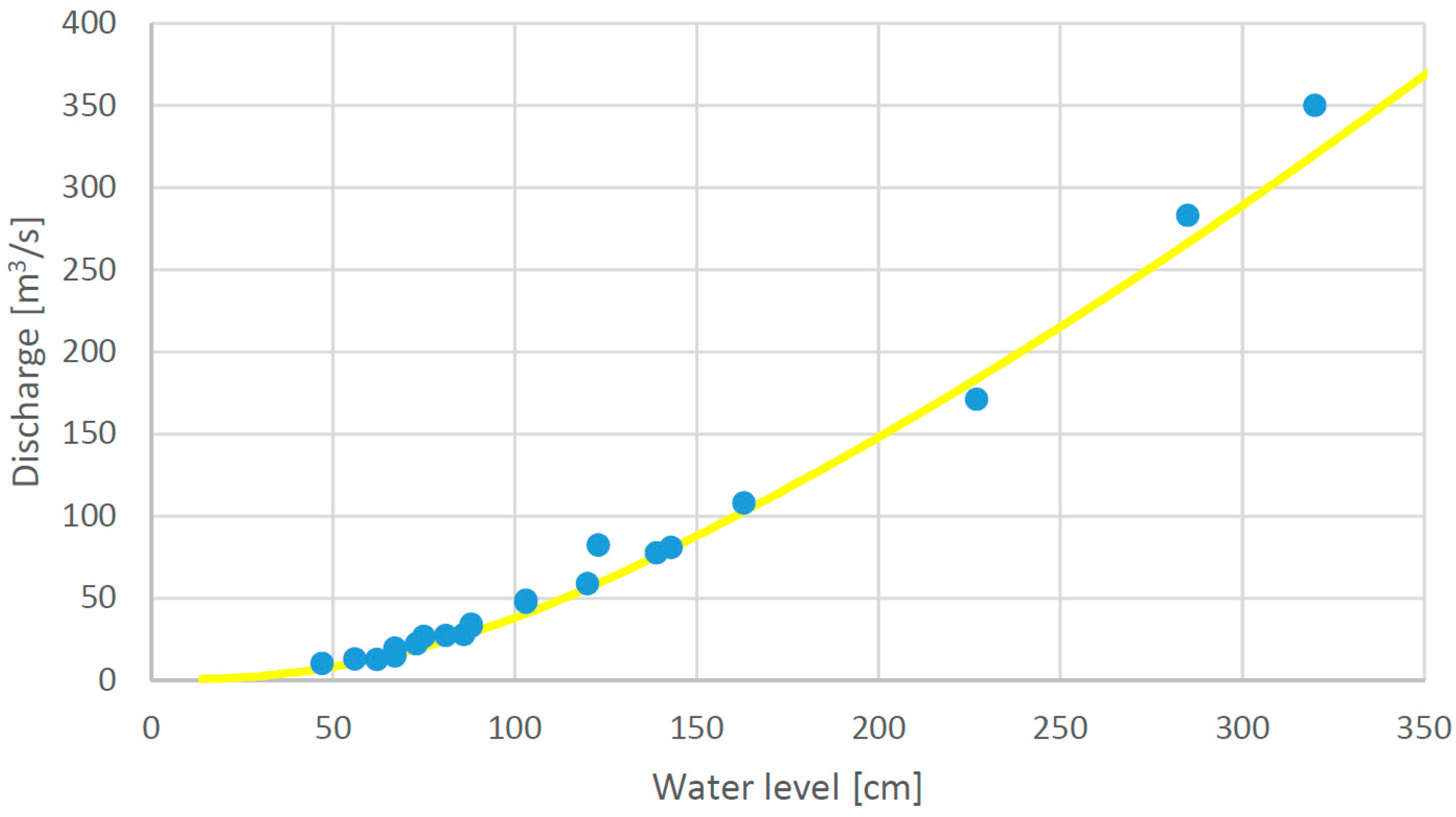
| River | Sava Dolinka | Sava Dolinka | Ledava | Nanoščica |
|---|---|---|---|---|
| Discharge gauging station | Kranjska Gora | Blejski most | Polana | Mali Otok |
| Catchment area (km2) | 40 | 509 | 209 | 51 |
| Mean discharge (m3/s) | 1.6 | 25.3 | 1.2 | 1.6 |
| Precipitation and air temperature station | Rateče | Rateče | Murska Sobota | Postojna |
| Station elevation | 864 m a.s.l. | 864 m a.s.l. | 187 m a.s.l. | 533 m a.s.l. |
| Mean annual precipitation (mm) | 1655 | 1655 | 841 | 1532 |
| Number of days with snow cover | 105 | 105 | 30 | 35 |
| Mean min., mean and max. air temperature (°C) | 2.5, 7.5, 13.7 | 2.5, 7.5, 13.7 | 6.3, 11.2, 16.8 | 5.5, 10.4, 15.7 |
| Station | Period | GR4J | GR6J | CemaNeige GR6J | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equation (1) | Equation (2) | Equation (3) | Equation (4) | Equation (1) | Equation (2) | Equation (3) | Equation (4) | Equation (1) | Equation (2) | Equation (3) | Equation (4) | ||
| Kranjska Gora | Calibration | 1.76 | 1.76 | 1.76 | 1.76 | 1.76 | 1.76 | 1.76 | 1.77 | 1.52 | 1.52 | 1.48 | 1.49 |
| Validation | 1.67 | 1.66 | 1.64 | 1.67 | 1.66 | 1.64 | 1.66 | 1.67 | 1.08 | 1.08 | 1.14 | 1.18 | |
| Polana | Calibration | 0.69 | 0.69 | 0.69 | 0.68 | 0.64 | 0.64 | 0.64 | 0.64 | 0.46 | 0.46 | 0.48 | 0.48 |
| Validation | 1.09 | 1.09 | 1.09 | 1.07 | 1.35 | 1.32 | 1.34 | 1.29 | 1.26 | 1.22 | 1.24 | 1.20 | |
| Mali otok | Calibration | 2.52 | 2.52 | 2.52 | 2.52 | 2.51 | 2.51 | 2.50 | 2.50 | 2.35 | 2.41 | 2.32 | 2.39 |
| Validation | 2.55 | 2.55 | 2.55 | 2.56 | 2.54 | 2.54 | 2.55 | 2.55 | 2.58 | 2.58 | 2.60 | 2.59 | |
| Blejski most | Calibration | 2.08 | 2.08 | 2.08 | 2.08 | 2.00 | 2.00 | 2.00 | 2.00 | 1.76 | 1.80 | 1.71 | 1.77 |
| Validation | 2.60 | 2.60 | 2.60 | 2.60 | 2.46 | 2.45 | 2.46 | 2.49 | 1.76 | 1.80 | 1.73 | 1.76 | |
| Model | Statistics | T | T, P | T, P, Q | T, P, Q, RC |
|---|---|---|---|---|---|
| GR4J | Mean | ~0% | <1% | <1% | 3% |
| Maximum | ~0% | 1% | 1% | 14% | |
| CemaNeige GR6J | Mean | ~0% | <1% | <1% | 2% |
| Maximum | ~0% | 1% | 1% | 13% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bezak, N.; Cerović, L.; Šraj, M. Impact of the Mean Daily Air Temperature Calculation on the Rainfall-Runoff Modelling. Water 2020, 12, 3175. https://doi.org/10.3390/w12113175
Bezak N, Cerović L, Šraj M. Impact of the Mean Daily Air Temperature Calculation on the Rainfall-Runoff Modelling. Water. 2020; 12(11):3175. https://doi.org/10.3390/w12113175
Chicago/Turabian StyleBezak, Nejc, Lazar Cerović, and Mojca Šraj. 2020. "Impact of the Mean Daily Air Temperature Calculation on the Rainfall-Runoff Modelling" Water 12, no. 11: 3175. https://doi.org/10.3390/w12113175
APA StyleBezak, N., Cerović, L., & Šraj, M. (2020). Impact of the Mean Daily Air Temperature Calculation on the Rainfall-Runoff Modelling. Water, 12(11), 3175. https://doi.org/10.3390/w12113175







