1. Introduction
Rainfall interception is recognized at present as one of the most underrated and underpriced processes in forest hydrology. In places where floor litter has developed on a near-ground surface, rainfall that falls on forest cover is intercepted by the litter layer and subsequently evaporates back into the atmosphere [
1,
2,
3]. This retention and redistribution process profoundly influences the water budget of forest areas, altering the amount of water available to percolate into the uppermost layer of forest soils [
4,
5,
6]. Compared to tree canopy interception, floor litter interception has received less attention because it is often regarded as a minor component of the water cycle [
7]. Forest litter refers to recently fallen and partially decomposed tree leaves, twigs, and small branches, distinct from humus, resting on the upper surface of soils [
8]. It forms a porous barrier that retains a small portion of the incident rainfall.
Researchers have been investigating floor litter interception since the middle of the 20th century; however, only recently has it received a significant amount of research attention [
2,
3]. Taking accurate measurements of litter interception capacity is challenging [
3,
7]. Field experiments can provide a reliable estimation of the interception loss but are inaccurate in their estimation of the interception capacity over time and space [
9,
10,
11,
12,
13]. Thus, laboratory experiments are often employed to assess litter interception loss [
4,
7,
14,
15,
16,
17,
18,
19]. Regardless of the approach, water intercepted by floor litter is of similar magnitude or sometimes higher than that intercepted by the canopy. A wide range of litter interception loss has been observed in previous studies, ranging from 1–2% to 50–70% of gross rainfall [
2,
3,
10,
14,
20,
21], although inconsistencies in measurement exist. The reason for these inconsistencies can be attributed to the variation in the litter type, litter thickness, and rainfall characteristics [
4,
7,
11,
15,
18,
19,
20,
21].
Floor litter is highly heterogeneous in terms of its physical structure and its accumulation is not evenly distributed over the soil surface. Furthermore, the interception capacity of floor litter can vary across tree species and depends entirely on the litter’s physiological and morphological characteristics [
22]. Broadleaf litter is generally large and curved in shape and thus can easily capture rainwater, while needle-leaf litter is well compacted and can block flow paths that run through the litter [
7,
19]. Broadleaf litter individually stores more water than needle litter during storm periods [
4,
7,
14]. In contrast, the loosely packed, flat litter layer in deciduous species intercepts less water than the clumped, needle litter accumulation in coniferous species [
16,
19]. The absolute amount of water retained is likely to depend on the thickness of the accumulated litter, where a thicker litter layer retains more water [
10,
15,
18].
Water retention is not only affected by the inherent nature of litter but also by rainfall characteristics, which influence the water storage capacity of floor litter. Although the amount of water stored is proportional to rainfall intensity, litter storage capacity shows a poor relationship with rainfall intensity [
16,
23]. This inverse relationship exists because more water is needed to saturate the deeper litter accumulation thoroughly [
10,
24]. Therefore, floor litter can retain a smaller rainfall percentage during a short, intense storm event than in a long, less intense event [
25,
26]. Li et al. [
25] and others [
17] found that the effects of rainfall intensity on interception capacity are not apparent, and no linear relationship exists across litter types.
The influence of rainfall on the extent of interception capacity has not yet been revealed as raindrop size, intensity, and the pattern of natural rainfall vary in space and time. Although research on litter interception is limited, several studies have attempted to quantify it under natural or artificial rainfall events. The variance and inhomogeneity of natural rainfall make it difficult to identify the fingerprint of rainfall on litter interception storage under in situ experiments [
25,
26,
27]. Over the past few decades, rainfall simulation experiments have been used in numerous hydrologic studies to quantitatively demonstrate the influence of rainfall characteristics on experimental variables [
4,
14,
23]. Using simulated rainfall enables a greater control of the rainfall variables and simplifies data collection during the experiment.
Although the interception capacity of rainfall by floor litter has been widely investigated, studies on the precise nature of hydrologic processes occurring in the litter layer during rainfall have not been conducted. Furthermore, the effects of litter and rainfall characteristics on water retention and drainage have not been adequately examined. In this regard, the present study conducts a laboratory investigation of retention and drainage processes as to whether or not the physical features of litter and rainfall characteristics would affect the hydrologic function of litter. The primary aim of the experiment is to quantitatively estimate the rainfall interception storage of various litter types under controlled conditions of rainfall and litter. The secondary aim is to examine the hydrologic processes of the litter layer over the short period of time by relating the retention and drainage processes to the litter’s physical traits and the rainfall characteristics.
2. Materials and Methods
2.1. Litter Collection and Characterization
Two contrasting types of litter were used in this study: needle-leaf litter and broadleaf litter. All litter samples were collected at Mt. Gwanak, which is approximately 1500 ha and is managed by the College of Agriculture and Life Sciences, Seoul National University. This forest is located in the southern part of Seoul in Korea and is at a height of 632 m a.s.l., consisting of young-growth and mixed-coniferous type stands. Its topography is relatively steep, and the dominant soil type is sandy loam.
Undecomposed litter was taken from six different sites: three litter samples beneath coniferous trees, and three beneath deciduous trees. Coniferous tree species included Abies holophylla Maxim., Pinus strobus, Pinus rigida Mill., while Quercus acutissima Carruth., Quercus variabilis Blume, and Sorbus alnifolia (Siebold & Zucc.) C. Koch represented broadleaf litter. Fallen leaves from the current year were manually collected from the ground surface beneath the mature trees. We also removed leaves with obvious symptoms of pathogen or herbivore attack. Most of the litter samples were collected in the period of October to November 2016, while some needle litter samples were supplemented in April 2017. All the collected litter samples were placed in sealed plastic bags and immediately transported to the laboratory for analysis.
The morphological characteristics of litter may vary with tree species. Apparent features, such as length and diameter, of the needle-leaf litter were measured manually and the measurements were repeated for 200 needles for each species, thereby accounting for the natural variations in its physical shape. The measurements were performed using a digital caliper and rounded to the nearest 0.1 mm. The needle’s all-side surface area and volume were estimated from the litter length and diameter, under the assumption that the pine-type needle has a cylindrical form with the terminal area neglected [
4]. The projected areas of 50 randomly selected broadleaf litters were measured with an LI-3000C leaf-area meter (LiCOR Inc., Lincoln, NE, USA) and used to determine the total surface area of individual litter. The leaf volume of the broadleaf litter was estimated by multiplying the surface area of the individual litter by its thickness. Leaf thickness was averaged from five measurement points that were randomly made with a digital caliper.
Because of the wide variation in the leaf morphology between tree species, this study used two reliable parameters, specific surface area (SSA) and surface-area-to-volume ratio (SAV), to distinguish the physical properties of the litter. A finite amount of water adheres to the litter surface as a result of surface tension. Therefore, SSA has been used extensively to examine the influences of litter traits on rainfall retention [
3,
28]. SSA is a geometric estimator representing the total surface area per unit mass of litter, thereby indicating the extent to which the litter surface interacts with its surroundings. The litter was dried in laboratory at nearly 23 °C temperature, 40% relative humidity for at least seven days and then weighed to determine its dry mass. SAV is a crucial litter parameter that best describes litter geometry and its relative dimensions. It refers to the ratio between the surface area and its volume [
29]. The SAV value of individual litter can be determined by separate measurements of the surface area and volume. Large SAVs increase the rates of energy and mass exchange in the gaseous phase, implying that litter can quickly become wet or dry in response to changes in the surrounding conditions.
2.2. Rainfall Simulation Experiment
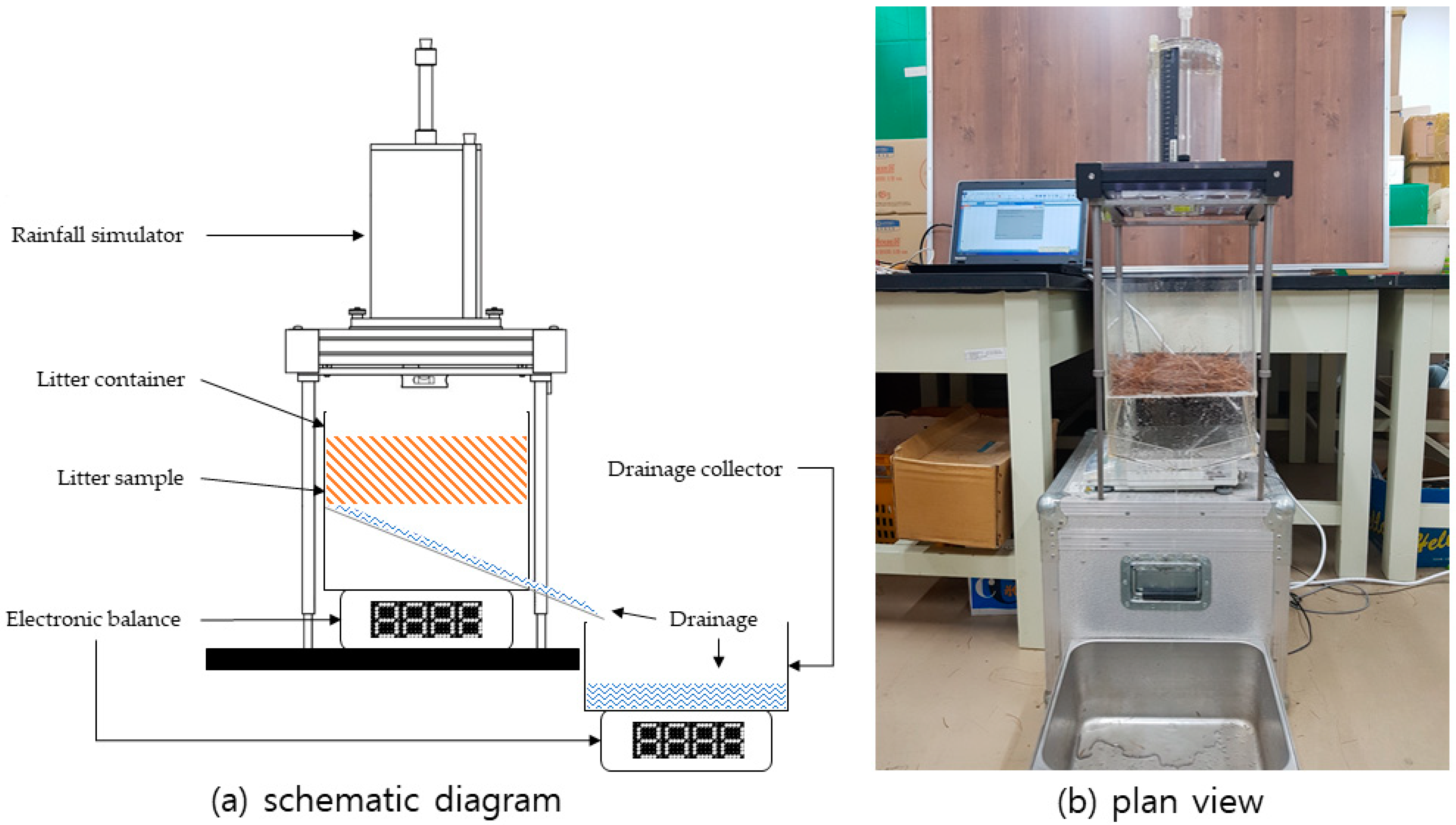
A rainfall simulation experiment was conducted to quantitatively demonstrate the effects of rainfall characteristics on litter interception storage. The experimental apparatus consisted of a portable rainfall simulator, a litter container, a drainage collector, and electronic balances (
Figure 1).
A portable rainfall simulator with a 0.25 m × 0.25 m sprinkling area (Eijkelkamp
®, Giesbeek, Netherlands) supplied simulated rainfall of assigned rainfall intensity and duration. The rainfall simulation pours water droplets with a mass of 0.106 g and a diameter of 5.9 mm, which is similar to the canopy drip of throughfall [
30].
Litter mass influences water storage and drainage [
14,
25]. Kang et al. [
31] observed a litter accumulation of 944 ± 512 g/m
2 in a deciduous forest in Korea, which is similar to a previous study [
15]. Therefore, a weight of 60 g (on average 960 g/m
2) of litter was used in the rainfall simulation experiments. Litter was placed in a 0.25 m × 0.25 m rectangular container beneath the portable simulator. The thickness of the litter layer varied with the density and consolidation of the layer.
Water moved along the macropore channels in the litter layer during the experiment. Assuming that floor litters are hygroscopic, the distribution of pore space influences the vertical or lateral movement of water. Therefore, porosity was calculated to enable a direct comparison with the extent of pore space in the litter layer [
32]:
where
is the litter layer’s porosity,
is the weight of the litter layer,
is the total volume of the litter layer, and
is litter density.
The litter container was placed on a CUX-4200H electronic balance (CAS®, Yangju, Korea), connected to a personal computer by a communication cable. When the rain began, the weight of the container was continuously recorded every 5 s. Part of the incident rainfall percolated through the pore channel of litter and consequently reached the drainage collector. The drainage rate was also measured at 5 s intervals from the drainage collector on the CUX-4200H electronic balance. Varying intensities of 50, 75, and 100 mm/h were designated as rainfall intensity parameters, and the rainfall simulator was operated at these intensities for 10, 20, 30, and 40 min. An intensity of 100 mm/h is approximately equivalent to a 100-year, 1-h design storm event in the Seoul region. The rainfall simulation experiment was repeated five times for each litter type under specified rainfall conditions. In total, 180 experiments were conducted in this study.
2.3. Interception Storage Measurement
Interception storage capacity is a predictive variable that quantitatively represents the retention ability of floor litter. It can be defined as the depth of water stored or retained on the litter surface and within the macropores of the litter layer [
27]. There are two types of interception storage [
15]. The maximum interception storage capacity (
is the amount of rainwater retained by litter temporarily before the rain stops. It represents the water stored by litter that can flow down to the uppermost soil layer and is therefore essential for understanding the soil water relationship. The minimum interception storage capacity (
) refers to the thin film of detained water held on the litter surface that is removed by evaporation only.
is a more crucial hydrological parameter than
because it indicates the ultimate retention capacity of floor litter [
14,
23].
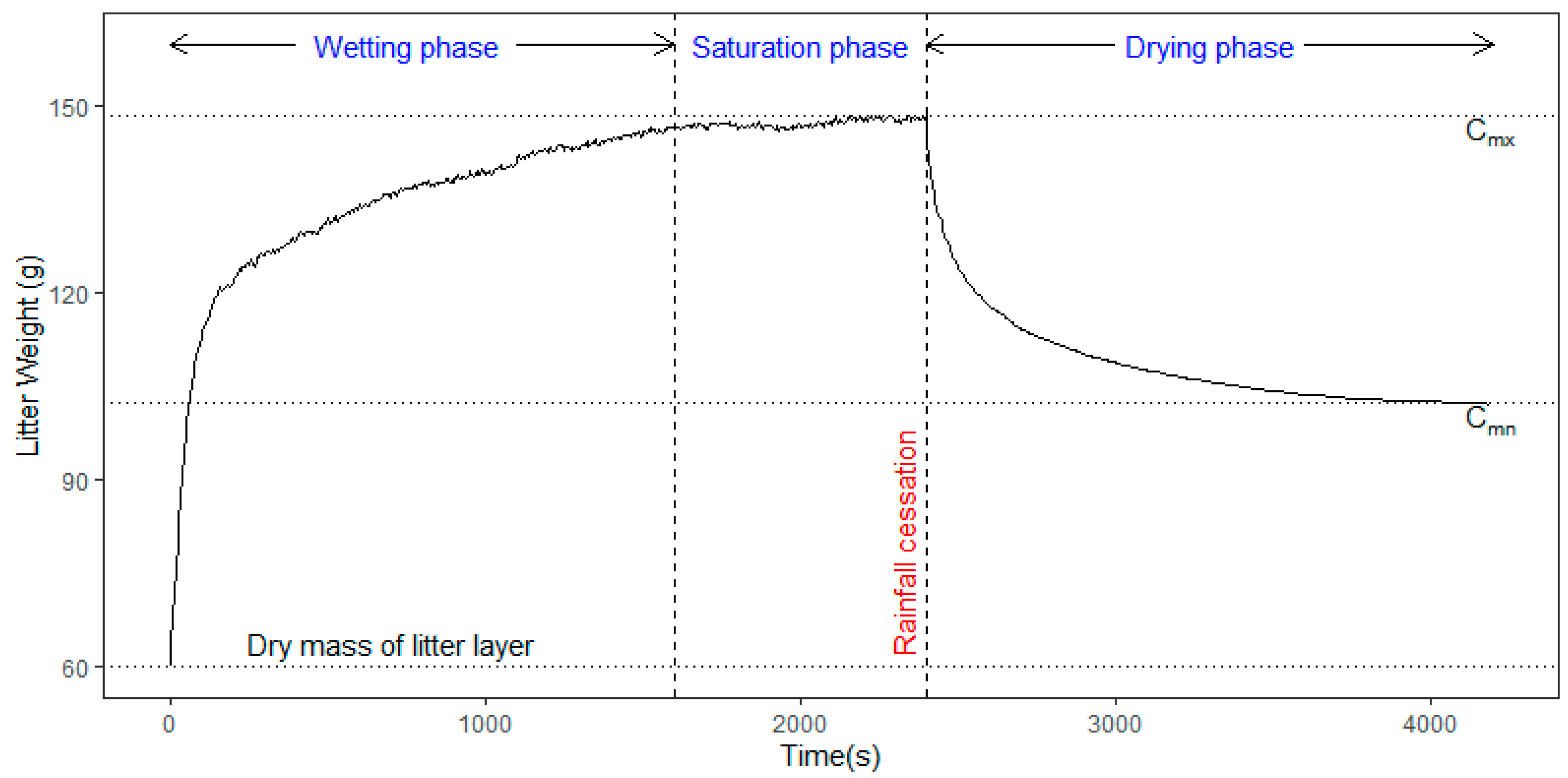
Through rainfall simulation experiments, the above-mentioned two storages were determined from the litter weight curve.
was experimentally obtained as the amount of detained water at an asymptotic stable line during rainfall and
was determined to be the water stored at the completion of post-rainfall drainage, as shown in
Figure 2.
2.4. Litter Drainage Estimation
Water retention and drainage processes occurring in the litter layer displayed three phases in terms of the timing and flux of water: wetting, saturation, and drying. As shown in
Figure 2, the amount of retained water increased rapidly during the wetting phase. This phase usually took place during the first stages of the rain over a short time. As the rain continued for a certain period, the water retained on the litter plateaued and reached the saturation phase. The saturation phase was relatively stable because the litter was too wet to retain more water and, consequently, excess water drained into the collector. When the rain stopped, a gravitational flow was produced in the pores until the surface tension and gravitation force established an equilibrium. During the drying phase, the drainage rate tended to decrease exponentially, similar to the infiltration curve.
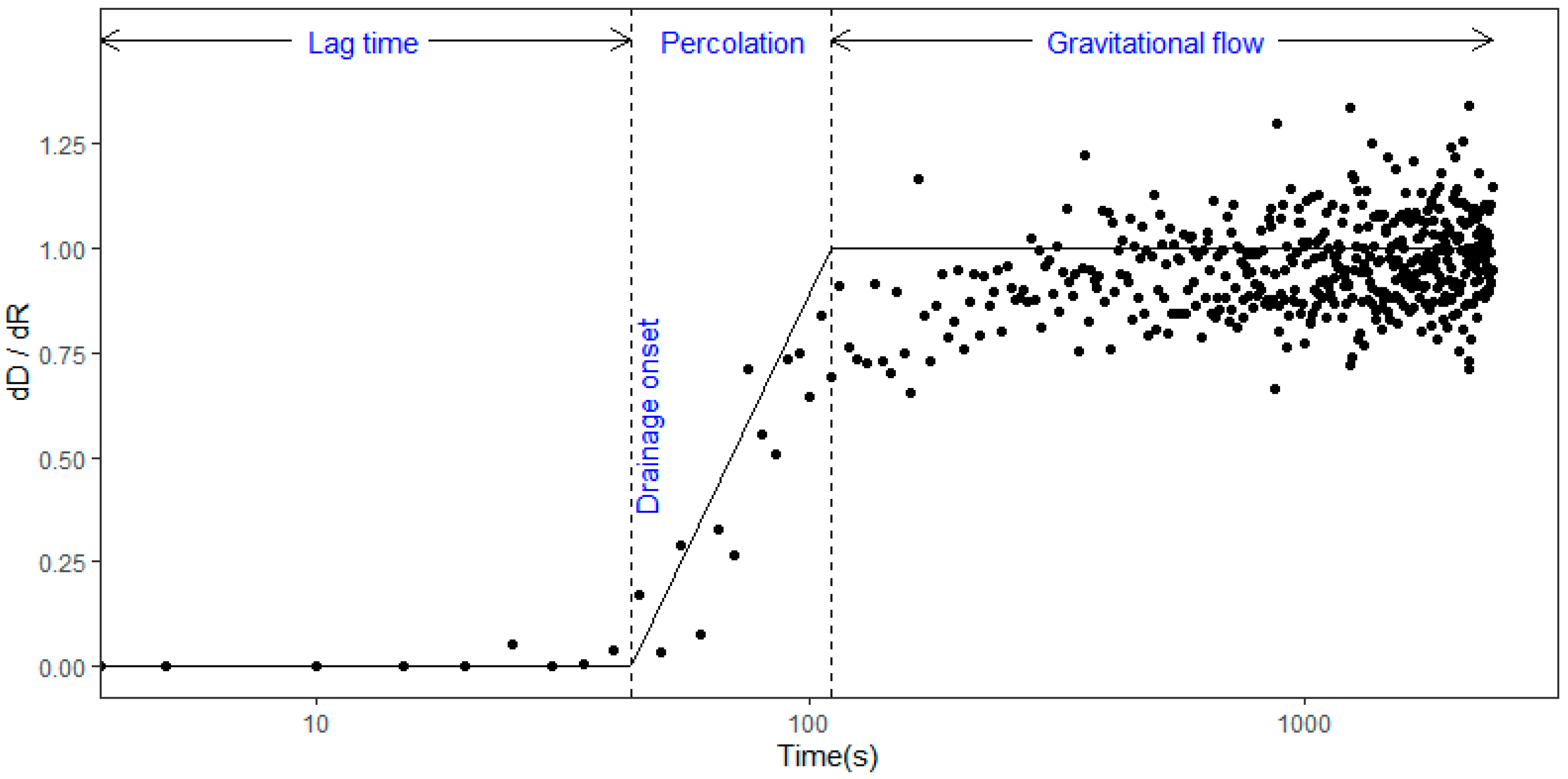
The wetting phase consists of the initial abstraction (lag time), percolation, and gravitational flow (
Figure 3). When rain begins to fall, all the rain can be stored for a short period as the initial abstraction. As shown in
Figure 3, the initial abstraction is commonly referred to as the lag time, which is the elapsed time for producing litter drainage. In succession to the lag time, percolation occurred through the litter layer [
33]. The percolation period was estimated from the time-varying flux of rainfall and drainage,
, where
and
dR are the deviations of drainage and rainfall rates for a 5-s interval, respectively. We assume that the value of
increases linearly for the period of percolation. Although the increase in rainfall is unbounded, drainage rate is bounded by the maximum interception storage and asymptotically approaches a constant value of
, as shown in
Figure 3. This asymptotic convergence occurs because a certain amount of liquid is gradually absorbed throughout the amorphous parts in cell walls of dead leaves [
3]. The gravitation flow is referred to as the dominant hydrologic process occurring in the litter layer during this period.
When the rain stops, water retained in the litter surface begins to evaporate. If evaporation is negligible, the post-rainfall retention of litter is determined by the competition of the available water (
subject to the gravitational force and the cohesive and/or adhesive forces of water. When the rain ceased, the retained water exponentially decreased as follows:
where
is the water retained in the litter layer at t-min after rain cessation,
are the maximum and minimum interception storage of the litter layer, and
k is the recession coefficient of litter drainage. The parameter
represents the time-dependent decline of water retained in the litter layer.
2.5. Statistical Analysis
Statistical differences among the groups were evaluated by one-way ANOVA or Kruskal-Wallis test (one-way ANOVA on ranks). If the treatments satisfied the assumptions of the ANOVA, i.e., the independence, normality and homogeneity of variances, the one-way ANOVA method was used. Otherwise, the Kruskal–Wallis test, a nonparametric method, was used.
In addition, a post hoc test was conducted when the results showed significant differences (
p < 0.05). A Tukey’s test was used for the post-hoc analysis of one-way ANOVA test. Meanwhile, a Mann-Whitney U test was used for that of the Kruskal-Wallis test. This nonparametric test allows two groups to be compared without assuming that the values are normally distributed [
34].
Thus, both Kruskal-Wallis and Mann-Whitney U tests were conducted for a comparison of physical traits and the interception storage capacity. The one-way ANOVA and Tukey’s tests were used for comparing the recession coefficient of litter drainage.
All statistical analyses were performed using R 4.0.2 (The R Foundation for Statistical Computing, Vienna, Austria) and Python 3.7.8 (The Python Software Foundation, Wilmington, DE, United States).
3. Results
3.1. Litter Physical Characteristics
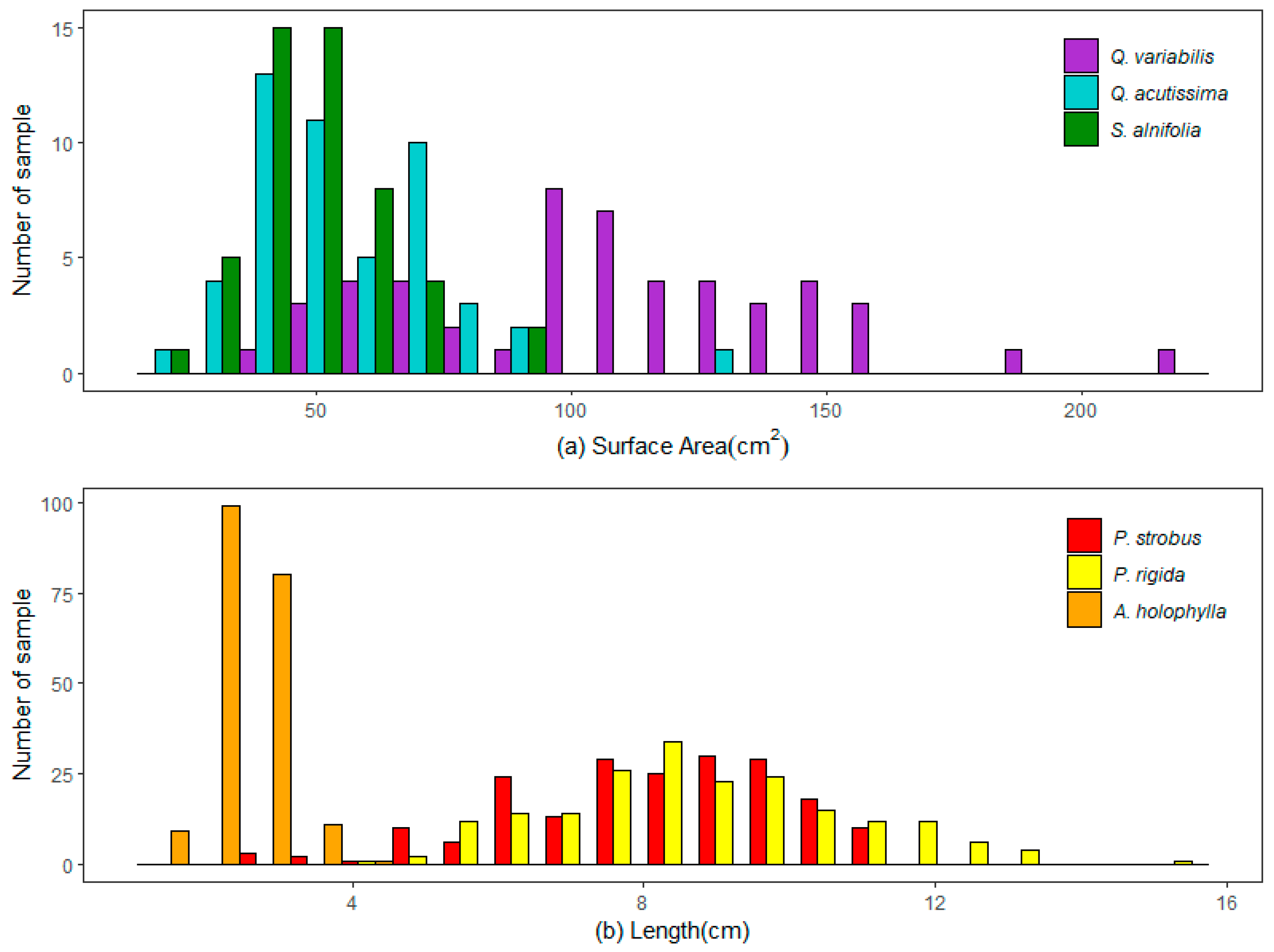
Leaf litter samples taken from three deciduous tree species were used in this study. The litters of
Q. variabilis and
Q. acutissima were characterized by a longer length and narrower width than the oval-shaped litter of
S. alnifolia. The projected surface area of the
Q. variabilis litter was significantly larger than that of the
S. alnifolia and
Q. acutissima litters. As shown in
Figure 4a, small litters with areas of less than 100 cm
2 contributed the most to the
Q. acutissima and
S. alnifolia litters but contributed only 38% to the
Q. variabilis litter.
Figure 4b shows the distinct difference in litter length distribution between
A. holophylla and pine litter (
P. rigida and
P. strobus). The majority of
A. holophylla litters were 2–3 cm in length. The needle length of pine trees ranged mostly from 4 cm to 13 cm, with an average length of 8.89 cm in
P. rigida and 8.19 cm in
P. strobus.
The mean and standard deviation values of density, SSA, and SAV in various litter types are presented in
Table 1. Significant differences were detected in the SSAs and SAVs between the broadleaf and needle-leaf litters (
p < 0.01); however, the difference was less significant in term of the litter density (
p < 0.05). Between the broadleaf or needle litter types, interspecific differences in the physical properties were observed (
p < 0.01), which are in partial agreement with the findings reported in previous studies [
2,
4,
35].
The P. rigida litter is considered to be the heaviest floor litter (0.661 g/cm3), while the density of the A. holophylla litter is 0.393 g/cm3, which is the lightest among the six litter types. Leaf surface area was significantly higher in the broadleaf litter than in the needle-leaf litter. The SSAs of the broadleaf litter varied from 167.83 cm2/g (Q. variabilis) to 283.88 cm2/g (S. alnifolia), while they ranged from 30.64 cm2/g (A. holophylla) to 176.87 cm2/g (P. strobus) in the case of needle-leaf litter. A similar variation was observed in the SAV values, which were higher in the order of S. alnifolia, Q. acutissima, and Q. variabilis for the broadleaf litter, and P. strobus, P. rigida, and A. holophylla for the needle-leaf litter.
Simulated rainfall was poured over the litter accumulation in the litter container. The litter layer’s characteristics, such as layer thickness and porosity, can affect the water retention capacity.
Table 2 displays the thickness and porosity of the litter layer for all the experiments. Litter thickness varied with litter density and porosity. The
A. holophylla litter layer had a lower thickness (1.37 cm) than the pine litter layers. The broadleaf litter layer thickness ranged from 10.84 cm in
Q. variabilis to 13.16 cm in
Q. acutissima. Porosities of the broadleaf litter layer were higher than those of the needle litter layer.
3.2. Litter Interception Storage
Litter interception storage is given by the equivalent depth of rainfall per unit thickness of the litter layer (
Table 3). For needle-leaf litter, the average
value per unit thickness of the litter layer was the highest in
A. holophylla (1.146 mm/cm), followed by
P. rigida (0.173 mm/cm) and
P. strobus (0.097 mm/cm). The water stored in the broadleaf litter layer ranged from 0.088 mm in
Q. acutissima to 0.098 mm in
Q. variabilis per effective depth of the layer, depending on species and rainfall intensity, which were considerably lower than those of the needle litters.
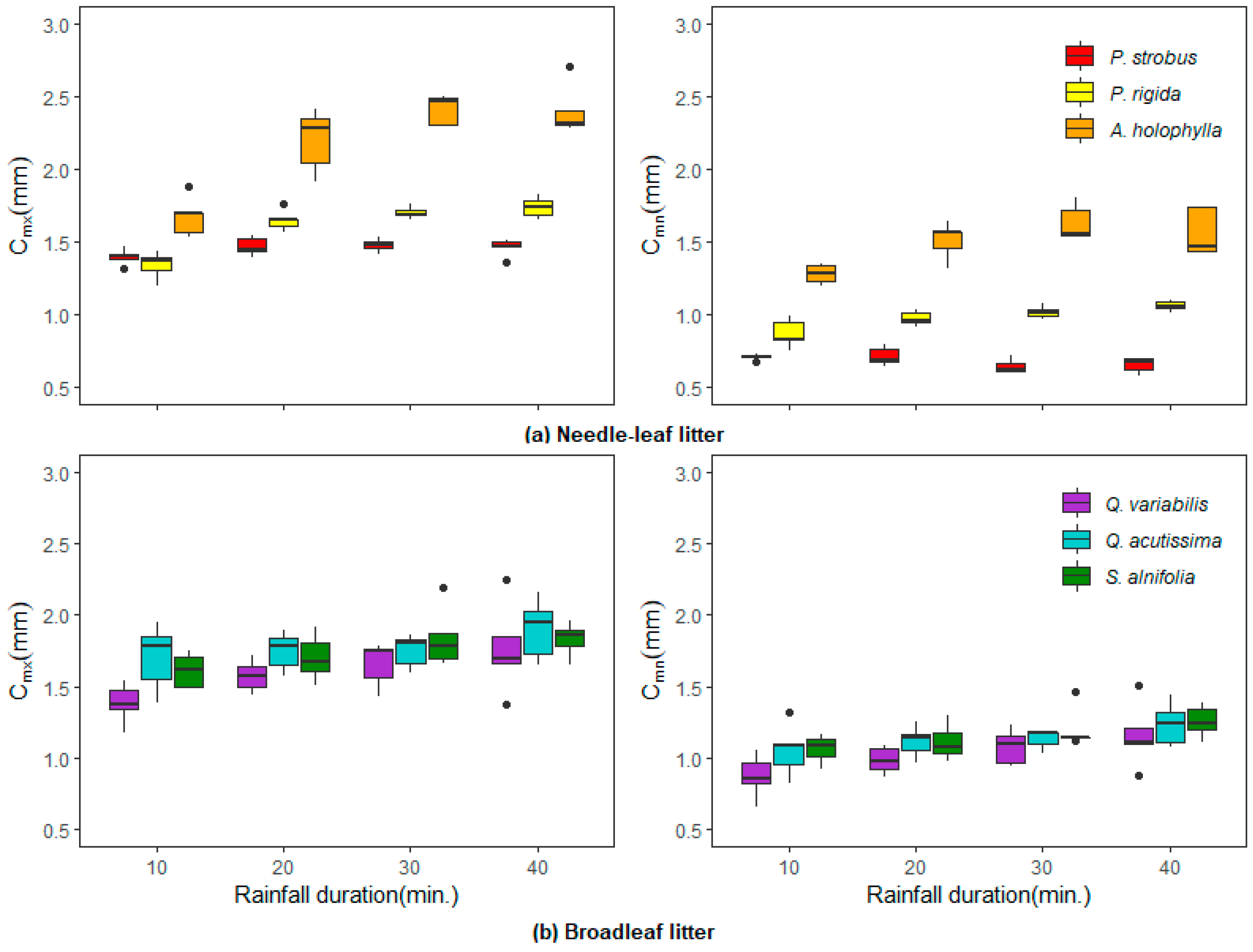
Figure 5 shows how the interception storage capacities (
) vary with litter type and rainfall duration at a constant intensity of 50 mm/h for a given period. As shown, the interception storage responses to rainfall duration varied among the litter types. The influence of needle-leaf litter was more evident than that of broadleaf litter. Both the
and
values were highest in the
A. holophylla litter and lowest in the
P. strobus litter for the needle-leaf litters, regardless of rainfall duration.
The averaged values in the A. holophylla litter varied from 1.67 mm for a 10-min duration to 2.42 mm for a 30-min duration, while the values ranged from 1.28 mm to 1.63 mm under the same rainfall characteristics. There were significant differences in the and values between needle-leaf litters (p < 0.05). However, unlike the needle-leaf litters, the values of and in the Q. acutissima and S. alnifolia litters occurred in the same group (p 0.05), and those of the Q. variabilis litter differed from other broadleaf litters. Slight increasing trends were observed in the and values with increasing rainfall for all the broadleaf litters.
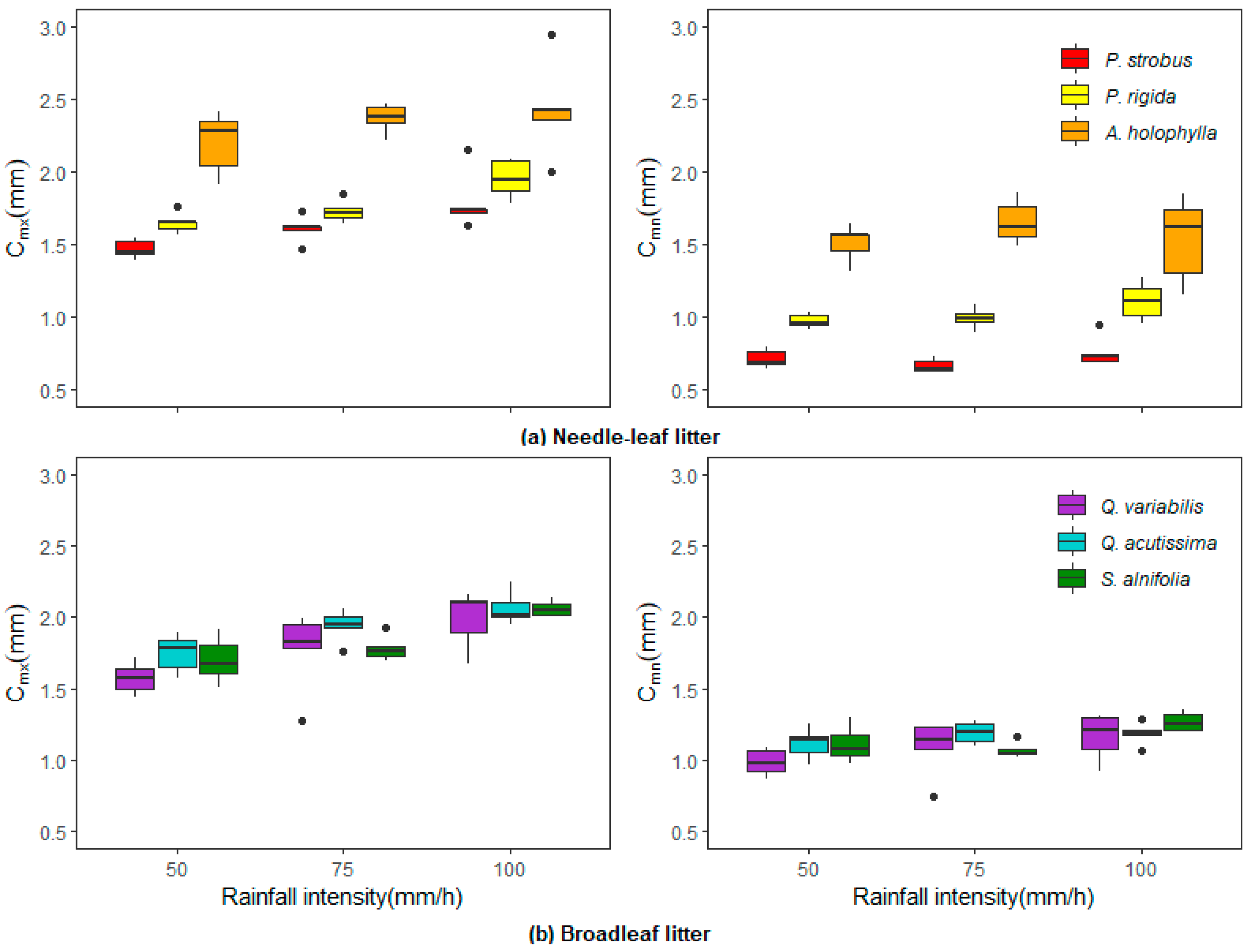
The influence of rainfall intensity on interception storage was also examined. Rainfall intensities of 50, 75, and 100 mm/h were poured for 20 min over various litter covers. As shown in
Figure 6, both
and
increased marginally with increasing rainfall intensity. However, the effect of rainfall intensity on
was more apparent. As mentioned previously,
is the sum of
and gravitational flow. Thus, several studies have reported a directly proportional relationship between
and rainfall intensity [
14,
15,
16]. The results of this study indicate that a two-fold increase in rainfall intensity (50 mm/h to 100 mm/h) caused
to increase by 6.5% for the needle litter and 12.7% for the broadleaf litter.
The effects of rainfall characteristics on litter interception storage were substantial. The extent of litter interception capacity is mainly dependent on the rainfall amount and its intensity and duration. The current study demonstrated that a higher intensity or longer duration of rainfall leads to an increase in the interception storage of the litter layer, which is similar to the findings of Sato et al. [
14], Putuhena and Cordery [
15], and others [
16,
25].
3.3. Litter Drainage
The amount of water retained in the litter is the result of the throughfall, evaporation and litter drainage. When assuming little or no evaporation loss for the experiment’s short duration, rainfall that exceeds the litter’s interception storage may begin to move downward, under gravitational forces, through the litter layer as litter drainage. During the experiment, litter drainage reached a stable condition (equivalent to the rainfall rate) after approximately 20–30 min, depending on the litter type and rainfall characteristics.
Table 4 presents the portion of the litter drainage corresponding to the rainfall amount. When the litter layer reached its saturation point, a nearly constant amount of water was drained. Litter drainage, expressed as a percentage of the total rainfall, for broadleaf litter with 50 mm/h of rainfall varied from 0.865% after 10 min to 0.966% after 40 min. At a rainfall intensity of 100 mm/h, litter drainage increased by approximately 0.026% at a 50 mm/h intensity for the same 20 min duration. Therefore, the drainage percentage increased with a longer duration or higher intensity of rainfall. However, for the rainfall-simulated experiments, the rainfall amount was found to be a crucial variable for producing litter drainage [
14,
19]. When compared with events producing the same rainfall amount, such as 25-mm rainfall events (30 min, 50 mm/h and 20 min, 75 mm/h) and 33.3-mm rainfall events (40 min, 50 mm/h and 20 min, 100 mm/h), the drainage of each litter was not significantly different.
Table 4 also indicates that the effects of litter type on drainage were not apparent.
3.4. Water Retention and Drainage Process of the Litter Layer
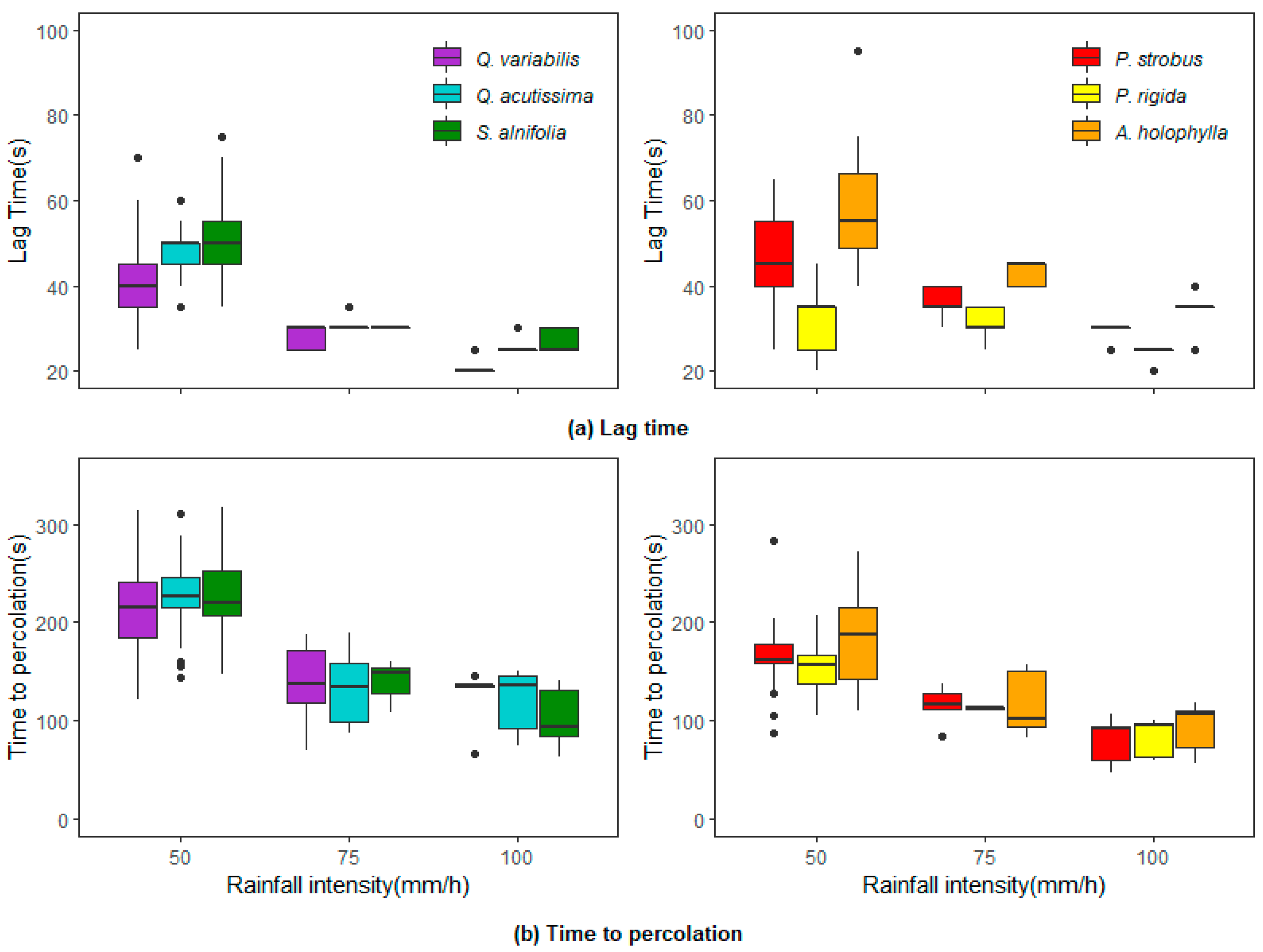
Figure 7a depicts the lag time for drainage onset under rainfall simulation experiments. The drainage onset occurred earliest with pine litters and was delayed longest by the
A. holophylla litter. Unlike the needle leaf litter, no significant differences in lag time existed for the broadleaf litter. For the rainfall experiments with an intensity of 50 mm/h and a 20-min duration, an average lag time of 53.0 s (equivalent to 0.74 mm) was required for the drainage onset in the
A. holophylla litter, followed by the
S. alnifolia litter (51.4 s),
Q. variabilis (48.3 s),
Q. acutissima litter (48.0 s),
P. strobus litter (37.0 s), and
P. rigida litter (35.0 s). As shown in
Figure 7a, the lag time varied with litter type, showing a slight decrease with an increase in rainfall intensity. Generally, fast drainage responses were typically associated with needle litter, while broadleaf litter was slower to respond. This phenomenon was also reported by Zhao et al. [
19] and Li et al. [
25]. They demonstrated that the broadleaf litter’s larger surface depression functions as a rainwater harvester at the beginning of a rainfall event.
The fraction of rainfall that moved through the litter layer as percolation and the litter container’s weight gradually increased with an increasing rainfall rate. The percolation period was defined as the time at which the
curve meets the threshold line. The percolation period lasted for 1.7–4.1 min for the broadleaf litter, and 1.3–3.3 min for the needle litter (
Figure 7b). This period indicates that most rainfall can be intercepted and retained by the litter layer, although a small portion of rainfall drips off.
The recession coefficient (
k) in Equation (2) was analyzed using the interception storage and drainage relationships.
Table 5 displays the best relationships of drainage recession limbs for each litter type, showing a sufficiently good agreement. The recession coefficients varied from 0.00202 in the
A. holophylla litter to 0.00236 in the
S. alnifolia litter, indicating no significant difference between litter types. Therefore, we propose a practical use recession coefficient of 0.00224 to estimate drainage flow from floor litter.
Table 5 indicates the absence of a significant difference in the post-rainfall drainage recession coefficient. This suggests that post-rainfall drainage from the saturated litter layer is governed by the force of gravity and not litter type.
4. Discussion
4.1. The Influence of Litter Type on Interception Capacity
The amount of intercepted water can be largely attributed to the physical differences across litter types. Morphologically, broadleaf litters have either oval or elliptical forms and form well-arranged stacks on the ground surface. Leaf bundles or fascicles are a distinct characteristic of needle-leaf litters. The number of needles per fascicle differs among tree species. A. holophylla litters comprise flattened needles that are singly attached around the twig. The P. rigida litter has fascicles of three needles, while P. strobus litters have five-needle fascicles.
Under the rainfall simulation experiments,
is controlled by the porosity and volume of litter, and the ability of water to penetrate through the exterior of the litter into the inner pores.
is related to litter’s physical features such as surface area, arrangement and litter surface [
4]. Sato et al. [
14] and others [
4] suggested that broadleaf litter stores substantially more water than needle-leaf litter. No significant differences in the interception storage were established for broadleaf litter. This is due to the fact that rainwater is mostly retained in the macropores of broadleaf litter when rain pours for a short period, which is not enough to saturate the litter tissue [
10]. Moreover, except for the
A.
holophylla litter, broadleaf litter retained more water than needle leaf litter. As shown in
Table 2, the lower porosity of
A. holophylla litter contributes to higher storage retention due to the greater resistance of the packed litter to the vertical movement of water [
36,
37].
The
A. holophylla litter has the advantage of retaining water within the layer due to its exceptionally accumulated litter structure with a relatively smaller length and lower porosity compared to pine litter. Thus, the adhesion and surface tension of water molecules are strong on the
A. holophylla layer. Rainfall applied to the
A. holophylla litter layer did not disperse sufficiently [
14], and the dense litter mat restricted water movement into the litter layer [
38]. The SAV value was approximately 1.6 times greater in
A. holophylla litter than in the pine litters. Litter interception storage, in general, was inversely related to SSA and SAV for the needle-leaf litter. In contrast, SSA and SAV’s influences were not significant for the broadleaf litter because water was stored on surface pits or leave concavities. The interception storage was also affected by the thickness of the litter layer [
10,
15]. This indicates that interception storage in needle litters is more strongly dependent on physical properties in comparison to broadleaf litters.
Additionally, the individual litter’s orientation or arrangement can affect the amount of water retained in the litter layer. For needle litter, the horizontally oriented layer retains more water than the curved or suspended layer. In this study, litter was horizontally piled in the litter container to ignore the effect of litter orientation.
4.2. Litter Drainage Characteristics
It is expected that no drainage occurs until rainfall exceeds the litter layer’s interception storage capacity. However, drainage from the litter container was observed even at the beginning of the rainfall (less than 1 min), which is most likely due to quick flow such as the preferential flow through macropores and bypass flow on the litter container walls. Some rainfall passed quickly through the litter layer’s macropores or flowed down along the container surface. However, the initial abstraction process was not fully investigated in this study because the experiment was conducted with a small, thin-layered litter layer. Nevertheless, initial abstraction is thought to be more considerable in the forest cover water cycle and thereby warrants further research.
When the rain continued to fall, the rainfall occupied the macropores of the litter layer until the litter reached saturation. During this period, drainage tended to increase logarithmically because the litter layer became partly saturated, and gravitational flow occurred under the force of gravity. Moreover, the timespan for gravitational flow generation is affected by the rainfall intensity and litter type. In the experiment, the drainage rate was always below the rainfall rate during the wetting phase.
When litter can be completely saturated under long rainfall durations, the average drainage rate is approximately equal to the rainfall rate. In most cases, the constant drainage rate did not attain a long duration of rainfall because water absorption into leaf tissues may have accounted for some of the gradual rainfall loss. The maximum drainage rate was nevertheless defined, as the water was discharged immediately before rain cessation. This made it possible to define the potential amount of water that reached the soil layer under various rainfall conditions.
4.3. Limitation and Future Application
We noted several limitations in this study. The rainfall intensities used in the experiments were relatively high. This led to a decrease in the litter’s retention ability compared to that exposed to lower-intensity natural rainfall [
14]. Furthermore, short rainfall duration caused a lower retention capacity [
25,
26], particularly in the
A. holophylla litter, because all needles of the litter layer may not have been wetted. Moreover, experiments were also conducted with a homogeneous litter, yet under natural conditions, floor litter consists of leaves, branches, and fruits of several trees and plants, rather than a single species. In natural conditions, lateral flow on inclined surfaces may occur, thereby affecting percolation and retention [
19,
23]. However, slope was not considered in the experiments and no measurements were made of the lateral movement of water. Retention or drainage processes occurring in the litter layer may be affected by these factors. The litter’s interception capacity is relatively constant for a specific tree species, but it can vary with geographical location, tree age, or canopy position. Additional precision can be achieved by enlarging the number of observations to compensate for variations in both the litter’s physical properties and its water retention ability.
The presence of litter layer on the ground is a characteristic feature of forest soils. Rainfall interception of litter layer is one of the hydrologic processes in forest watersheds. The changes in water stored within the floor litter is determined by summing direct rainfall as throughfall, drip from the foliage, stems, and branches, lateral flow out of the layer, and percolation from the litter layer into the upper soil layer. In addition,
corresponds to the threshold value of percolation through the litter layer, which controls the litter drainage during rainfall events. Leaf litter, characterized by the interception storage and drainage capacity here, are important in determining what happens in forest floors and examining how the vegetation influences the hydrologic cycle of forested watersheds. However, there have been few attempts to develop the hydrologic models regarding the interception storage-drainage relationship of floor litter [
33,
37] because the knowledge of the process has not yet been fully explored [
27]. Here, we presented the simplified rainfall-interception relationship of floor litter with the rainfall simulation experiments, but more research is needed to overcome the above-mentioned drawbacks.
5. Conclusions
Floor litter plays an essential role in forest hydrological cycles by capturing a fraction of rainfall and evaporating it into the atmosphere. During a short period of rainfall events, litter’s water retention ability may be affected by the physical properties of the litter, amount of litter, and rainfall characteristics. In this study, rainfall simulation experiments were conducted to experimentally explore the influences of litter type and rainfall patterns on water retention and drainage in the litter layer. Three types of broadleaf and needle-leaf litters were investigated to demonstrate how the litter’s physical features can influence the rainfall interception process.
The interception storage capacity of needle litters varied significantly with the litter type. The A. holophylla litter showed the highest values for the maximum and minimum interception storage regardless of the rainfall intensity and duration. Moreover, small A. holophylla litter retained more water than the other litters owing to its much lower thickness and porosity. No significant differences in interception storage existed across the broadleaf litter types. Rainfall interception of broadleaf litter occurred on the surface storage of horizontal or sub-horizontal leaves, particularly in concavities. It was also revealed that the amount of water retained by litter is a function of the intensity and duration of rainfall. A higher intensity or longer duration of rainfall events can increase the interception storage capacity of litter on all broadleaf and needle-leaf litters.
The amount of rainfall available for initial abstraction and percolation in the litter layer varied according to litter type and rainfall pattern. However, after rainfall cessation, the recession limbs did not vary significantly according to litter type and rainfall characteristics. This implies that the force of gravity is the primary factor governing post-rainfall drainage from the saturated litter layer.