Accuracy and Transferability of Artificial Neural Networks in Predicting in Situ Root-Zone Soil Moisture for Various Regions across the Globe
Abstract
:1. Introduction
2. Materials and Methods
2.1. In Situ Soil Moisture Datasets from ISMN
- -
- Soil moisture data lie within the temporal range (January 2013–December 2019) to maximize common temporal coverage. Some stations do not have data that cover the whole temporal interval (absence of measurements, gaps generated after quality control) but are still selected as long as they fall into that period. The total number of considered records is 10,054,406 hourly values. The representativeness and size of the training dataset is an important criterion since ANNs are data-driven methods [27].
- -
- A station is selected when soil moisture data are available at a depth of 5 cm for SSM and depths ranging between 30 and 60 cm for RZSM. Stations do not always have the same sensor installation and layout. Some stations have horizontal sensors (depthfrom = depthto), whereas, for other stations, soil moisture sensors are disposed vertically (depthfrom <> depthto). In the latter case, stations that fall into the interval [30, 60 cm] were chosen.
- -
- A station is selected if it has at least 3000 hourly soil moisture values (cf. Section 2.2.2 and Section 3.2).
2.2. Methods
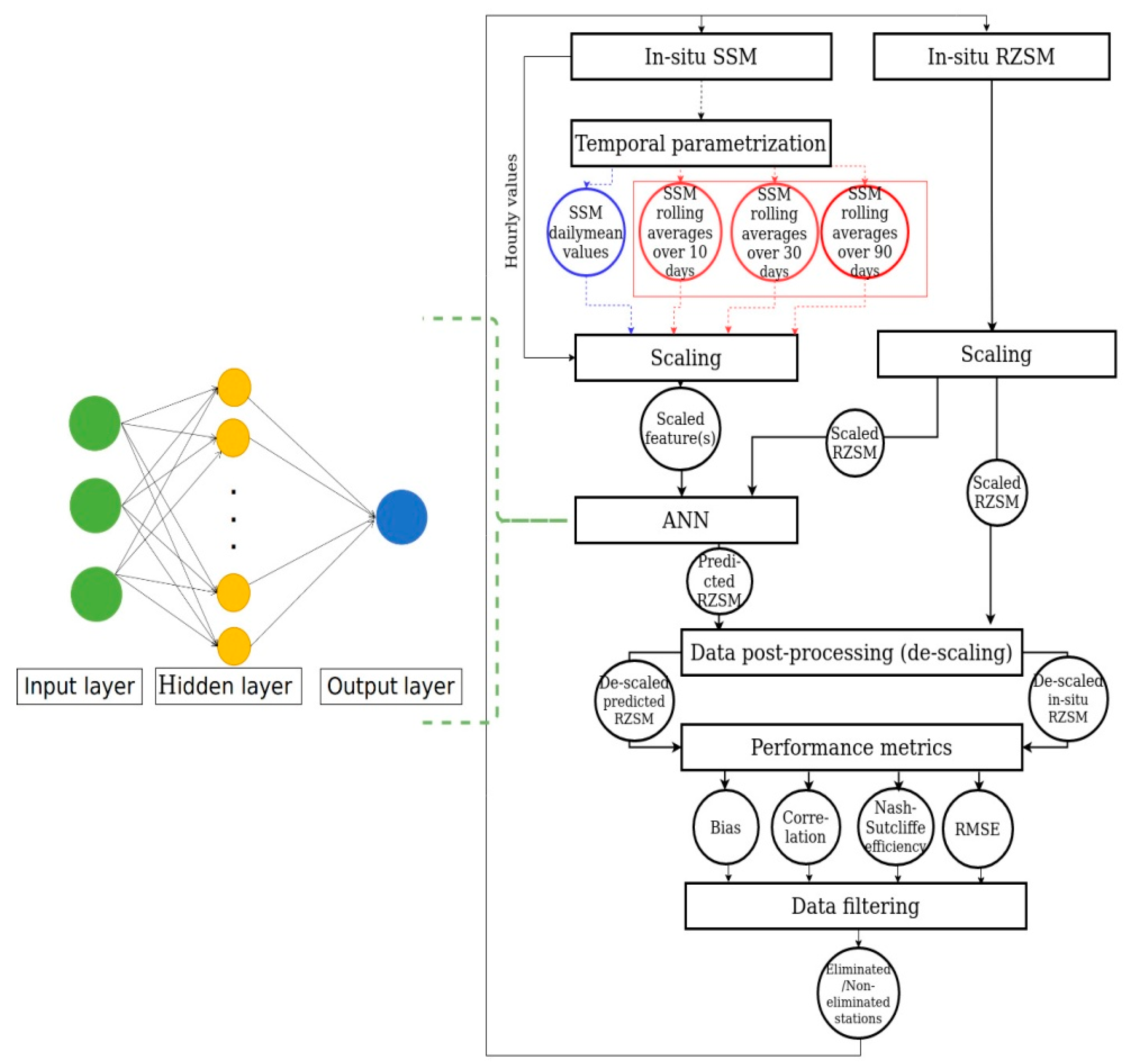
2.2.1. Configuration of the Artificial Neural Network
2.2.2. Features and Scaling
- -
- ANNH: A one-feature ANN such as the feature is the hourly values of SSM.
- -
- ANND: A one-feature ANN such as the feature is the daily mean values of SSM.
- -
- ANNRAV: A three-feature ANN such as the three features is the SSM backward rolling average values over 10, 30, and 90 days.
- -
- SSCA (Standard scaling): Standard scaling or Z-score normalization transforms the distribution of a dataset such that the mean and standard deviation of the observations are 0 and 1, respectively, using Equation (2):
- -
- MMSCA (MinMax scaling): This scaling scheme constrains the range of each input feature or each output of a neural network. This is usually performed by rescaling the features or outputs from one range of values to a new range of values. Generally, the features are rescaled to lie within a range of 0 to 1 or from −1 to 1. The rescaling is often accomplished by using a linear interpolation formula such as [34]:
2.2.3. Training and Test Configuration
- -
- ANN-TOT refers to a training/test approach where 70% of the whole global dataset (70% of the stations of all networks) forms the training set, the remaining 30% of the global dataset consists of a validation set, and the test set is made up of the whole dataset.
- -
- ANN-Neti refers to a training/test approach where 70% of the values belonging to the stations of a given network (Neti) form the training set, the remaining 30% of values remaining in Neti serve as a validation set, and the test set is made up of the whole dataset.
- -
- ANN-(TOT-Neti) refers to a training/test approach where 70% of the whole global dataset minus the values of a given network (Neti) form the training set, the remaining 30% of the global dataset minus measurements of Neti serve as a validation set, and the test set is made up of the whole dataset.
2.2.4. Performance Indicators
Individual Station Performance Metrics
Skill Indices
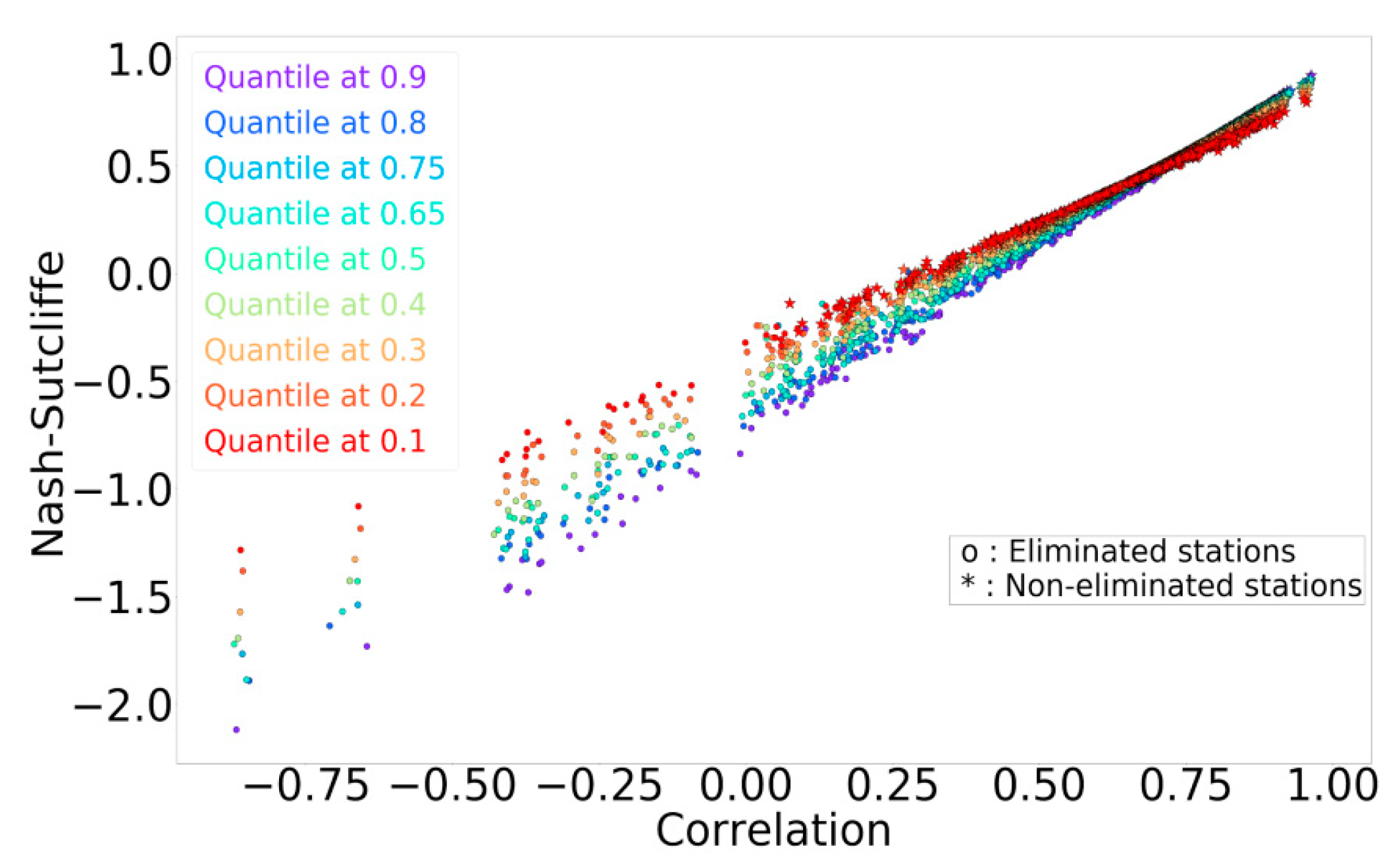
2.2.5. Data Filtering
3. Results and Discussion
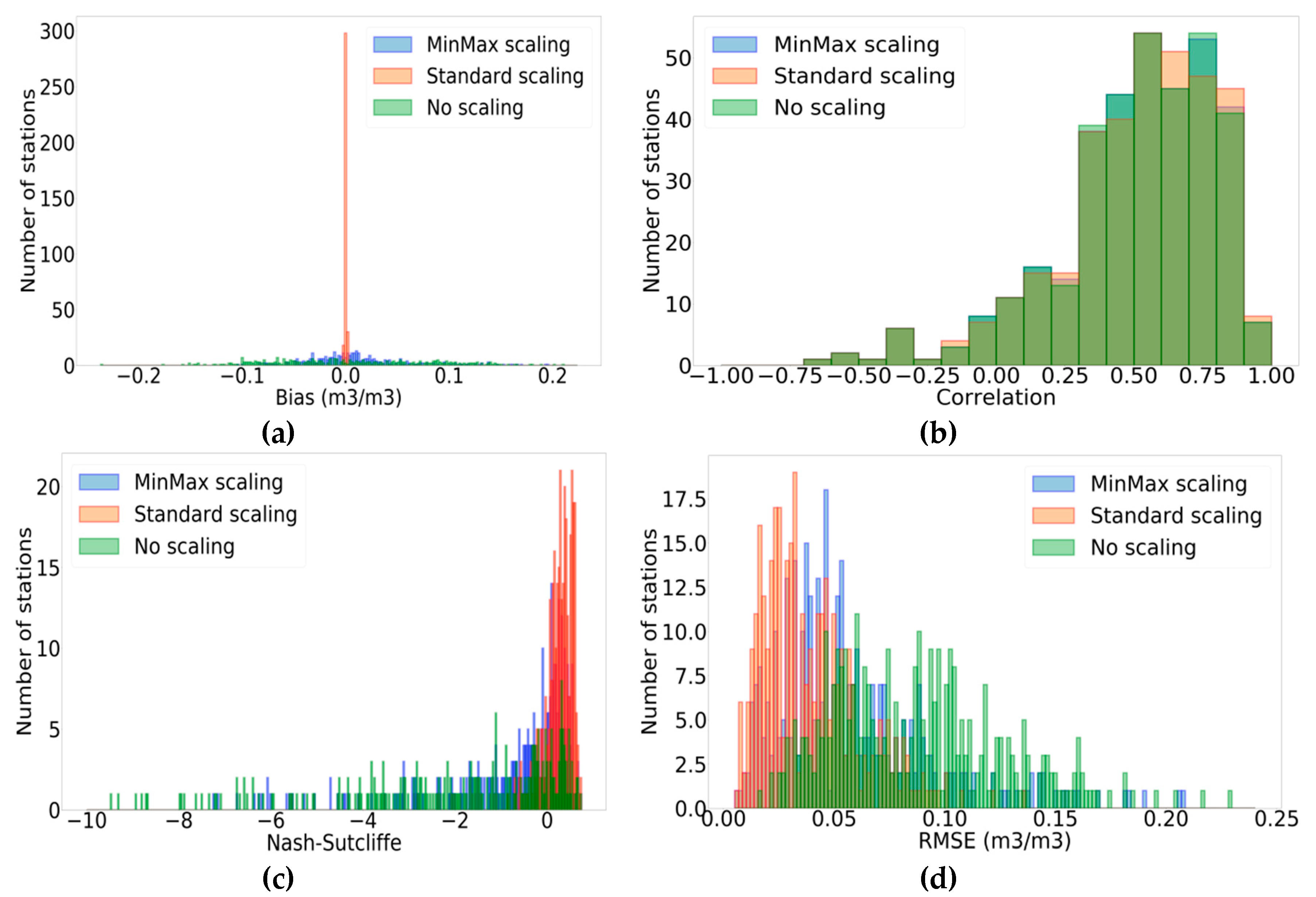
3.1. Impact of Scaling
- -
- Bias is considerably reduced with the application of SSCA. This is expected, as the SSCA method by construction tends to eliminate bias. These values ranged between −0.002 and 0.002 m3/m3 for SSCA, whereas MMSCA yielded bias values between −0.105 and 0.196 m3/m3.
- -
- Correlation values are quite similar for the two scaling methods. An insignificant difference of less than 0.001 for correlation values is obtained by MMSCA and SSCA for approximately 60% of the stations (206 stations). Approximately 52% of the stations (181 stations) have higher correlation values with SSCA, approximately 6% of the stations (23 stations) have the same correlation values for both scaling methods, and the remaining stations (142 stations) have higher correlation values with MMSCA.
- -
- RMSE values are also improved with SSCA in comparison with MMSCA mainly due to the enhancement of bias correction. Approximately 87% of the stations (302 stations) show lower RMSE values with SSCA, approximately 7% of the stations (25 stations) have invariable RMSE values, and the remaining stations (19 stations) have better RMSE values with MMSCA. The maximum decrease (and thus, improvement) in RMSE is recorded for the “Reynolds Homestead” station (“SCAN” network) with SSCA such that the decrease is equal to 0.145 m3/m3. RMSE values yielded by SSCA and no scaling are consistent with previous results advanced in [27] for RZSM estimates at a depth of 50 cm in the case of the “SCAN” network. Actually, the authors in [27] used linear rescaling to compare ANN-simulated soil moisture (generated by SMOS data) to the reference datasets (GLDAS-1/Noah output). The ANN-simulated RZSM values were bias-corrected to match the mean and standard deviation of the reference set. The authors in [27] obtained a mean RMSE of 0.054 m3/m3 following bias correction against a mean RMSE of 0.082 m3/m3 without bias correction. In our case, for the network “SCAN”, SSCA gives a mean RMSE equal to 0.042 m3/m3 against a mean RMSE of 0.090 m3/m3 without scaling. For SSCA, RMSE is equal to the unbiased root mean square error (ubRMSE) since bias is eliminated by construction. In fact, the relation between these two metrics is as follows:
- -
- NSE values are drastically improved when the SSCA is applied. Approximately 91% of the stations (315 stations) have better NSE values. The best improvements are recorded for stations “PrairieView#1” and “GuilarteForest”, which belong to the network “SCAN”, such as NSE differences (SSCA-MMSCA), which are equal to 86.827 and 85.483, respectively. The difference in behavior between correlation and NSE can be explained by the fact that NSE is a function of RMSE (Equation (8)). Given that RMSE is considerably reduced for most stations with SSCA, NSE is improved.
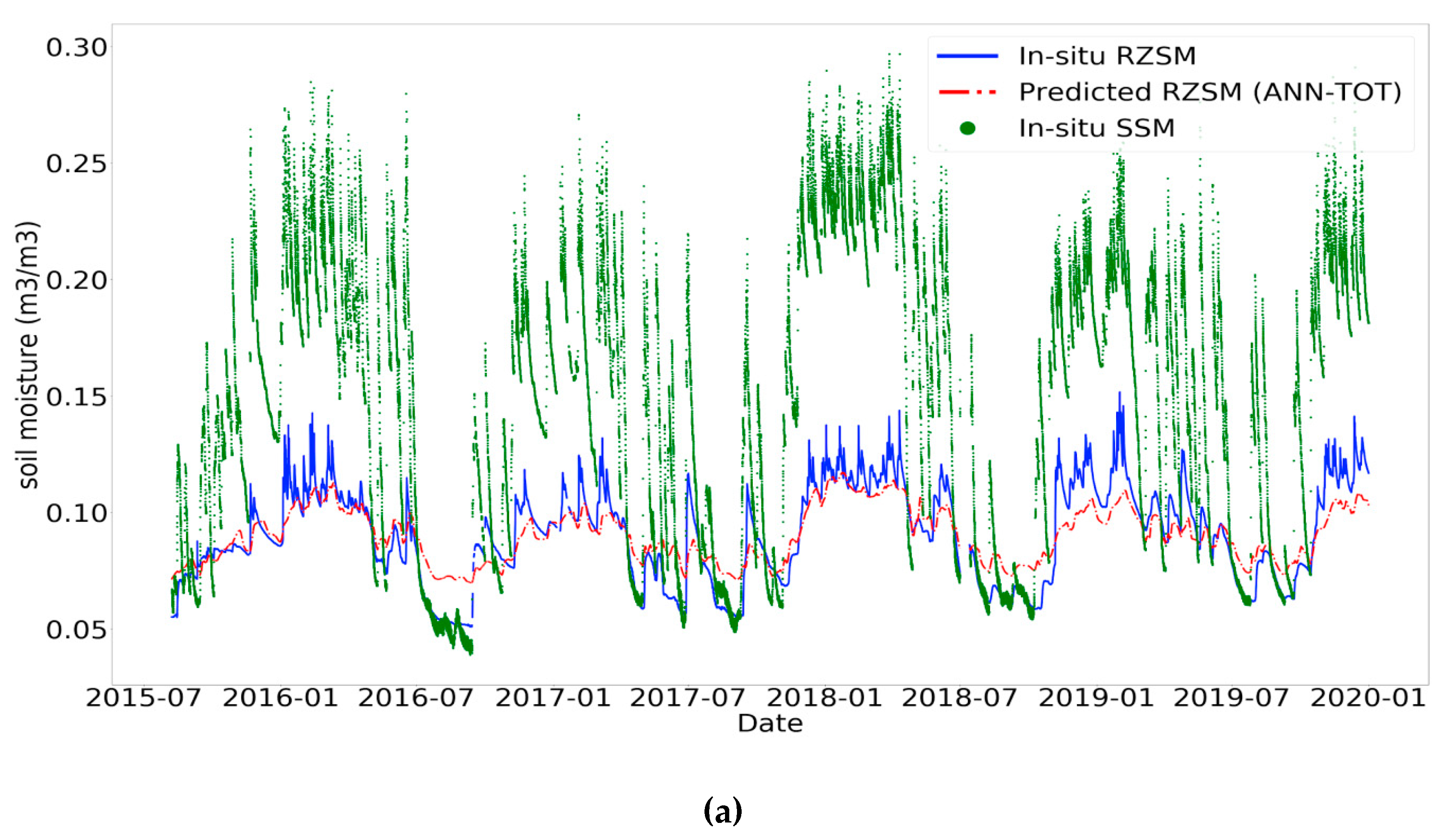
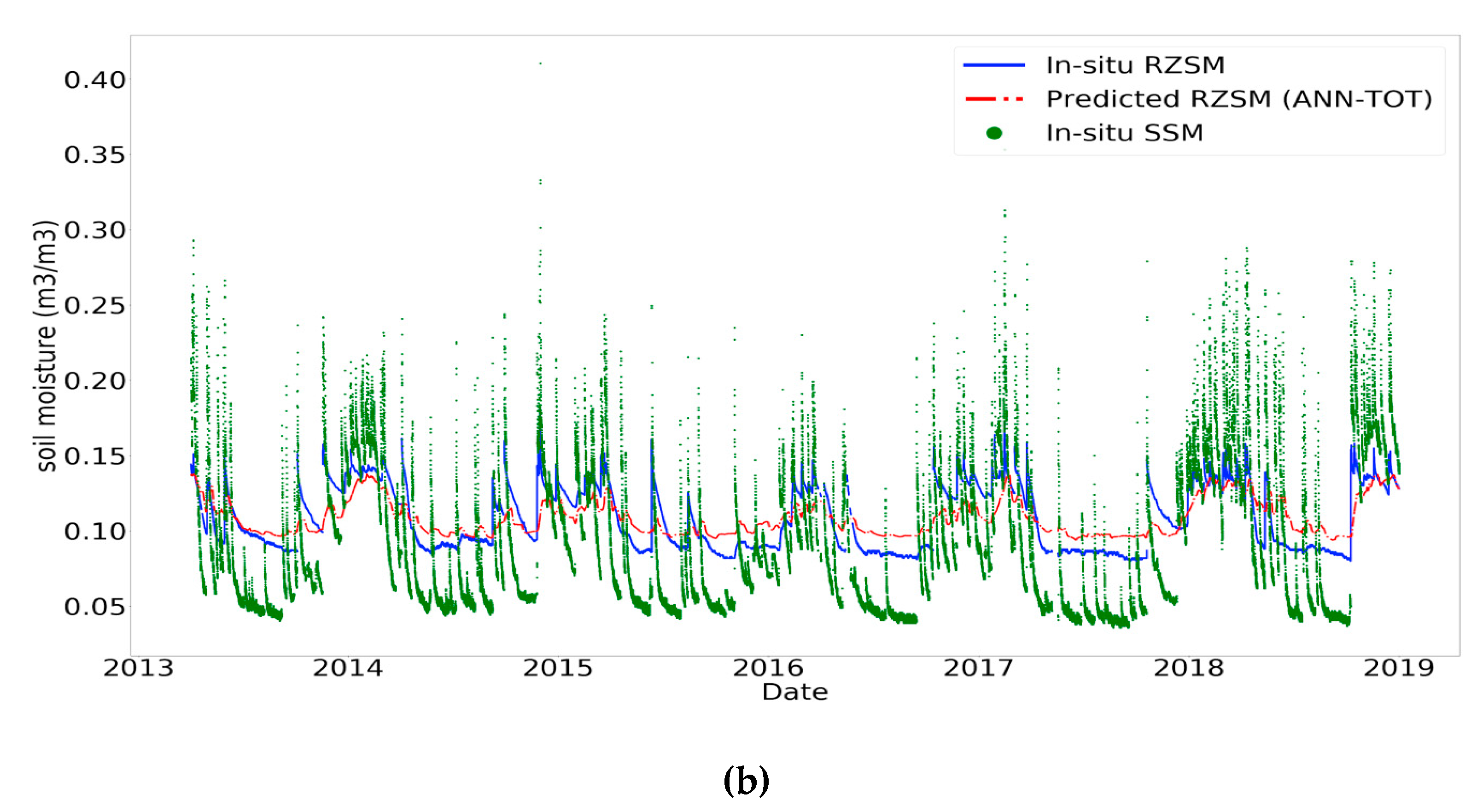
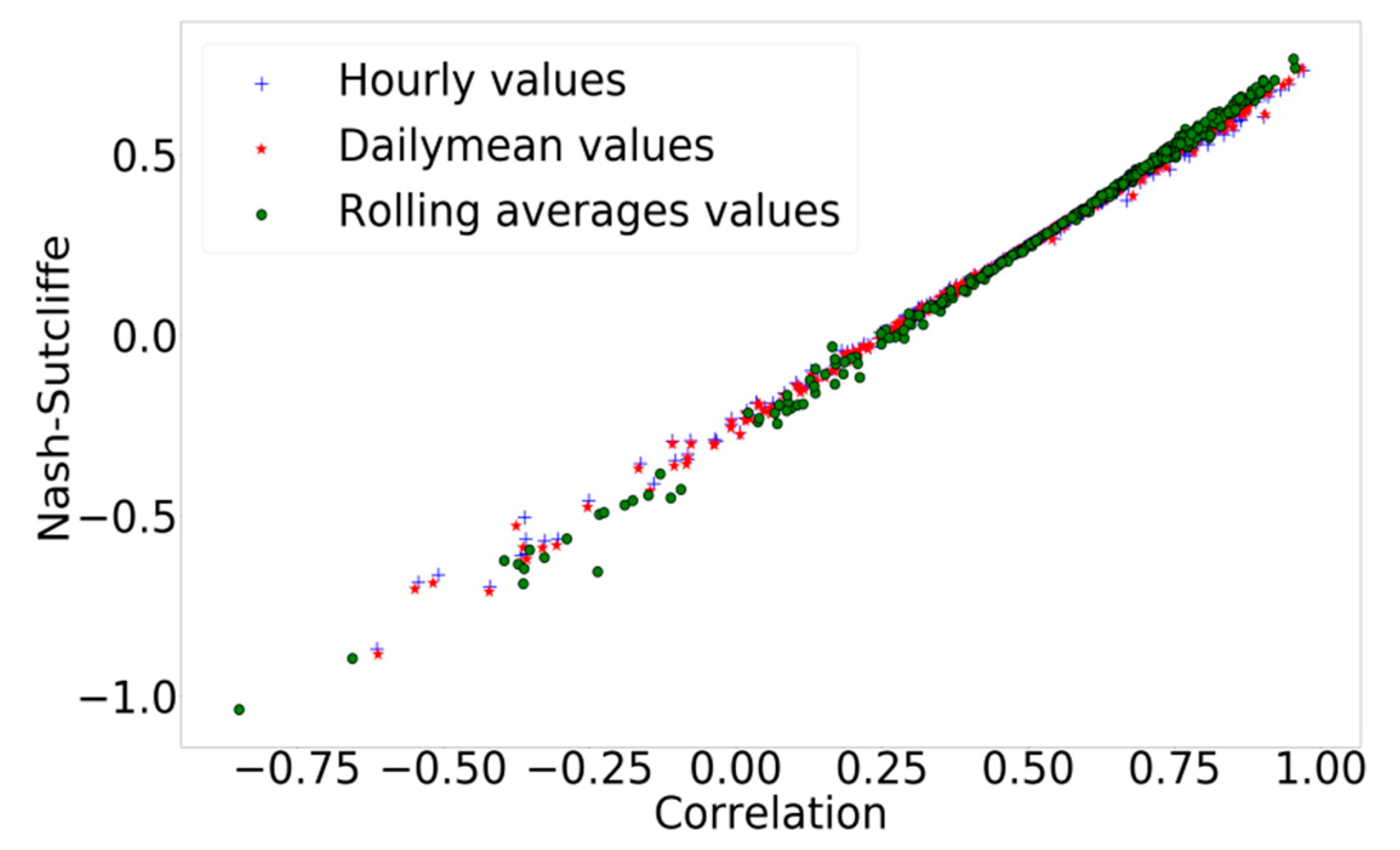
3.2. Impact of the Temporal Information
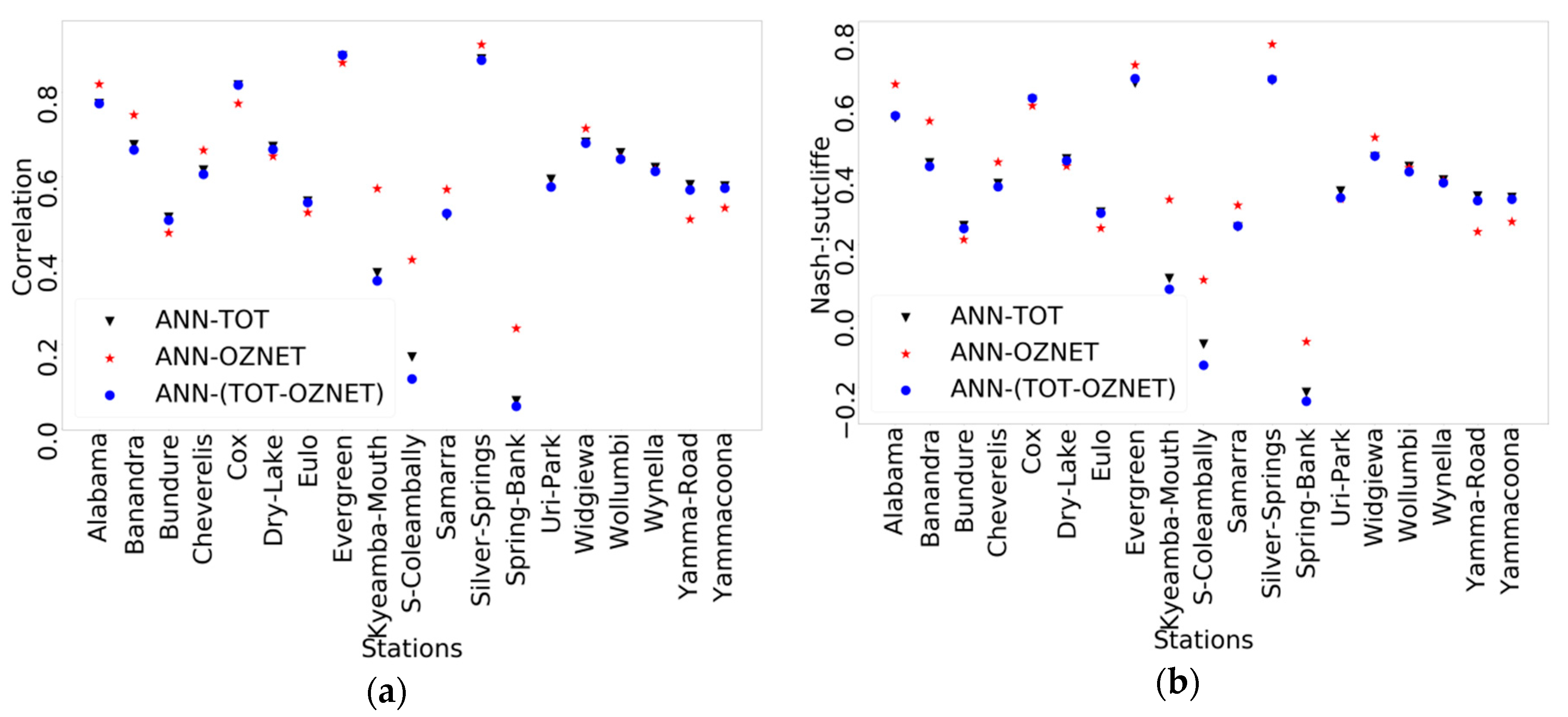
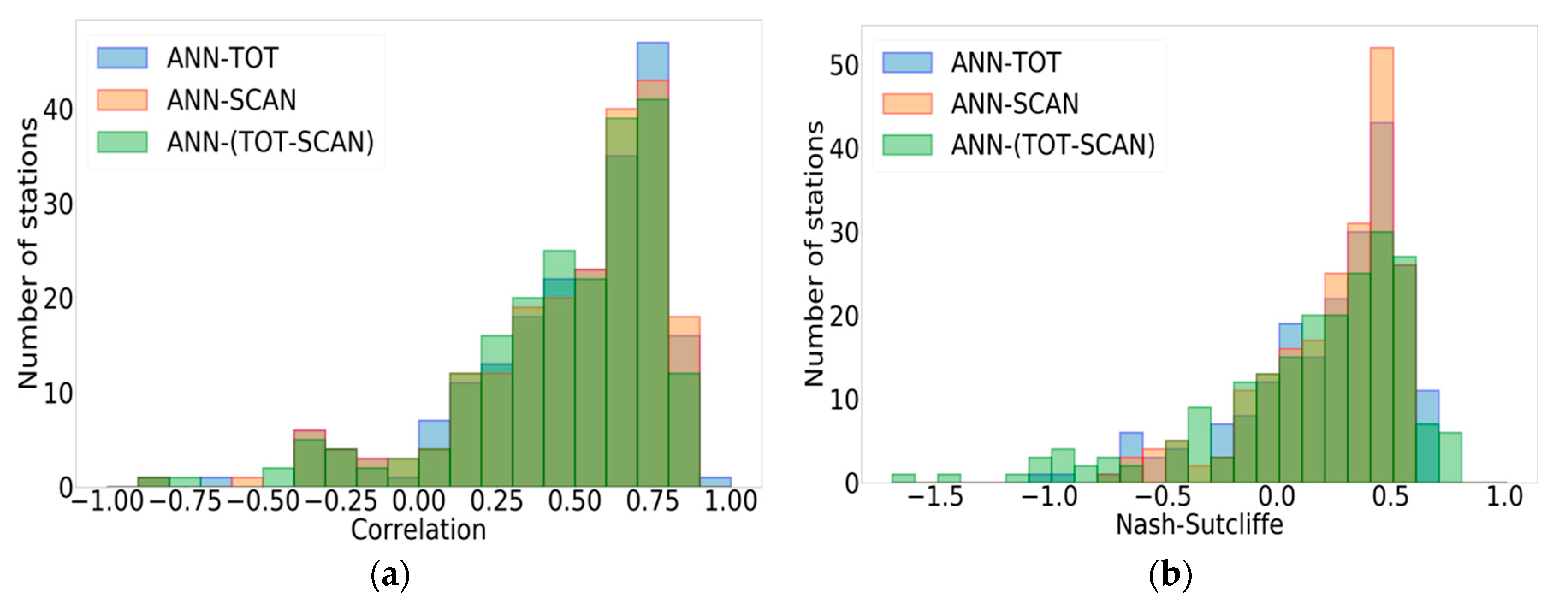
3.3. Impact of the Training Approach
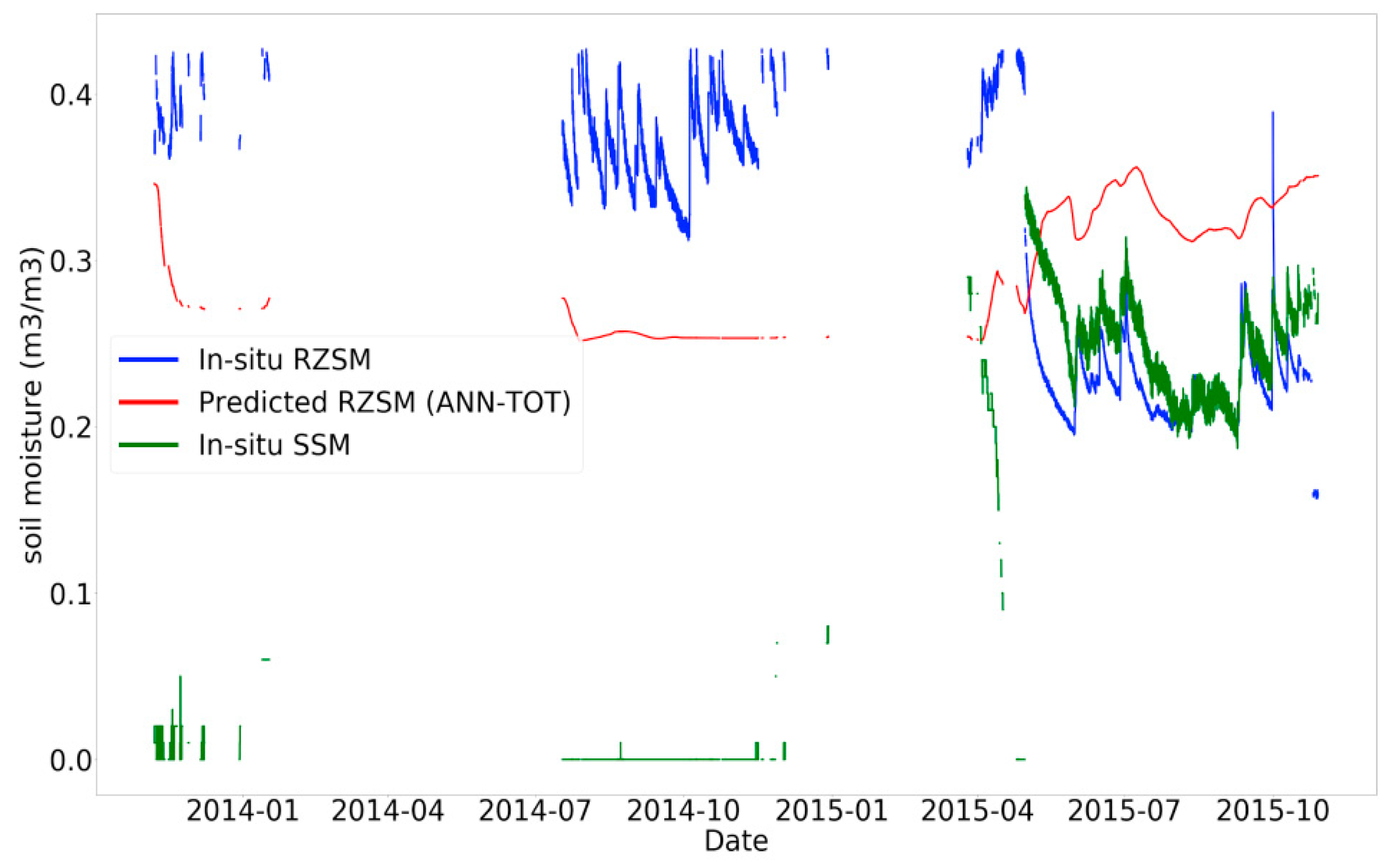
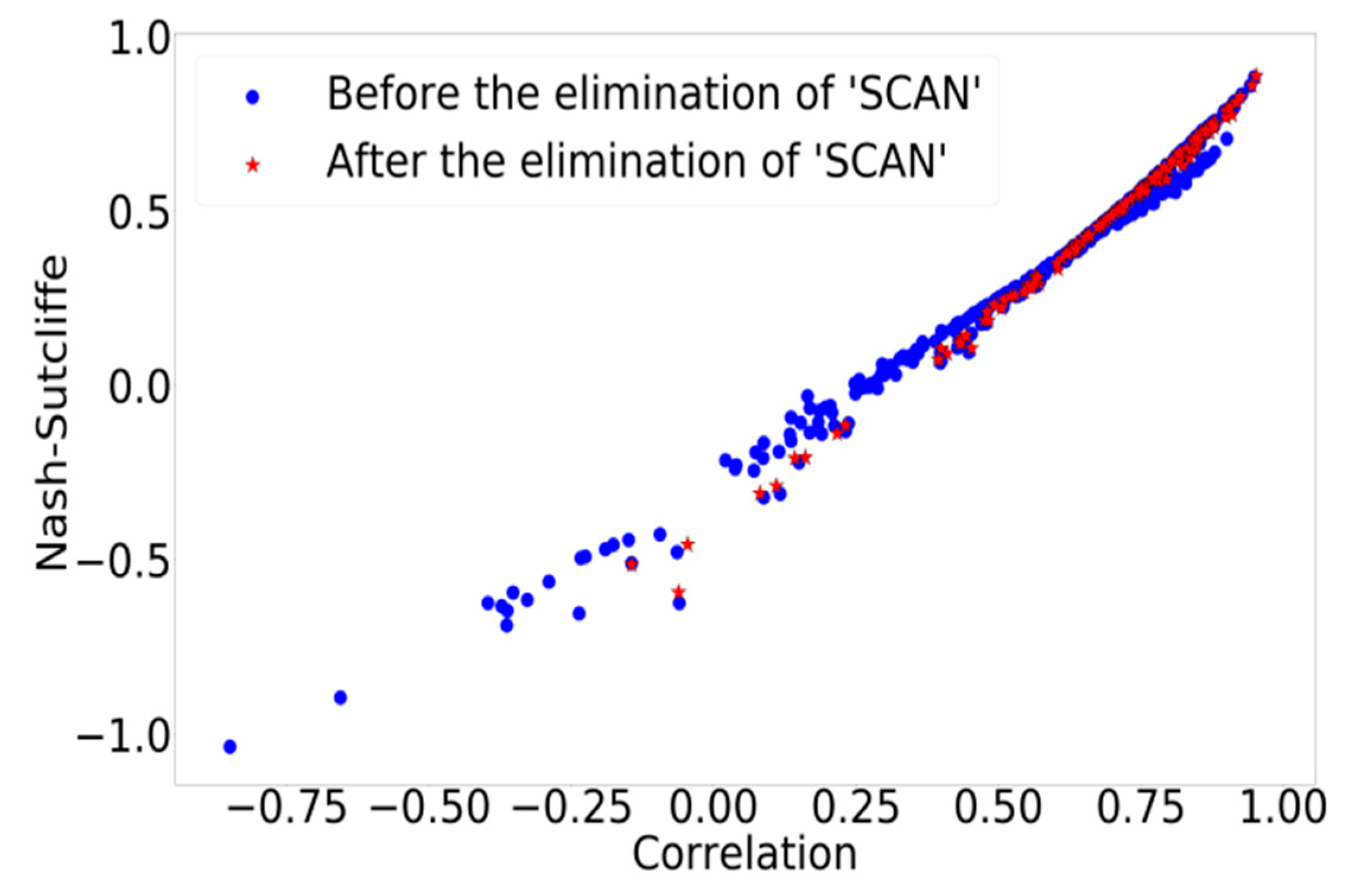
3.4. Data Filtering
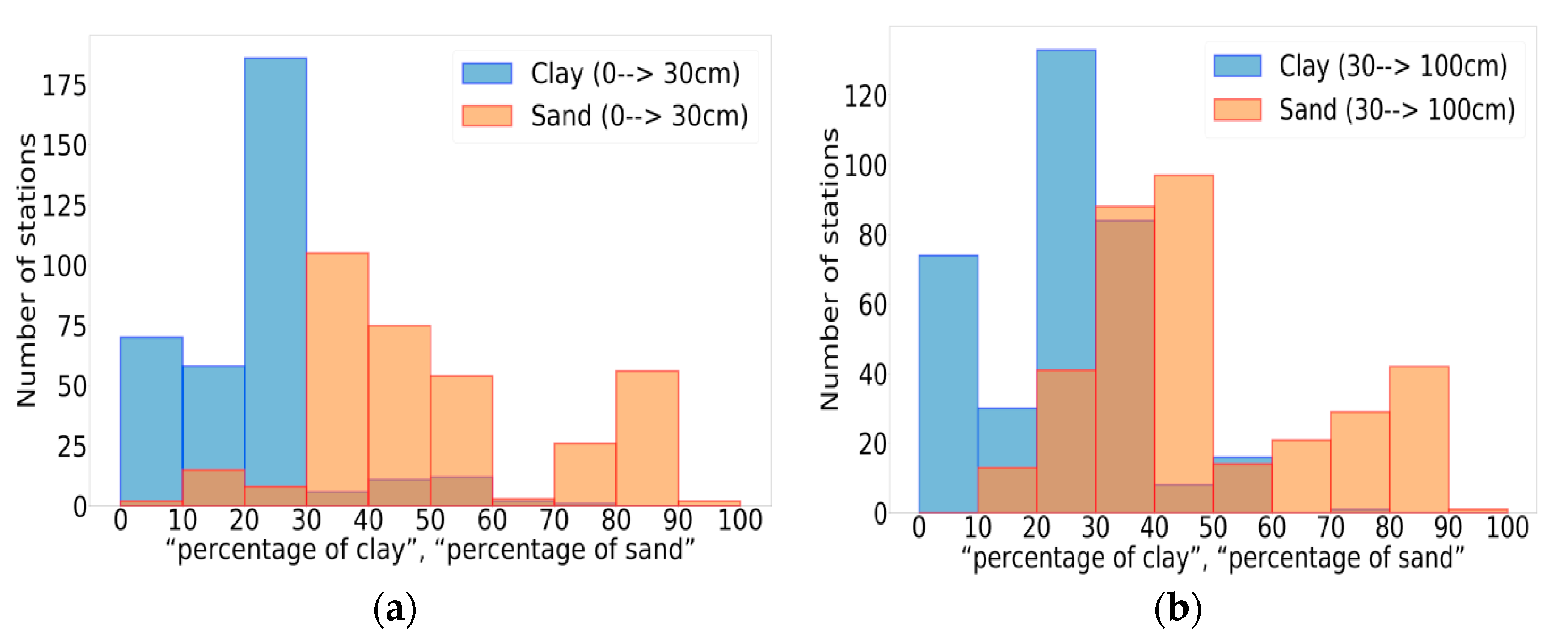
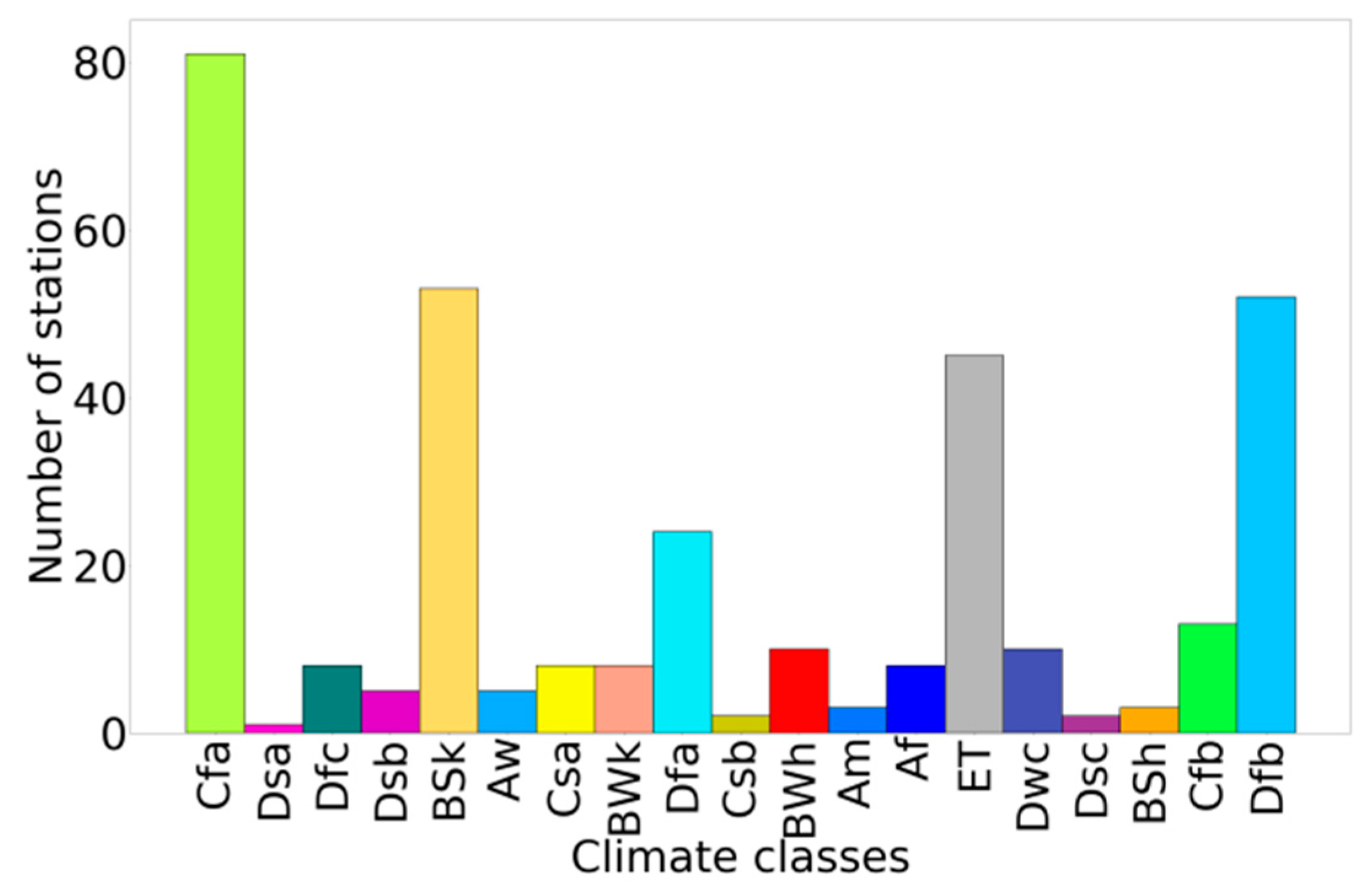
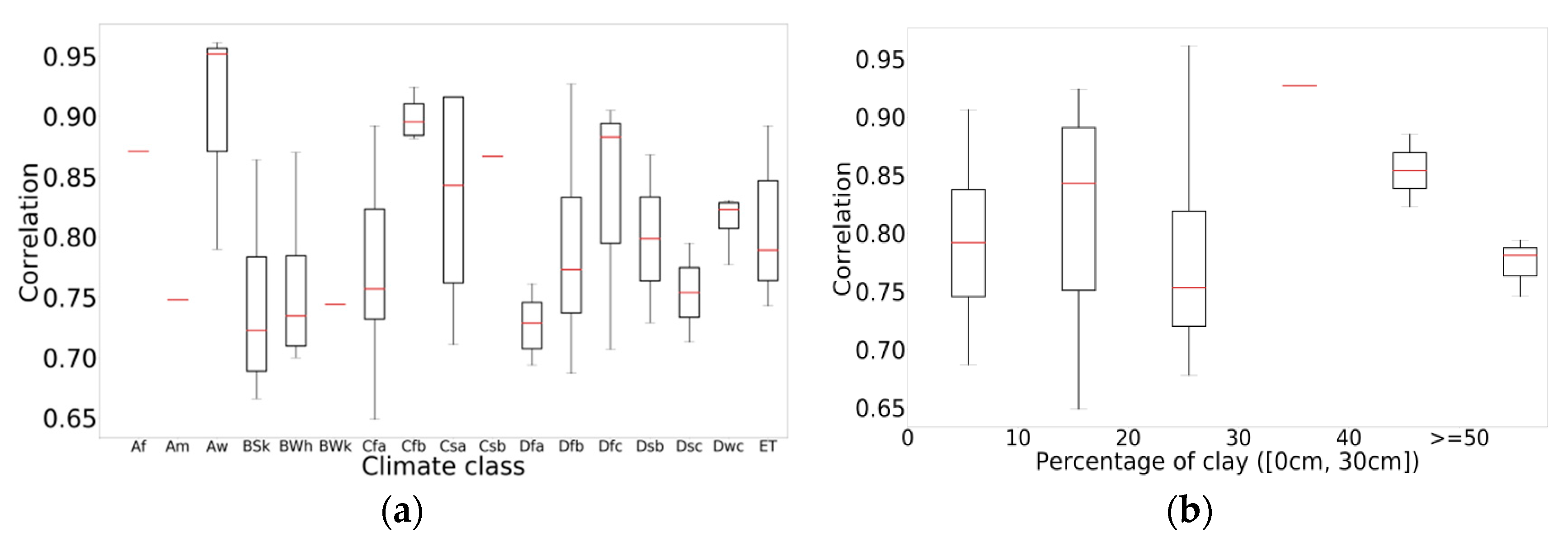
3.5. Impact of Climate and Soil Texture
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil Moisture for Hydrological Applications: Open questions and New Opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; van Oevelen, P.; et al. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef] [Green Version]
- Haubrock, S.-N.; Chabrillat, S.; Lemmnitz, C.; Kaufmann, H. Surface soil moisture quantification models from reflectance data under field conditions. Int. J. Remote Sens. 2008, 29, 3–29. [Google Scholar] [CrossRef]
- Mladenova, I.E.; Bolten, J.D.; Crow, W.; Sazib, N.; Reynolds, C. Agricultural Drought Monitoring via the Assimilation of SMAP Soil Moisture Retrievals Into a Global Soil Water Balance Model. Front. Big Data 2020, 3, 10. [Google Scholar] [CrossRef] [Green Version]
- Manfreda, S.; Brocca, L.; Moramarco, T.; Melone, F.; Sheffield, J. A physically based approach for the estimation of root-zone soil moisture from surface measurements. Hydrol. Earth Syst. Sci. 2014, 18, 1199–1212. [Google Scholar] [CrossRef] [Green Version]
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J.-C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 12, 1323–1337. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Wu, P.; Zhao, X.; Zhang, B.; Wang, J.; Shi, Y. Estimating the spatial means and variability of root-zone soil moisture in gullies using measurements from nearby uplands. J. Hydrol. 2013, 476, 28–41. [Google Scholar] [CrossRef]
- Han, E.; Merwade, V.; Heathman, G.C. Application of data assimilation with the Root Zone Water Quality Model for soil moisture profile estimation in the upper Cedar Creek, Indiana. Hydrol. Process. 2012, 26, 1707–1719. [Google Scholar] [CrossRef]
- Lekshmi, S.U.S.; Singh, D.N.; Baghini, M.S. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements of the Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; de Rosnay, P.; Jann, A.; Schneider, S.; et al. The ASCAT Soil Moisture Product: A Review of its Specifications, Validation Results, and Emerging Applications. Metz 2013, 22, 5–33. [Google Scholar] [CrossRef] [Green Version]
- Ceballos, A.; Scipal, K.; Wagner, W.; Martínez-Fernández, J. Validation of ERS scatterometer-derived soil moisture data in the central part of the Duero Basin, Spain. Hydrol. Process. 2005, 19, 1549–1566. [Google Scholar] [CrossRef]
- Wagner, W.; Naeimi, V.; Scipal, K.; de Jeu, R.; Martínez-Fernández, J. Soil moisture from operational meteorological satellites. Hydrogeol. J. 2007, 15, 121–131. [Google Scholar] [CrossRef]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.-C.; Bizzarri, B.; Wigneron, J.-P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Hydrol. Res. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Sabater, J.M.; Jarlan, L.; Calvet, J.-C.; Bouyssel, F.; De Rosnay, P. From Near-Surface to Root-Zone Soil Moisture Using Different Assimilation Techniques. J. Hydrometeor. 2007, 8, 194–206. [Google Scholar] [CrossRef]
- Masson, V.; Le Moigne, P.; Martin, E.; Faroux, S.; Alias, A.; Alkama, R.; Belamari, S.; Barbu, A.; Boone, A.; Bouyssel, F.; et al. The SURFEXv7.2 land and ocean surface platform for coupled or offline simulation of earth surface variables and fluxes. Geosci. Model Dev. 2013, 6, 929–960. [Google Scholar] [CrossRef] [Green Version]
- Noilhan, J.; Mahfouf, J.-F. The ISBA land surface parameterisation scheme. Glob. Planet. Chang. 1996, 13, 145–159. [Google Scholar] [CrossRef]
- Oleson, W.; Lawrence, M.; Bonan, B.; Flanner, G.; Kluzek, E.; Lawrence, J.; Levis, S.; Swenson, C.; Thornton, E.; Dai, A.; et al. Technical Description of version 4.0 of the Community Land Model (CLM); NCAR: Boulder, CO, USA, 2010. [Google Scholar] [CrossRef]
- Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E. AquaCrop—The FAO Crop Model to Simulate Yield Response to Water: II. Main Algorithms and Software Description. Agron. J. 2009, 101, 438–447. [Google Scholar] [CrossRef] [Green Version]
- Battude, M.; Al Bitar, A.; Brut, A.; Tallec, T.; Huc, M.; Cros, J.; Weber, J.-J.; Lhuissier, L.; Simonneaux, V.; Demarez, V. Modeling water needs and total irrigation depths of maize crop in the south west of France using high spatial and temporal resolution satellite imagery. Agric. Water Manag. 2017, 189, 123–136. [Google Scholar] [CrossRef]
- Pleim, J.E.; Xiu, A. Development of a Land Surface Model. Part II: Data Assimilation. J. Appl. Meteor. 2003, 42, 1811–1822. [Google Scholar] [CrossRef] [Green Version]
- Tanty, R.; Desmukh, T.S. MANIT BHOPAL Application of Artificial Neural Network in Hydrology—A Review. IJERT 2015, V4, IJERTV4IS060247. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Parasuraman, K. On the relevance of using artificial neural networks for estimating soil moisture content. J. Hydrol. 2008, 362, 1–18. [Google Scholar] [CrossRef]
- Kolassa, J.; Reichle, R.H.; Liu, Q.; Alemohammad, S.H.; Gentine, P.; Aida, K.; Asanuma, J.; Bircher, S.; Caldwell, T.; Colliander, A.; et al. Estimating surface soil moisture from SMAP observations using a Neural Network technique. Remote Sens. Environ. 2018, 204, 43–59. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.; Kornelsen, K.C.; Coulibaly, P. Estimating Root Zone Soil Moisture at Continental Scale Using Neural Networks. J. Am. Water Resour. Assoc. 2017, 53, 220–237. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Ramchoun, H.; Amine, M.; Idrissi, J.; Ghanou, Y.; Ettaouil, M. Multilayer Perceptron: Architecture Optimization and Training. IJIMAI 2016, 4, 26. [Google Scholar] [CrossRef]
- Oyebode, O.; Stretch, D. Neural network modeling of hydrological systems: A review of implementation techniques. Nat. Resour. Modeling 2019, 32, e12189. [Google Scholar] [CrossRef] [Green Version]
- Heaton, J. Introduction to Neural Networks with Java; Heaton Research, Inc.: St. Louis, MO, USA, 2008; ISBN 9781604390087. [Google Scholar]
- Chai, S.-S.; Walker, J.; Makarynskyy, O.; Kuhn, M.; Veenendaal, B.; West, G. Use of Soil Moisture Variability in Artificial Neural Network Retrieval of Soil Moisture. Remote Sens. 2009, 2, 166–190. [Google Scholar] [CrossRef] [Green Version]
- Yonaba, H.; Anctil, F.; Fortin, V. Comparing Sigmoid Transfer Functions for Neural Network Multistep Ahead Streamflow Forecasting. J. Hydrol. Eng. 2010, 15, 275–283. [Google Scholar] [CrossRef]
- Bishop, C.M.; Bishop, P. Neural Networks for Pattern Recognition; Clarendon Press: Oxford, UK, 1995; ISBN 9780198538646. [Google Scholar]
- Koster, R.D.; Guo, Z.; Yang, R.; Dirmeyer, P.A.; Mitchell, K.; Puma, M.J. On the Nature of Soil Moisture in Land Surface Models. J. Clim. 2009, 22, 4322–4335. [Google Scholar] [CrossRef] [Green Version]
- Crow, W.T.; Miralles, D.G.; Cosh, M.H. A Quasi-Global Evaluation System for Satellite-Based Surface Soil Moisture Retrievals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2516–2527. [Google Scholar] [CrossRef]
- Priddy, K.L.; Keller, P.E. Artificial Neural Networks: An Introduction; SPIE Press: Bellingham, WA, USA, 2005; ISBN 9780819459879. [Google Scholar]
- Jayalakshmi, T.; Santhakumaran, A. Statistical Normalization and Back Propagation for Classification. IJCTE 2011, 89–93. [Google Scholar] [CrossRef]
- Dabrowska-Zielinska, K.; Musial, J.; Malinska, A.; Budzynska, M.; Gurdak, R.; Kiryla, W.; Bartold, M.; Grzybowski, P. Soil Moisture in the Biebrza Wetlands Retrieved from Sentinel-1 Imagery. Remote Sens. 2018, 10, 1979. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, W.A.; Xaver, A.; Vreugdenhil, M.; Gruber, A.; Hegyiová, A.; Sanchis-Dufau, A.D.; Zamojski, D.; Cordes, C.; Wagner, W.; Drusch, M. Global Automated Quality Control of In Situ Soil Moisture Data from the International Soil Moisture Network. Vadose Zone J. 2013, 12, vzj2012.0097. [Google Scholar] [CrossRef]
- Jackson, T.J.; Hawley, M.E.; O’Neill, P.E. Preplanting Soil Moisture Using Passive Microwave Sensors1. Jawra J. Am. Water Resour. Assoc. 1987, 23, 11–19. [Google Scholar] [CrossRef]
- Kornelsen, K.C.; Coulibaly, P. Root-zone soil moisture estimation using data-driven methods. Water Resour. Res. 2014, 50, 2946–2962. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Stroud, P.D. A Recursive Exponential Filter For Time-Sensitive Data; Los Alamos National Laboratory: Los Alamos, Mexico, 1999.
- Gao, X.; Zhao, X.; Brocca, L.; Pan, D.; Wu, P. Testing of observation operators designed to estimate profile soil moisture from surface measurements. Hydrol. Process. 2019, 33, 575–584. [Google Scholar] [CrossRef]
- Arya, L.M.; Richter, J.C.; Paris, J.F. Estimating profile water storage from surface zone soil moisture measurements under bare field conditions. Water Resour. Res. 1983, 19, 403–412. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.D. Three-dimensional soil moisture profile retrieval by assimilation of near-surface measurements: Simplified Kalman filter covariance forecasting and field application. Water Resour. Res. 2002, 38, 37-1–37-13. [Google Scholar] [CrossRef] [Green Version]
- Hirschi, M.; Mueller, B.; Dorigo, W.; Seneviratne, S.I. Using remotely sensed soil moisture for land–atmosphere coupling diagnostics: The role of surface vs. root-zone soil moisture variability. Remote Sens. Environ. 2014, 154, 246–252. [Google Scholar] [CrossRef] [Green Version]
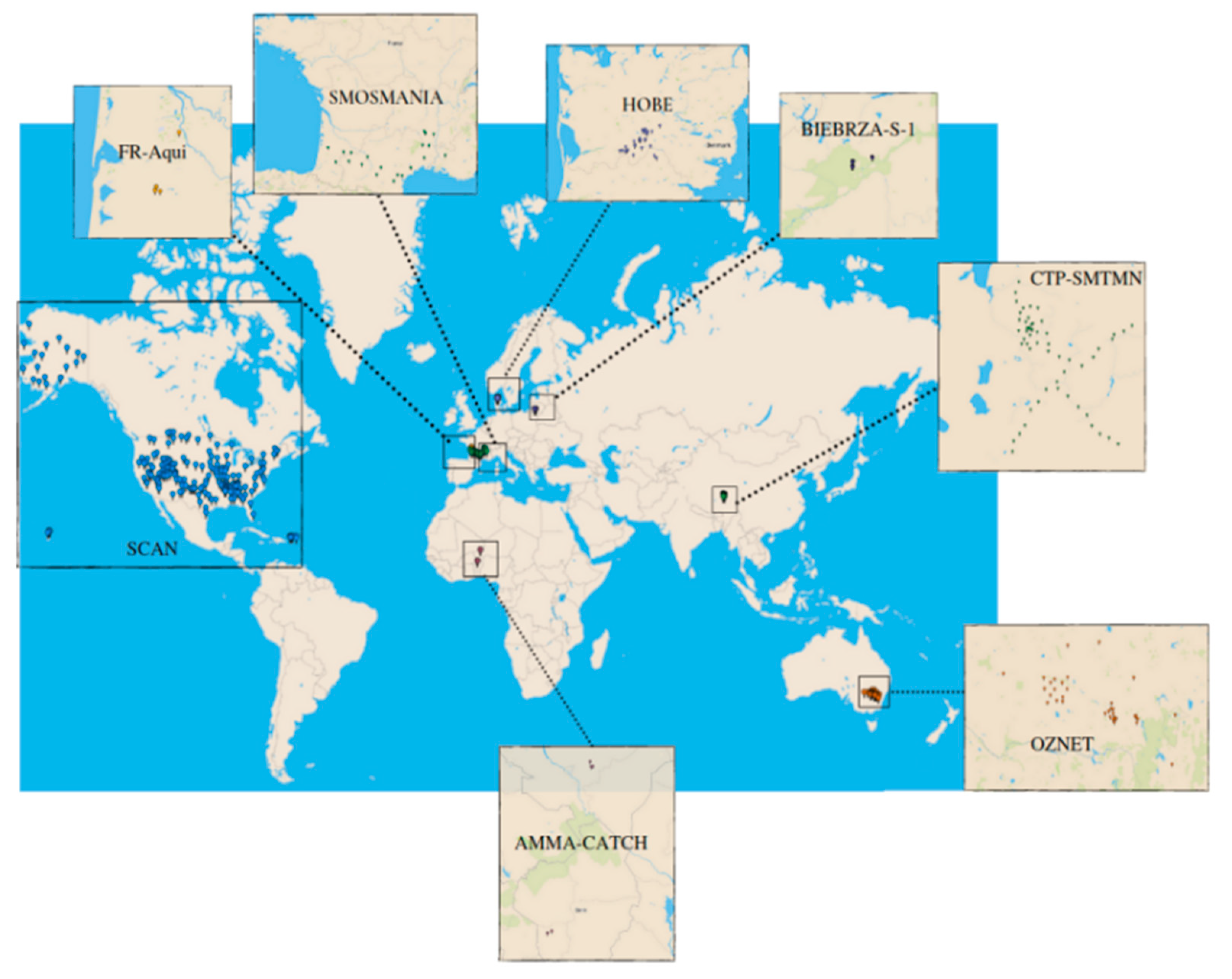
| Network | Country | Number of Selected Stations | Selected RZSM Depth (cm) | SM Sensors | Length of Record (Hourly) |
|---|---|---|---|---|---|
| AMMA-CATCH | Benin, Niger | 5 (3 in Benin +2 in Niger) | 40 | CS616 | 191,997 |
| BIEBRZA-S-1 | Poland | 3 | 50 | GS-3 | 11,401 |
| CTP-SMTMN | China | 54 | 40 | EC-TM/5TM | 716,139 |
| HOBE | Denmark | 29 | 55 | Decagon-5TE | 819,591 |
| FR-Aqui | France | 5 | 30, 34, 50 | ThetaProbe ML2X | 200,087 |
| OZNET | Australia | 19 | 30 | Hydra Probe-CS616 | 519,938 |
| SCAN | USA | 209 | 50 | Hydraprobe-Sdi-12/Ana | 6,777,222 |
| SMOSMANIA | France | 22 | 30 | ThetaProbe ML2X | 818,031 |
| Training Test | ANN-AMMA-CATCH | ANN-BIEBRZA-S-1 | ANN-CTP-SMTMN | ANN-FR-Aqui | ANN-HOBE | ANN-OZNET | ANN-SCAN | ANN-SMOSMANIA |
|---|---|---|---|---|---|---|---|---|
| AMMA-CATCH | +1.12% | +0.10% | +0.61% | +0.61% | 0% | 0% | −1.02% | +0.51% |
| BIEBRZA-S-1 | −0.66% | +3.53% | −2.21% | −0.55% | −0.55% | −3.31% | −1.88% | +0.99% |
| CTP-SMTMN | −0.88% | −3.62% | +0.77% | −0.33% | +0.33% | +0.11% | −0.99% | −0.21% |
| FR-Aqui | +0.46% | −3.56% | −1.26% | +2.53% | −1.49% | −3.1% | −2.76% | −2.07% |
| HOBE | −2.40% | −1.49% | −1.03% | −1.83% | +0.34% | −0.92% | −1.26% | −0.34% |
| OZNET | −5.03% | −6.42% | −1.51% | −5.28% | −0.50% | +1.26% | −1.89% | −3.02% |
| SCAN | −1.5% | −1.39% | −1.07% | −1.07% | −0.43% | −0.64% | +0.11% | −1.28% |
| SMOSMANIA | +0.57% | −1.82% | +0.11% | −0.57% | +1.82% | −1.25% | −3.65% | +3.53% |
| Training Test | ANN-(TOT- AMMA-CATCH) | ANN-(TOT-BIEBRZA-S-1) | ANN-(TOT-CTP-SMTMN) | ANN-(TOT- FR-Aqui) | ANN-(TOT- HOBE) | ANN-(TOT- OZNET) | ANN-(TOT- SCAN) | ANN-(TOT- SMOSMANIA) |
|---|---|---|---|---|---|---|---|---|
| AMMA-CATCH | −0.20% | −0.10% | −0.31% | −0.20% | 0% | 0% | 0.92% | 0% |
| BIEBRZA-S-1 | −0.44% | −0.44% | −0.66% | −0.22% | −0.44% | −0.33% | −0.33% | −0.11% |
| CTP-SMTMN | 0% | 0% | −0.33% | 0.11% | 0% | 0% | 0.66% | 0.22% |
| FR-Aqui | −0.46% | −0.35% | −0.46% | −0.58% | −0.12% | −0.12% | 1.61% | −0.12% |
| HOBE | −0.11% | −0.11% | −0.23% | −0.11% | −0.23% | −0.11% | 0.34% | 0.11% |
| OZNET | 0% | −0.13% | −0.38% | 0% | −0.13% | −0.38% | −0.13% | 0.25% |
| SCAN | 0% | 0% | 0.11% | 0% | 0% | 0% | −0.53% | 0% |
| SMOSMANIA | −0.12% | −0.23% | −0.81% | 0% | 0% | 0.12% | 2.77% | 0.69% |
| q | Number of ES | Number of NES |
|---|---|---|
| 0.9 | 308 | 38 |
| 0.8 | 275 | 71 |
| 0.75 | 254 | 92 |
| 0.65 | 224 | 122 |
| 0.5 | 170 | 176 |
| 0.4 | 141 | 205 |
| 0.3 | 105 | 241 |
| 0.2 | 71 | 275 |
| 0.1 | 38 | 308 |
| Q | Number of ES | Number of NES | Correlation | NSE | RMSE |
|---|---|---|---|---|---|
| 0.9 | 308 | 38 | 48.7% of ES 73.68% of NES | 28.57% of ES 100% of NES | 34.41% of ES 100% of NES |
| 0.8 | 275 | 71 | 44.72% of ES 63.38% of NES | 26.18% of ES 97.18% of NES | 36.72% of ES 97.18% of NES |
| 0.75 | 254 | 92 | 47,24% of ES 70.65% of NES | 24.8% of ES 95.65% of NES | 17.71% of ES 88.04% of NES |
| 0.65 | 224 | 122 | 41.07% of ES 63.93% of NES | 19.19% of ES 88.53% of NES | 11.16% of ES 78.69% of NES |
| 0.5 | 170 | 176 | 47.06% of ES 66.48% of NES | 14.71% of ES 88.07% of NES | 10.59% of ES 73.86% of NES |
| 0.4 | 141 | 205 | 41.13% of ES 60.98% of NES | 14.18% of ES 78.05% NES | 7.09% of ES 63.41% of NES |
| 0.3 | 105 | 241 | 39.05% of ES 66.39% of NES | 13.33% of ES 78% of NES | 7.62% of ES 60.17% of NES |
| 0.2 | 71 | 275 | 25.35% of ES 60% of NES | 11.26% of ES 73.45% of NES | 0% of ES 50.18% of NES |
| 0.1 | 38 | 308 | 23.68% of ES 63.31% of NES | 13.16% of ES 67.85% of NES | 0% of ES 39.94% of NES |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souissi, R.; Al Bitar, A.; Zribi, M. Accuracy and Transferability of Artificial Neural Networks in Predicting in Situ Root-Zone Soil Moisture for Various Regions across the Globe. Water 2020, 12, 3109. https://doi.org/10.3390/w12113109
Souissi R, Al Bitar A, Zribi M. Accuracy and Transferability of Artificial Neural Networks in Predicting in Situ Root-Zone Soil Moisture for Various Regions across the Globe. Water. 2020; 12(11):3109. https://doi.org/10.3390/w12113109
Chicago/Turabian StyleSouissi, Roïya, Ahmad Al Bitar, and Mehrez Zribi. 2020. "Accuracy and Transferability of Artificial Neural Networks in Predicting in Situ Root-Zone Soil Moisture for Various Regions across the Globe" Water 12, no. 11: 3109. https://doi.org/10.3390/w12113109







