Deformation and Stability Characteristics of Layered Rock Slope Affected by Rainfall Based on Anisotropy of Strength and Hydraulic Conductivity
Abstract
:1. Introduction
2. Materials and Methods
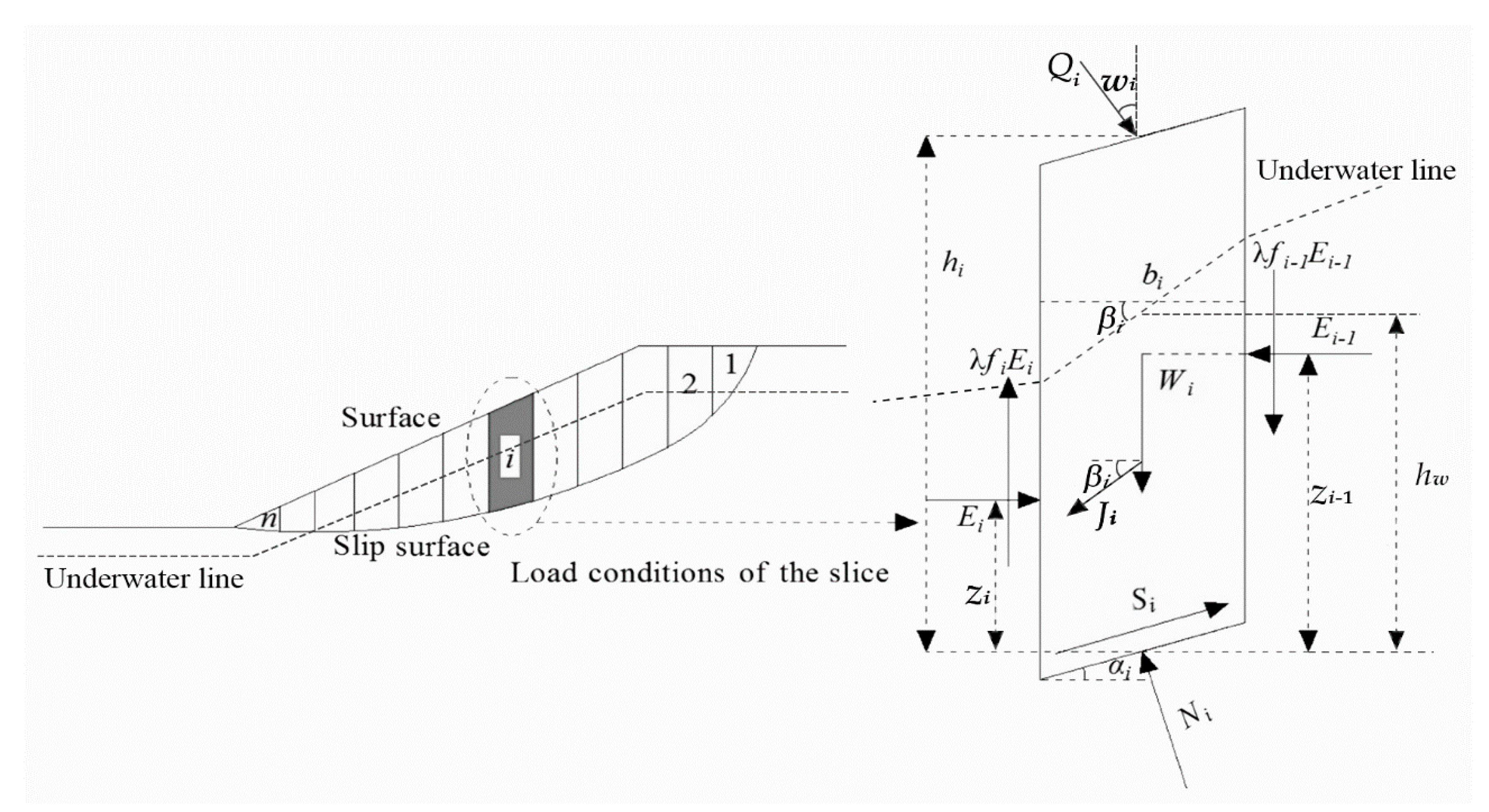
2.1. Control Differential Equation
2.2. Theory of Fluid–Solid Coupling
2.3. Establishment of the Factor of Safety for Unsaturated Rock
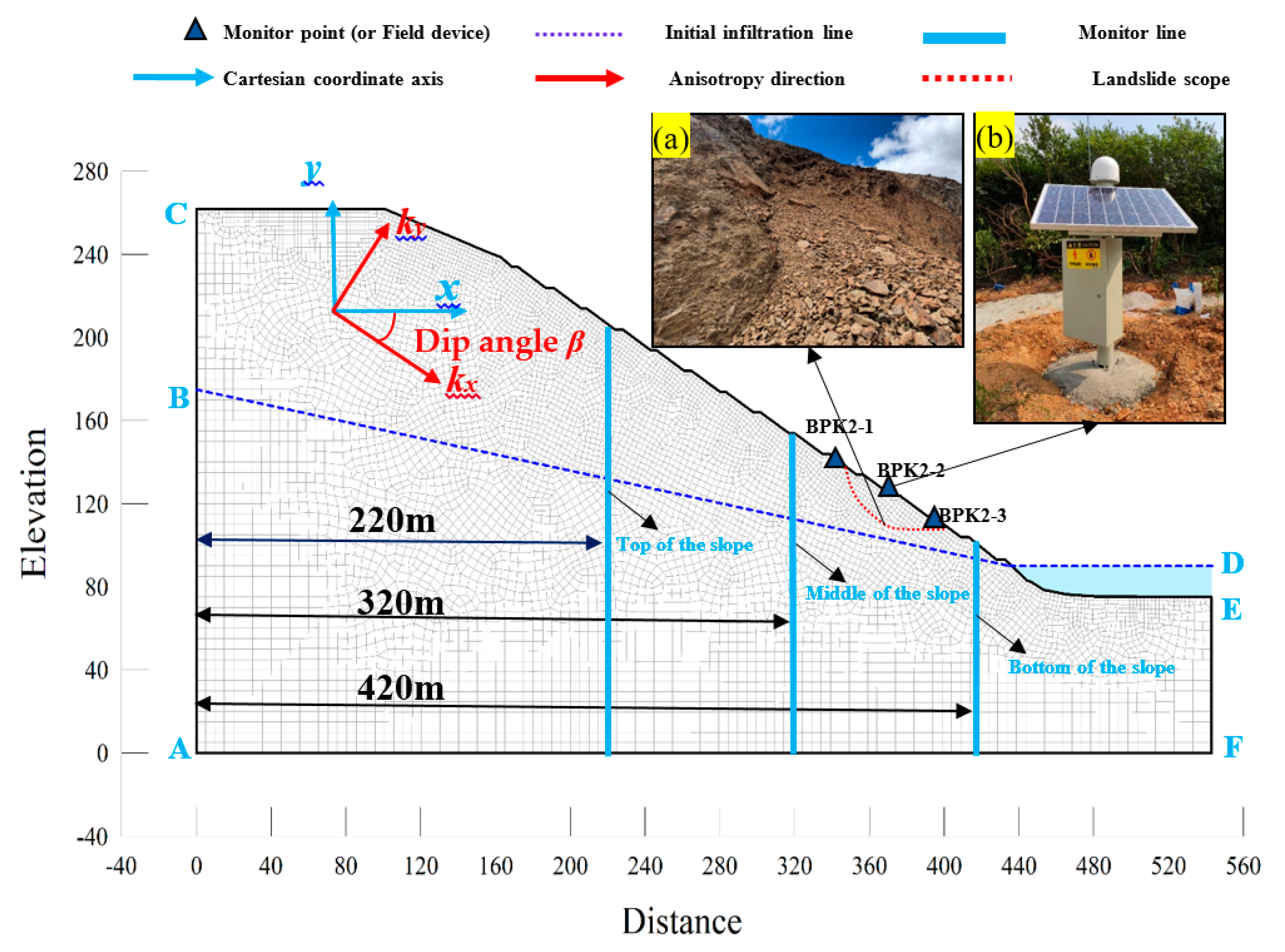
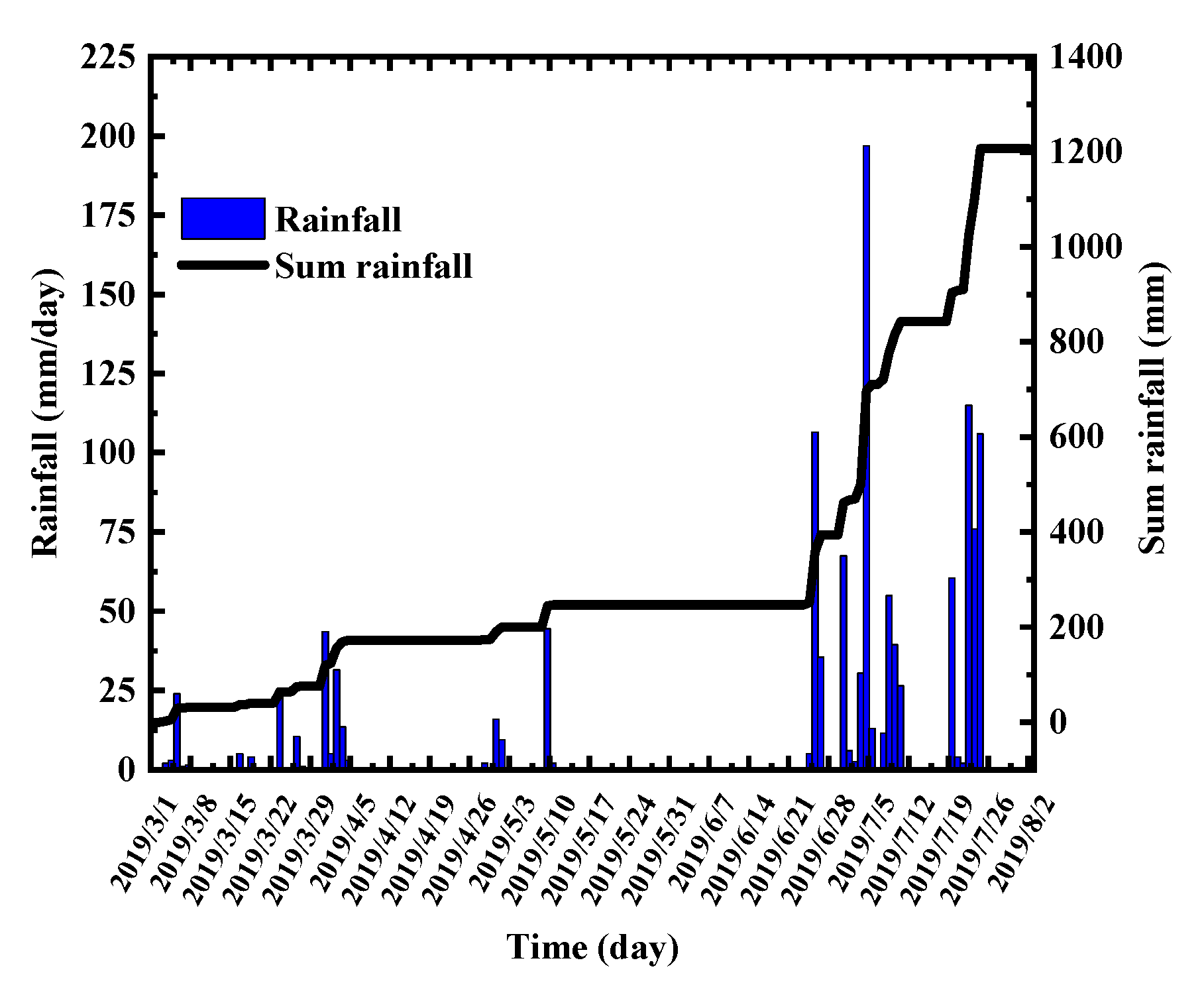
2.4. Establishment of the Numerical Calculation Model
2.5. Determination of the Maximum Initial Matric Suction
2.6. Establishment of Unsaturated Permeability Coefficient
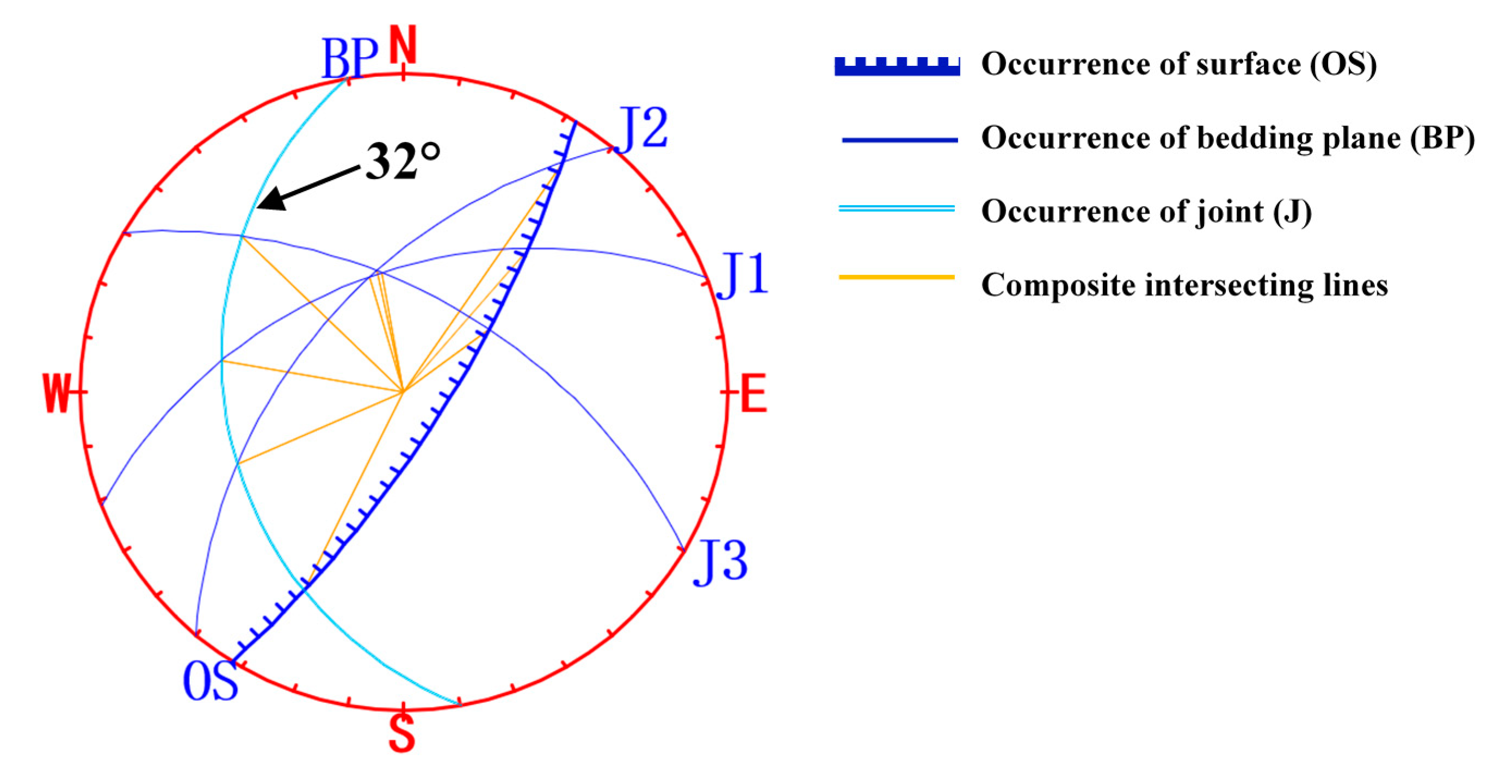
2.7. Definition of Anisotropy and the Calculation Conditions
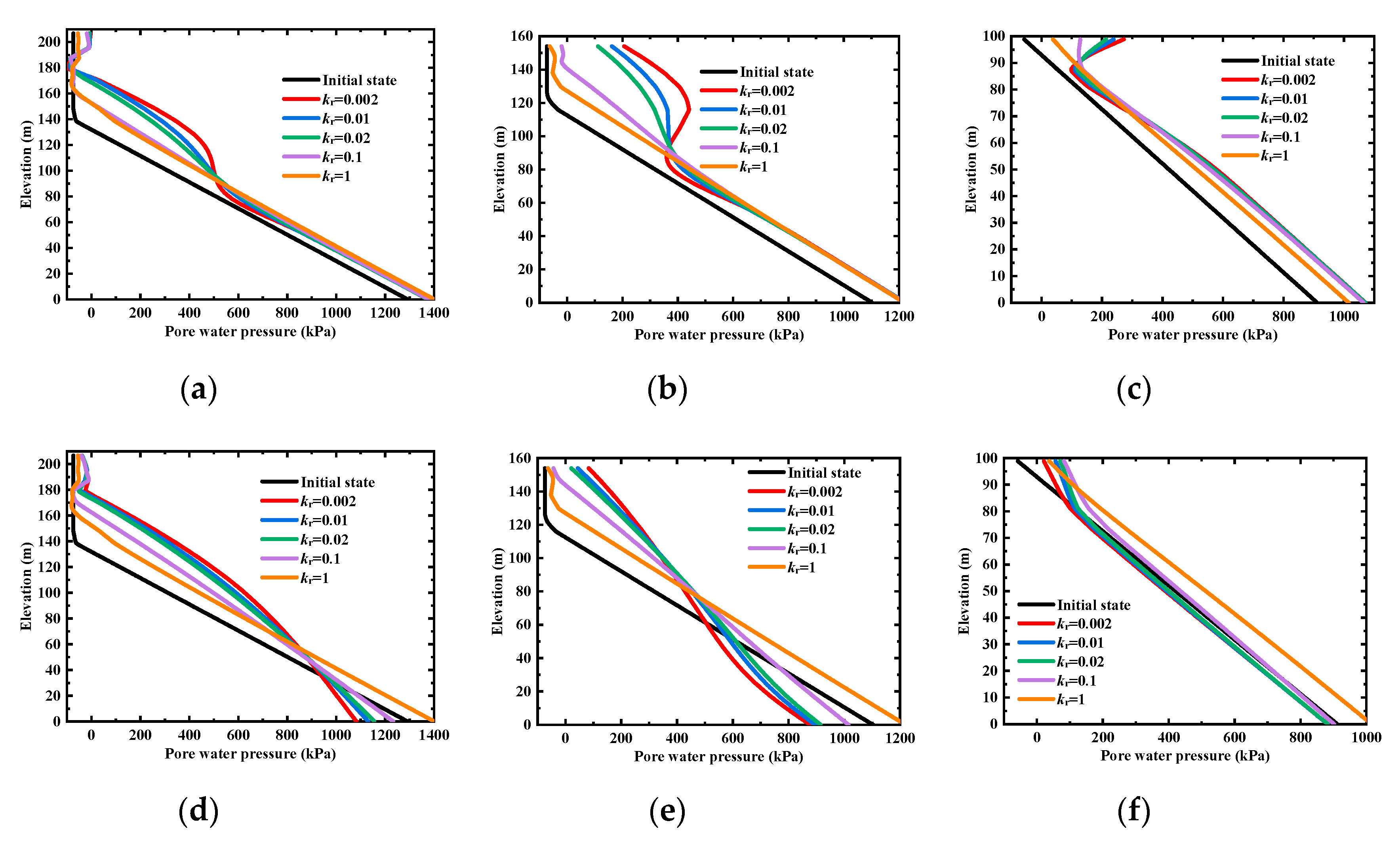
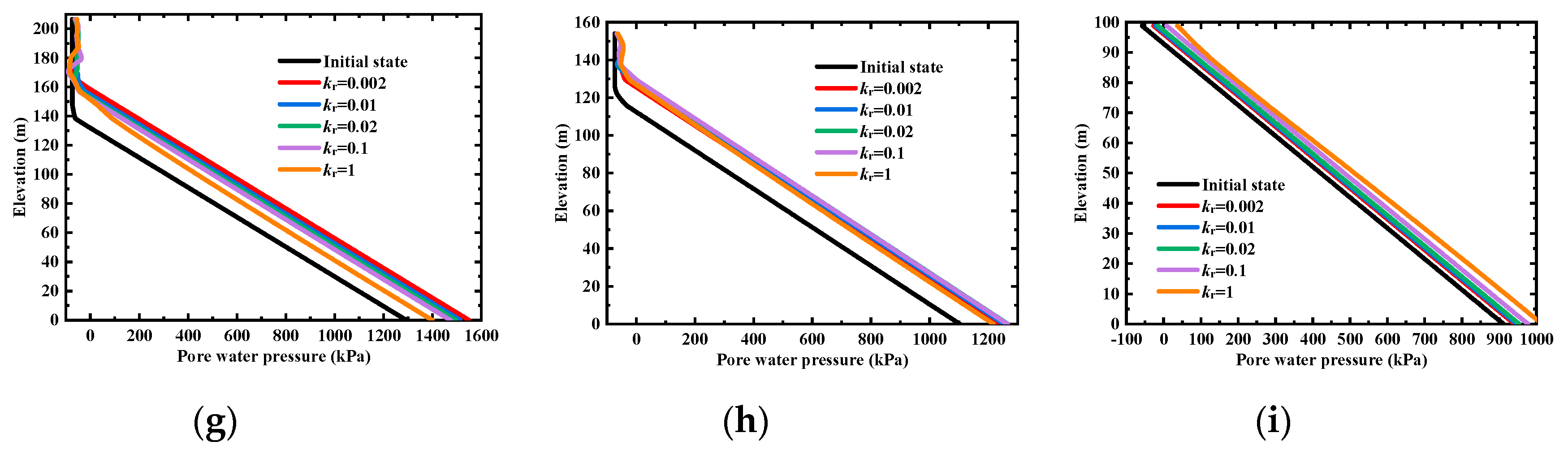
3. Results
3.1. Effects of the Hydraulic Conductivity and Strength Anisotropy on the Deformation Characteristics
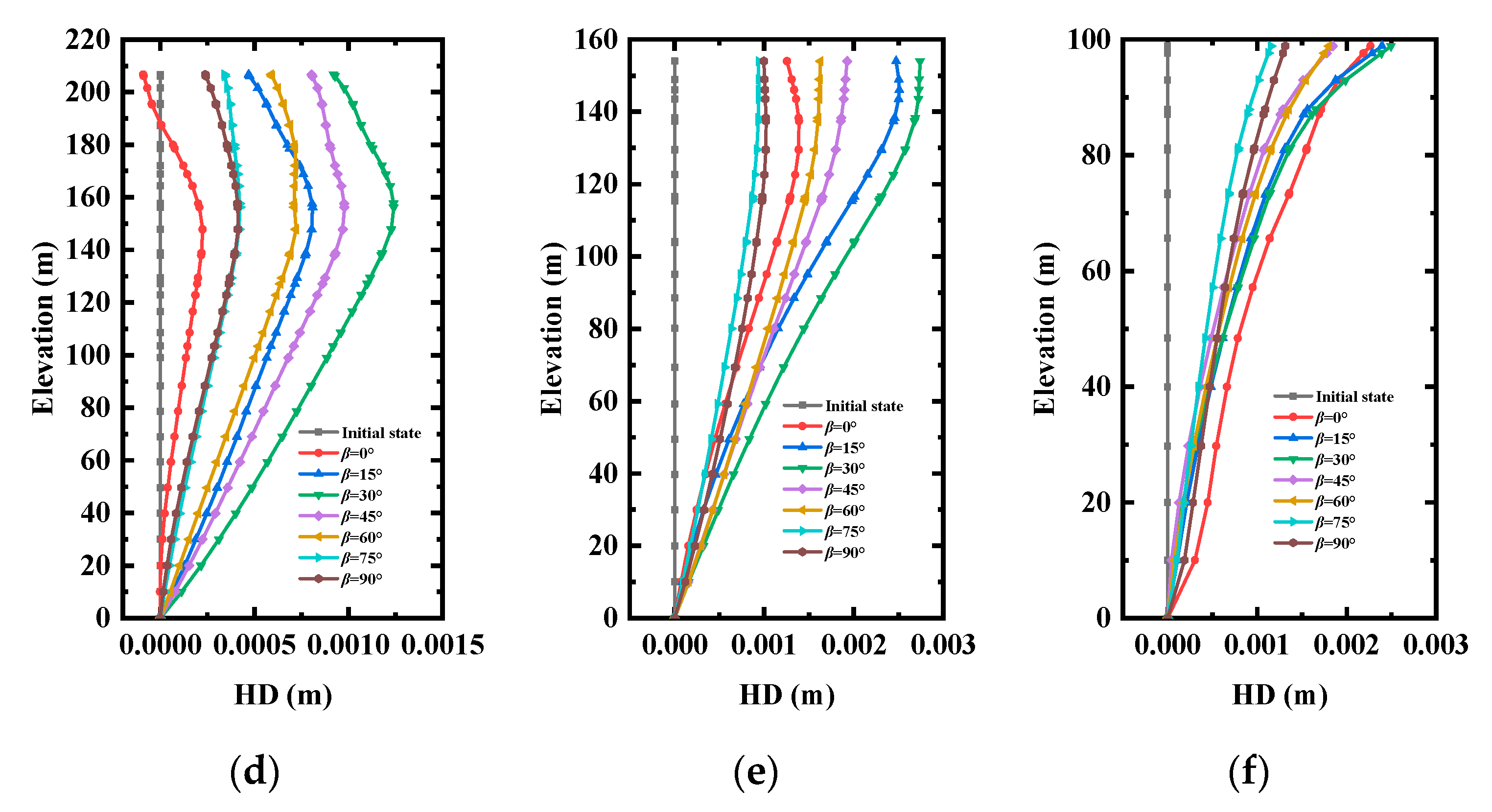
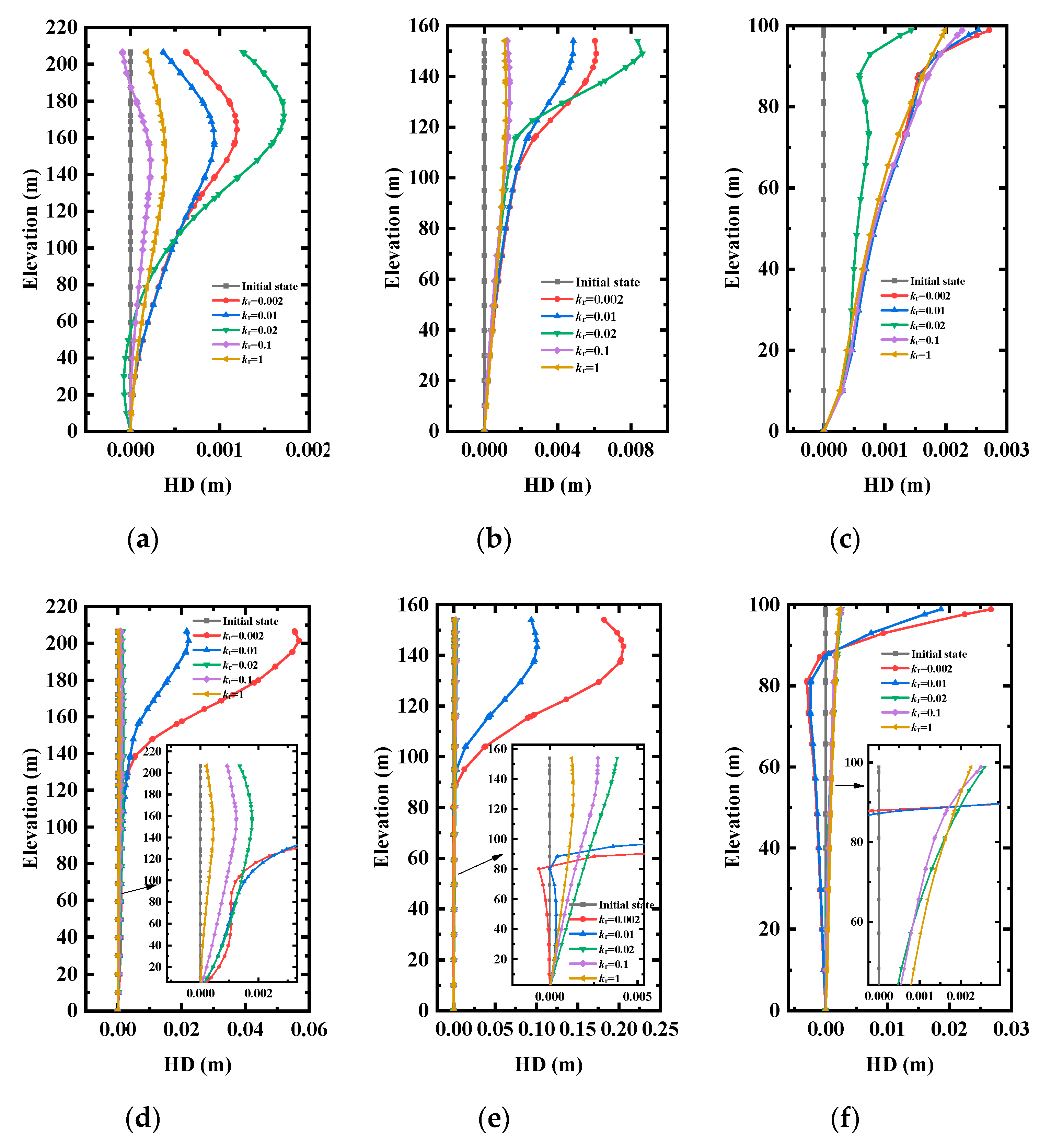
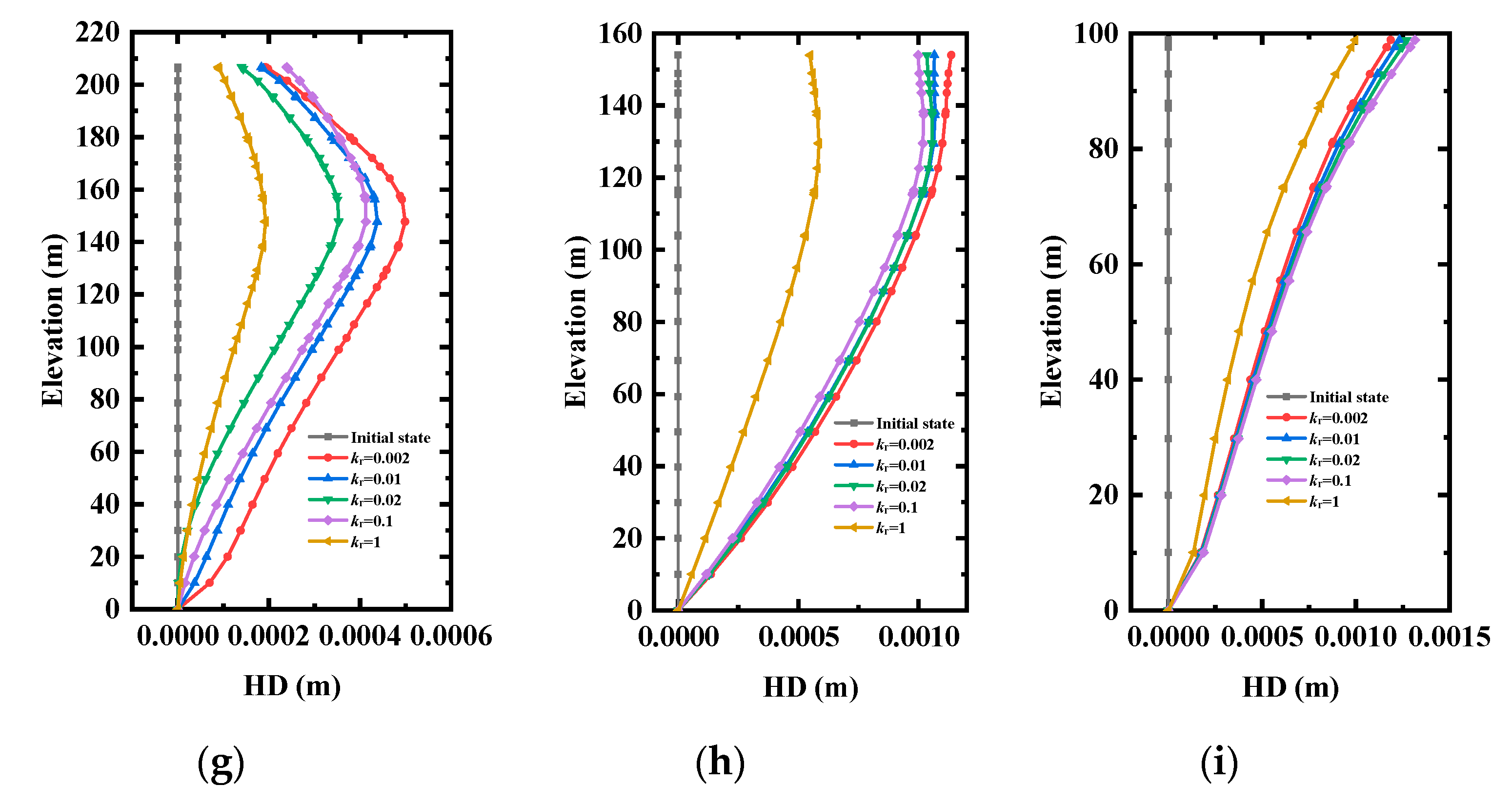
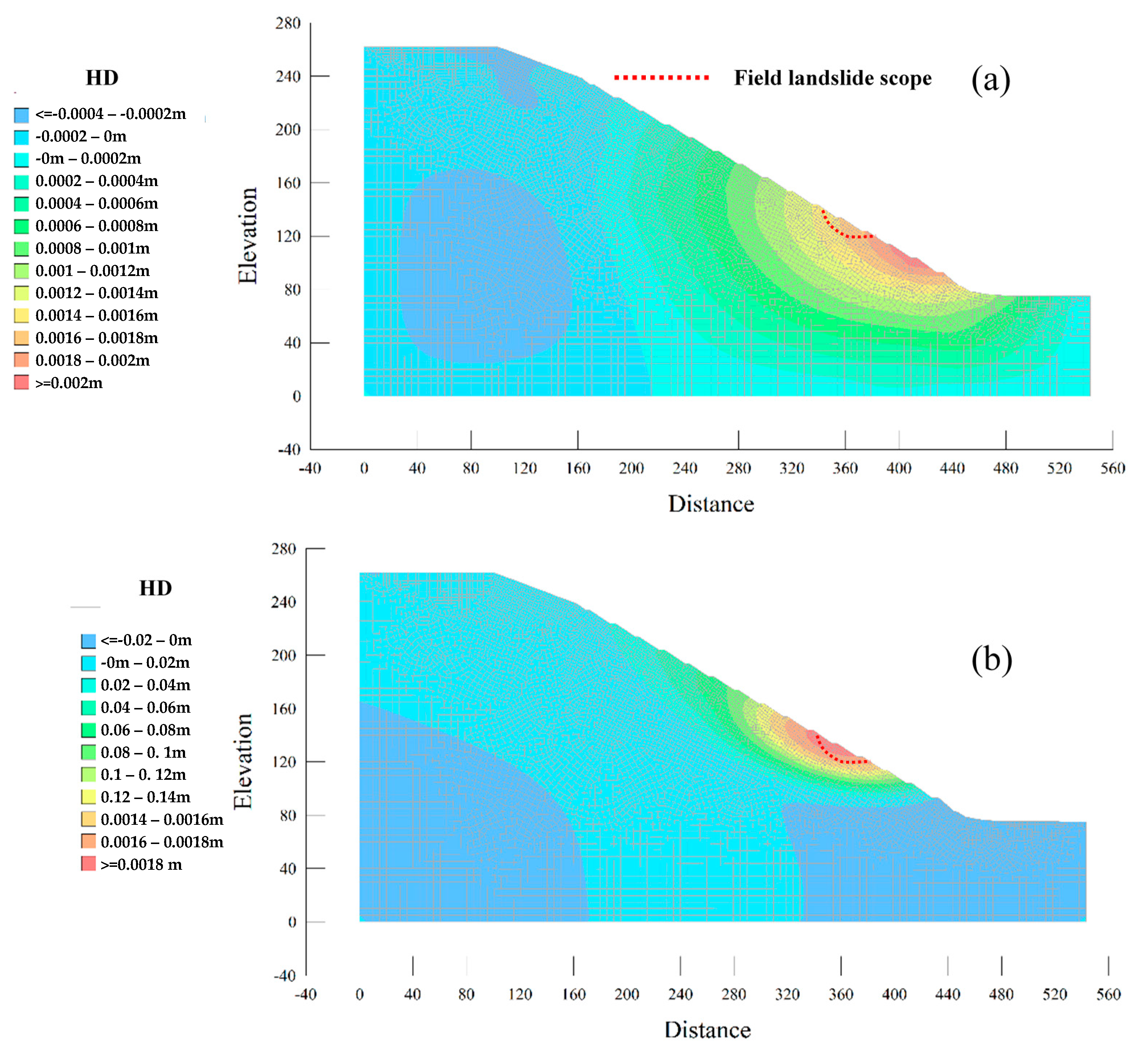
3.1.1. Analysis of the Horizontal Displacement of Monitoring Line
3.1.2. Analysis of the Horizontal Displacement of Monitoring Point
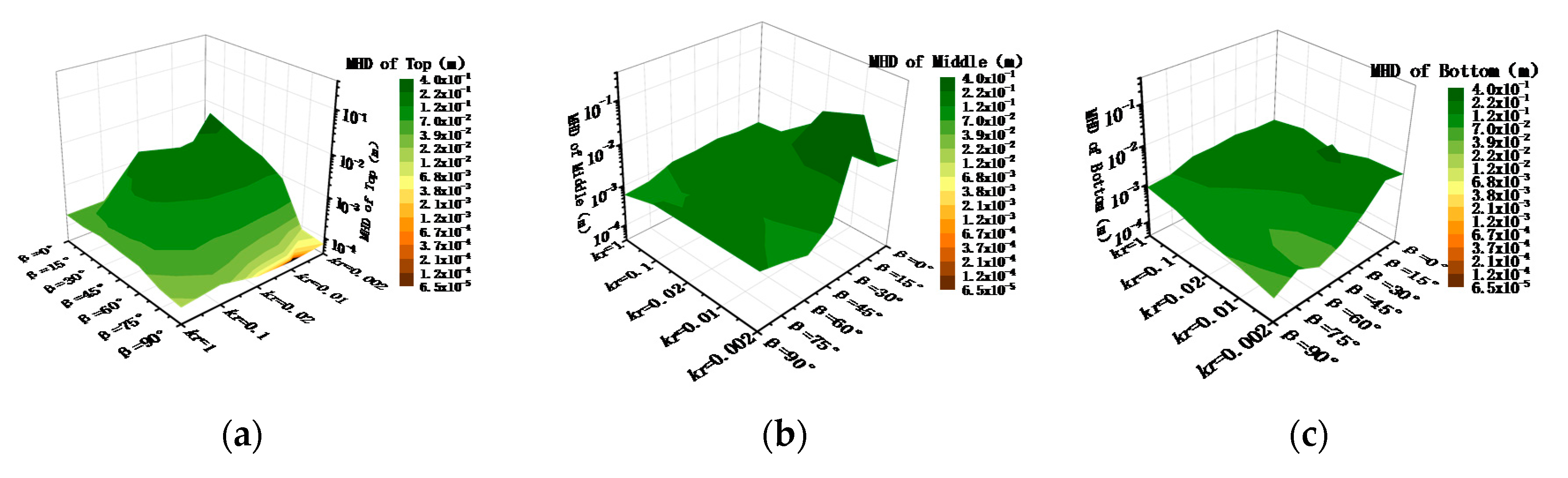
3.1.3. Analysis of the Maximum Horizontal Displacement
3.2. Effects of the Hydraulic Conductivity and Strength Anisotropy on the Stability of the Rock Slope
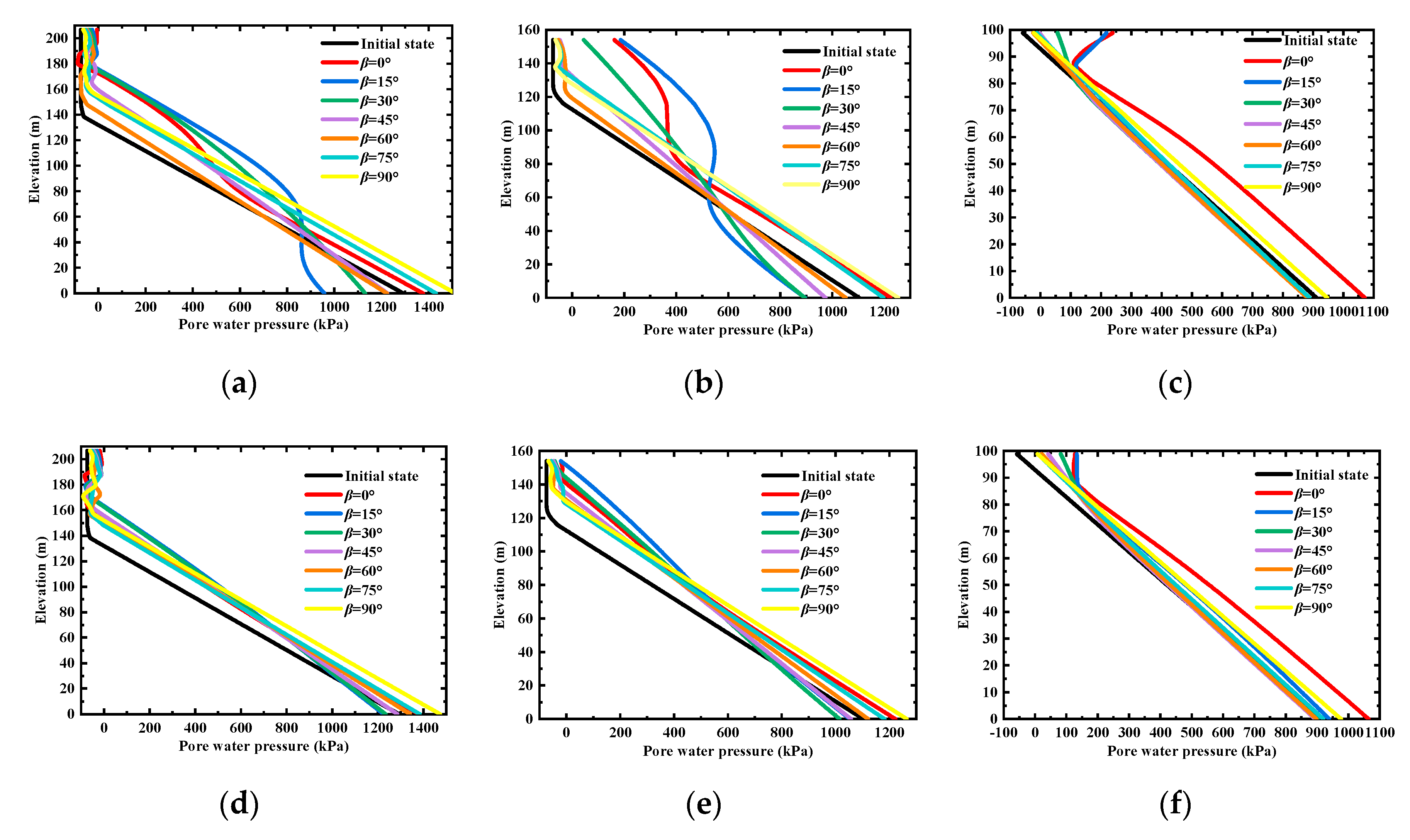
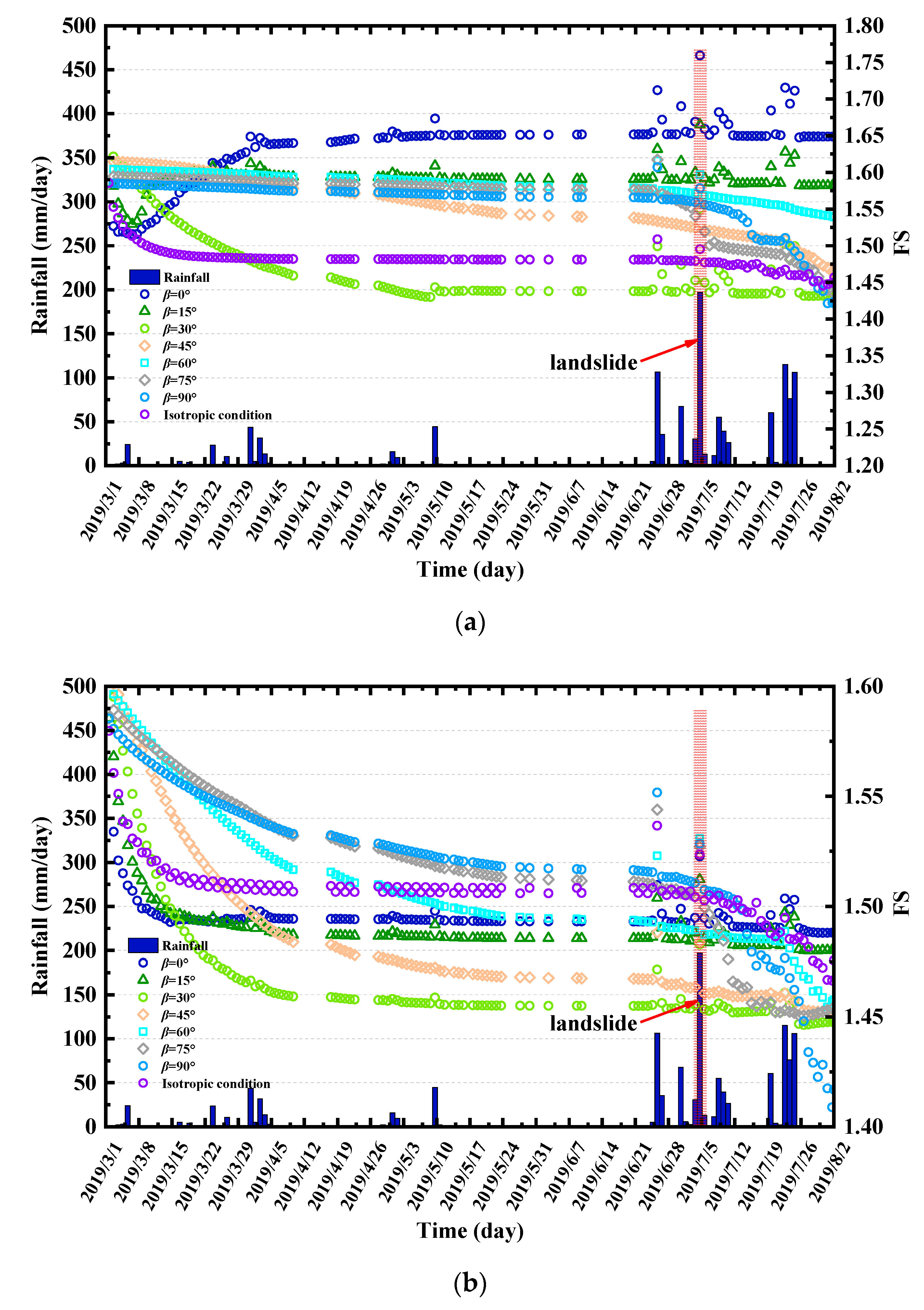
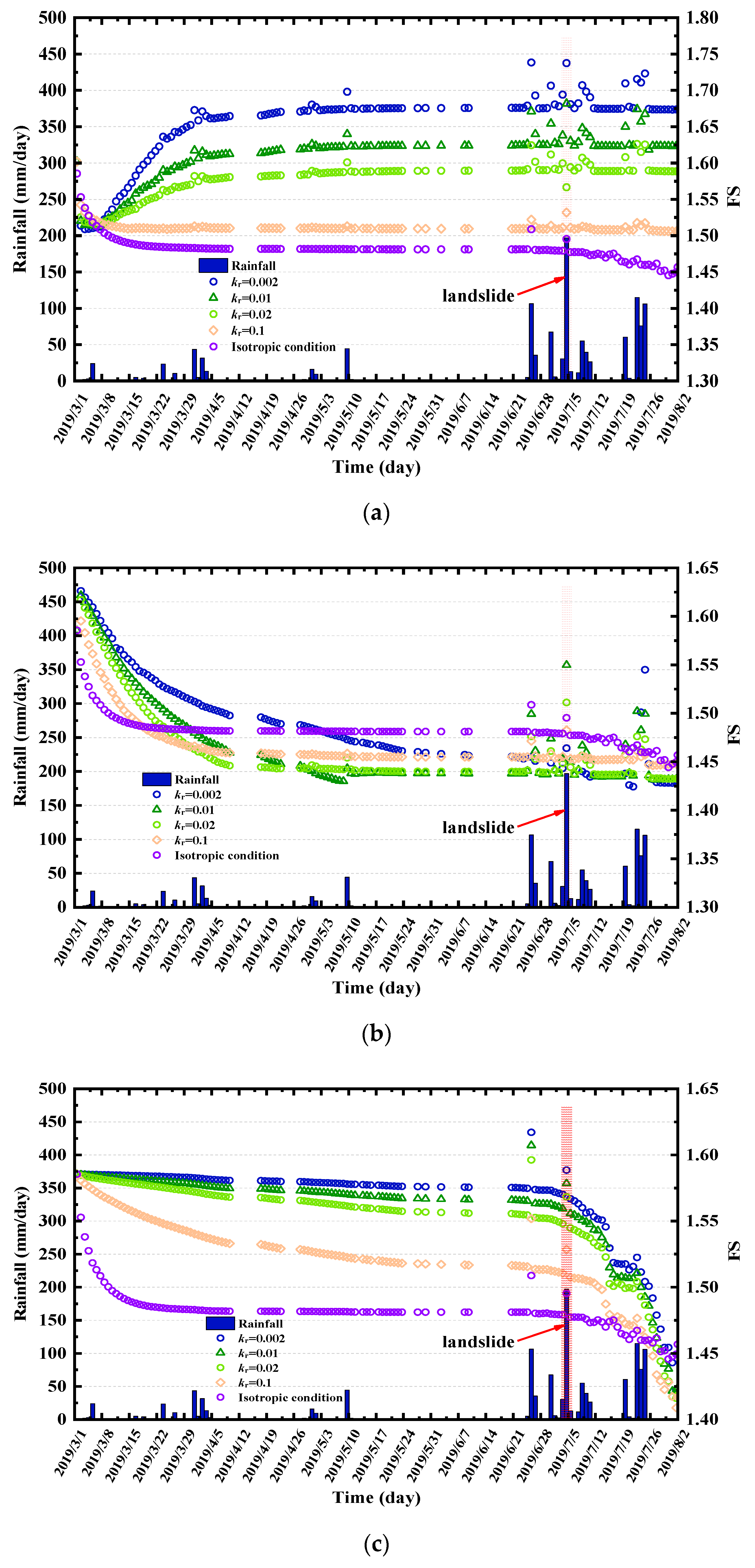
3.2.1. Analysis of the Factor of Safety
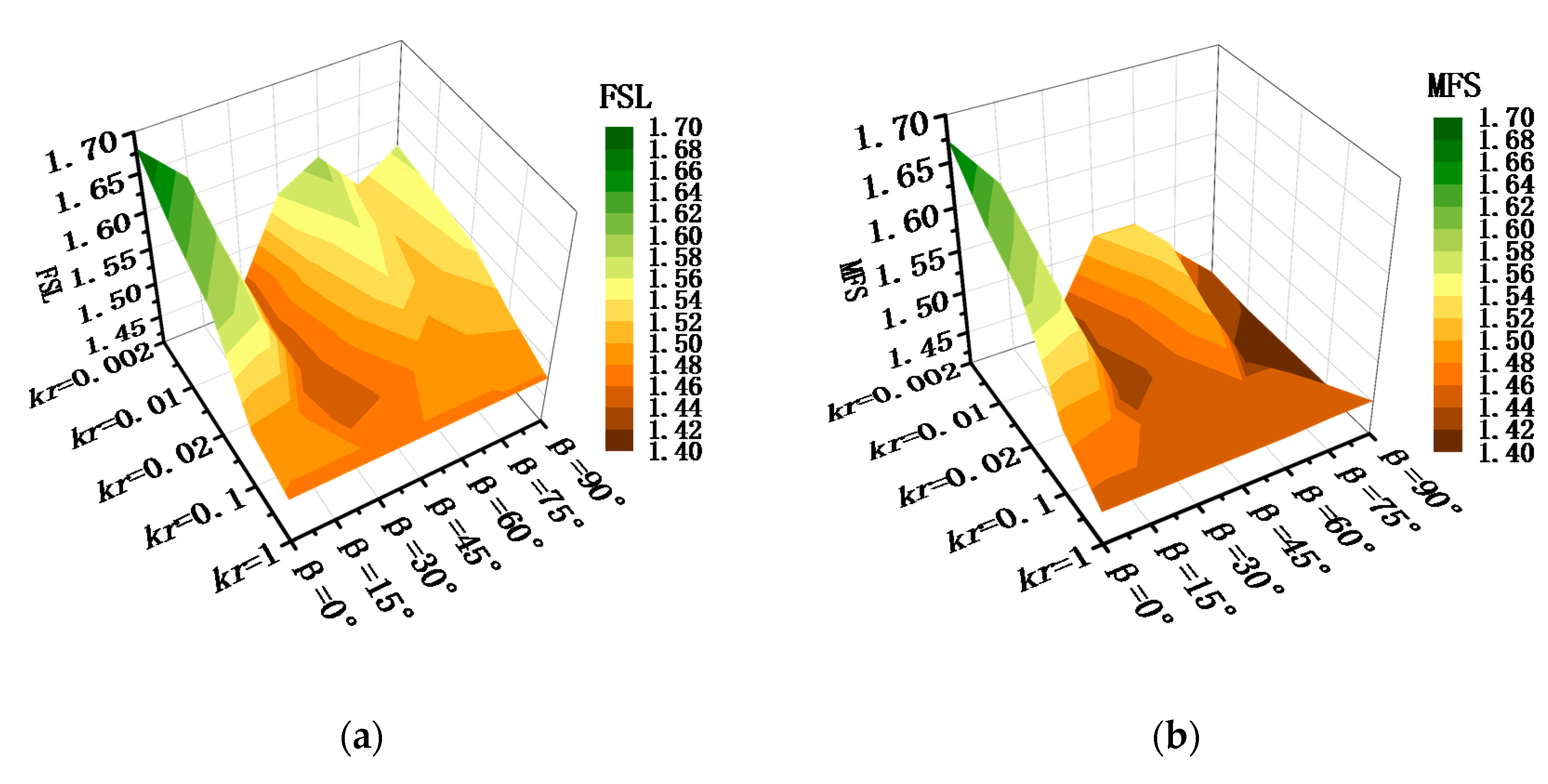
3.2.2. Analysis of the Minimum Factor of Safety
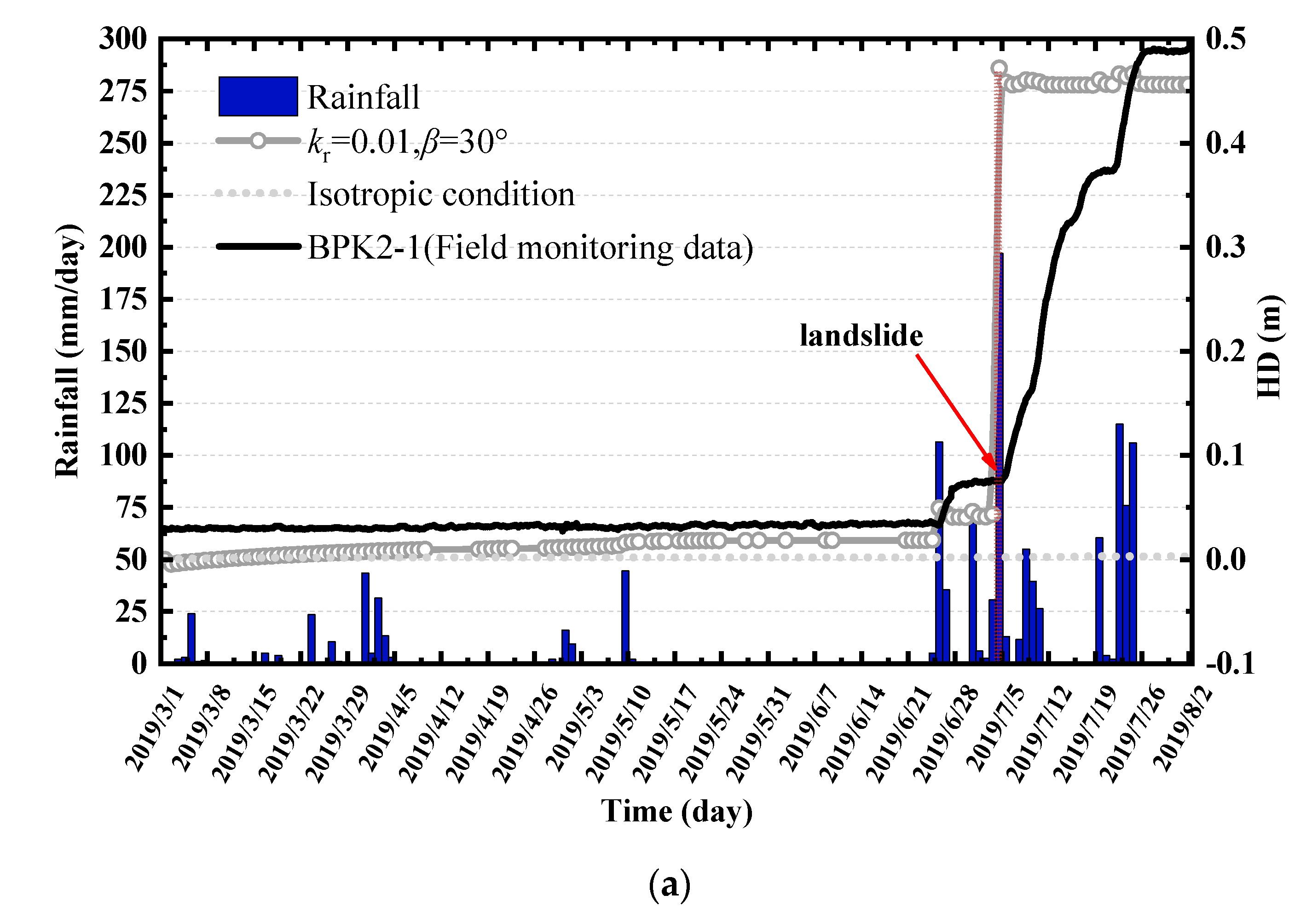
4. Discussion
5. Conclusions
- (1)
- The strength conversion equations of elastic modulus and Poisson’s ratio were feasible, and the rock slope model could accurately predict the occurrence time, horizontal displacement, and scope of the landslide;
- (2)
- The different anisotropy ratios and dip angles of the bedding plane were found to have major impacts on the deformation and stability of the layered rock slope;
- (3)
- The horizontal displacement (HD) and maximum horizontal displacement (MHD) were determined to characterize the deformation characteristics of the rock slope. Considering the layered rock slope as a homogeneous medium could underestimate its HD and MHD. When the dip angle was 30°, the MHD reached the maximum. When the anisotropy angle was close to 60°, and the MHD reached its minimum;
- (4)
- The factor of safety (FS), the minimum factor of safety (MFS), and the factor of safety of landslide (FSL) were determined to characterize the stability characteristics of the rock slope. When the dip angle was 30°, the FS, MFS, and FSL of the rock slope reached the minimum. However, when the rock slope was treated as an isotropic medium, the FS, MFS, and FSL were overestimated;
- (5)
- The changing law of the anisotropy ratio was not obvious, and it was difficult to verify by field data. This could be a focus of future research work. The obtained results are likely to provide a theoretical basis for the prediction and monitoring of layered rock landslide.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yeh, P.T.; Lee, K.Z.Z.; Chang, K.T. 3D Effects of permeability and strength anisotropy on the stability of weakly cemented rock slopes subjected to rainfall infiltration. Eng. Geol. 2020, 266. [Google Scholar] [CrossRef]
- Wei, X.S.; Fan, W.; Chai, X.Q.; Cao, Y.B.; Nan, Y.L. Field and numerical investigations on triggering mechanism in typical rainfall-induced shallow landslides: A case study in the Ren River catchment, China. Nat. Hazards 2020. [Google Scholar] [CrossRef]
- Yu, S.; Ren, X.; Zhang, J.; Wang, H.; Wang, J.; Zhu, W. Seepage, Deformation, and Stability Analysis of Sandy and Clay Slopes with Different Permeability Anisotropy Characteristics Affected by Reservoir Water Level Fluctuations. Water 2020, 12, 201. [Google Scholar] [CrossRef] [Green Version]
- Yeh, H.F.; Tsai, Y.J. Analyzing the Effect of Soil Hydraulic Conductivity Anisotropy on Slope Stability Using a Coupled Hydromechanical Framework. Water 2018, 10, 905. [Google Scholar] [CrossRef] [Green Version]
- Bai, D.; Tang, J.; Lu, G.; Zhu, Z.; Liu, T.; Fang, J. The design and application of landslide monitoring and early warning system based on microservice architecture. Geomat. Nat. Hazards Risk 2020, 11, 928–948. [Google Scholar] [CrossRef]
- Greco, R.; Marino, P.; Santonastaso, G.F.; Damiano, E. Interaction between Perched Epikarst Aquifer and Unsaturated Soil Cover in the Initiation of Shallow Landslides in Pyroclastic Soils. Water 2018, 10, 17. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.Y.; Tang, J.J.; Tian, S.J.; Jiang, Y.J. Rainfall-induced rapid and long-runout catastrophic landslide on July 23, 2019 in Shuicheng, Guizhou, China. Landslides 2020, 17, 2161–2171. [Google Scholar] [CrossRef]
- Jordanova, G.; Gariano, S.L.; Melillo, M.; Peruccacci, S.; Brunetti, M.T.; Auflic, M.J. Determination of Empirical Rainfall Thresholds for Shallow Landslides in Slovenia Using an Automatic Tool. Water 2020, 12, 15. [Google Scholar] [CrossRef]
- Xia, C.; Lu, G.; Bai, D.; Zhu, Z.; Luo, S.; Zhang, G. Sensitivity Analyses of the Seepage and Stability of Layered Rock Slope Based on the Anisotropy of Hydraulic Conductivity: A Case Study in the Pulang Region of Southwestern China. Water 2020, 12, 2314. [Google Scholar] [CrossRef]
- Singh, P.K.; Singh, K.K.; Singh, T.N. Slope failure in stratified rocks: A case from NE Himalaya, India. Landslides 2016, 14, 1319–1331. [Google Scholar] [CrossRef]
- Dong, J.J.; Tu, C.H.; Lee, W.R.; Jheng, Y.J. Effects of hydraulic conductivity/strength anisotropy on the stability of stratified, poorly cemented rock slopes. Comput. Geotech. 2012, 40, 147–159. [Google Scholar] [CrossRef]
- Chen, Y.F.; Yu, H.; Ma, H.Z.; Li, X.; Hu, R.; Yang, Z. Inverse modeling of saturated-unsaturated flow in site-scale fractured rocks using the continuum approach: A case study at Baihetan dam site, Southwest China. J. Hydrol. 2020, 584, 124693. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Z. Introduction to rock hydraulics. Geol. Hazards Environ. Prot. 1997, 6, 56. [Google Scholar]
- Collins, B.D.; Znidarcic, D. Stability Analyses of Rainfall Induced Landslides. J. Geotech. Geoenviron. Eng. 2004, 130, 362–372. [Google Scholar] [CrossRef]
- Barton, N.; Quadros, E. Anisotropy is Everywhere, to See, to Measure, and to Model. Rock Mech. Rock Eng. 2015, 48, 1323–1339. [Google Scholar] [CrossRef]
- Hu, S.C.; Tan, Y.L.; Zhou, H.; Guo, W.Y.; Hu, D.W.; Meng, F.Z.; Liu, Z.G. Impact of Bedding Planes on Mechanical Properties of Sandstone. Rock Mech. Rock Eng. 2017, 50, 2243–2251. [Google Scholar] [CrossRef]
- Yin, P.F.; Yang, S.Q. Experimental investigation of the strength and failure behavior of layered sandstone under uniaxial compression and Brazilian testing. Acta Geophys. 2018, 66, 585–605. [Google Scholar] [CrossRef]
- Jin, Z.; Li, W.; Jin, C.; Hambleton, J.; Cusatis, G. Anisotropic elastic, strength, and fracture properties of Marcellus shale. Int. J. Rock Mech. Min. Sci. 2018, 109, 124–137. [Google Scholar] [CrossRef] [Green Version]
- Fjær, E.; Nes, O.M. The impact of heterogeneity on the anisotropic strength of an outcrop shale. Rock Mech. Rock Eng. 2014, 47, 1603–1611. [Google Scholar] [CrossRef]
- Wu, Y.; Li, X.; He, J.; Zheng, B. Mechanical Properties of Longmaxi Black Organic-Rich Shale Samples from South China under Uniaxial and Triaxial Compression States. Energies 2016, 9, 1088. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.F.; Wei, K.; Liu, W.; Hu, S.H.; Hu, R.; Zhou, C.B. Experimental Characterization and Micromechanical Modelling of Anisotropic Slates. Rock Mech. Rock Eng. 2016, 49, 3541–3557. [Google Scholar] [CrossRef]
- Gholami, R.; Rasouli, V. Mechanical and elastic properties of transversely isotropic slate. Rock Mech. Rock Eng. 2014, 47, 1763–1773. [Google Scholar] [CrossRef]
- Xu, G.; He, C.; Su, A.; Chen, Z. Experimental investigation of the anisotropic mechanical behavior of phyllite under triaxial compression. Int. J. Rock Mech. Min. Sci. 2018, 104, 100–112. [Google Scholar] [CrossRef]
- Ramamurthy, T.; Rao, G.V.; Singh, J. Engineering behaviour of phyllites. Eng. Geol. 1993, 33, 209–225. [Google Scholar] [CrossRef]
- Ding, C.D.; Hu, D.W.; Zhou, H.; Lu, J.J.; Lv, T. Investigations of P-Wave velocity, mechanical behavior and thermal properties of anisotropic slate. Int. J. Rock Mech. Min. Sci. 2020, 127, 13. [Google Scholar] [CrossRef]
- Nasseri, M.H.B.; Rao, K.S.; Ramamurthy, T. Anisotropic strength and deformational behavior of Himalayan schists. Int. J. Rock Mech. Min. Sci. 2003, 40, 3–23. [Google Scholar] [CrossRef]
- Debecker, B.; Vervoort, A. Experimental observation of fracture patterns in layered slate. Int. J. Fract. 2009, 159, 51–62. [Google Scholar] [CrossRef]
- Geng, Z.; Chen, M.; Jin, Y.; Yang, S.; Yi, Z.C.; Fang, X.; Du, X.Y. Experimental study of brittleness anisotropy of shale in triaxial compression. J. Nat. Gas Sci. Eng. 2016, 36, 510–518. [Google Scholar] [CrossRef]
- Gonzaga, G.G.; Leite, M.H.; Corthésy, R. Determination of anisotropic deformability parameters from a single standard rock specimen. Int. J. Rock Mech. Min. Sci. 2008, 45, 1420–1438. [Google Scholar] [CrossRef]
- Yu, S.; Ren, X.; Zhang, J.; Wang, H.; Zhang, Z. Sensibility Analysis of the Hydraulic Conductivity Anisotropy on Seepage and Stability of Sandy and Clayey Slope. Water 2020, 12, 277. [Google Scholar] [CrossRef] [Green Version]
- Morgenstern, N.R.; Price, V.E. The Analysis of the Stability of General Slip Surfaces. Géotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Oo, H.Z.; Ai, L.Z.; Qiu, Z. Numerical Analysis of River Bank Slope Stability during Rapid Drawdown of Water Level. Study Civ. Eng. Archit. 2013, 2, 98–103. [Google Scholar]
- Johansson, J.M.A.; Edeskr, T. Effects of external water-level fluctuations on slope stability. Electron. J. Geotech. Eng. 2014, 19, 2437–2463. [Google Scholar]
- Mandal, A.K.; Li, X.; Shrestha, R. Influence of Water Level Rise on the Bank of Reservoir on Slope Stability: A Case Study of Dagangshan Hydropower Project. Geotech. Geol. Eng. 2019, 37, 5187–5198. [Google Scholar] [CrossRef]
- Tang, D.; Li, D.; Zhou, C. Slope stability analysis considering the antecedent rainfall process. Rock Soil Mech. 2013, 34, 3239–3248. [Google Scholar]
- Fredlund, D.G.; Morgenstern, N.R.; Widger, R.A. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Genuchten, V.T.M. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media; Colorado State University, Hydrology and Water Resources Program: Fort Collins, CO, USA, 1964; pp. 1–27. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Zuo, S.; Wang, S.; Qu, C.; Zhao, Y. Laboratory uniaxial compression test analysis of layered anisotropic rock mass. J. Yangtze River Sci. Res. Inst. 2016, 5, 58–62. [Google Scholar]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Guo, Q.G.; Che, A. Research on relationship of rock mass integrity index and rock mass elastic modulus. Chin. J. Rock Mech. Eng. 2011, 9, 3914–3919. [Google Scholar]
- Jiang, Z.; Xiong, X.; Zeng, L. Unsaturated seepage analysis of slope under rainfall condition based on FLAC3D. Geotech. Mech. 2014, 35, 855–861. [Google Scholar]
- Montrasio, L.; Valentino, R.; Meisina, C. Soil Saturation and Stability Analysis of a Test Site Slope Using the Shallow Landslide Instability Prediction (SLIP) Model. Geotech. Geol. Eng. 2018. [Google Scholar] [CrossRef]
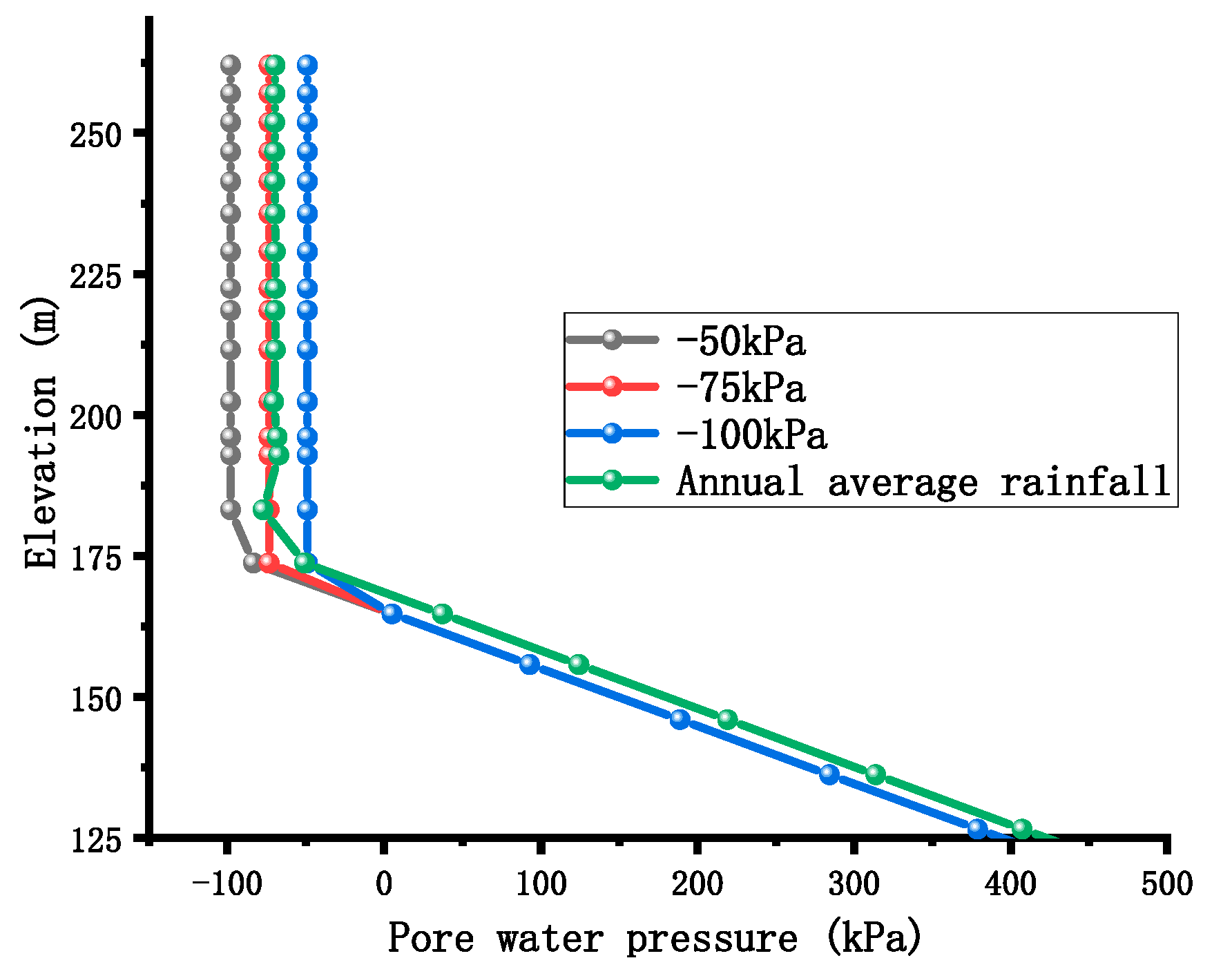
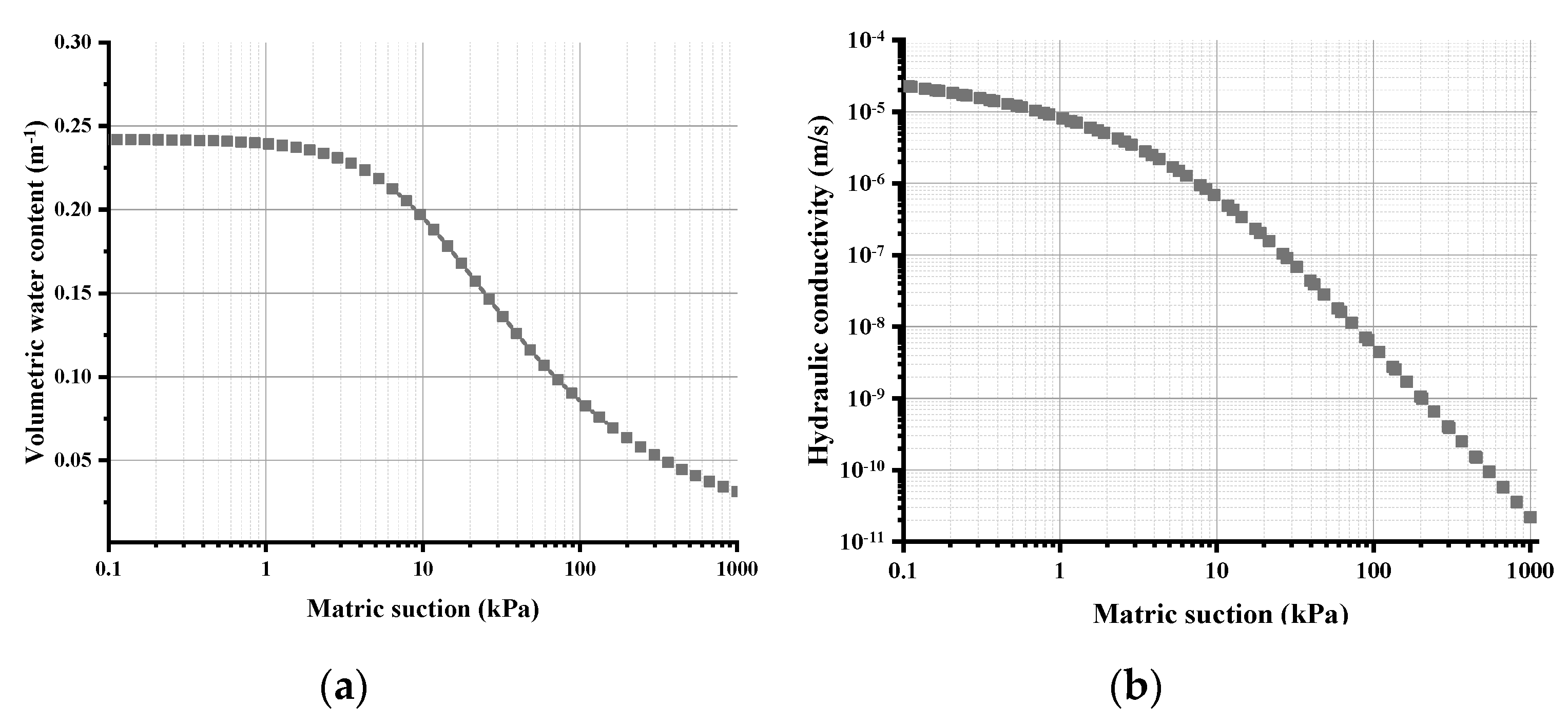

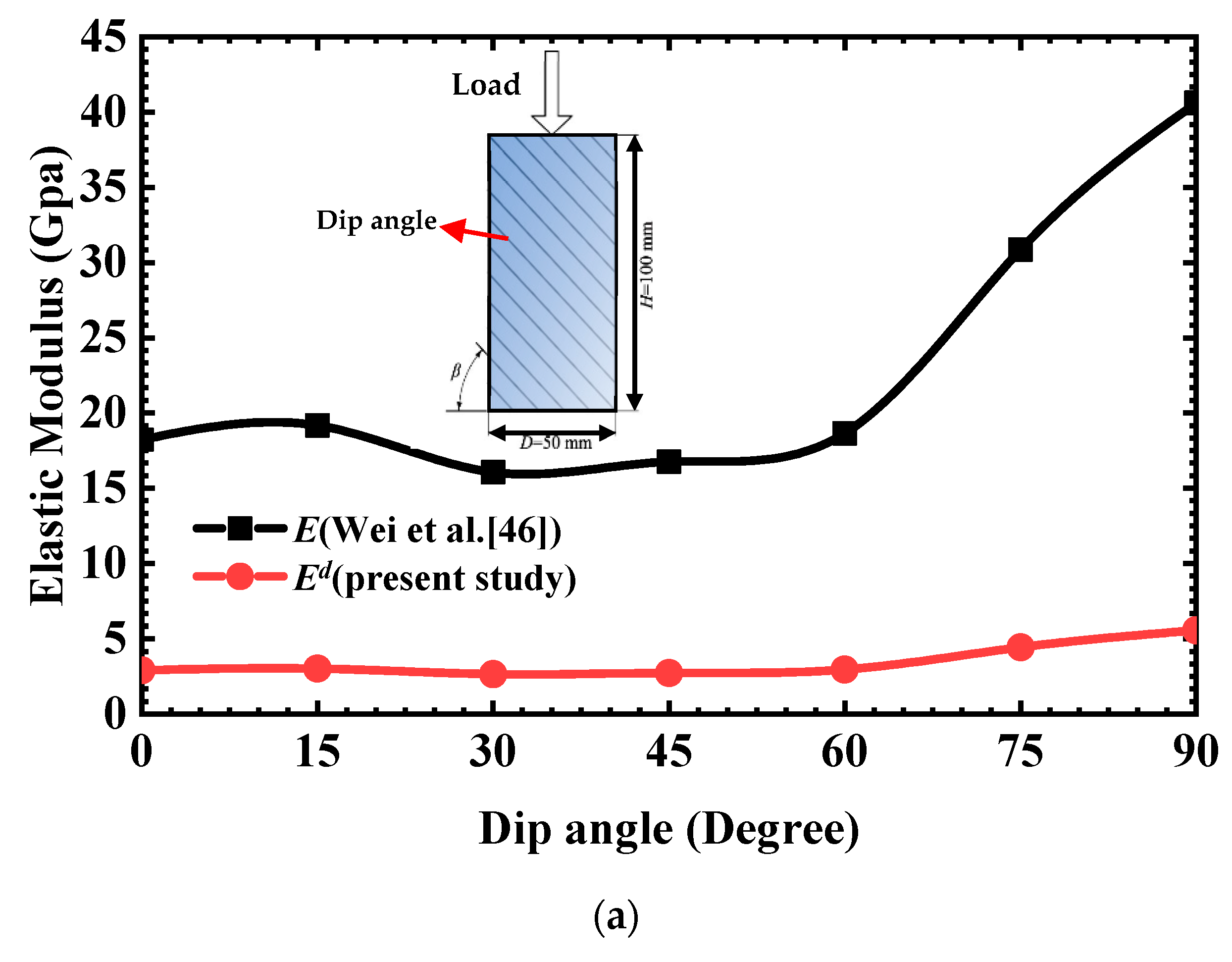
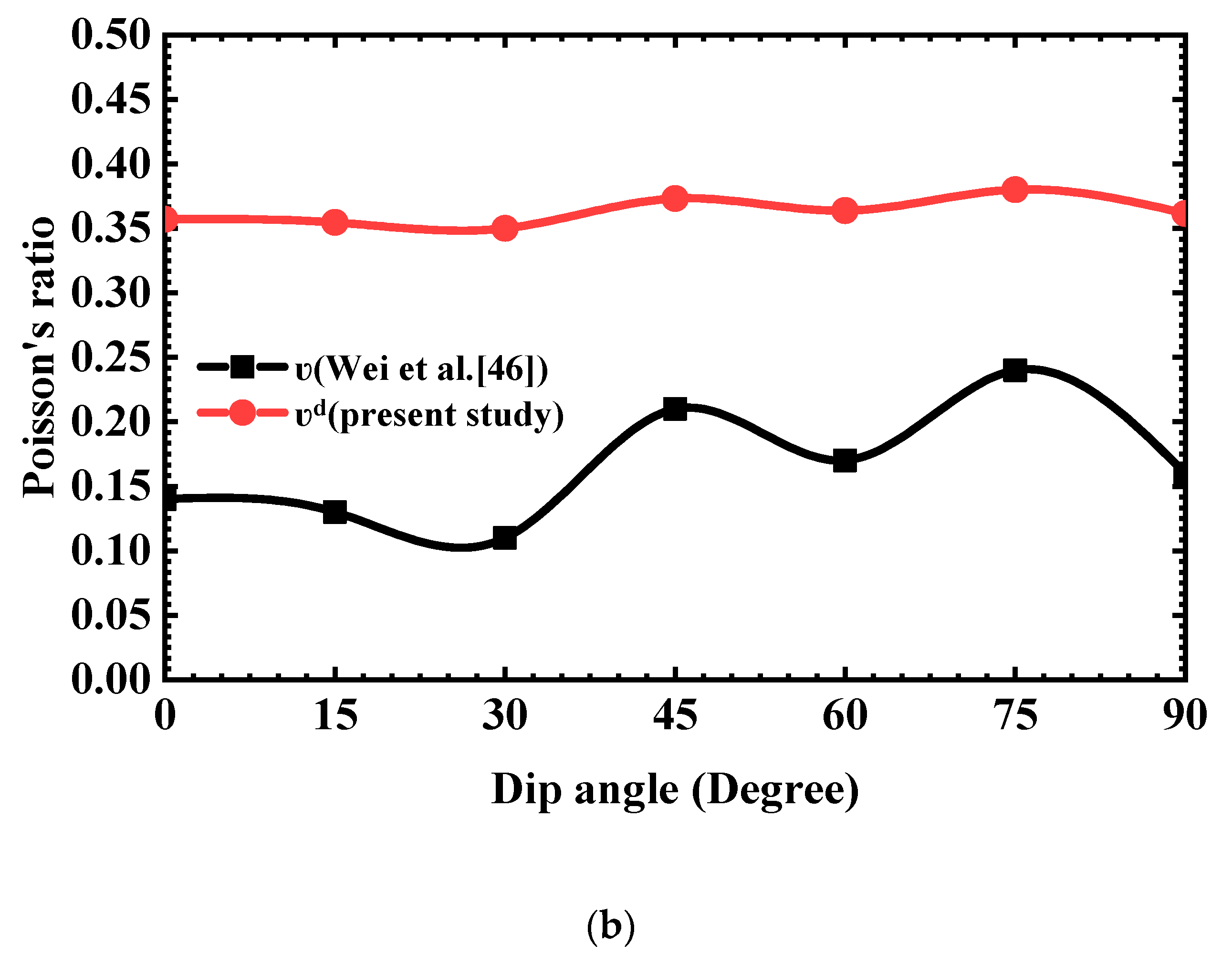


| Layer | Materials | Fitting Parameters | Hydraulic Conduction Coefficient | ||||
|---|---|---|---|---|---|---|---|
| A (kPa) | m | n | θs | θr | k (m/s) | ||
| I | Strongly weathered carbonaceous slate | 10 | 0.33 | 1.5 | 0.242 | 0.001 | 8.08 × 10−5 |
| Rock Types | Anisotropy Ratio kr = ky/kx | Anisotropic Angle/ Dip Angle β (°) | Elastic Modulus Ed (GPa) | Poisson Ratio vd | Unit Weight (kN/m3) | Cohesion (kPa) | Friction Angle (°) |
|---|---|---|---|---|---|---|---|
| seriously weathered carbonaceous slate | 22.4 | 93.6 | 33.3 |
| MHD | Only Considering kr | Only Considering β | Considering Both kr and β |
|---|---|---|---|
| Slope top | 23% | 118% | 2.25 × 105% |
| Slope middle | 86% | 127% | 3.38 × 105% |
| Slope bottom | 81% | 123% | 1.17 × 105% |
| MHD | Only Considering kr | Only Considering β | Considering Both kr and β |
|---|---|---|---|
| FSL | 7% | 16% | 16.4% |
| MFS | 6% | 17% | 17.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, C.; Lu, G.; Zhu, Z.; Wu, L.; Zhang, L.; Luo, S.; Dong, J. Deformation and Stability Characteristics of Layered Rock Slope Affected by Rainfall Based on Anisotropy of Strength and Hydraulic Conductivity. Water 2020, 12, 3056. https://doi.org/10.3390/w12113056
Xia C, Lu G, Zhu Z, Wu L, Zhang L, Luo S, Dong J. Deformation and Stability Characteristics of Layered Rock Slope Affected by Rainfall Based on Anisotropy of Strength and Hydraulic Conductivity. Water. 2020; 12(11):3056. https://doi.org/10.3390/w12113056
Chicago/Turabian StyleXia, Chengzhi, Guangyin Lu, Ziqiang Zhu, Lianrong Wu, Liang Zhang, Shuai Luo, and Jie Dong. 2020. "Deformation and Stability Characteristics of Layered Rock Slope Affected by Rainfall Based on Anisotropy of Strength and Hydraulic Conductivity" Water 12, no. 11: 3056. https://doi.org/10.3390/w12113056
APA StyleXia, C., Lu, G., Zhu, Z., Wu, L., Zhang, L., Luo, S., & Dong, J. (2020). Deformation and Stability Characteristics of Layered Rock Slope Affected by Rainfall Based on Anisotropy of Strength and Hydraulic Conductivity. Water, 12(11), 3056. https://doi.org/10.3390/w12113056




