Estimating Design Floods at Ungauged Watersheds in South Korea Using Machine Learning Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Prediction Models
2.2.1. Linear Regression Model
2.2.2. Principal Component Analysis (PCA)
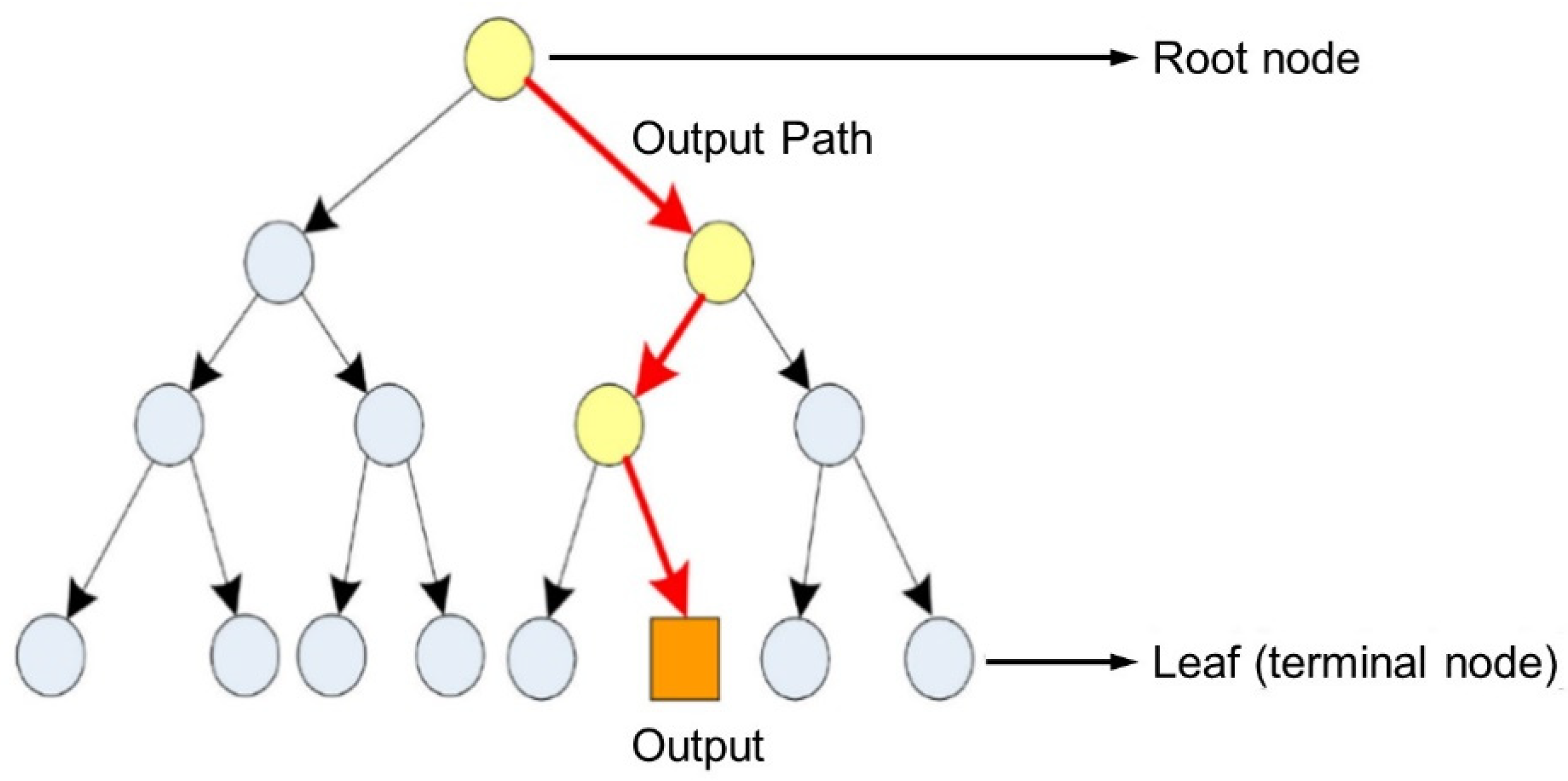
2.2.3. Decision Tree
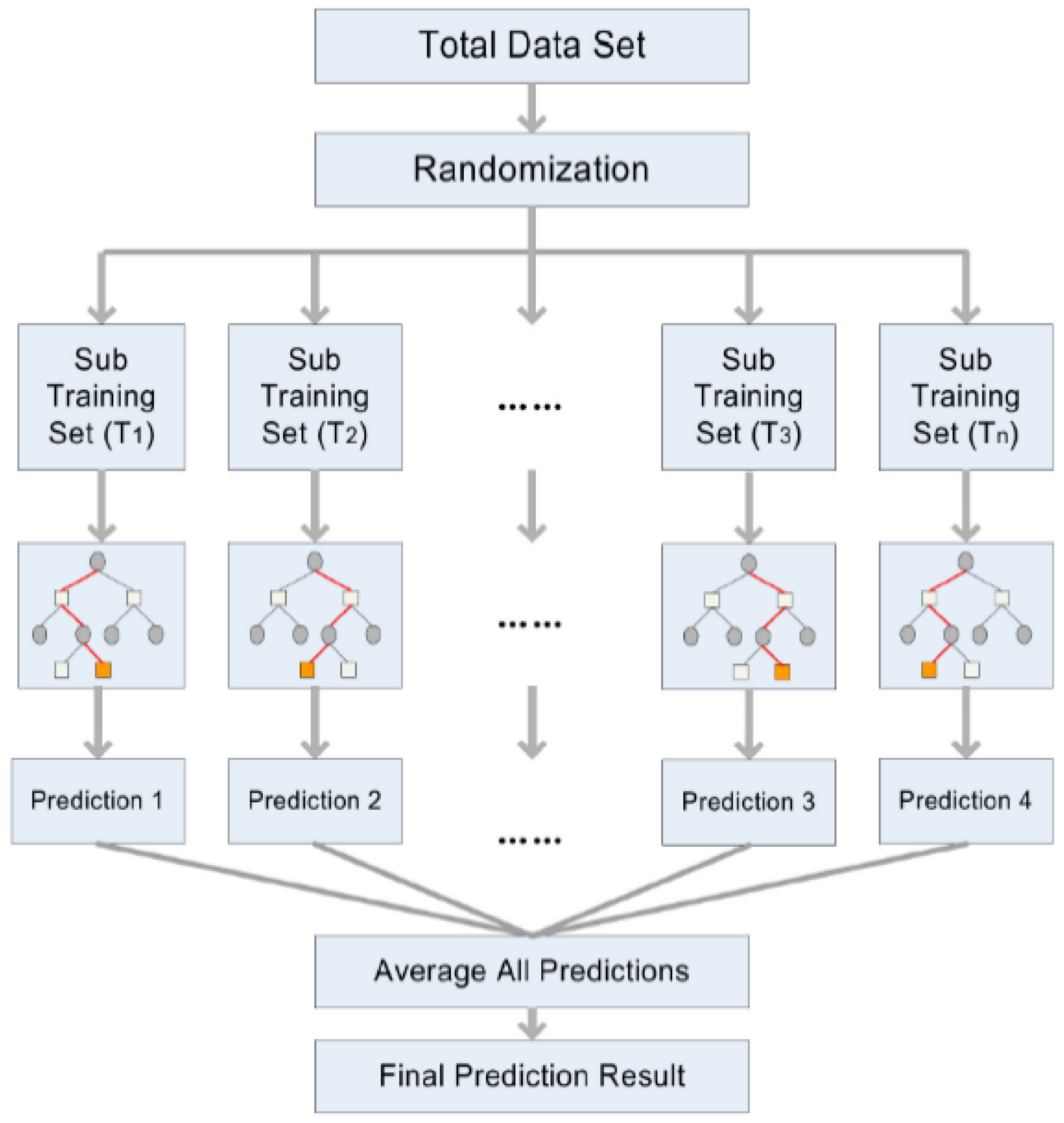
2.2.4. Random Forest (RF)
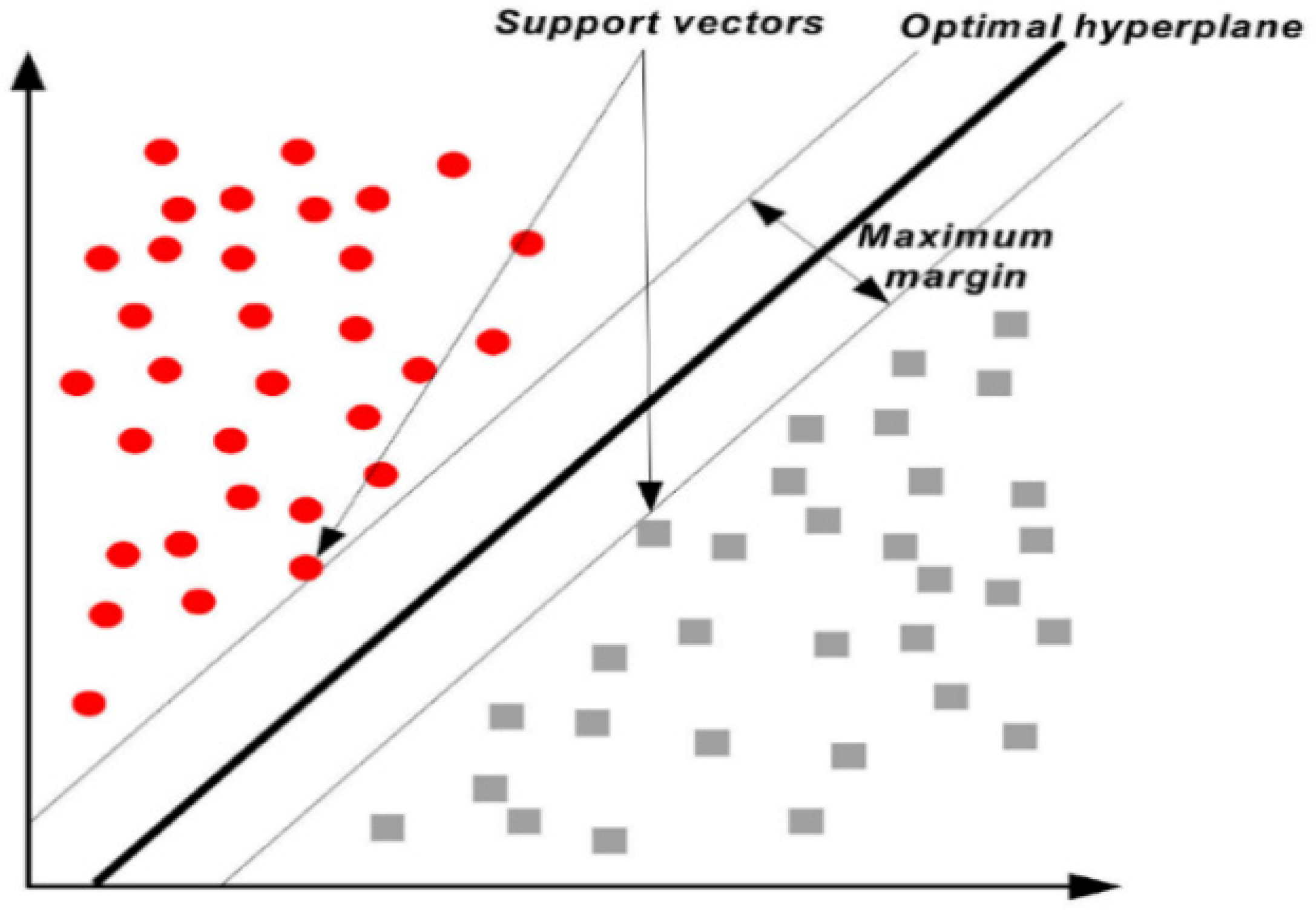
2.2.5. Support Vector Machine (SVM)
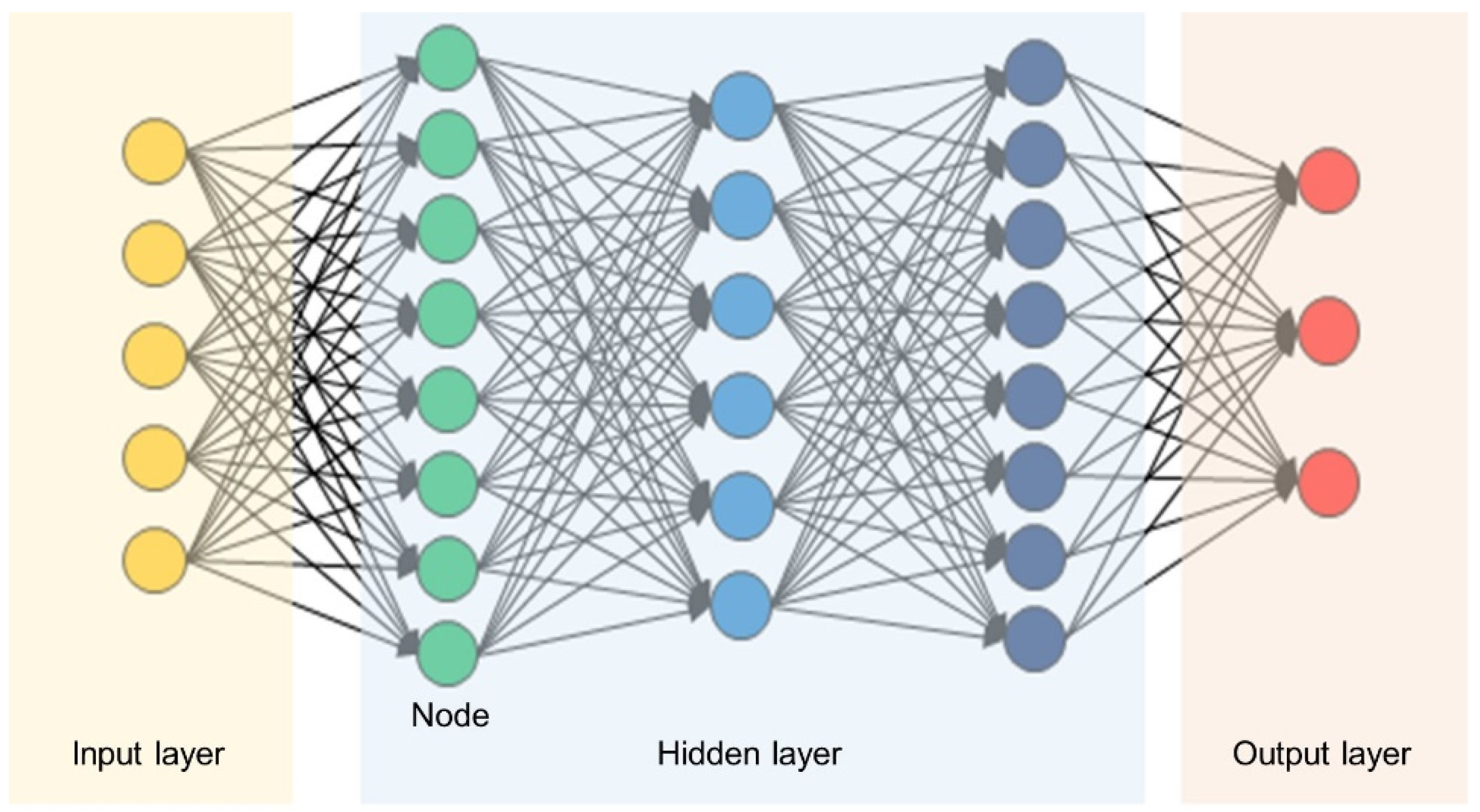
2.2.6. Deep Neural Network (DNN)
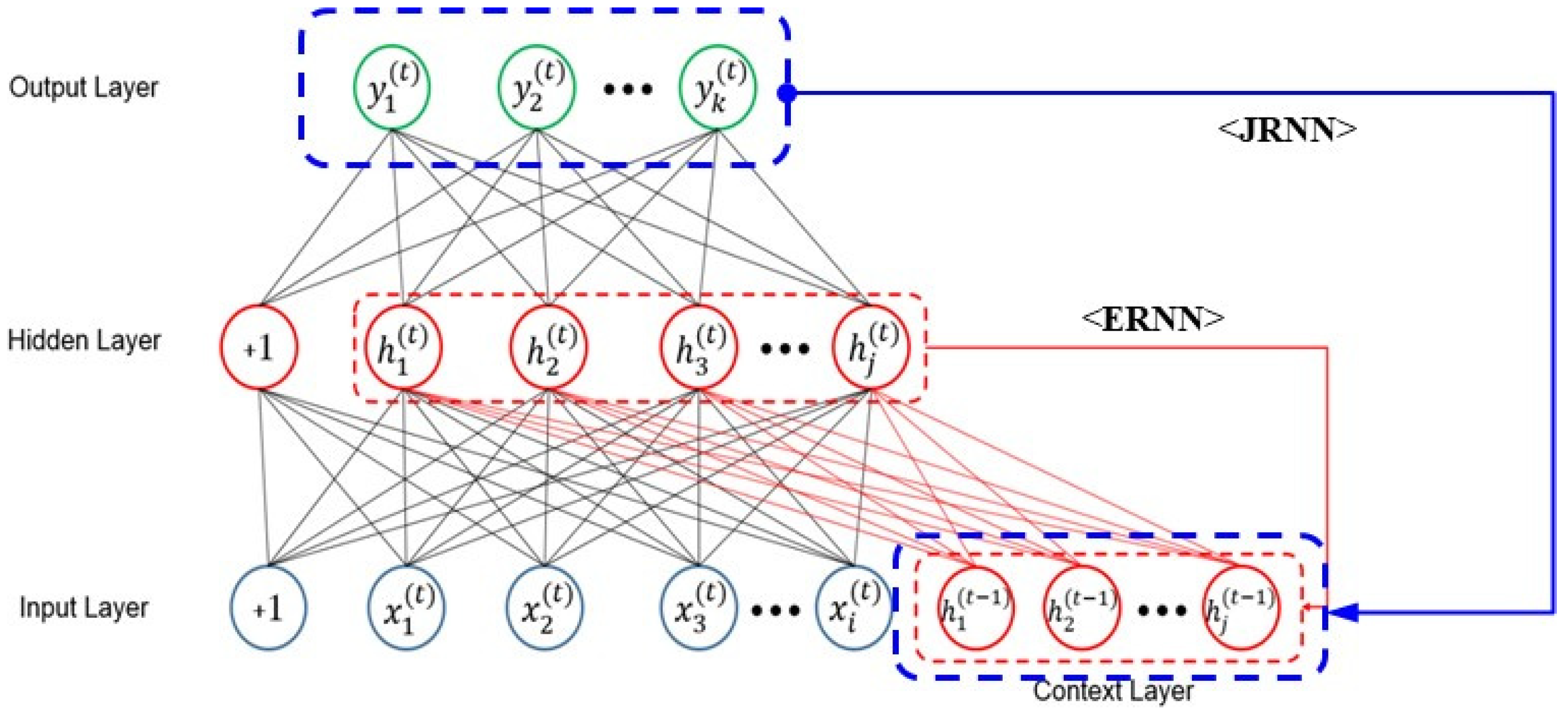
2.2.7. Recurrent Neural Network
2.3. Validation and Performance Assessment
3. Results and Discussion
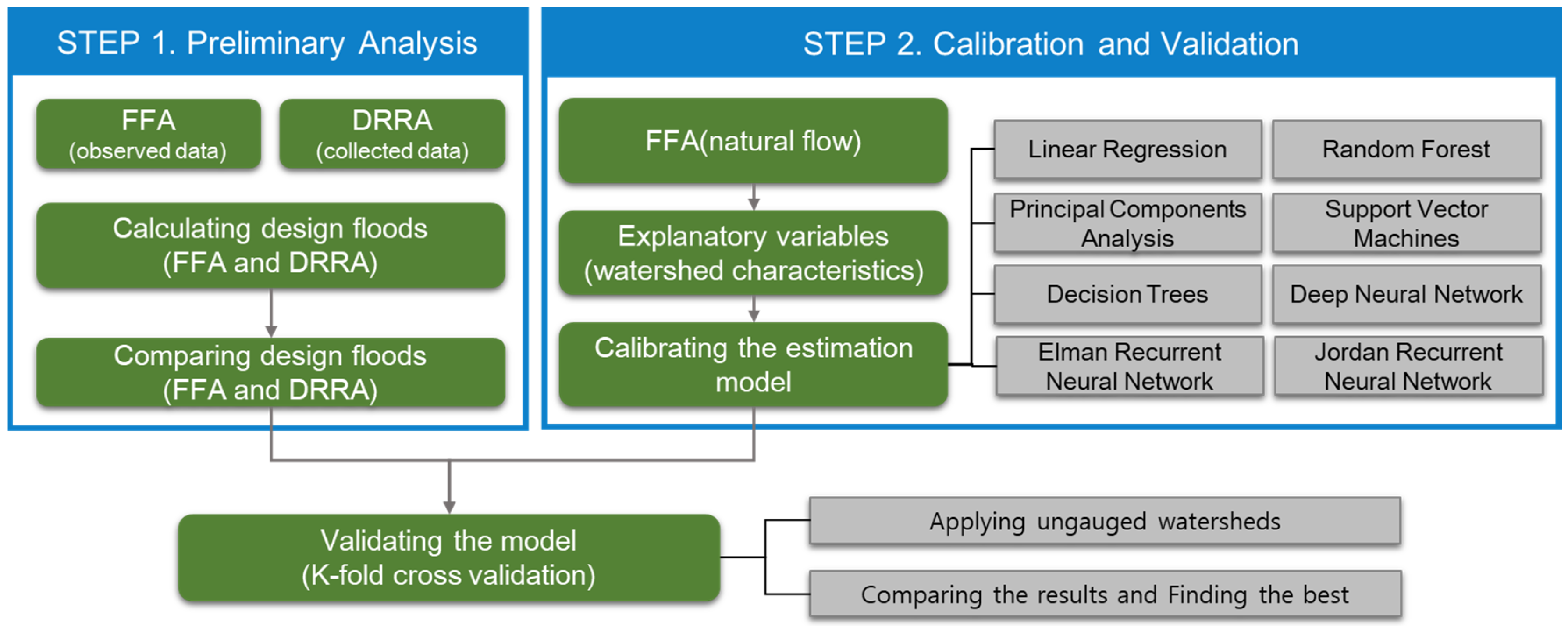
3.1. Preliminary Analysis (Step 1)
3.2. Calibration of Machine Learning-Based Models (Step 2)
3.2.1. Target and Explanatory Variables
3.2.2. Design Flood Estimation with PCA and LR
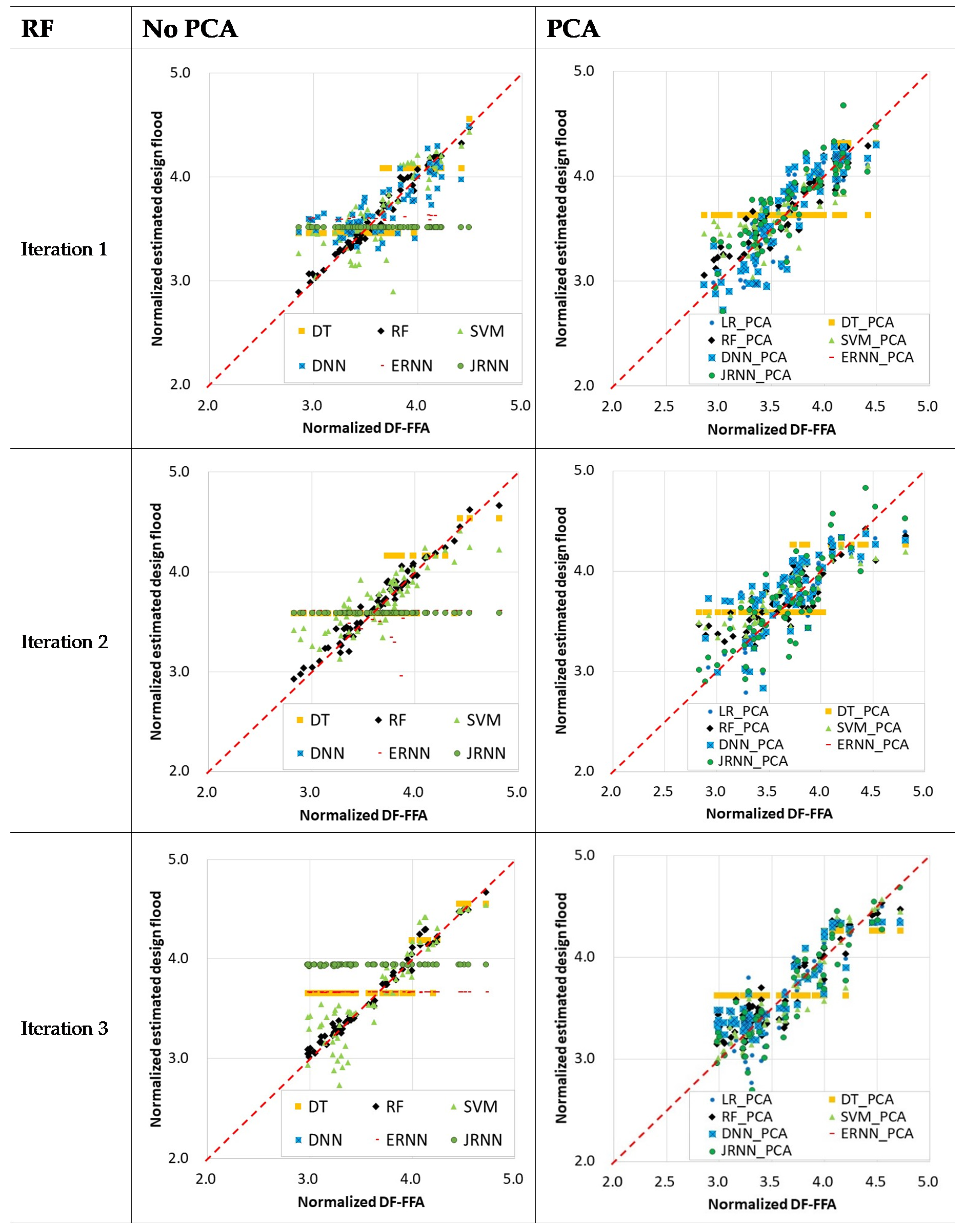
3.2.3. Design Flood Estimation with Machine Learnings
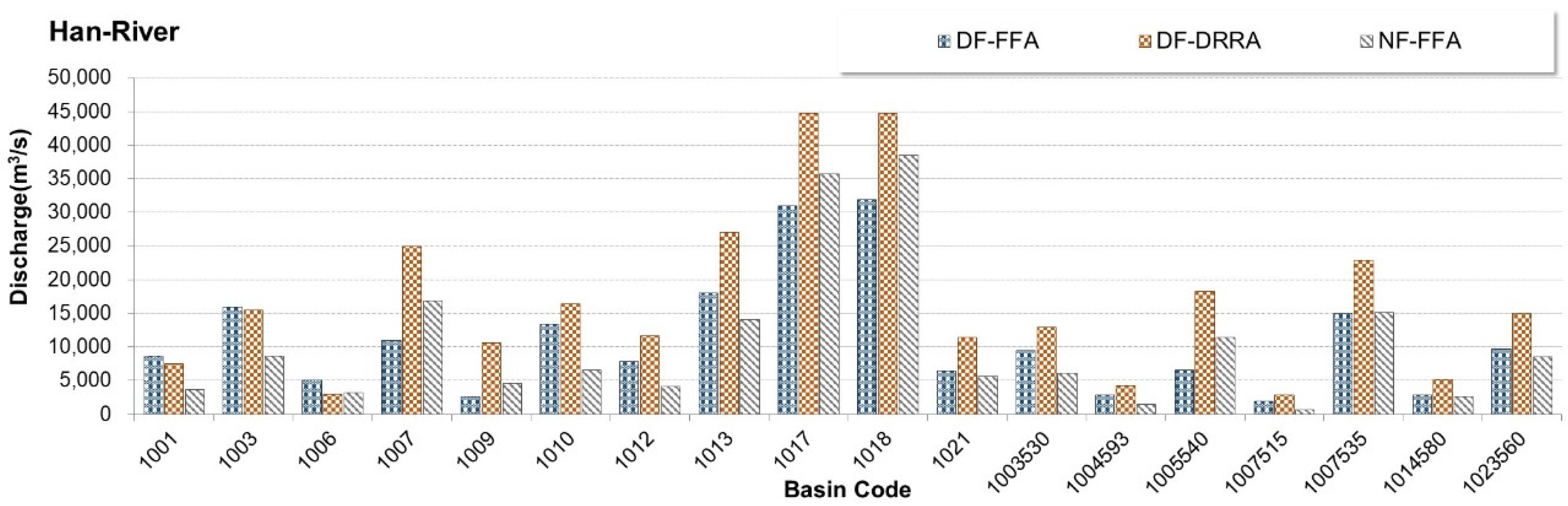
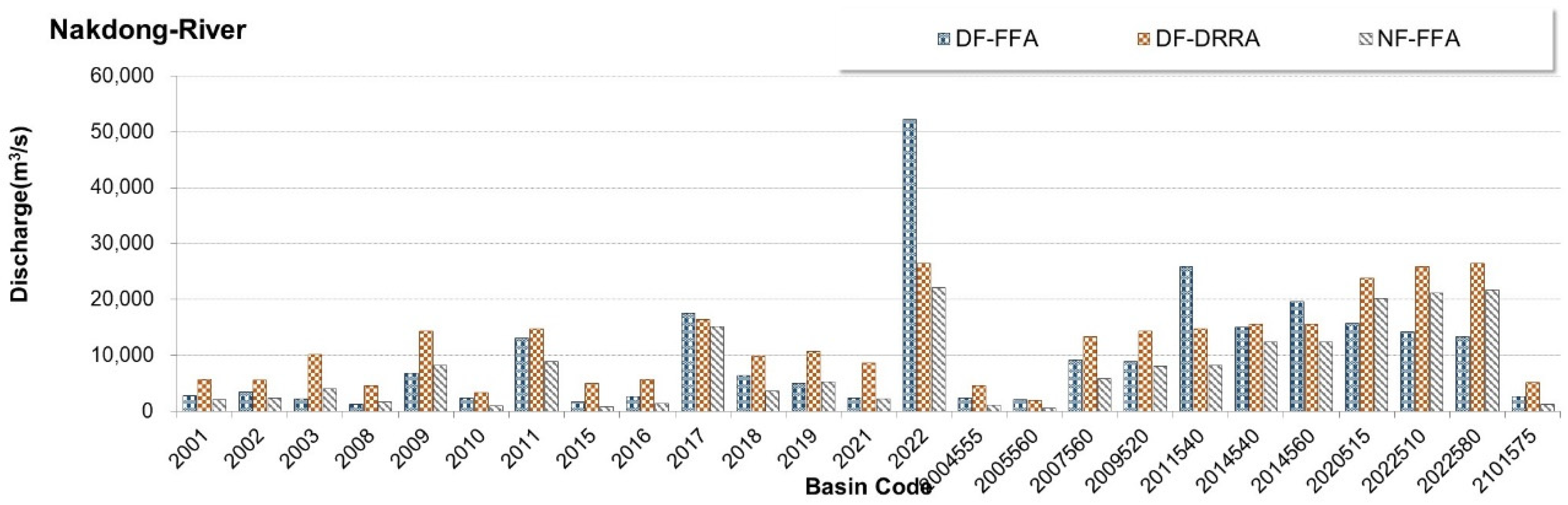
3.3. Validation of Machine Learning-Based Models (Step 2)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, N.W.; Lee, J.-Y.; Park, D.H.; Kim, T.-W. Evaluation of future flood risk according to RCP scenarios using a regional flood frequency analysis for ungauged watersheds. Water 2019, 11, 992. [Google Scholar] [CrossRef] [Green Version]
- Flynn, K.M.; Kirby, W.H.; Hummel, P.R. User’s Manual for Program. PeakFQ, Annual Flood-Frequency Analysis Using Bulletin 17B Guidelines; U.S. Geological Survey: Reston, VA, USA, 2006.
- Institute of Hydrology. Flood Estimation Handbook; Institute of Hydrology: Wallingford, UK, 1999. [Google Scholar]
- Centre for Ecology & Hydrology. European Procedures for Flood Frequency Estimation; European Cooperation in Science and Technology: Lancaster, UK, 2012. [Google Scholar]
- Burnham, M.W. Adoption of Flood Flow Frequency Estimates at Ungaged Location, Training Document 11; US Army Corps of Engineers: Institute for Water Resources: Davis, CA, USA, 1980. [Google Scholar]
- Cunnane, C. Statistical Distributions for Flood Frequency Analysis; World Meteorological Organization Operational: Geneva, Switzerland, 1989; Volume 33, p. 718. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Potter, K.W.; Lattenmaier, D.P. A comparison of regional flood frequency estimation methods using are sampling method. Water Resour. Res. 1990, 26, 415–424. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Tasker, G.D. Regional hydrologic analysis 1. Ordinary, weighted and generalized least squares compared. Water Resour. Res. 1985, 21, 1421–1432. [Google Scholar] [CrossRef]
- Tong, S.; Chang, E. Support vector machine active learning for image retrieval. In Proceedings of the Ninth ACM International Conference on Multimedia, Ottawa, ON, Canada, 1 October 2001; pp. 107–118. [Google Scholar]
- Ahmed, N.K.; Atiya, A.F.; Gayar, N.E.; El-Shishiny, H. An empirical comparison of machine learning models for time series forecasting. Econom. Rev. 2010, 29, 594–621. [Google Scholar] [CrossRef]
- Ak, R.; Fink, O.; Zio, E. Two machine learning approaches for short-term wind speed time-series prediction. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 1734–1747. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.; Qian, X.; Song, H.; Xing, Y.; Li, Z.; Tan, J. Soil moisture investigation utilizing machine learning approach based experimental data and Landsat5-TM images: A case study in the Mega City Beijing. Water 2018, 10, 423. [Google Scholar] [CrossRef] [Green Version]
- Randall, M.; Fensholt, R.; Zhang, Y.; Bergen Jensen, M. Geographic object based image analysis of WorldView-3 Imagery for Urban Hydrologic Modelling at the catchment scale. Water 2019, 11, 1133. [Google Scholar] [CrossRef] [Green Version]
- Marjanović, M.; Kovačević, M.; Bajat, B.; Voženílek, V. Landslide susceptibility assessment using SVM machine learning algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar] [CrossRef]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Choubin, B.; Borji, M.; Mosavi, A.; Sajedi-Hosseini, F.; Singh, V.P.; Shamshirband, S. Snow avalanche hazard prediction using machine learning methods. J. Hydrol. 2019, 577, 123929. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef] [Green Version]
- Chang, F.-J.; Chen, P.-A.; Lu, Y.-R.; Huang, E.; Chang, K.-Y. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Yu, P.-S.; Yang, T.-C.; Chen, S.-Y.; Kuo, C.-M.; Tseng, H.-W. Comparison of random forests and support vector machine for real-time radar-derived rainfall forecasting. J. Hydrol. 2017, 552, 92–104. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Chang, F.J. Explore an evolutionary recurrent ANFIS for modelling multi-step-ahead flood forecasts. J. Hydrol. 2019, 570, 343–355. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.; Chang, L.C.; Chang, F.-J. Exploring a long short-term memory based encoder-decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure and Transport (MOLIT). Long-Term Comprehensive Plan for Water Resources; MOLIT: Seoul, Korea, 2006.
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Choi, C.; Kim, J.; Kim, J.; Kim, H.S. Development of combined heavy rain damage prediction models with machine learning. Water 2019, 11, 2516. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Wiley, J.F.R. Deep Learning Essentials; Packt Publishing Ltd.: Birmingham, UK, 2016. [Google Scholar]
- Elman, J.L. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Jordan, M.I. A Parallel Distributed Processing Approach; Tech. Rep. No. 8604; University of California, Institute for Cognitive Science: San Diego, CA, USA, 1986. [Google Scholar]
- Jordan, M.I.; Rosenbaum, D.A. Action Technology; Rep. No. 8826; University of Massachusetts, Department of Computer Science: Amherst, MA, USA, 1988. [Google Scholar]
- Marquardt, D.W. Generalized inverses, ridge regression, biased linear estimation, and nonlinear estimation. Technometrics 1973, 12, 591–612. [Google Scholar] [CrossRef]
- Tay, F.E.; Cao, L. Application of support vector machines in financial time series forecasting. Omega 2001, 29, 309–317. [Google Scholar] [CrossRef]




| x1 | DF-DRRA | x2 | NF-FFA |
| x3 | Watershed area | x4 | River length |
| x5 | Watershed circumference | x6 | Mean watershed width |
| x7 | Shape factor | x8 | Maximum elevation difference |
| x9 | Return period | - | - |
| RF | NRMSE | MAE | RMSLE | MAPE |
|---|---|---|---|---|
| Iteration 1 | 3.63 | 702.77 | 0.06 | 0.11 |
| Iteration 2 | 12.31 | 1243.03 | 0.08 | 0.17 |
| Iteration 3 | 3.40 | 841.26 | 0.06 | 0.11 |
| Iteration 4 | 3.95 | 642.61 | 0.08 | 0.14 |
| Iteration 5 | 4.81 | 1249.81 | 0.07 | 0.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-Y.; Choi, C.; Kang, D.; Kim, B.S.; Kim, T.-W. Estimating Design Floods at Ungauged Watersheds in South Korea Using Machine Learning Models. Water 2020, 12, 3022. https://doi.org/10.3390/w12113022
Lee J-Y, Choi C, Kang D, Kim BS, Kim T-W. Estimating Design Floods at Ungauged Watersheds in South Korea Using Machine Learning Models. Water. 2020; 12(11):3022. https://doi.org/10.3390/w12113022
Chicago/Turabian StyleLee, Jin-Young, Changhyun Choi, Doosun Kang, Byung Sik Kim, and Tae-Woong Kim. 2020. "Estimating Design Floods at Ungauged Watersheds in South Korea Using Machine Learning Models" Water 12, no. 11: 3022. https://doi.org/10.3390/w12113022






