Multi-Year Index-Based Insurance for Adapting Water Utility Companies to Hydrological Drought: Case Study of a Water Supply System of the Sao Paulo Metropolitan Region, Brazil
Abstract
1. Introduction
2. Study Area and Water Utility Financial Crisis Context
3. Materials and Methods
3.1. Risk Transfer Scheme Features
3.2. MTRH-SHS Module Structure Descriptions
3.2.1. Hazard Module
3.2.2. Vulnerability Module
3.2.3. Financial Module
4. Results
4.1. Actuarially Fair Premiums
4.2. Premium Ambiguity
4.3. Insurance Fund Performance Indices
5. Discussions and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Acronyms and Definitions
| Definition | |
| WEAP | Water evaluation and planning system (software for water resources planning) |
| MYI | Multi-year insurance |
| SPMR | Sao Paulo Metropolitan Region |
| SABESP | Sao Paulo State Water Utility Company |
| SUSEP | Government agency responsible for authorization, control, and inspection of insurance markets in Brazil |
| MTRH-SHS | Modelo de Transferência de Riscos Hidrológicos of the Department of Hydraulics and Sanitation at Sao Paulo University |
| Dd | Drought duration |
| Rp | Return period |
| RCM | Regional climate model (as Eta; used to downscale global climate model projections) |
| n | Annual contractual period |
| GDP | Gross domestic product |
| CPI | Consumer Price Index |
| Net margin | Ratio between net profit and revenue |
| Net profit | Difference between income and expenses generated over a period |
| GCM | Global climate model (such as HadGEM2-ES, MIROC5, and BESM) |
| RCP | Representative concentration pathway (pessimistic and optimistic scenarios) |
| SD, NSD | Stationary demand, non-stationary demand |
| TLM | Threshold level method |
| SDF | Severity duration frequency |
| Actuarially fair premium | Premium is equal to expected claims |
| LR | Loss ratio |
| SC | Solvency coefficient |
| EC | Efficiency coefficient |
| Residual risk | Risk portion that prevails after reaching maximum limit of possible risk coverage |
References
- Pichs-Madruga, Y.; Sokona, E.; Farahani, S.; Kadner, K.; Seyboth, A.; Adler, I.; Baum, S.; Brunner, P.; Eickemeier, B.; Kriemann, J.; et al. IPCC, 2014: Summary for Policymakers. In Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- WMO. Atlas of Mortality and Economic Losses from Weather, Climate and Water Extremes; Publications Board World Meteorological Organization (WMO): Geneva, Switzerland, 2014; ISBN 978-92-63-11123-4. [Google Scholar]
- Di Giulio, G.M.; Bedran-Martins, A.M.B.; Vasconcellos, M.D.P.; Ribeiro, W.C.; Lemos, M.C. Mainstreaming climate adaptation in the megacity of São Paulo, Brazil. Cities 2017, 72, 237–244. [Google Scholar] [CrossRef]
- Huang, S.; Li, P.; Huang, Q.; Leng, G.; Hou, B.; Ma, L. The propagation from meteorological to hydrological drought and its potential influence factors. J. Hydrol. 2017, 547, 184–195. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Yao, H.; Gao, L.; Chen, Y.; Liu, M. Non-linear relationship of hydrological drought responding to meteorological drought and impact of a large reservoir. J. Hydrol. 2017, 551, 495–507. [Google Scholar] [CrossRef]
- Stahl, K.; Kohn, I.; Blauhut, V.; Urquijo, J.; De Stefano, L.; Acacio, V.; Dias, S.; Stagge, J.H.; Tallaksen, L.M.; Kampragou, E.; et al. Impacts of European drought events: Insights from an international database of text-based reports. Nat. Hazards Earth Syst. Sci. 2016, 16, 801–819. [Google Scholar] [CrossRef]
- Schäfer, L.; Waters, E.; Kreft, S.; Zissener, M. Making Climate Risk Insurance Work for the Most Vulnerable: Seven Guiding Principles; United Nations University Institute for Environment and Human Security: Bonn, Germany, 2016. [Google Scholar]
- Mello, K.; Randhir, T. Diagnosis of water crises in the metropolitan area of São Paulo: Policy opportunities for sustainability. Urban Water J. 2017, 15, 53–60. [Google Scholar] [CrossRef]
- Nobre, C.A.; Marengo, J.A. Water Crises and Megacities in Brazil: Meteorological Context of the São Paulo Drought of 2014–2015; Global Water Forum: Brasilia, Brazil, 2016. [Google Scholar]
- Soriano, E.; Torres, L.; Gregorio, D.I.; Coutinho, M.P.; Bacellar, L.; Santos, L. Water Crisis in Sao Paulo Evaluated Under the Disaster’s point of view. Ambient. Soc. 2016, 19, 21–42. [Google Scholar] [CrossRef]
- Empinotti, V.L.; Budds, J.; Aversa, M. Governance and water security: The role of the water institutional framework in the 2013–15 water crisis in São Paulo, Brazil. Geoforum 2019, 98, 46–54. [Google Scholar] [CrossRef]
- GESP. Relatório da Administração 2016—Companhia de Saneamento Básico do Estado de São Paulo—SABESP; Report: Companhia de Saneamento Básico do Estado de São Paulo—SABESP; SABESP: Sao Paulo, Brazil, 2016. [Google Scholar]
- Doncaster, C.P.; Tavoni, A.; Dyke, J.G. Using Adaptation Insurance to Incentivize Climate-change Mitigation. Ecol. Econ. 2017, 135, 246–258. [Google Scholar] [CrossRef]
- Kunreuther, H.; Michel-Kerjan, E. Economics of Natural Catastrophe Risk Insurance. In Handbooks in Economics: Economics of Risk and Uncertainty; Machina, M.J., Viscusi, K.W., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 651–699. ISBN 9780444536853. [Google Scholar]
- Savitt, A. Insurance as a tool for hazard risk management? An evaluation of the literature. Nat. Hazards 2017, 86, 583–599. [Google Scholar] [CrossRef]
- Daron, J.D.; Stainforth, D.A. Assessing pricing assumptions for weather index insurance in a changing climate. Clim. Risk Manag. 2014, 1, 76–91. [Google Scholar] [CrossRef]
- Zhu, W. A model of catastrophe risk pricing and its empirical test School of Finance. Insur. Math. Econ. 2017, 77, 14–23. [Google Scholar] [CrossRef]
- Guzman, D.A. Hydrological Risk Transfer Planning under the Drought “Severity-Duration-Frequency” Approach as a Climate Change Impact Mitigation Strategy; Sao Paulu Univeristy: Sao Paulo, Brazil, 2018. [Google Scholar]
- Mohor, G.S.; Mendiondo, E.M. Economic indicators of hydrologic drought insurance under water demand and climate change scenarios in a Brazilian context. Ecol. Econ. 2017, 140, 66–78. [Google Scholar] [CrossRef]
- Haddad, E.A.; Teixeira, E. Economic impacts of natural disasters in megacities: The case of floods in Sao Paulo, Brazil. Habitat Int. 2015, 45, 106–113. [Google Scholar] [CrossRef]
- SABESP. Sistema Cantareira. Available online: http://www2.ana.gov.br/Paginas/servicos/saladesituacao/v2/SistemaCantareira.aspx (accessed on 31 December 2016).
- ANA; DAEE. Subsídios Para a Análise do Pedido de Outorga do Sistema Cantareira e Para a Definição das Condições de Operação dos Seus Reservatórios; ANA/DAEE Technical Note: Estado de São Paulo, Brazil, 2004. [Google Scholar]
- Nobre, C.A.; Marengo, J.A.; Seluchi, M.E.; Cuartas, A.; Alves, L.M. Some Characteristics and Impacts of the Drought and Water Crisis in Southeastern Brazil during 2014 and 2015. J. Water Resour. Prot. 2016, 8, 252–262. [Google Scholar] [CrossRef]
- Milano, M.; Reynard, E.; Muniz-miranda, G.; Guerrin, J. Water Supply Basins of São Paulo Metropolitan Region: Hydro-Climatic Characteristics of the 2013–2015 Water Crisis. Water 2018, 10, 1517. [Google Scholar] [CrossRef]
- Taffarello, D.; Samprogna Mohor, G.; do Carmo Calijuri, M.; Mendiondo, E.M. Field investigations of the 2013–14 drought through quali-quantitative freshwater monitoring at the headwaters of the Cantareira System, Brazil. Water Int. 2016, 8060, 1–25. [Google Scholar] [CrossRef]
- Meyer, V.; Becker, N.; Markantonis, V.; Schwarze, R.; Van Den Bergh, J.C.J.M.; Bouwer, L.M.; Bubeck, P.; Ciavola, P.; Genovese, E.; Green, C.; et al. Review article: Assessing the costs of natural hazards-state of the art and knowledge gaps. Nat. Hazards Earth Syst. Sci. 2013, 13, 1351–1373. [Google Scholar] [CrossRef]
- Zeff, H.B.; Characklis, G.W. Managing water utility financial risks through third-party index insurance contracts. Water Resour. Res. 2013, 49, 4939–4951. [Google Scholar] [CrossRef]
- SABESP. Relatório da Administração 2017; Technical Note; SABESP: Sao Paulo, Brazil, 2017. [Google Scholar]
- Mohor, G.S. Seguros Hídricos como Mecanismos de Adaptação às Mudanças do Clima para Otimizar a Outorga de Uso da Água. Master’s Thesis, Sao Paulo University, Sao Paulo, Brazil, 2016. [Google Scholar]
- World Bank. Lesotho WEAP Manual; License: Creative Commons Attribution CC BY 3.0 IGO; World Bank: Washington, DC, USA, 2017. [Google Scholar]
- Dereczynski, C.; Chan Chou, S.; Lyra, A.; Sondermann, M.; Regoto, P.; Tavares, P.; Chagas, D.; Gomes, J.L.; Rodrigues, D.C.; Skansi, M.d.l.M. Downscaling of climate extremes over South America—Part I: Model evaluation in the reference climate. Weather Clim. Extrem. 2020, 29, 100273. [Google Scholar] [CrossRef]
- Almagro, A.; Oliveira, P.T.S.; Rosolem, R.; Hagemann, S.; Nobre, C.A. Performance evaluation of Eta/HadGEM2-ES and Eta/MIROC5 precipitation simulations over Brazil. Atmos. Res. 2020, 244, 105053. [Google Scholar] [CrossRef]
- Chou, S.C.; Lyra, A.; Mourão, C.; Dereczynski, C.; Pilotto, I.; Gomes, J.; Bustamante, J.; Tavares, P.; Silva, A.; Rodrigues, D.; et al. Evaluation of the Eta Simulations Nested in Three Global Climate Models. Am. J. Clim. Chang. 2014, 3, 438–454. [Google Scholar] [CrossRef]
- Chou, S.C.; Lyra, A.; Mourão, C.; Dereczynski, C.; Pilotto, I.; Gomes, J.; Bustamante, J.; Tavares, P.; Silva, A.; Rodrigues, D.; et al. Assessment of Climate Change over South America under RCP 4.5 and 8.5 Downscaling Scenarios. Am. J. Clim. Chang. 2014, 3, 512–527. [Google Scholar] [CrossRef]
- SABESP. COMUNICADO—03/16: Marco Tarifario RMSP. 2016. Available online: http://site.sabesp.com.br/site/uploads/file/clientes_servicos/comunicado_03_2016.pdf (accessed on 1 August 2017).
- De Oliveira, J.B.; Camargo, M.; Rossi, M.; Filho, B.C. Mapa Pedológico do Estado de São Paulo, 1st ed.; Embrapa, IAC: Campinas, Brazil, 1999; ISBN 8585564032. [Google Scholar]
- Molin, P.G.; Miranda, F.T.S.; Sampaio, J.V.; Fransozi, A.A.; Ferraz, S.D.B. Mapeamento de uso e Cobertura do Solo da Bacia do Rio Piracicaba, SP: Anos 1990, 2000 e 2010; Technical Report no. 207; Circular Tecnica/Instituto de Pesquisas e Estudos Florestais: Sao Paulo, Brazil, 2015. [Google Scholar]
- Holbig, C.A.; Mazzonetto, A.; Borella, F.; Pavan, W.; Fernandes, J.M.C.; Chagas, D.J.; Gomes, J.L.; Chou, S.C. PROJETA platform: Accessing high resolution climate change projections over Central and South America using the Eta model. Agrometeoros 2019, 26, 7. [Google Scholar] [CrossRef]
- UNISDR. Insurance Development Forum: Defining the Protection Gap “Working Group on Metrics & Indicators”. Available online: https://www.unisdr.org/files/globalplatform/591d4fcfd34e8Defining_the_Protection_Gap_Working_Paper.pdf (accessed on 1 December 2016).
- Surminski, S.; Bouwer, L.M.; Linnerooth-Bayer, J. How insurance can support climate resilience. Nat. Clim. Chang. 2016, 6, 333–334. [Google Scholar] [CrossRef]
- Paudel, Y.; Botzen, W.J.W.; Aerts, J.C.J.H.; Dijkstra, T.K. Risk allocation in a public—Private catastrophe insurance system: An actuarial analysis of deductibles, stop-loss, and premiums. J. Flood Risk Manag. 2015, 8, 116–134. [Google Scholar] [CrossRef]
- Laurentis, G.L. de Modelo De Transferência De Riscos Hidrológicos Como Estratégia De Adaptação Às Mudanças Globais Segundo Cenários De Vulnerabilidade Dos Recursos Hídricos. Master’s Thesis, Escola de Engenharia de São Carlos, Sao Paulo, Brazil, 2012. [Google Scholar]
- Graciosa, M.C. Modelo de Seguro Para Riscos Hidrológicos com Base em Simulação Hidráulico-Hidrológica como Ferramenta Para Gestão do Risco de Inundações. Ph.D. Thesis, University of São Paulo, Sao Paulo, Brazil, 2010. [Google Scholar]
- Sung, J.H.; Chung, E.S. Development of streamflow drought severity-duration-frequency curves using the threshold level method. Hydrol. Earth Syst. Sci. 2014, 18, 3341–3351. [Google Scholar] [CrossRef]
- Dalezios, N.R.; Loukas, A.; Vasiliades, L. Severity-duration-frequency analysis of droughts and wet periods in Greece. Hydrol. Sci. J. 2000, 45, 751–769. [Google Scholar] [CrossRef]
- Santos, C.A.S.; Rocha, F.A.; Ramos, T.B.; Alves, L.M.; Mateus, M.; de Oliveira, R.P.; Neves, R. Using a hydrologic model to assess the performance of regional climate models in a semi-arid Watershed in Brazil. Water 2019, 11, 170. [Google Scholar] [CrossRef]
- Firoz, A.B.M.; Nauditt, A.; Fink, M.; Ribbe, L. Quantifying human impacts on hydrological drought using a combined modelling approach in a tropical river basin in Central Vietnam. Hydrol. Earth Syst. Sci. 2018, 22, 547–565. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Madsen, H.; Clausen, B. On the definition and modelling of streamflow drought duration and deficit volume. Hydrol. Sci. J. 1997, 42, 15–33. [Google Scholar] [CrossRef]
- Zaidman, M.D.; Keller, V.; Young, A.R.; Cadman, D. Flow-duration-frequency behaviour of British rivers based on annual minima data. J. Hydrol. 2003, 277, 195–213. [Google Scholar] [CrossRef]
- Rojas, L.P.T.; Díaz-Granados, M. The construction and comparison of regional drought severity-duration-frequency curves in two Colombian River basins-study of the Sumapaz and Lebrija Basins. Water 2018, 10, 1453. [Google Scholar] [CrossRef]
- Bachmair, S.; Kohn, I.; Stahl, K. Exploring the link between drought indicators and impacts. Nat. Hazards Earth Syst. Sci. 2015, 15, 1381–1397. [Google Scholar] [CrossRef]
- Hou, W.; Chen, Z.Q.; Zuo, D.D.; Feng, G. lin Drought loss assessment model for southwest China based on a hyperbolic tangent function. Int. J. Disaster Risk Reduct. 2018, 33, 477–484. [Google Scholar] [CrossRef]
- Mens, M.J.P.; Gilroy, K.; Williams, D. Developing system robustness analysis for drought risk management: An application on a water supply reservoir. Nat. Hazards Earth Syst. Sci. 2015, 15, 1933–1940. [Google Scholar] [CrossRef]
- Garrido, R. Price Setting for Water Use Charges in Brazil Price Setting for Water Use Charges in Brazil. Int. J. Water Resour. Dev. 2005, 21, 99–117. [Google Scholar] [CrossRef]
- SABESP. Regulamento do Sistema Tarifário da Sabesp. Available online: http://site.sabesp.com.br/site/interna/Default.aspx?secaoId=183 (accessed on 1 December 2018).
- Mays, L.W.; Tung, Y.-K. Economics for Hydrosystems. In Hydrosystemas Engineering and Management; McGraw-Hill: New York, NY, USA, 2002; pp. 23–50. [Google Scholar]
- Vaghela, C.R.; Vaghela, A.R. Synthetic Flow Generation. Int. J. Eng. Res. Apl. 2014, 4, 66–71. [Google Scholar]
- Hisdal, H.; Tallaksen, L.M.; Clausen, B.; Peters, E.; Gustard, A. Hydrological Drought Characteristics. In Developments in Water Science: Hydrological Drought, Processes and Estimation Methods for Streamflow and Groundwater; Tallaksen, L.M., Van Lanen, H.A.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2004; pp. 139–198. ISBN 0-444-51767-7. [Google Scholar]
- SUSEP. Como é Calculado o Prêmio de Seguro? Available online: http://www.susep.gov.br/setores-susep/cgpro/coseb (accessed on 1 August 2017).
- Kunreuther, H.; Pauly, M.V.; McMorrow, S. Insurance & Behavioral Economics: Improving Desicions in the Most Misunderstood Industry, 1st ed.; Cambridge University Press: New York, NY, USA, 2013; ISBN 9781107013445. [Google Scholar]
- Kunreuther, H.; Useem, M. Learning Fromm Catastrophes: Strategies for Reaction and Response, 1st ed.; Wharton School Publishing: Upper Saddle River, NJ, USA, 2010; ISBN 9780137044856. [Google Scholar]
- Şen, Z. Applied Drought Modeling, Prediction, and Mitigation; Şen, Z., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; ISBN 9780128021767. [Google Scholar]
- Dionne, G. Risk Sharing and Pricing in the Reinsurance Market, 2nd ed.; Dionne, G., Ed.; Springer: Montreal, QC, Canada, 2013; ISBN 9781461401551. [Google Scholar]
- Contador, C.R. Economia do Seguro: Fundamentos e Aplicações, 1st ed.; Atlas: Sao Paulo, Brazil, 2007; ISBN 8522448108. [Google Scholar]
- Hudson, P.; Botzen, W.J.W.; Feyen, L.; Aerts, J.C.J.H. Incentivising flood risk adaptation through risk based insurance premiums: Trade-offs between affordability and risk reduction. Ecol. Econ. 2016, 125, 1–13. [Google Scholar] [CrossRef]
- Leblois, A.; Le Cotty, T.; Maître d’Hôtel, E. How Might Climate Change Influence farmers’ Demand for Index-Based Insurance? Ecol. Econ. 2020, 176, 106716. [Google Scholar] [CrossRef]
- Miao, R. Climate, insurance and innovation: The case of drought and innovations in drought-tolerant traits in US agriculture. Eur. Rev. Agric. Econ. 2020, 1–35. [Google Scholar] [CrossRef]
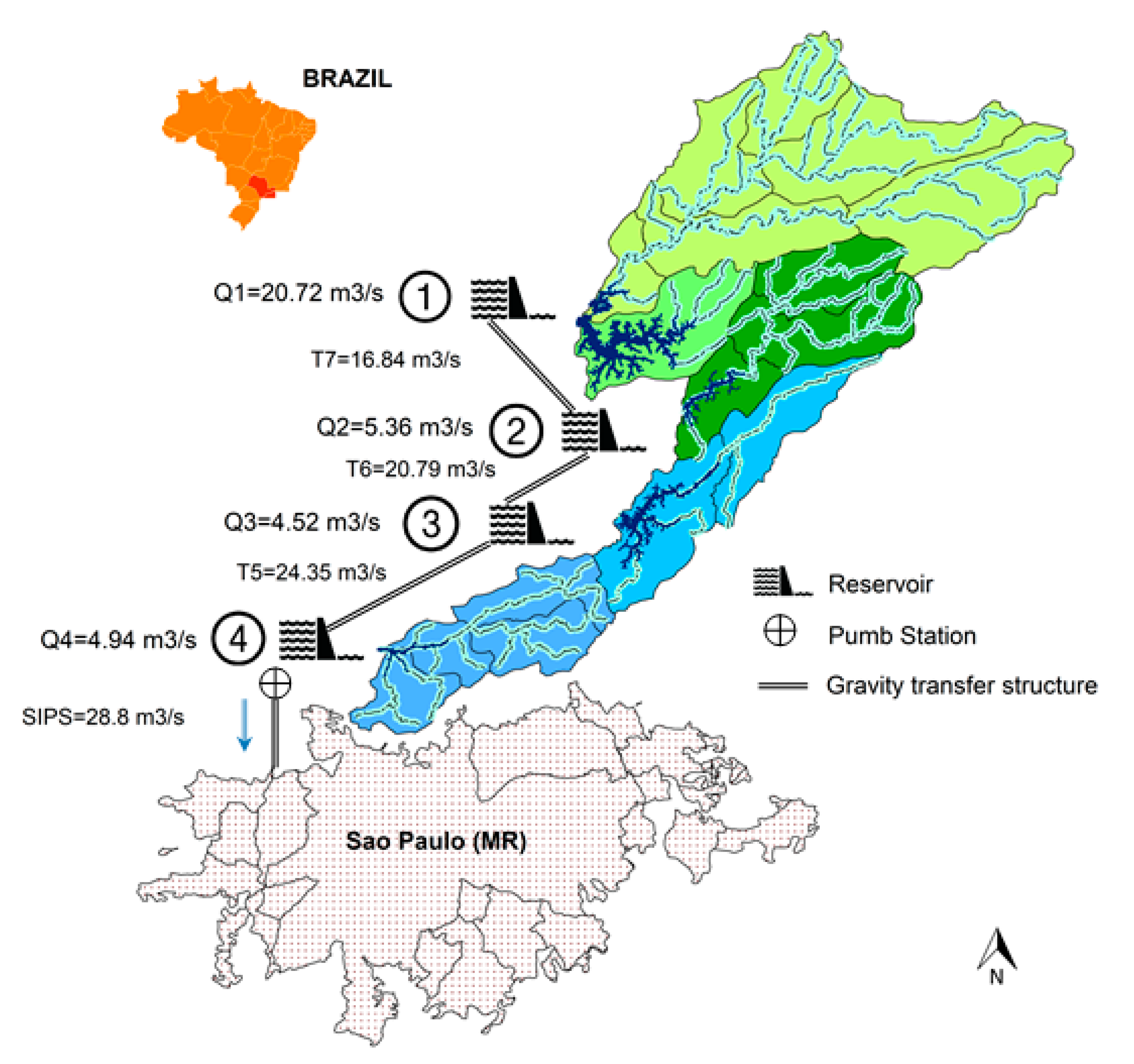
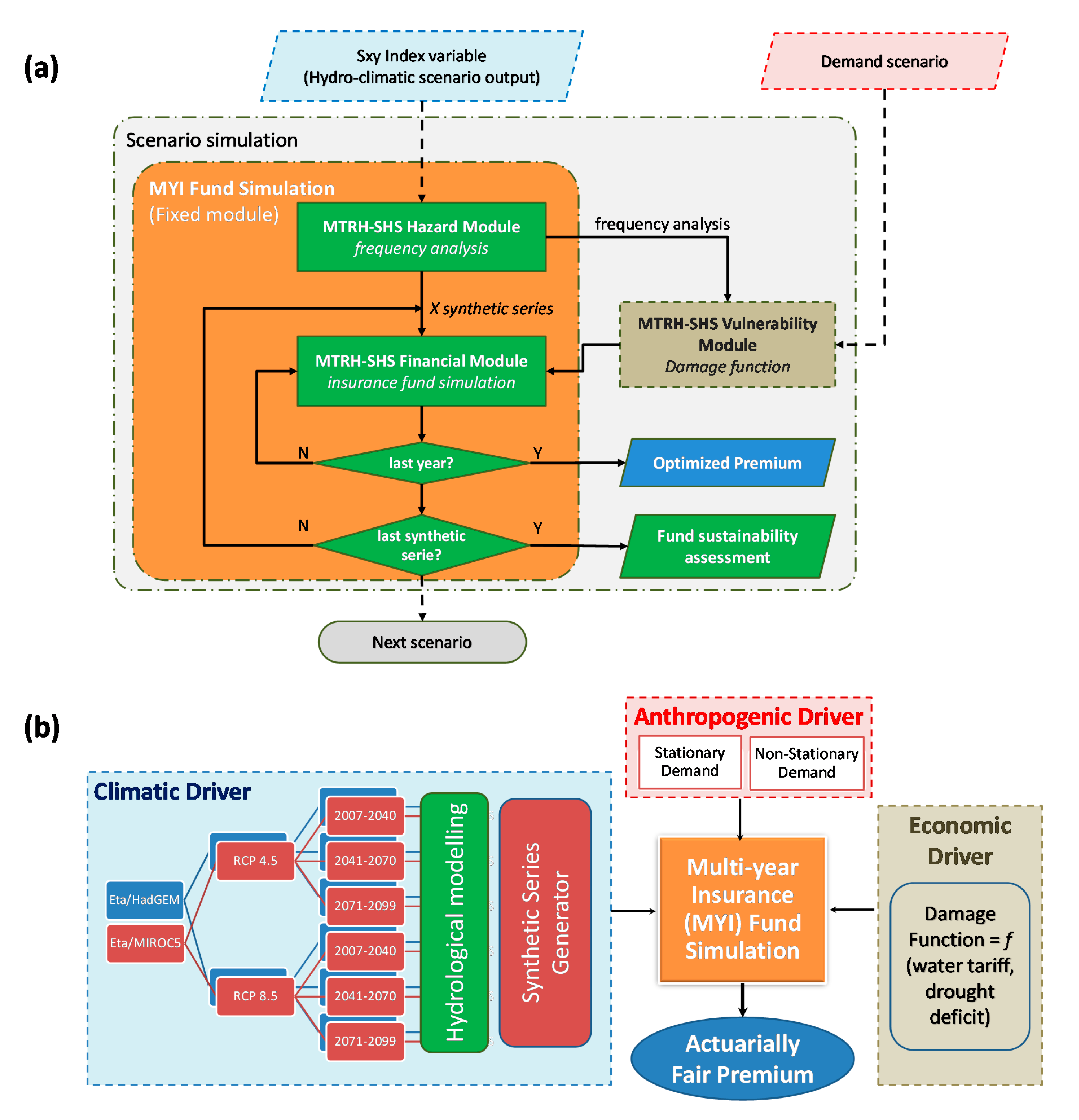
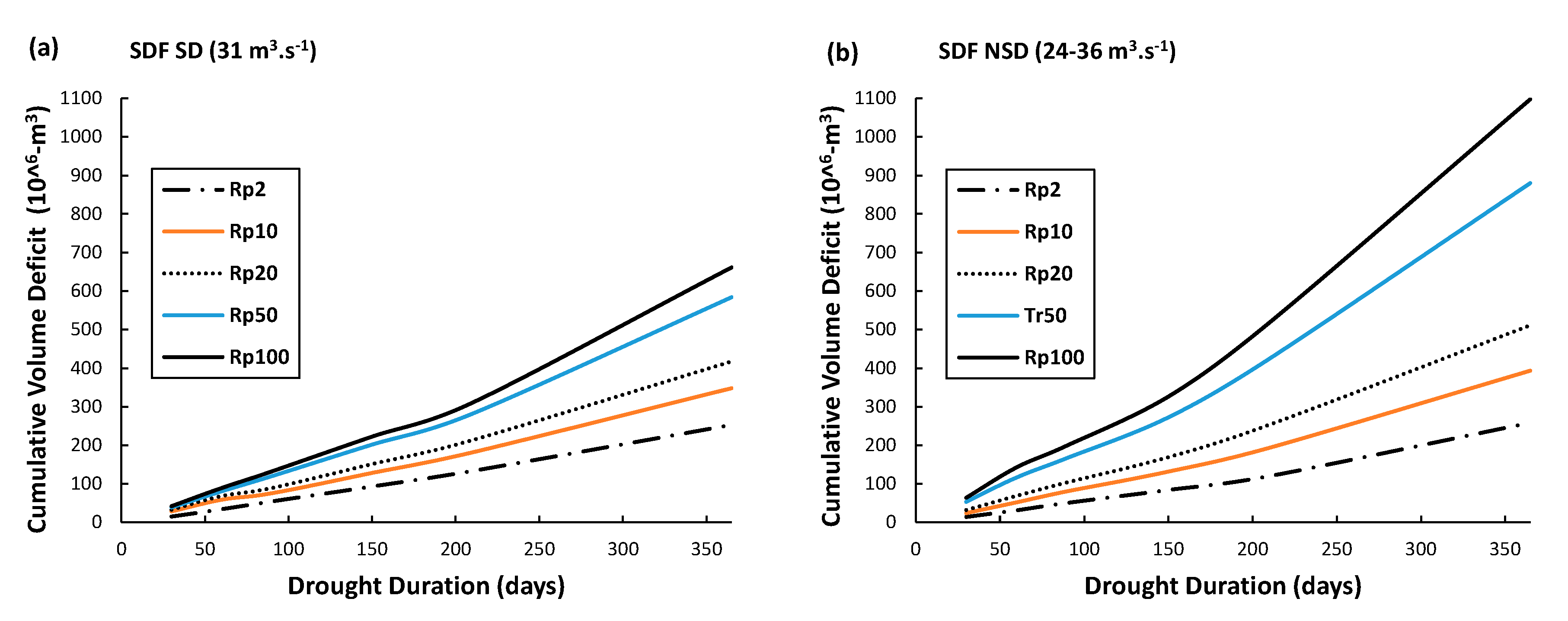
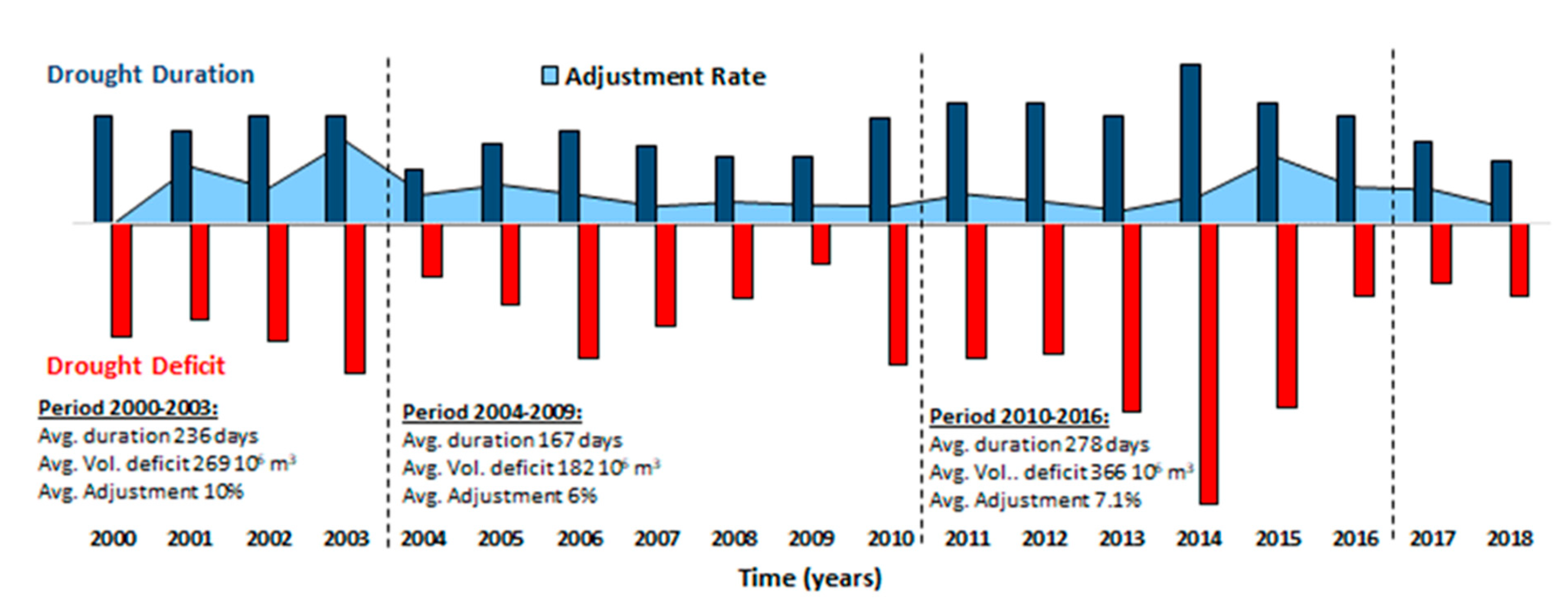
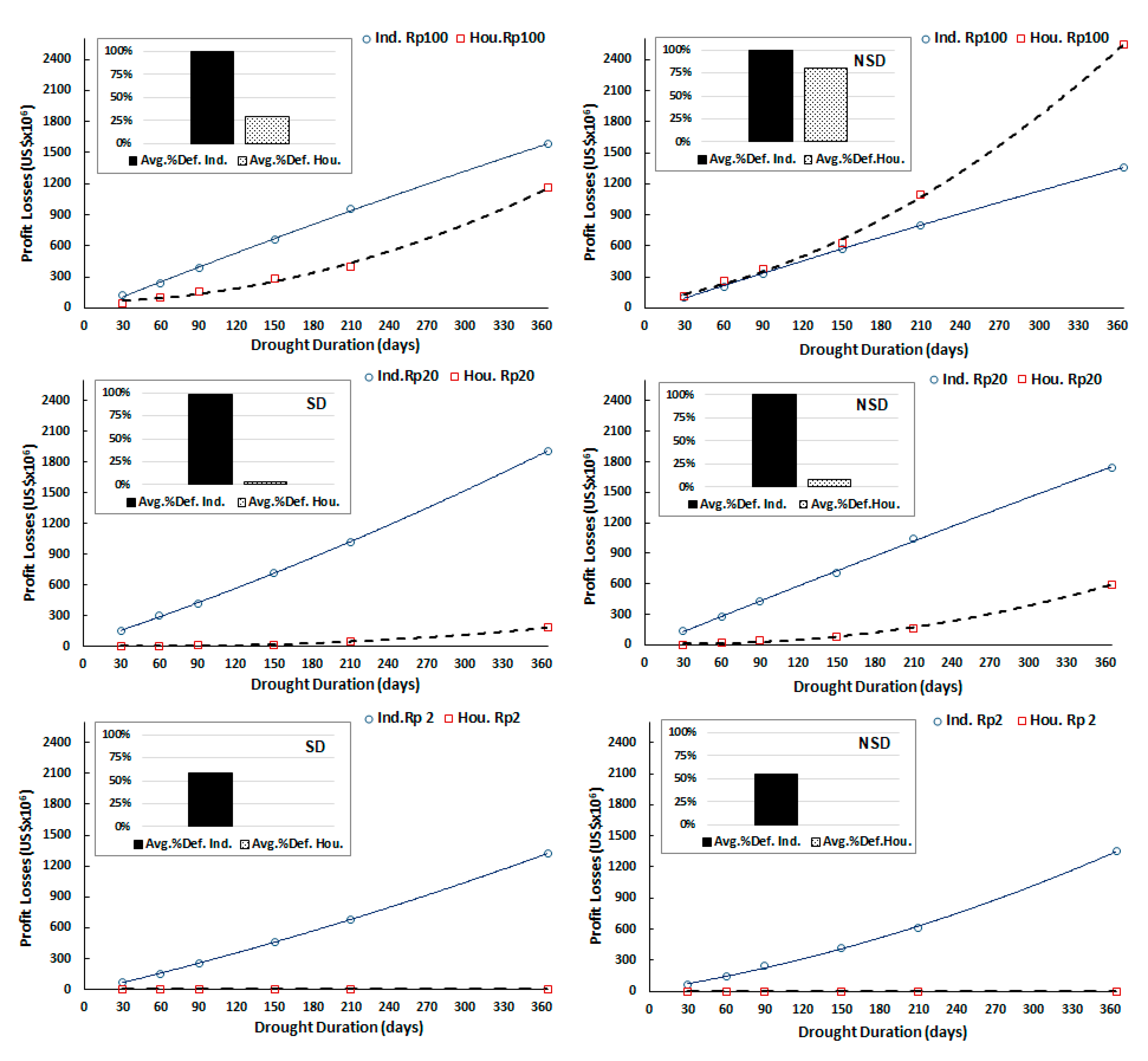
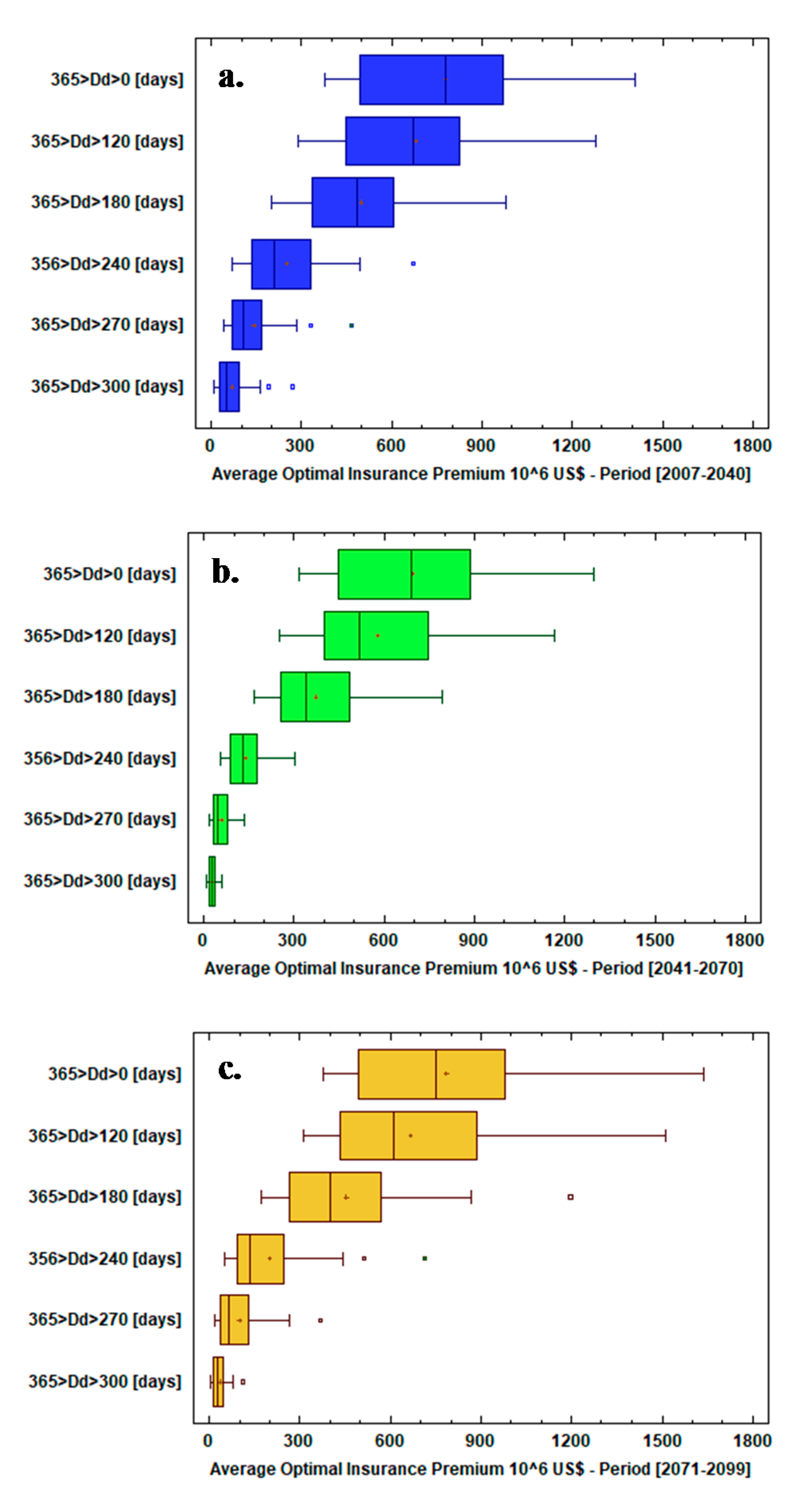
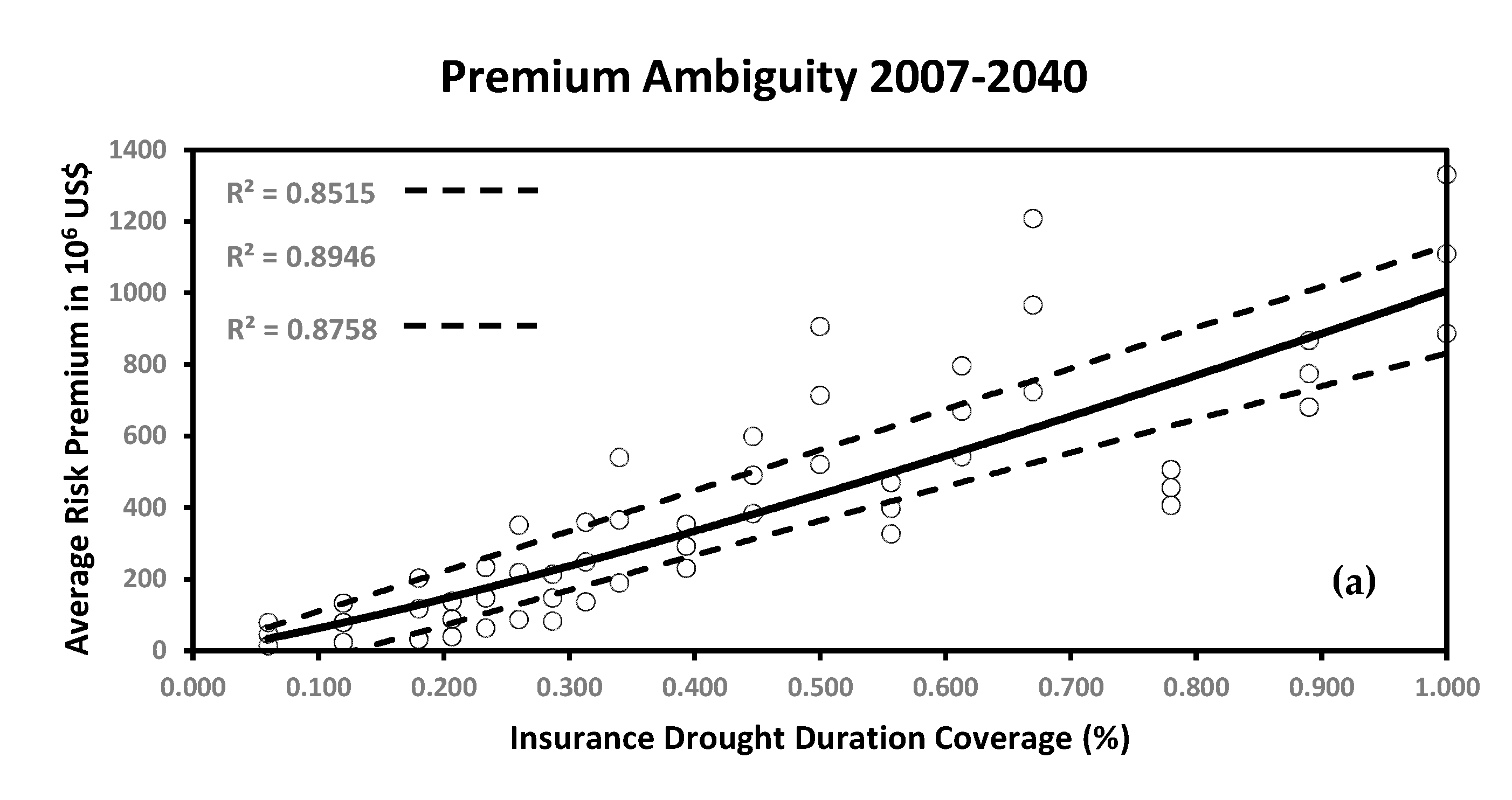
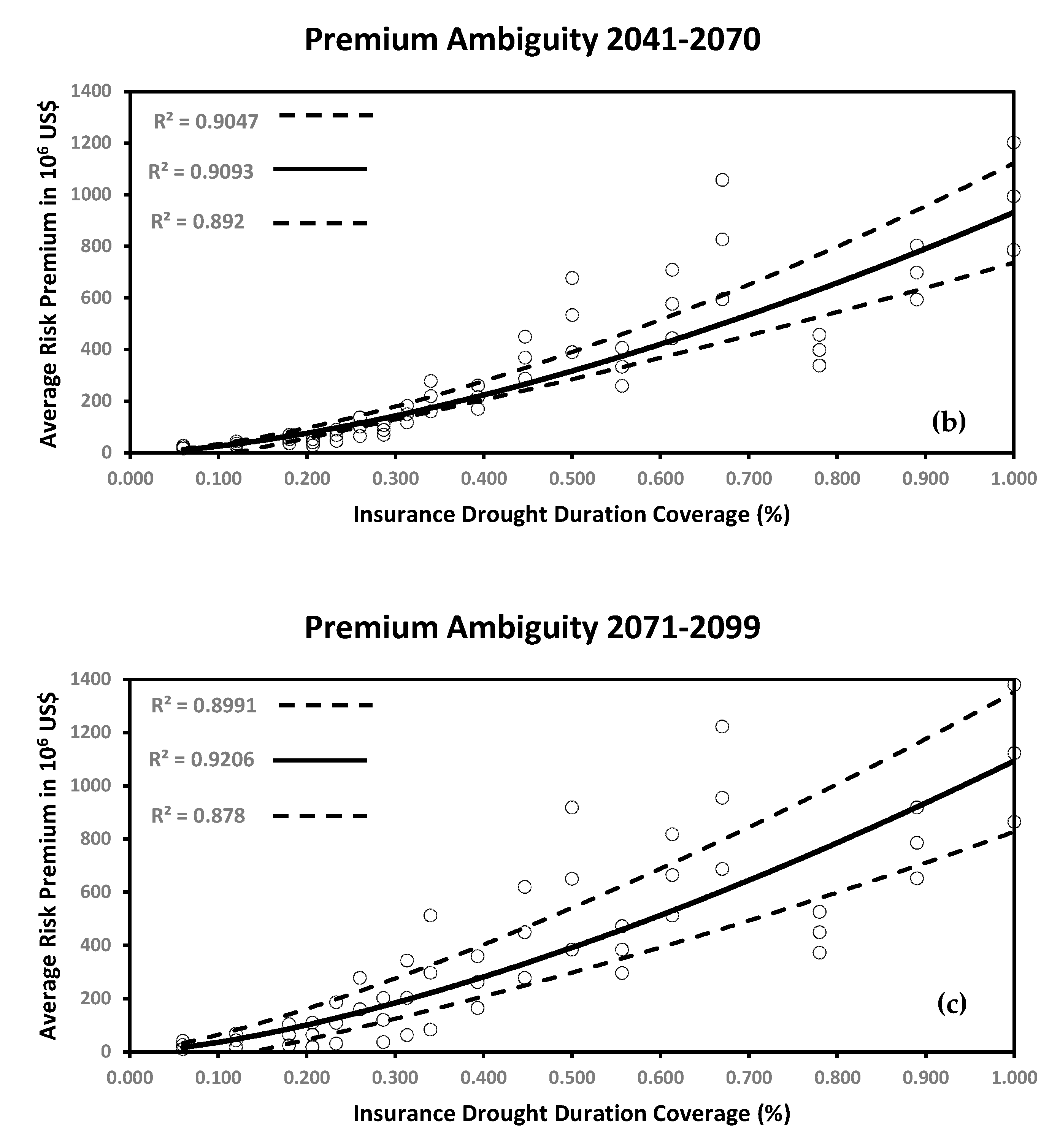
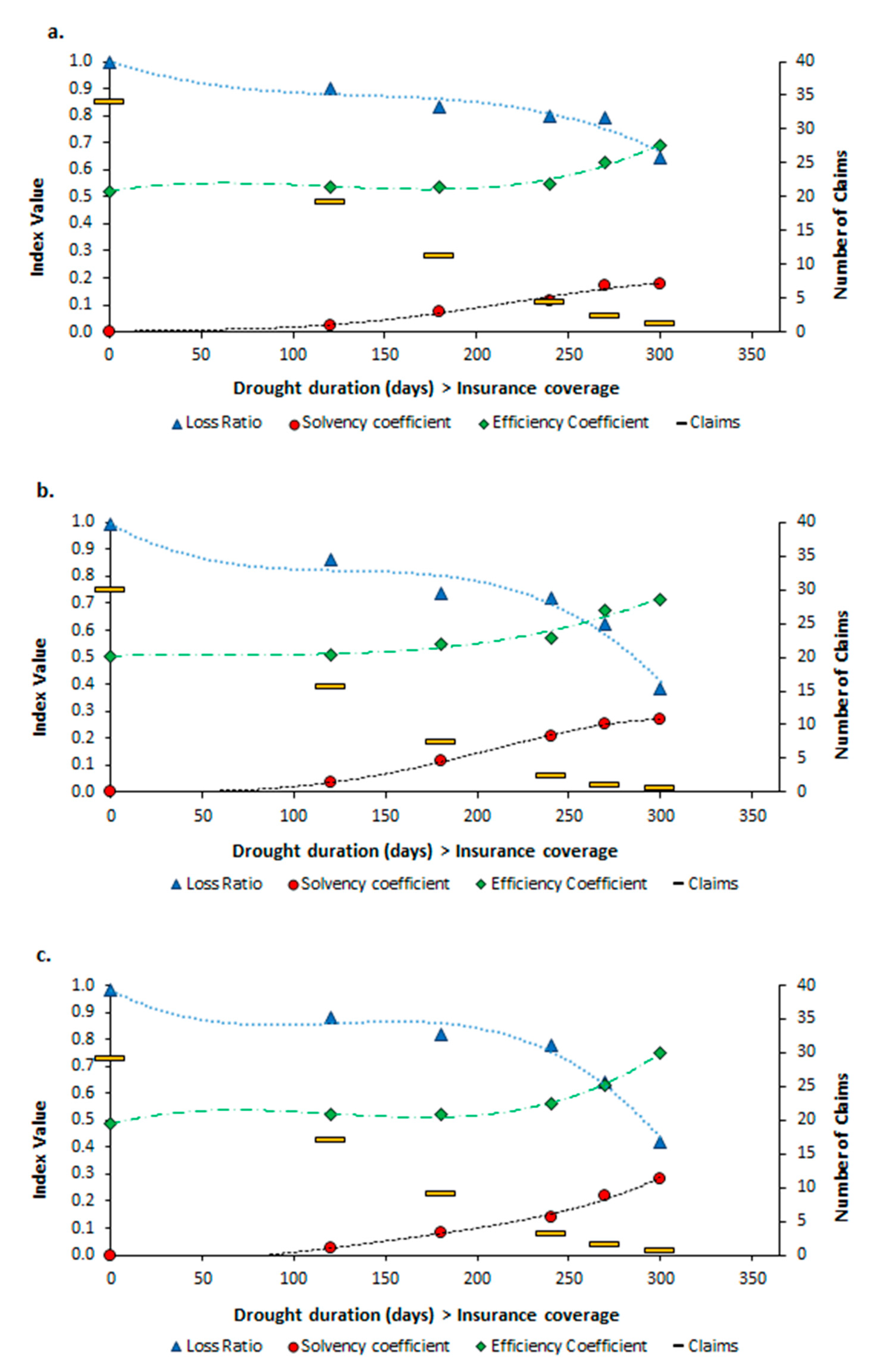
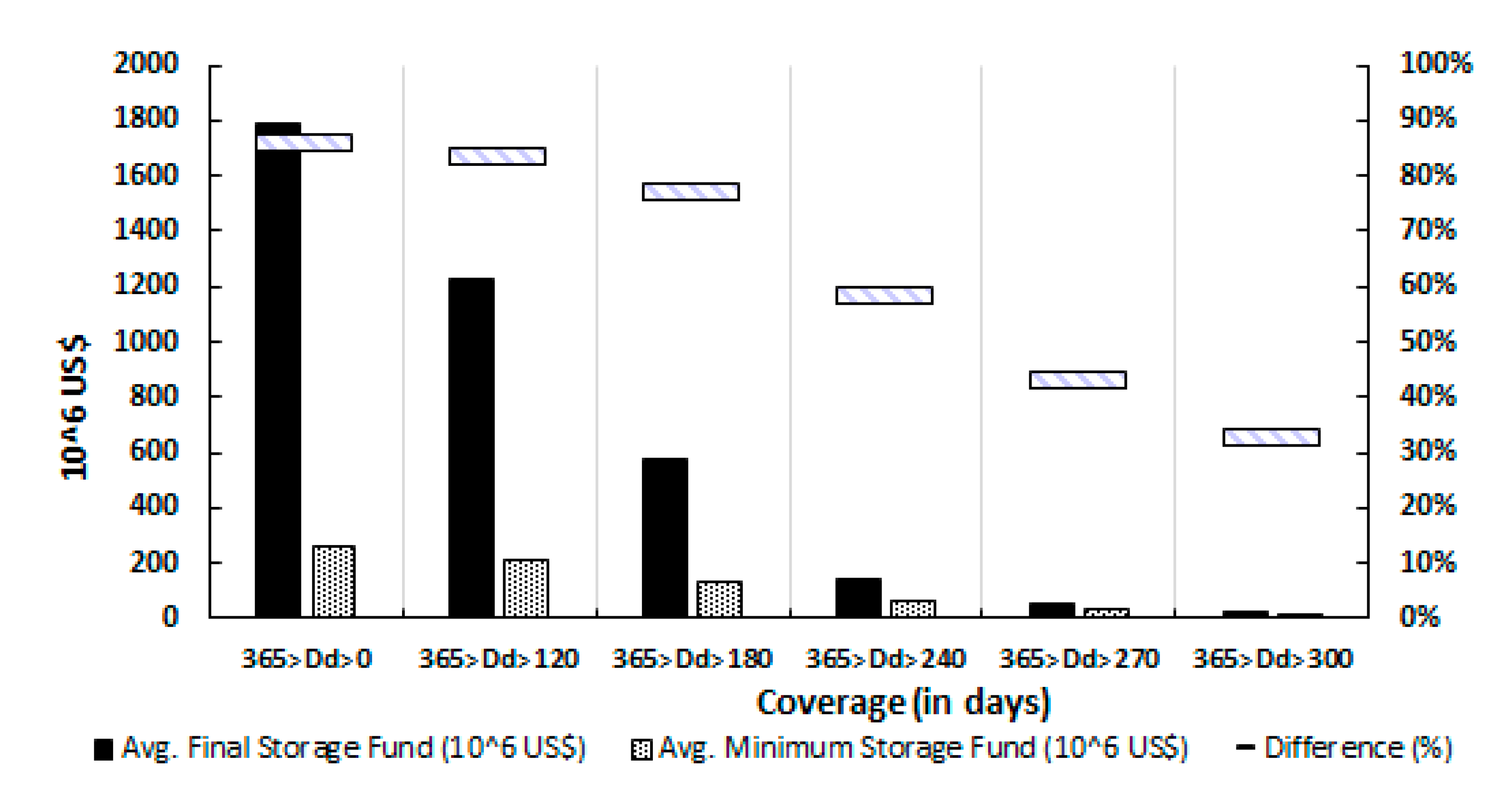
| Index | 2012 (Before) | 2013 (During) | 2014 (During) | 2015 (During) | 2016 (After) | 2017 (After) |
|---|---|---|---|---|---|---|
| Net margin (%) | 17.8 | 17.0 | 8.1 | 4.6 | 20.9 | 17.2 |
| Net profit (106 USD) * | 479.2 | 481.9 | 226.24 | 134.3 | 738.3 | 631.2 |
| Feature | Description |
|---|---|
| Insurance regulations | Administration of private insurance (SUSEP) in Brazil:
|
| Hazard approach | Hydrological drought |
| Insurance sector | Private insurance (disaster coverage for businesses) |
| Coverage (what and who) | What: Business interruption cost [26]; revenue losses related to selling water in household and industrial sectors during hydrological deficit until 100-year return period (Rp) [40,41] Who: Public services (water utility company revenue losses) |
| Coverage scale | Meso-scale (the Sao Paulo Metropolitan Region (SPMR)), lumped as watershed system model |
| Insurance planning scenarios |
|
| Purchase requirement | Compulsory under an MYI contract scheme |
| Premium setting | Risk actuarially fair premium (free of administrative costs) |
| Hydrological variable * | Intra-annual droughts: 0 days < drought duration (Dd) < 365 days, from the monthly threshold level method (TLM) analysis |
| Loss function * | Empirically based curves as a function of annual maximum drought duration (days) and tariff policy price adopted during deficit periods (USD) |
| Insurance performance indexes | Loss ratio, efficiency, and solvency coefficients |
| Drought Duration (Days) * | Water Tariff Adjustment Adopted (%) | Average Price (USD/m3) | Cantareira System Robustness Characteristic Scenarios |
|---|---|---|---|
| 0 to 31 | 0 | 3.38 | 100% water availability base scenario |
| 0 to 90 | 6 | 3.58 | 100% water availability |
| 0 to 180 | 10 | 3.71 | Water availability with storage dependency |
| 0 to 365 | 17 | 3.95 | Water deficit (multi-year droughts) |
| Hydroclimatological Scenario x | Avg. Annual Premium (106 USD) | Demand Scenarios (%) * | Avg. Annual Premium (GDP %) ** | Potential Annual Bonus Discount (106 USD) | Avg. Loans (106 USD) |
|---|---|---|---|---|---|
| Rp 100–365 > 0, 2007–2099 SD–NSD | |||||
| 4.5 Eta/MIROC5 | 938–1636 | 42 | 0.27–0.47 | 268–1133 | 20–43 |
| 4.5 Eta/HadGEM | 779–1362 | 43 | 0.22–0.40 | 161–1044 | 70–127 |
| 8.5 Eta/MIROC5 | 889–1408 | 37 | 0.25–0.42 | 405–1408 | 8–49 |
| 8.5 Eta/HadGEM | 701–1128 | 38 | 0.20–0.33 | 141–479 | 26–149 |
| Rp 100–365 > 180, 2007–2099 SD–NSD | |||||
| 4.5 Eta/MIROC5 | 578–1198 | 52 | 0.16–0.35 | 27–86 | 204–517 |
| 4.5 Eta/HadGEM | 378–980 | 61 | 0.11–0.29 | 2–208 | 310–551 |
| 8.5 Eta/MIROC5 | 458–951 | 51 | 0.13–0.28 | 9–137 | 289–666 |
| 8.5 Eta/HadGEM | 356–570 | 38 | 0.11–0.16 | 3–14 | 342–520 |
| Rp 100–365 > 300, 2007–2099 SD–NSD | |||||
| 4.5 Eta/MIROC5 | 21–110 | 81 | 0.005–0.04 | 0–0 | 99–315 |
| 4.5 Eta/HadGEM | 36–269 | 87 | 0.01–0.07 | 0–3.5 | 131–593 |
| 8.5 Eta/MIROC5 | 9–82 | 89 | 0.002–0.02 | 0–0.3 | 51–244 |
| 8.5 Eta/HadGEM | 29–93 | 69 | 0.009–0.02 | 0–0 | 117–275 |
| Rp 2–365 > 0, 2007–2099 SD–NSD | |||||
| 4.5 Eta/MIROC5 | 427–584 | 27 | 0.13–0.16 | 117–394 | 10–14 |
| 4.5 Eta/HadGEM | 352–484 | 27 | 0.10–0.14 | 59–497 | 35–46 |
| 8.5 Eta/MIROC5 | 403–505 | 20 | 0.11–0.15 | 185–560 | 3–17 |
| 8.5 Eta/HadGEM | 316–409 | 23 | 0.09–0.11 | 47–231 | 13–48 |
| Rp 2–365 > 180, 2007–2099 SD–NSD | |||||
| 4.5 Eta/MIROC5 | 269–425 | 38 | 0.07–0.13 | 8–48 | 100–186 |
| 4.5 Eta/HadGEM | 176–345 | 49 | 0.05–0.11 | 0.4–71 | 150–202 |
| 8.5 Eta/MIROC5 | 212–338 | 37 | 0.06–0.09 | 2–87 | 133–239 |
| 8.5 Eta/HadGEM | 166–203 | 18 | 0.04–0.05 | 1.2–8 | 158–181 |
| Rp 2–365 > 300, 2007–2099 SD–NSD | |||||
| 4.5 Eta/MIROC5 | 10–38 | 74 | 0.002–0.011 | 0–0 | 48–109 |
| 4.5 Eta/HadGEM | 18–92 | 80 | 0.005–0.02 | 0–1.2 | 63–203 |
| 8.5 Eta/MIROC5 | 5–28 | 82 | 0.0015–0.009 | 0–0.1 | 25–83 |
| 8.5 Eta/HadGEM | 14–32 | 56 | 0.004–0.010 | 0–0 | 56–94 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzmán, D.A.; Mohor, G.S.; Mendiondo, E.M. Multi-Year Index-Based Insurance for Adapting Water Utility Companies to Hydrological Drought: Case Study of a Water Supply System of the Sao Paulo Metropolitan Region, Brazil. Water 2020, 12, 2954. https://doi.org/10.3390/w12112954
Guzmán DA, Mohor GS, Mendiondo EM. Multi-Year Index-Based Insurance for Adapting Water Utility Companies to Hydrological Drought: Case Study of a Water Supply System of the Sao Paulo Metropolitan Region, Brazil. Water. 2020; 12(11):2954. https://doi.org/10.3390/w12112954
Chicago/Turabian StyleGuzmán, Diego A., Guilherme S. Mohor, and Eduardo M. Mendiondo. 2020. "Multi-Year Index-Based Insurance for Adapting Water Utility Companies to Hydrological Drought: Case Study of a Water Supply System of the Sao Paulo Metropolitan Region, Brazil" Water 12, no. 11: 2954. https://doi.org/10.3390/w12112954
APA StyleGuzmán, D. A., Mohor, G. S., & Mendiondo, E. M. (2020). Multi-Year Index-Based Insurance for Adapting Water Utility Companies to Hydrological Drought: Case Study of a Water Supply System of the Sao Paulo Metropolitan Region, Brazil. Water, 12(11), 2954. https://doi.org/10.3390/w12112954





