Assessment of the Impact of Sand Mining on Bottom Morphology in the Mekong River in An Giang Province, Vietnam, Using a Hydro-Morphological Model with GPU Computing
Abstract
1. Introduction
- (1)
- First, the computational times on a single-core CPU machine are too slow to meet the simulation’s on-demand requirements. We thus parallelize our solver using massively multi-core GPUs to accelerate the computing speed, which is evaluated with a strong-scaling factor.
- (2)
- Second, we assess the changes in bottom morphology in the Mekong River in An Giang province under sand mining.
2. Materials and Methods
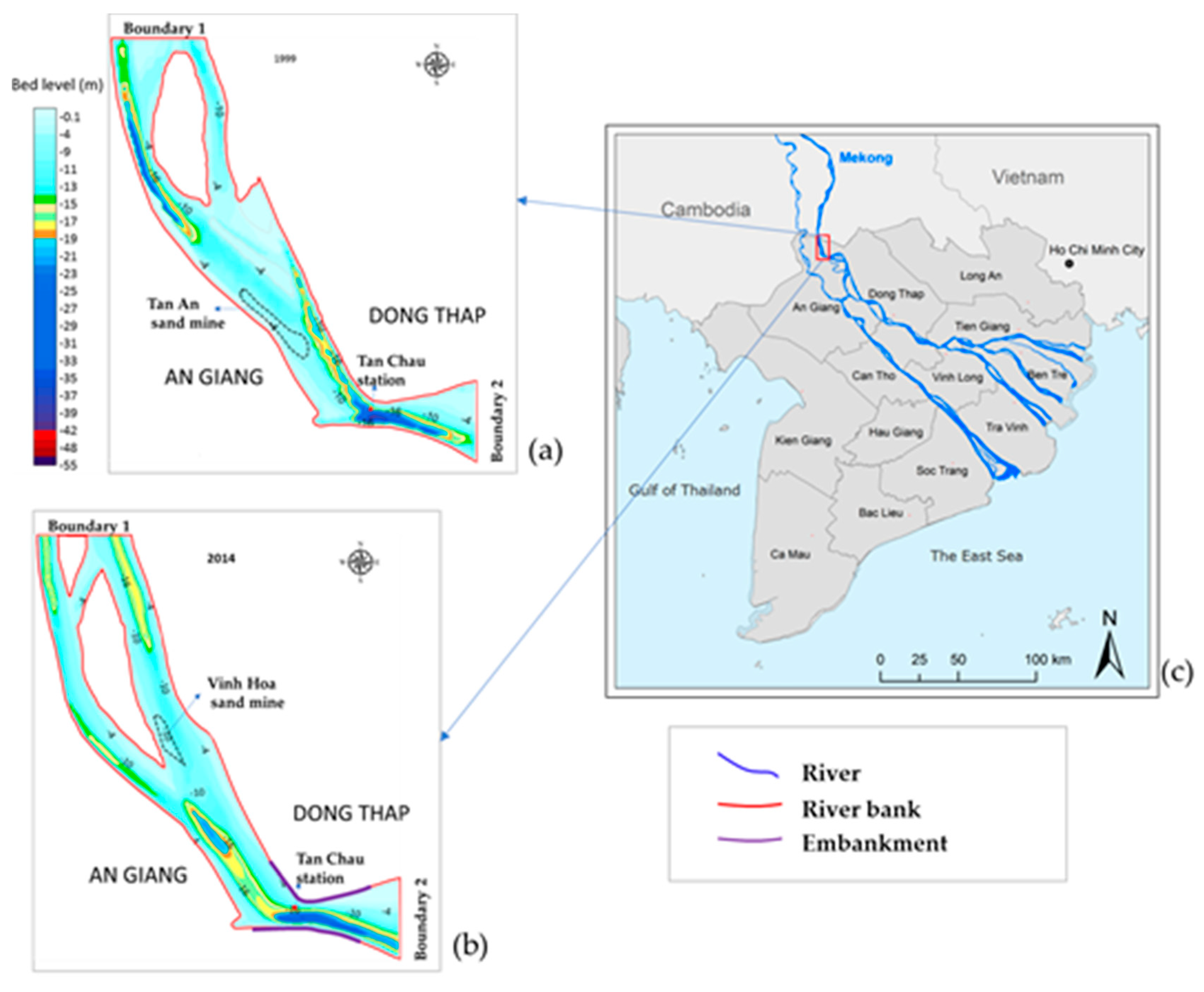
2.1. Study Area
2.2. Numerical Model
2.2.1. Reynolds Equation in the Ox and Oy Directions
2.2.2. Suspended Sediment Transport Equation
2.2.3. Bed Load Continuity Equation with Sand Mining Component:
2.3. Graphics Processing Unit (GPU)
3. Setting up the Model
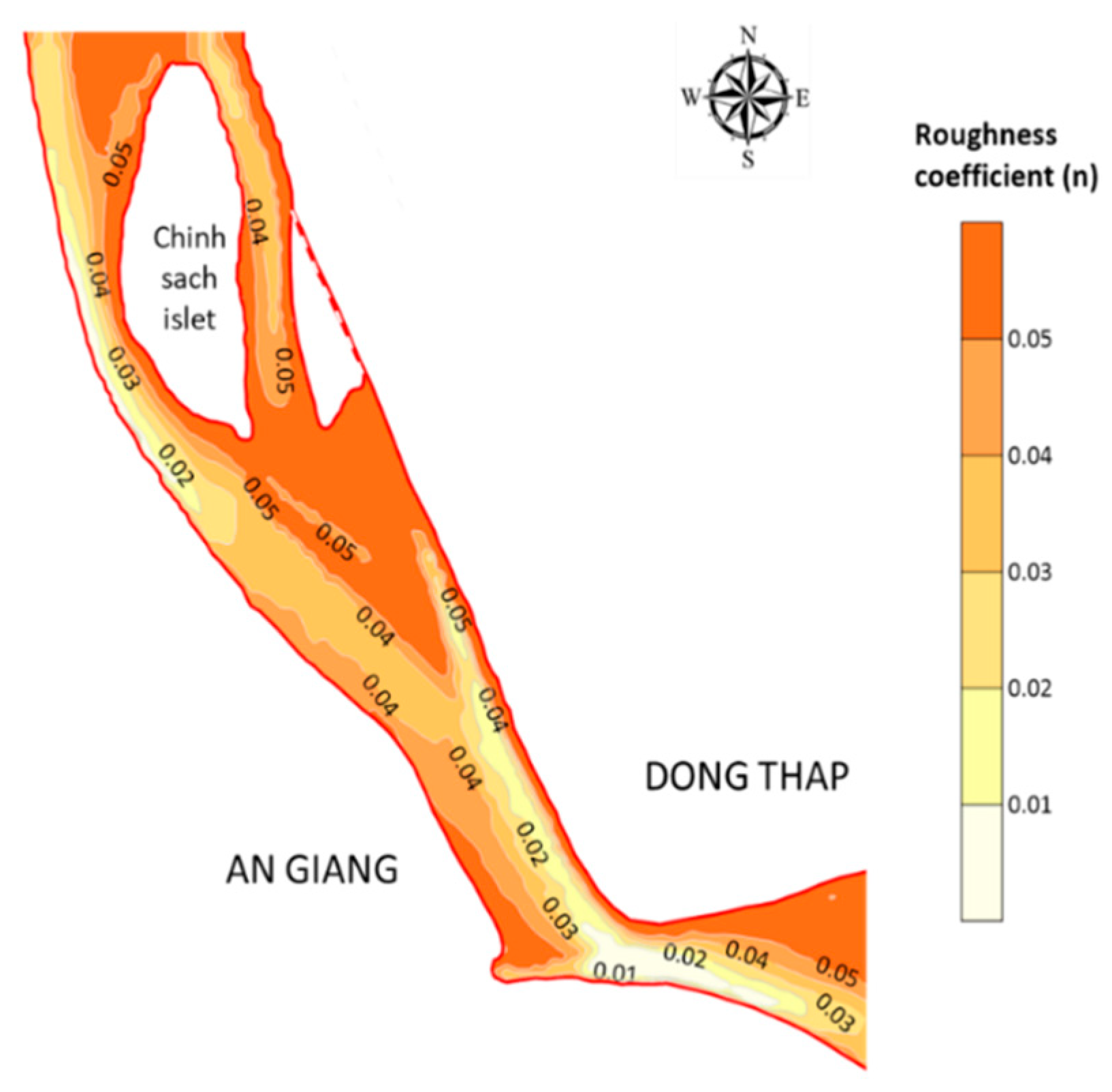
3.1. Study Area Mesh
3.2. Initial and Boundary Conditions
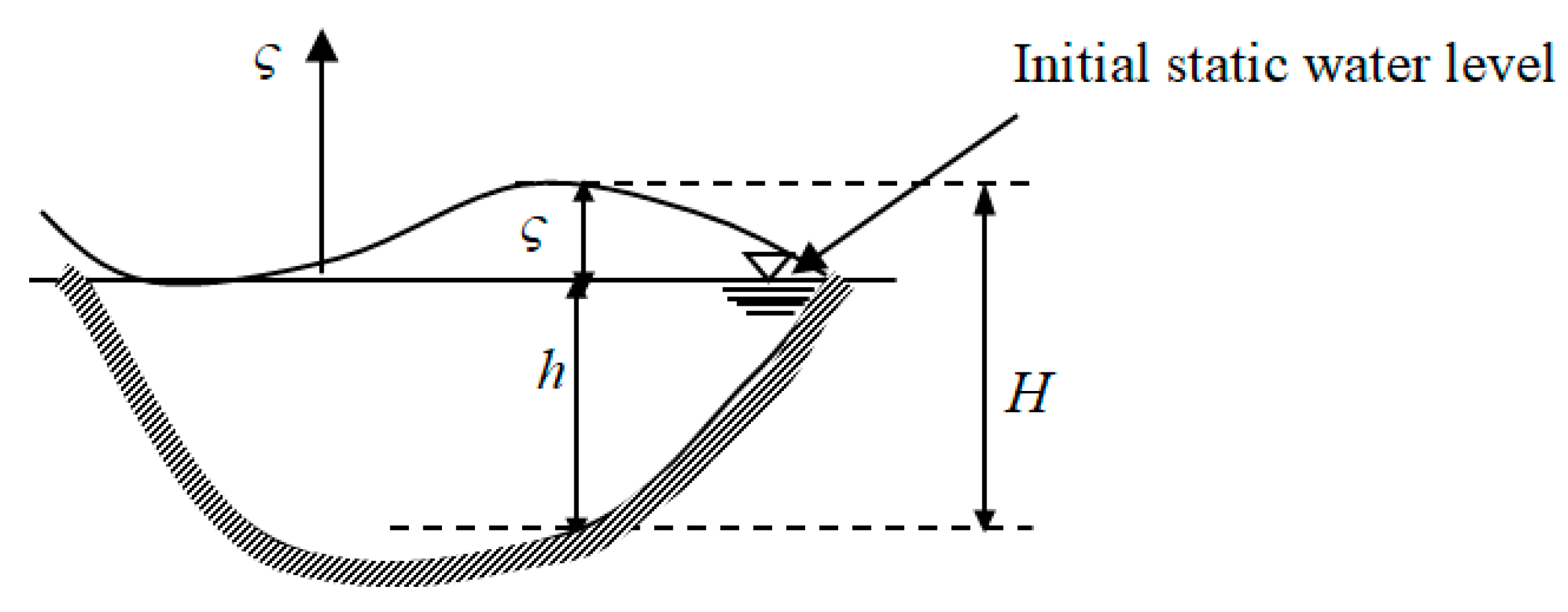
3.2.1. Initial Conditions
3.2.2. Boundary Conditions
The Open Boundary
Solid Wall Boundary
4. Results and Discussion
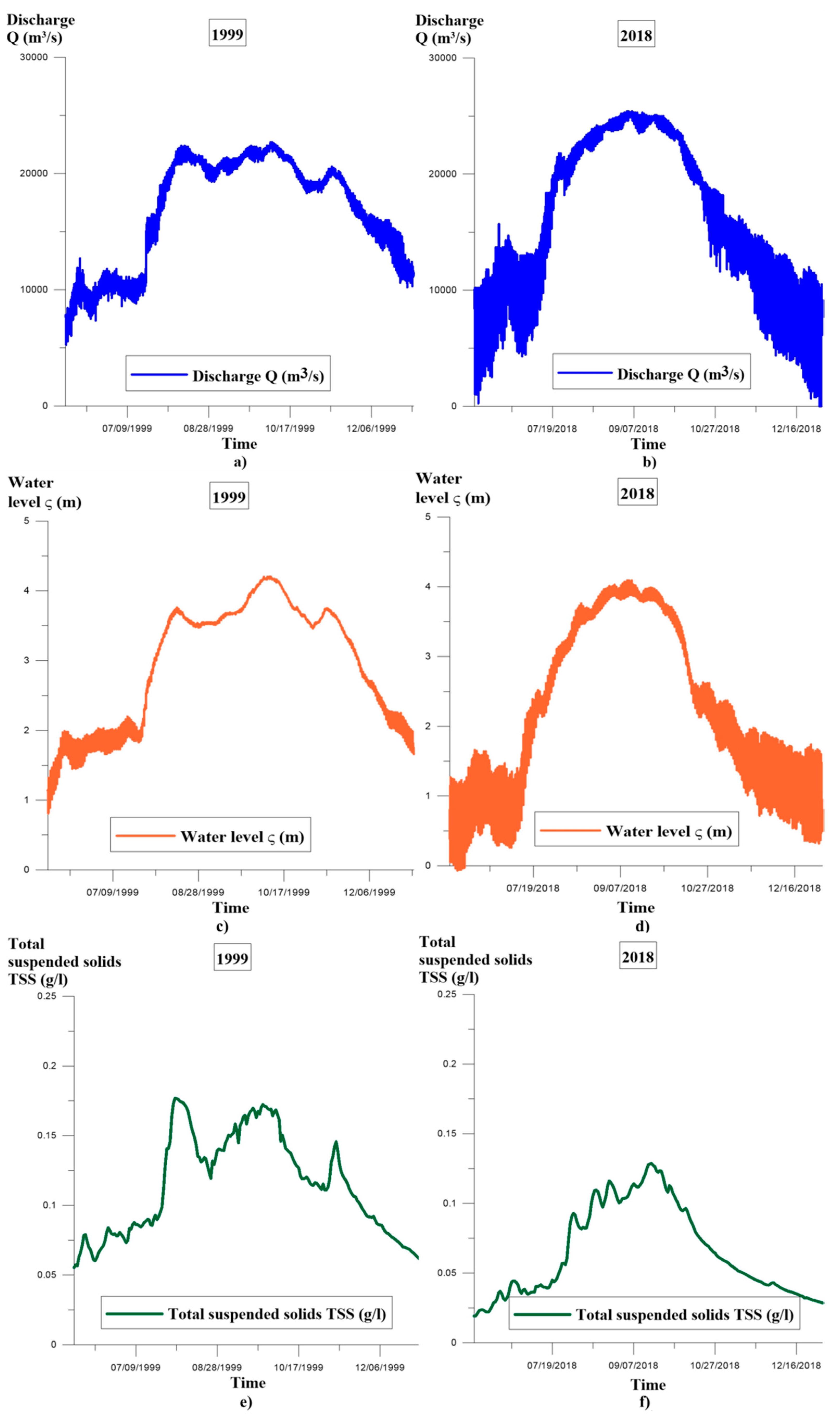
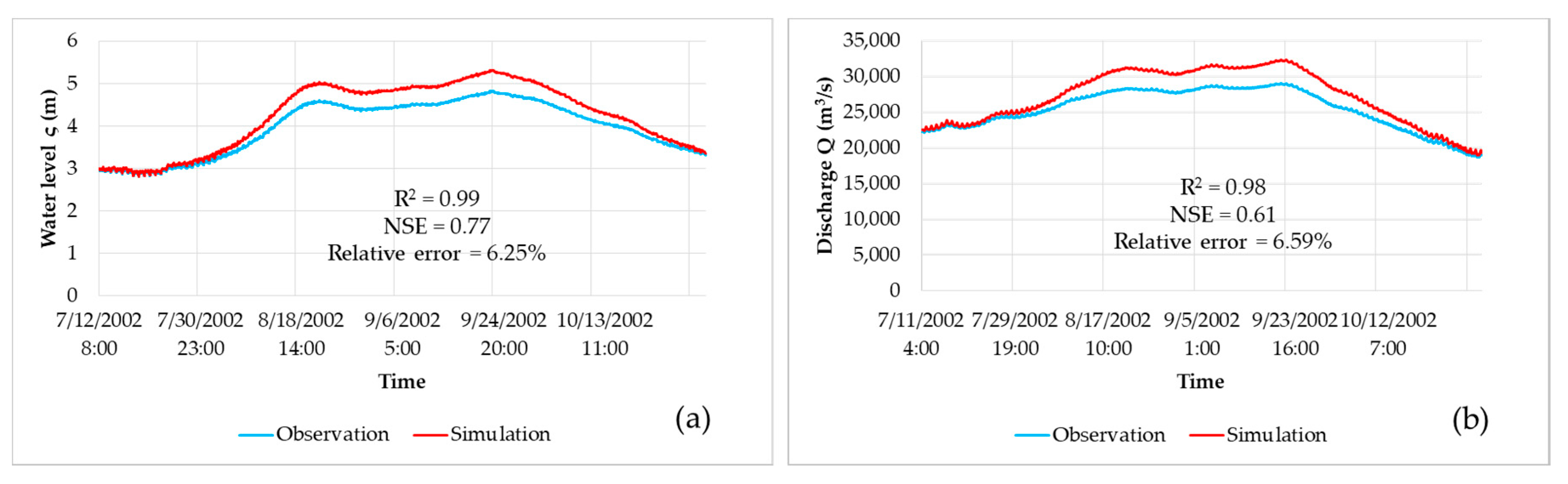
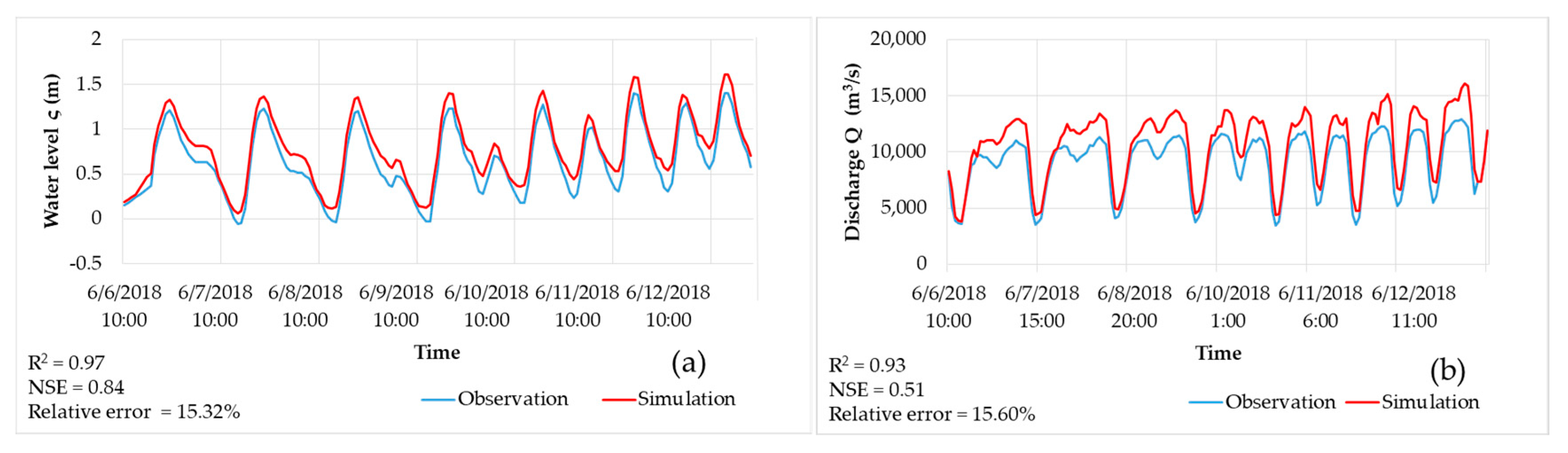
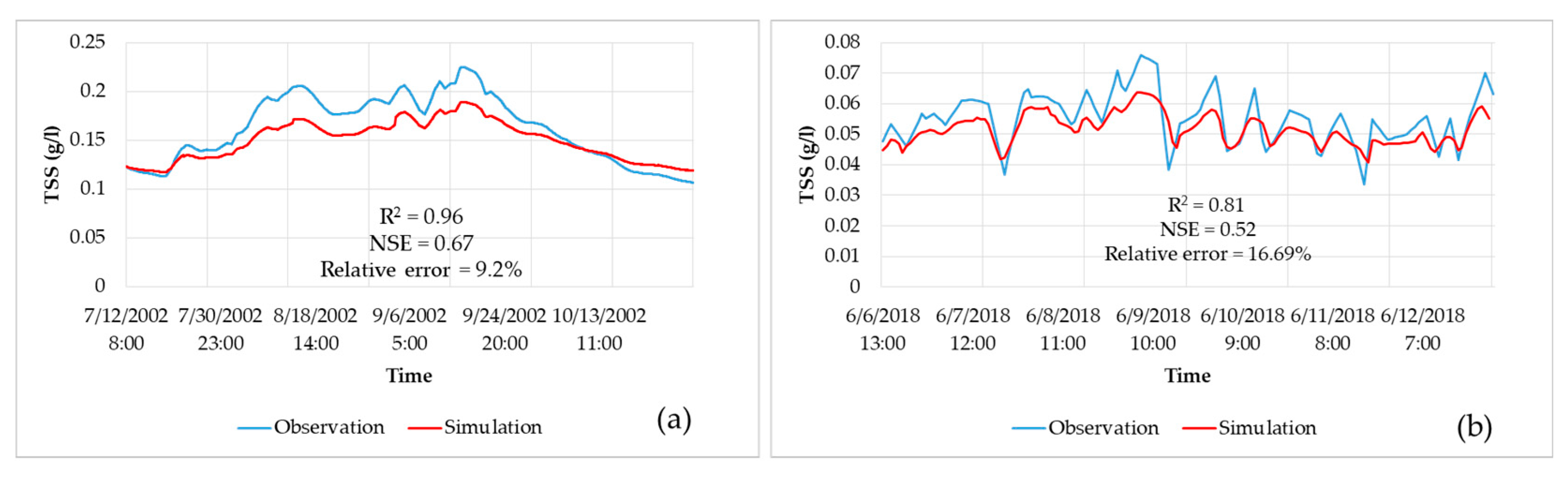
4.1. Calibration and Validation
4.1.1. Hydraulic Model
4.1.2. Sediment Transport Model
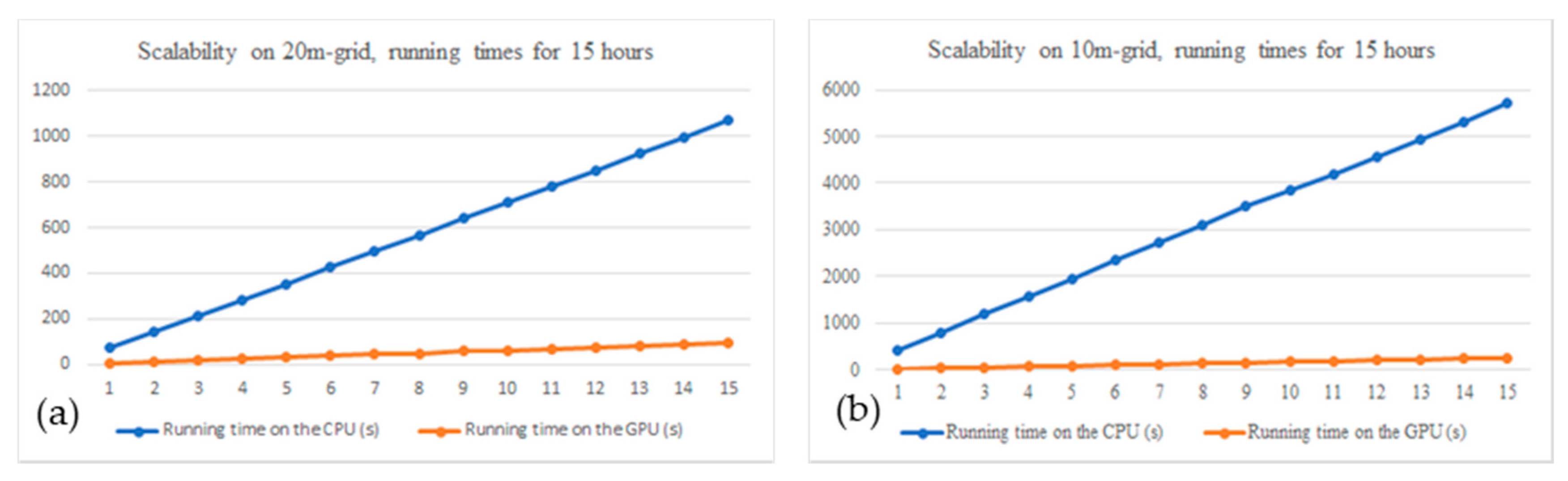
4.2. Improved Computing Speed When Combining GPUs
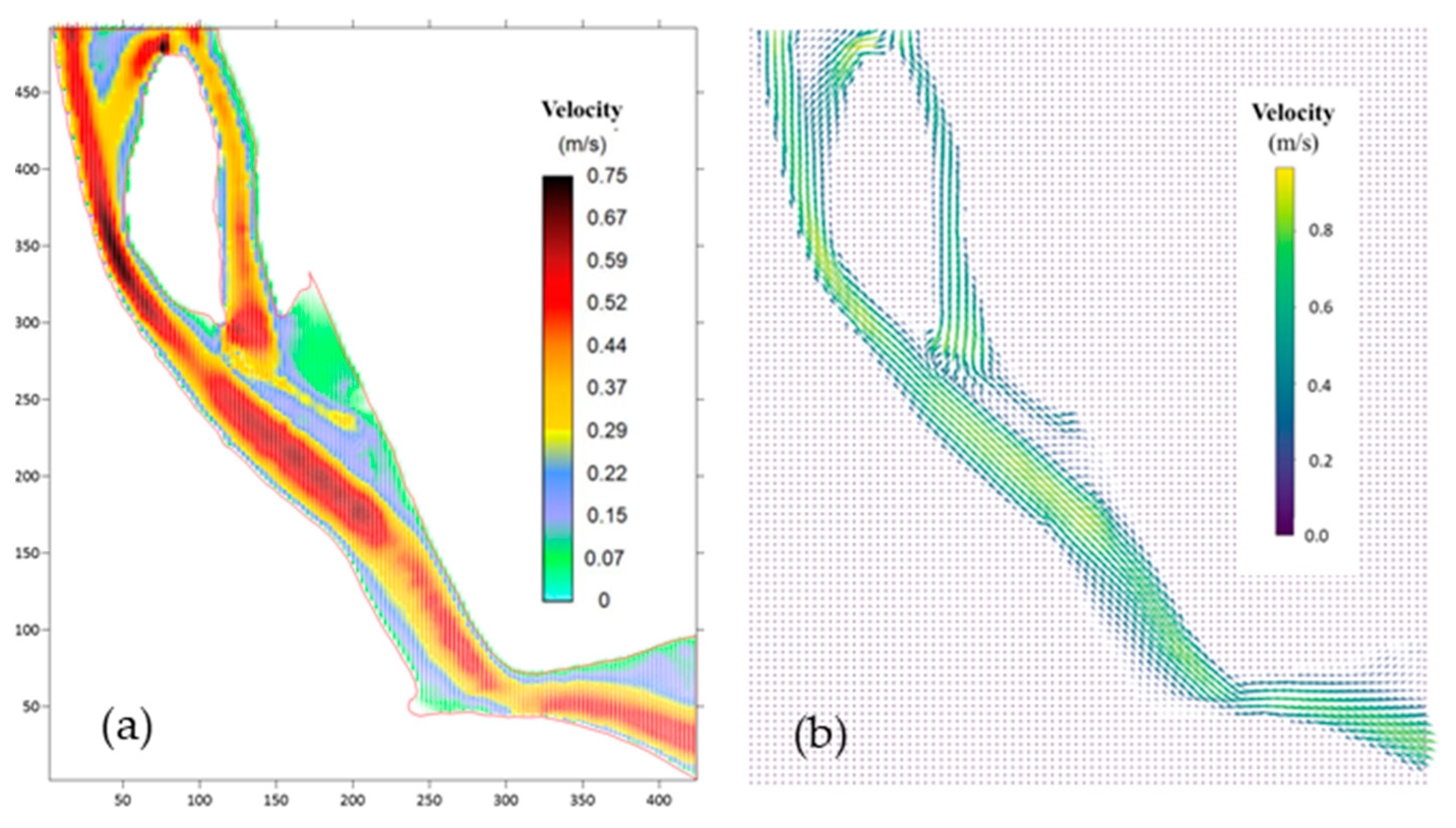
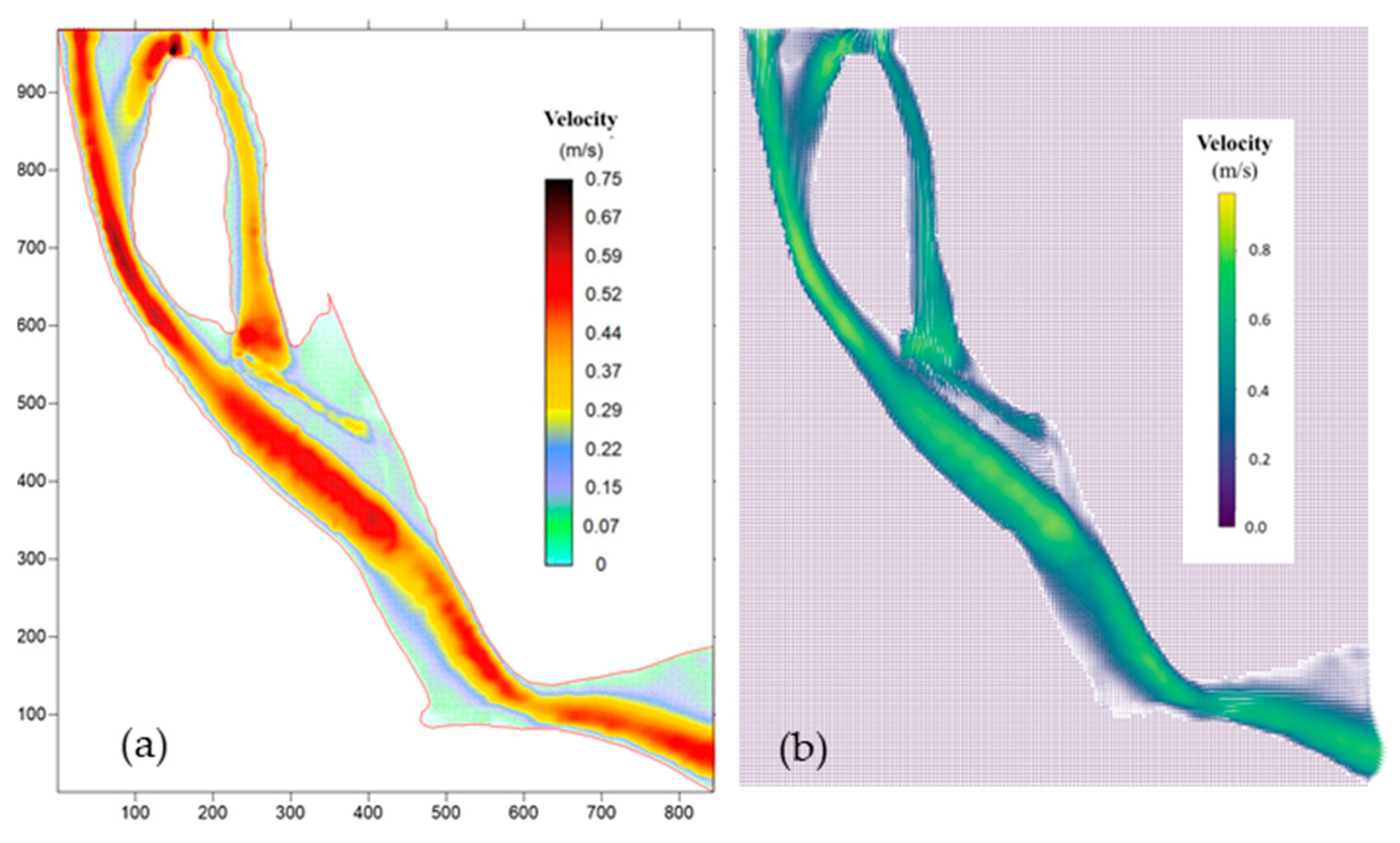
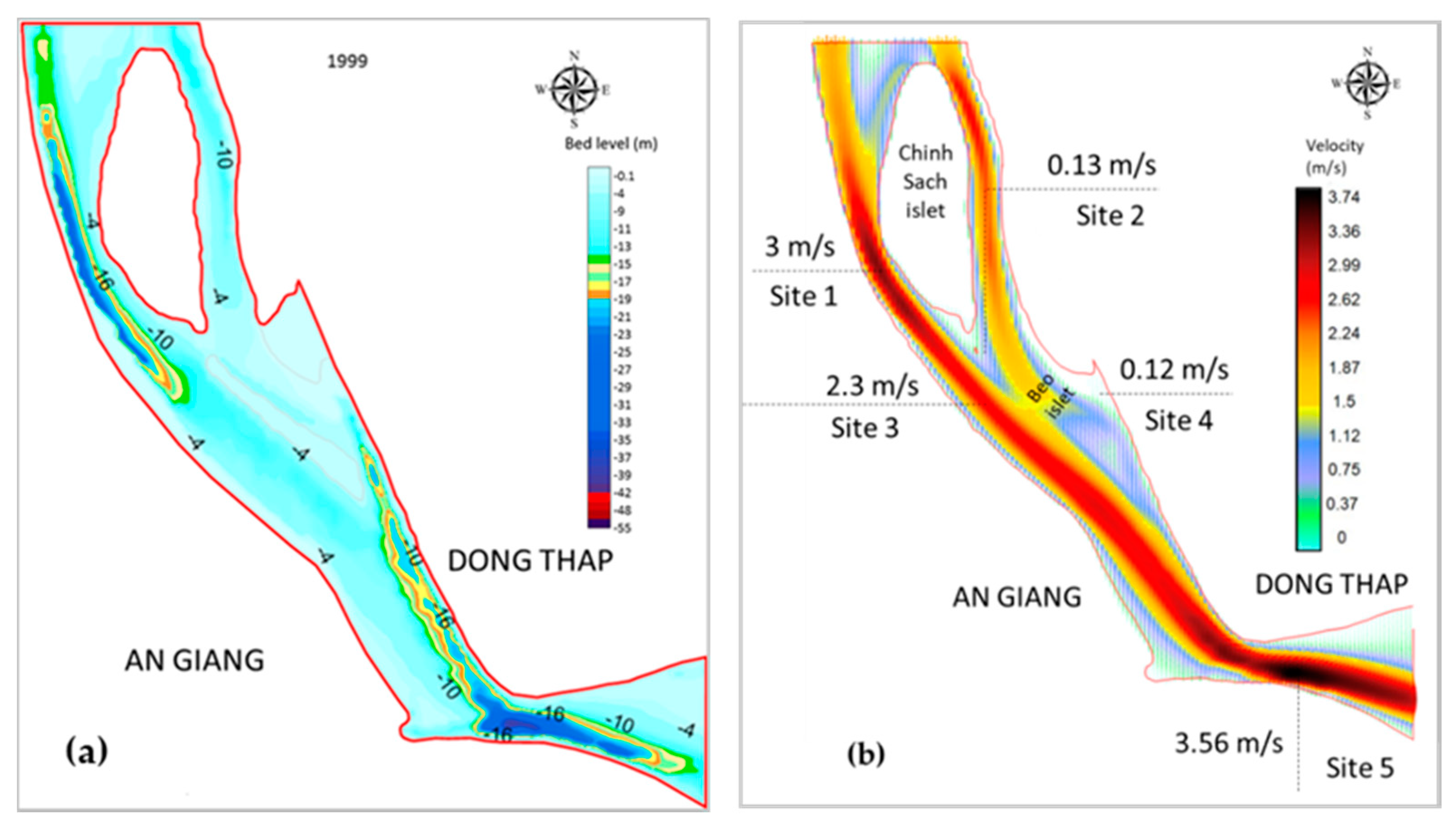
4.3. The Hydraulic Simulation of the Tien River Segment in Mekong Delta
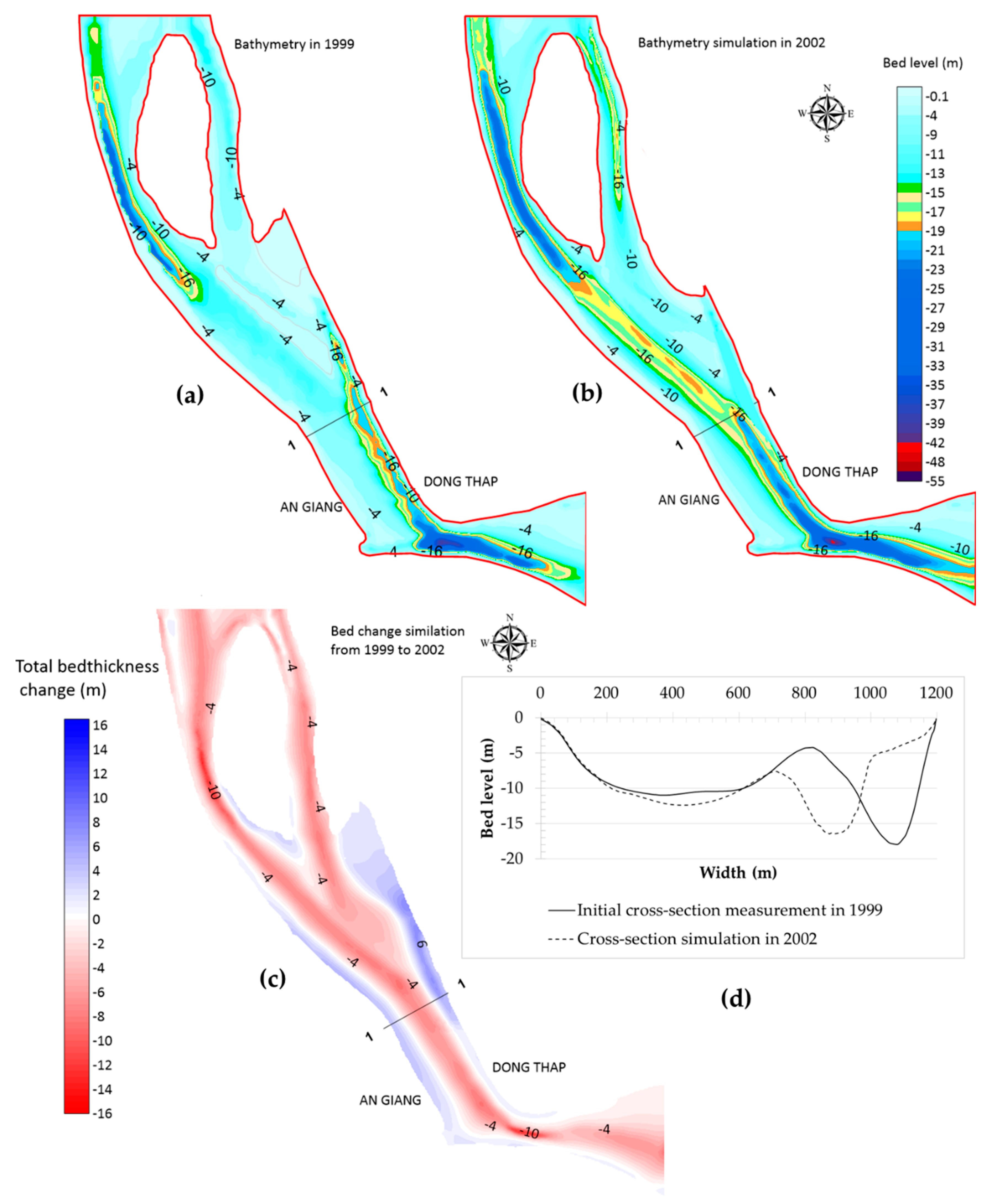
4.4. Results of Bottom Changes and Analysis
- SC1: From 1999 to 2002 was the time before the sand mines started operating.
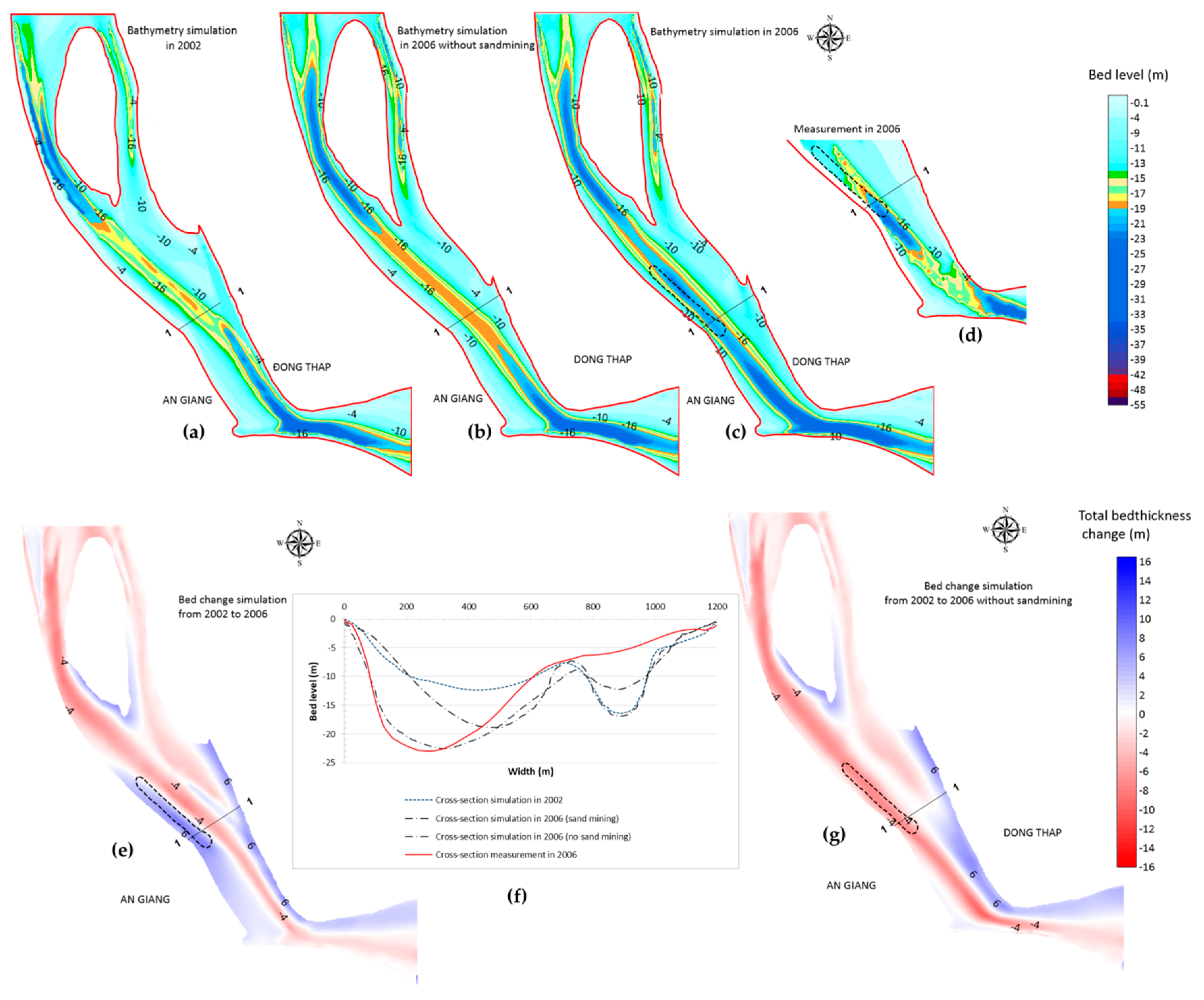
- SC2A: From 2002 to 2006 was the time that Tan An sand mine was in operation.
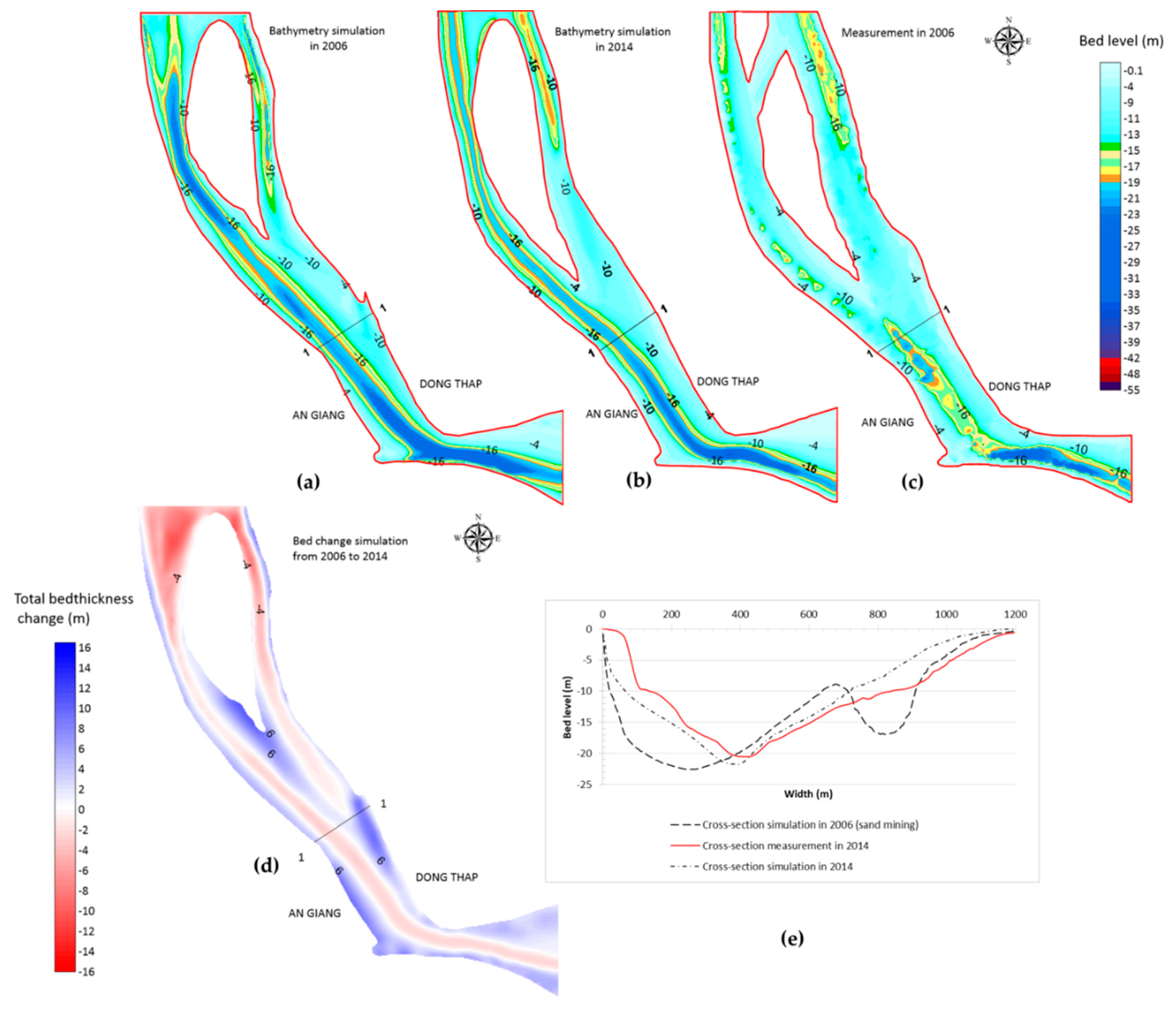
- SC3: From 2006 to 2014, there was no sand quarry in the study area.
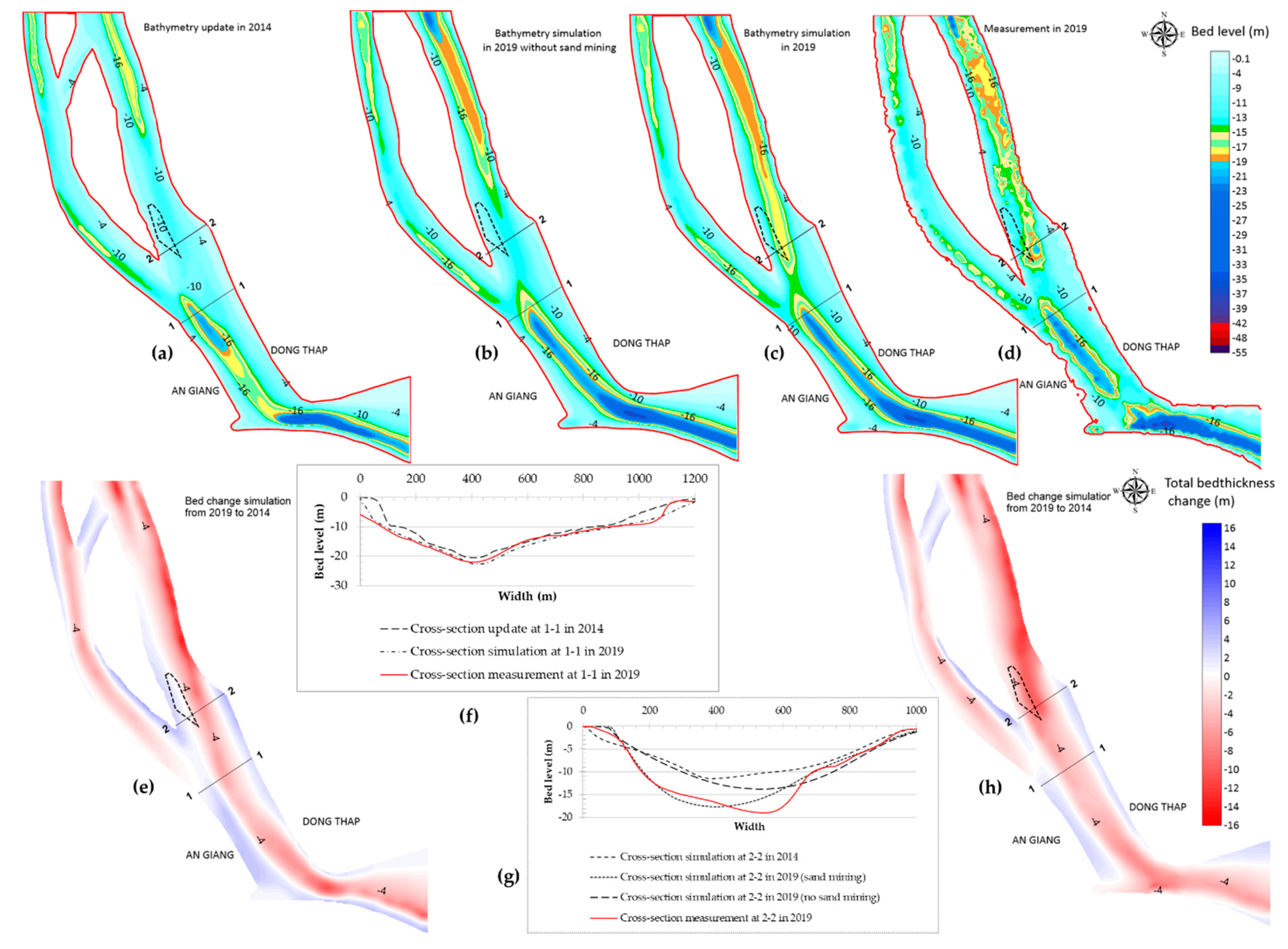
- SC4A: From 2014 to 2019, the Vinh Hoa sand mine is in operation.
- SC2B: From 2002 to 2006, there was no sand mining at Tan An sand mine.
- SC4B: From 2014 to 2019, there was no sand mining at Vinh Hoa sand mine.
4.4.1. From 1999 to 2002 (SC1)
4.4.2. From 2002 to 2006 (SC2A and SC2B)
4.4.3. From 2006 to 2014 (SC3)
4.4.4. From 2014 to 2019 (SC4A and SC4B)
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclatures
| u | Depth-averaged horizontal velocity components in x-direction (m/s) |
| ν | Depth-averaged horizontal velocity components in y-direction (m/s) |
| ς | Fluctuation of the water surface, compared to a “zero” level (m) |
| h | Static depth from the still water surface to the bed (m) |
| K | Friction bed coefficient |
| A | Eddy horizontal viscosity coefficient (m2/s) |
| g | Acceleration gravity (m/s2) |
| C | Depth-averaged concentration of the suspended load (m3/m3) |
| Kx | Dispersion coefficient in the Ox direction (m2/s) |
| Ky | Dispersion coefficient in the Oy direction (m2/s) |
| H | Average depth used in the model (H=h+ ς) (m) |
| γv | Velocity coefficient for the depth; calculated from |
| Z | Suspension number defined after Van Rijn (1993), |
| χ | Von Karman constant = 0.4 |
| u | Bed shear velocity, |
| Ch | Chezy coefficient, |
| Ks | Bed roughness, Ks = 3D90 |
| D90 | Diameter of particle that is equal to or less than 90% of the mass of the particles present |
| S | Standing for erosion and deposition rates (m/s). |
| M | Sediment size-dependent coefficient after Van Rijn (1993): 0,00001 (kg/m2/s) |
| Cb | Concentration of bedload, (m3/m3) |
| ωsm | Particle fall velocity in a mixture of water and sediment (m/s), |
| ωs | Particle fall velocity, |
| D | Mean diameter of the particle (m) |
| ν | Kinematic viscosity coefficient (m2/s) |
| τe | Critical bed shear stress for erosion at the bottom (N/m2) |
| τd | Critical bed shear stress for deposition at the bottom (N/m2) |
| τb | Bed shear stress (N/m2), |
| fw | Friction coefficient of Darcy – Weisbach, calculated from the Chezy formula; |
| ρ | Mass density of water, (kg/m3) |
| ρs | Density of particles, (kg/m3) |
| nr | Roughness coefficient |
| εp | Void ratio of sediment |
| D* | Dimensionless particle parameter |
| T | Dimensionless bed shear stress: |
| u*,cr | Critical depth-averaged flow velocity based on Shields (m/s), |
| qb | Bedload |
| hi | Bottom depth at the calculation node (m) |
| Δx | The distance between two nodes (m) |
| np | Perpendicular to the shoreline |
References
- Baena-Escudero, R.; Rinaldi, M.; García-Martínez, B.; Guerrero-Amador, I.C.; Nardi, L. Sediment mining in alluvial channels: Physical effects and management perspective. Geomorphology 2019, 337, 15–30. [Google Scholar] [CrossRef]
- Chen, D.; Acharya, K.; Stone, M. Sensitivity analysis of nonequilibrium adaptation parameters for modeling mining-pit migration. J. Hydraul. Eng. 2010, 136, 806–811. [Google Scholar] [CrossRef]
- Kim, C. Impact analysis of river aggregate mining on river environment. KSCE J. Civil Eng. 2005, 9, 45–48. [Google Scholar] [CrossRef]
- Kondolf, G.M. Hungry water: Effects of dams and gravel mining on river channels. Environ. Manag. 1997, 21, 533–551. [Google Scholar] [CrossRef]
- Martín-Vide, J.P.; Ferrer-Boix, C.; Ollero, A. Incision due to gravel mining: Modeling a case study from the Gallegoriver, Spain. Geomorphology 2010, 117, 261–271. [Google Scholar] [CrossRef]
- Bandita, B.; Arup, K.S.; Bimlesh, K. Mining pit migration of an alluvial channel: Experimental and numerical investigations. ISH J. Hydraul. Eng. 2020, 26, 448–456. [Google Scholar] [CrossRef]
- Bandita, B.; Bimlesh, K.; Arup, K.S. Dynamic characterization of the migration of a mining pit in an alluvial channel. Int. J. Sediment Res. 2019, 34, 155–165. [Google Scholar] [CrossRef]
- Yuill, B.T.; Gaweesh, A.; Allison, M.A.; Meselhe, E.A. Morphodynamic evolution of a lower Mississippi River channel bar after sand mining. Earth Surf. Process. Landf. 2016, 41, 526–542. [Google Scholar] [CrossRef]
- Jia, P.; Dong, C.; Brendan, T.Y. Modeling Evolution of a Large Mining Pit in the Lower Mississippi River. In Proceedings of the World Environmental and Water Resources Congress, Pittsburgh, Pennsylvania, 19–23 May 2019; pp. 287–295. [Google Scholar]
- Van Rijn, L.C. Sedimentation of dredged channels by currents and waves. J. Waterw. Port Coast. Ocean Eng. 1986, 112, 541–559. [Google Scholar] [CrossRef]
- Adamson, P.T.; Rutherfurd, I.D.; Peel, M.; Conlan, I.A. The hydrology of the Mekong River. In The Mekong; Elsevier: Amsterdam, The Netherlands, 2009; pp. 53–76. [Google Scholar]
- Gupta, A.; Liew, S.C. The Mekong from satellite imagery: A quick look at a large river. Geomorphology 2007, 85, 259–274. [Google Scholar] [CrossRef]
- Halls, A.S.; Conlan, I.; Wisesjindawat, W.; Phouthavongs, K.; Viravong, S.; Chan, S.; Vu, V.A. Atlas of Deep Pools in the Lower Mekong River and Some of its Tributaries; Mekong River Commission: Phnom Penh, Cambodia, 2013. [Google Scholar]
- Jordan, C.; Tiede, J.; Lojek, O.; Visscher, J.; Apel, H.; Nguyen, H.Q.; Schlurmann, T. Sand mining in the Mekong Delta revisited-current scales of local sediment deficits. Sci. Rep. 2019, 9, 17823. [Google Scholar] [CrossRef]
- Bravard, J.P.; Goichot, M.; Gaillot, S. Geography of sand and gravel mining in the Lower Mekong River. First survey and impact assessment. EchoGéo 2013, 26. [Google Scholar] [CrossRef]
- Hackney, C.; Darby, S.; Parsons, D.; Leyland, J.; Best, J.; Aalto, R.; Nicholas, A. Unsustainable in-channel sand mining threatens sand delivery to the Mekong delta. In Proceedings of the 20th EGU General Assembly, Vienna, Austria, 4–13 April 2018. [Google Scholar]
- Best, J.; Hackney, C.R.; Darby, S.E.; Parsons, D.R.; Leyland, J.; Aalto, R.E.; Nicholas, A.P.; Houseago, R.C. River bank instability induced by unsustainable sand mining in the Mekong River. In Proceedings of the AGU Fall Meeting 2019, San Francisco, CA, USA, 9–13 December 2019; American Geophysical Union: Washington, DC, USA, 2019. [Google Scholar]
- Hoai, H.C.; Bay, N.T.; Khoi, D.N.; Nga, T.N.Q. Analyzing the causes producing the rapidity of river bank erosion in Mekong Delta. Vietnam J. Hydro-Meteorol. 2019, 7, 42–50. (In Vietnamese) [Google Scholar]
- Filip, H. Studies of the morphological activity of rivers as illustrated by the River Fyris, Bulletin. Geol. Inst. Upsalsa 1935, 25, 221–527. [Google Scholar]
- Kondolf, G.M.; Schmitt, R.J.; Carling, P.; Darby, S.; Arias, M.; Bizzi, S.; Castelletti, A.; Cochrane, T.A.; Gibson, S.; Kummu, M.; et al. Changing sediment budget of the Mekong: Cumulative threats and management strategies for a large river basin. Sci. Total Environ. 2018, 625, 114–134. [Google Scholar] [CrossRef] [PubMed]
- Babu, K.; Dwarakish, G.; Jayakumar, S. Modeling of sediment transport along Mangalore coast using mike 21. In Proceedings of the International Conference on Coastal and Ocean Technology, Chennai, India, 10–12 December 2003. [Google Scholar]
- Daghigh, H.; Khaniki, A.K.; Bidokhti, A.A.; Habibi, M. Prediction of bed ripple geometry under controlled wave conditions: Wave-flume experiments and MIKE21 numerical simulations. Indian J. Geo-Mar. Sci. 2017, 46, 529–537. [Google Scholar]
- Jia, Y.; Wang, S.S. Numerical model for channel flow and morphological change studies. J. Hydraul. Eng. 1999, 125, 924–933. [Google Scholar] [CrossRef]
- Kopmann, R.; Merkel, U.H. Using reliability analysis in morphodynamic simulation with TELEMAC-2D/SISYPHE. In Proceedings of the XIXth TELEMAC-MASCARET User Conference, Oxford, UK, 18–19 October 2012. [Google Scholar]
- Villaret, C.; Hervouet, J.M.; Kopmann, R.; Merkel, U.; Davies, A.G. Morphodynamic modeling using the Telemac finite-element system. J. Comput. 2013, 53, 105–113. [Google Scholar] [CrossRef]
- Safarzadeh, A.; Neyshabouri, A.S.; Dehkordi, A. 2D Numerical Simulation of Fluvial Hydrodynamics and Bed Morphological Changes. In AIP Conference Proceedings; American Institute of Physics: College Park, MA, USA, 2009. [Google Scholar]
- Ahn, J.; Lyu, S. Analysis of flow and bed change on hydraulic structure using CCHE2D: Focusing on Changnyong-Haman. J. Korea Water Resour. Assoc. 2013, 46, 707–717. [Google Scholar] [CrossRef][Green Version]
- Bay, N.T.; Khoi, D.N.; Kim, T.T.; Phung, N.K. Research on bottom morphology and Lithodynamic processes in the coastal area using the numerical Model: Case Studies of Can Gio and Cua Lap, Southern Vietnam. Vietnam J. Hydro-Meteorol. 2018, 2, 43–53. [Google Scholar]
- Bay, N.T.; Toan, T.T.; Phung, N.K.; Nguyen-Quang, T. Numerical investigation on the sediment transport trend of Can Gio Coastal Area (Southern Vietnam). J. Mar. Environ. Eng. 2012, 9, 191–211. [Google Scholar]
- Guan, M.; Liang, Q. A two-dimensional hydro-morphological model for river hydraulics and morphology with vegetation. Environ. Model. Softw. 2017, 88, 10–21. [Google Scholar] [CrossRef]
- Ikeda, S. Sediment transport and sorting at bends. River Meand. 1989, 12, 103–125. [Google Scholar]
- Van Rijn, L.C. Sediment Transport, Part II: Suspended Load Transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Wu, W. Depth-averaged two-dimensional numerical modeling of unsteady flow and nonuniform sediment transport in open channels. J. Hydraul. Eng. 2004, 130, 1013–1024. [Google Scholar] [CrossRef]
- Wu, W.; Shields, F.D., Jr.; Bennett, S.J.; Wang, S.S. A depth-averaged two-dimensional model for flow, sediment transport, and bed topography in curved channels with riparian vegetation. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Bay, N.T.; Kim, T.T.; Hoai, H.C.; Tai, P.A.; Huy, N.D.Q.; Phung, N.K. HYDIST model and the approach of solving sediment concentration at open boundaries. Vietnam J. Hydro-Meteorol. 2019, 704, 57–64. (In Vietnamese) [Google Scholar] [CrossRef]
- Mattamana, B.A.; Varghese, S.; Paul, K. River Sand Inflow Assessment and Optimal Sand Mining Policy Development. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 305–317. [Google Scholar]
- Yao, J.; Zhang, D.; Li, Y.; Zhang, Q.; Gao, J. Quantifying the hydrodynamic impacts of cumulative sand mining on a large river-connected floodplain lake: Poyang Lake. J. Hydrol. 2019, 579, 124156. [Google Scholar] [CrossRef]
- Obot, O.I.; Ekpo, I.F.; David, G.S. The Effect of Sand Mining on the Physico-Chemical Parameters of Ikot Ekpan River, Akwa Ibom State, Nigeria. J. Aquat. Sci. Mar. Biol. 2019, 2, 21–24. [Google Scholar]
- Okorie, P.U.; Acholonu, A.D.W. Effect of Commercial Sand Mining on Water Quality Parameters of Nworie River in Owerri, Nigeria. Proc. Niger. Acad. Sci. 2018, 11, 1–8. [Google Scholar]
- Cui, M. Compact alternating direction implicit method for two-dimensional time fractional diffusion equation. J. Comput. Phys. 2012, 231, 2621–2633. [Google Scholar] [CrossRef]
- Gong, C.; Bao, W.; Tang, G.; Jiang, Y.; Liu, J. Computational challenge of fractional differential equations and the potential solutions: A survey. Math. Probl. Eng. 2015, 2015, 258265. [Google Scholar] [CrossRef]
- Harris, M. Fast fluid dynamics simulation on the GPU. In ACM SIGGRAPH 2005 Courses on—SIGGRAPH ’05; Addison-Wesley Professional: Boston, MA, USA, 2005; Volume 220, pp. 637–666. [Google Scholar]
- Mei, X.; Decaudin, P.; Hu, B.-G. Fast hydraulic erosion simulation and visualization on GPU. In Proceedings of the 15th Pacific Conference on Computer Graphics and Applications (PG’07), Maui, HI, USA, 29 October–2 November 2007. [Google Scholar]
- Guidolin, M.; Kapelan, Z.; Savic, D.; Giustolisi, O. High performance hydraulic simulations with epanet on graphics processing units. In Proceedings of the 9th International Conference on Hydroinformatics, Tianjin, China, 7–11 September 2010. [Google Scholar]
- Wu, Z.Y.; Eftekharian, A.A. Parallel artificial neural network using CUDA-Enabled GPU for extracting hydraulic domain knowledge of large water distribution systems. In Proceedings of the World Environmental and Water Resources Congress, Palm Springs, CA, USA, 22–26 May 2011; pp. 79–92. [Google Scholar] [CrossRef]
- Dorsey, J.; Edelman, A.; Jensen, H.W.; Legakis, J.; Pedersen, H.K. Modeling and rendering of weathered stone. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 8–13 August 1999. [Google Scholar]
- Liu, Y.Q.; Zhu, H.B.; Liu, X.H.; Wu, E.H. Real-time simulation of physically based on-surface flow. Vis. Comput. 2005, 21, 727–734. [Google Scholar] [CrossRef]
- Gupta, A. Chapter 3—Geology and landforms of the Mekong basin. In The Mekong. Aquatic Ecology; Campbell, I.C., Ed.; Academic Press: Cambridge, MA, USA, 2009; pp. 29–51. [Google Scholar]
- Hai, H.Q. Correlation of erosion—Aggradation in areas along Tien and Hau Rivers. Vietnam J. Earth Sci. 2011, 33, 37–44. (In Vietnamese) [Google Scholar] [CrossRef]
- Kuenzer, C.; Guo, H.; Huth, J.; Leinenkugel, P.; Li, X.; Dech, S. Flood mapping and flood dynamics of the Mekong Delta: ENVISAT-ASAR-WSM based time series analyses. Remote Sens. 2013, 5, 687–715. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Aqua Publications: Amsterdam, The Netherlands, 1993; Volume 1006. [Google Scholar]
- Douglas, J. On the Numerical Integration of ∂^2u∂x^2+∂^2u∂y^2=∂u∂t by Implicit Methods. J. Soc. Ind. Appl. Math. 1955, 3, 42–65. [Google Scholar]
- Thomas, L. Elliptic Problems in Linear Differential Equations Over a Network: Watson Scientific Computing Laboratory; Columbia University: New York, NY, USA, 1949. [Google Scholar]
- Valero-Lara, P.; Martínez-Pérez, I.; Sirvent, R.; Martorell, X.; Peña, A.J. cuThomasBatch and cuThomasVBatch, CUDA Routines to compute batch of tridiagonal systems on NVIDIA GPUs. Concurr. Comput. Pract. Exp. 2018, 30, e4909. [Google Scholar] [CrossRef]
- The 2-Clause BSD License. Available online: http://www.opensource.org/licenses/bsd-license.php (accessed on 20 July 2019).
- National Center for Computational Hydroscience and Engineering (CCHE). CCHE2D: Two-Dimensional Hydrodynamic and Sediment Transport Model for Unsteady Open Channel Flows Over Loose Bed; Technical Report No. NCCHE-TR-2001-1; National Center for Computational Hydroscience and Engineering (CCHE): University, MS, USA, 2001. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Mehta, A.J.; Hayter, E.J.; Parker, W.R.; Krone, R.B.; Teeter, A.M. Cohesive sediment transport. I: Process description. J. Hydraul. Eng. 1989, 115, 1076–1093. [Google Scholar] [CrossRef]
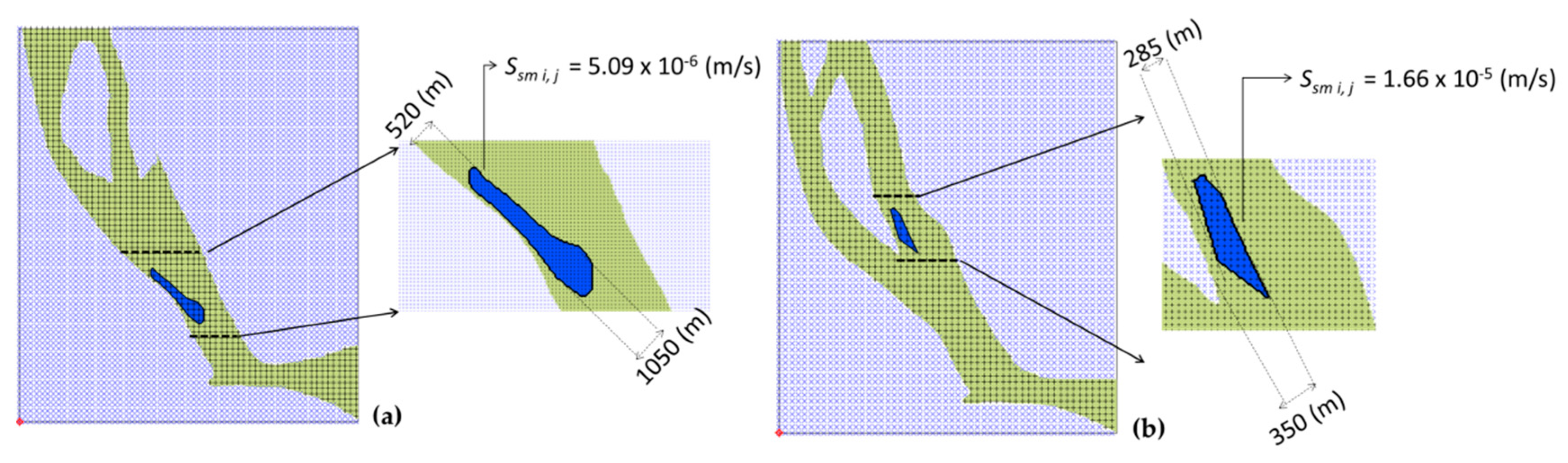
| Sand Mine | Annual Output (m3/year) | Square (m2) | Average Exploitation Rate (m/s)-Ssm(i, j) | |||||
|---|---|---|---|---|---|---|---|---|
| 1999–2001 | 2002–2006 | 2007–2014 | 2014–2019 | |||||
| SC1 | SC2A | SC2B | SC3 | SC4A | SC 4B | |||
| Tan An | 200,000 | 910,000 | 0 | 5.09 × 10-6 | 0 | 0 | 0 | 0 |
| Vinh Hoa | 200,000 | 279,000 | 0 | 0 | 0 | 0 | 1.66 × 10-5 | 0 |
| Parameter | Value |
|---|---|
| Time step (Δt) | 2 s |
| Mean diameter of particle (D) | 0.01 mm |
| Diameter of particle 90% of the mass of particles present (D90) | 0.04 mm |
| Density of particles (ρs) | 2600 kg/m3 |
| Kinematic viscosity coefficient (ν) | m2/s |
| Critical shear stress for deposition (τd) | 0.35 N/m2 |
| Critical shear stress for erosion (τe) | 0.04 N/m2 |
| 20-m Grid | 10 m-Grid | |||||
|---|---|---|---|---|---|---|
| Hours of Simulation | Running Time on the CPU (s) | Running Time on the GPU (s) | Accelerating Factor | Running Time on the CPU (s) | Running Time on the GPU (s) | Accelerating Factor |
| 1 | 72.00 | 6 | 12 | 409.00 | 16 | 26 |
| 2 | 141.00 | 12 | 11.75 | 806.00 | 32 | 25 |
| 3 | 213.00 | 19 | 11.21052632 | 1,196.00 | 49 | 24 |
| 4 | 282.00 | 25 | 11.28 | 1,568.00 | 66 | 24 |
| 5 | 353.00 | 31 | 11.38709677 | 1,953.00 | 82 | 24 |
| 6 | 425.00 | 38 | 11.18421053 | 2,340.00 | 99 | 24 |
| 7 | 496.00 | 44 | 11.27272727 | 2,724.00 | 116 | 23 |
| 8 | 567.00 | 50 | 11.34 | 3,110.00 | 132 | 24 |
| 9 | 638.00 | 57 | 11.19298246 | 3,494.00 | 148 | 24 |
| 10 | 709.00 | 63 | 11.25396825 | 3,852.00 | 165 | 23 |
| 11 | 780.00 | 69 | 11.30434783 | 4,198.00 | 181 | 23 |
| 12 | 851.00 | 76 | 11.19736842 | 4,572.00 | 198 | 23 |
| 13 | 922.00 | 82 | 11.24390244 | 4,946.00 | 215 | 23 |
| 14 | 995.00 | 89 | 11.17977528 | 5,323.00 | 232 | 23 |
| 15 | 1,068.00 | 95 | 11.24210526 | 5,697.00 | 248 | 23 |
| ... | ... | ... | ... | ... | ... | ... |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thi Kim, T.; Huong, N.T.M.; Huy, N.D.Q.; Tai, P.A.; Hong, S.; Quan, T.M.; Bay, N.T.; Jeong, W.-K.; Phung, N.K. Assessment of the Impact of Sand Mining on Bottom Morphology in the Mekong River in An Giang Province, Vietnam, Using a Hydro-Morphological Model with GPU Computing. Water 2020, 12, 2912. https://doi.org/10.3390/w12102912
Thi Kim T, Huong NTM, Huy NDQ, Tai PA, Hong S, Quan TM, Bay NT, Jeong W-K, Phung NK. Assessment of the Impact of Sand Mining on Bottom Morphology in the Mekong River in An Giang Province, Vietnam, Using a Hydro-Morphological Model with GPU Computing. Water. 2020; 12(10):2912. https://doi.org/10.3390/w12102912
Chicago/Turabian StyleThi Kim, Tran, Nguyen Thi Mai Huong, Nguyen Dam Quoc Huy, Pham Anh Tai, Sumin Hong, Tran Minh Quan, Nguyen Thi Bay, Won-Ki Jeong, and Nguyen Ky Phung. 2020. "Assessment of the Impact of Sand Mining on Bottom Morphology in the Mekong River in An Giang Province, Vietnam, Using a Hydro-Morphological Model with GPU Computing" Water 12, no. 10: 2912. https://doi.org/10.3390/w12102912
APA StyleThi Kim, T., Huong, N. T. M., Huy, N. D. Q., Tai, P. A., Hong, S., Quan, T. M., Bay, N. T., Jeong, W.-K., & Phung, N. K. (2020). Assessment of the Impact of Sand Mining on Bottom Morphology in the Mekong River in An Giang Province, Vietnam, Using a Hydro-Morphological Model with GPU Computing. Water, 12(10), 2912. https://doi.org/10.3390/w12102912





