Effects of Pressure and Nozzle Size on the Spray Characteristics of Low-Pressure Rotating Sprinklers
Abstract
1. Introduction
2. Materials and Methods
2.1. Sprinkler
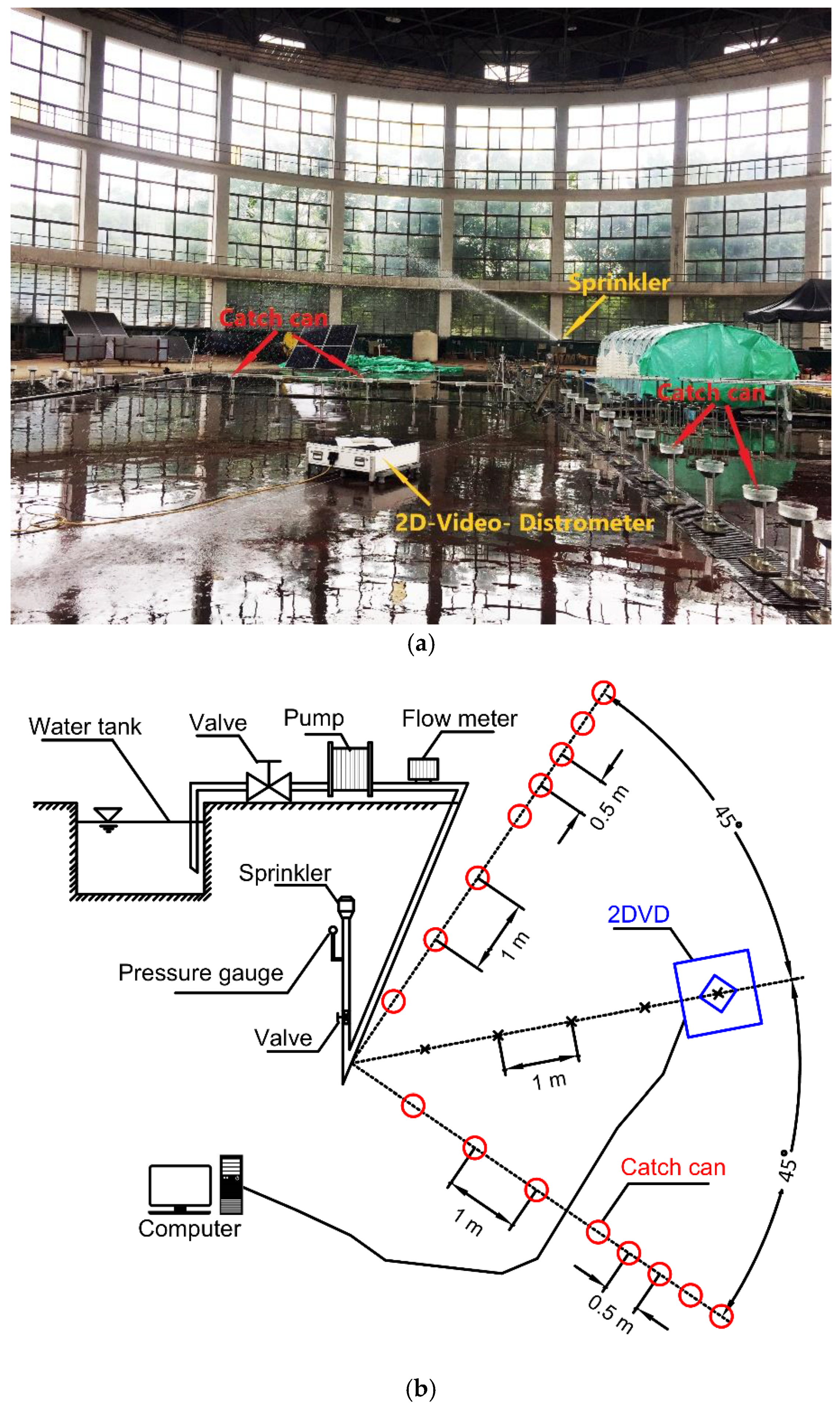
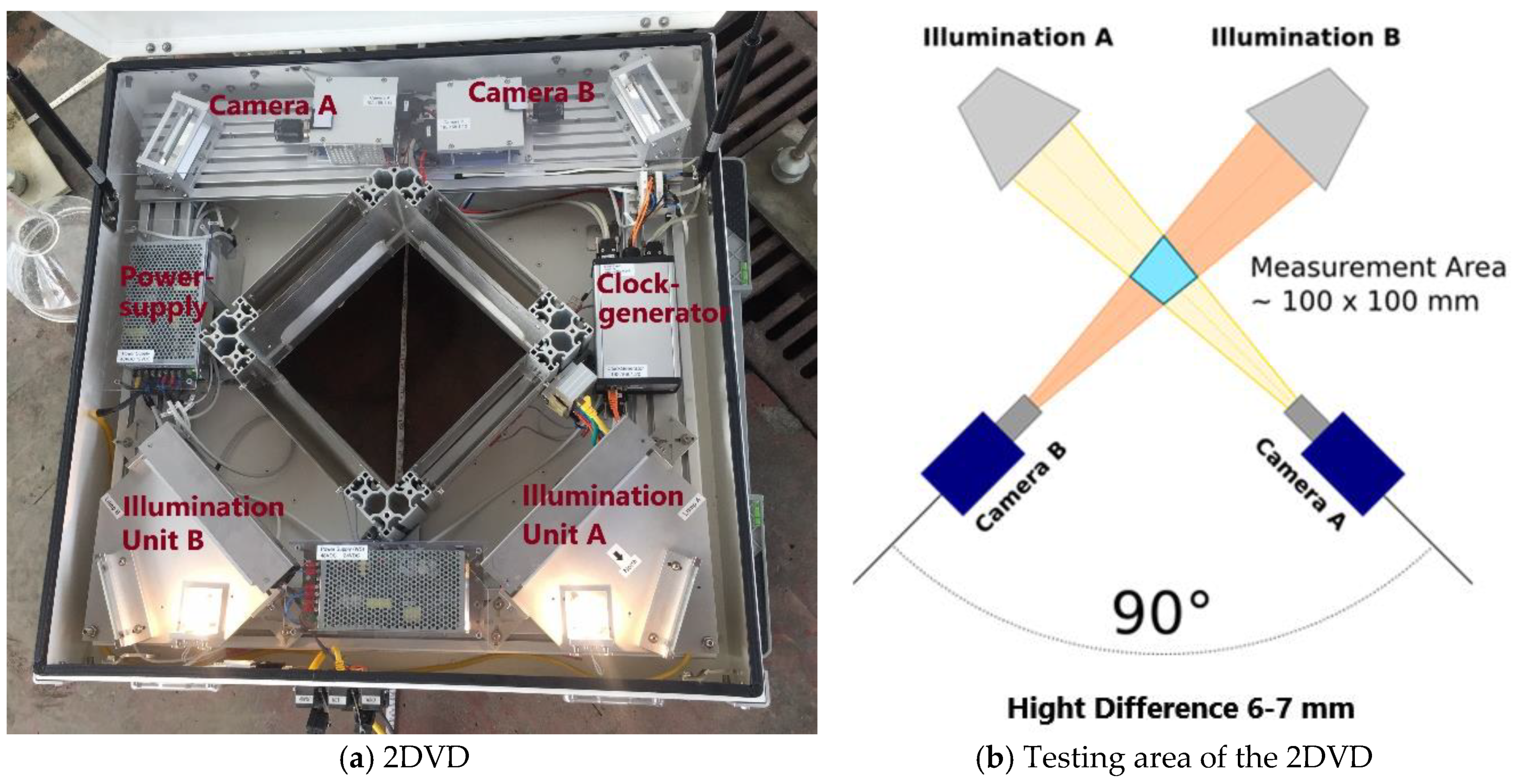
2.2. Experimental Setup and Procedure
2.3. Data Analysis
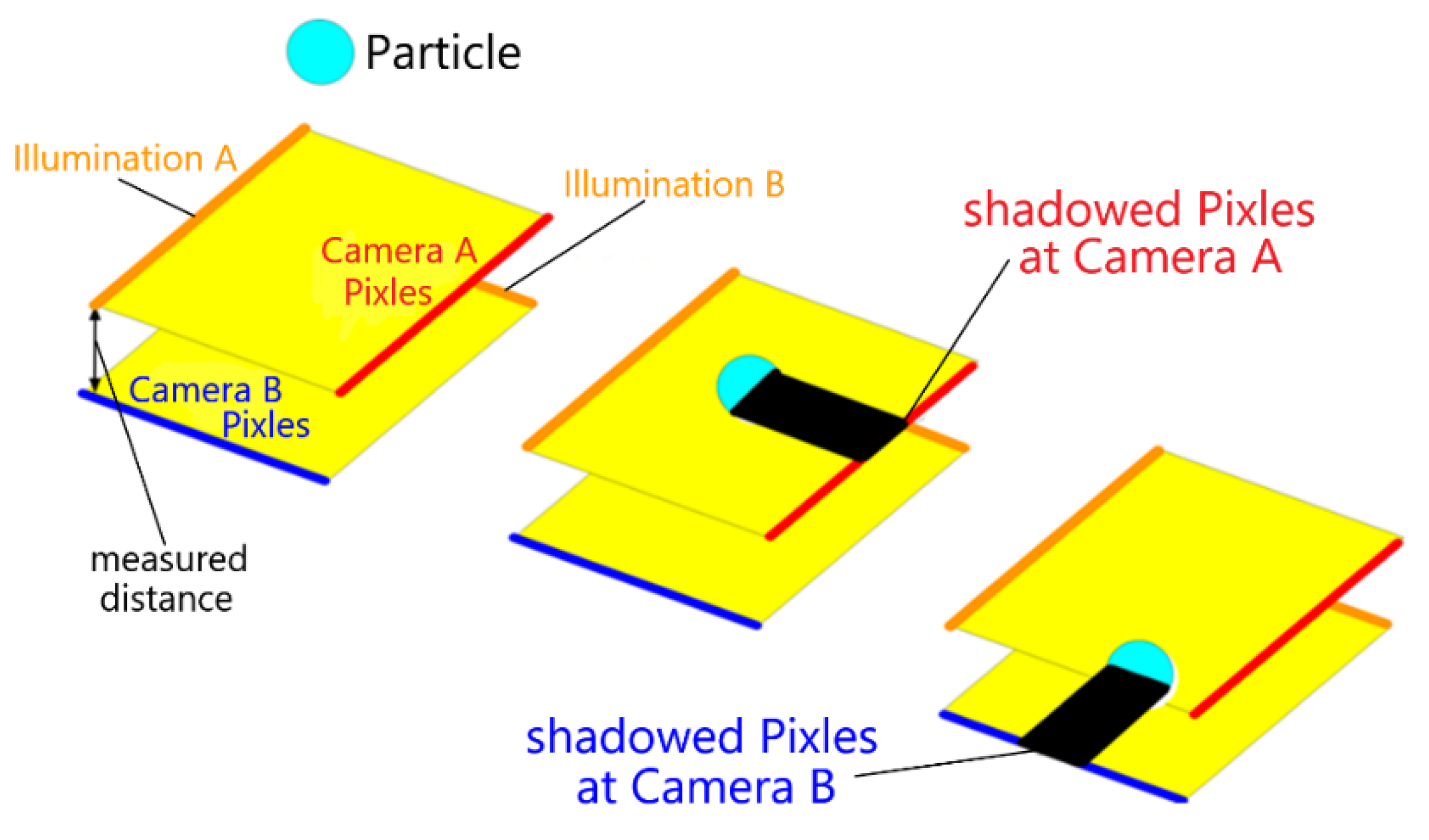
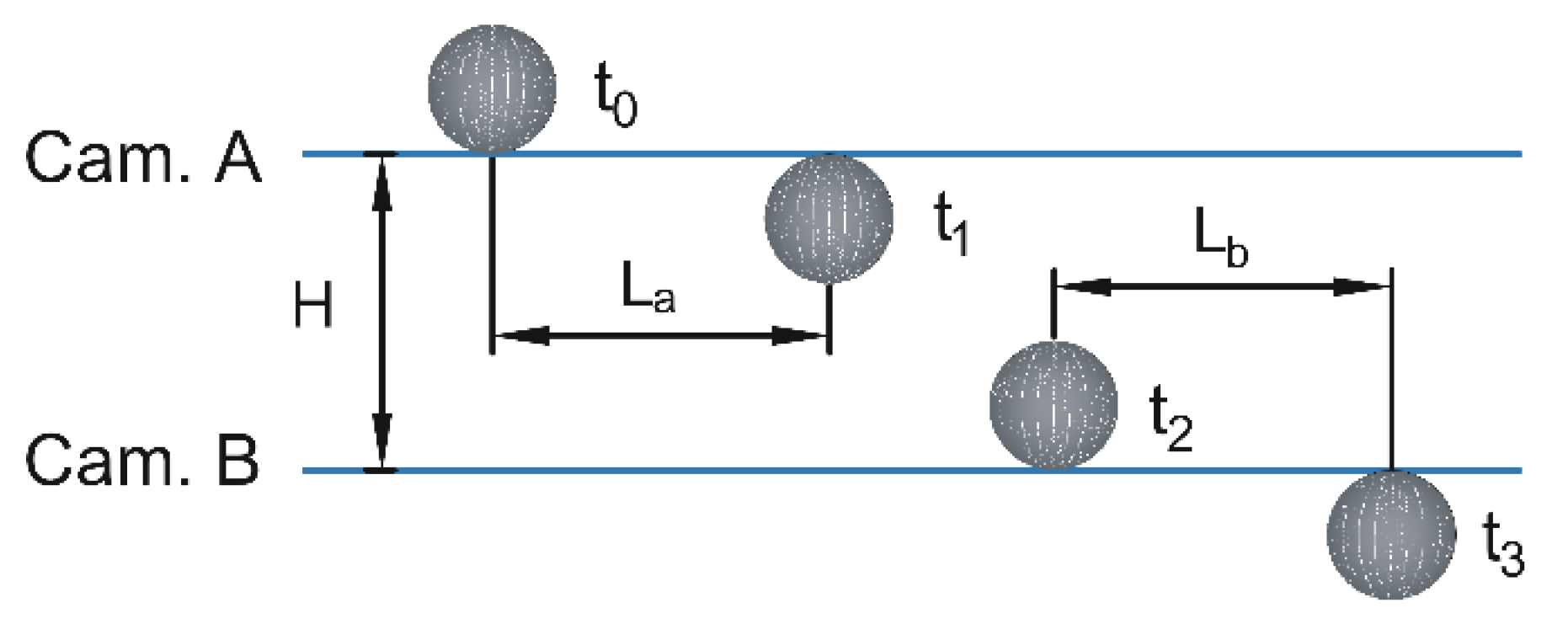
2.3.1. Droplet Size and Drop Velocity
2.3.2. Droplet Angle
2.3.3. Kinetic Energy
2.3.4. Performance function
3. Results and Analysis
3.1. Sprinkler Rotation
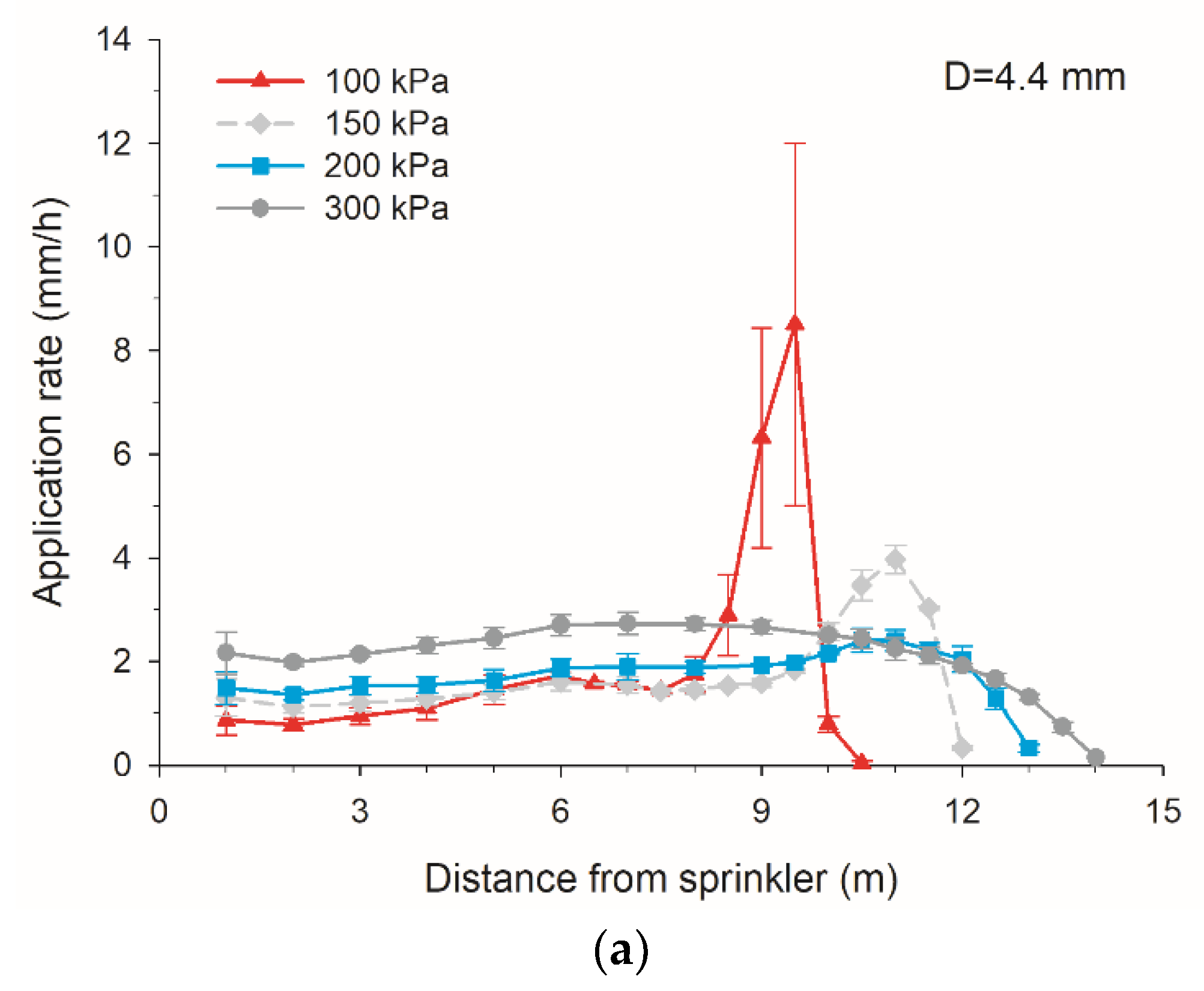
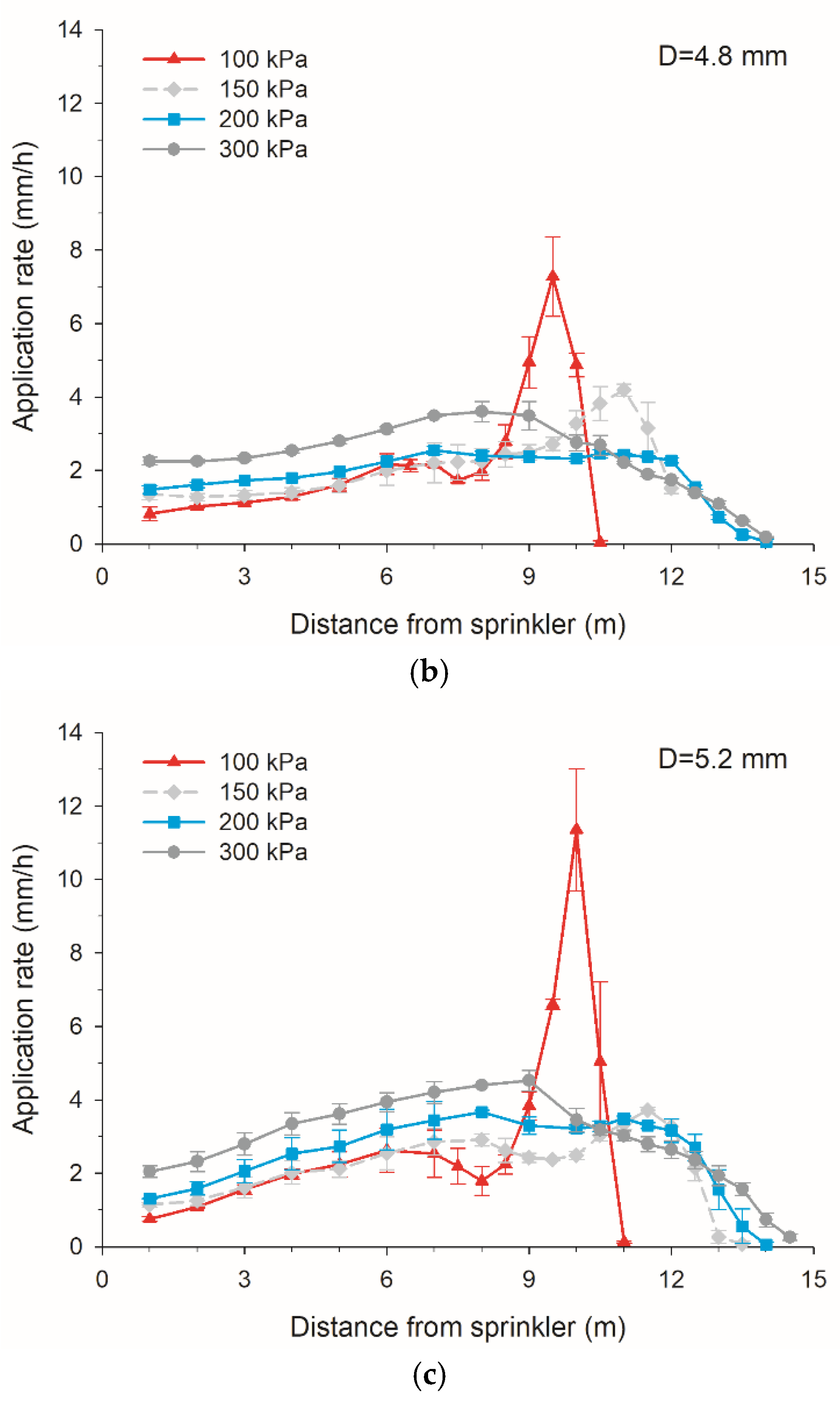
3.2. Radial Water Application Rate
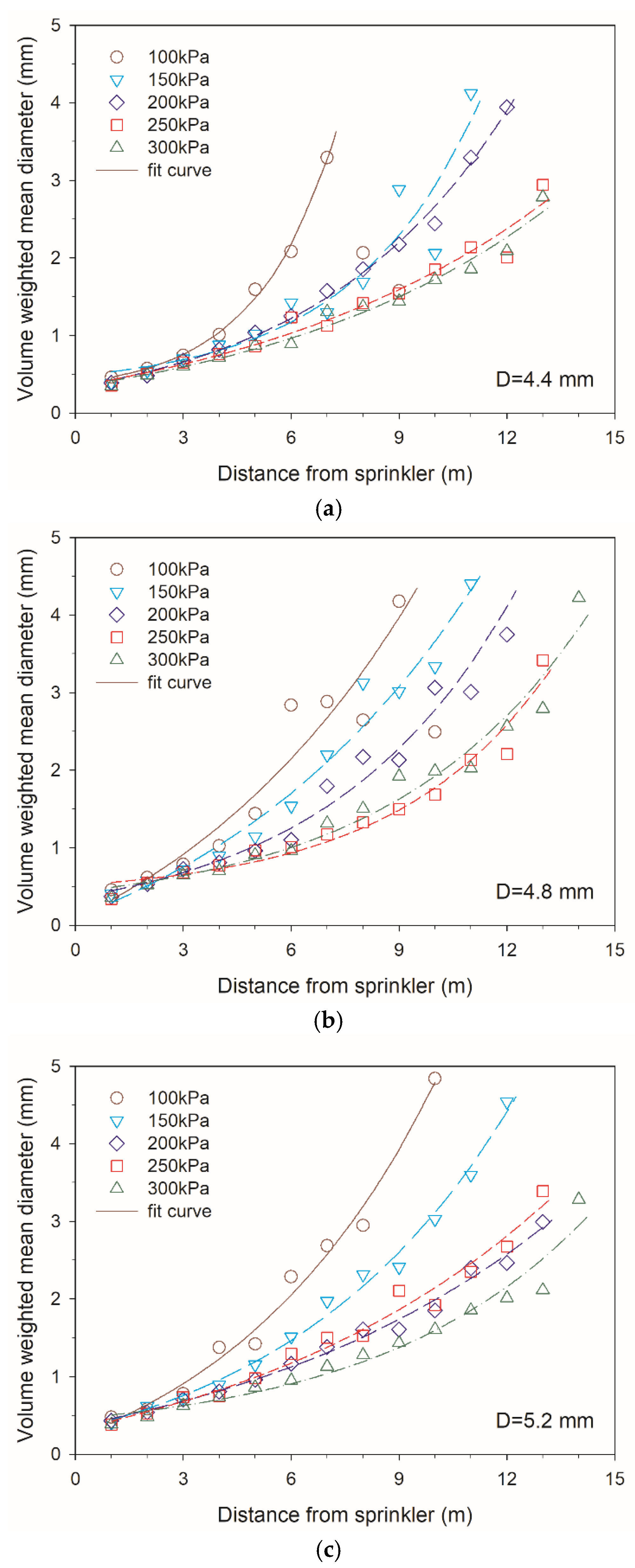
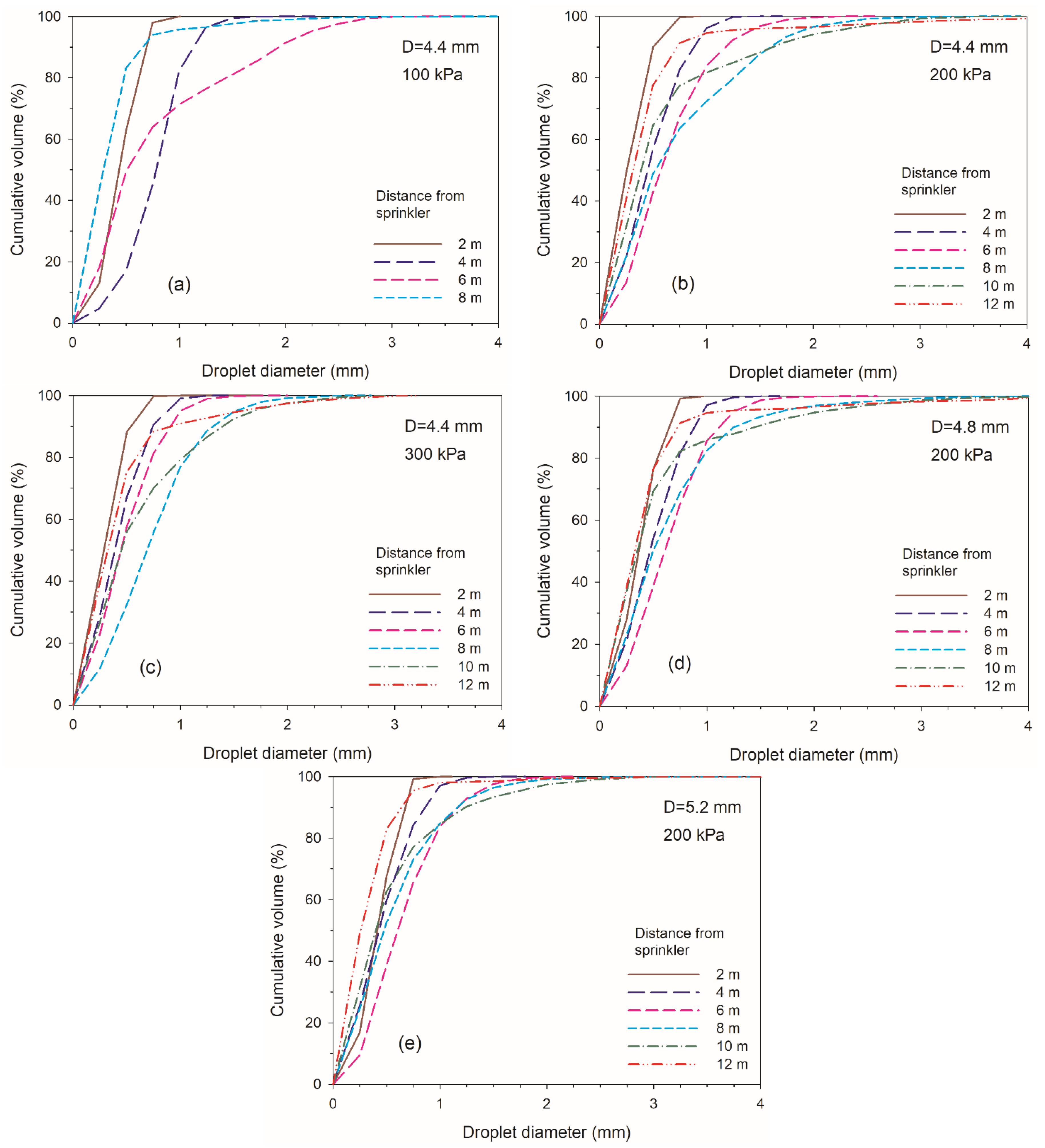
3.3. Droplet Size
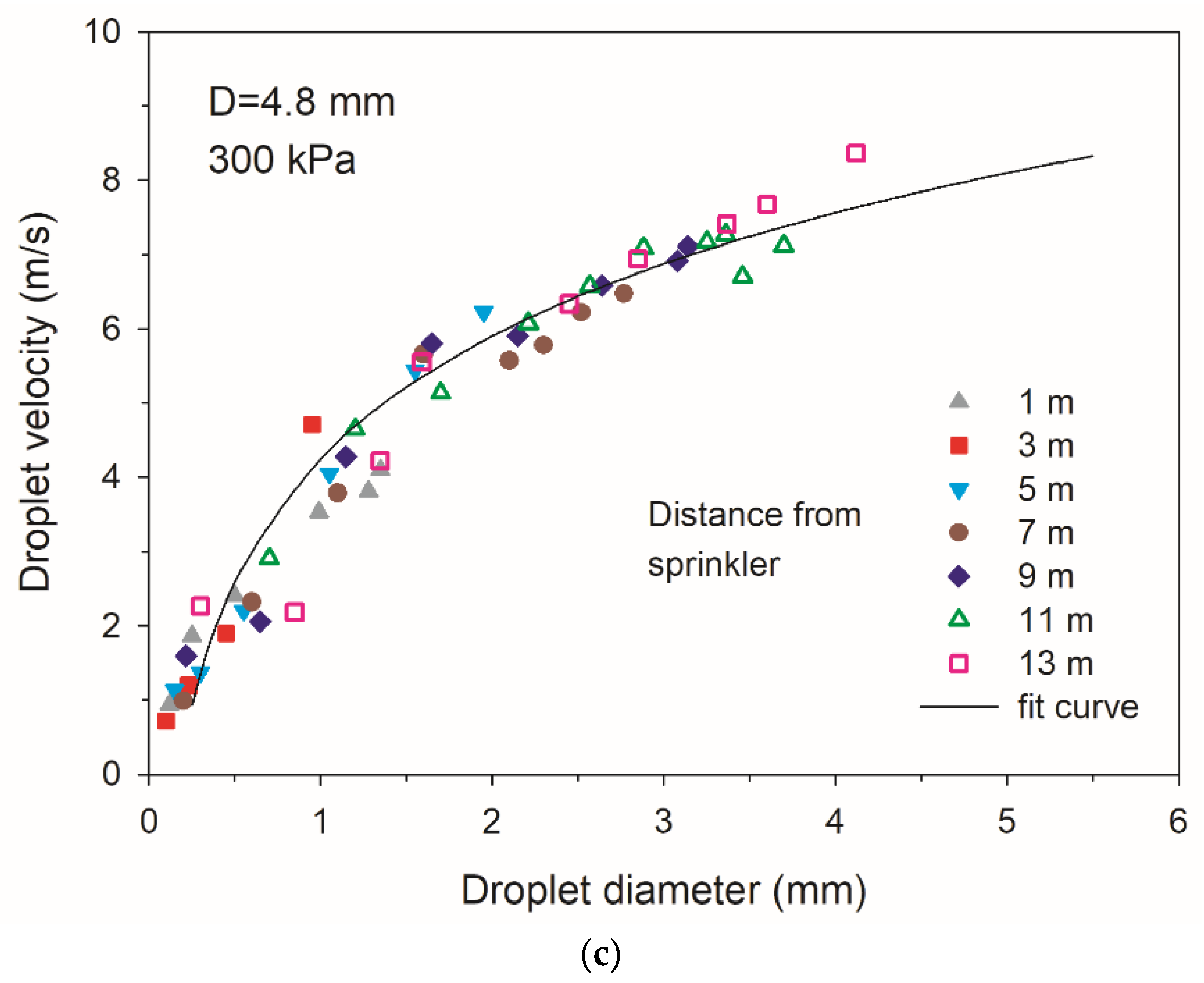
3.4. Droplet Velocity
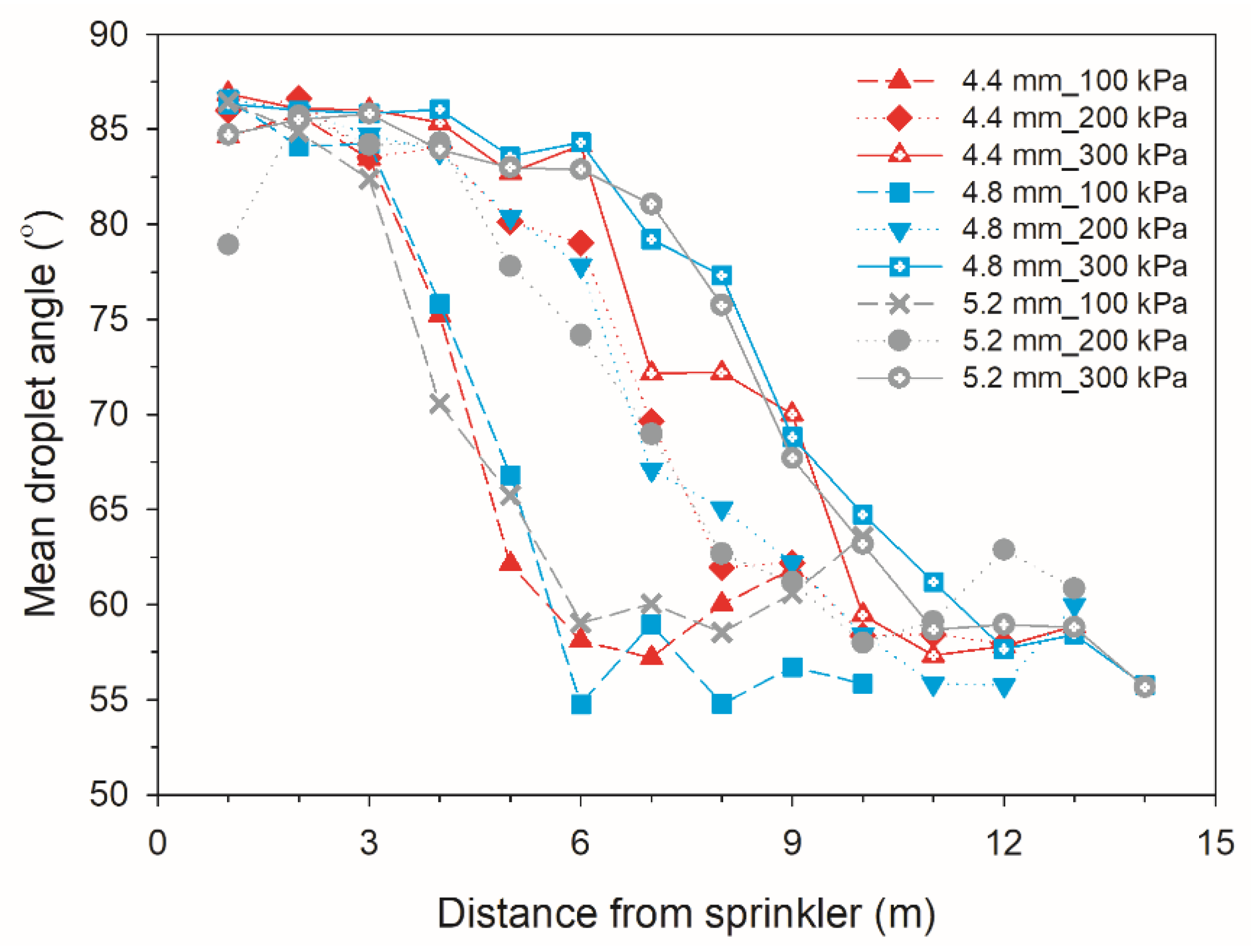
3.5. Droplet Angle
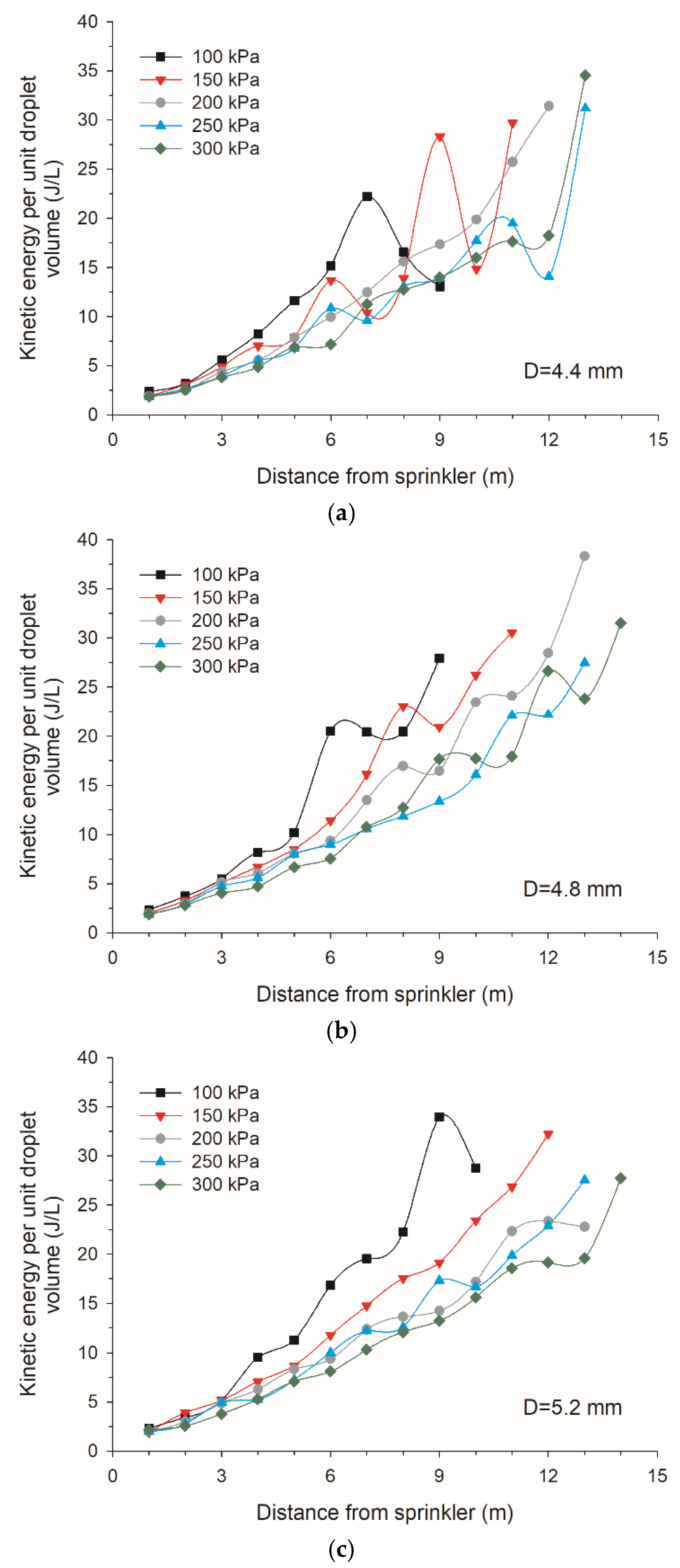
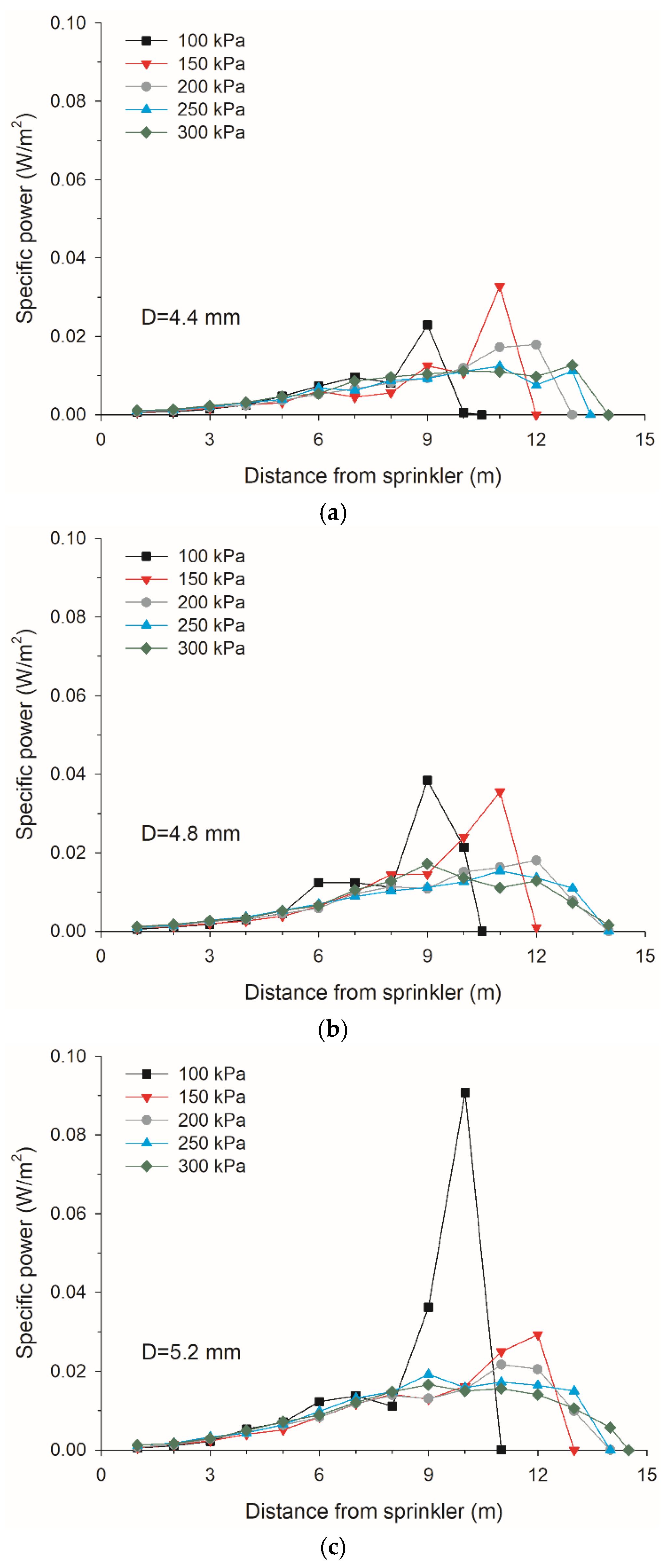
3.6. Kinetic Energy
4. Discussion
5. Conclusions
- (a)
- The relations among mean droplet diameter, working pressure, sprinkler nozzle, and distance from sprinkler were indicated by the droplet diameter model in this paper. The relationships between the droplet velocity and droplet diameter were described by a logarithmic function model. The correlation coefficients of these models reached as high as 0.9 under different working pressures and nozzle sizes.
- (b)
- An empirical equation was developed to estimate the kinetic energy per unit droplet volume at different distances from the sprinkler as functions of the working pressure and nozzle size. With an increase in working pressure, the peak specific power and application rate decreased while the rotation speed and droplet trajectory angle increased.
- (c)
- The working pressure of the sprinkler should not be below 150 kPa since the quality of the water application decreased under the lowest working pressure of 100 kPa. It is necessary to select the nozzles adapted to the working pressure of the sprinkler irrigation system.
Author Contributions
Funding
Conflicts of Interest
References
- Tal, A. Rethinking the sustainability of Israel’s irrigation practices in the drylands. Water Res. 2016, 90, 387–394. [Google Scholar] [CrossRef] [PubMed]
- UNESCO. The United Nations World Water Development Report 2014: Water and Energy; The United Nations world water development report; UNESCO Pub.: Paris, France, 2014. [Google Scholar]
- Zhou, B.; Li, Y.K.; Xue, S.; Feng, J. Variation of microorganisms in drip irrigation systems using high-sand surface water. Agric. Water Manag. 2019, 218, 37–47. [Google Scholar] [CrossRef]
- Lal, R. Carbon emission from farm operations. Environ. Int. 2004, 30, 981–990. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chen, R. An improved finite element model for the hydraulic analysis of drip irrigation subunits considering local emitter head loss. Irrig. Sci. 2020, 38, 147–162. [Google Scholar] [CrossRef]
- Zapata, N.; Robles, O.; Playán, E.; Paniagua, P.; Romano, C.; Salvador, R.; Montoya, F. Low-pressure sprinkler irrigation in maize: Differences in water distribution above and below the crop canopy. Agric. Water Manag. 2018, 203, 353–365. [Google Scholar] [CrossRef]
- Moreno, M.A.; Ortega, J.F.; Córcoles, J.I.; Martínez, A.; Tarjuelo, J.M. Energy analysis of irrigation delivery systems: Monitoring and evaluation of proposed measures for improving energy efficiency. Irrig. Sci. 2010, 28, 445–460. [Google Scholar] [CrossRef]
- Zhang, L.; Merkley, G.P.; Pinthong, K. Assessing whole-field sprinkler irrigation application uniformity. Irrig. Sci. 2013, 31, 87–105. [Google Scholar] [CrossRef]
- Dieter, C.A.; Maupin, M.A.; Caldwell, R.R.; Harris, M.A.; Ivahnenko, T.I.; Lovelace, J.K.; Barber, N.L.; Linsey, K.S. Estimated use of water in the United States in 2015. US Geol. Surv. Circ. 2018, 1441, 36. [Google Scholar]
- Robles, O.; Playán, E.; Cavero, J.; Zapata, N. Assessing low-pressure solid-set sprinkler irrigation in maize. Agric. Water Manag. 2017, 191, 37–49. [Google Scholar] [CrossRef]
- Cai, Y.H.; Wu, P.T.; Zhang, L.; Zhu, D.L.; Wu, S.J.; Zhao, X.; Dong, Z. Prediction of flow characteristics and risk assessment of deep percolation by ceramic emitters in loam. J. Hydrol. 2018, 566, 901–909. [Google Scholar] [CrossRef]
- Jiménez-Bello, M.A.; Royuela, A.; Manzano, J.; Prats, A. García; Martínez-Alzamora, F. Methodology to improve water and energy use by proper irrigation scheduling in pressurised networks. Agric. Water Manag. 2015, 149, 91–101. [Google Scholar] [CrossRef]
- Martínez, J.M.; Martínez, R.S.; Martínbenito, J.M.T. Analysis of water application cost with permanent set sprinkler irrigation systems. Irrig. Sci. 2004, 23, 103–110. [Google Scholar] [CrossRef]
- Sayyadi, H.; Nazemi, A.H.; Sadraddini, A.A.; Delirhasannia, R. Characterising droplets and precipitation profiles of a fixed spray-plate sprinkler. Biosyst. Eng. 2014, 119, 13–24. [Google Scholar] [CrossRef]
- Robles-Rovelo, C.O.; Ruiz, N.Z.; Tolosa, J.B.; Félix-Félix, J.R.; Latorre, B. Characterization and Simulation of a Low-Pressure Rotator Spray Plate Sprinkler Used in Center Pivot Irrigation Systems. Water 2019, 11, 1684. [Google Scholar] [CrossRef]
- Li, Y.C.; Hui, X.; Yan, H.J.; Chen, D.Y. Effects of Travel Speed and Collector on Evaluation of the Water Application Uniformity of a Center Pivot Irrigation System. Water 2020, 12, 1916. [Google Scholar] [CrossRef]
- Zhang, L.; Fu, B.Y.; Ren, N.W.; Huang, Y. Effect of pulsating pressure on water distribution and application uniformity for sprinkler irrigation on sloping land. Water 2019, 11, 913. [Google Scholar] [CrossRef]
- Kincaid, D.C. Spray drop kinetic energy from irrigation sprinklers. Trans. ASAE 1996, 39, 847–853. [Google Scholar] [CrossRef]
- Liu, J.P.; Liu, X.F.; Zhu, X.Y.; Yuan, S.Q. Droplet characterisation of a complete fluidic sprinkler with different nozzle dimensions. Biosyst. Eng. 2016, 148, 90–100. [Google Scholar] [CrossRef]
- Lima, J.L.M.P.D.; Torfs, P.J.J.F.; Singh, V.P. A mathematical model for evaluating the effect of wind on downward-spraying rainfall simulators. CATENA 2002, 46, 221–241. [Google Scholar] [CrossRef]
- Yan, H.J.; Bai, G.; He, J.Q.; Lin, G. Influence of droplet kinetic energy flux density from fixed spray-plate sprinklers on soil infiltration, runoff and sediment yield. Biosyst. Eng. 2011, 110, 213–221. [Google Scholar] [CrossRef]
- Young, R.A.; Wiersma, J.L. The role of rainfall impact in soil detachment and transport. Water Resour. Res. 1973, 9, 1629–1636. [Google Scholar] [CrossRef]
- Angulo Martínez, M.; Barros, A.P. Measurement uncertainty in rainfall kinetic energy and intensity relationships for soil erosion studies: An evaluation using PARSIVEL disdrometers in the Southern Appalachian Mountains. Geomorphology 2015, 228, 28–40. [Google Scholar] [CrossRef]
- Thompson, A.L.; Gilley, J.R.; Norman, J.M. A sprinkler water droplet evaporation and plant canopy model: 2. Model application. Trans. ASAE 1993, 36, 743–750. [Google Scholar] [CrossRef]
- Schneider, A.D. Efficiency and uniformity of the LEPA and spray sprinkler methods: A review. Trans. ASAE 2000, 43, 937–944. [Google Scholar] [CrossRef]
- Ge, M.S.; Wu, P.T.; Zhu, D.L.; Zhang, L. Analysis of kinetic energy distribution of big gun sprinkler applied to continuous moving hose-drawn traveler. Agric. Water Manag. 2018, 201, 118–132. [Google Scholar] [CrossRef]
- ISO 15886-3. Agricultural Irrigation Equipment—Sprinklers—Part 3: Characterization of Distribution and Test Methods; ISO: Geneva, Switzerland, 2016. [Google Scholar]
- ASAE Standards. Procedure for Sprinkler Testing and Performance Reporting; ASAE S398.1.; ASABE: St Joseph, MI, USA, 1985. [Google Scholar]
- Playán, E.; Salvador, R.; Faci, J.M. Day and night wind drift and evaporation losses in sprinkler solid-sets and moving laterals. Agric. Water Manag. 2005, 76, 139–159. [Google Scholar] [CrossRef]
- Seginer, I. Water distribution from medium pressure sprinklers. J. Irrig. Drain. E-ASCE 1963, 89, 13–30. [Google Scholar]
- King, B.A.; Bjorneberg, D.L. Characterizing droplet kinetic energy applied by moving spray-plate center-pivot irrigation sprinklers. Trans. ASABE 2010, 53, 137–145. [Google Scholar] [CrossRef]
- King, B.A. Moving spray-plate center-pivot sprinkler rating index for assessing runoff potential. Trans. ASABE 2016, 59, 225–237. [Google Scholar]
- Liu, J.P.; Zhu, X.Y.; Yuan, S.Q.; Wan, J.H.; Chikangaise, P. Hydraulic performance assessment of sprinkler irrigation with rotating spray plate sprinklers in indoor experiments. J. Irrig. Drain. E-ASCE 2018, 144, 06018005. [Google Scholar] [CrossRef]
- Ge, M.S.; Wu, P.T.; Zhu, D.L.; Zhang, L. Comparisons of spray characteristics between vertical impact and turbine drive sprinklers—A case study of the 50PYC and HY50 big gun-type sprinklers. Agric. Water Manag. 2020, 228, 105847. [Google Scholar] [CrossRef]
- Montero, J.; Tarjuelo, J.M.; Carrión, P. Sprinkler droplet size distribution measured with an optical spectropluviometer. Irrig. Sci. 2003, 22, 47–56. [Google Scholar] [CrossRef]
- Ashgriz, N.; Li, X.; Sarchami, A. Instability of liquid sheets. In Handbook of Atomization and Sprays; Ashgriz, N., Ed.; Springer: New York, NY, USA, 2011; pp. 75–95. [Google Scholar]
- Thompson, A.L.; James, L.G. Water droplet impact and its effect on infiltration. Trans. ASAE 1985, 28, 1506–1510. [Google Scholar] [CrossRef]


| Rotation Time (s/Rotation) | |||||
|---|---|---|---|---|---|
| Nozzle Size (mm) | Working Pressure (kPa) | ||||
| 100 | 150 | 200 | 250 | 300 | |
| 4.4 | 184.86 | 97.50 | 64.57 | 47.23 | 38.27 |
| 4.8 | 113.25 | 73.09 | 51.80 | 39.65 | 30.94 |
| 5.2 | 162.86 | 92.14 | 58.62 | 41.08 | 30.80 |
| Nozzle Size (mm) | Working Pressure (kPa) | Relational Expression | R2 |
|---|---|---|---|
| 4.4 | 100 | 0.934 | |
| 200 | 0.950 | ||
| 300 | 0.837 | ||
| 4.8 | 100 | 0.969 | |
| 200 | 0.963 | ||
| 300 | 0.965 | ||
| 5.2 | 100 | 0.920 | |
| 200 | 0.902 | ||
| 300 | 0.928 |
| Nozzle Size (mm) | Pressure (kPa) | ARm_i (m) | SPm_i (m) | ARm (mm h−1) | SPm (W m−2) |
|---|---|---|---|---|---|
| 4.4 | 100 | 9.5 | 9 | 8.507 | 0.023 |
| 150 | 11 | 11 | 3.975 | 0.033 | |
| 200 | 10.5 | 12 | 2.410 | 0.018 | |
| 250 | 10.5 | 11 | 2.432 | 0.012 | |
| 300 | 7 | 13 | 2.735 | 0.013 | |
| 4.8 | 100 | 9.5 | 9 | 7.280 | 0.038 |
| 150 | 11 | 11 | 4.190 | 0.036 | |
| 200 | 10.5 | 12 | 2.450 | 0.018 | |
| 250 | 8 | 11 | 3.125 | 0.015 | |
| 300 | 8 | 9 | 3.605 | 0.017 | |
| 5.2 | 100 | 10 | 10 | 11.354 | 0.091 |
| 150 | 11.5 | 12 | 3.720 | 0.029 | |
| 200 | 8 | 11 | 3.672 | 0.022 | |
| 250 | 8 | 9 | 4.224 | 0.019 | |
| 300 | 9 | 9 | 4.525 | 0.017 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Li, H.; Wang, J.; Guo, X. Effects of Pressure and Nozzle Size on the Spray Characteristics of Low-Pressure Rotating Sprinklers. Water 2020, 12, 2904. https://doi.org/10.3390/w12102904
Chen R, Li H, Wang J, Guo X. Effects of Pressure and Nozzle Size on the Spray Characteristics of Low-Pressure Rotating Sprinklers. Water. 2020; 12(10):2904. https://doi.org/10.3390/w12102904
Chicago/Turabian StyleChen, Rui, Hong Li, Jian Wang, and Xin Guo. 2020. "Effects of Pressure and Nozzle Size on the Spray Characteristics of Low-Pressure Rotating Sprinklers" Water 12, no. 10: 2904. https://doi.org/10.3390/w12102904
APA StyleChen, R., Li, H., Wang, J., & Guo, X. (2020). Effects of Pressure and Nozzle Size on the Spray Characteristics of Low-Pressure Rotating Sprinklers. Water, 12(10), 2904. https://doi.org/10.3390/w12102904




