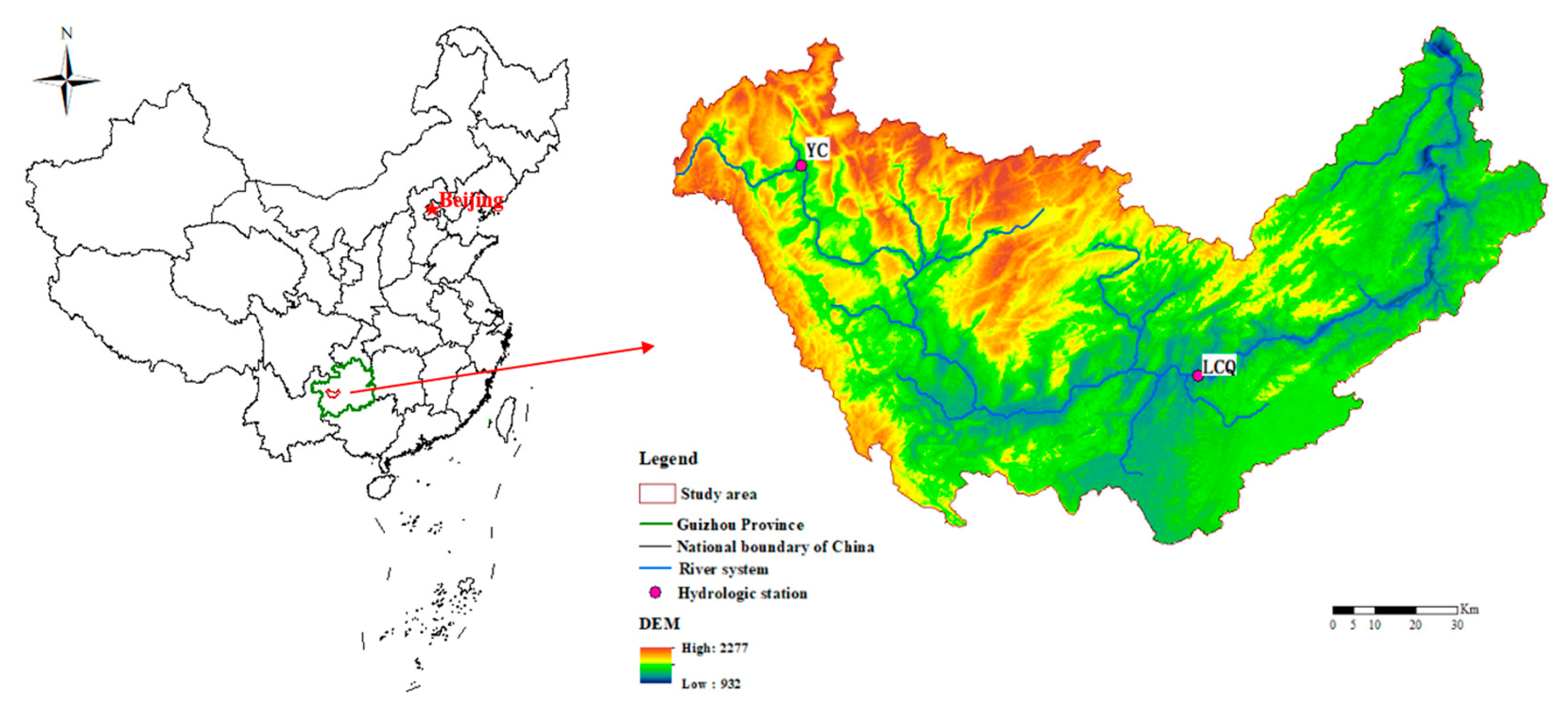
4.1. Comprehensive Analysis of the Dominant Factors and Interactions for the Different Geomorphic Types
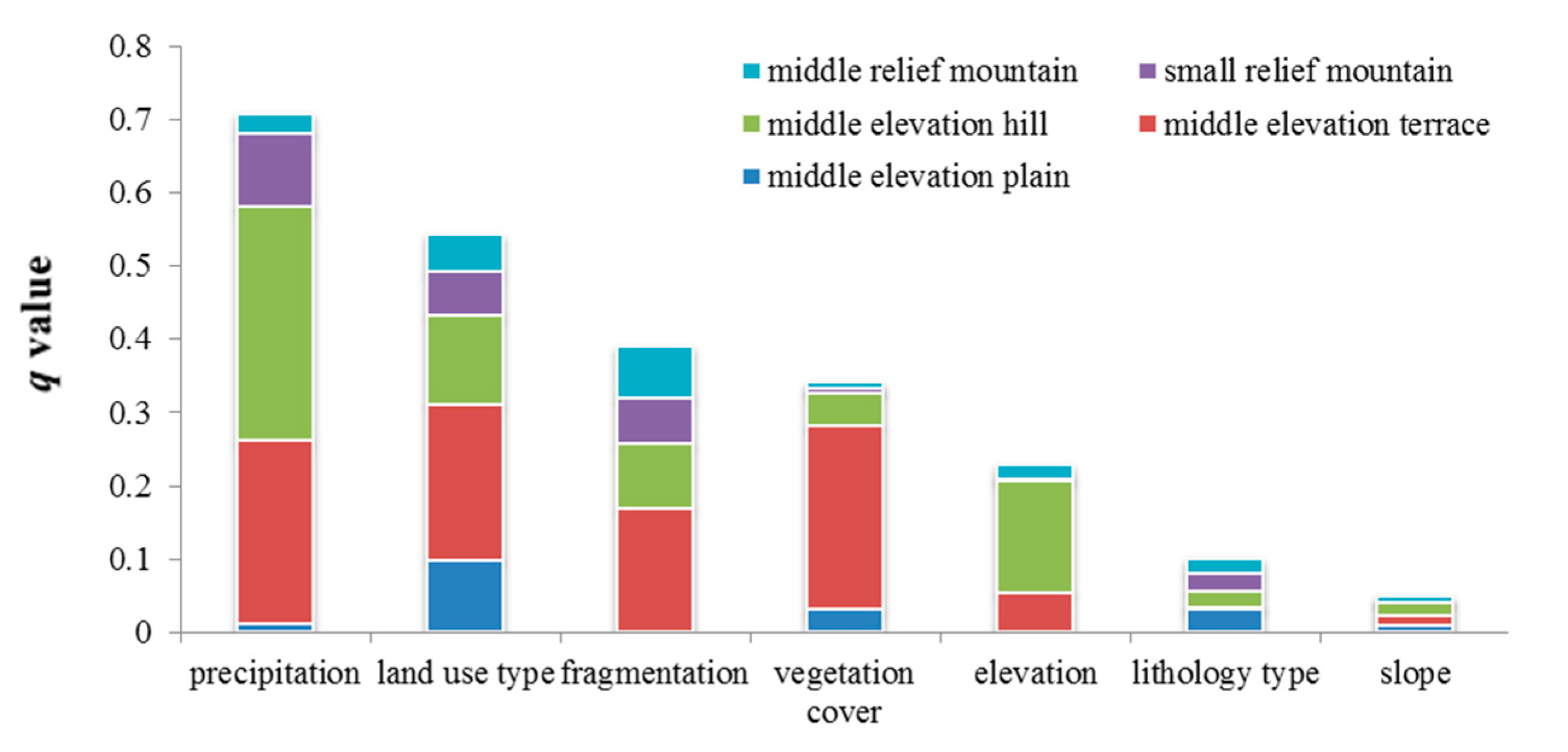
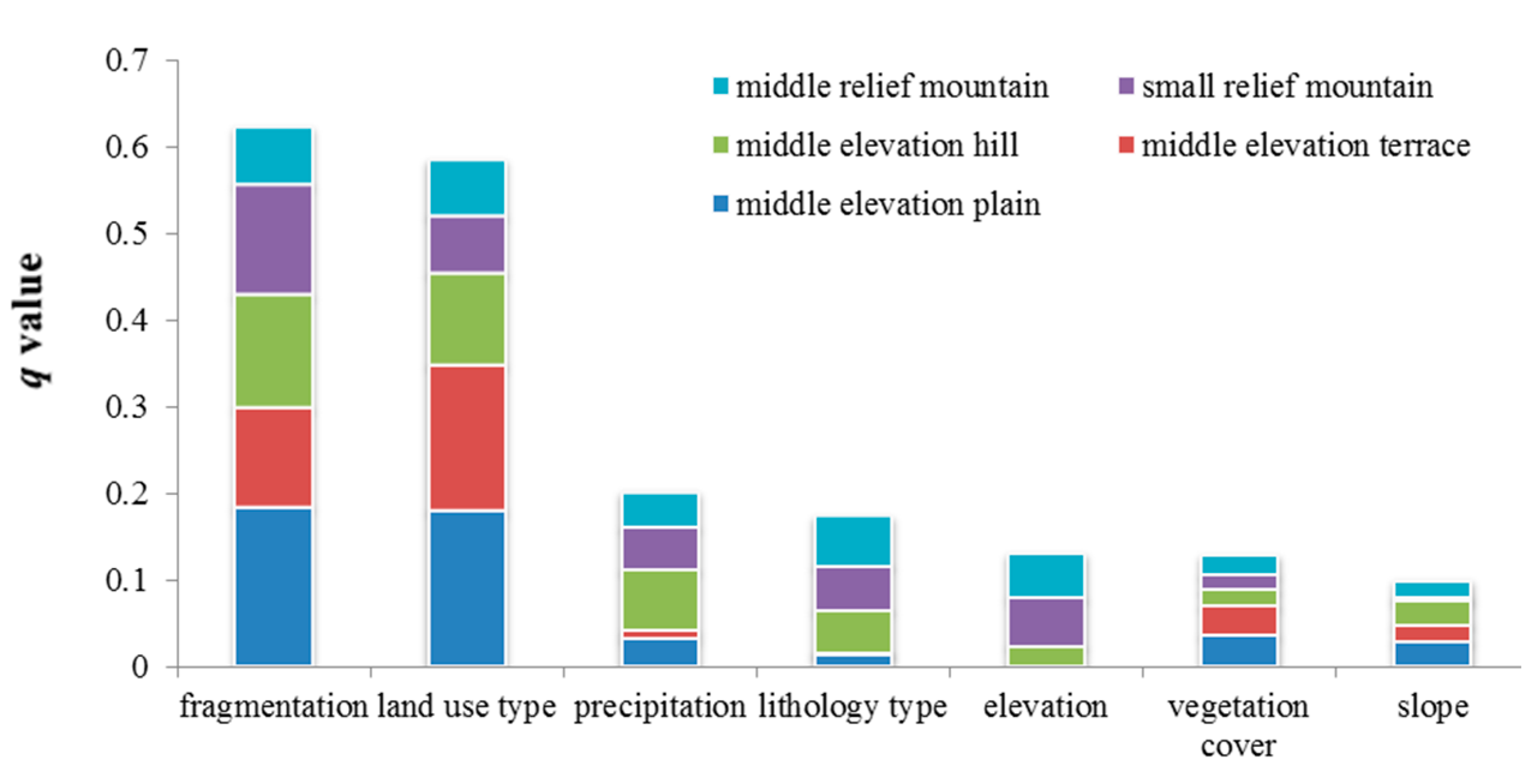
Middle elevation plain region. In the middle elevation plain region, land use type and landscape fragmentation are more important than the other factors in controlling the spatial distribution of the total river runoff and groundwater, with
q values concentrated in the range of 12–18.5%. In addition to these two dominant factors, vegetation cover, precipitation, and slope also play roles in the dominant interactions. The interaction modes were further explored according the interaction criteria (
Table 7). In this area with low elevation and gentle topography, the high
q values of land use types and landscape fragmentation reflect the significant of human activities on runoff [
41]. The results show that the interaction modes of the hydrological variables are also pair-wise among the dominant factors (land use type and landscape fragmentation) and vegetation cover, slope, and precipitation, with primarily nonlinear enhancement, which indicates that the mutual effect of two factors strengthen their individual influences on the spatial variation. The impact of interaction between these two key elements further confirms the dominant influence of them. Only the second dominant mode of total river runoff, and the first dominant mode of groundwater exhibit bifactor enhancement, which is rather weak compared to nonlinear enhancement. Furthermore, the bifactor enhancement mode of these three conditions is the interaction between land use type and landscape fragmentation, that is, the effect of the interaction between these two factors is less than the sum of the two completely individual factors. Landscape fragmentation is calculated using the land use type, so they may have the same effect as their partial overlap, which also illustrates that the different mode of interaction mainly depends on the mechanism of action of two interaction factors.
Middle elevation terrace region. In this geomorphic type region, land use type, vegetation cover, landscape fragmentation, and precipitation are the dominant factors, with
q values in the range of 11.4–25.1%. Further, it is still land use type that has the greatest impact. In addition, according to the interaction criteria, we found that the effects of the interaction modes among these dominant factors on the total river runoff, surface runoff, and groundwater are all nonlinear enhancement (
Table 8). This indicates that the effects of the interactions between the factors are greater than the sum of the two individual factors. Under this geomorphologic condition, the two elements promote each other to affect runoff. What stands out is that landscape fragmentation superimposed with vegetation cover, precipitation, and land use type on surface runoff have interaction degrees of up to 60.3%, 50.7%, and 49.6%, respectively, which is 18.7%, 9.2%, and 11.9% more than the sum of the
q values of the individual factors. This also indicates that in the middle elevation terrace region, it is more conductive to the interactions between these elements, which will further have a more significant impact on surface runoff.
Middle elevation hill region. There are several different results for the middle elevation hill region. In addition to the three key factors of land use types, landscape fragmentation, and precipitation, which are similar to the results for the middle elevation plain and middle elevation terrace regions, elevation is an important factor. The
q values of these factors are in the range of 12.2–31.9%. Among them, the influence of precipitation on surface runoff reaches 31.9%. In hilly regions with fluctuations, the influence of human activities is weakened, while objective environmental conditions begin to play an important role, such as precipitation, and elevation. For the pairwise interactions of the above leading factors, the interaction modes, which is different from the previous two geomorphic types, are mainly bifactor enhancement, and the third dominant mode of surface runoff and the first and second dominant modes of groundwater exhibit nonlinear enhancement (
Table 9). Furthermore, this also shows that the interaction between the two factors will be weakened in the middle elevation hill region.
Small relief mountain region. In the small relief mountain region, precipitation, landscape fragmentation, and land use type are the main factors, with
q values in the range of 11–22.7%. We found that based on the
q values, the effect of precipitation is larger compared to the geomorphic type regions discussed above. In addition to these three factors, lithology becomes an important fact in the top three interactions, which is different from the middle elevation regions. For example, the third interaction for total river runoff is a combination of land use type and lithologic type, with a
q value of 30.2%. However, the individual explanatory power of land use type is 11%, and that of lithologic type is only 5.2%. This also confirms that the interaction between factors can significantly enhance the effects of the factors. According to the interaction criteria, of the interaction between two factors can strengthen the influences of the two individual factors. Half exhibit bifactor enhancement, and half exhibit nonlinear enhancement (
Table 10). In small relief mountain region, precipitation and lithology began to play an important role. On the one hand, it is possibly influenced by weaken human activities; on the other hand, the mountain microclimate changes frequently and changeable [
42], and the lithology condition are relatively complex.
Middle relief mountain region. In the middle relief mountain region, the influence of each factor on the runoff distribution is weaker than in the other geomorphic type regions. Precipitation and landscape fragmentation are the dominant factors. Precipitation, lithology, and elevation become more important on runoff, which may due to frequent and complex microclimate changing. The factor combinations of the top three interactions are also different. The interactions between precipitation and elevation, precipitation and lithologic type, landscape fragmentation and precipitation, and landscape fragmentation and elevation have larger effects on the spatial distribution, rather than the interaction between land use type and landscape fragmentation being the main factor. The interaction modes of the different factor combinations are primarily nonlinear enhancement (
Table 11), except for the third dominant interaction for total river runoff, which exhibits bifactor enhancement. In high-elevation mountain areas, the influence of human activities is relatively small, and the interaction between different natural environmental elements is less affected by other unnatural factors.
4.2. Thoughts on the Rules of the Influencing Factors and Their Interactions for the Different Geomorphic Types
Considering the effects of the dominant factors and their interactions on the hydrological variables in the various geomorphic type regions, we found that the results of the factor detector provide an obvious rule and logical explanations, and there are three interesting interaction effects. First, for the top three dominant interactions, several factors have little effect on each other, but the effects of the interactions are significantly improved. For example, in the middle elevation plain region, the influence of each individual factor in the top two combinations (land use type and vegetation cover, land use type and slope) on the spatial distribution of the runoff is less than 10% (1–9.9%), but the interaction influences reach up to 25%, i.e., an increase of 90%. A similar situation occurs for the influence on surface runoff in the middle relief mountain region. This indicates that the interactions between two factors have a positive promoting effect on the spatial distribution of the runoff.
Second, the top three dominant interactions are not all ordered by the degree of influence of their individual factors. Several factors play a less important role alone, while in an interaction with other factors, their effect on the runoff was significantly increased. For instance, in the middle elevation hill region, landscape fragmentation and land use type are the greatly influencing factors on the spatial distribution of the groundwater. However, in the top dominant interactions, precipitation combined with the other factors have the highest influences and are much stronger than the combination of landscape fragmentation and land use type.
Third, based on the single-factor analysis, we found that although land use type and landscape fragmentation both have a significant influence on the runoff in the five geomorphic type regions, the interaction modes of these two factors are usually bifactor enhancement, rather than nonlinear enhancement. Because landscape fragmentation is calculated using the land use type data, there is a partial overlap of the influences of the two factors on the spatial distribution of the runoff. One thing needs to be explained is that landscape fragmentation represents the degree of fragmentation of landscape pattern, and analysis for land use types is to study the influence of different types on runoff. However, the reasons for these results are only preliminarily explained in a superficial way in this study, and an in-depth study on this issue was not conducted in this paper. This will be further explored in future research to fully understand the interaction mechanisms between the different factors and how they influence the various hydrological variables through such interaction mechanisms.