Improved δ-SPH Scheme with Automatic and Adaptive Numerical Dissipation
Abstract
1. Introduction
2. Governing Equations
3. Numerical Methods
3.1. -SPH and -SPH Methods
3.2. -LES-SPH Method
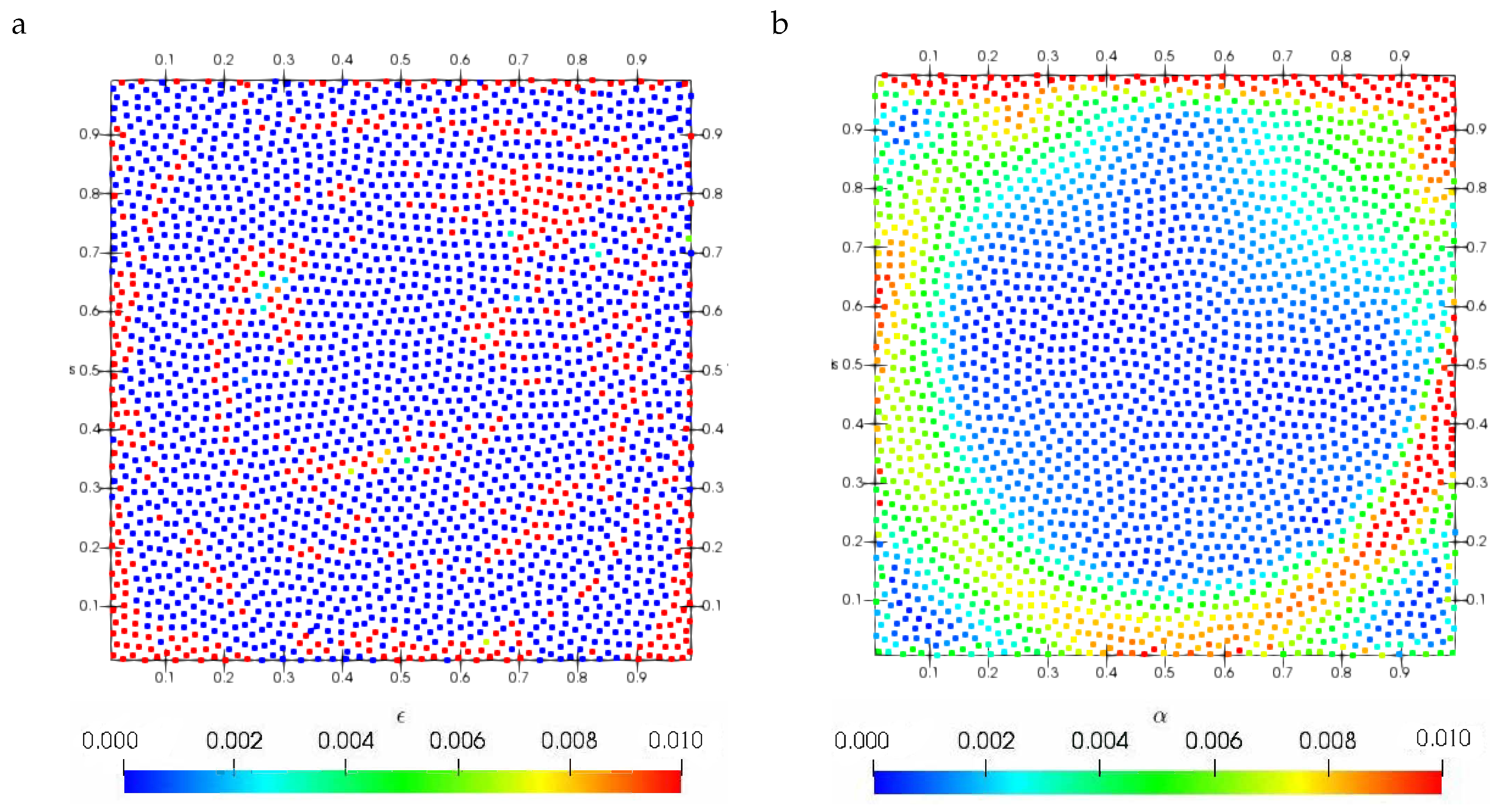
3.3. A New -ADA-SPH Scheme
4. Numerical Examples
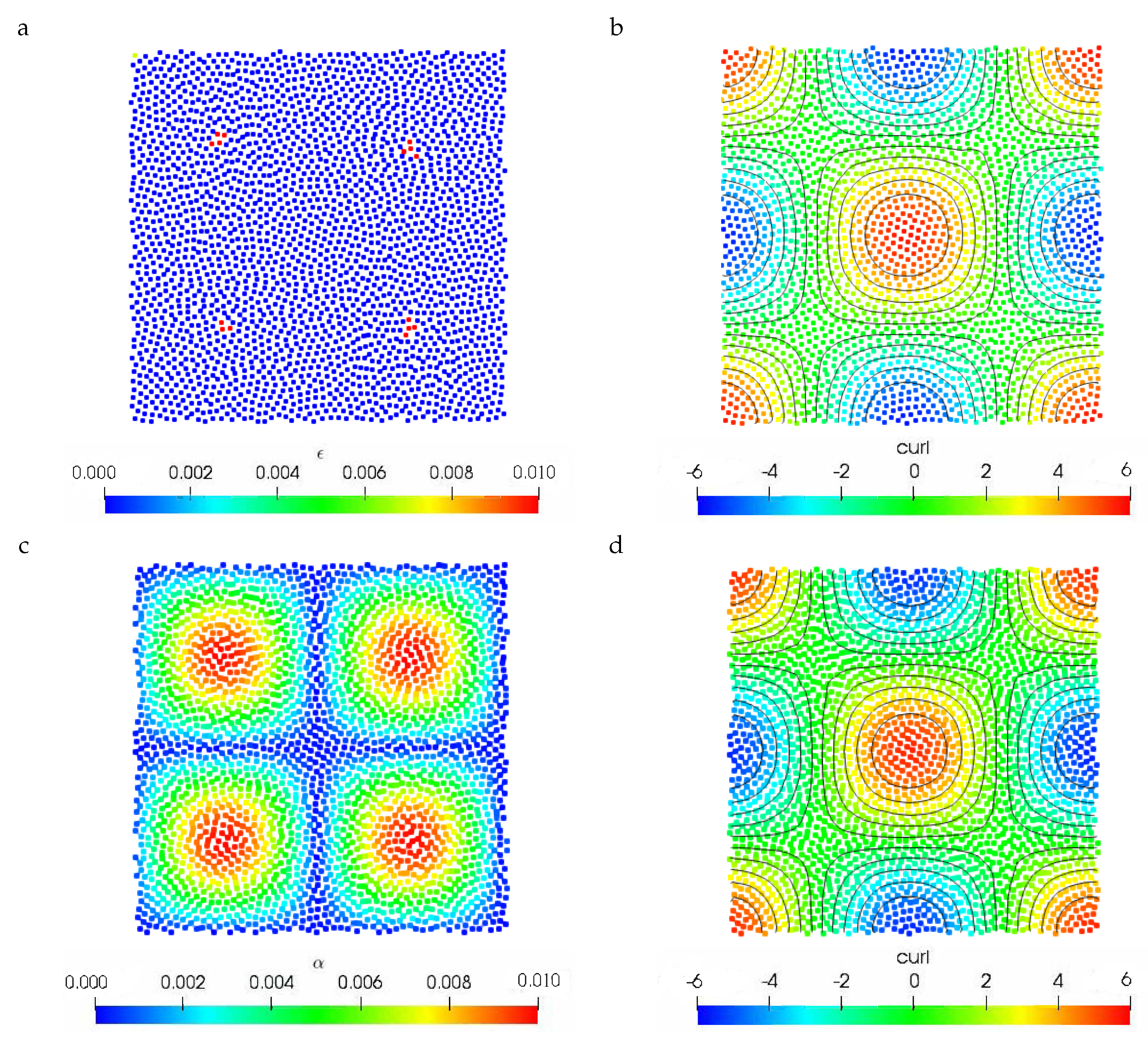
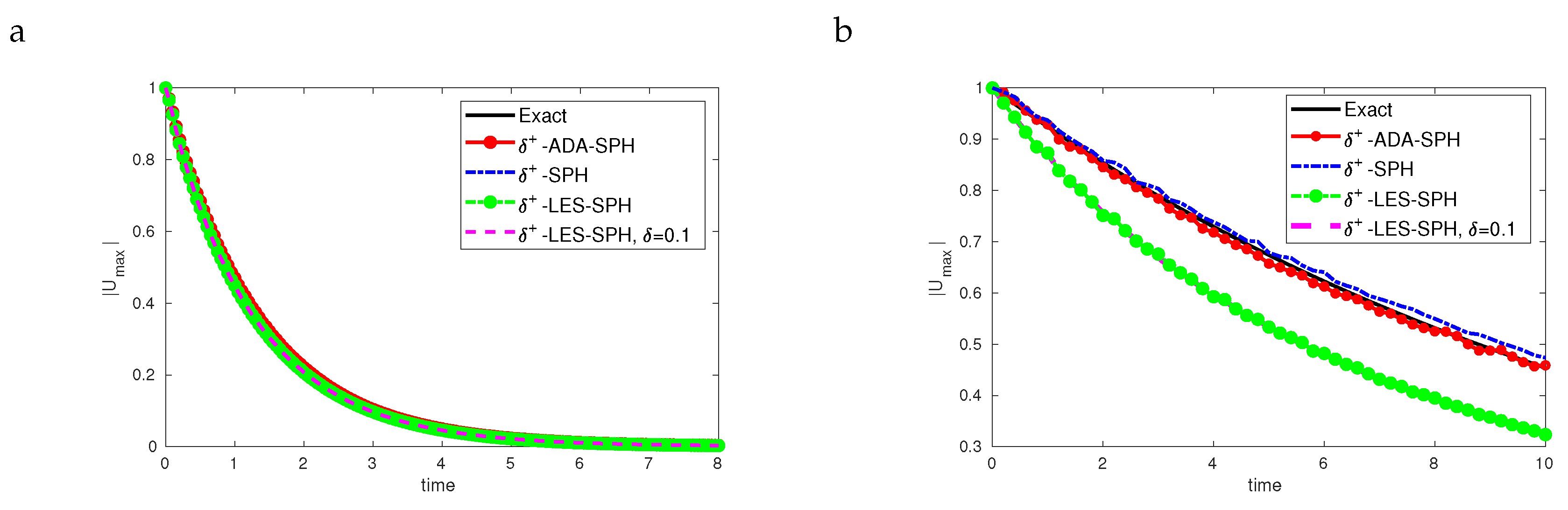
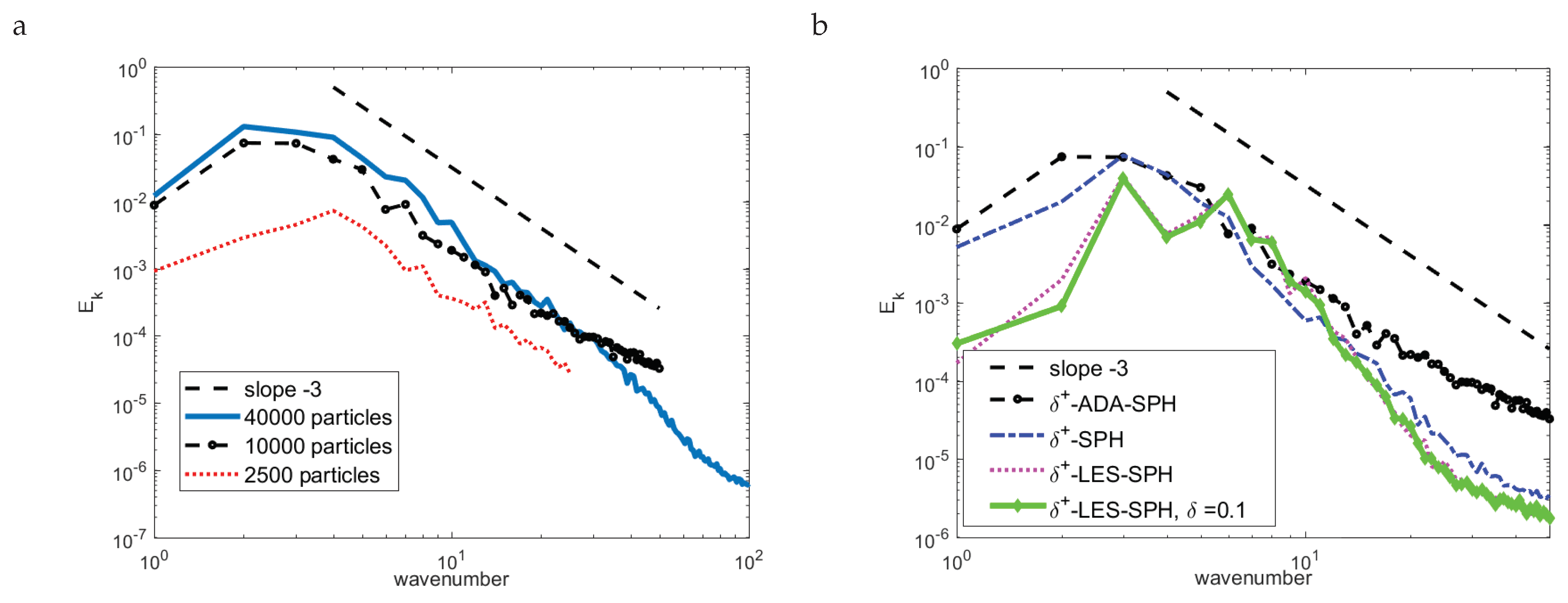
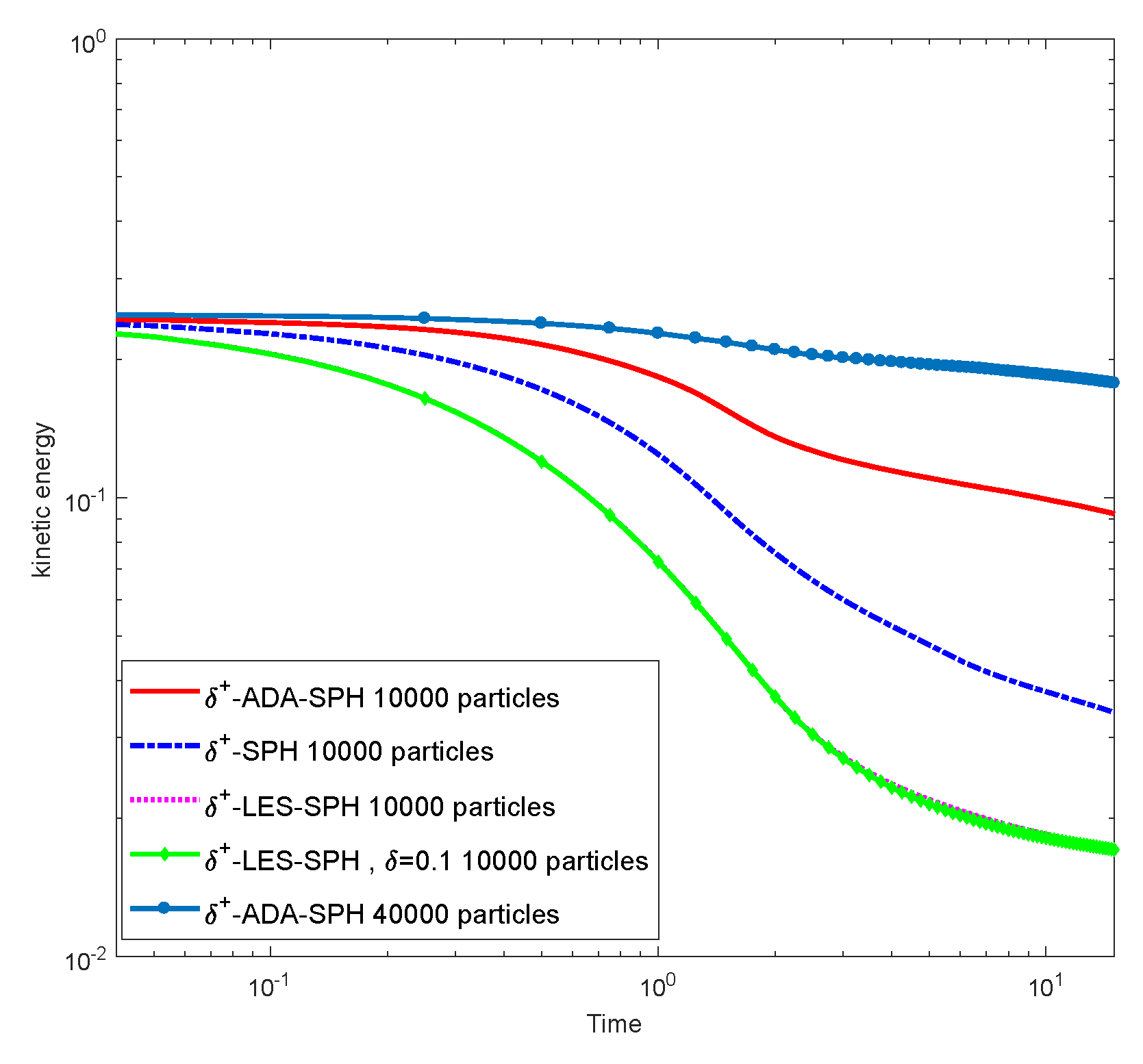
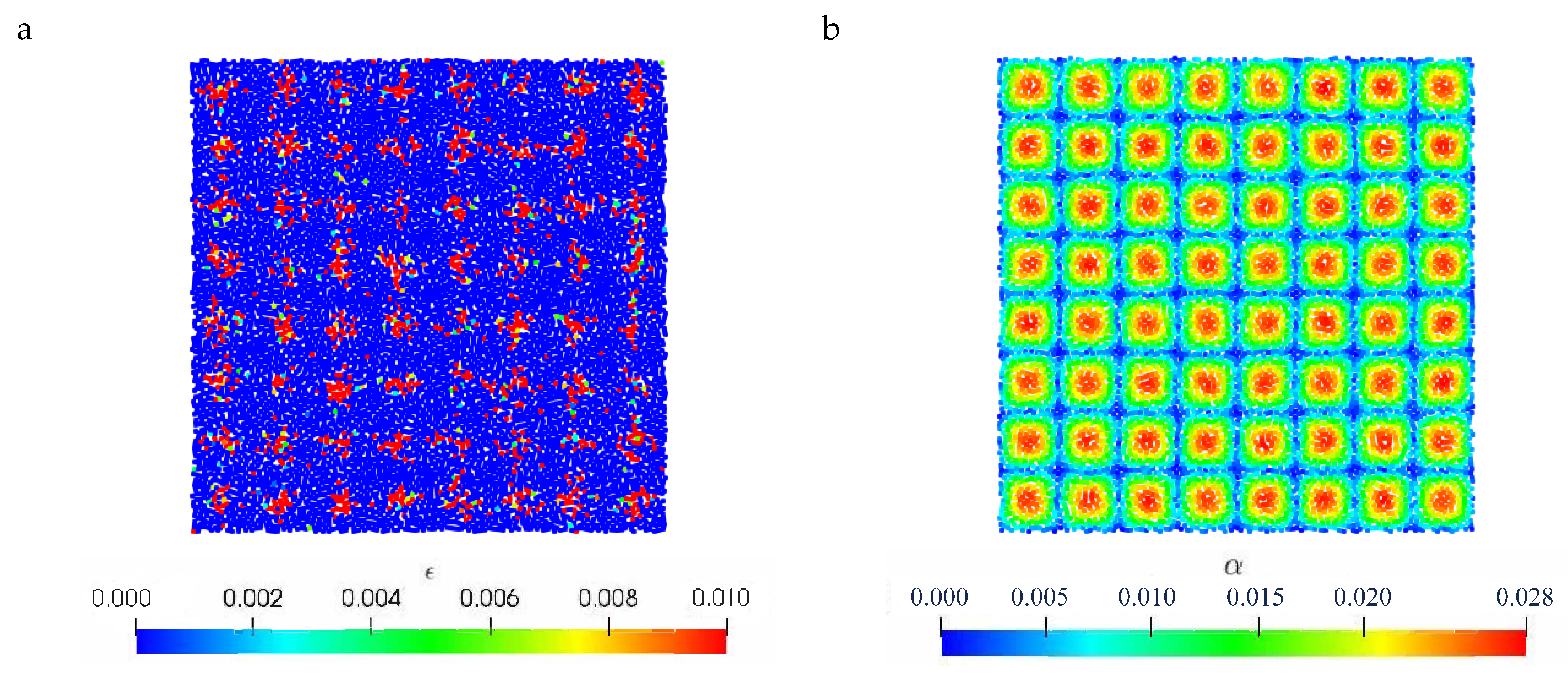
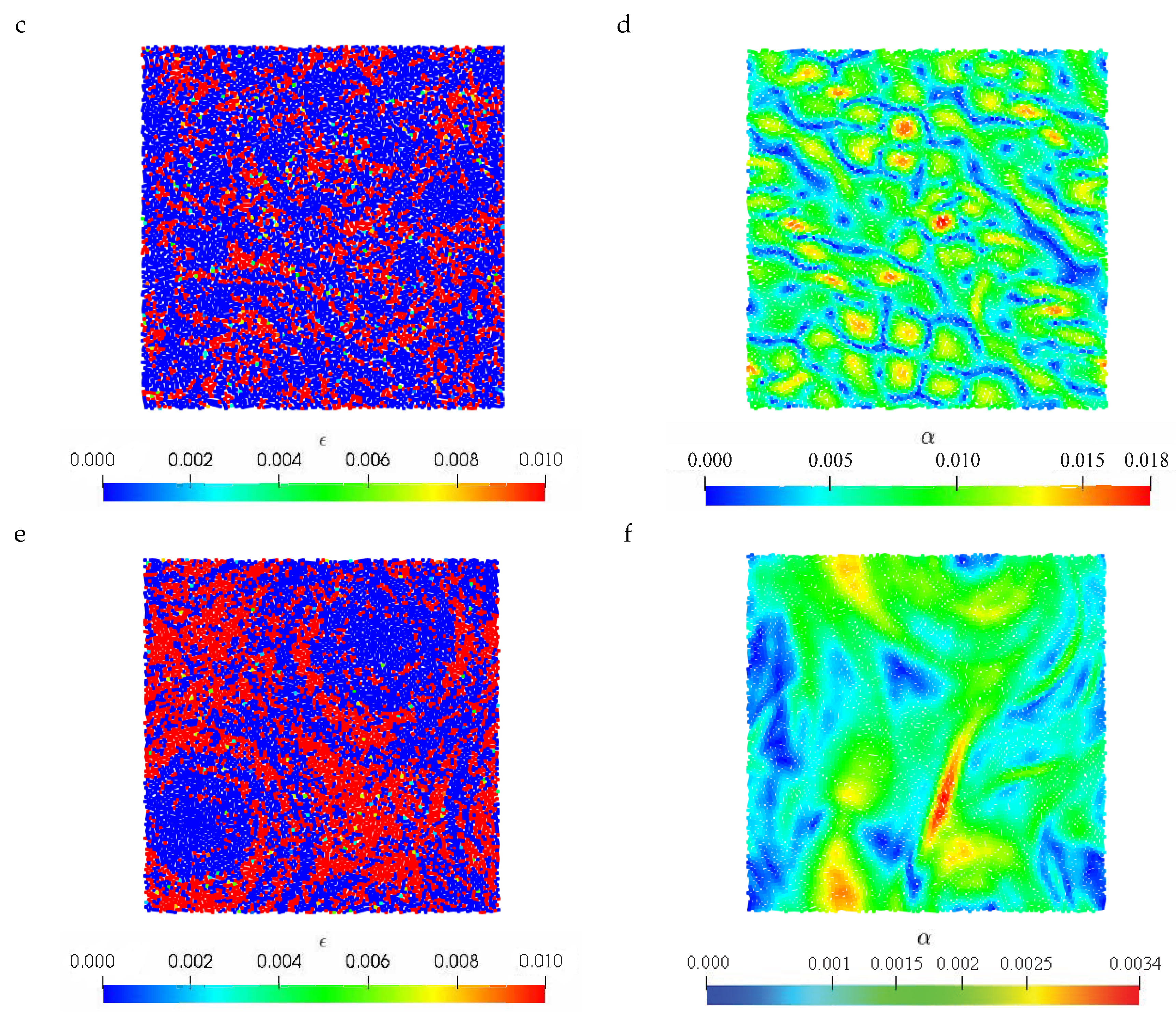
4.1. Viscous Two-Dimensional Taylor–Green Flow
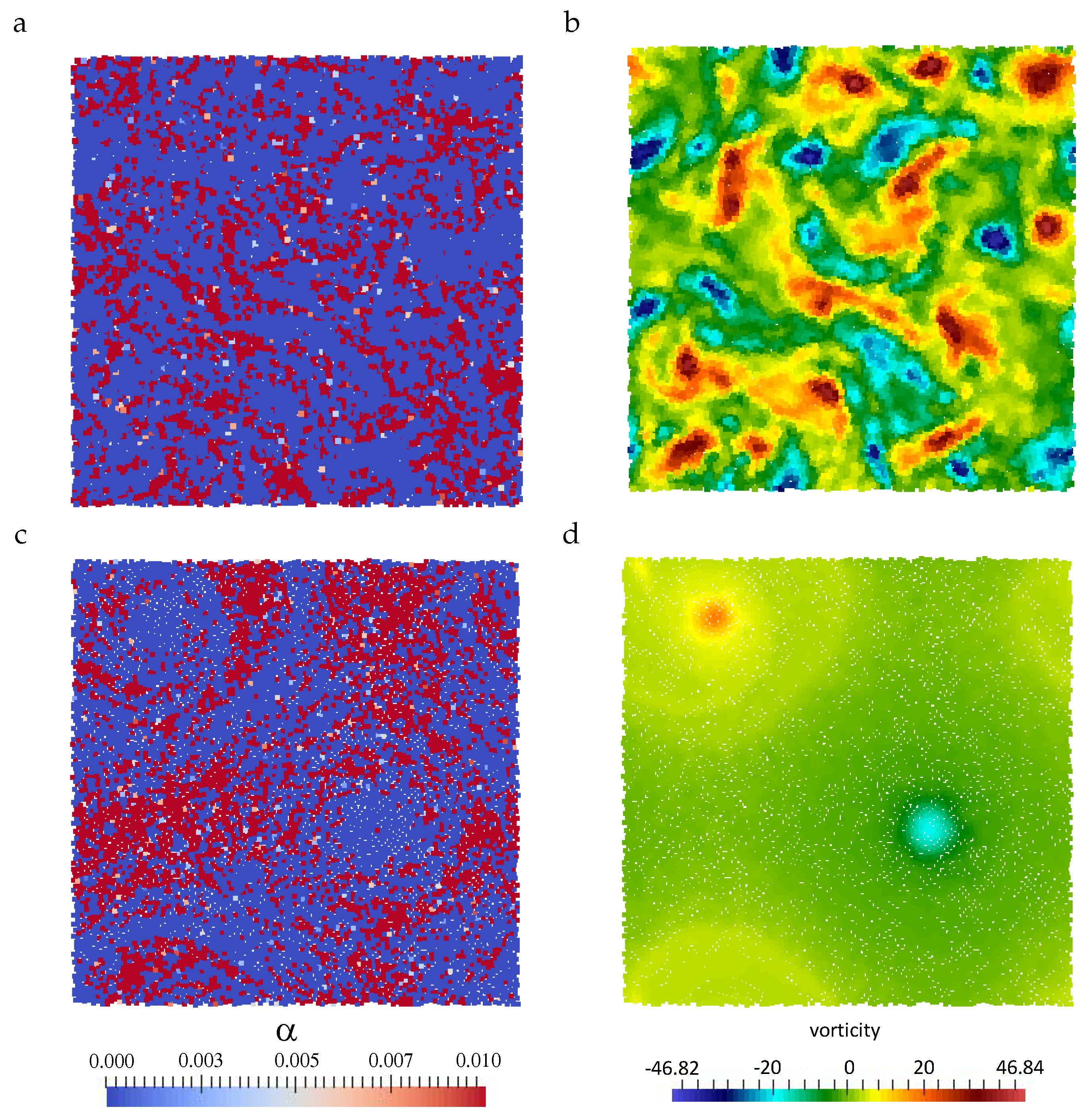
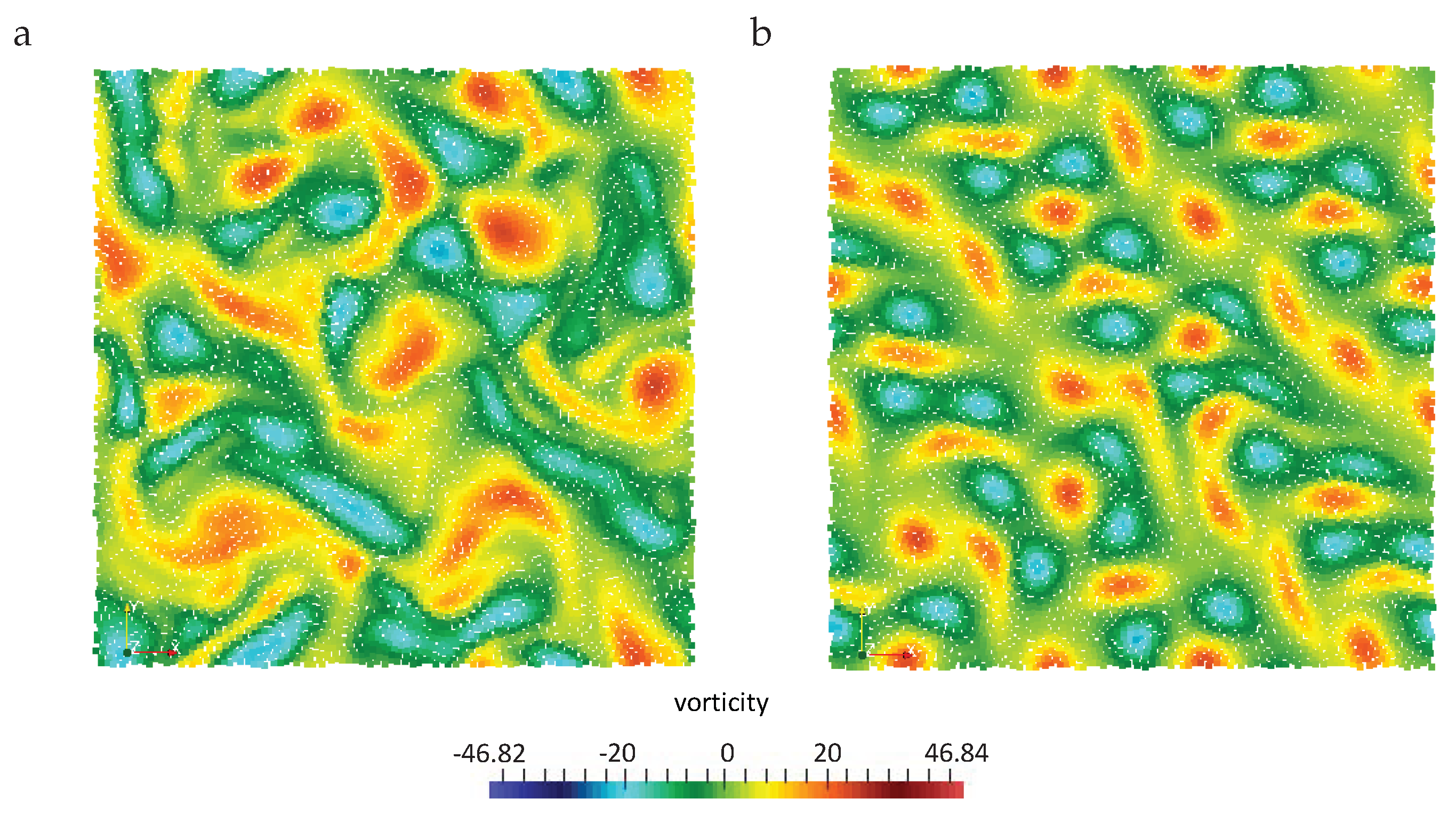
4.2. Inviscid Two-Dimensional Taylor–Green Flow
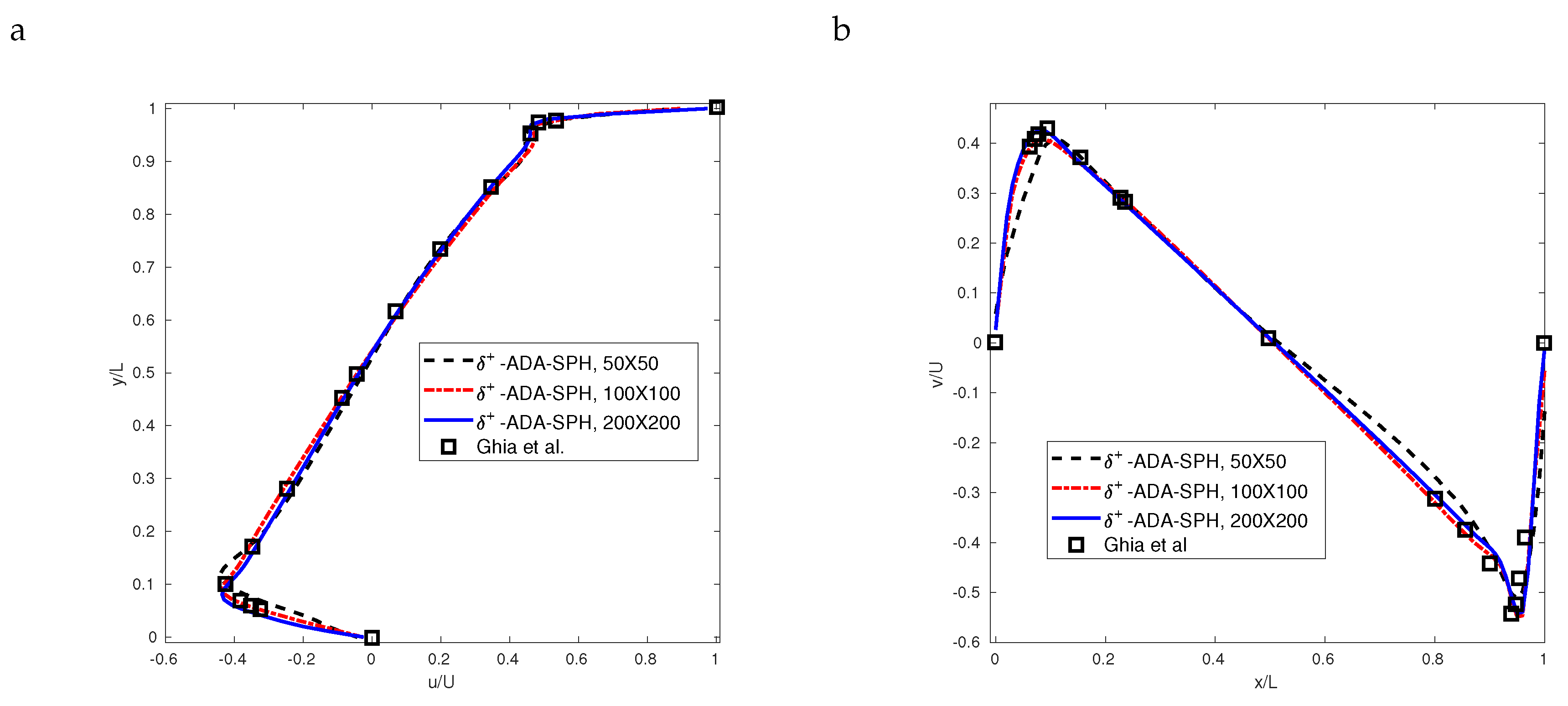
5. Lid-Driven Cavity Flow
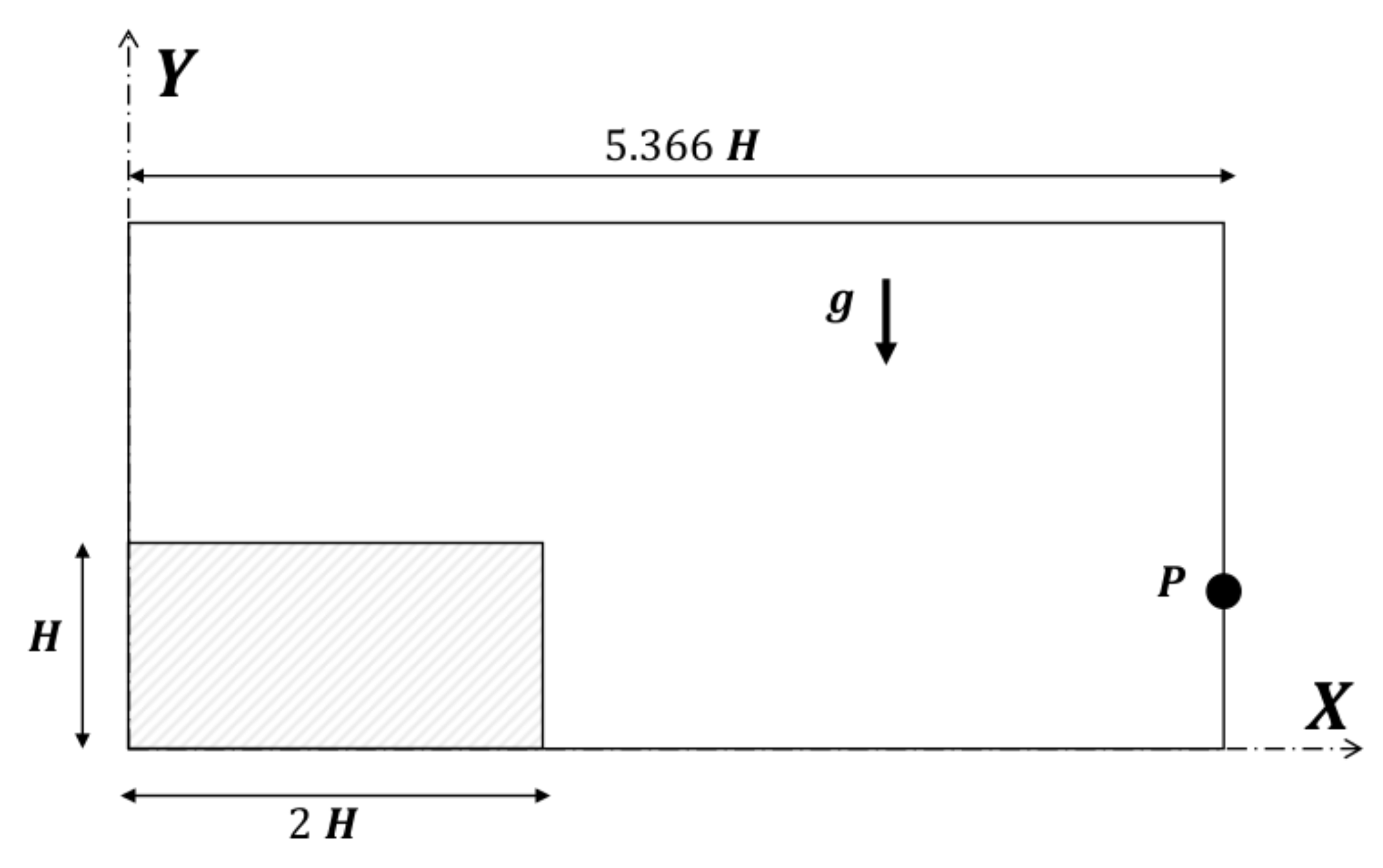
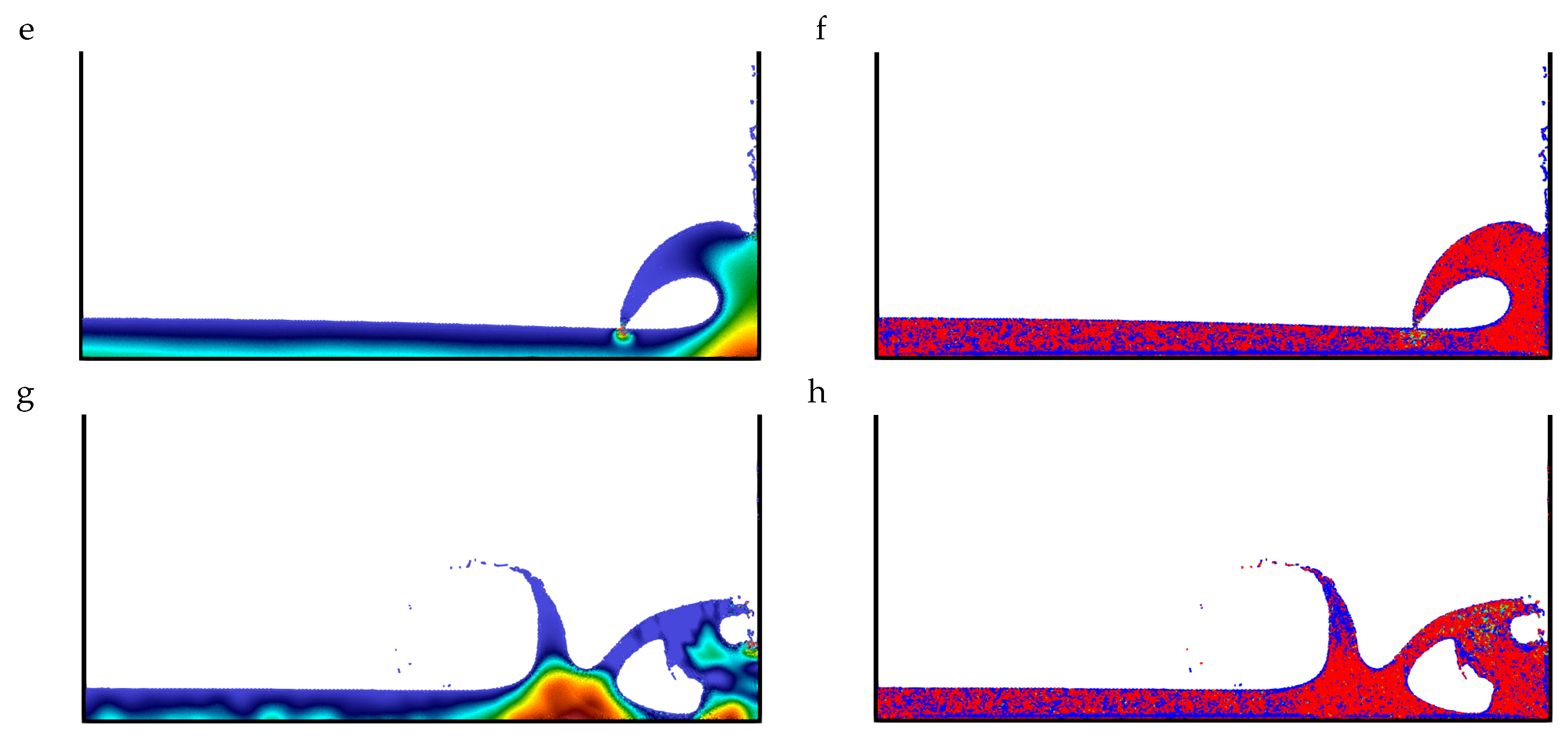
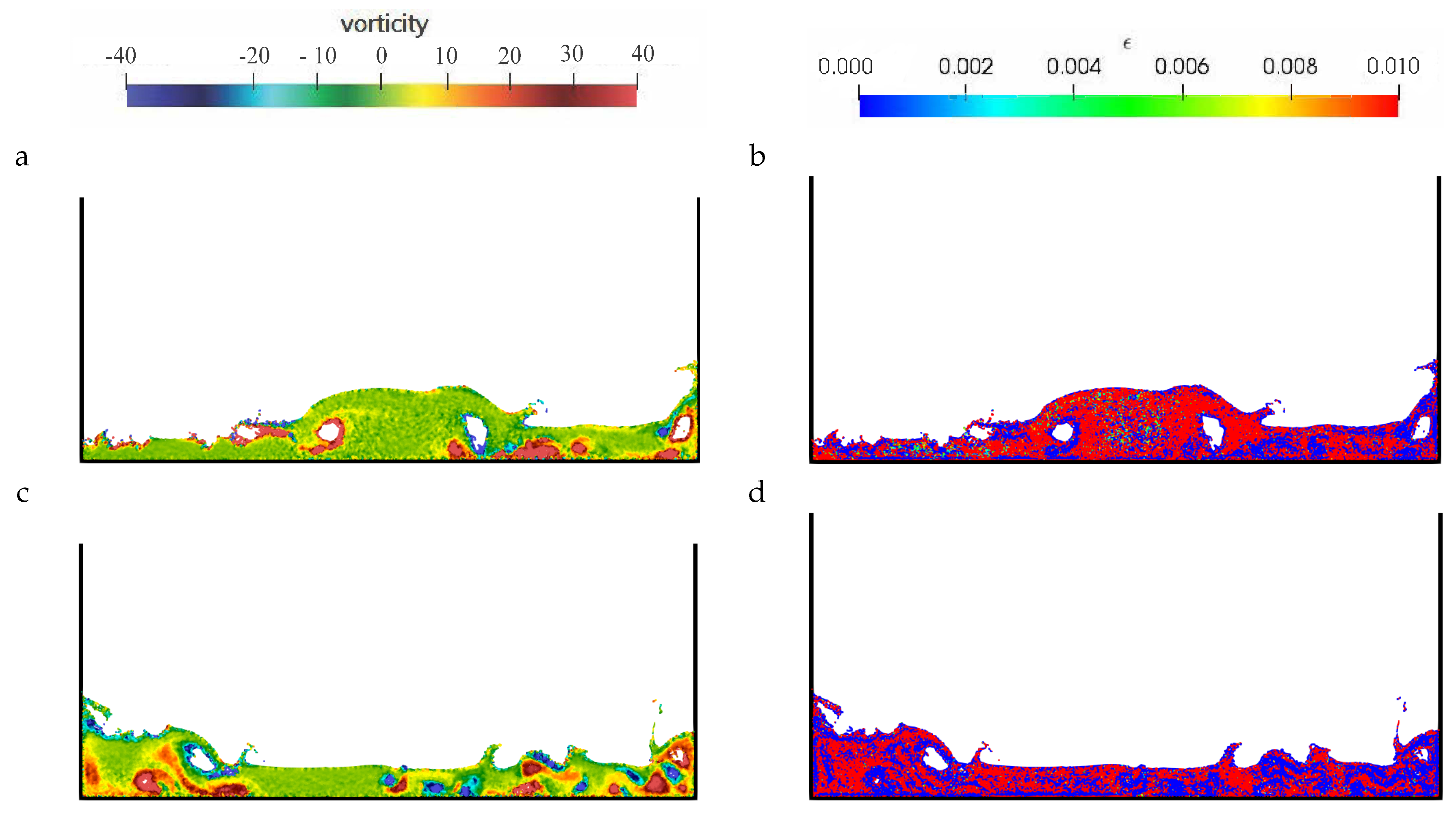
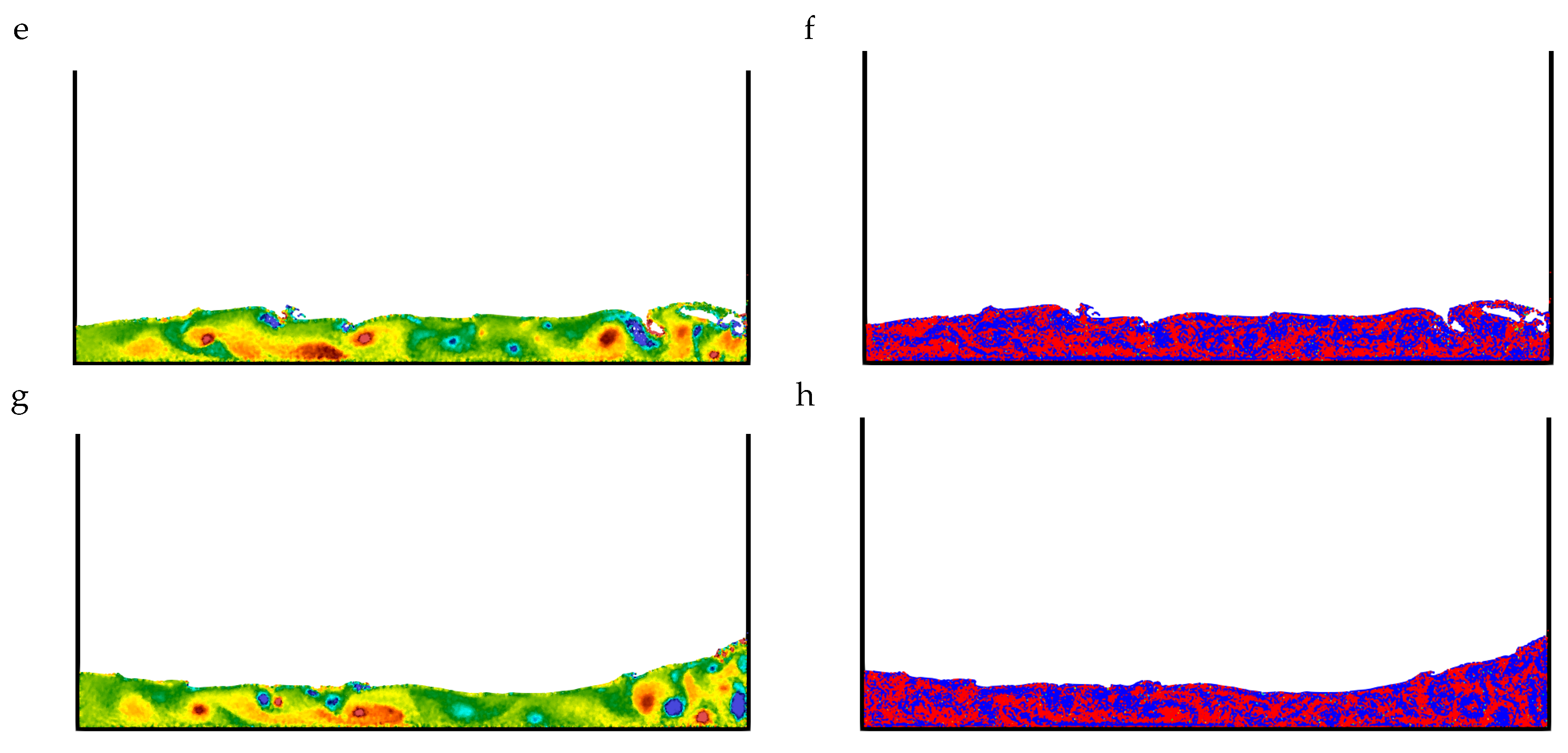
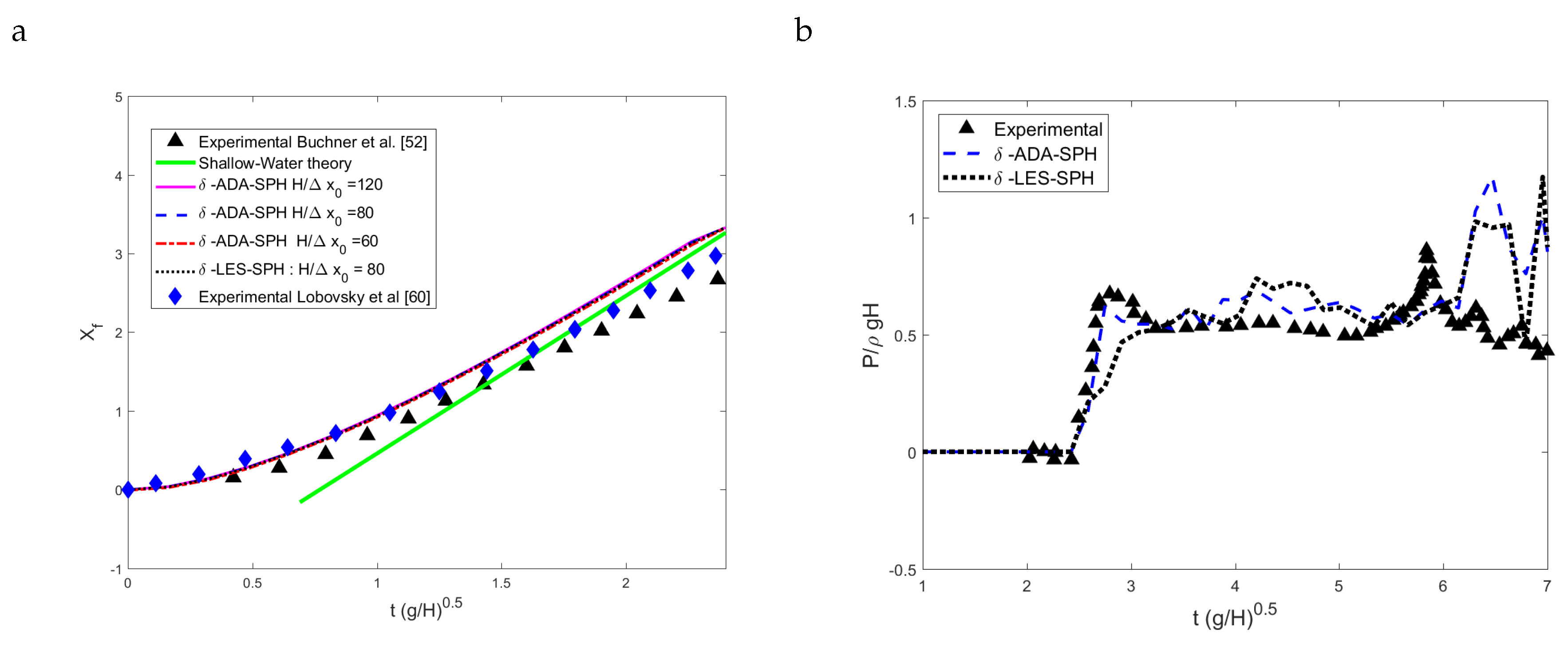
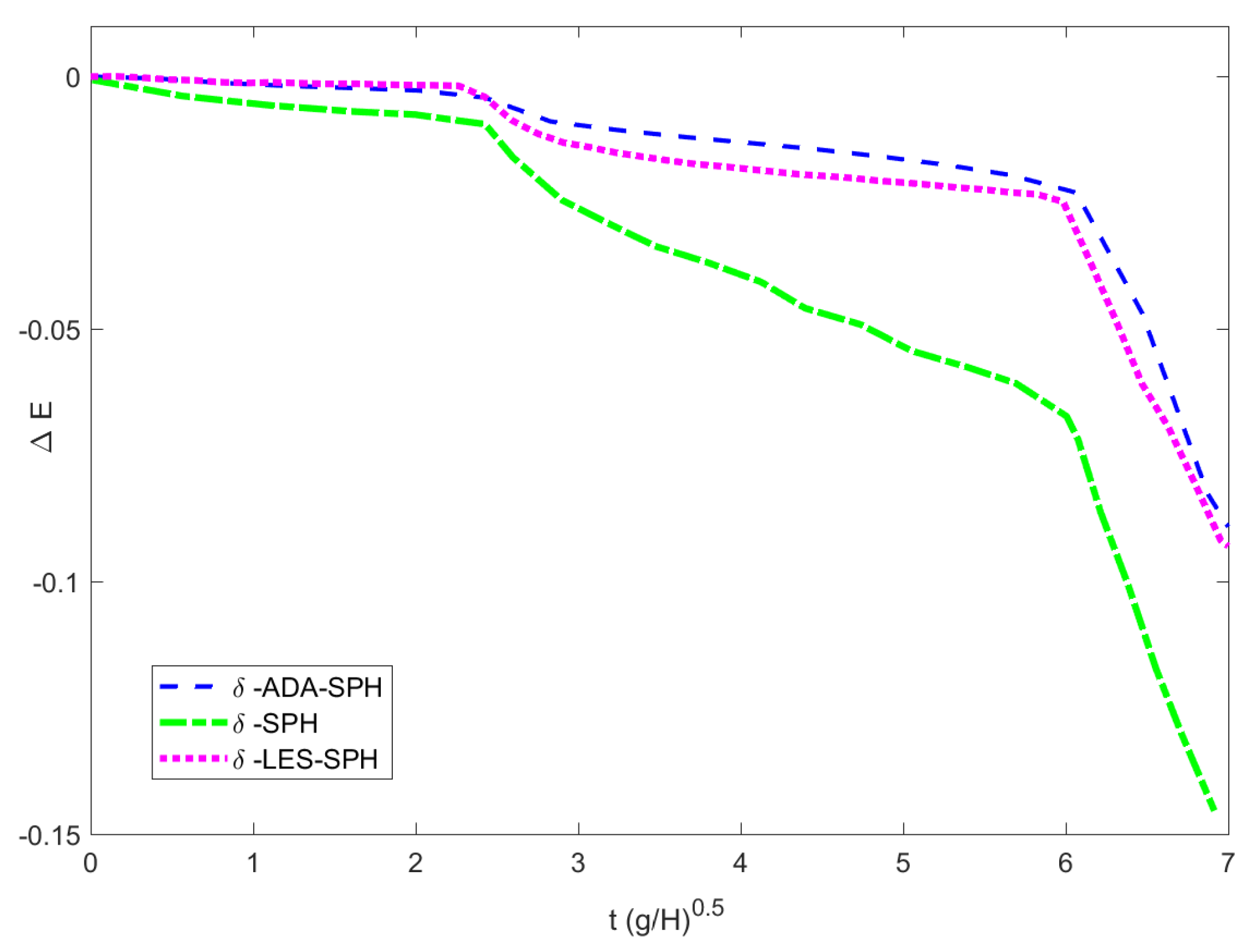
Two-Dimensional Dam-Break Flow
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M.; Rogers, B.D.; Dalrymple, R.A.; Crespo, A.J. State-of-the-art of classical SPH for free-surface flows. J. Hydraul. Res. 2010, 48, 6–27. [Google Scholar] [CrossRef]
- Price, D.J. Smoothed particle hydrodynamics and magnetohydrodynamics. J. Comput. Phys. 2012, 231, 759–794. [Google Scholar] [CrossRef]
- Violeau, D.; Rogers, B. Smoothed particle hydrodynamics (SPH) for free-surface flows: Past, present and future. J. Hydraul. Res. 2010, 48, 6–279. [Google Scholar] [CrossRef]
- Vila, J. On Particle Weighted Methods and Smooth Particle Hydrodynamics. Math. Model. Methods Appl. Sci. 1999, 9, 161–209. [Google Scholar] [CrossRef]
- Inutsuka, S.I. Reformulation of smoothed particle hydrodynamics with Riemann solver. J. Comput. Phys. 2002, 179, 238–267. [Google Scholar] [CrossRef]
- Sirotkin, F.; Yoh, J. A Smoothed Particle Hydrodynamics method with approximate Riemann solvers for simulation of strong explosions. Comput. Fluids 2013, 88, 418–429. [Google Scholar] [CrossRef]
- Avesani, D.; Dumbser, M.; Bellin, A. A new class of Moving-Least-Squares WENO-SPH schemes. J. Comput. Phys. 2014, 270, 278–299. [Google Scholar] [CrossRef]
- Hopkins, P. New Class of Accurate, Mesh-Free Hydrodynamic Simulation Methods. Mon. Not. R. Astron. Soc. 2015, 450, 53–110. [Google Scholar] [CrossRef]
- Nogueira, X.; Ramírez, L.; Clain, S.; Loubère, R.; Cueto-Felgueroso, L.; Colominas, I. High-accurate SPH method with Multidimensional Optimal Order Detection limiting. Comput. Methods Appl. Mech. Eng. 2016, 310, 134–155. [Google Scholar] [CrossRef]
- Ramírez, L.; Nogueira, X.; Khelladi, S.; Krimi, A.; Colominas, I. A very accurate Arbitrary Lagrangian-Eulerian meshless method for Computational Aeroacoustics. Comput. Methods Appl. Mech. Eng. 2018, 342, 116–141. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, X.; Adams, N.A. A weakly compressible SPH method based on a low-dissipation Riemann solver. J. Comput. Phys. 2017, 335, 605–620. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S.; Molteni, D. Free-surface flows solved by means of SPH schemes with numerical diffusive terms. Comput. Phys. Commun. 2010, 181, 532–549. [Google Scholar] [CrossRef]
- Sun, P.; Colagrossi, A.; Marrone, S.; Zhang, A. The δplus-SPH model: Simple procedures for a further improvement of the SPH scheme. Comput. Methods Appl. Mech. Eng. 2017, 315, 25–49. [Google Scholar] [CrossRef]
- Di Mascio, A.; Antuono, M.; Colagrossi, A.; Marrone, S. Smoothed particle hydrodynamics method from a large eddy simulation perspective. Phys. Fluids 2017, 29, 035102. [Google Scholar] [CrossRef]
- Sun, P.; Colagrossi, A.; Marrone, S.; Antuono, M.; Zhang, A. Multi-resolution Delta-plus-SPH with tensile instability control: Towards high Reynolds number flows. Comput. Phys. Commun. 2018, 224, 63–80. [Google Scholar] [CrossRef]
- Meringolo, D.D.; Marrone, S.; Colagrossi, A.; Liu, Y. A dynamic δ-SPH model: How to get rid of diffusive parameter tuning. Comput. Fluids 2019, 179, 334–355. [Google Scholar] [CrossRef]
- Li, C.G.; Tsubokura, M. An implicit turbulence model for low-Mach Roe scheme using truncated Navier–Stokes equations. J. Comput. Phys. 2017, 345, 462–474. [Google Scholar] [CrossRef]
- Nogueira, X.; Ramírez, L.; Fernández-Fidalgo, J.; Deligant, M.; Khelladi, S.; Chassaing, J.C.; Navarrina, F. An a posteriori-implicit turbulent model with automatic dissipation adjustment for Large Eddy Simulation of compressible flows. Comput. Fluids 2020, 197, 104371. [Google Scholar] [CrossRef]
- Tantikul, T.; Domaradzki, J. Large eddy simulations using truncated Navier–Stokes equations with the automatic filtering criterion. J. Turbul. 2010, 11, N21. [Google Scholar] [CrossRef]
- Domaradzki, J.A.; Loh, K.C.; Yee, P.P. Large eddy simulations using the subgrid-scale estimation model and truncated Navier–Stokes dynamics. Theor. Comput. Fluid Dyn. 2002, 15, 421–450. [Google Scholar] [CrossRef]
- Sun, G.; Domaradzki, J.A. Implicit LES using adaptive filtering. J. Comput. Phys. 2018, 359, 380–408. [Google Scholar] [CrossRef]
- Hu, X.; Adams, N. A SPH model for incompressible turbulence. arXiv 2012, arXiv:1204.5097. [Google Scholar] [CrossRef][Green Version]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touzé, D.; Graziani, G. δ-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G.; Lam, K. Constructing smoothing functions in smoothed particle hydrodynamics with applications. J. Comput. Appl. Math. 2003, 155, 263–284. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Monaghan, J.J. SPH without a tensile instability. J. Comput. Phys. 2000, 159, 290–311. [Google Scholar] [CrossRef]
- Sun, P.; Colagrossi, A.; Marrone, S.; Antuono, M.; Zhang, A.M. A consistent approach to particle shifting in the δ-Plus-SPH model. Comput. Methods Appl. Mech. Eng. 2019, 348, 912–934. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Deardorff, J.W. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Meringolo, D.D.; Liu, Y.; Wang, X.Y.; Colagrossi, A. Energy balance during generation, propagation and absorption of gravity waves through the δ-LES-SPH model. Coast. Eng. 2018, 140, 355–370. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical diffusive terms in weakly-compressible SPH schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703. [Google Scholar] [CrossRef]
- Kennedy, C.A.; Carpenter, M.H.; Lewis, R.M. Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations. Appl. Numer. Math. 2000, 35, 177–219. [Google Scholar] [CrossRef]
- Taylor, G.I.; Green, A.E. Mechanism of the production of small eddies from large ones. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1937, 158, 499–521. [Google Scholar]
- Colagrossi, A.; Bouscasse, B.; Antuono, M.; Marrone, S. Particle packing algorithm for SPH schemes. Comput. Phys. Commun. 2012, 183, 1641–1653. [Google Scholar] [CrossRef]
- Hu, X.; Adams, N.A. An incompressible multi-phase SPH method. J. Comput. Phys. 2007, 227, 264–278. [Google Scholar] [CrossRef]
- Hu, X.; Adams, N.A. A constant-density approach for incompressible multi-phase SPH. J. Comput. Phys. 2009, 228, 2082–2091. [Google Scholar] [CrossRef]
- Tabeling, P. Two-dimensional turbulence: A physicist approach. Phys. Rep. 2002, 362, 1–62. [Google Scholar] [CrossRef]
- Kraichnan, R.H.; Montgomery, D. Two-dimensional turbulence. Rep. Prog. Phys. 1980, 43, 547. [Google Scholar] [CrossRef]
- Ghia, U.; Ghia, K.N.; Shin, C. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Erturk, E. Discussions on driven cavity flow. Int. J. Numer. Methods Fluids 2009, 60, 275–294. [Google Scholar] [CrossRef]
- Perumal, D.A.; Dass, A.K. Multiplicity of steady solutions in two-dimensional lid-driven cavity flows by lattice Boltzmann method. Comput. Math. Appl. 2011, 61, 3711–3721. [Google Scholar] [CrossRef]
- Wahba, E. Steady flow simulations inside a driven cavity up to Reynolds number 35,000. Comput. Fluids 2012, 66, 85–97. [Google Scholar] [CrossRef]
- Leroy, A.; Violeau, D.; Ferrand, M.; Kassiotis, C. Unified semi-analytical wall boundary conditions applied to 2-D incompressible SPH. J. Comput. Phys. 2014, 261, 106–129. [Google Scholar] [CrossRef]
- Martin, J.C.; Moyce, W.J.; Martin, J.; Moyce, W.; Penney, W.G.; Price, A.; Thornhill, C. Part IV. An experimental study of the collapse of liquid columns on a rigid horizontal plane. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1952, 244, 312–324. [Google Scholar]
- Zhou, Z.; De Kat, J.; Buchner, B. A nonlinear 3D approach to simulate green water dynamics on deck. In Proceedings of the Seventh International Conference on Numerical Ship Hydrodynamics, Nantes, France, 19–22 July 1999; pp. 1–15. [Google Scholar]
- Buchner, B. Green Water on Ship-Type Offshore Structures. Ph.D. Thesis, Delft University of Technology Delft, Delft, The Netherlands, 2002. [Google Scholar]
- Adami, S.; Hu, X.Y.; Adams, N.A. A generalized wall boundary condition for smoothed particle hydrodynamics. J. Comput. Phys. 2012, 231, 7057–7075. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Mokos, A.; Rogers, B.D.; Stansby, P.K.; Domínguez, J.M. Multi-phase SPH modelling of violent hydrodynamics on GPUs. Comput. Phys. Commun. 2015, 196, 304–316. [Google Scholar] [CrossRef]
- Chen, Z.; Zong, Z.; Liu, M.; Zou, L.; Li, H.; Shu, C. An SPH model for multiphase flows with complex interfaces and large density differences. J. Comput. Phys. 2015, 283, 169–188. [Google Scholar] [CrossRef]
- Greco, M. A Two-Dimensional Study of Green-Water Loading. Ph.D. Thesis, Department of Marine Hydrodynamics, Faculty of Marine Technology, Norwegian University of Science and Technology, Trondheim, Norway, 2001. [Google Scholar]
- Krimi, A.; Khelladi, S.; Nogueira, X.; Deligant, M.; Ata, R.; Rezoug, M. Multiphase smoothed particle hydrodynamics approach for modeling soil–water interactions. Adv. Water Resour. 2018, 121, 189–205. [Google Scholar] [CrossRef]
- Cherfils, J.M. Développements et Applications de la Méthode SPH aux Écoulements Visqueux à Surface Libre. Ph.D. Thesis, Université du Havre, Le Havre, France, 2011. [Google Scholar]
- Ritter, A. Die fortpflanzung der wasserwellen. Z. Des Vereines Dtsch. Ing. 1892, 36, 947–954. [Google Scholar]
- Lobovskỳ, L.; Botia-Vera, E.; Castellana, F.; Mas-Soler, J.; Souto-Iglesias, A. Experimental investigation of dynamic pressure loads during dam break. J. Fluids Struct. 2014, 48, 407–434. [Google Scholar] [CrossRef]
- Rezavand, M.; Zhang, C.; Hu, X. A weakly compressible SPH method for violent multi-phase flows with high density ratio. J. Comput. Phys. 2020, 402, 109092. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krimi, A.; Ramírez, L.; Khelladi, S.; Navarrina, F.; Deligant, M.; Nogueira, X. Improved δ-SPH Scheme with Automatic and Adaptive Numerical Dissipation. Water 2020, 12, 2858. https://doi.org/10.3390/w12102858
Krimi A, Ramírez L, Khelladi S, Navarrina F, Deligant M, Nogueira X. Improved δ-SPH Scheme with Automatic and Adaptive Numerical Dissipation. Water. 2020; 12(10):2858. https://doi.org/10.3390/w12102858
Chicago/Turabian StyleKrimi, Abdelkader, Luis Ramírez, Sofiane Khelladi, Fermín Navarrina, Michael Deligant, and Xesús Nogueira. 2020. "Improved δ-SPH Scheme with Automatic and Adaptive Numerical Dissipation" Water 12, no. 10: 2858. https://doi.org/10.3390/w12102858
APA StyleKrimi, A., Ramírez, L., Khelladi, S., Navarrina, F., Deligant, M., & Nogueira, X. (2020). Improved δ-SPH Scheme with Automatic and Adaptive Numerical Dissipation. Water, 12(10), 2858. https://doi.org/10.3390/w12102858







