Abstract
With the increase in global urbanization, satellite imagery and other types of geospatial data have been extensively used in urban landscape change research, which includes environmental modeling in order to assess the change impact on urban watersheds. For urban hydrological modeling, as a focus of this study, several related research questions are raised: (1) How sensitive are runoff simulation to land use and land cover change patterning? (2) How will input data quality impact the simulation outcome? (3) How effective is integrating and synthesizing various forms of geospatial data for runoff modeling? These issues were not fully or adequately addressed in previous related studies. With the aim of answering these questions as research objectives, we conducted a spatial land use and land cover (LULC) change analysis and an urban runoff simulation in the Blue River watershed in the Kansas City metropolitan area between 2003 and 2017. In this study, approaches were developed to incorporate the Hydrologic Engineering Center Hydrologic Modeling System (HEC-HMS) model with remote sensing, geographic information systems (GIS), and radar rainfall data. The impact of data quality on the model simulation outcome was also analyzed. The results indicate that there are no significant differences between simulated runoff responses in the two study years (2003 and 2017) due to spatial and temporal heterogeneity of urbanization processes in the region. While the metropolitan area has been experiencing remarkable urban development in the past few decades, the gain in built-up land in the study watershed during the study period is insignificant. On the other hand, the gain in vegetated land caused by forestation activities is offset by a decrease in farmland and grassland. The results show that increasing spatial data resolution does not necessarily or noticeably improve the HEC-HMS model performance or outcomes. Under these conditions, using Next Generation Weather Radar (NEXRAD) rainfall data in the simulation provides a satisfactory fit in hydrographs’ shapes, peak discharge amounts and time after calibration efforts, while they may overestimate the amount of rainfall as compared with gauge data. This study shows that the developed approach of synthesizing satellite, GIS, and radar rainfall data in hydrological modeling is effective and useful for incorporating urban landscape and precipitation change data in dynamic flood risk assessment at a watershed level.
1. Introduction
Flooding is one of the most severe and damaging natural hazards. As revealed by the Emergency Events Database (EM-DAT) Center for Research on the Epidemiology of Disasters (CRED) [1], from 2005 to 2014, floods accounted for 46% of all natural disasters and affected about 85 million people. During the 20th century, floods were the number-one natural disaster in the United States in terms of the number of lives lost and property damage [2]. As reported by the Federal Emergency Management Agency (FEMA), from 1978 to 2016, the total amount of paid losses for significant flood events was about USD 46.6 billion. Although this may indicate that climate change is responsible for the increase in flood occurrence and damages, this process is primarily intensified by urbanization [3]. According to the World Urbanization Report [4], 54% of the world’s population lives in urban areas, and it is projected that ongoing urbanization and population growth will add 2.5 billion people to the urban population by 2050. The world’s urban percentage increased from 43% in 1990 to 54% in 2014, and it is expected to grow to 66% by 2050. In urban watersheds, the scenario of urbanization is that impervious surfaces, including roads, sidewalks, parking lots, airports, buildings, etc., are replacing the natural soil layer and, as a result, reducing infiltration, which leads to a decrease in travel time and the generation of rapid overland flow. This human modification of land use and land cover (LULC) can significantly influence the watershed hydrological conditions and increases the peak discharge and runoff, which affect people’s lives and properties. At the end of the 1960s, researchers began to focus on understanding the effect of intensive deforestation and urbanization on river systems [5]. The research was carried out to determine the effect of land use/cover change on urban flooding risk [6,7,8,9,10]. Saghafian et al. [9] found that the deterioration of vegetated land cover led to an increase in flood peak and volume.
All of these human developments and related LULC change issues have led to the necessity of reliable flood and hydrological runoff modeling and predictions for advance warning and protection. Du et al. [11] applied an integrated simulation of land use changes and hydrological processes to investigate the impact of urbanization on the volume of direct runoff. The simulation results indicate that land use change has significantly increased direct runoff over the past two decades. Romero and Ordenes [12] concluded that the increased impervious areas in rural lands were causing flash floods. Olaide M et al. [13] used satellite images to determine the LULC change and how it influences urban flooding. The study found that marginal areas and vegetation were converted to residential areas, which increased the total impervious cover and generally increased the peak runoff. Various contributions have applied hydrological models to estimate and evaluate the impact of LULC change on the urban runoff process, flood magnitude, and frequency [7,8,10,14,15,16]. The Hydrologic Engineering Center Hydrologic Modeling System (HEC-HMS) is one of the semi-distributed models that take into account the spatial variation in the watershed parameters to simulate the rainfall-runoff processes of the watershed systems. The model has been widely applied for simulating runoff in flood risk assessment studies—for example, in [9,17]. Further, Oleyiblo and Li [18] indicated that the model accurately simulated the flood volume and peak time and is a powerful tool for flood forecasting. Koneti et al. [19] applied HEC-HMS for runoff simulation and found that the model better simulated the runoff at the sub-basin scale. Although there have been numerous urban runoff modeling efforts, as exampled above, our review suggests that there was a lack of understanding of the impact of spatial and temporal heterogeneity of urban development processes on runoff model outcomes. At the regional level, there are often “hot spots” and “cool spots” of urban development in both spatial and temporal domains. How sensitive are the urban runoff models, specifically HEC-HMS, in their ability to reflect these variations in urbanization processes, as indicated by the patterning of LULC change? In previous studies, this issue was not fully and adequately addressed.
In the past decade or so, hydrological modeling has been improved with the development of remote sensing, geographic information systems (GIS), and fine-resolution geospatial data, including satellite imagery, digital elevation models (DEM), and radar rainfall data. The accuracy of spatial information is critical for effective landscape and hydrologic modeling [20,21,22], and model outcomes and their interpretation are heavily dependent on the availability of input data at a given scale [23]. Although the concept of incorporating satellite imagery and other geospatial data into hydrological modeling is not a recent development, the availability of fine spatial resolution data and the development of modeling and computational tools make it possible to obtain more detailed information needed for landscape and flood risk assessment. In this regard, we find that there is a lack of tests of the feasibility and effectiveness of integrating various forms of geospatial data in a unified runoff simulation. Further, our review indicates that the impact of the quality of geospatial data, specifically different spatial resolutions, on the model outcome has not been fully examined in previous studies, particularly in an urban watershed such as our case study area.
The response of LULC to precipitation varies spatially; thus, spatially distributed rainfall data, such as Next Generation Weather Radar (NEXRAD), are critical in distributed hydrological models, such as HEC-HMS for accurate runoff computation, which requires calculating the mean areal precipitation (MAP) for the watershed. Using this dataset, computing MAP explicitly considers the spatial variability of rainfall compared with ground-based gauge rainfall [24]. Some previous studies have tested the performance of different NEXRAD precipitation products against the ground-based gauge data in hydrological modeling, and results have shown the superiority of NEXRAD data because of their ability to capture the rainfall spatial variations for better outcomes [25,26,27]. Only a few studies have attempted to couple NEXRAD Level 3 rainfall with the HEC-HMS model for the assessment of LULC change impact on urban flooding. For example, Knebl et al. [17] used NEXRAD data in HEC-HMS simulations and found that the model tended to overestimate the runoff, and the calibration runs improved the overall results. On the other hand, McCormick [28] found that the NEXRAD data were effective for utilization with HEC-HMS, and the model produced reasonable results. Given these different findings, a further understanding of this issue is essential.
In summary, all the issues described above raised the research questions: (1) How sensitive are runoff simulation to land use and land cover change patterning? (2) How will input data quality impact the simulation outcome? (3) How effective are integrating and synthesizing various forms of geospatial data for runoff modeling? To address these questions, this study aims to (1) detect LULC changes and assess the impact of the change patterns on the watershed hydrological response (runoff); (2) examine the impact of data quality on simulation outcomes; (3) test the suitability of NEXRAD rainfall data when being used in integration with other geospatial datasets in runoff modeling.
2. Materials and Methods
2.1. Case Study Area: The Blue River Watershed
The case study area (Figure 1) selected for the simulation is the Blue River watershed. It is a fifth-order stream basin that covers about one-half of the Kansas City metropolitan area south of the Missouri River. It extends about 686 square kilometers through two states (Missouri and Kansas), four counties (Johnson and Wyandotte in Kansas; Jackson and Cass in Missouri), and 11 municipalities [29], representing diverse LULC types. Most of the watershed consists of silt loams and silty clay loams, and more than a third of the watershed is under the urban land complex category. Approximately 60 to 70% of this category are impervious surfaces, which also contain silt loams and silty clay loam soils. These types of soil are associated with moderate to high runoff rates according to the hydrologic soil groups of the Natural Resources Conservation Service (NRCS) [30]. Generally, the Kansas City Metropolitan area has experienced remarkable urban development in the past few decades, which resulted in a significant increase in impervious surfaces (built-up land). However, this changing trend has varied spatially and temporally. As such, we selected this watershed for our case study, which has more diverse land use and development activities and a history of frequent floods, in order to better examine the LULC impact on the model outcome.
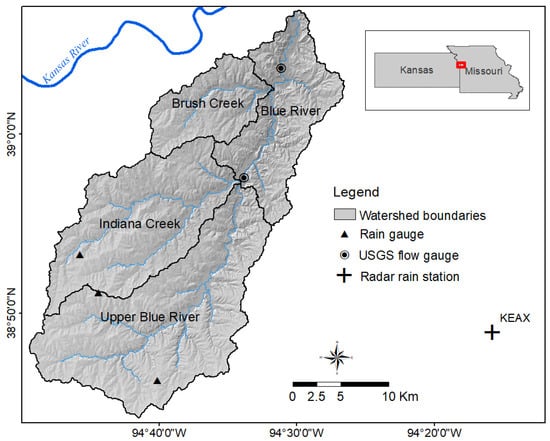
Figure 1.
Location of the study area, the Blue River watershed, with major sub-watersheds and the locations of rain gauges, USGS streamflow gauges, and the Kansas City Radar rain station.
2.2. Methodology
Runoff-rainfall modeling requires a variety of spatial data inputs related to, for example, land use and land cover, terrain, soil, precipitation, and streamflow data records. These datasets are used as inputs for the HEC-HMS model. The method in this study can be described in several major stages (Figure 2). It first derives the LULC maps with 6, 20, and 30 m spatial resolution using the Maximum Likelihood classification (MLC) and performs a change detection analysis, which is followed by delineating the drainage networks with 3 and 30 m spatial resolution DEMs. The process then prepares the soil data in order to derive the Soil Conservation Service (SCS) curve number (CN) values and then prepares NEXRAD rainfall data. The final step includes the model setup and simulation run.
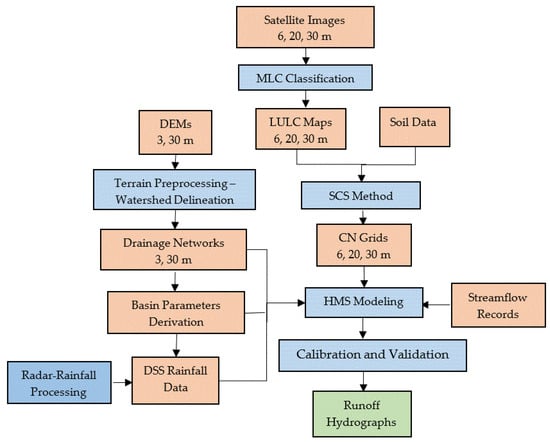
Figure 2.
Data processing and modeling procedures: orange boxes indicate data inputs with different spatial resolutions, blue indicates processing, and green indicates final simulation outputs.
2.2.1. LULC Classification, Accuracy Assessment, and Change Detection
Four satellite images with various resolutions were used to derive the LULC maps of 2003 and 2017 and to monitor the land use/cover change over time. For the year 2003, a SPOT image (20 m) and LANDSAT image (30 m) were used; for the year 2017, SPOT (6 m) and LANDSAT (30 m) images were utilized (Table 1). ERDAS IMAGINE 2016, an image processing software of HEXAGON Geospatial that performs advanced remote sensing analysis and spatial modeling, was used for image preprocessing, classification, and accuracy assessment in this study. A satellite image preprocessing technique, such as geometric correction, was applied to all four images. Using the SPOT 2017 image as a georeferenced image, an image-to-image registration was conducted on the SPOT 2003 image and LANDSAT 2003 and 2017 images, resulting in an accuracy of below 0.5 root-mean-square error for each image. The selection of dates was based on the availability of images. The MLC classification was applied to derive land use and land cover maps, one of the required inputs for HEC-HMS. MLC is the most common classification used with remote sensing data [31]. It is based on the probability that a pixel belongs to a particular class and considers the variability of classes using a covariance matrix [32]. Spectral signature samples were carefully collected to ensure proper representation of the class spectral reflectance to obtain reasonable estimates of the conditional mean vector and covariance matrix. This process enables more accurate classification results. The error matrix method, the most effective and widely accepted measure to evaluate the accuracy of thematic maps, was used to evaluate the accuracy of the classification results. It compares information from reference sites with information on the classified map for a number of sample areas. Kappa is another measure of image classification accuracy that is based on the difference between the actual agreement in the error matrix (the agreement between the classification and the reference data) and the agreement expected by chance [33]. In this process, 250 reference points were randomly assigned to each of the four classified images. Some other available images from previous studies and Google Earth historical images were utilized for further verification of the reference points.

Table 1.
List of satellite images used in the study.
The classification scheme was determined to better reflect major land use/cover types in the study area and also represent the common types of land use/cover used for the SCS CN method in modeling the runoff. They include water, forestland, farmland/grassland, and built-up areas. The water class includes rivers, lakes, and ponds. The built-up area class contains all impervious surfaces, such as buildings, driveways, paved parking lots, etc. The farmland/grassland category represents farms, grass, and bare soil land, whereas the forestland class represents woods and trees. For change detection analysis, post-classification change detection was performed on classified SPOT and LANDSAT images using ERDAS IMAGINE 2018. Resampling was conducted on the SPOT 2003 (20 m) image to obtain a uniform 6 m cell size for both images. There was no need to resample LANDSAT images because both have the same spatial resolution (30 m).
2.2.2. Watershed Delineation
For the purpose of comparison, USGS DEMs with two resolutions were utilized to delineate the watershed drainage network in order to investigate the impact of different spatial resolution data inputs on the simulation results. The first is LiDAR-derived DEM data with a 1/9 arc-second (3 m) horizontal resolution with a vertical accuracy of 0.87 m, and the second dataset has one arc-second (30 m) horizontal resolution with a vertical accuracy of about 3 m. The HEC-GeoHMS toolkit was used to delineate the drainage network with both DEMs. HEC-GeoHMS is a geospatial hydrologic model extension for ArcMap released by the US Army Corps of Engineers [34]. The tool allows the modelers to analyze digital terrain data, derive stream and watershed drainage networks, and construct and prepare inputs for hydrological model software, such as HEC-HMS [35]. Using this tool, terrain preprocessing was performed in multiple steps, starting with filling the sinks and ending with delineating the catchment. A threshold value of 0.25% was chosen to define the streams in both DEMs. Terrain preprocessing outputs are composed of both raster and vector data, which are the primary inputs for the HEC-GeoHMS model setup. By defining the basin outlet point, the tool created the watershed boundaries and the stream networks and computed parameters. Two drainage watershed systems were extracted from both DEMs.
2.2.3. NEXRAD Rainfall Data Processing
For model calibration, hourly NEXRAD Level III rainfall data, obtained from the National Weather Service (NWS) Weather Surveillance Radar Doppler units (WSR-88D) [36], were utilized. The accuracy of NEXRAD precipitation data is based on the Z-R relationship model that is used to estimate rainfall from reflectivity. An automated GIS-based approach was applied to prepare and process the data. A multi-step procedure was implemented utilizing NCEL Radar Software, ArcGIS 10.7, and the standard UNIX Command. The decoding step produced about 2700 radar images for the selected events. Precipitation grids are required to be in the Data Storage System format (HEC-DSS) for use in the HEC-HMS model. HEC-DSS is a dataset system designed to effectively store and retrieve sequential data, such as textual or gridded time-series data [37]. Figure 3 shows some selected rainfall images for the 2017 flood event of the one-hour NEXRAD precipitation data after processing.
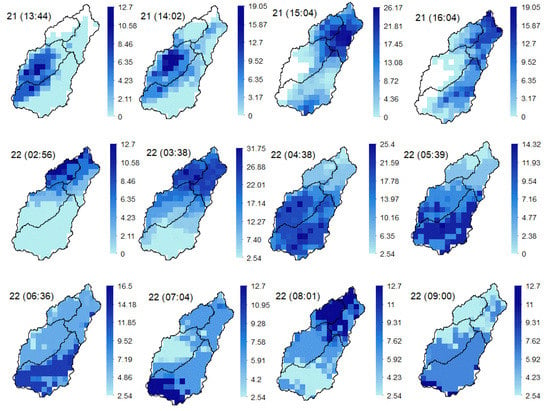
Figure 3.
Spatially distributed cumulative precipitation (mm) of selected available one-hour NEXRAD Level III images (4 km) for the August 2017 flood event in the UTC time zone after processing.
2.3. Runoff Simulation
2.3.1. Urban Runoff Model: HEC-HMS
The watershed model prepared by HEC-GeoHMS is shown in Figure 4. The watershed is divided into the four major sub-watersheds to accurately calculate and simulate the runoff. For model calibration and validation, we used three flooding events, which were reported as flash flood events according to NOAA Storm Events Database [38]. The selected events for model calibration occurred in the periods of 2–6 June 2005 and 21–23 August 2017. The 2008 event was selected for model validation, which occurred from 29 to 31 July 2008 (Table 2). The available hourly and daily gauge data from NOAA/National Climatic Center [39] were used to evaluate NEXRAD Level III precipitation. Observed streamflow data from two USGS discharge gauges were available for all events. The study simulated the runoff hydrographs using HEC-HMS. For the accuracy of the runoff simulation, four separate models were used in the simulation to represent each element of the runoff process, including runoff volume, direct runoff, channel flow, and baseflow. The SCS CN loss method was utilized to compute the runoff volume. It estimates precipitation excess according to cumulative precipitation, soil type, land use/cover types, and antecedent moisture [24]. Soils were classified into A, B, C, and D categories according to their minimum infiltration rates, based on the hydrological soil group (HSG) (more details in National Engineering Handbook and TR-55 report [40,41]). The Soil Survey Geographic (SSURGO) data, available from the United States Department of Agriculture (USDA) [42], were prepared based on both the SSURGO and GeoHMS user’s manual instructions (Figure 4). Using the four SPOT and LANDSAT imagery-generated LULC maps and the soil data, the CN value for each cell in the elevation grid and the average CN value for each sub-watershed were calculated.
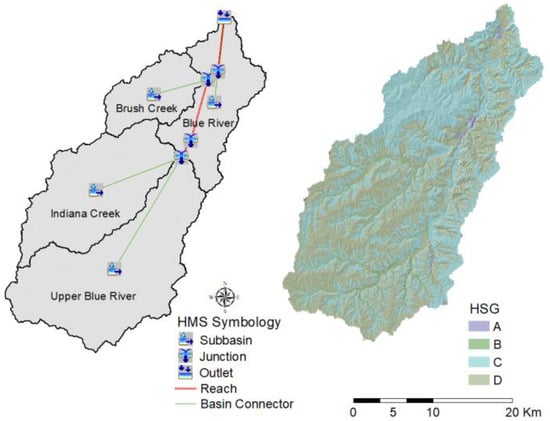
Figure 4.
The watershed model created by HEC-GeoHMS, and Hydrological soil group based on SSURGO data.

Table 2.
Total precipitation (mm) based on radar rainfall obtained from KC station.
The ModClark model was selected to simulate the direct runoff of the excess precipitation in the watershed to be utilized with NEXRAD precipitation data. The ModClark algorithm is the modified version of the Clark unit hydrograph that is suitable for the use of spatially distributed precipitation data (Figure 5). This distributed parameter model accounts explicitly for variation in runoff travel time and storage. In this method, a grid is overlaid on the watershed, which allows for calculating the distances from all regions of the watershed to the outlet to compute the inflow and outflow. The model then combines them to determine the direct runoff hydrograph [43,44].
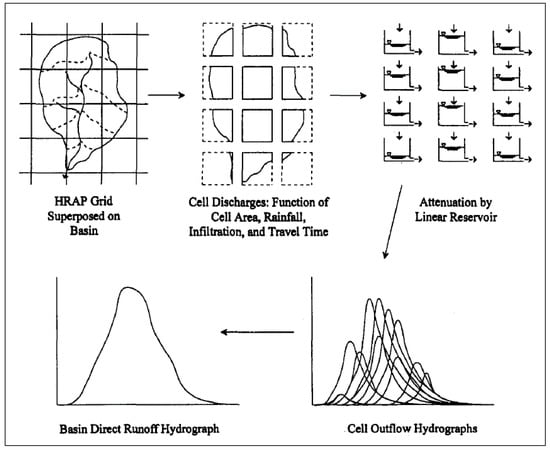
Figure 5.
ModClark model’s conceptual structure; adopted from [44].
The application of the model requires Storage coefficient R and Time of concentration tc. R represents the temporary storage rainfall excess while the drainage is processing to the outlet. It can be calculated by dividing the flow at the inflection point on the hydrograph’s falling limb by the time derived from the flow. Alternatively, it can be estimated as:
Time of concentration tc was estimated according to the SCS TR-55 method using HEC-GeoHMS for each cell of the model and is derived as:
where tc is the time of concentration for the subwatershed and a function of basin length and slope, dcell the travel distance from the cell to the outlet, and dmax the travel distance from the cell furthest from the outlet. For routing (channel flow) modeling, the Lag method was applied. It is widely used, mainly in urban drainage channels, and is calculated as:
where Ot = outflow hydrograph ordinate at time t; It = inflow hydrograph ordinate at time t; lag = time by which the inflow ordinates are to be lagged. As with other parameters, it can be estimated with the availability of observed streamflow hydrographs as the elapsed time between the time of hydrograph peaks. Baseflow was modeled using the Constant Monthly Baseflow method that represents the baseflow as a constant flow, which may vary monthly. Monthly baseflow values from the available USGS streamflow gauges were calculated for each flood event [24].
2.3.2. Model Performance
The model performance was evaluated by assigning the following indicators:
Nash–Sutcliffe Efficiency (E)
E indicates how well the result of observed flow versus the simulated flow fits the 1:1 line. The value of E ranges between 1.0 (perfect fit) and −∞. An efficiency value below zero means that the value of the observed data would have been a better predictor than the model [45].
Percent Bias (EPBIAS)
EPBIAS measures the average tendency of the simulated data to be larger or smaller than their observed counterparts. A low value indicates a more accurate simulation. Positive results mean underestimation, whereas negative values mean overestimation [46].
The Root-Mean-Square Error Standard Deviation (RMSE Std Dev)
The resulting value of the RMSE Std Dev varies from 0, as an optimal fit, to a larger positive value. The lower the value, the better the simulation performance [46].
3. Results and Discussion
3.1. LULC Maps, Classification Accuracy, and Change Detection
Figure 6 shows the classified LULC maps using SPOT and LANDSAT 2003 images and 2017 images. The use of the higher spatial resolution image (SPOT 6 m), as compared with the lower spatial resolution images (SPOT 20 m), improved the overall classification accuracy.
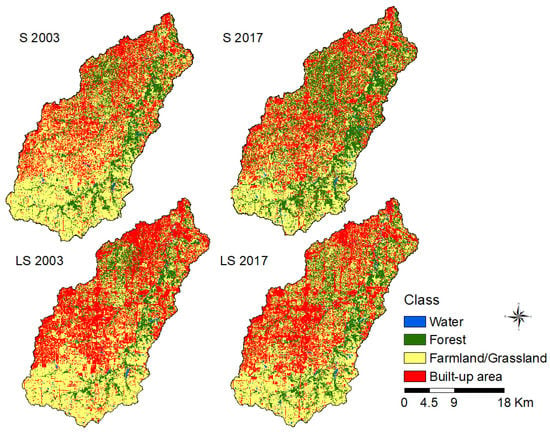
Figure 6.
Classified images of SPOT (S) and LANDSAT (LS) (2003 and 2017).
Table 3 and Table 4 summarize the classification accuracy assessment results, including producer’s and user’s accuracies for each image. The overall classification accuracy results with SPOT images increased from 85% (2003) to 92% (2017). The overall accuracy results with LANDSAT images are 87.60% for the 2003 image and 84% for the 2017 image. The calculated classification accuracies show satisfactory results for the purpose of this study, in which LULC maps with different resolutions are produced as inputs for the runoff modeling. SPOT and LANDSAT imagery classification results show an increase in water bodies and forestland and a decrease in farmland/grassland. There is a marginal gain in built-up area (Table 5). As a result, during the study period, farmland and grassland remained the largest land use type, followed by forestland, built-up area, and water bodies.

Table 3.
Accuracy assessment results of SPOT images.

Table 4.
Accuracy assessment results of LANDSAT images.

Table 5.
Total change in LULC obtained from classified images.
Change detection statistics were calculated and are shown in Table 6 and Table 7. Both classifications reveal an increase in the water class (0.19% from SPOT imagery and 0.15% from LANDSAT imagery). Forestland increased by a higher percentage (11% from SPOT imagery and 4% from LANDSAT imagery). These change patterns might have been caused by efforts to restore the Blue River watershed’s ecosystem, such as a partnership project, called Renew the Blue, that restores riparian forests, upland habitats, and wetlands in the study watershed [47]. The increase in forestland through forestation activities was mostly at the cost of losing farmland and grassland, according to image classification results. A small decrease in built-up areas might also be associated with the gain in forestland. The built-up area class shows, in SPOT classification results, a decrease of 0.02%, which can be considered as no change, while LANDSAT classification results indicate that the decrease in built-up areas was about 3.67%. These change patterns are consistent with the similar findings of Ji et al.’s [48] study, which found that, between 1992 and 2010, forestland increased by about 4%; farmland and grassland decreased by about 16%; built-up areas increased by about 10%.

Table 6.
Major LULC class changes from 2003 to 2017 from SPOT images.

Table 7.
Major LULC class changes from 2003 to 2017 from LANDSAT images.
Table 6 and Table 7 represent the total land cover transformation between 2003 and 2017. For instance, according to SPOT imagery classification results, forestland increased at the expense of farmland/grassland (89.5 km2) and built-up areas (22.25 km2). The total loss of farmland and grassland was about 167.61 km2; 89.5 km2 was converted to forest or trees, and the rest (76.15 km2) was converted to built-up areas. In general, forestland has increased the most, whereas the farmland/grassland class has decreased the most. According to LANDSAT imagery classification results, the farmland/grassland class was the larger contributor to the increase in forestland, and both forestland and built-up area classes contributed to the loss of farmland/grassland. The farmland/grassland class was the main land use type in both SPOT and LANDSAT results after 2003. In 2003, the built-up area was the second-largest land use; however, by 2017, forestland became the second-largest land cover in the watershed. Both results show an increase in water bodies, and in general, all classes contributed to this increase. This change detection analysis is essential for understanding the effect of past and current LULC regimes and the effect of LULC change that has been taking place in the watershed and its response to flood events. The study of Ji et al. [48] indicated that all watersheds in the entire metropolitan area gained about 7% in built-up areas from 1992 to 2010. The above change statistics suggest that our study area (Blue River watershed) had a relatively low rate of urban development and more complex vegetation change patterning during the study period from 2003 to 2017. Naturally, further examination of whether the runoff simulation outcome can reflect such LULC change patterning was carried out, as described in Section 3.5.
3.2. Watershed Extraction and CN Values
Total stream length and watershed catchment area are often used to measure the level of details extracted from DEMs [20,49,50,51]. The watershed drainage networks extracted from 3 and 30 m DEMs are shown in Figure 7. The 3 m DEM represents a total stream length of 230 km and a catchment area of 685.56 km2, whereas the 30 m DEM represents a total stream length of 178.60 km and a catchment area of 685.59 km2. The 3 m DEM is sensitive to minor topographic variations, so it captures more details of topographic features. With a vertical resolution of less than 1 m (0.87 m), the 3 m DEM modeled about 51.4 km more streams. Even though the 3 m DEM modeled more stream length, the difference between both results can be considered insignificant. The 3 m DEM produced a more detailed stream network and slightly lower values of basin parameters compared with the 30 m DEM; however, the difference between both DEM results is not significant. Additionally, both DEMs produced the same watershed total area. This outcome agrees with the findings of other studies that have compared the impact of different DEM resolutions on hydrologic and hydraulic modeling results [51,52,53]. Thus, for hydrologic modeling, the use of a moderate-resolution DEM provides reasonable results.
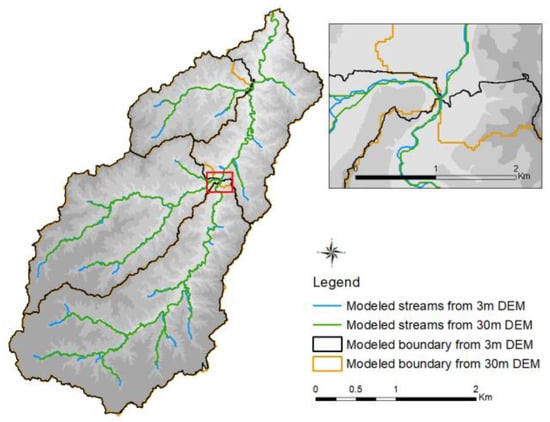
Figure 7.
Watershed boundaries and drainage streams extracted from 3 and 30 m DEMs.
Estimated CN values using SPOT and LANDSAT LULC maps are shown in a color range from 30 to 100 in Figure 8. Utilizing LULC maps with different spatial resolutions to estimate the CN values produced different results. LANDSAT LULC maps produced slightly higher values. The watershed, in general, has a high CN value even though the built-up area occupies just about 30–35%, and much of the area is vegetated land, which is occupied by farmland, grassland, and forestland. The reason for this is that the majority of the soil covering the watershed is from categories C and D, based on HSG, which usually have low infiltration and high potential runoff.
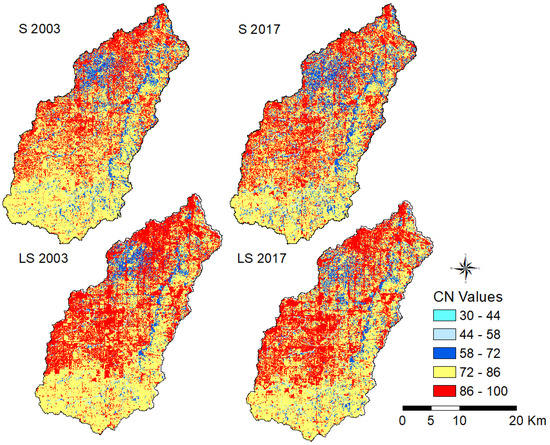
Figure 8.
CN values estimated from SPOT (S) and LANDSAT (LS) LULC maps.
3.3. NEXRAD Level III Validation
NEXRAD data were validated against gauge rainfall records from three ground-based gauges that were only available for Upper Blue River and Indiana Creek sub-watersheds. Scatter plots in Figure 9 show a significant correlation between NEXRAD and gauge precipitation data for 2008 (R2 = 0.8) and 2017 events (R2 = 0.6), while there is a less significant correlation for the 2005 event (R2 = 0.30). The Upper Blue River sub-watershed data for the 2008 event display the highest correlation, with an R2 value of 0.8. In contrast, for the 2005 event, both Upper Blue River and Indiana Creek sub-watersheds show the lowest correlation (R2 = 0.3). There were some missing data in the gauge records for this event, which affected the correlation results. Validation outcomes of NEXRAD and gauge precipitation usually do not reveal a good relationship because of the possible errors in both of them [26,54,55]. Figure 10 compares the total precipitation of NEXRAD with gauge data. NEXRAD precipitation amounts were overestimated for two flood events compared with gauge rainfall. There is no difference between gauge and NEXRAD rainfall data for 2005 event for both sub-watersheds; however, it is about 0.4 percent for the 2008 event. For the 2017 event, the difference is about 0.2 percent for Indiana Creek and 0.5 percent for Upper Blue River sub-watersheds. The overestimation is probably a result of area (radar grid cell) and point (gauge) errors [54]. On the other hand, the gauge precipitation might be underestimated due to issues with gauge funnels, which might have been temporarily blocked by grass, bird debris, or other objects, and as a result, the precipitation could be missing or delayed and underestimated [55].
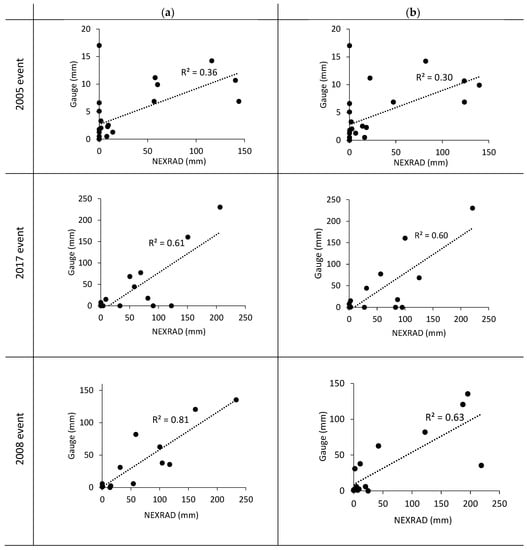
Figure 9.
Scatter plots of hourly NEXRAD and gauge rainfall data of the flood events for (a) Upper Blue and (b) Indian Creek.
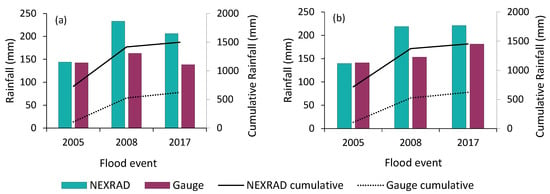
Figure 10.
NEXRAD and gauge rainfall data of the flood events for two sub-watersheds (a) Upper Blue River and (b) Indiana Creek.
3.4. Model Calibration and Validation
The preliminary simulated runoff hydrographs show a reasonable overall fit with observed data for the watershed. Although the runoff was overestimated in the validation results, the calibration attempts provided better results. Calibration and validation results at the Blue River watershed outlet are shown in Figure 11.
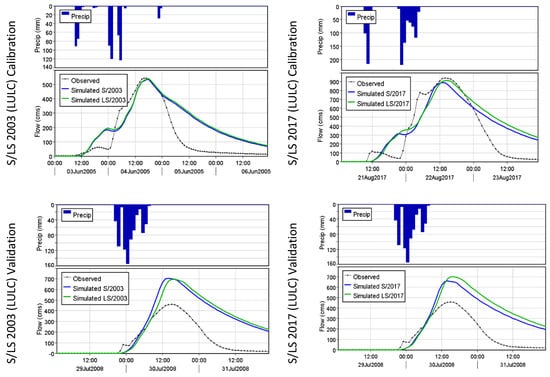
Figure 11.
Calibrated and validated hydrographs at the Blue River watershed outlet for SPOT (S) and LANDSAT (LS) LULC conditions.
Model calibration is the derivation of a set of model parameter values that produces the best fit to the observed data; on the other hand, the validation process is running the model for different events without changing the parameters. Calibrated models of 2005 and 2017 events provide better simulation results compared to the 2008 validation models (uncalibrated). There is almost no difference between the observed and calibrated amounts of peak discharge, whereas there is a 0.16 to 0.35 percent difference in direct runoff volume. Validation models provide relatively satisfactory results, although the peak discharge and runoff might be overestimated due to the precipitation amount overestimation in the NEXDAD data. The difference between observed and simulated peak discharge is about 0.36 percent, and direct runoff 0.5 percent. Better estimation for the rainfall amount in NEXRAD data could mitigate the runoff volume and simulate the peak discharge more accurately.
At a sub-watershed level, the model tended to overestimate the runoff for some sub-watersheds, but for the rest of the sub-watersheds, the model more accurately estimated the runoff. Compared with the observed data, the calibrated hydrographs indicate relatively good performance. The difference in statistical results between all models with different data input resolutions and LULC conditions is not significant. All models simulated the runoff in a similar fashion. For instance, the results for the model with lower resolution and 2003 LULC data are E = 0.6, EPBIAS 60%, and RMSE Std Dev = 0.6, and the results for the model with higher resolution and 2017 LULC data are E = 0.7, EPBIAS = 32%, and RMSE Std Dev = 0.5. Thus, using moderate-resolution data (e.g., 30 m) for modeling can still provide satisfactory simulation outcomes. The validation hydrographs of the 2008 event might have been overestimated due to the overestimation of the rainfall in the NEXRAD data. All validation models performed similarly. For example, the results for the model with lower resolution and 2003 LULC data are E = −0.9, EPBIAS 121%, and RMSE Std Dev = 1.4, and the results for the model with higher resolution and 2017 LULC are E = −0.7, EPBIAS = 120%, and RMSE Std Dev = 1.3.
3.5. Impact of LULC Change and Data Quality on Runoff
Using CN values estimated from 2003 (20 and 30 m) LULC maps and basin parameters extracted from 3 and 30 m DEMs, models 1 and 2, simulated with the 2005 event produced similar runoff hydrograph results. With CN values estimated from 2017 (6 and 30 m) LULC maps and basin parameters extracted from 3 m and 30 m DEMs, respectively, models 1.2 and 2.2 simulated with the 2017 event produced close runoff hydrograph results as well. In addition, running models 1 and 2 with the 2017 event and models 1.2 and 2.2 with the 2005 event generated closer results. In other words, all models, when simulating with the corresponding flood events, generated similar runoff hydrographs. For instance, as shown in Table 8, when simulating the 2005 event under the 2003 LULC condition (Model 1), the results show watershed discharges of 19,217.3 (cms), and under the 2017 LULC condition (Model 1.2), discharges of 19,201.9 (cms) are observed. There is almost no difference between the two discharge amounts. This insignificant variance demonstrates that the simulation reflects outcomes that are consistent with the LULC change patterns in the study area and period. As discussed before, the built-up area in the watershed did not change notably during the study period, while the increase in forestland was offset by decreased farmland/grassland.

Table 8.
Simulated peak discharge under 2003 and 2017 LULC conditions at the Blue River outlet.
Comparing the results of model 1.2, which uses higher spatial resolution data, with model 2.2, which uses lower resolution data, reveals that for each flood event all simulated values are close. For instance, in model 1.2 (uses 6 m LULC and 3 m DEM data), the simulated peak discharge is 33,103.3 cms for the 2017 event, while simulation with model 2.2 (with 30 m LULC and DEM data) results in a peak discharge of 33,295.7 cms. This also shows consistency with the low variation in the CN value and DEM processing outputs derived from different spatial resolution data, which led to similar simulation outputs and performance statistics. In addition, the HEC-HMS model is a generalized model system and applies mathematical models to represent the watershed flow; hence, small differences between derived inputs from 3 and 30 m DEMs or 6 and 30 m images are not enough to notably affect the model outputs. In previous studies, the impact of spatial and temporal heterogeneity of urban development processes on runoff model outcomes was not fully and adequately addressed, particularly in an urban watershed, such as in our case study area. There is a lack of understanding of the impact of different spatial resolutions on the model outcome and the suitability of coupling NEXRAD rainfall with the HEC-HMS model to assess LULC change impact on urban flooding. Our study attempts to further address this issue. In our 14-year study period, we found that the LULC in the Blue River watershed did not significantly change. Since 2003, the buildup area occupied about 1/3 of the watershed, and the majority of the area is vegetated land (forestland, farmland, and grassland). This less dynamic regime of the LULC in the watershed led to similar responses to precipitation and storm events. For runoff simulation applications, it is useful to utilize the standard available data resolution (e.g., 30 m) for satellite images to generate LULC data and CN values, or for DEMs to extract watershed parameters, which may cost less compared with data with higher spatial resolution. As LULC, NEXRAD data vary spatially, which provides a more accurate representation of the rainfall over each area compared with the ground-based gauge data that represent the rainfall amount only in the location area. In our case study, the use of (4 km) NEXRAD precipitation data for the simulation provides reasonably accurate runoff hydrographs. Using the dataset may contribute to runoff overestimation or underestimation due to the uncertainty and error that is usually associated with radar precipitation. At a sub-watershed scale, we found that using HEC-HMS, NEXRAD data can represent the rainfall amount and simulate the runoff for small sub-watersheds more accurately than large ones. Tests of other types of NEXRAD Level III precipitation data, such as the products of “dual-pol,” which clearly identify and detect rainfall, might reduce rainfall overestimation and provide better results.
4. Conclusions
In this study, urban runoff was simulated in an urban watershed that has diverse LULC and development activities, and its streams tend to be frequently flooded. The study aims to understand how LULC change patterning and the quality of input geospatial data affect the simulation outcomes as well as examine the effectiveness of NEXRAD rainfall data in such modeling settings. The study results reveal that the simulation with the HEC-HMS model sensitively responds to the spatial and temporal patterning of LULC dynamics indicated by the change rate of imperious surfaces and vegetated land-use processes. Specifically, the simulation outcomes reflect the slow-down period of urban development and associated ecological restoration efforts in the case study watershed during the study period. The study indicates that the developed simulation approach can better tolerate small variations in derived input parameters, such as CN values, watershed boundaries, parameters, and stream networks, suggesting that input data with a moderate spatial resolution (e.g., 30 m) are suitable for urban runoff simulation at a watershed scale. Further, this study illustrates that, in such modeling, applying spatially distributed precipitation data, such as the one-hour NEXRAD Level III data, provide reliable and satisfactory outcomes after calibration efforts, particularly in hydrograph shape, peak discharge amounts, and time. In addition, the rainfall amount overestimation in NEXRAD data results in higher peak discharge and runoff volume as compared with observed data. Finally, the study proves the feasibility and effectiveness of incorporating satellite imagery-based LULC maps with related geospatial data, including DEM and distributed radar precipitation, in hydrological simulation to assess the watershed’s hydrological response to flooding events.
Author Contributions
Conceptualization, A.E. and W.J.; methodology, A.E. and W.J.; software, A.E. and W.J.; validation, A.E. and W.J.; formal analysis, A.E.; investigation, A.E.; resources, A.E. and W.J.; data curation, A.E.; writing—original draft preparation, A.E.; writing—review and editing, A.E. and W.J.; visualization, A.E.; supervision, W.J.; project administration, A.E. and W.J.; funding acquisition, A.E. and W.J. All authors have read and agreed to the published version of the manuscript.
Funding
SPOT 2017 image purchase was funded by the University of Missouri–Kansas City School of Graduate Studies Research Grant. The other SPOT images were acquired through a previous remote sensing study, which was supported by the US EPA Grant CD 97701501 and by the grant of the Friends of the Library of the University of Missouri—Kansas City. A.E. received financial support from Umm AL-Qura University.
Acknowledgments
We thank the anonymous reviewers for their constructive comments and suggestions to improve the early version of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Database|EM-DAT. Available online: https://www.emdat.be/database (accessed on 9 March 2018).
- Perry, C.A. Significant Flood in the United States during 20th Centuru-USGS Measures a Centuru of Floods; USGS Fact Sheet 024-00: Washington, DC, USA, 2000. [Google Scholar]
- Mori, K.; Perrings, C. Optimal management of the flood risks of floodplain development. Sci. Total Environ. 2012, 431, 109–121. [Google Scholar] [CrossRef]
- UN. World Urbanization Prospects the 2014 Revision; United Nations, Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2014; Available online: https://population.un.org/wup/Publications/Files/WUP2014-Report.pdf (accessed on 9 March 2017).
- Patric, J.H.; Reinhart, K.G. Hydrologic effects of deforesting two mountain watersheds in West Virginia. Water Resour. Res. 1971, 7, 1182–1188. [Google Scholar] [CrossRef]
- Wheater, H.S.; Shaw, T.L.; Rutherford, J.C. Storm runoff from small lowland catchments in southwest England. J. Hydrol. 1982, 55, 321–337. [Google Scholar] [CrossRef]
- Ewen, J.; Parkin, G. Validation of catchment models for predicting land-use and climate change impacts. 1 method. J. Hydrol. 1996, 175, 583–594. [Google Scholar] [CrossRef]
- Niehoff, D.; Fritsch, U.; Bronstert, A. Land-use impacts on storm-runoff generation: Scenarios of land-use change and simulation of hydrological response in a meso-scale catchment in SW-Germany. J. Hydrol. 2002, 267, 80–93. [Google Scholar] [CrossRef]
- Saghafian, B.; Farazjoo, H.; Bozorgy, B.; Yazdandoost, F. Flood intensification due to changes in land use. Water Resour. Manag. 2008, 22, 1051–1067. [Google Scholar] [CrossRef]
- Sharma, C.S.; Behera, M.D.; Mishra, A.; Panda, S.N. Assessing flood induced land-cover changes using remote sensing and fuzzy approach in eastern gujarat (India). Water Resour. Manag. 2011, 25, 3219–3246. [Google Scholar] [CrossRef]
- Du, S.; Van Rompaey, A.; Shi, P.; Wang, J. A dual effect of urban expansion on flood risk in the pearl river delta (China) revealed by land-use scenarios and direct runoff simulation. Nat. Hazards 2015, 77, 111–128. [Google Scholar] [CrossRef]
- Romero, H.; Ordenes, F. Emerging urbanization in the southern andes: Environmental impacts of urban sprawl in santiago de chile on the andean piedmont. Mt. Res. Dev. 2004, 24, 197–201. [Google Scholar] [CrossRef]
- Olaide, M.A.; Blessing, K.N.; Joseph, E.; Hilda, U.O.; Nnaemeka, M.I.; Rejoice, I.E. Impacts of urban land use changes on flood events in warri, delta state nigeria. IOSR J. Environ. Sci. Toxicol. Food Technol. 2014, 8, 37–45. [Google Scholar] [CrossRef]
- Miller, S.N.; Kepner, W.G.; Mehaffey, M.H.; Hernandez, M.; Miller, R.C.; Goodrich, D.C.; Devonald, K.; Heggem, D.T.; Miller, W.P. Integrating landscape assessment and hydrologic modeling for land cover change analysis. J. Am. Water Resour. Assoc. 2002, 38, 915–929. [Google Scholar] [CrossRef]
- Fohrer, N.; Haverkamp, S.; Frede, H.-G. Assessment of the effects of land use patterns on hydrologic landscape functions: Development of sustainable land use concepts for low mountain range areas. Hydrol. Process. 2005, 19, 659–672. [Google Scholar] [CrossRef]
- Blöschl, G.; Ardoin-Bardin, S.; Bonell, M.; Dorninger, M.; Goodrich, D.; Gutknecht, D.; Matamoros, D.; Merz, B.; Shand, P.; Szolgay, J. At what scales do climate variability and land cover change impact on flooding and low flows? Hydrol. Process. 2007, 21, 1241–1247. [Google Scholar] [CrossRef]
- Knebl, M.R.; Yang, Z.-L.; Hutchison, K.; Maidment, D.R. Regional scale flood modeling using NEXRAD rainfall, GIS, and HEC-HMS/RAS: A case study for the San Antonio river basin summer 2002 storm event. J. Environ. Manag. 2005, 75, 325–336. [Google Scholar] [CrossRef] [PubMed]
- Oleyiblo, J.O.; Li, Z. Application of HEC-HMS for flood forecasting in Misai and Wan’an catchments in China. Water Sci. Eng. 2010, 3, 14–22. [Google Scholar]
- Koneti, S.; Sunkara, S.L.; Roy, P.S. Hydrological modeling with respect to impact of land-use and land-cover change on the runoff dynamics in godavari river basin using the HEC-HMS model. ISPRS Int. J. Geo-Inf. 2018, 7, 206. [Google Scholar] [CrossRef]
- Murphy, P.N.C.; Ogilvie, J.; Meng, F.-R.; Arp, P. Stream network modelling using lidar and photogrammetric digital elevation models: A comparison and field verification. Hydrol. Process. 2008, 22, 1747–1754. [Google Scholar] [CrossRef]
- Ogden, F.L.; Garbrecht, J.; DeBarry, P.A.; Johnson, L.E. GIS and distributed watershed models. II: Modules, interfaces, and models. J. Hydrol. Eng. 2001, 6, 515–523. [Google Scholar] [CrossRef]
- Clarke, S.; Burnett, K. Comparison of digital elevation models for aquatic data development. Photogramm. Eng. Remote Sens. 2003, 69, 1367–1375. [Google Scholar] [CrossRef]
- Wagenet, R.J.; Hutson, J.L. Scale-dependency of solute transport modeling/GIS applications. J. Environ. Qual. 1996, 25, 499–510. [Google Scholar] [CrossRef]
- USA Army Corps of Engineers. HEC-HMS Technical Reference Manual; Hydrologic Engineering Center: Davis, CA, USA, 2000; Available online: https://www.hec.usace.army.mil/software/hec-hms/documentation/HEC-HMS_Technical%20Reference%20Manual(CPD-74B).pdf (accessed on 19 March 2018).
- Li, Z.; Yang, D.; Hong, Y.; Qi, Y.; Cao, Q. Evaluation of radar-based precipitation estimates for flash flood forecasting in the three gorges region. Proc. Int. Assoc. Hydrol. Sci. 2015, 368, 89–95. [Google Scholar] [CrossRef][Green Version]
- Cho, Y.; Engel, B.A. NEXRAD quantitative precipitation estimations for hydrologic simulation using a hybrid hydrologic model. J. Hydrometeorol. 2017, 18, 25–47. [Google Scholar] [CrossRef]
- Myungjin, L.; Kang, N.; Joo, H.; Kim, S.; Lee, J. Hydrological modeling approach using radar-rainfall ensemble and multi-runoff-model blending technique. Water 2019, 11, 850. [Google Scholar] [CrossRef]
- McCormick, B.C. Distributed Hydrologic Modeling of the Upper Roanoke River Watershed Using GIS and NEXRAD. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2003. [Google Scholar]
- Wilkison, D.H.; Armstrong, D.J.; Norman, R.D.; Poulton, B.C.; Furlong, E.T.; Zaugg, S.D. Water Quality in the Blue River Basin, Kansas City Metropolitan Area, Missouri and Kansas, July 1998 to October 2004; Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2006; Volume 06-5147, p. 170.
- Missouri Department of Natural Resources, W.P.P. Total Maximum Daily Load (TMDL) for Blue River and Indian Creek Jackson County, Missouri. Available online: https://dnr.mo.gov/env//wpp/docs/0417-0418-0419-0420-0421-blue-r-indian-ck-tmdl.pdf (accessed on 13 September 2020).
- Richards, J.A. Remote Sensing Digital Image Analysis: An Introduction, 5th ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-30061-5. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective; Prentice Hall: Upper Saddle River, NJ, USA, 2005; ISBN 978-0-13-145361-6. [Google Scholar]
- Congalton, R.G.; Green, K.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008; ISBN 978-0-429-14397-7. [Google Scholar]
- HEC-GeoHMS. Available online: https://www.hec.usace.army.mil/software/hec-geohms/ (accessed on 15 April 2020).
- HEC-HMS. Available online: https://www.hec.usace.army.mil/software/hec-hms/ (accessed on 15 April 2020).
- National Oceanic and Atmospheric Administration. Available online: https://www.noaa.gov/ (accessed on 15 April 2020).
- CEIWR-HEC. HEC-DSSVue HEC Data Storage System Visual Utility Engine User’s Manual; USA Army Corps of Engineers: Davis, CA, USA, 2009; Available online: https://www.hec.usace.army.mil/software/hec-dssvue/documentation/User’sManual_2.0/HEC-DSSVue_20_Users_Manual.pdf (accessed on 9 September 2019).
- Storm Events Database|National Centers for Environmental Information. Available online: https://www.ncdc.noaa.gov/stormevents/ (accessed on 15 April 2020).
- Menne, M.J.; Durre, I.; Korzeniewski, B.; McNeal, S.; Thomas, K.; Yin, X.; Anthony, S.; Ray, R.; Russell, S.V.; Byron, E.G.; et al. Global Historical Climatology Network-Daily (GHCN-Daily). NOAA Natl. Clim. Data Cent. 2012. [Google Scholar] [CrossRef]
- SCS. US. National Engineering Handbook: Section 4: Hydrology, Soil Conservation Service; USDA: Washington, DC, USA, 1985. Available online: https://data.nodc.noaa.gov/cgi-bin/iso?id=gov.noaa.ncdc:C00861 (accessed on 22 July 2019).
- Cronshey, R. Urban Hydrology for Small Watersheds Technical Release 55. USDA, SCS, Engineering Division. 1986; p. 160. Available online: https://www.nrcs.usda.gov/Internet/FSE_DOCUMENTS/stelprdb1044171.pdf (accessed on 22 July 2019).
- Soil Survey|NRCS Soils. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/main/soils/survey/ (accessed on 22 October 2018).
- Peters, J.C.; Easton, D.J. Runoff simulation using radar rainfall data1. JAWRA J. Am. Water Resour. Assoc. 1996, 32, 753–760. [Google Scholar] [CrossRef]
- Kull Daniel, W.; Feldman Arlen, D. Evolution of clark’s unit graph method to spatially distributed runoff. J. Hydrol. Eng. 1998, 3, 9–19. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Save the Blue River. Available online: https://www.joinrenewtheblue.org (accessed on 31 July 2020).
- Ji, W.; Xu, X.; Murambadoro, D. Understanding urban wetland dynamics: Cross-scale detection and analysis of remote sensing. Int. J. Remote Sens. 2015, 36, 1763–1788. [Google Scholar] [CrossRef]
- Day, T.J. Observed mixing lengths in mountain streams. J. Hydrol. 1977, 35, 125–136. [Google Scholar] [CrossRef]
- Callow, J.N.; Van Niel, K.P.; Boggs, G.S. How does modifying a DEM to reflect known hydrology affect subsequent terrain analysis? J. Hydrol. 2007, 332, 30–39. [Google Scholar] [CrossRef]
- Yang, P.; Ames, D.P.; Fonseca, A.; Anderson, D.; Shrestha, R.; Glenn, N.F.; Cao, Y. What is the effect of LiDAR-derived DEM resolution on large-scale watershed model results? Environ. Model. Softw. 2014, 58, 48–57. [Google Scholar] [CrossRef]
- Charrier, R.; Li, Y. Assessing resolution and source effects of digital elevation models on automated floodplain delineation: A case study from the camp creek watershed, missouri. Appl. Geogr. 2012, 34, 38–46. [Google Scholar] [CrossRef]
- Fekete, B.M.; Vörösmarty, C.J.; Lammers, R.B. Scaling gridded river networks for macroscale hydrology: Development, analysis, and control of error. Water Resour. Res. 2001, 37, 1955–1967. [Google Scholar] [CrossRef]
- Xie, H.; Zhou, X.; Vivoni, E.R.; Hendrickx, J.M.H.; Small, E.E. GIS-based NEXRAD stage III precipitation database: Automated approaches for data processing and visualization. Comput. Geosci. 2005, 31, 65–76. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H.; Sharif, H.; Zeitler, J. Validating NEXRAD MPE and stage III precipitation products for uniform rainfall on the upper guadalupe river basin of the texas hill country. J. Hydrol. 2008, 348, 73–86. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).