Incorporating Uncertainty of the System Behavior in Flood Risk Assessment—Sava River Case Study
Abstract
1. Introduction
2. Materials and Methods
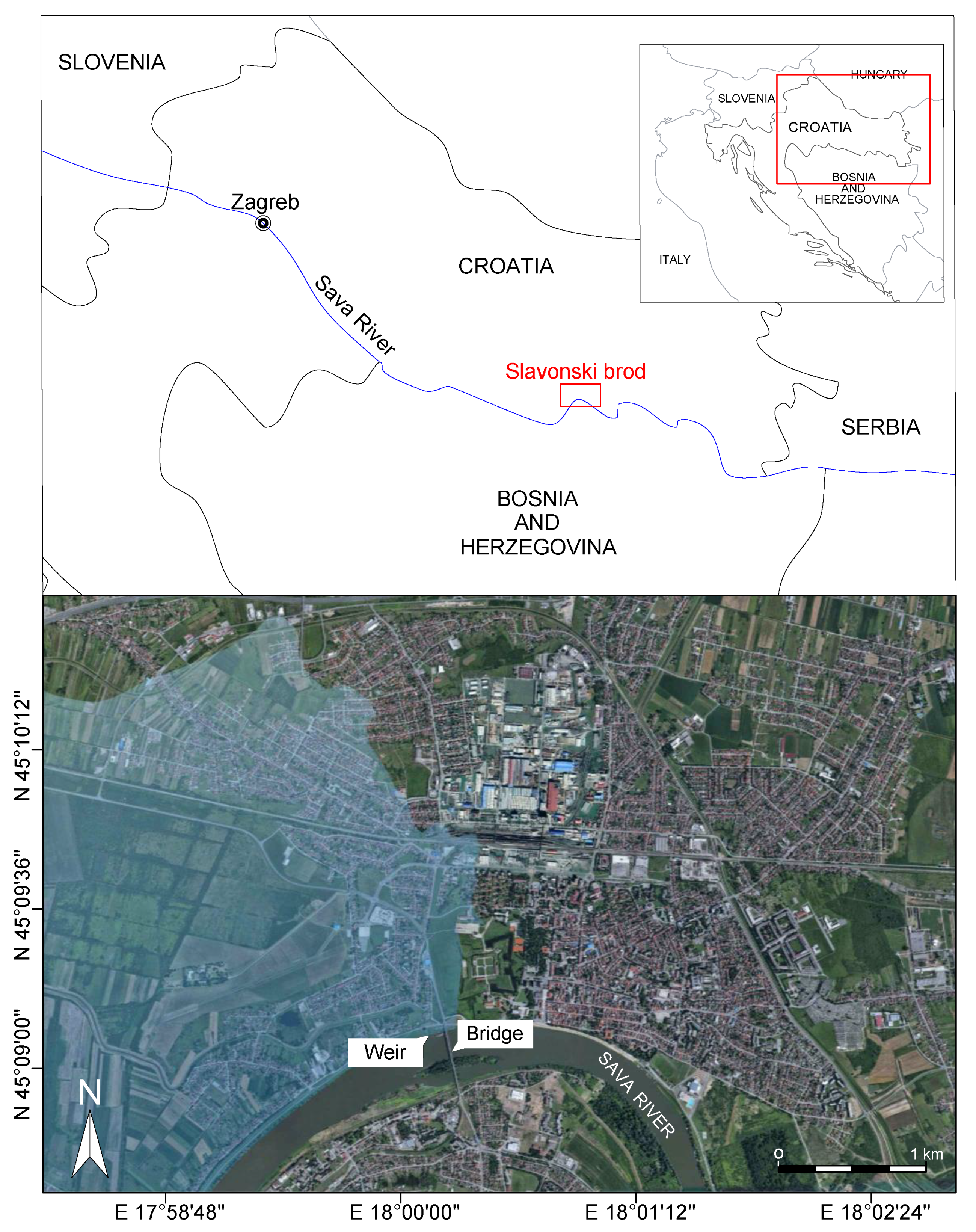
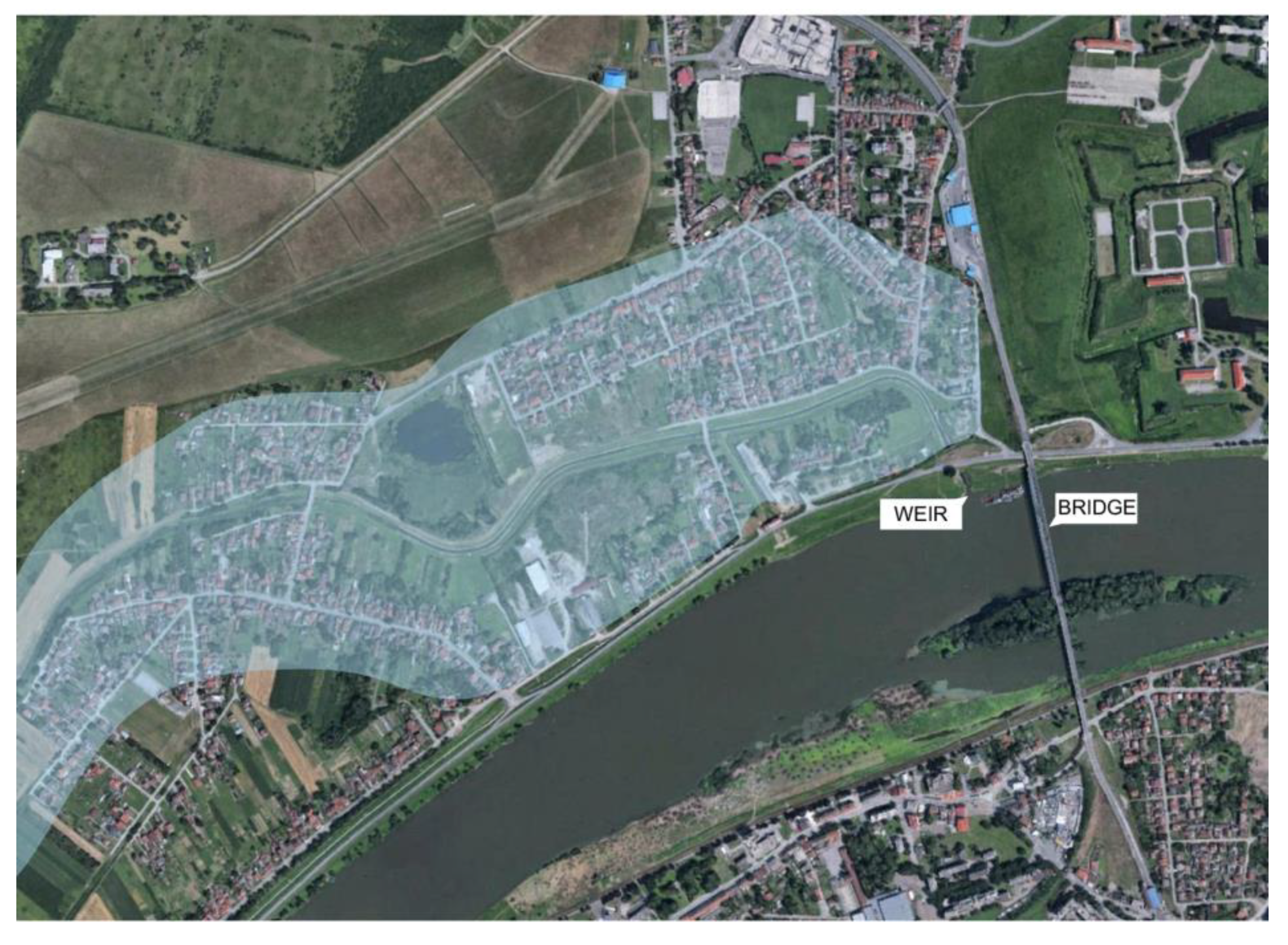
2.1. Case Study Area
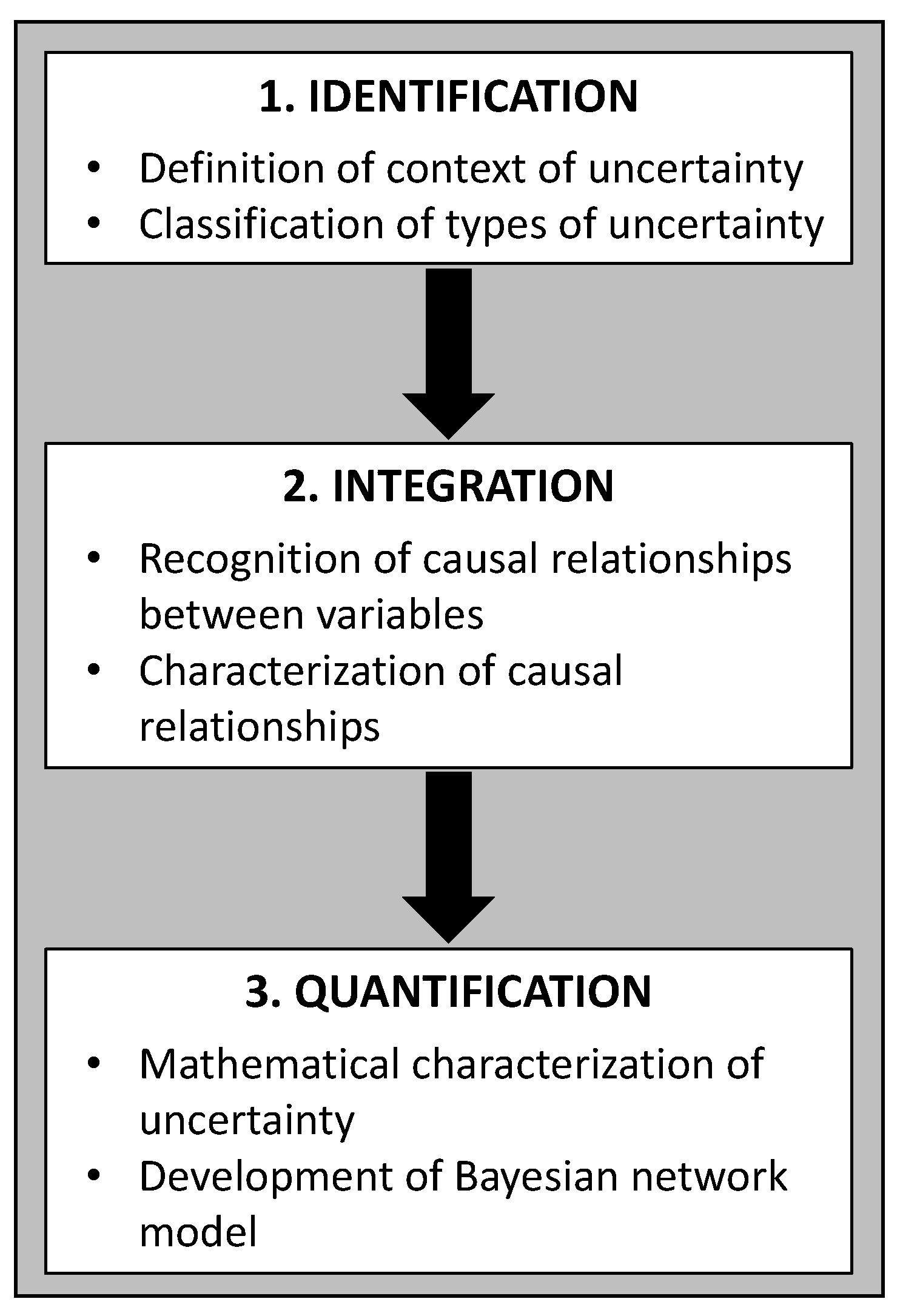
2.2. Framework for Uncertainty Analysis
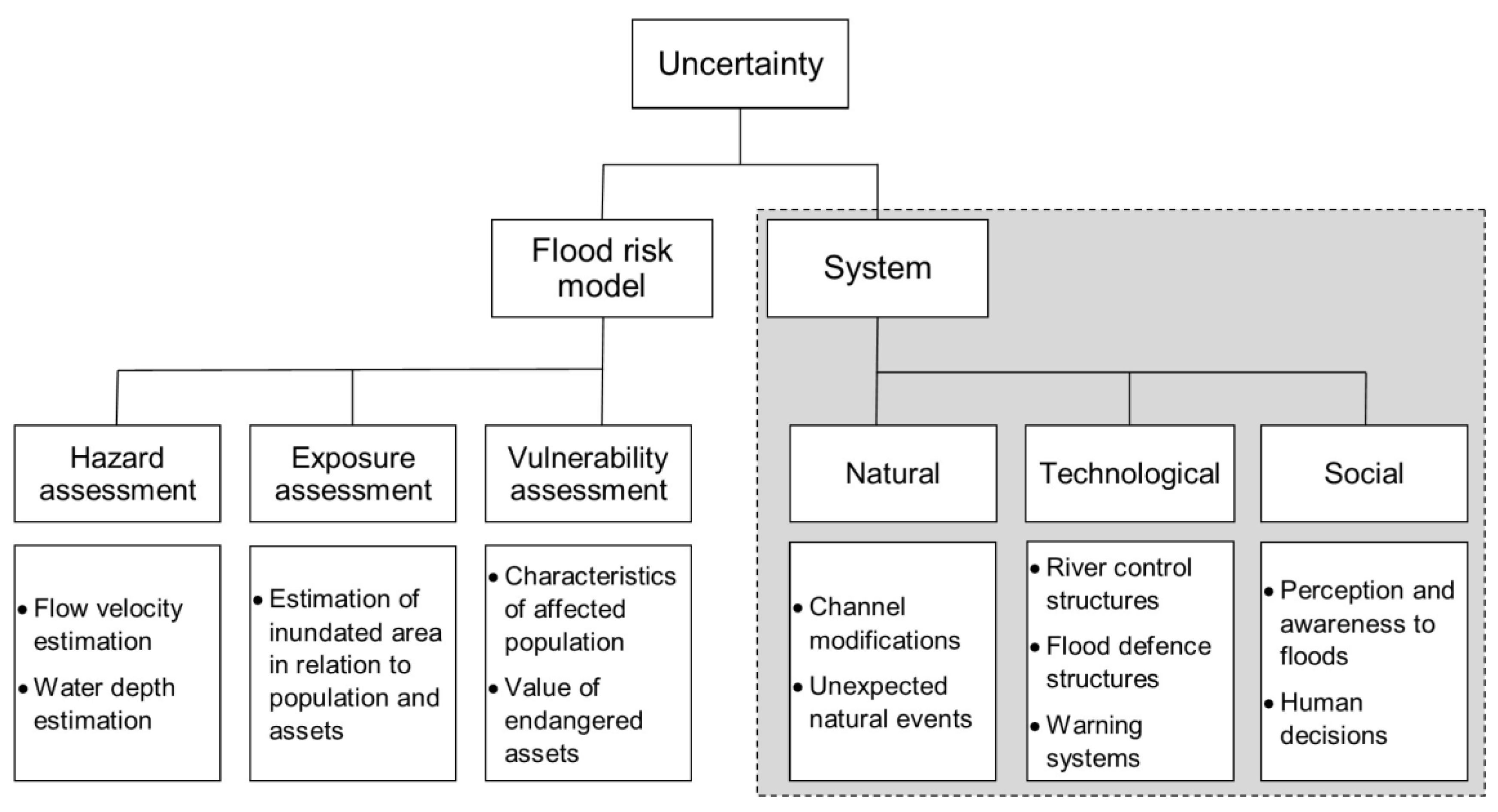
2.2.1. Identification of Uncertainty
2.2.2. Integration of the Identified Sources of Uncertainty
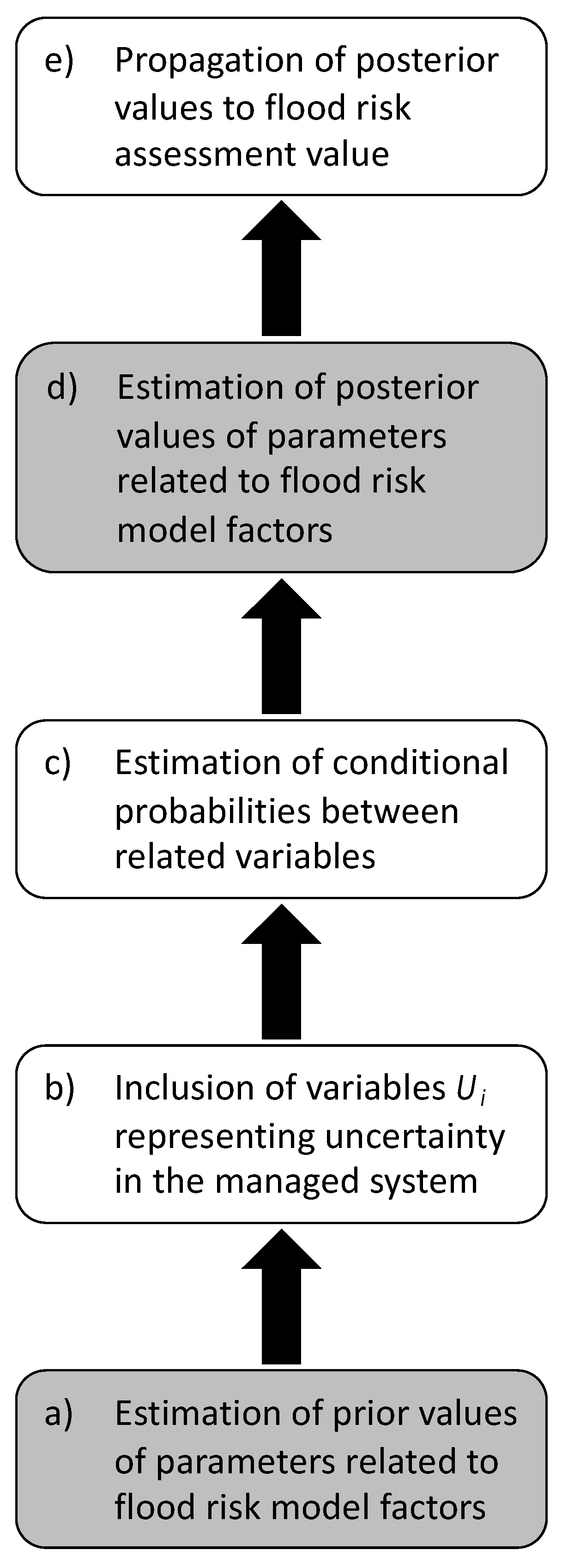
2.2.3. Quantification of Uncertainty
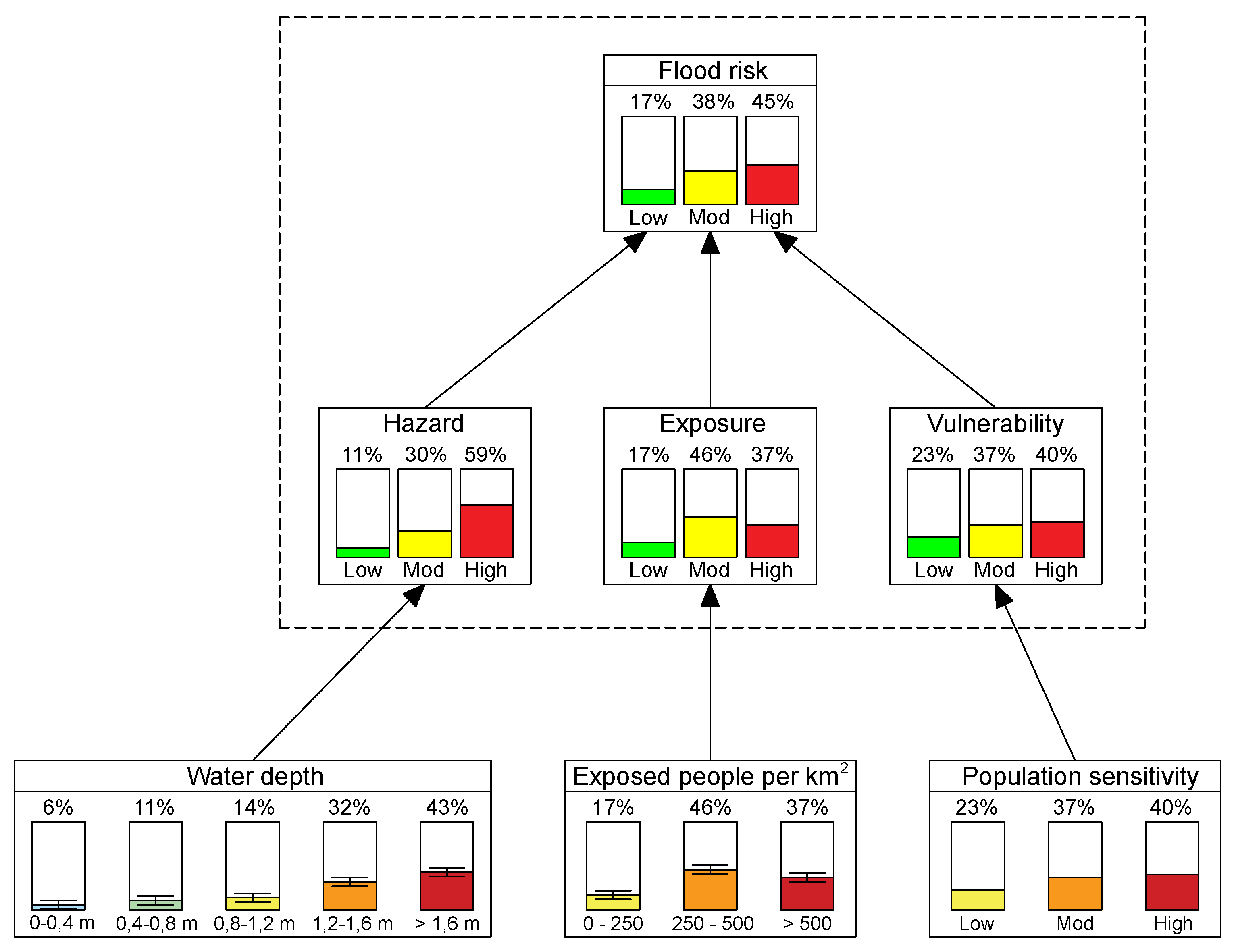
- (a)
- In the first step the prior values of parameters that are related to flood risk model factors (dark grey, fixed variables in Figure 6) are estimated for a chosen flood event. This is performed by using the results of flood models, available data, and/or expert judgement;
- (b)
- In the second step, the set of variables marked as U1 … Ui in Figure 5 is included, representing sources of uncertainty in the managed system. This considers assigning the appropriate mathematical function to each variable, based on the experts’ judgements, modelling results, and/or historical data and events;
- (c)
- The following step considers estimation of conditional probabilities between variables Ui and parameters related to flood risk model factors (marked dark grey in Figure 5);
- (d)
- Once the conditional probabilities are estimated, the further step is estimation of the posterior values of parameters related to flood risk model factors, quantifying the impact of variables Ui on these particular parameters;
- (e)
- In the final step, the posterior results from the previous step are propagated to flood risk factors (dark grey variables in Figure 5), obtaining the flood risk value and completing the analysis.
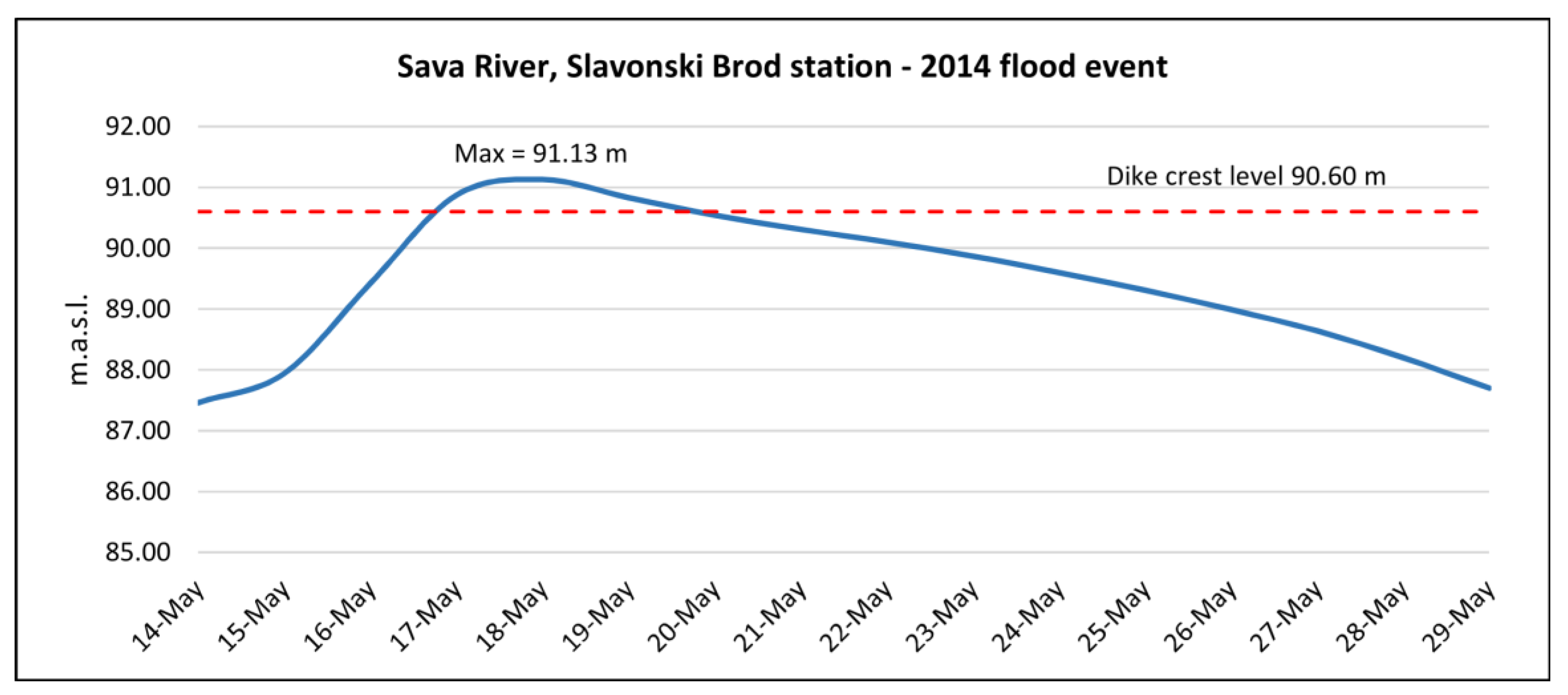
3. Framework Validation and Results
3.1. Identification of Sources of Uncertainty for the Slavonski Brod Area
3.2. Integration of the Identified Sources of Uncertainty
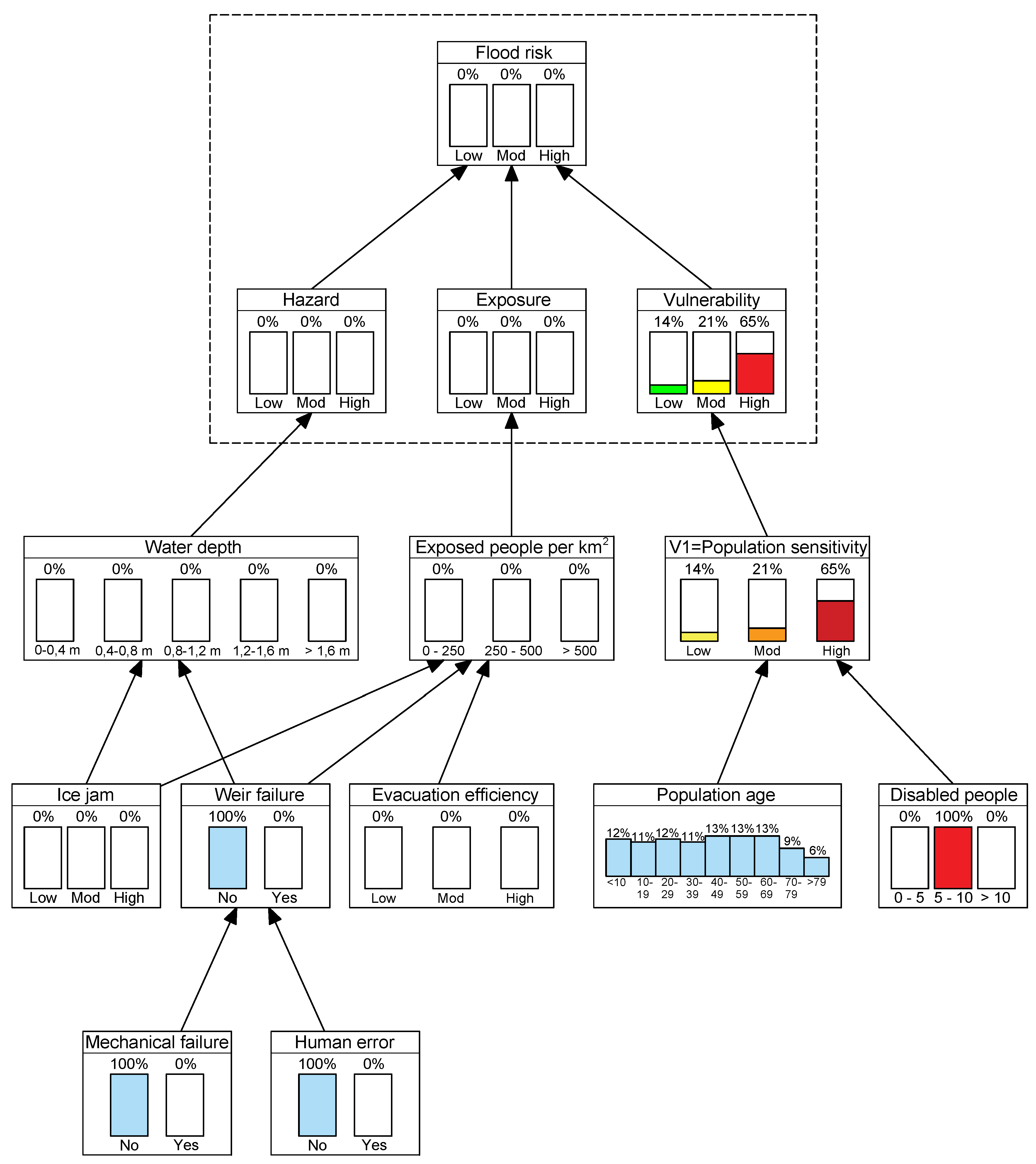
3.3. Quantification of Uncertainty in the Flood Risk Assessment for the Slavonski Brod Area
4. Discussion
5. Concluding Remarks
- The proposed approach for the Sava River case study in Croatia shows that additional sources of uncertainty representing the system behavior could appear in the managed area for future flood events.
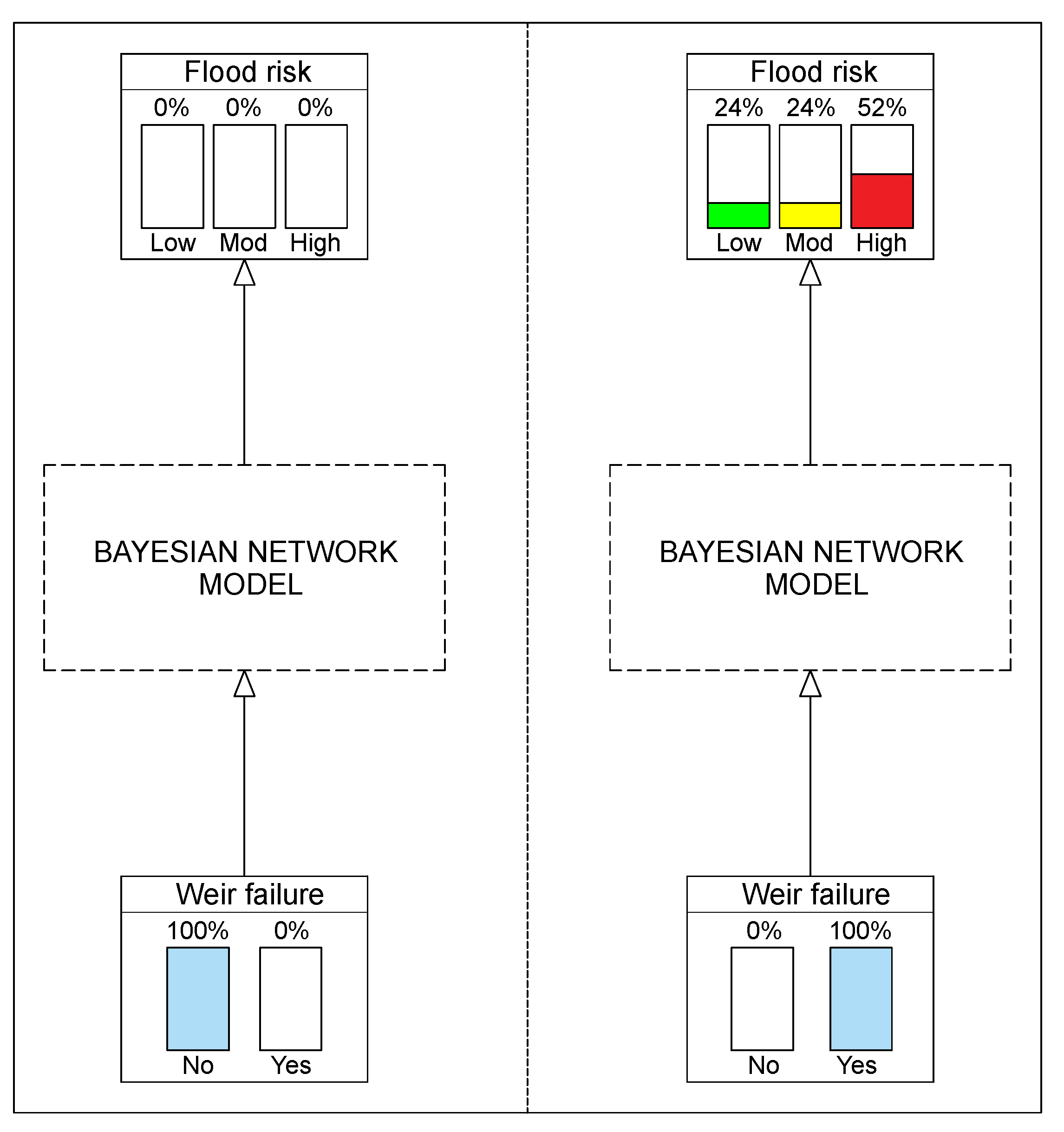
- Considering the scenario of infrastructure failure of the present weir alone, the Sava river would flood approximately 1 km2 of the safe area, resulting in 52% of high risk, 24% of moderate risk, and 24% of low risk on the flooded area.
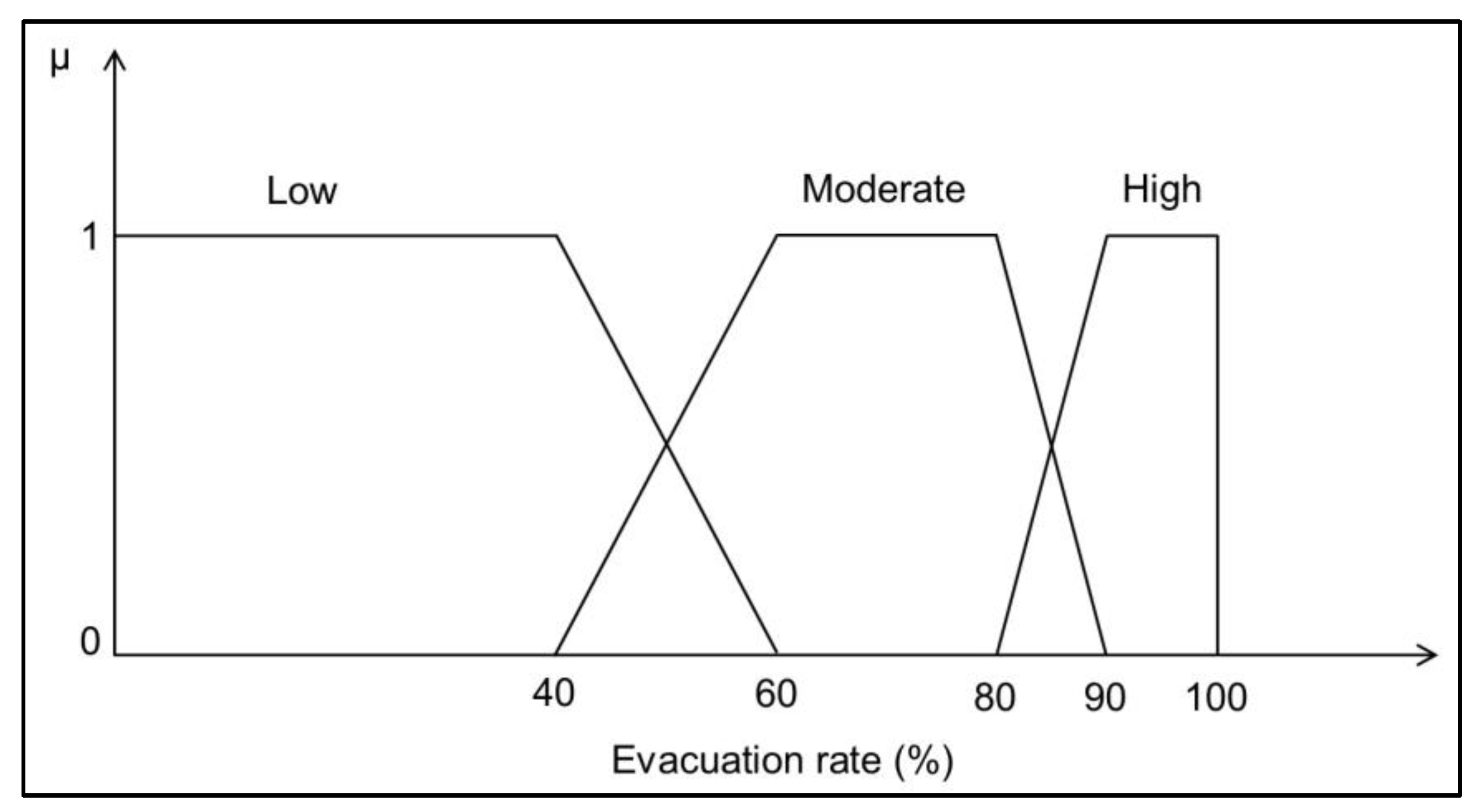
- By combining the evacuation efficiency, as a nonstructural measure, with the weir failure event, the results indicate that for an estimated evacuation rate of 82%, the flood risk is shifted towards the low risk stage, decreasing the high flood risk value from 52% to 24%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pistrika, A.; Tsakiris, G. Flood risk assessment: A methodological framework. In Proceedings of the EWRA Symposium “Water Resources Management: New Approaches and Technologies”, Chania, Greece, 13–22 June 2007. [Google Scholar]
- Jonkman, S.N.; Vrijling, J.K.; Vrouwenvelder, A.C.W.M. Methods for the estimation of loss of life due to floods: A literature review and a proposal for a new method. Nat. Hazards 2008, 46, 353–389. [Google Scholar] [CrossRef]
- Merz, B.; Hall, J.; Disse, M.; Schumann, A. Fluvial flood risk management in a changing world. Nat. Hazards Earth Syst. Sci. 2010, 10, 509–527. [Google Scholar] [CrossRef]
- Hutter, G.; Schanze, J. Learning how to deal with uncertainty of flood risk in long-term planning. Int. J. River Basin Manag. 2008, 6, 175–184. [Google Scholar] [CrossRef]
- Neuhold, C.; Stanzel, P.; Nachtnebel, H.P. Incorporating river morphological changes to flood risk assessment: Uncertainties, methodology and application. Nat. Hazards Earth Syst. Sci. 2009, 9, 789–799. [Google Scholar] [CrossRef]
- De Moel, H.; Aerts, J.C.J.H. Effect of uncertainty in land use, damage models and inundation depth on flood damage estimates. Nat. Hazards 2011, 58, 407–425. [Google Scholar] [CrossRef]
- Beven, K.; Lamb, R.; Leedal, D.; Hunter, N. Communicating uncertainty in flood inundation mapping: A case study. Int. J. River Basin Manag. 2015, 13, 285–295. [Google Scholar] [CrossRef]
- Wagenaar, D.J.; de Bruijn, K.M.; Bouwer, L.M.; de Moel, H. Uncertainty in flood damage estimates and its potential effect on investment decisions. Nat. Hazards Earth Syst. Sci. 2016, 16, 1–14. [Google Scholar] [CrossRef]
- Apel, H.; Thieken, A.H.; Merz, B.; Blöschl, G. Flood risk assessment and associated uncertainty. Nat. Hazards Earth Syst. Sci. 2004, 4, 295–308. [Google Scholar] [CrossRef]
- Apel, H.; Merz, B.; Thieken, A.H. Quantification of uncertainties in flood risk assessments. Int. J. River Basin Manag. 2008, 6, 149–162. [Google Scholar] [CrossRef]
- Van Der Most, H.; Wehrung, M. Dealing with uncertainty in flood risk assessment of dike rings in The Netherlands. Nat. Hazards 2005, 36, 191–206. [Google Scholar] [CrossRef]
- Hall, J.W.; Meadowcroft, I.C.; Sayers, P.B.; Bramley, M.E. Integrated flood risk management in England and Wales. Nat. Hazards Rev. 2003, 4, 3. [Google Scholar] [CrossRef]
- Merz, B.; Vorogushyn, S.; Lall, U.; Viglione, A.; Blöschl, G. Charting unknown waters—On the role of surprise in flood risk assessment and management. Water Resour. Res. 2015, 51, 6399–6416. [Google Scholar] [CrossRef]
- Plate, E.J. Flood risk and flood management. J. Hydrol. 2002, 267, 2–11. [Google Scholar] [CrossRef]
- Wood, E. An analysis of flood levee reliability. Water Resour. Res. 1977, 13, 665–671. [Google Scholar] [CrossRef]
- Jonkman, S.N.; Kok, M.; Vrijling, J.K. Flood risk assessment in The Netherlands: A case study for dike ring South Holland. Risk Anal. 2008, 28, 1357–1374. [Google Scholar] [CrossRef] [PubMed]
- Brilly, M.; Polic, M. Public perception of flood risks, flood forecasting and mitigation. Nat. Hazards Earth Syst. Sci. 2005, 5, 345–355. [Google Scholar] [CrossRef]
- Simonovic, S.P.; Ahmad, S. Computer-based Model for Flood Evacuation Emergency Planning. Nat. Hazards 2005, 34, 25–51. [Google Scholar] [CrossRef]
- Hall, J.W. Flood Risk Management: Decision Making Under Uncertainty. In Applied Uncertainty Analysis for Flood Risk Management; Beven, K., Hall, J., Eds.; Imperial College Press: London, UK, 2014; pp. 3–24. [Google Scholar]
- Merz, B. Flood Risk Analysis. Oxf. Res. Encycl. Nat. Hazard Sci. 2017. [Google Scholar] [CrossRef]
- Höllermann, B.; Evers, M. Perception and handling of uncertainties in water management—A study of practitioners’ and scientists’ perspectives on uncertainty in their daily decision-making. Environ. Sci. Policy 2017, 71, 9–18. [Google Scholar] [CrossRef]
- Kaplan, S.; Garrick, B.J. On the quantitative definition of risk. Risk Anal. 1981, 1, 11–27. [Google Scholar] [CrossRef]
- Van den Hoek, R.E.; Brugnach, M.; Mulder, J.P.M.; Hoekstra, A.Y. Analysing the cascades of uncertainty in flood defence projects: How ‘‘not knowing enough’’ is related to ‘‘knowing differently’’. Glob. Environ. Chang. 2014, 24, 373–388. [Google Scholar] [CrossRef]
- Spachinger, K.; Dorner, W.; Metzka, R.; Serrhini, K.; Fuchs, S. Flood Risk and Flood Hazard Maps—Visualisation of Hydrological Risks. IOP Conference Series: Earth and Environmental Science, Volume 4. In Proceedings of the 24th Conference of the Danubian Countries on the Hydrological Forecasting and Hydrological Bases of Water Management, Bled, Slovenia, 2–4 June 2008; IOP Conference Series: Earth and Environmental Science. IOP Publishing Ltd.: Bristol, UK, 2008; Volume 4. [Google Scholar] [CrossRef]
- Preliminary Flood Risk Assessment in the Sava River Basin, International Sava River Basin Commission. 2014. Available online: http://www.savacommission.org/dms/docs/dokumenti/documents_publications/publications/other_publications/pfra/preliminary_flood_risk_assessment_in_the_sava_river_basin_20140701.pdf (accessed on 17 June 2020).
- Committee on Decision Making Under Uncertainty, Board on Population Health and Public Health Practice, Institute of Medicine. Environmental Decisions in the Face of Uncertainty; The National Academies Press: Washington, DC, USA, 2013; p. 130. [Google Scholar]
- Kolen, B.; Van Gelder, P.H.A.J.M. Risk-Based Decision-Making for Evacuation in Case of Imminent Threat of Flooding. Water 2018, 10, 1429. [Google Scholar] [CrossRef]
- Faulkner, H.; Parker, D.; Green, C.; Beven, K. Developing a Translational Discourse to Communicate Uncertainty in Flood Risk between Science and the Practitioner. AMBIO 2007, 36, 692–703. [Google Scholar] [CrossRef]
- Hall, J.; Solomatine, D. A framework for uncertainty analysis in flood risk management decisions. Int. J. River Basin Manag. 2008, 6, 85–98. [Google Scholar] [CrossRef]
- Molinari, D.; Ballio, F.; Menoni, S. Modelling the benefits of flood emergency management measures in reducing damages: A case study on Sondrio, Italy. Nat. Hazards Earth Syst. Sci. 2013, 13, 1913–1927. [Google Scholar] [CrossRef]
- Chang, M.; Tseng, Y.; Chen, J. A scenario planning approach for the flood emergency logistics preparation problem under uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 737–754. [Google Scholar] [CrossRef]
- Morss, R.E.; Wilhelmi, O.V.; Downton, M.W.; Gruntfest, E. Flood risk, uncertainty, and scientific information for decision making: Lessons from an Interdisciplinary Project. Bull. Am. Meteorol. Soc. 2005, 86, 1593–1602. [Google Scholar] [CrossRef]
- Floods in May 2014 in the Sava River Basin, Brief Overview of Key Events and Lessons Learned, International Sava River Basin Commission. 2015. Available online: http://www.savacommission.org/dms/docs/dokumenti/documents_publications/publications/other_publications/sava_floods_report.pdf (accessed on 18 June 2020).
- Funtowicz, S.O.; Ravetz, J.R. Science for the Post-Normal Age. Futures 1993, 25, 739–755. [Google Scholar] [CrossRef]
- Ling, C.W. Characterising Uncertainty: A Taxonomy and an Analysis of Extreme Events. Master’s Thesis, School of Engineering and Applied Science, University of Virginia, Charlottesville, VA, USA, 1993. [Google Scholar]
- Simonović, S.P. Risk in sustainable water resources management. In Sustainability of Water Resources under Increasing Uncertainties, Proceedings of Rabat Symposium S1; IAHS Publications: Rabat, Morocco, 1997; Volume 240, pp. 3–17. [Google Scholar]
- Simonović, S.P. Systems Approach to Management of Disasters, Methods and Applications; Wiley: Hoboken, NJ, USA, 2011; pp. 98–100. [Google Scholar]
- Walker, W.E.; Harremoes, P.; Rotmans, J.; van der Sluijs, J.P.; van Asselt, M.B.A.; Janssen, P.; Krayer von Krauss, M.P. Defining Uncertainty A Conceptual Basis for Uncertainty Management in Model-Based Decision Support. Integr. Assess. 2003, 4, 5–17. [Google Scholar] [CrossRef]
- Van Asselt, M.B.A. Perspectives on Uncertainty and Risk: The PRIMA Approach to Decision Support; Springer: New York, NY, USA, 2000; pp. 85–88. [Google Scholar]
- Brugnach, M.; Dewulf, A.; Pahl-Wostl, C.; Taillieu, T. Towards a relational concept of uncertainty: About knowing too little, knowing too differently, and accepting not to know. Ecol. Soc. 2008, 13, 30. [Google Scholar] [CrossRef]
- Baecher, G.B.; Christian, J.T. Natural Variation, Limited Knowledge, and the Nature of Uncertainty in Risk Analysis. In Proceedings of the Risk-Based Decision making in Water Resources IX, Santa Barbara, CA, USA, 15–20 October 2000. [Google Scholar]
- Kron, W. Flood Risk = Hazard × Exposure × Vulnerability. In Proceedings of the 2nd International Conference on Flood Defence, Beijing, China, 10–13 September 2002; Wu, B.S., Wang, Z.Y., Wang, G.Q., Huang, G.H., Fang, H.W., Huang, J.C., Eds.; Science Press: New York, NY, USA, 2002; pp. 82–97. [Google Scholar]
- Kron, W. Flood Risk = Hazard • Values • Vulnerability. Water Int. 2005, 30, 58–68. [Google Scholar] [CrossRef]
- 2009 UNISDR Terminology on Disaster Risk Reduction, International Strategy for Disaster Risk Reduction, United Nations. Available online: https://www.preventionweb.net/files/7817_UNISDRTerminologyEnglish.pdf (accessed on 22 February 2020).
- Brugnach, M.; Dewulf, A.; Pahl-Wostl, C.; Taillieu, T. Towards a relational concept of uncertainty: Incorporating the human dimension. In Proceedings of the International Conference in Adaptive and Integrated Water Management, Basel, Switzerland, 12–15 November 2007; pp. 1–25. [Google Scholar]
- Ren, C.; Yang, C.; Jin, S. Agent-Based Modeling and Simulation on Emergency Evacuation. In Complex Sciences. Complex 2009. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Zhou, J., Ed.; Springer: Berlin/Heidelberg, Germany; Volume 5. [CrossRef]
- Merz, B.; Thieken, A.H. Flood risk analysis: Concepts and challenges. Osterr. Wasser Abfallwirtsch. 2004, 56, 27–34. [Google Scholar]
- Rinderknecht, S.L.; Borsuk, M.E.; Reichert, P. Bridging uncertain and ambiguous knowledge with imprecise probabilities. Environ. Model. Softw. 2012, 36, 122–130. [Google Scholar] [CrossRef]
- Akter, T.; Simonović, S.P. Aggregation of fuzzy views of a large number of stakeholders for multi-objective flood management decision-making. J. Environ. Manag. 2005, 77, 133–143. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Kraft, D.H.; Pasi, G.; Bordogna, G. Vagueness and uncertainty in information retrieval: How can fuzzy sets help. In Proceedings of the 2006 International Workshop on Research Issues in Digital Libraries (IWRIDL’06), Kolkata, India, 12–15 December 2006; Association for Computing Machinery: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Arunraj, N.S.; Mandal, S.; Maiti, J. Modeling uncertainty in risk assessment: An integrated approach with fuzzy set theory and Monte Carlo simulation. Accid. Anal. Prev. 2013, 55, 242–255. [Google Scholar] [CrossRef]
- Li, Q. Fuzzy approach to analysis of flood risk based on variable fuzzy sets and improved information diffusion methods. Nat. Hazards Earth Syst. Sci. 2013, 13, 239–249. [Google Scholar] [CrossRef]
- Quevedo, J.R.N. Fuzzy sets. A way to represent ambiguity and subjectivity. Boletín Matemáticas 2017, 24, 57–88. [Google Scholar]
- Humphreys, M.; Jacobs, A. Mixing Methods: A Bayesian Approach. Am. Political Sci. Rev. 2015, 109, 653–673. [Google Scholar] [CrossRef]
- Balbi, S.; Villa, F.; Mojtahed, V.; Hegetschweiler, K.T.; Giupponi, C. A spatial Bayesian network model to assess the benefits of early warning for urban flood risk to people. Nat. Hazards Earth Syst. Sci. 2016, 16, 1323–1337. [Google Scholar] [CrossRef]
- Barton, D.N.; Saloranta, T.; Moe, S.J.; Eggestad, H.O.; Kuikka, S. Bayesian belief networks as a meta-modelling tool in integrated river basin management—Pros and cons in evaluating nutrient abatement decisions under uncertainty in a Norwegian river basin. Ecol. Econ. 2008, 66, 91–104. [Google Scholar] [CrossRef]
- Straub, D. Natural hazards risk assessment using Bayesian networks. In Proceedings of the Ninth International Conference on Structural Safety and Reliability, Rome, Italy, 19–23 June 2005. [Google Scholar]
- Vogel, K.; Riggelsen, C.; Korup, O.; Scherbaum, F. Bayesian network learning for natural hazard analyses. Nat. Hazards Earth Syst. Sci. 2014, 14, 2605–2626. [Google Scholar] [CrossRef]
- Wu, J.; Fang, W.; Hu, Z.; Hong, B. Application of Bayesian Approach to Dynamic Assessment of Flood in Urban Underground Spaces. Water 2018, 10, 1112–1132. [Google Scholar] [CrossRef]
- Kandel, A. Fuzzy Mathematical Techniques with Applications; Addison-Wesley Publishing Company: Reading, MA, USA, 1986; pp. 72–84. [Google Scholar]
- Maskey, S. Modelling Uncertainty in Flood Forecasting Systems. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 24 May 2004. [Google Scholar]
- Čavlović, Z. Obrana od leda na Savi. Hrvat. Vodoprivr. 2012, 198, 54–55. (In Croatian) [Google Scholar]
- Spatial Plans of the City of Slavonski Brod Area. Available online: https://www.slavonski-brod.hr/index.php/vazeci-prostorni-planovi (accessed on 22 April 2020).
- Croatian Bureau of Statistics. Available online: https://www.dzs.hr/default_e.htm (accessed on 14 April 2020).
- Kolen, B.; Helsloot, I. Decision-making and evacuation planning for flood risk management in The Netherlands. Disasters 2014, 38, 610–635. [Google Scholar] [CrossRef]
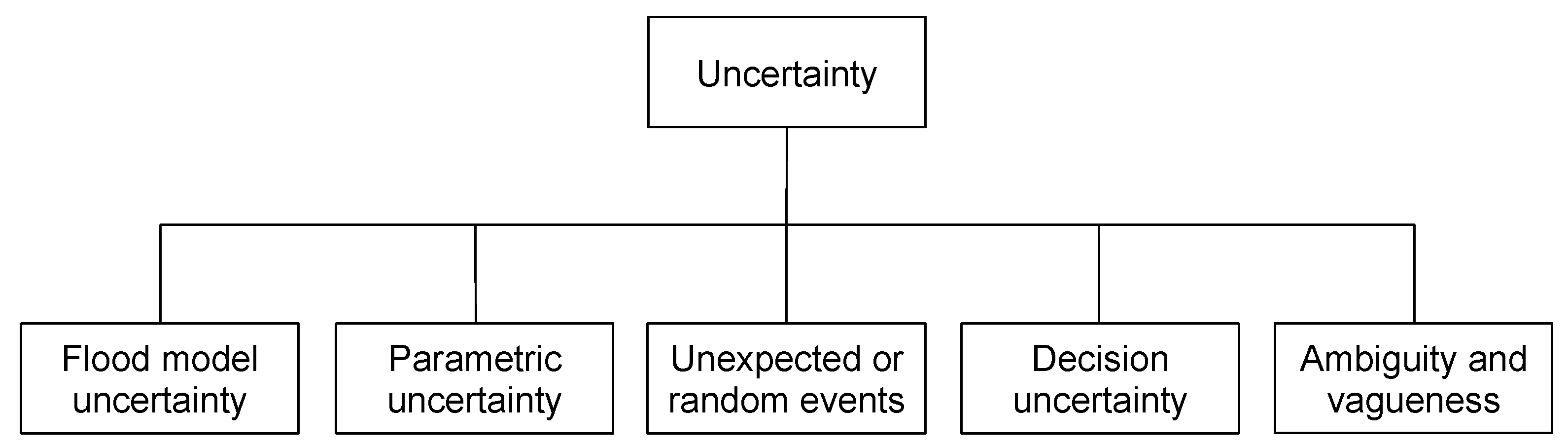


| Funtowicz and Ravetz [34] | Ling [35], Simonovic [36,37] | Walker et al. [38] | Van Asselt [39], Brugnach et al. [40] | Baecher and Christian [41] |
|---|---|---|---|---|
| Inexactness, unreliability, and border with ignorance | Variability and ambiguity | Location, level, and nature of uncertainty | Incomplete knowledge, unpredictability, ambiguity | Inherent randomness, incomplete knowledge |
| Flood Model Uncertainty | Parametric Uncertainty | Unexpected or Random Events | Decision Uncertainty | Ambiguity and Vagueness |
|---|---|---|---|---|
| Sensitivity analysis | Probability distribution | Boolean variable, probability distribution | Boolean variable, probability distribution | Fuzzy set theory |
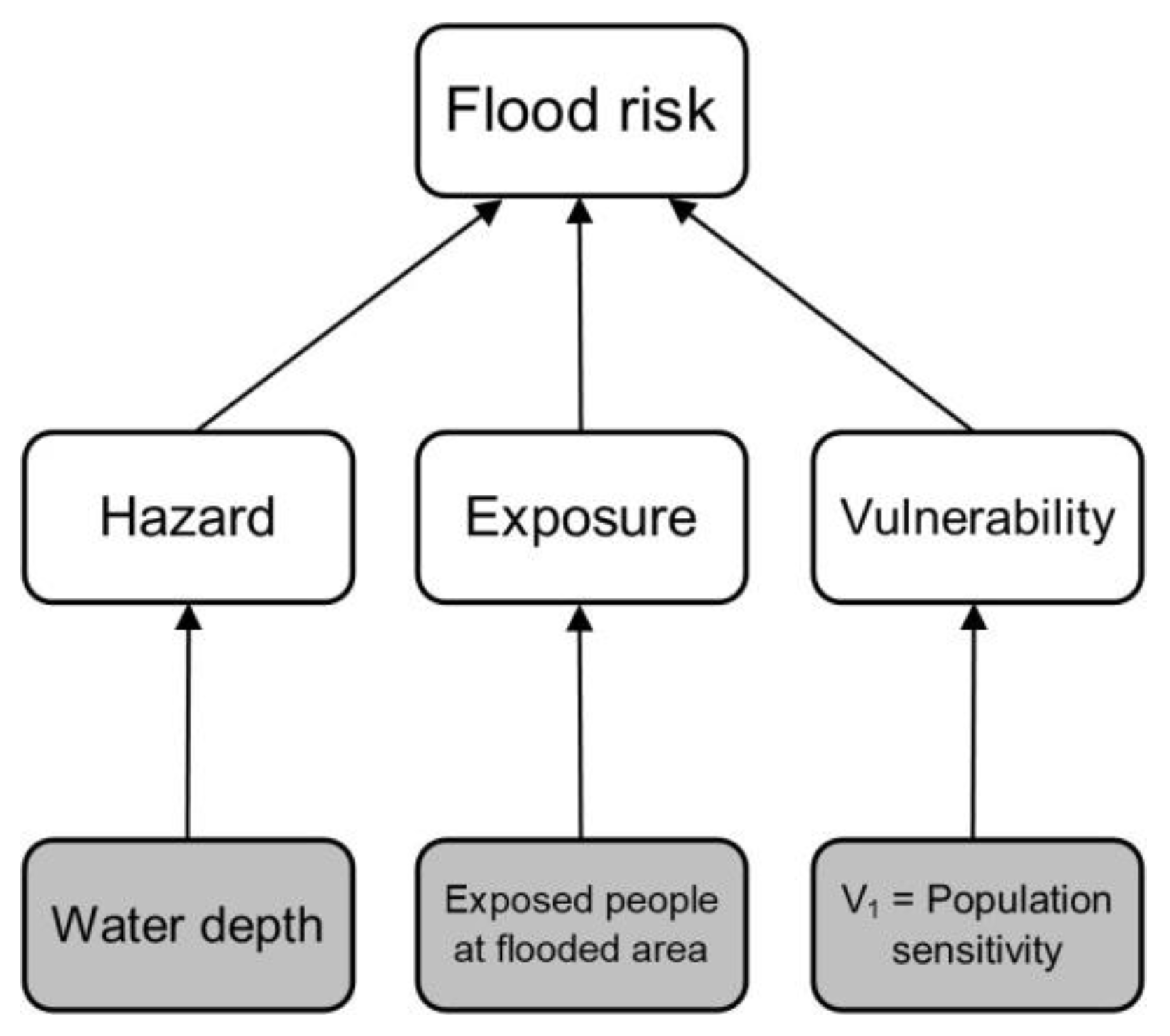
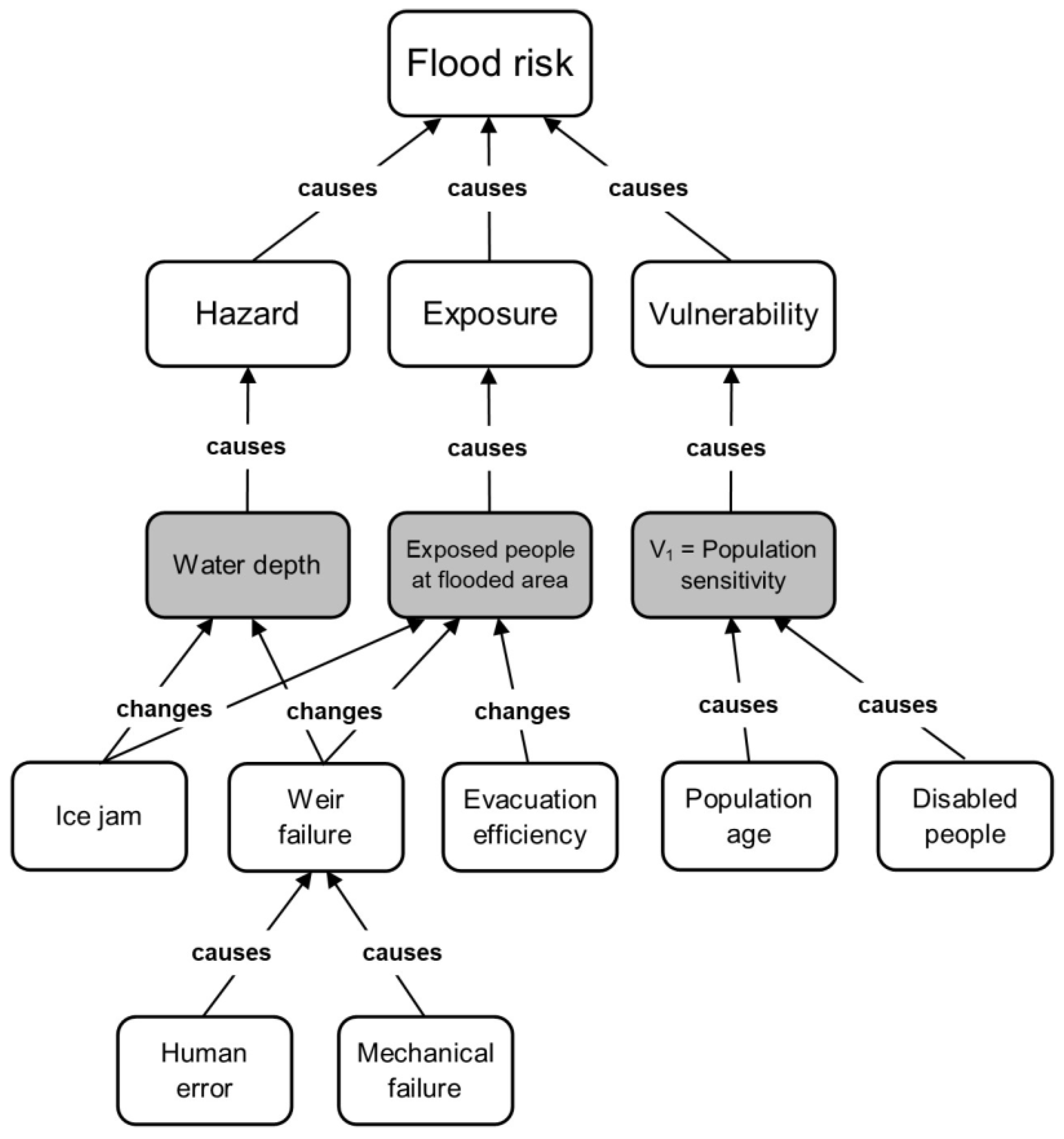
| Sources of Uncertainty | Context | Type | |
|---|---|---|---|
| Flood risk model | Water depth distribution Estimation of water depth distribution over an inundated area. | Hazard assessment | Flood model |
| Number of people exposed to flooding Estimation of flood extent proportions in relation to population density on an inundated area. | Exposure assessment | Flood model/parametric | |
| Population sensitivity to floods Assessment of exposed population sensitivity in respect to population age and number of disabled people. | Vulnerability assessment | Parametric | |
| System | Ice jam Appearance of ice on the river surface jamming on the bridge pillars. | Natural | Unexpected or random event |
| Weir failure Possibility of weir closure failure due to mechanical error on the operating mechanism, or due to human operating error. | Technological/social | Unexpected or random event/decision uncertainty | |
| Evacuation efficiency Rate of evacuation of people from endangered area before the incoming flood. | Social | Decision uncertainty/ambiguity | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kekez, T.; Knezić, S.; Andričević, R. Incorporating Uncertainty of the System Behavior in Flood Risk Assessment—Sava River Case Study. Water 2020, 12, 2676. https://doi.org/10.3390/w12102676
Kekez T, Knezić S, Andričević R. Incorporating Uncertainty of the System Behavior in Flood Risk Assessment—Sava River Case Study. Water. 2020; 12(10):2676. https://doi.org/10.3390/w12102676
Chicago/Turabian StyleKekez, Toni, Snježana Knezić, and Roko Andričević. 2020. "Incorporating Uncertainty of the System Behavior in Flood Risk Assessment—Sava River Case Study" Water 12, no. 10: 2676. https://doi.org/10.3390/w12102676
APA StyleKekez, T., Knezić, S., & Andričević, R. (2020). Incorporating Uncertainty of the System Behavior in Flood Risk Assessment—Sava River Case Study. Water, 12(10), 2676. https://doi.org/10.3390/w12102676






