Modeled Land Atmosphere Coupling Response to Soil Moisture Changes with Different Generations of Land Surface Models
Abstract
1. Introduction
2. Model Description
2.1. The Modular Platform TerrSysMP
2.2. The COSMO Weather Prediction Model
2.3. TERRA-ML
2.4. CLM
3. Experiment Setup
3.1. Idealized Simulations
3.2. Soil-Vegetation Structure
3.3. Initial Conditions
4. Results
4.1. Soil Moisture Response to Initial Soil Moisture
4.2. Overall Model State Response to Initial Soil Moisture
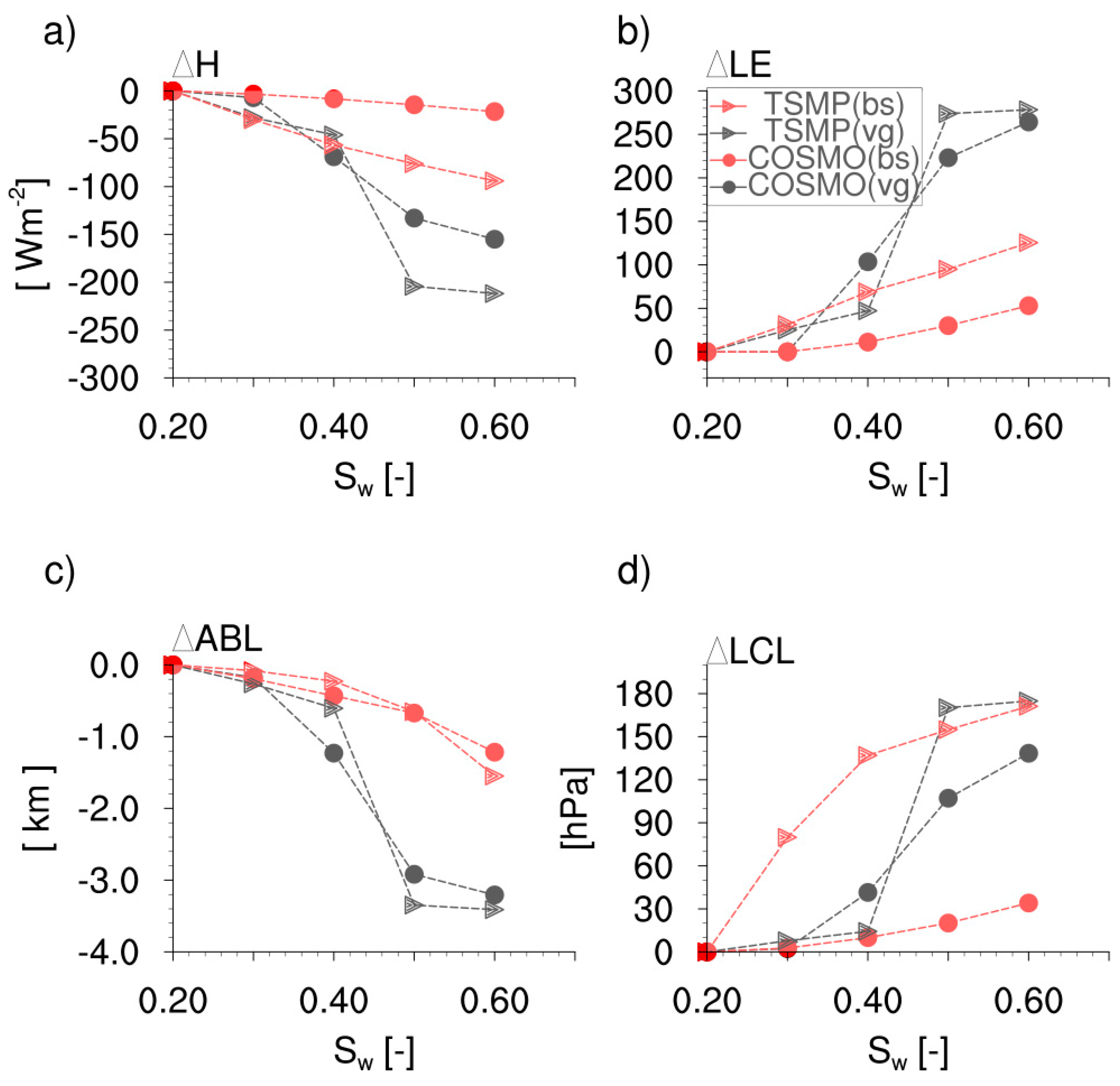
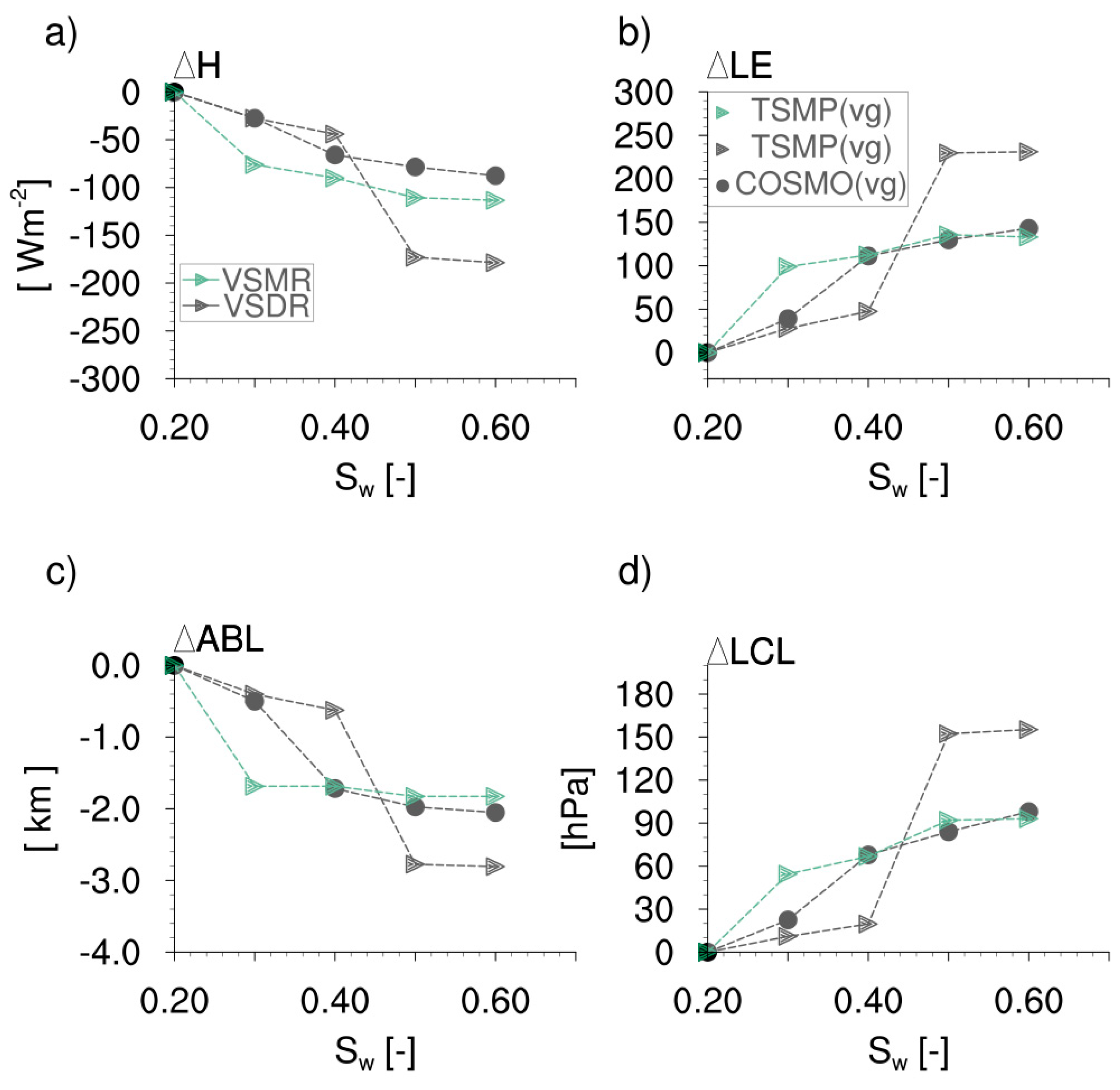
4.2.1. Surface Fluxes
4.2.2. ABL Quantities
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Seuffert, G.; Gross, P.; Simmer, C.; Wood, E.F. The influence of hydrologic modeling on the predicted local weather: Two-way coupling of a mesoscale weather prediction model and a land surface hydrologic model. J. Hydrometeorol. 2002, 3, 505–523. [Google Scholar] [CrossRef]
- Jin, J.; Miller, N.L.; Schlegel, N. Sensitivity Study of Four Land Surface Schemes in the WRF Model. Adv. Meteorol. 2010, 2010, 167436. [Google Scholar] [CrossRef]
- Davin, E.L.; Stöckli, R.; Jaeger, E.B.; Levis, S.; Seneviratne, S.I. COSMO-CLM2: A new version of the COSMO-CLM model coupled to the Community Land Model. Clim. Dyn. 2011, 37, 1889–1907. [Google Scholar] [CrossRef]
- Chen, F.; Liu, C.; Dudhia, J.; Chen, M. A sensitivity study of high resolution regional climate simulations to three land surface models over the western United States. J. Geophys. Res. Atmos. 2014, 119, 7271–7291. [Google Scholar] [CrossRef]
- Santanello, J.A., Jr.; Peters-Lidard, C.D.; Kennedy, A.; Kumar, S.V. Diagnosing the nature of land–atmosphere coupling: A case study of dry/wet extremes in the US southern Great Plains. J. Hydrometeorol. 2013, 14, 3–24. [Google Scholar] [CrossRef]
- Shrestha, P.; Sulis, M.; Masbou, M.; Kollet, S.; Simmer, C. A scale-consistent Terrestrial System Modeling Platform based on COSMO, CLM and ParFlow. Mon. Weather Rev. 2014, 142, 3466–3483. [Google Scholar] [CrossRef]
- Keune, J.; Gasper, F.; Goergen, K.; Hense, A.; Shrestha, P.; Sulis, M.; Kollet, S. Studying the influence of groundwater representations on land surface-atmosphere feedbacks during the European heat wave in 2003. J. Geophys. Res. Atmos. 2016, 121, 13301–13325. [Google Scholar] [CrossRef]
- Sulis, M.; Keune, J.; Shrestha, P.; Simmer, C.; Kollet, S. Quantifying the impact of subsurface-land surface physical processes on the predictive skill of subseasonal mesoscale atmospheric simulations. J. Geophys. Res. Atmos. 2018, 123, 9131–9151. [Google Scholar] [CrossRef]
- Shrestha, P.; Kurtz, W.; Vogel, G.; Schulz, J.-P.; Sulis, M.; Hendricks Franssen, H.-J.; Kollet, S.; Simmer, C. Connection between root zone soil moisture and surface energy flux partitioning using modeling, observations, and data assimilation for a temperate grassland site in Germany. J. Geophys. Res. Biogeosci. 2018, 123, 2839–2862. [Google Scholar] [CrossRef]
- Grasselt, R.; Schüttemeyer, D.; Warrach-Sagi, K.; Ament, F.; Simmer, C. Validation of TERRA-ML with discharge measurements. Meteorol. Z. 2008, 17, 763–773. [Google Scholar] [CrossRef]
- Doms, G.; Förstner, J.; Heise, E.; Herzog, H.-J.; Raschendorfer, M.; Reinhardt, T.; Ritter, B.; Schrodin, R.; Schulz, J.-P.; Vogel, G. A Description of the Nonhydrostatic Regional Model LM, Part II: Physical Parameterization. 2007. Available online: http://www.cosmo-model.org (accessed on 8 April 2015).
- Schulz, J.-P.; Vogel, G.; Becker, C.; Kothe, S.; Rummel, U.; Ahrens, B. Evaluation of the ground heat flux simulated by a multi-layer land surface scheme using high-quality observations at grass land and bare soil. Meteorol. Z. 2016, 25, 607–620. [Google Scholar] [CrossRef]
- Oleson, K.W.; Niu, G.Y.; Yang, Z.L.; Lawrence, D.M.; Thornton, P.E.; Lawrence, P.J.; Stockli, R.; Dickinson, R.E.; Bonan, G.B.; Levis, S.; et al. Improvements to the Community Land Model and their impact on the hydrological cycle. J. Geophys. Res. 2008, 113, 01021. [Google Scholar] [CrossRef]
- Baldauf, M.; Seifert, A.; Förstner, J.; Majewski, D.; Raschendorfer, M.; Reinhardt, T. Operational convective-scale numerical weather prediction with the COSMO model: Description and sensitivities. Mon. Weather Rev. 2011, 139, 3887–3905. [Google Scholar] [CrossRef]
- Valcke, S. The OASIS3 coupler: A European climate modelling community software. Geosci. Model Dev. 2013, 6, 373–388. [Google Scholar] [CrossRef]
- Valcke, S.; Craig, T.; Coquart, L. OASIS3-MCT User Guide, OASIS3-MCT 2.0. CERFACS/CNRS SUC URA NO. 1875. Available online: http://www.cerfacs.fr/oa4web/oasis3-mct/oasis3mct_UserGuide.pdf (accessed on 8 April 2015).
- Gasper, F.; Goergen, K.; Shrestha, P.; Sulis, M.; Rihani, J.; Geimer, M.; Kollet, S.J. Implementation and scaling of the fully coupled Terrestrial Systems Modeling Platform (TerrSysMP v1.0) in a massively parallel supercomputing environment—A case study on JUQUEEN (IBM Blue Gene/Q). Geosci. Model Dev. 2014, 7, 2531–2543. [Google Scholar] [CrossRef]
- Shrestha, P.; Sulis, M.; Simmer, C.; Kollet, S. Effects of horizontal grid resolution on evapotranspiration partitioning using TerrSysMP. J. Hydrol. 2018, 557, 910–915. [Google Scholar] [CrossRef]
- Poll, S.; Shrestha, P.; Simmer, C. Modelling convectively induced secondary circulations in the terra incognita with TerrSysMP. Q. J. R. Meteorol. Soc. 2017, 143, 2352–2361. [Google Scholar] [CrossRef][Green Version]
- Steppeler, J.; Doms, G.; Schättler, U.; Bitzer, H.W.; Gassmann, A.; Damrath, U.; Gregoric, G. Meso-gamma scale forecasts using the nonhydrostatic model LM. Meteorol. Atmos. Phys. 2003, 82, 75–96. [Google Scholar] [CrossRef]
- Doms, G.; Förstner, J.; Heise, E.; Herzog, H.-J.; Mironov, D.; Raschendorfer, M.; Reinhardt, T.; Ritter, B.; Schrodin, R.; Schulz, J.-P.; et al. A Description of the Nonhydrostatic Regional Model LM, Part II: Physical Parameterization. 2011. Available online: http://www.cosmo-model.org (accessed on 23 May 2016).
- Ritter, B.; Geleyn, J.F. A comprehensive radiation scheme for numerical weather prediction models with potential applications in climate simulations. Mon. Weather Rev. 1992, 120, 303–325. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Blackadar, A.K. The vertical distribution of wind and turbulent exchange in neutral atmosphere. J. Geophys. Res. 1962, 67, 3095–3102. [Google Scholar] [CrossRef]
- Raschendorfer, M. The new turbulence Parameterization of LM. COSMO Newslett. 2001, 1, 89–97. Available online: http://www.cosmo-model.org (accessed on 8 April 2015).
- Dickinson, R.E. Modeling evapotranspiration for three-dimensional global climate models. Clim. Process. Clim. Sensit. Geophys. Monogr. 1984, 29, 58–72. [Google Scholar]
- Jarvis, P.G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. B 1976, 273, 593–610. [Google Scholar] [CrossRef]
- Stewart, J.B. Modelling surface conductance of pine forest. Agric. For. Meteorol. 1988, 43, 19–35. [Google Scholar] [CrossRef]
- Sellers, P.J.; Berry, J.A.; Collatz, G.J.; Field, C.B.; Hall, F.G. Canopy reflectance, photosynthesis, and transpiration. III. A reanalysis using improved leaf models and a new canopy integration scheme. Remote Sens. Environ. 1992, 42, 187–216. [Google Scholar] [CrossRef]
- Collatz, G.; Ball, J.T.; Grivet, C.; Berry, J.A. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: A model that includes a laminar boundary layer. Agric. For. Meteorol. 1991, 54, 107–136. [Google Scholar] [CrossRef]
- Shrestha, P. TerrSysMP Pre-Processing and Post-Processing System. CRC/TR32 Database (TR32DB). Available online: https://www.tr32db.uni-koeln.de/data.php?dataID=1873 (accessed on 28 March 2019).
- John, J.A.; Draper, N.R. An alternative family of transformations. Appl. Stat. 1980, 29, 190–197. [Google Scholar] [CrossRef]
- Garratt, J.R. The atmospheric boundary layer. Earth-Sci. Rev. 1994, 37, 89–134. [Google Scholar] [CrossRef]
- Ma, M.; Pu, Z.; Wang, S.; Zhang, Q. Characteristics and numerical simulations of extremely large atmospheric boundary-layer heights over an arid region in north-west China. Bound.-Layer Meteorol. 2011, 140, 163–176. [Google Scholar] [CrossRef]
- Vogel, G.; Shrestha, P.; Schulz, J.-P.; Becker, C.; Rummel, U. Modelluntersuchungen zum Einfluss der Abschattung der Solarstrahlung durch die Vegetation auf die Erdbodentemperaturen in Falkenberg. MOL-RAO Aktuell. Available online: http://www.dwd.de/DE/forschung/atmosphaerenbeob/lindenbergersaeule/publikationen/publikationen_node.html (accessed on 1 September 2015).
- Davin, E.L.; Maisonnave, E.; Seneviratne, S.I. Is land surface processes representation a possible weak link in current Regional Climate Models? Environ. Res. Lett. 2016, 11, 074027. [Google Scholar] [CrossRef]
- Sulis, M.; Williams, J.L.; Shrestha, P.; Diederich, M.; Simmer, C.; Kollet, S.; Maxwell, R.M. Coupling Groundwater, Vegetation, and Atmospheric Processes: A Comparison of Two Integrated Models. J. Hydrometeorol. 2017, 18, 1489–1511. [Google Scholar] [CrossRef]
- Simmer, C.; Thiele-Eich, I.; Masbou, M.; Amelung, W.; Bogena, H.; Crewell, S.; Diekkrüger, B.; Ewert, F.; Hendricks Franssen, H.-J.; Huisman, J.A.; et al. Monitoring and modeling the terrestrial system from pores to catchments—The transregional collaborative research center on patterns in the soil-vegetation-atmosphere system. Bull. Am. Meteorol. Soc. 2014, 96, 1765–1787. [Google Scholar] [CrossRef]
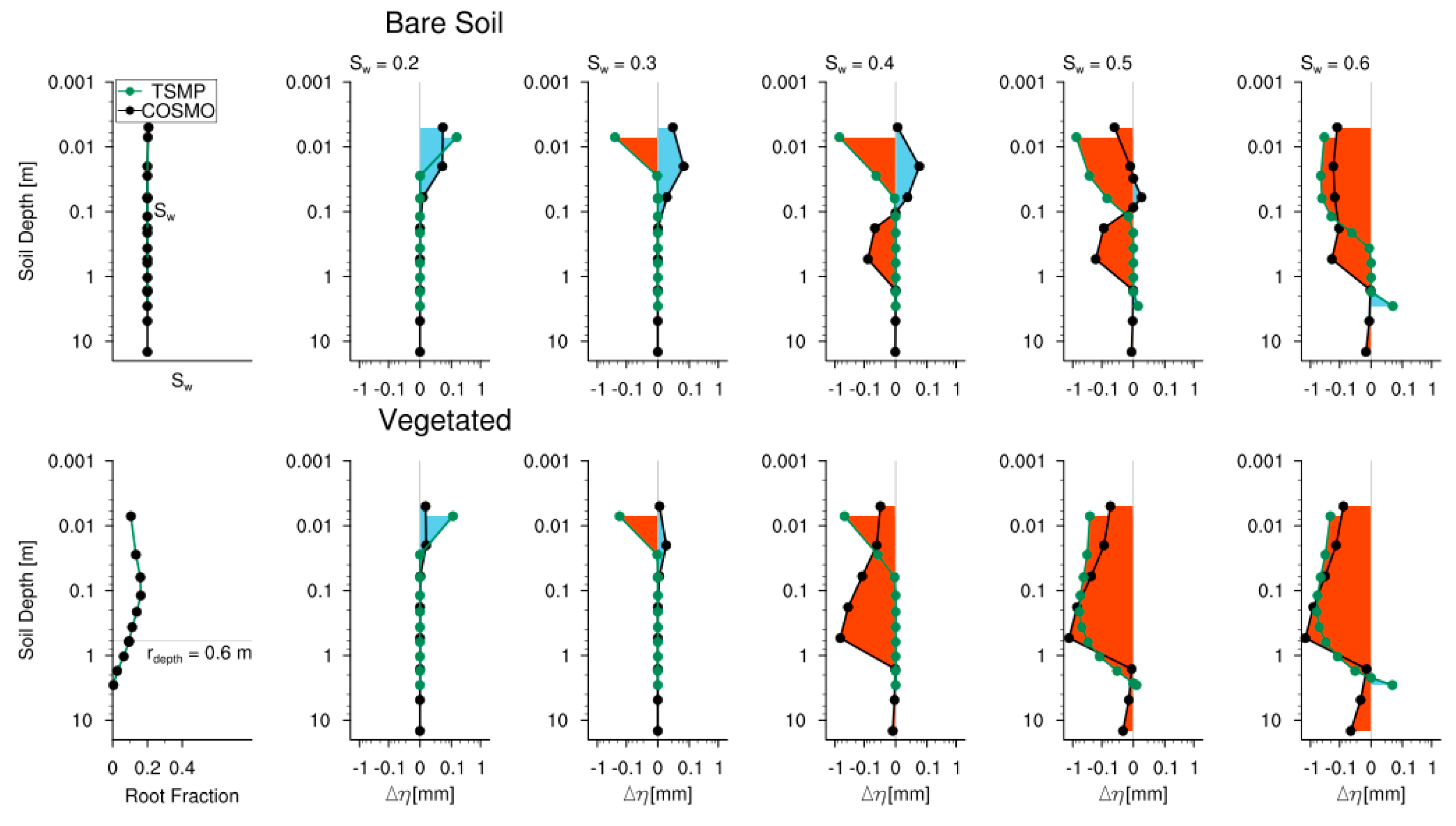
| CSDR (Vertically Constant Relative Soil Saturation and Default Root Distribution) |
| Land Use Types: Bare Soil and Vegetated Five Soil Moisture Initialization: Vertically constant profiles |
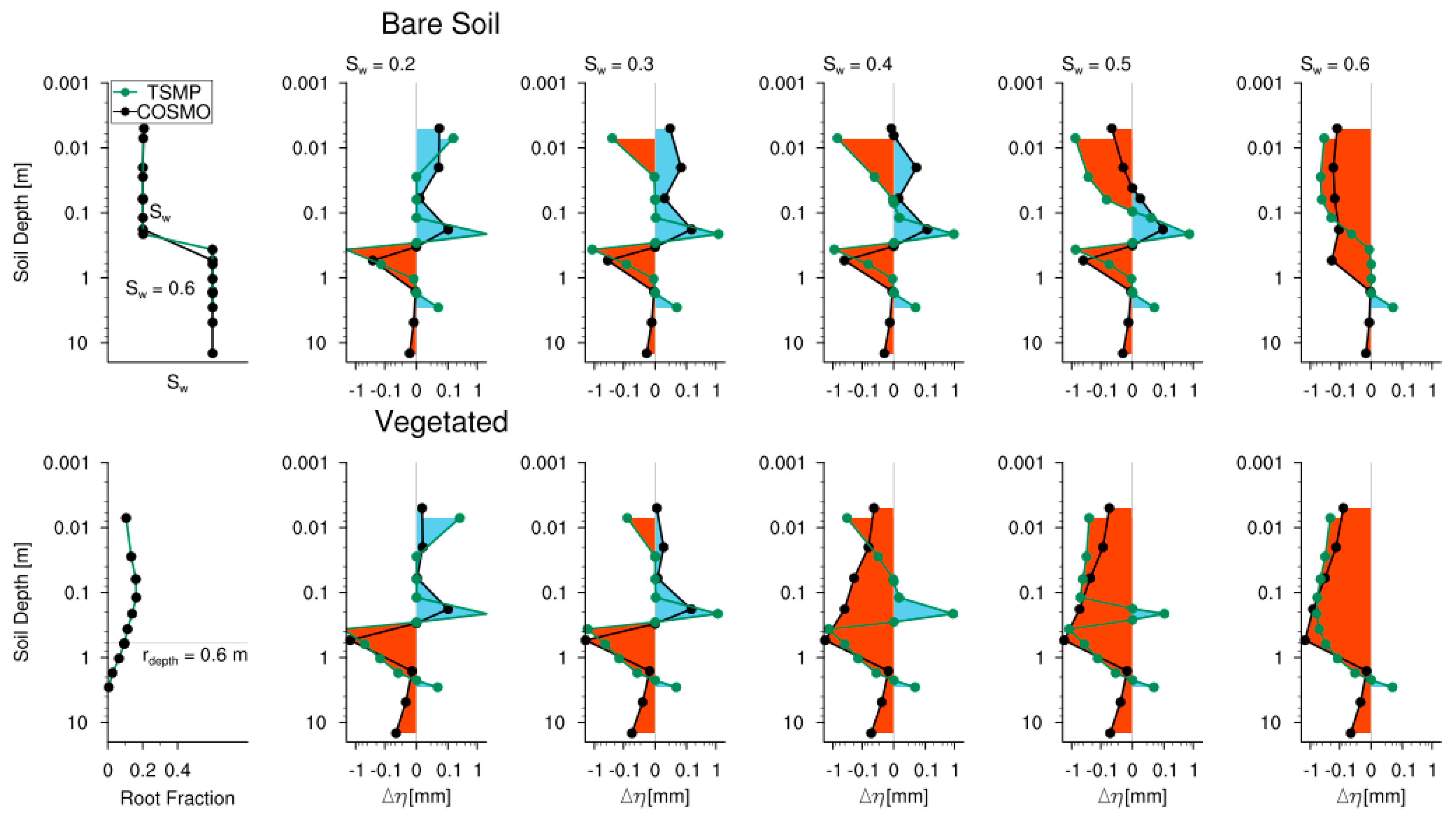
| VSDR (Vertically Varying Relative Soil Saturation and Default Root Distribution) |
| Land Use Types: Bare Soil and Vegetated Soil Moisture Initialization: Vertically varying profiles , |
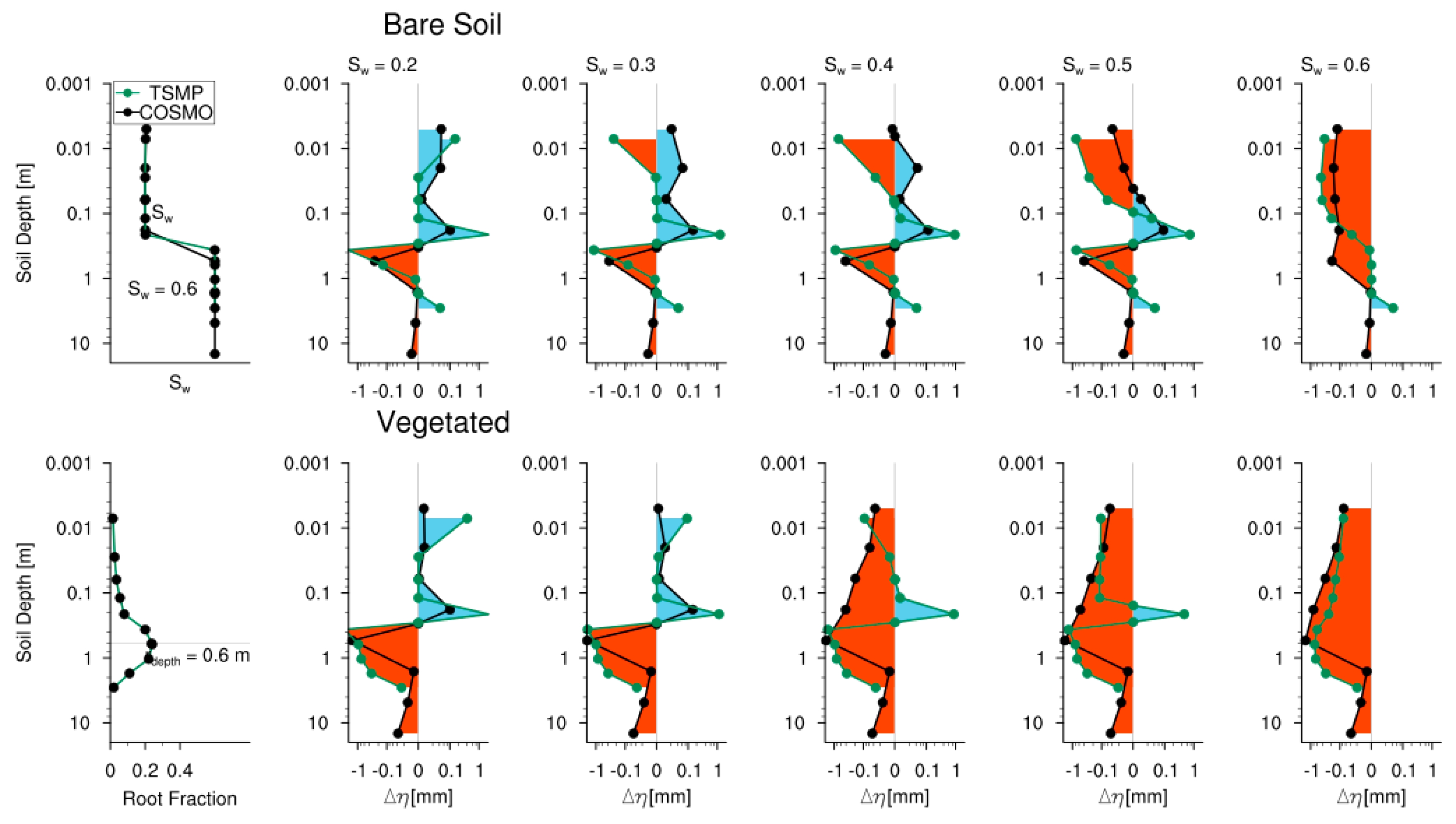
| VSMR (Vertically Varying Relative Soil SATURATION and Modified Root Distribution) |
| Two Land Use Types: Bare Soil, Vegetated with modified root distribution for TSMP Five Soil Moisture Initialization: Vertically varying profiles , |
| 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| bs | vg | bs | vg | bs | vg | bs | vg | bs | vg | |
| CSDR Experiment | ||||||||||
| COSMO | +0.09 | +0.01 | +0.09 | + 0.01 | −0.04 | −1.19 | −0.28 | −2.43 | −0.74 | −2.87 |
| TSMP | +0.15 | +0.11 | −0.25 | −0.17 | −0.75 | −0.50 | −1.10 | −3.11 | −1.38 | −3.10 |
| VSDR Experiment | ||||||||||
| COSMO | −0.08 | −1.45 | −0.13 | −1.85 | −0.26 | −2.59 | −0.36 | −2.75 | −0.74 | −2.87 |
| TSMP | +0.19 | −0.83 | −0.22 | −1.12 | −0.72 | −1.39 | −1.06 | −3.11 | −1.38 | −3.10 |
| VSMR Experiment | ||||||||||
| COSMO | −0.08 | −1.45 | −0.13 | −1.85 | −0.26 | −2.59 | −0.36 | −2.75 | −0.74 | −2.87 |
| TSMP | +0.19 | −2.23 | −0.22 | −2.88 | −0.72 | −3.00 | −1.06 | −3.14 | −1.38 | −3.09 |
| 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| bs | vg | bs | vg | bs | vg | bs | vg | bs | vg | |
| CSDR Experiment | ||||||||||
| COSMO | −199 | −157 | −196 | −155 | −189 | −137 | −182 | −116 | −172 | −108 |
| TSMP | −154 | −151 | −127 | −146 | −110 | −142 | −105 | −98 | −102 | −96 |
| VSDR Experiment | ||||||||||
| COSMO | −196 | −137 | −191 | −129 | −185 | −116 | −180 | −111 | −172 | −108 |
| TSMP | −154 | −141 | −127 | −135 | −110 | −131 | −105 | −97 | −102 | −96 |
| VSMR Experiment | ||||||||||
| COSMO | −196 | −137 | −191 | −129 | −185 | −116 | −180 | −111 | −172 | −108 |
| TSMP | −154 | −120 | −127 | −106 | −110 | −102 | −105 | −97 | −102 | −96 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrestha, P.; Simmer, C. Modeled Land Atmosphere Coupling Response to Soil Moisture Changes with Different Generations of Land Surface Models. Water 2020, 12, 46. https://doi.org/10.3390/w12010046
Shrestha P, Simmer C. Modeled Land Atmosphere Coupling Response to Soil Moisture Changes with Different Generations of Land Surface Models. Water. 2020; 12(1):46. https://doi.org/10.3390/w12010046
Chicago/Turabian StyleShrestha, Prabhakar, and Clemens Simmer. 2020. "Modeled Land Atmosphere Coupling Response to Soil Moisture Changes with Different Generations of Land Surface Models" Water 12, no. 1: 46. https://doi.org/10.3390/w12010046
APA StyleShrestha, P., & Simmer, C. (2020). Modeled Land Atmosphere Coupling Response to Soil Moisture Changes with Different Generations of Land Surface Models. Water, 12(1), 46. https://doi.org/10.3390/w12010046




